Journal of Modern Physics
Vol.05 No.18(2014), Article ID:52635,4 pages
10.4236/jmp.2014.518206
Generally Covariant Duality and Tachyon of Cosmological Nature
Dao Vong Duc1, Phu Chi Hoa2
1Institute of Physics, Hanoi, Vietnam
2Dalat University, Dalat, Vietnam
Email: dvduc@iop.vast.ac.vn, hoapc@dlu.edu.vn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 October 2014; revised 12 November 2014; accepted 5 December 2014
ABSTRACT
In this work the concept of generally covariant duality is treated with the introduction of generalized Levi-Civita tensor within the framework of vierbein formalism. The equations for the attached Lorentz scalar fields are derived from vierbein postulate. It is shown that the masses of the associated particles including that with negative square mass are completely determined by Einstein’s cosmological constant.
Keywords:
General Relativity, Cosmology, Tachyon

1. Motivation
Recently there have been many attempts to approach the problem of unification of fundamental interactions on the base of Extended General Relativity [1] . The starting insight is that all the fundamental interactions are originated from the nature of space-time itself as the gravitational interaction is.
On the other side, superstring theory [2] [3] is also considered as a promising approach to the construction of the unification theory. Among the most notable theoretical consequences of string theory is the existence of tachyon-scalar particle having negative square mass. In this connection we would mention that according to the results obtained in Refs. [4] - [6] the existence of tachyons could be originated from the compactification of time- like extradimensions.
The aim of this work is to consider the concept of generally covariant duality in General Relativity with the introduction of generalized Levi-Civita tensor and to study the specific properties of the attached fields within the framework of vierbein formalism.
It is shown that the masses of the associated particles, in particular tachyon-like particle, are completely determined by Einstein’s cosmological constant.
2. Generally Covariant Duality
In special Relativity the Duality concept is treated by means of the 4-rank Levi-Civita tensor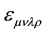 . The well known example is the relation
. The well known example is the relation
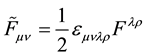 (1)
(1)
for electromagnetic field strength tensor
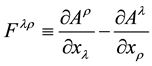
with the identification
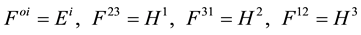
for electric 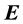 and magnetic
and magnetic 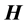 fields, Equation (1) represents Maxwell’s equations.
fields, Equation (1) represents Maxwell’s equations.
General Relativity requires the generalized version of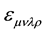 , which is to be some fully antisymmetric 4-rank tensor denoted by
, which is to be some fully antisymmetric 4-rank tensor denoted by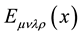 . In this connection the covariant wedge product of two vectors
. In this connection the covariant wedge product of two vectors 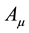 and
and 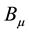 is to be defined as:
is to be defined as:
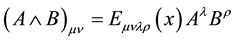 (2)
(2)
and in correspondence the relation (1) is modified to become
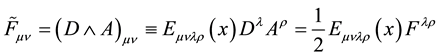 (3)
(3)
where D denotes covariant derivative,
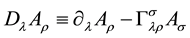
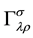 being affine connection.
being affine connection.
Let the tensor 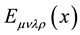 under consideration have
under consideration have 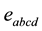 as its vierbein component, namely:
as its vierbein component, namely:

where 




Together with 

with the convention
Like for Riemann metric 
(


where B(x) and C(x) are some one-component fields and 
they transform according to the rule:

J being Jacobian transformation determinant.
The Formula (8) tells that the fields B(x) and C(x) are scalar with respect to Lorentz transformation only, but
instead 


space inverse transformation, 

From Equations (4)-(7) it follows that the fields B(x) and C(x) have the following vierbein structure:

where 







Note also that:

In this sense B(x) and C(x) might be referred to as dual partners.
3. Dual Equations
We now derive the equations for B(x) and C(x), starting from vierbein postulate

From the vierbein structure (4) and (6) this gives:

By inserting (7) into (13) we have:

And hence:

From the expression of 

Up to first order in gravitational constant 

where
Equations (15) with the expressions (17) inserted gives:

On the other hand, by performing similar calculations for the Ricci tensor we obtain:

Hence, Equations (18) can be rewritten as:

By inserting here the expression of R,

derived from Einstein’s equation with cosmological constant

(

where

Equation (23) tells that the fields B(x) and C(x) have square mass equaling

This corresponds to the following Lagrangian terms describing the fields B(x) and C(x) interacting with the gravitational field:

This also means that one of them is tachyon-like particle unless
4. Conclusion
In this work we consider the concept of Generally Covariant Duality. The focus point is the generalization of flat Levi-Civita tensor for the case of curved Riemann space-time. This leads to some kind of pseudoscalar fields of cosmological nature with the masses closely related to Einstein’s cosmological constant. In particular among them there is tachyon-like particle having negative square mass. Taking into account that the cosmological constant has a close relation to dark energy, one might think about the possibility for tachyon to be among the candidates for dark matter.
References
- del Aguila, F., de Azcarraga, J.A. and Albabez, L.E. (1985) Supersymmetry, Supergravity and Related Topics. World Scientific, Singapore City.
- Green, M.B., Schwarz, J.H. and Witten, E. (1987) Superstring Theory. Cambridge University Press, Cambridge.
- Furlan, G., Jengo, R., Pati, J.C., Sciama, D.W., Sergin, E. and Shafi, Q. (1997) Superstrings, Supergravity and Unified Theories. World Scientific, Singapore City.
- Duc, D.V. and Giao, N.M. (2013) A Mechanism for Mass Creation from Extradimensions. arXiv-hepth/1301-1405.
- Duc, D.V. and Giao, N.M. (2013) Journal of Modern Physics, 4, 991. http://dx.doi.org/10.4236/jmp.2013.47133
- Duc, D.V., Giao, N.M. and Dung, T.T. (2014) Journal of Physical Science and Applications, in Print.





