ABSTRACT

A solution of nonlocal EPR correlation between counter-propagating pair of polarization entangled photons emitted from a common source at S and detected at points P and Q is sought outside the EPR’s reality criterion of local causality but within the framework of time-symmetric quantum electrodynamics allowing the bi-directional signal transmission P ↔ S ↔ Q on the double-light cone where the future and the past cones share common light paths connecting the photon source S and the detection points P and Q.

Keywords:Quantum Theory, Time-Symmetry, Relativity, Causality, Locality, Correlation, Retrocausation, Paradox

1. Introduction

Since the advent of quantum mechanics in the mid-1920s there have been continued interpretational controversies surrounding its counter-intuitive nature such as the wave-particle duality and the instantaneous collapse [1] of the particle wave function at the detection point. But the paradox of nonlocal EPR correlation [2] between distant events without nonlocal interactions has been more problematic in recent times by Bell’s experimental nonlocality test [3] proposed in 1964, though the paradox was first noticed by Schrödinger [1] and discussed in the dialogue between Einstein [2] and Bohr [4] at 1935 Solvay Council. In emphasis of the signal transmission in EPR correlation Cavaicanti and Wiseman [5] asked: “What Bohr could have told Einstein at Solvay had he known about Bell experiments?” In his recollection in 1990 Bell [6] wrote: “Suppose quantum mechanics were found to resist precise formulation. Suppose that when formulation beyond “FAPP” (For All Practical Purposes) [7] is attempted, we find an unmovable finger obstinately pointing outside the subject....to the Mind of the Observer..., or only Gravitation?” We here show that the solution of quantum paradoxes can be found outside the EPR’s reality criterion of local causality but within the framework of time-symmetric quantum electrodynamics for finite spacetime.

2. EPR Correlation in EPR Loophole

At the Solvay council EPR asked: “Are there spooky actions at a distance in quantum mechanics?” Recently, Yin et al. [8] led by Q. Zhang measured a superluminal speed of spooky actions between counter-propagating pair of photons emitted from an optically pumped atom in spin 0 state. During the measurement the locality and the freedom-of-choice loopholes of previous experiments were maximally closed by observing a 12-hour continuous violation of Bell’s numerical expression (inequality) to EPR’s reality criterion of local causality and separability of distant events. Let the spacetime positions of the photon source and the detection points be S(x_S, t_S), P(x_P, t_P) and Q(x_Q, t_Q). Then the lower bound of the speed c_S of the spooky actions [9] [10]

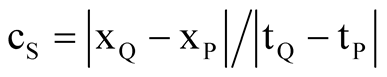(1)

can be superluminal as |t_Q − t_P| → 0. Here we can see a local and causal link P ← S → Q (t_S < t_P ≈ t_Q) and the nonlocal and acausal (spooky) link P → Q (t_P < t_Q). Let ε_P and ε_Q be the unit polarization vectors of photons measured at P and Q. The experiments verified the quantum expectations of the correlation function

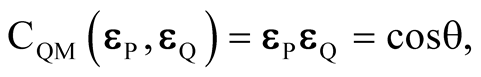(2)

where θ is the Hilbert space angle between ε_P and ε_Q, and showed a clear rejection of classical theories obeying Bell’s inequalities. The experiments also confirmed the insensitivity of C_QM to observer’s delayed decision as to which direction to measure each photon’s polarization at P and Q after the photon left the source at S-too late for a message to reach the opposite photon, [7] making the causal link P ← S → Q improbable and the bi-directional link P ↔ S ↔ Q probable in the loophole of EPR’s reality criterion of local causality between P and Q.

3. EPR Correlation on Double-Light Cone

Dirac [11] defined the two-point correlation function or propagator Δ(x, t) between S(0, 0) and P(x, t), and visualized the signal transmission S ↔ P on the light cone with the origin S as vertex:

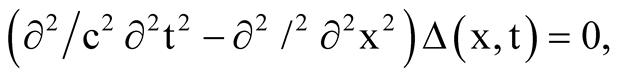(3)

(4)

where α(t) = t/|t| = 1 (t > 0); = −1 (t < 0). There an electron at S moves under the retarded (causal) action Δ_ret of a charged particle at P on the past light cone δ(ct + x) of S as well as the advanced (retrocausal) action Δ_adv of a charged particle at Q on the future light cone δ(ct − x) of S, giving the radiation damping of the electron at S. Likewse, the bi-directional EPR link, P(x_P, t_P) ↔ S(x_S, t_S) ↔ Q(x_Q, t_Q), can be visualized on the future light cone of S by replacing the step function α(t) by the square (step-up and down) function β(t) = 0 (t < t_S); = 1 (t_S < t < t_P/Q); = 0 (t > t_P/Q)

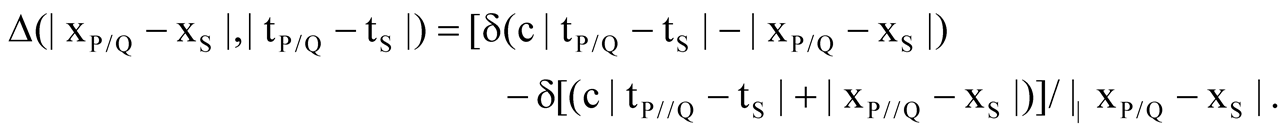(5)

The double-light cone [δ_ret − δ_adv] in Equation (5) tells that the spacetime points P/Q are reached by retarded waves expi(ωt − kt) from S while advanced waves expi(ωt + kx) from P/Q reach S on the past light cone of P/Q, forming a bi-directional sinusoidal wave, expiωtsinkx, standing in phase between S and P/Q with nodes fixed in space at x = nπ/k (n = integer) where the probability of finding a photon vanishes.

4. Bi-Directional Microscope

“Is the star there when nobody looks” asked Tetrode [12] . At the 1947 Solvay Council Heisenberg proposed a thought experiment measuring the electron position on microscope’s object plane. There the photon wave collapsing at S in the retina of the observer entails the retrocollapse (appearance) of an electron at P scattering the photon. That is, the electron is not at P when nobody looks at S. This point was emphasized by Weizäcker [13] in his delayed-choice thought experiment measuring the photon momentum on the focal plane of Heisenberg’s microscope. If the microscope is very long, the observer at S can make choice as to which property of the electron, position or momentum, to measure after the scattering process has taken place at P. To see the bi-directional signal transmission S ↔ P in microscope we write Equation (5) in momentum space [14]

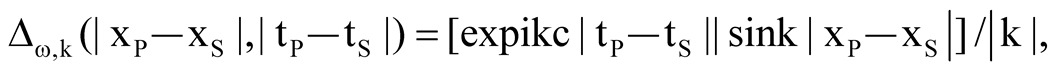(6)

getting an uncertainty relation between photon momentum p = ħk and the microscope length

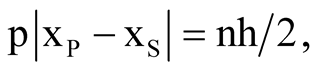(7)

where n is the number of intermediate points between two successive nodes of the sinusoidal wave between S and P where a photon can be found with maximum probability.

5. EPR Correlation and Observer

Standard quantum electrodynamics requires the photon propagator Δ to satisfy asymptotic conditions Δ(x, t) → 0 as t → ±∞ to avoid divergent self-energy of radiating electron and building-up of higher energy levels of radiating metastable atom, and gives the same amplitude of transition C_AMP for an optically pumped atom at S emitting two EPR photons (e → 2γ) of given polarizations ε_P and ε_Q on the future light cone δ(ct − x) of S and for two photons incoming from the past light cone δ(ct + x) of S pumping the metastable atom (2γ → e) at S in spin 0 Bell state [3] (inverse-EPR process) [15] :

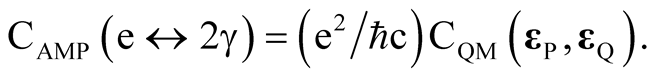(8)

While interpretational problem does not arise in the willed preparation of pumping (2γ → e), the EPR paradox appears after the measurement of polarizations (e → 2γ). But we can see in the observer’s mind a retrocausal connection P → S ← Q: “Given the measured polarization data of individual photons at P and Q retrodict (disentangle) the incompletely specified (entangled) Bell state at S” and, conversely, the causal connection P ← S → Q: “Given the disentangled Bell state at S predict the individual polarizations at P and Q”. The bi-directional causal connection P ↔ S ↔ Q can directly be seen in sum over skeleton (with nodes) histories approximation to Feynman’s path integral construction of quantum mechanical paths between S and P/Q in delayed-choice thought experiments visualizing the insensitivity of C_QM to the distance between P and Q and to the timing of the optical switch, which is generally closed but opens during the passage of the post-selected photon, placed at any point (node) along the paths of the detected photons.

6. Conclusion

We have shown that the EPR paradox arises outside the EPR’s reality criterion of local causality, and is solved within the framework of time-symmetric and relativistic quantum electrodynamics for finite spacetime with singular boundary conditions [16] at the photon source and the detectors allowing the bi-directional signal transmission on the double-light cone where the past and the future coexist. We note that the time-symmetric and nonrelativistic quantum mechanics allows the bi-directional signal transmission and the visualization of wave-particle dual nature of the electron in the single-electron double-slit interference experiment [17] .

References