Journal of Modern Physics
Vol.5 No.6(2014), Article ID:45323,42 pages DOI:10.4236/jmp.2014.56053
Gravitational Fields: Another Fortunate Manifestation of the Higgs Mechanism
Jacob Schaff
Universidade Federal do Rio Grande do Sul (UFRGS), Instituto de Fsica, Porto Alegre, Brazil
Email: schaf@if.ufrgs.br
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 7 December 2013; revised 5 January 2014; accepted 1 February 2014
ABSTRACT
The present work discusses, in a comprehensible language and simple mathematics, the origin of the gravitational physics in the light of new recent experimental observations, achieved with the help of the tightly synchronized clocks of the GPS. These observations reveal that real space, ruling the inertial motion of matter and the propagation of light, is moving round the earth and round the sun according to a Keplerian velocity field, consistent with the local main astronomical motions. This Keplerian velocity field of real space is the quintessence of the gravitational fields and appropriately induces the observed gravitational dynamics. Such real space needs not to be invented. It is well at hand in the Quantum Field Theory (QFT), underlying the Standard Elementary Particle Model (SEPM). The QFT entails the idea that space is filled up with the Higgs condensate (HC), a very powerful quantum space (QS). The HC is a Bose-Einstein (BE) condensate of the zero spin Higgs bosons. By coupling to the HC, the elementary particles get inertial mass by the Higgs mechanism, that is, get mechanical properties. This will say that the HC rules the inertial motion of matter and the propagation of light and hence is the locally ultimate reference for rest and for motion of matter and light. The present work acknowledges that, likewise the Meissner effect in superconductors develops macroscopic screening currents, forcing magnetic fields out from superconductors, the Higgs mechanism too entails a macroscopic manifestation in the form of the Keplerian velocity field of the QS round each matter body throughout the universe, consistent with the local main astronomical motions. This Keplerian velocity field screens and thrusts the matter fields out from the HC by squeezing them into a minimum of volume. It is shown that this Keplerian velocity field of the QS appropriately induces the observed gravitational dynamics on earth, in the solar system as well as the galactic gravitational dynamics without the need of dark matter. It also provides an antigravitation mechanism accelerating the expansion of the universe. It finally is shown that this spacedynamics correctly and appropriately gives origin, in terms of simple and genuine physical effects, to all the other observed effects, caused by the gravitational fields on the propagation of light and on the rate of the clocks.
Keywords:Gravity, Gravitational Physics, Gravitational Fields, Gravitational Effects, Dark Matter, Dark Energy

1. Introduction
After a short outline of the most important achievements and shortcomings of the current theories of space and gravitation, the present work investigates in Section 2 the nature of space and of gravitation in the light of the recent new experimental observations, achieved with the help of the tightly synchronized atomic clocks of the Global Positioning System (GPS). In Section 3 it is shown that this new view about the nature of space is well endorsed by the ideas of Quantum Field Theory underlying the Standard Elementary Particle Model, according to which the Higgs condensate filling up the whole of space is responsible for the inertial mass of the elementary particles and hence rules the inertial motion of matter and the propagation of light. Section 4 outlines the foundations of the new conception of space matter and gravitation, coherent with the recent experimental observations described in Section 2 and the theoretical view, described in Section 3. The subsequent Sections 5 - 8 apply the new conception to resolve the gravitational dynamics and the origin of the effects of the gravitational fields in general. Section 5 solves the gravitational dynamics on earth, in the solar system and in the galaxy. Section 6 discusses the origin of the accelerated expansion of the universe in terms of the dominant anti-gravitational interaction between galaxies, predicted by the new conception. Section 7 outlines the effects of the gravitational fields on the propagation of light and on the rate of clocks. Finally, Section 8 shows that the new gravitational mechanism systematically reproduces correctly the known experimental observations, caused by the gravitational fields.
Experiments of mechanics have shown that Newton’s laws of mechanics are good in all inertial references, which has led to the Galilean principle of relativity. According to this principle, local experiments of mechanics cannot reveal the state of uniform motion of a laboratory along a straight line. The failure of the Michelson light anisotropy experiments to detect effects, due to the motion of earth with respect to the ether, in the turnover of the ninetieth to the twentieth century, seen as a universal, static and absolute reference, convinced Einstein that local electromagnetic experiments too cannot reveal the state of uniform motion of the laboratory. Einstein was a positivist, rejecting whatever cannot be evidenced by experiment. With base in the null results of the light anisotropy experiments, he rejected the existence of ether and any objective reality of space, concluding that Maxwell’s Equations must be good in all inertial references. Moreover, as Maxwell’s Equations give the velocity of light, the velocity of light must be the same with respect to all possible inertial references. According to Einstein’s principle of relativity, no absolute and no preferred inertial references exist. Hence, only relative motions between bodies are physically relevant and no absolute motions can be defined. Accordingly, all inertial references are democratically equivalent and the laws of physics must be the same in all inertial references [1] . Einstein’s view about the nature of space and gravitation prevails to present date.
In reality, the Galilean principle of relativity is an abstraction, because free bodies in our laboratories never move uniformly along straight lines, unless the effect of gravity is constrained away. However, if the free-fall and the motions of force-free bodies along curved paths within gravitational fields are not due to the action of real Newtonian gravitational forces, but are ruled by the principle of inertia, as Einstein rightly asserted later in his theory of gravitation, then these motions too are congruent with the Galilean principle of relativity and local experiments of mechanics cannot reveal the state of motion of such free bodies. Inertial motion of bodies along curved paths within gravitational fields leads inexorably to the conclusion that within gravitational fields the inertial references (IRs) are local and dynamic. They are local because any two force-free bodies at different positions accelerate with respect to each other and the IRs are dynamic because any force-free body accelerates toward the gravitational center. Einstein’s free falling elevator indeed is locally an inertial reference, however a different one at each point of space. Obviously an IR cannot spontaneously accelerate toward the gravitational center. The free-fall necessarily involves an intrinsic inertial dynamics of the gravitational fields. The only realistic way to make the elevator accelerate toward the gravitational center without the action of a force, is the local IR to be rotating in the ordinary space round an overhead axis at a local characteristic angular velocity. In this case the resting elevator necessarily is implicitly moving oppositely along a circular path round the overhead axis within the local rotating IR. This motion is implicit because it cannot be specified with respect to ordinary space. If no structure acts the upward centripetal force, necessary to maintain the elevator in the implicit circular path, it inevitably will move instantaneously and uniformly (for an infinitesimal time interval) along a straight line within the local IR, exactly as any free body does within an IR. However, as the local IR is rotating in the ordinary space, this straight line will rotate together with it. Consequently the momentum of the elevator acquires an increasing downward component and centrifugally accelerates toward the gravitational center (please see the full details of this inertial dynamics in Section 5).
The idea of local rotating IRs may seem nonsensical because, according to learned physics, a rotating reference frame is a non-inertial reference. However, why are the apparently static and non-rotating earth based laboratories non-inertial references? The challenge of the present work is showing that if the real space, ruling the inertial motion of matter and the propagation of light, is itself moving and rotating, then the reference frames, rotating with it round the same rotation axis, are inertial references and frames not rotating with it (static in the ordinary space) are non-inertial references. Visibly the earth based laboratories are of this last kind.
The idea of a real and moving space, ruling the inertial motion of matter and the propagation of light, is not inane. The Quantum Field Theory (QFT), underlying the Standard Elementary Particle Model (SEPM), entails the idea that space is filled up with the Higgs condensate [2] -[4] , a quantum space (QS) ruling the inertial motion of the elementary particles and the propagation of light (please see details in Section 3). Moreover, several recent and trustworthy experimental observations, achieved with the help of the tightly synchronized clocks of the GPS [5] -[7] , clearly show that the real space, ruling the propagation of light and the rate of clocks, is moving round earth round the sun etc., according to a Keplerian velocity field consistent with the local main astronomical motions (please see details in Section 2 and also in Ref. [8] ). The major goal of the present work is showing that the gravitational dynamics on earth, in the solar system and throughout the universe as well as all the effects of the gravitational fields on the propagation of light and on the rate of clocks is a simple, natural and genuine physical outcome of the motion and warping of the real QS, ruling the inertial motion of matter and the propagation of light, in the ordinary three dimensions round each astronomical body throughout the universe, according to a Keplerian velocity field, consistent with the local main astronomical motions.
In his interpretation of the Michelson light anisotropy experiments, Einstein has overlooked an issue that is crucial in experimental physics. The Michelson experiments were performed within the non-inertial earth based laboratories, which necessarily involves implicit kinematical circumstances that Einstein totally ignored in the epoch. Obviously, before a reliable interpretation can be given to the null results of the Michelson light anisotropy experiments, it is absolutely essential to precisely know the true kinematical circumstances of the earth based laboratories with respect to a possible spatial medium, ruling the inertial motion of matter and the propagation of light and creating the inertial dynamics observed within the gravitational fields.
Einstein gave attention to these kinematical circumstances of the earth based laboratories only later in his theory of gravitation, the General Theory of Relativity (GR). The central idea of GR is that gravitational effects somehow are equivalent to inertial effects [1] . This conclusion relies on the general observation that all matter objects having inertial mass exert gravitation and within our earth-based laboratories experience identical gravitational acceleration, independently from their form, size, mass, charge or constitution. However, in order to put the equivalence of gravitational and inertial effects effectively into play, the apparently resting earth-based laboratories must inexorably be moving under an upward acceleration. Moreover, the gravitational (inertial) pull is largest in laboratories resting in the gravitational field with respect to the ordinary space coordinates. To find out how an earth-based laboratory, resting in the ordinary space, undergoes physically genuine motions and accelerations certainly is among the most challenging and also the most revealing issues in fundamental physics.
In the Special Theory of Relativity (STR) Einstein has linked the three-dimensional space and time together into a four-dimensional space-time, in which the time axis is orthogonal to the ordinary space axes. Within the four dimensional space-time continuum the three-dimensional universe is inherently moving at the velocity of light along the time axis. This assumption, although purely intuitive, has opened plenty of new theoretical possibilities. Motion along the time axis cannot be specified with respect to the ordinary universe and must be described in terms of imaginary numbers, which mathematically means that it is along a direction orthogonal to the ordinary space coordinates. Einstein often insisted that the time axis is a genuine fourth dimension and that motion along the time axis is on the same foot as motion in the ordinary space. By this assumption Einstein has introduced motion (dynamics) where no motion at all is seen in the ordinary space.
The linking of space and time has introduced additional degrees of freedom that cannot be described in the ordinary three-dimensional space and in the relativistic quantum mechanics, they allow for the appearance of implicit dynamic states like for instance the intrinsic angular momentum (spin). However, Dirac’s relativistic quantum mechanics of the electron, besides predicting the electron spin and the anti-particle of the electron (the positron), also predicts non-observed negative energy states. This shows that the implicit dynamics was not introduced correctly into the equation and that something is flawed in the relativistic conception. Apparently there are too many degrees of freedom, too many dimensions and components. Negative energy of free particles is a very odd outcome that visibly is the fruit of the way the energy-momentum 4-vector is defined by combining the resting energy (creation energy) of the particle with its ordinary momentum.
With base in the assumption that the velocity of light is the same with respect to all possible inertial references, Einstein stipulated transformations of time intervals and spatial distances with the relative velocity of the inertial references in such a way that the velocity of light is isotropic and the same with respect to all possible inertial references. Hence, observers looking a same physical event in the four-dimensional spacetime from all different inertial references, observe the same outcomes. These transformations of the space and time coordinates turned out to be homogeneous linear transformations parameterized by the relative velocity, that is, hyperbolic rotations of the space and time coordinates in Minkowski spacetime that now are well known as the Lorentz Transformations. The fact that these transformations directly predicted the null results of the Michelson light anisotropy experiments, together with the experimental observation of time dilation in muon decay and the lowered frequency of the radiation from speeding hydrogen atoms [9] corresponded well to the predictions of the STR was acknowledged as experimental support to the theory.
According to the STR displacements, velocities and momenta must be described in terms of four components, 4-vectors in the four-dimensional spacetime. The fact that these 4 vectors are invariant under Lorentz transformations is the great and much celebrated achievement of the TR that assured its success. However, this achievement relies totally and critically on the one assumption: “The velocity of light is the same with respect to all inertial references”. This sameness emerges from Einstein’s interpretation of the null results of the Michelson light anisotropy experiments. However, according to Einstein’s own words, any experiment that shows this assumption to be false, fatally will ruin the whole theory.
In order to explain the gravitational phenomena in terms of the equivalence of inertial and gravitational effects, Einstein in his GR vent on modifying the metric of spacetime. However, in this case the cause of the modifications is not relative velocity but the gravitational potential. He has set up an equation that specifies the corrections to the space and time coordinates within the spherically symmetric region of a gravitational field, a kind of geometrical algorithm in terms of the metric tensor. These transformations however could not be linear anymore, as in the STR, leading to curved (non-Euclidean) geometry. Within the curved spacetime, gravitation is due to continuous rotation of the direction of the components of the 4-momentum 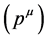 as a function of time, causing mixing between the time-like and the radial component, generating an increasing velocity toward the gravitational center. However, the geometrodynamics of GR, while being able to precisely simulate and predict the motion of bodies within the gravitational fields, it is intangible and visibly does not disclose the true physics background operating it. GR, instead of appointing genuine physical causes rotating the components of the 4-momentum
as a function of time, causing mixing between the time-like and the radial component, generating an increasing velocity toward the gravitational center. However, the geometrodynamics of GR, while being able to precisely simulate and predict the motion of bodies within the gravitational fields, it is intangible and visibly does not disclose the true physics background operating it. GR, instead of appointing genuine physical causes rotating the components of the 4-momentum 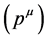 of the force-free bodies within gravitational fields, constructs the spacetime geometry that incorporates their effects, making the curved motions seem natural. Another troubling point is that, strangely the TR needs to involve two completely different causes for time dilation. The present work will unify the cause. Time dilation is caused only by the velocity with respect to the QS (Higgs condensate).
of the force-free bodies within gravitational fields, constructs the spacetime geometry that incorporates their effects, making the curved motions seem natural. Another troubling point is that, strangely the TR needs to involve two completely different causes for time dilation. The present work will unify the cause. Time dilation is caused only by the velocity with respect to the QS (Higgs condensate).
GR predicts the orbital motions of planets, the gravitational deflection of light, the gravitational slowing of clocks, the perihelion precession of elliptic orbits, the excess time delay of radar signals in go-return roundtrips within the solar system and many other effects. Many physicists repute GR as the definitive explanation of gravity. However, in recent years an increasing number of clear-cut experimental observations, achieved with the help of the tightly synchronized clocks of the Global Positioning System (GPS) [5] -[7] , cannot be explained by the TR (please see Section 2 for details). This proves that something is very flawed in the relativistic scenario and that it does not disclose the true natures of space and of the gravitational physics. Visibly the geometric model of GR symmetrizes space and the gravitational fields too much; thereby eliminating small anisotropies that in fact exist and now are being discovered.
The foundations of the STR get into really serious troubles within the context of the Quantum Field Theory (QFT) underlying the Standard Elementary Particle Model (SEPM). Visibly, the denial of the objective reality of space has removed from nature the effects of the motions of the real QS that play a fundamental role in the physical phenomena, more visibly in the gravitational physics. Another sequel of this denial is that the TR, although linking the rest energy  to rest mass
to rest mass  by Einstein’s most famous equation
by Einstein’s most famous equation 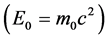 and stipulating its corrections with relative velocity, cannot explain the origin of the inertial mass. The relativistic gauge theories can provide no inertial mass to the elementary particles. In recent years QFT, underlying the SEPM, is amending these flaws by introducing the Higgs condensate thereby somehow restoring the objective reality of space (please see details in Section 3). By coupling to the Higgs condensate the elementary particles get inertial mass. This is known as the Higgs mechanism. The Higgs mechanism is closely analogous to the Meissner effect in superconductivity, by which superconductors confine the electromagnetic (EM) field, making it short-range and providing the photons with rest mass within superconductors. Altogether these experimental facts prove that the TR is in serious conflict with the experimental observations. Moreover, GR cannot explain the gravitational dynamics of the galaxies, nor does it provide a physical mechanism to explain the accelerated expansion of the universe.
and stipulating its corrections with relative velocity, cannot explain the origin of the inertial mass. The relativistic gauge theories can provide no inertial mass to the elementary particles. In recent years QFT, underlying the SEPM, is amending these flaws by introducing the Higgs condensate thereby somehow restoring the objective reality of space (please see details in Section 3). By coupling to the Higgs condensate the elementary particles get inertial mass. This is known as the Higgs mechanism. The Higgs mechanism is closely analogous to the Meissner effect in superconductivity, by which superconductors confine the electromagnetic (EM) field, making it short-range and providing the photons with rest mass within superconductors. Altogether these experimental facts prove that the TR is in serious conflict with the experimental observations. Moreover, GR cannot explain the gravitational dynamics of the galaxies, nor does it provide a physical mechanism to explain the accelerated expansion of the universe.
On the other hand, the QFT underlying the SEPM has been extremely successful in elucidating the structure and the interactions of elementary particles. Thanks to QFT the structure of the elementary particles, the electromagnetic, weak nuclear and strong nuclear interactions are now fairly well understood. However, all efforts to explain the gravitational interaction in terms of quantum exchange interaction, mediated by gravitons, failed. The troubles of Quantum Gravity (QG) begin within the theory itself and become even worse in the experimental verifications. Gravitons contrarily than photons do not conform to the superposition principle. Therefore the graviton-graviton interaction leads to non-renormalisable divergences. Moreover, the gravitons never have been detected, which indicates that such particles simply do not exist. QG too cannot explain the gravitational dynamics of the galaxies and the accelerated expansion of the universe.
The centuries old troubles with the nature of space and gravitation and the endless rivalry and impasse of GR and QG about the gravitational physics is unacceptable. In spite of the shortcomings of GR and the insurmountable difficulties of QG, these theories still are acclaimed by the establishment as valid explanations of the gravitational physics. To Einstein’s glory, his original model of space and gravitation survived all the challenges to present date, showing that his discernment was well beyond his time. Certainly also to his dislike, the TR in our times has become like religion. On the other hand however, several new and trustworthy experimental facts are pointing out to a new conception of space, matter and gravitation radically different from that of the establishment. Moreover, new concepts ready in the QFT are opening the way to settle all these troubles at once.
In the next Section 2 it is shown that several clear-cut experimental observations, achieved with the help of the tightly synchronized atomic clocks of the GPS, attest that the real QS, ruling the inertial motion of matter and the propagation of light, is effectively moving according to a Keplerian velocity field round earth and round the sun.
2. Recent Experimental Observations That Reveal the Spacedynamic Nature of the Gravitational Fields
2.1. The One-Way Anisotropy of Light
According to an assertion often seen in the literature, all the reports claiming to have measured the one-way velocity of light, are in fact two-way measurements. However, some recent new measurements with the help of the tightly synchronized GPS clocks fall well out this rule. Collective and simultaneous synchronization of the highly stable atomic clocks in the 24 GPS satellites and on earth by using Einstein’s synchronization technique involves two-way travels of electromagnetic (EM) or light signals together with the assumption that their velocity is the same in the go and in the return journeys. By this method the GPS clocks and the clocks in the earth based stations can be synchronized altogether simultaneously to within 0.1 ns (time for light to travel 3 cm). In case of low orbit satellites, clock synchronization can even be up to an order of magnitude better.
With the help of the tightly synchronized atomic clocks in satellites the one-way signal travel time from one satellite to the other, the velocity of the electromagnetic (EM) signals (light) can be measured with precision enough. Note that such one-way measurements involve first order effects. Especially clear-cut measurements of the one-way velocity of electromagnetic signals (light) were achieved using the twin satellites of the Gravity Recovery and Climate Experiment (GRACE) [5] . These twin satellites move in the same sense at nearly 8 km/sec along coplanar and practically identical circular polar orbits at 500 km of altitude, separated from each other by 200 km and their positions being monitored by the GPS within 3 cm. These satellites are equipped for many tasks. One of them is measuring microgravity effects. To this purpose they need to be equipped with highly stable atomic clocks synchronized to better than 0.16 ns. The satellites continuously exchange EM signals between them in both senses.
It is observed that the signal transit time from the leading satellite to the rear satellite corresponds to a shortening by more than 5 m (17 ns), while the signal transit time from the rear satellite to the leading satellite is lengthened by more than 5 m (17 ns). These discrepancies correspond in both cases exactly to the distance moved by the receiving satellite during the signal transit time and are consistent with backward signal anisotropy of nearly 8 km/sec with respect to the satellites. This anisotropy is two orders of magnitude larger than the experimental precision of the experiment and shows that the EM signal (light) has a well-defined and isotropic North-South velocity  within the geostatic non-rotating reference, the same with respect to which the satellites are moving at 8 km/sec. This one way anisotropy observation in both senses unambiguously proves that the space that rules the propagation of light is not moving with respect to Earth along the North-South direction. The observed anisotropy is uniquely due to the motion of the satellites and hence no additional effects need to be considered. This anisotropy of the one-way velocity of light unquestionably proves that a spatial medium exists, possibly the Higgs condensate, that propagates light at a characteristic constant velocity c. This existence breaks irremediably by the first time the century old believe that the velocity of light is intrinsically constant and isotropic with respect to all possible inertial references. It also implies that earth based anisotropy experiments may show no North-South light anisotropy because the above measured anisotropy is due to the motion of the GRACE satellites.
within the geostatic non-rotating reference, the same with respect to which the satellites are moving at 8 km/sec. This one way anisotropy observation in both senses unambiguously proves that the space that rules the propagation of light is not moving with respect to Earth along the North-South direction. The observed anisotropy is uniquely due to the motion of the satellites and hence no additional effects need to be considered. This anisotropy of the one-way velocity of light unquestionably proves that a spatial medium exists, possibly the Higgs condensate, that propagates light at a characteristic constant velocity c. This existence breaks irremediably by the first time the century old believe that the velocity of light is intrinsically constant and isotropic with respect to all possible inertial references. It also implies that earth based anisotropy experiments may show no North-South light anisotropy because the above measured anisotropy is due to the motion of the GRACE satellites.
The immediate consequence of this anisotropy of the one-way velocity of light is the absolute need of revising the interpretation of all the light anisotropy experiments performed in the past century. Most of the Michelson experiments intended to measure the light anisotropy due to the orbital and cosmic motion of earth. Systematically all these experiments obtained nominally null results. Now this must be interpreted as proving that the earth globe has no resultant velocity with respect to the quantum space (QS) ruling the propagation of light. Obviously this can make a sense only if this QS moves with earth round the sun, according to a Keplerian velocity field consistent with the planetary motions and with the solar system round the galactic center etc.
It would be an error not to mention here that some Michelson light anisotropy experiments, using highly sensitive Michelson interferometers rotating within the earth based laboratories, aimed measuring the anisotropy of light with respect to the earth based laboratory itself and practically all of them found small positive anisotropies of about 8 km/sec. Figure 1 displays the most complete anisotropy results obtained by D. Miller in his late and nonstop measurements day and night [10] . These results show that the value and direction of the small anisotropy of light with respect to the laboratory is nearly constant the whole day and the whole year and as will be seen, is due to the Keplerian velocity field of the QS, in the sense of the Moon’s orbital motion, generating the local earth’s gravitational field.
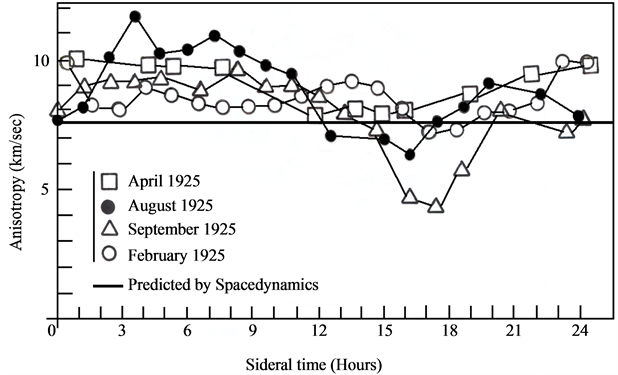
Figure 1. Ultimate light anisotropy data obtained by D. Miller. The small but systematic sinusoidal variation in the anisotropy along the 24 hours visibly is due to a cause not rotating with earth.
These anisotropy results give evidence that the QS, ruling the propagation of light, is moving through the earth-based laboratories at nearly 8 km/sec. This motion can only be along a West-East direction. Otherwise this observation would run into conflict with the above highly reliable one-way anisotropy of light. Apparently, the small variation of Miller’s results along the 24 hours, which may be spurious or due to an unknown cause, has lead him to conclude that the anisotropy is along a direction somewhat different from the West-East direction. In the epoch, Miller’s small anisotropy results could in no way be understood within the ether view and therefore were considered wholly spurious or simply ignored.
2.2. The Non-Synchronous Arrival of the Wave Fronts of Millisecond Pulsar Signals to Equidistant Earth Based Antennas
Another recent experimental observation that also clearly conflicts with the intrinsic constancy and isotropy of light came about during the implementation of set ups for Very Long Baseline Interferometry (VLBI) radio astronomy observations [6] [7] . By this interferometric method the resolution of images can be improved by orders of magnitude. The condition is that reception of the signals from distant objects by the earth based telescopes or antennas are synchronous. This can be achieved to within 0.1 ns with the help of the GPS clocks. The signals, recorded in the distant observatories, can be combined coherently with the help of computers, generating the improved images. According to the theory of relativity (TR), arrival of electromagnetic signals from distant millisecond pulsars to earth based antennas, equidistant from the source, should be synchronous. While along directions transverse to the earth’s orbital motion the arrival of the pulsar signal wave fronts to the equidistant antennas effectively are observed to be synchronous, along the earth’s orbital motion they reach the foregoing antenna up to 4.2 μs before the rear antenna. This relatively enormous discrepancy exceeds the time resolution of the experiment by more than three orders of magnitude contradicting the TR.
In the current theories, the aberration of star light is explained in terms of the orbital velocity of earth across the incident starlight, taking into account the relativistic addition of velocities. However, while this can explain the aberration phenomenon, it cannot explain the non-synchronous arrival of the millisecond pulsar wave fronts to equidistant antennas along the earth’s orbital motion. The pulsar signals are EM waves, a coherent superposition of a large amount of photons. The non-synchronous arrival to equidistant earth based antennas inexorably involves genuine refraction of the pulsar wave fronts in the environment of the solar system. Please see Equations (4) and Section 8.9 for a simple and genuine physical explanation of this relatively enormous discrepancy.
2.3. The Absence of Effects of the Solar Gravitational Potential on the GPS Clocks
A third and most revealing observation that cannot be explained by GR is the absence of effects of the solar gravitational potential on the GPS clocks. This is the well-known noon-midnight problem. The 24 GPS satellites are moving round earth in six equidistant circular 12 hour period orbits inclined 55 degrees with respect to the earth’s equator. The earth’s rotation axis is inclined 23 degrees away from the normal to the earth’s orbital plane. Hence, during the earth’s orbital motion the satellites, whose orbital plane has a component parallel to the earth-sun axis, pass 6 hs at the part of the orbit closer to the sun and then 6 hs at the part of the orbit more distant from the sun.
The effect of the solar gravitational potential  on the rate of the GPS clocks, predicted by GR, is given by
on the rate of the GPS clocks, predicted by GR, is given by 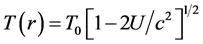 where
where 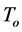 is the time period in the absence of a gravitational potential and
is the time period in the absence of a gravitational potential and 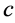 is the velocity of light. To first approximation this time dilation effect is proportional to
is the velocity of light. To first approximation this time dilation effect is proportional to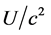 . Such gravitational time dilation effects have been well observed on the atomic clocks within the earth’s gravitational field and certainly would be shown by clocks fixed within the solar gravitational field too.
. Such gravitational time dilation effects have been well observed on the atomic clocks within the earth’s gravitational field and certainly would be shown by clocks fixed within the solar gravitational field too.
For the atomic clocks in the GPS satellites having orbital plane closest to the earth-sun axis, GR predicts a total delay accumulated during the 6 hours of closest approach from the sun larger than 24 ns, which would be recovered during the subsequent 6 hours farthest from the sun. The resulting 12 hour periodic sinusoidal deviation in the time display of these clocks is more than two orders of magnitude larger than the stability of the clocks and, if present, would be very easily observed. Nevertheless, contradicting the prediction of GR, no sign of such variation is observed [6] [7] . Note that this gravitational time dilation, predicted by GR, cannot be canceled by variation of the time dilation, due to changes of velocity of the satellite with respect to the solar non-rotating reference, because this would be two orders of magnitude larger and too is not observed. Observations show that the rate of the terrestrial and GPS clocks is ruled exclusively by the earth’s gravitational field. This is fortunate, because otherwise the use of the GPS would be much more complicated. GR cannot explain the absence of this time dilation because the gravitational potential is a scalar that depends on position but not on the orbital velocity of earth.
The observed absence of effects due to the solar gravitational potential on the GPS clocks has very drastic consequences on the current views about the nature of space and of the gravitational fields. On the other hand, it will be seen to fully corroborate the new interpretation of the light anisotropy experiments proposed in the above Section 2.1.
Time dilation is well known to be caused by motion as evidenced by the well known increased lifetimes of speeding Muons and the redshifts of the radiation emitted by speeding Hydrogen atoms [9] . In the STR this time dilation effect is imputed to the relative velocity 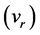 with respect to the observer. To first approximation this effect is proportional to
with respect to the observer. To first approximation this effect is proportional to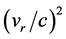 . Obviously the gravitational slowing of the atomic clocks within the earth based laboratories cannot be due to relative velocity because these clocks rest with respect to the laboratory observer. However, if motions cause time dilation, why then does the orbital motion of earth suppress the time dilation caused by the solar gravitational field on the earth-based and GPS clocks? Absurdly in one case motion causes time dilation and in the other case it suppresses it. This contradiction lets clear that time dilation is not caused by relative velocity, nor is it caused by gravitational potential. Time dilation visibly is caused by a velocity of a more fundamental nature.
. Obviously the gravitational slowing of the atomic clocks within the earth based laboratories cannot be due to relative velocity because these clocks rest with respect to the laboratory observer. However, if motions cause time dilation, why then does the orbital motion of earth suppress the time dilation caused by the solar gravitational field on the earth-based and GPS clocks? Absurdly in one case motion causes time dilation and in the other case it suppresses it. This contradiction lets clear that time dilation is not caused by relative velocity, nor is it caused by gravitational potential. Time dilation visibly is caused by a velocity of a more fundamental nature.
Some authors [11] suggest that the absence of effects of the solar gravitational field on the GPS clocks is due to the fact that these clocks together with earth are free-falling in the solar gravitational field. However, from this viewpoint, these same GPS clocks are also free-falling in the earth’s gravitational field and notwithstanding are slowed by the earth’s field by a quite significant and well observed amount. The assertion that a free falling clock is not affected by the gravitational field relies on the idea that gravitational time dilation is caused by acceleration, likewise alleged by several authors to resolve the famous twin paradox. However, acceleration has been tested up to 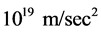 by muon decay experiments in cyclotrons [12] with the clear-cut conclusion that accelerations do not cause time dilation.
by muon decay experiments in cyclotrons [12] with the clear-cut conclusion that accelerations do not cause time dilation.
The observed slowing of the atomic clocks on earth must be related with the observed small constant anisotropy of light of nearly 8 km/sec. Both effects are observed within the earth based laboratories and both are proportional to 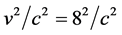 (
(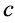 is in km/sec). Similarly the absence of effects due to the solar gravitational potential on the GPS clocks and all the clocks orbiting (with earth) round the sun must be related with the absence of light anisotropy due to the orbital motion of earth as is well known. The mysterious implicit velocity
is in km/sec). Similarly the absence of effects due to the solar gravitational potential on the GPS clocks and all the clocks orbiting (with earth) round the sun must be related with the absence of light anisotropy due to the orbital motion of earth as is well known. The mysterious implicit velocity 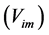 that causes the small light anisotropy of nearly 8 km/sec within the earth based laboratories is the same that causes the observed small decrease of the clock rates on earth. On the other hand, the orbital motion of earth (30 km/sec) that suppresses the gravitational time dilation due to the solar gravitational field, also suppresses the light anisotropy on earth, caused by the implicit velocity
that causes the small light anisotropy of nearly 8 km/sec within the earth based laboratories is the same that causes the observed small decrease of the clock rates on earth. On the other hand, the orbital motion of earth (30 km/sec) that suppresses the gravitational time dilation due to the solar gravitational field, also suppresses the light anisotropy on earth, caused by the implicit velocity 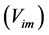 due to the solar gravitational field. This singles out velocity as the unified cause of time dilation. It is the usual velocity in the case of clocks speeding in the ordinary free space and it is this mysterious implicit velocity
due to the solar gravitational field. This singles out velocity as the unified cause of time dilation. It is the usual velocity in the case of clocks speeding in the ordinary free space and it is this mysterious implicit velocity 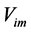 in the case of clocks fixed within gravitational fields.
in the case of clocks fixed within gravitational fields.
The only possible way to provide physical reality to this implicit velocity 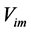 is acknowledging the existence of a real spatial medium (Higgs condensate) that rules the inertial motion of matter and the propagation of light and hence is the ultimate (locally absolute) reference for rest and for motions of matter. This real spatial medium is moving in the ordinary three dimensions round earth (at
is acknowledging the existence of a real spatial medium (Higgs condensate) that rules the inertial motion of matter and the propagation of light and hence is the ultimate (locally absolute) reference for rest and for motions of matter. This real spatial medium is moving in the ordinary three dimensions round earth (at  on surface) in the sense of the Moon’s orbital motion as well as round the sun according to a velocity field consistent with the earth’s orbital velocity
on surface) in the sense of the Moon’s orbital motion as well as round the sun according to a velocity field consistent with the earth’s orbital velocity  etc. These velocity fields will be seen to appropriately create the gravitational field of earth and of the sun and naturally explain all these observations on the velocity of light and the rate of the clocks. It also fully corroborates the propositions made in Section 2.1 in relation to the null results odd the Michelson light anisotropy experiments.
etc. These velocity fields will be seen to appropriately create the gravitational field of earth and of the sun and naturally explain all these observations on the velocity of light and the rate of the clocks. It also fully corroborates the propositions made in Section 2.1 in relation to the null results odd the Michelson light anisotropy experiments.
Obviously earth cannot be kinematically privileged in detriment to all the other planets of the solar system and astronomical bodies in general throughout the universe. Earth is not the only planet commoving with the real QS in the velocity field round the sun. All the planets must be closely commoving with the real QS. This will say that real QS must be moving according to a Keplerian velocity field round the sun:
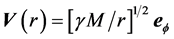 (1)
(1)
where 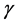 is the gravitational constant,
is the gravitational constant, 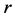 is the radial spherical coordinate and
is the radial spherical coordinate and 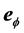 is the unit vector along the azimuthal spherical coordinate. This Keplerian velocity field is a cylindrical velocity field consistent with the local main astronimical motions, the magnitude of the velocity for a given
is the unit vector along the azimuthal spherical coordinate. This Keplerian velocity field is a cylindrical velocity field consistent with the local main astronimical motions, the magnitude of the velocity for a given  has the same value for all
has the same value for all  and all
and all  and hence its magnitude is spherically symmetric. Such a Keplerian velocity field of real QS will be seen to circulate round each matter concentration throughout the universe, generating the respective gravitational fields.
and hence its magnitude is spherically symmetric. Such a Keplerian velocity field of real QS will be seen to circulate round each matter concentration throughout the universe, generating the respective gravitational fields.
The disk shape of the solar system and of the galaxies as well as of the satellites round planets show that the orbits of the natural astronomical bodies in general are all closely concentrated within the equatorial plane of the respective Keplerian velocity field. This minimizes their velocity with respect to the QS. These orbital motions are largely determined by the circular motion of real QS in the Keplerian velocity field and hence these bodies very closely rest with respect to the moving real QS. This explains why the light anisotropy experiments searching for light anisotropy due to the orbital and cosmic motions of earth gave closely null results. The circular orbital motions of the planets need not to be explained anymore because it is space itself that so moves. The very slow velocity of the planets of the solar system, in the order of only hundreds of m/sec, with respect to the moving real QS is ruled by the principle of inertia. These very low velocities give rise to the very small deviations from the circular equatorial orbits that will be explained. The vertical free fall is an extreme case of elliptic orbit in which the opposite implicit velocity 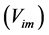 of the body with respect to real QS just compensates the Keplerian velocity.
of the body with respect to real QS just compensates the Keplerian velocity.
The experimental evidence that the QS, ruling the inertial motion of matter and the propagation of light, is circulating round earth and round the sun according to a Keplerian velocity field certainly is a significant and very intriguing result. However, what is really wonderful is the fact that this Keplerian velocity field of the QS is precisely the one that correctly creates the observed gravitational dynamics on earth, in the solar system and also generates correctly the galactic gravitational dynamics without the need of dark matter, as will be shown in Section 5. In Sections 7 and 8 it also will be shown that this Keplerian velocity field of the QS systematically and correctly generates in terms of well known physics all the observed effects of the gravitational fields on the propagation of light and on the rate of clocks, including all the new effects recently discovered with the help of the GPS.
The idea that a real QS, ruling the propagation of light and the inertial motion of matter and moving in the ordinary three-dimensions, certainly is queer from the viewpoint of the theory of relativity, because it introduces local preferred references, in fact a different one for each point of space. However, at the same time it ascertains that each astronomical body very nearly rests with respect to the respective local preferred reference, which explains the null results of the Michelson light anisotropy experiments that have been claimed to corroborate the theory of relativity. The velocity of earth with respect to the QS in the solar Keplerian velocity field is only about 100 m/sec. Moreover, the solar system will be seen to nearly rest with respect to the QS in the galactic velocity field (please see Section 5.3 for details). The only relevant velocity of the earth based laboratories with respect to the real QS is the one due to the local velocity field creating the gravitational field of earth itself. This velocity varies from 7.4 km/sec at the equator to 7.91 km/sec near the poles. The effect of this velocity 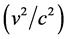 on the velocity of light and on the rate of clocks is extremely small, in the order of only
on the velocity of light and on the rate of clocks is extremely small, in the order of only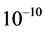 .
.
Excepting the Michelson light anisotropy experiments and some Mössbauer experiments, the sensitivity of all the other so called relativistic experiments is much too low to evidence such low effects. The velocities in all of the conventional relativistic experiments are many orders of magnitude larger than the 7.5 km/sec of the earth based laboratories with respect to the real QS (hydrogen atoms in the Ives-Stillwell experiment 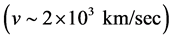 [9] , the increased lifetimes of Muons in cosmic rays
[9] , the increased lifetimes of Muons in cosmic rays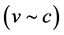 , the relativistic mass of electrons and protons from particle accelerators
, the relativistic mass of electrons and protons from particle accelerators 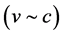 or of the relativistic energy term in atomic and nuclear states). In all of these experiments, it is impossible to discern the effects of the relatively very low velocity of less than 8 km/sec of the laboratory with respect to real QS from the effects of the enormous relative velocity with respect to the laboratory observer (QS). Therefore, all these so called relativistic effects can easily be reinterpreted as effects due to the velocity with respect to real QS, replacing the usual relative velocity with respect to the laboratory observer by the velocity with respect to real QS that are indistinguishably similar.
or of the relativistic energy term in atomic and nuclear states). In all of these experiments, it is impossible to discern the effects of the relatively very low velocity of less than 8 km/sec of the laboratory with respect to real QS from the effects of the enormous relative velocity with respect to the laboratory observer (QS). Therefore, all these so called relativistic effects can easily be reinterpreted as effects due to the velocity with respect to real QS, replacing the usual relative velocity with respect to the laboratory observer by the velocity with respect to real QS that are indistinguishably similar.
Only very recently have the measuring techniques achieved sensitivity enough to discern the very small effects, in the order of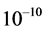 , due to actual velocities of the earth based laboratories with respect to real QS. The very high precision and stability of the atomic clocks and their close synchronization have played a fundamental role in all of such measurements. With the help of these synchronized clocks, several effects have been measured that clearly contradict predictions of the TR. Besides the troubles of the current theoretical view with experimental observations lurks another even much more serious trouble. These theories cannot account for the observed gravitational dynamics of galaxies and provide no physical grounds for the accelerated expansion of the universe (Sections 5.3 and 6 appoint appropriate solutions).
, due to actual velocities of the earth based laboratories with respect to real QS. The very high precision and stability of the atomic clocks and their close synchronization have played a fundamental role in all of such measurements. With the help of these synchronized clocks, several effects have been measured that clearly contradict predictions of the TR. Besides the troubles of the current theoretical view with experimental observations lurks another even much more serious trouble. These theories cannot account for the observed gravitational dynamics of galaxies and provide no physical grounds for the accelerated expansion of the universe (Sections 5.3 and 6 appoint appropriate solutions).
Experimental observations like those just described above are very difficult to find in the literature. They remain buried to the majority of the scientific community because of severe difficulties to get them published. During the last half century there is growing up an odd scientific policy in which experimental observations, not fitting into the currently accepted view, are seen as flawed and simply are ignored by the establishment. Editors of mainstream journals systematically decline publication of articles reporting experimental observations or theoretical views anyway conflicting with the establishment in the name of protecting the good reputation of their journals. Such reports can be found only in very low impact journals or in the internet. This is indeed a very pernicious policy. In the present work it is shown that the above clear-cut experimental observations reveal a genuine and realistic scenario of the universe that is completely different from that actually defended by the establishment and in which literally all of the impasses afflicting the current theories simply do not come up. In the next Section 3, it will be shown how this macroscopic spacedynamics emerges soundly within the context of the QFT.
3. The Higgs Condensate as Quantum Space and a Residual Macroscopic Manifestation of the Higgs Mechanism as the Quintessence of the Gravitational Fields
In a previous work [8] it has been shown that motion of real space, ruling the inertial motion of matter and the propagation of light, round earth and round the sun according to a Keplerian velocity field, consistent with the local main astronomical motions, appropriately creates the gravitational dynamics and all the observed effects caused by the gravitational fields. Obviously no classical medium has the required physical properties to rule the propagation of light and the inertial motion of matter, let alone the observed gravitational dynamics of the astronomical systems. Quantum fluids, contrarily than classical fluids, quantize all their excitations, which gives them surprising and very interesting dynamical properties. Although inviscidly flowing and deforming like usual fluids, they exhibit a characteristic dynamical stiffness by which they resist to all new changes of the state of motion. This makes the actual state of motion persistent. However, usual quantum fluids are all much too frail to support the material phenomena.
The idea here is not to discuss the theory of the elementary particles, but making use of the practical aspects of the Higgs mechanism and showing that the Higgs condensate (HC) complies with all the requisites to play the role of the real space, ruling the inertial motion of mater and the propagation of light. The HC is a Bose-Einstein (BE) condensate of zero spin Higgs bosons, a real and very robust Quantum Space (QS) stable up to 1015 degrees Kelvin. According to Quantum Field Theory (QFT), this QS is responsible for providing mass and hence mechanical properties to the elementary particles by the Higgs mechanism. This will say that this QS rules the inertial motion of matter and the propagation of light and hence is the ultimate reference for rest and for motion of matter and light. The Higgs mechanism, likewise the Meissner effect in superconductors, too must involve an extended macroscopic counterpart in the form of a velocity field of the condensate. This macroscopic counterpart has received much too little attention by the scientific community. Visibly this macroscopic manifestation of the Higgs mechanism corresponds to a Keplerian velocity field of the QS round the astronomical bodies, thereby creating appropriately the observed gravitational dynamics.
QFT has extensively been guided by the well known phenomenologies of the usual quantum fluids, especially the superconducting condensate [13] and this may also guide us now in this new affair. If the gravitational fields are a macroscopic manifestation of the Higgs mechanism, it is especially interesting to learn from the macroscopic features of the usual quantum fluids.
3.1. The Most Relevant Features of Superconducting Condensates and Superfluids
Usual quantum fluids are Bose-Einstein (BE) condensates of integer spin particles (bosons). In spite of being infinitely deformable and perfectly inviscid for steady state motions, quantum fluids possess a peculiar quantum phase stiffness that enables them to exhibit transient longitudinal as well as transverse elastic properties, resembling those of solids. In superconductors BE condensation becomes possible only with pairing of conduction electrons into Cooper pairs with zero spin and electric charge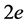 . On condensing into an energy state underneath the Fermi level, the Cooper pairs become completely entangled, indistinguishable and may tunnel throughout the volume of the superconductor. In the Ginsburg-Landau (GL) phenomenological theory [14] the charged superconducting condensate is described by a complex (two component) macroscopic order parameter
. On condensing into an energy state underneath the Fermi level, the Cooper pairs become completely entangled, indistinguishable and may tunnel throughout the volume of the superconductor. In the Ginsburg-Landau (GL) phenomenological theory [14] the charged superconducting condensate is described by a complex (two component) macroscopic order parameter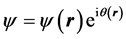 , where
, where 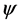 is the amplitude,
is the amplitude,  is the phase in three-dimensional space and
is the phase in three-dimensional space and 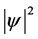 or
or 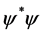 is the local condensate density.
is the local condensate density.
BE condensation occurs at low temperature because of the quantum phase correlation (BE correlation) between the wave functions of the bosonic particles. When the temperature of the system becomes sufficiently low, the phase correlation between the particle wave functions enforces long-range phase coherence, breaking the global 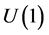 gauge symmetry in which the particle wave functions assume all among an infinite number of possible phases between zero and
gauge symmetry in which the particle wave functions assume all among an infinite number of possible phases between zero and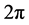 , one arbitrary and specific phase
, one arbitrary and specific phase  say. In superconductors about
say. In superconductors about 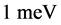 of energy is released per Cooper pair during BE condensation. In such low temperatures the phase correlation gives rise to a negative potential energy (bonding) term the value of which increases with the condensate density as
of energy is released per Cooper pair during BE condensation. In such low temperatures the phase correlation gives rise to a negative potential energy (bonding) term the value of which increases with the condensate density as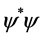 . Another positive potential energy (anti-bonding) term arises from repulsive core interaction between the bosons (they are not simply plane waves, but entail spin, charge etc.) that increases as
. Another positive potential energy (anti-bonding) term arises from repulsive core interaction between the bosons (they are not simply plane waves, but entail spin, charge etc.) that increases as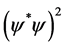 . The coefficient of the bonding term
. The coefficient of the bonding term 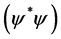 is considerably larger than that of the anti-bonding term. Therefore the minimum of the effective potential energy occurs not for
is considerably larger than that of the anti-bonding term. Therefore the minimum of the effective potential energy occurs not for , as usual, but for a finite value of
, as usual, but for a finite value of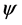 . This is well known as the so called Mexican Sombrero Potential. In this quantum coherent state, the long range GL order parameter
. This is well known as the so called Mexican Sombrero Potential. In this quantum coherent state, the long range GL order parameter 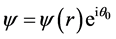 represents the resting condition of the condensate.
represents the resting condition of the condensate.
Because of the BE phase correlation, any local displacement of the phase within a part of the volume of the condensate with respect to the overall phase of the order parameter introduces phase disorder. This involves (elastic) energy, because it must conquer with the local phase correlation and climb up in the potential energy. It is important to realize that local phase displacements are inherently associated with local motion of the condensate and hence elastic phase stiffness corresponds also to motional stiffness. This phase stiffness is transient. It manifests it only during changes of the phase and of the flow velocity. Once excited, the motion becomes persistent. This phase stiffness enables quantum fluids to propagate phase perturbations (longitudinal and transverse oscillations) even moving and continuously deforming. A phase gradient 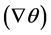 along any path causes the condensate to flow along the phase gradient (normally along a closed path) with velocity proportional to the magnitude of the gradient.
along any path causes the condensate to flow along the phase gradient (normally along a closed path) with velocity proportional to the magnitude of the gradient.
Phase gradients of the particle wave functions and of the superconducting order parameter are caused by an interacting field. In superconductors a gradient of the scalar potential (electric field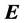 ) and or the vector potential
) and or the vector potential 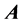 associated with magnetic field are well known to cause phase displacements of the (macroscopic) superconducting order parameter. While the phase gradient along the static electric field increases with time, the phase along the static vector potential increases only with distance. While a constant phase gradient leads to uniform flow of the condensate, a phase gradient changing with time corresponds to accelerated motion of the condensate. Phase displacements of the superconducting order parameter play a fundamental role in the electrodynamics of superconductors.
associated with magnetic field are well known to cause phase displacements of the (macroscopic) superconducting order parameter. While the phase gradient along the static electric field increases with time, the phase along the static vector potential increases only with distance. While a constant phase gradient leads to uniform flow of the condensate, a phase gradient changing with time corresponds to accelerated motion of the condensate. Phase displacements of the superconducting order parameter play a fundamental role in the electrodynamics of superconductors.
Superconductivity and magnetic fields are intrinsically incompatible with each other because the vector potential associated with the magnetic field causes local phase displacements that destroy the phase coherence of the electron wave functions as well as the pairing correlation. This breaks the Cooper pairs and tends to locally reestablish gauge symmetry. In type II superconductors, magnetic field in the form of quantized flux tubes coexist with superconductivity by sharing space and forming a mixed normal/superconducting state. The vector potential associated with the magnetic field displaces the phase of the superconducting order parameter creating phase disorder (screening currents), tending to destroy locally superconductivity and recovering gauge symmetry. The superconducting condensate tends to minimize its energy improving phase coherence by expulsing the magnetic field out from the superconductor, or compressing it into microscopic quantized flux tubes. This is the Meissner effect that confines the electromagnetic field, making it short-range and giving rest-mass to the photons (quasi-particles) within superconductors. The magnetic field within the flux tubes creates a screening interface layer (quantized Abrikosov vortices [15] ) that completes screening of the magnetic field and or the BE correlation within the London penetration depth. The intensity of the screening currents round the vortices falls off exponentially with distance from the fluxon nucleus. The screening currents must not be conceived as classical motion of individual Cooper pairs but as a local drift velocity field of the superconducting condensate that involves the Cooper pairs collectively. This antagonism between condensate and fields causing deleterious phase distortions seems to be a feature common to all quantum fluids.
Stationary circulation fields of the condensate (currents) along closed loops that may be caused by a vector potential field, contain a locked-in phase displacement.
 (2)
(2)
where 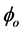 is the unit of quantized magnetic flux. Single valuedness requires that the total phase displacements
is the unit of quantized magnetic flux. Single valuedness requires that the total phase displacements 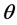 round the loops be an integer number
round the loops be an integer number  of
of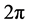 . Equation (2) rules the intrinsic quantization of excitations in quantum fluids, the origin of which is different from that of the usual quantization due to particle confinement by potential barriers. Phase correlation and conservation of existing phase displacements gives rise to another very peculiar feature of quantum fluids. Any motion (phase displacement) involves energy that is quantized for circulation fields along closed loops. However, once excited, these circulation fields become persistent. For instance, if a current is excited in a superconducting coil by an applied electromotive force, it will flow forever and only can be stopped by an opposing electromotive force. Because of the perfect conservativeness of the quantum fluids, such circulation fields with a locked-in phase displacement, known as quasi-particles are quantized and very stable. Rotons, Maxons and vortices are well known quasi-particles in superfluids and superconductors.
. Equation (2) rules the intrinsic quantization of excitations in quantum fluids, the origin of which is different from that of the usual quantization due to particle confinement by potential barriers. Phase correlation and conservation of existing phase displacements gives rise to another very peculiar feature of quantum fluids. Any motion (phase displacement) involves energy that is quantized for circulation fields along closed loops. However, once excited, these circulation fields become persistent. For instance, if a current is excited in a superconducting coil by an applied electromotive force, it will flow forever and only can be stopped by an opposing electromotive force. Because of the perfect conservativeness of the quantum fluids, such circulation fields with a locked-in phase displacement, known as quasi-particles are quantized and very stable. Rotons, Maxons and vortices are well known quasi-particles in superfluids and superconductors.
For macroscopic use of superconductivity several important new features come into play. While within superconductors the Meissner effect confines the local magnetic field into microscopic flux tubes, flux expulsion is a macroscopic counterpart of the Meissner effect. Circulation fields of the superconducting condensate (super-currents) are inherently associated with magnetic field. Hence, due to the Meissner magnetic flux expulsion, electric currents in a superconductor can flow only within a thin surface layer the depth of the London penetration length. Expulsion of large bundles of magnetic fluxons from the interior of type-II superconductors involves a macroscopic Lorentz (reaction) force field. Under a sufficiently dense fluxon distribution, besides repulsion between the quantized Abrikosov current vortices, the residual collective vector potential field (including the curl-free part [16] [17] ) excites macroscopic screening currents (velocity field of the condensate) round the bundle. In order to minimize the condensation energy, the superconductor thrusts the screening currents and the magnetic flux by a macroscopic Lorentz (reaction) force field along the flux density gradient and normally expels it out from the superconductor. However, in non-homogeneous superconductors, in which the amplitude of the superconducting order parameter has internally weaker or non-superconducting regions (due to inhomogeneous bulk temperature or to lower transition temperature), the Lorentz (reaction) force field may sweep and compress the magnetic flux into these weaker superconducting regions. The compressed magnetic flux weakens even more the superconductivity within these regions. The sweeping of flux toward the interior gives place for new flux to be admitted from outside through the boundary, which is the well known high field paramagnetic Meissner effect [18] .
3.2. The Higgs Condensate as Quantum Space
Usual Bose-Einstein (BE) condensates are all much too frail to play the role of real space. The quantum space (QS) or quantum vacuum, propagating light and responsible for the inertial behavior of matter as well as inducing the gravitational dynamics, must be an extremely robust and powerful spatial medium, stable up to extremely high temperatures. Obviously no classical medium complies with these requisites. However, the QFT, underlying the SEPM, entails the idea that space is filled up with the scalar Higgs field, a complex 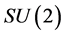 doublet. After the electro-weak symmetry is broken at
doublet. After the electro-weak symmetry is broken at 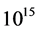 degrees Kelvin, spontaneous breaking of the global
degrees Kelvin, spontaneous breaking of the global 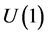 symmetry leads to BE condensation of the surviving zero spin Higgs bosons, releasing about a hundred of GeV per condensed Higgs boson. The Higgs condensate (HC) is a quantum fluid, likewise the superconducting condensate. It however is stable up to
symmetry leads to BE condensation of the surviving zero spin Higgs bosons, releasing about a hundred of GeV per condensed Higgs boson. The Higgs condensate (HC) is a quantum fluid, likewise the superconducting condensate. It however is stable up to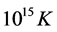 . The HC, analogously as the superconducting condensate, exhibits phase rigidity, inviscidness for steady state motion, quantization of all excitations etc., however in a scale multiplied by 15 orders of magnitude. Hence the HC plainly fulfills all the requisites to play the role of the QS ruling all the material and gravitational phenomena.
. The HC, analogously as the superconducting condensate, exhibits phase rigidity, inviscidness for steady state motion, quantization of all excitations etc., however in a scale multiplied by 15 orders of magnitude. Hence the HC plainly fulfills all the requisites to play the role of the QS ruling all the material and gravitational phenomena.
In the relativistic gauge theory, all the elementary particles are originally gauge particles that have no rest-mass and move at the velocity of light. No rest-mass means no rest-energy and no local stationary states. However, nature tells a different story. Experiments showed that the weak nuclear interaction is short-range and that the gauge bosons (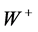 ,
,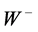 and
and ), mediating it have large masses. These observational facts demanded for a physical mechanism making this interaction short-range and providing inertial mass to the
), mediating it have large masses. These observational facts demanded for a physical mechanism making this interaction short-range and providing inertial mass to the ,
, 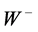 and
and 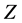 bosons. The well known fact that the Meissner effect makes the electromagnetic (EM) interaction short-range and gives mass to the photons (gauge particles) within superconductors was the key phenomenon suggesting a way to settle the problem. Analogously as the superconducting condensate confines the electromagnetic field by the Meissner effect, making it short-range and giving rest-mass to the photons within superconductors, a condensate, filling up the whole space, had to be conceived that confines the weak nuclear field, making it short-range and giving mass to the
bosons. The well known fact that the Meissner effect makes the electromagnetic (EM) interaction short-range and gives mass to the photons (gauge particles) within superconductors was the key phenomenon suggesting a way to settle the problem. Analogously as the superconducting condensate confines the electromagnetic field by the Meissner effect, making it short-range and giving rest-mass to the photons within superconductors, a condensate, filling up the whole space, had to be conceived that confines the weak nuclear field, making it short-range and giving mass to the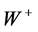 ,
, 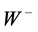 and
and  bosons. Actually this condensate is believed to be the HC and the mechanism, analog to the Meissner effect, is the Higgs Mechanism. The close similarity in the phenomenologies of the HC and the superconducting condensate comes from the fact that both are quantum fluids.
bosons. Actually this condensate is believed to be the HC and the mechanism, analog to the Meissner effect, is the Higgs Mechanism. The close similarity in the phenomenologies of the HC and the superconducting condensate comes from the fact that both are quantum fluids.
The HC excludes the weak nuclear field from the quantum space by the Higgs mechanism, confining it into a minimum distance of about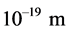 , providing the
, providing the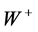 ,
,  and
and 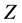 bosons with large rest masses. Quarks and leptons that port weak hypercharges too interact with the HC by a Yukawa like coupling, thereby getting inertial mass and all their parameters becoming quantized. The HC is to the weak and strong nuclear fields what the superconducting condensate is to magnetic fields. This lets clear that the HC effectively is responsible for the mechanical properties of the elementary particles, ruling the inertial motion of matter and the propagation of light and hence locally represents the ultimate reference for rest and for motion of matter and light. On the other hand, the HC, on moving itself according to a macroscopic differential velocity field, plays the role of the QS inducing the inertial dynamics observed within the gravitational fields.
bosons with large rest masses. Quarks and leptons that port weak hypercharges too interact with the HC by a Yukawa like coupling, thereby getting inertial mass and all their parameters becoming quantized. The HC is to the weak and strong nuclear fields what the superconducting condensate is to magnetic fields. This lets clear that the HC effectively is responsible for the mechanical properties of the elementary particles, ruling the inertial motion of matter and the propagation of light and hence locally represents the ultimate reference for rest and for motion of matter and light. On the other hand, the HC, on moving itself according to a macroscopic differential velocity field, plays the role of the QS inducing the inertial dynamics observed within the gravitational fields.
The QFT formally tells how the elementary particles get mass. This however does not tell what inertial mass really is. Within the context of the Higgs mechanism, the inertial mass can only be a manifestation of the phase correlation, the same that leads to the spontaneous breaking of the 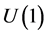 gauge symmetry and to the BE condensation. This same phase correlation also is what assures the persistence of the actual state of motion of the particles (inertia) and the intrinsic quantization of all excitations in the HC. From this viewpoint, inertial mass and the conservation of the linear and angular momentum of matter bodies are forcibly consequence of the persistence and conservation of all motions in the HC. Excitation of any closed circulation field in the HC (elementary particle) costs a well defined (quantized) amount of energy, the creation energy of the particle. However, once excited, it automatically becomes persistent.
gauge symmetry and to the BE condensation. This same phase correlation also is what assures the persistence of the actual state of motion of the particles (inertia) and the intrinsic quantization of all excitations in the HC. From this viewpoint, inertial mass and the conservation of the linear and angular momentum of matter bodies are forcibly consequence of the persistence and conservation of all motions in the HC. Excitation of any closed circulation field in the HC (elementary particle) costs a well defined (quantized) amount of energy, the creation energy of the particle. However, once excited, it automatically becomes persistent.
According to QFT, a field (particle) interacting with the HC, becomes short-range and gets mass. There however is a problem. The HC is really a quantum fluid in which no parts are distinguishable. Moreover, there is no outside. Hence, interaction implies exchanging energy with the condensate, which means heating up the whole condensate or exciting (evaporating) particles out from it. This however involves prohibiting large amounts of energy. Coupling of the elementary particles to the HC becomes affordable only if they already are excitations (quasi-particles) of the HC itself, that is, if the particles are in their essence local dynamical states (quantized circulation fields) of the HC itself because this involves attainable energy. Such local dynamical states involve necessarily both a real dynamics of the particles, describable in the ordinary space, as well as an imaginary dynamics. The imaginary dynamics arises because of implicit motion of the particle, not describable with respect to the ordinary space, and due to motion of the condensate (QS) itself. This implicit dynamics however is observable indirectly through corresponding physical effects. This links the inertial mass of the particles directly to the phase correlation and conservativeness of the Higgs condensate. In other words, the quantized resting energy of an elementary particle is the energy necessary to overcome the local phase correlation and to excite the local dynamical state of the HC itself. In this context inertial mass and conservation of the linear and angular momentum turn out to be simply consequence of the persistent modes of the HC.
Likewise the superconducting condensate is antagonistic to magnetic fields; the HC is antagonistic to the weak nuclear fields because it causes phase disorder increasing energy above the minimum. The HC however is not antagonistic to the electromagnetic and gravitational fields because they cause no phase disorder in the HC. The HC contains no electric charges and hence cannot screen electromagnetic fields. It also does not screen the gravitational fields. Hence, while the weak and strong nuclear fields become extremely short-range, confined to less than 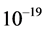 meters, the electromagnetic interactions although long range rarely become relevant in a macroscopic scale because of mutual screening of positively and negatively charged particles. The only interaction that effectively remains long range is the gravitational interaction and hence it is completely dominant in an astronomical scale.
meters, the electromagnetic interactions although long range rarely become relevant in a macroscopic scale because of mutual screening of positively and negatively charged particles. The only interaction that effectively remains long range is the gravitational interaction and hence it is completely dominant in an astronomical scale.
The constitution of the superconducting condensate and of the Higgs condensate is quite different and they act in different milieus. However, both are very similar quantum fluids. This is visibly the good reason of the remarkable resemblance between their microscopic phenomenologies, connected respectively with the Meissner effect and with the Higgs mechanism. There seems to be no reason why this should be fundamentally different in their macroscopic manifestations. Likewise the Meissner effect has a macroscopic counterpart, the Higgs mechanism too must have one. If a large bundle of magnetic fluxons inducing screening currents is present in a superconductor, the superconductor minimizes its energy by thrusting the magnetic flux along the gradient of the flux density out from the superconductor or into weaker superconducting regions [18] . Analogously the matter fields of large concentrations of matter may induce phase disorder of the Higgs order parameter and a screening velocity field of the HC. The Higgs condensate permeates all of space and there is no outside. The Higgs condensate minimizes its energy by developing a macroscopic force field, thrusting the matter fields along the matter density gradient toward regions where the Higgs order parameter has already been depressed by a large concentration of matter. The screening velocity field of the Higgs condensate round matter bodies is to be seen as the Keplerian velocity field of the QS and the corresponding force field is the gravitational field, which in fact will be seen to be a centrifugal (fictitious) force field toward the gravitational center. The next section introduces the new conception of space, matter and gravitation that complies with the discussions in the previous sections and straightforwardly solves the gravitational physics.
4. Foundations of the New Conception That Properly Solves the Centuries Old Troubles with the Gravitational Physics
4.1. The Foundations of the New Conception of Space, Matter and Gravitation
In the positivist view of the TR, elementary particles originally have inertial mass and are objectively real by themselves, while space has no objective reality at all. The present work explores a scenario in which the ontological hierarchy of matter and space is the very opposite. In the new conception the quantum space (QS) is objectively real by itself and is moving in the ordinary three dimensions, while matter particles and light are only propagating perturbations in this real moving QS, that is, are local persistent and propagating dynamical states of this real QS itself. This concept is not inane. Such QS is well at hand in the context of the QFT, underlying the SEPM. The QS is a Bose-Einstein (BE) condensate of the zero spin (neutral) Higgs bosons. The Higgs condensate (HC) is an extremely robust quantum fluid spatial medium, stable up to about 1015 degrees Kelvin. According to the QFT, this HC is responsible for providing inertial mass and thus mechanical properties to the elementary particles by the Higgs mechanism. If the HC rules the inertial motion of matter and the propagation of light, it is much more than simply an ether propagating light. It is the support of all material phenomena and thus the local absolute and ultimate reference for rest and for motions of matter and light. Therefore only motions with respect to the local HC may give rise to physical effects.
According to the TR the velocity of light is intrinsically constant and isotropic with respect to all possible inertial references. However, recent experimental observations, achieved with the help of the tightly synchronized clocks of the GPS [5] -[7] (please see Section 2), reveal very clearly that the QS, ruling the inertial motion of matter and the propagation of light, is moving round earth and round the sun according to the Keplerian velocity field [Equation (1)], consistent with the local main astronomical motions. They also corroborate that the velocity of light is constant and isotropic not with respect to all observers and all inertial references; however with respect to the local moving real QS that propagates light. Einstein has related time dilation effects to relative velocity with respect to the observer and later also to the gravitational potential. However, these recent experimental observations show that time dilation is caused not by relative velocity and also not by the gravitational potential, however by velocity with respect to the QS.
In the view of the present new conception the Higgs mechanism, analogously as the Meissner effect in superconductors, too entails a macroscopic manifestation in the form of a Keplerian velocity field of the HC (screening currents) thereby squeezing the matter fields into compact bodies. Motion of the QS according to a Keplerian velocity field [Equation (1)] round each matter concentration throughout the universe, consistent with the local main natural astronomical motions is the quintessence of the gravitational fields. In this spacedynamics earth, the solar system, the galaxy and the astronomical bodies in general are very closely resting with respect to the moving QS, which explains the null results of the light anisotropy experiments and the observed absence of gravitational time dilation on the GPS clocks. This QS-dynamics will be shown to appropriately generate the observed gravitational dynamics on earth, within the solar system as well as the galactic gravitational dynamics without the need of dark matter.
Matter bodies, resting in the ordinary space within a Keplerian velocity field of the QS, have physically genuine motions with respect to the moving QS that cannot be described with respect to ordinary space and must be expressed in terms of imaginary numbers, which means orthogonality to the ordinary motions. The Keplerian velocity field, generating the earth’s gravitational field achieves nearly 8 km/sec on the earth’s surface. Earth based laboratories have this relatively very low velocity with respect to the QS (less than 8 km/sec). Hence, the very large relative velocities (in particle beams) in the usual relativistic experiments are almost equally large velocities with respect to the QS. The effect of the very low velocity of the earth based laboratories is in the order of only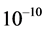 , much too low to be evidenced by the usual relativistic experiments. Very few Michelson light anisotropy experiments have achieved resolution enough to barely detect these small effects. Only in recent years have the atomic clocks achieved resolution enough (down to
, much too low to be evidenced by the usual relativistic experiments. Very few Michelson light anisotropy experiments have achieved resolution enough to barely detect these small effects. Only in recent years have the atomic clocks achieved resolution enough (down to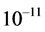 ) to unambiguously detect such small effects. With the help of these precise atomic clocks the gravitational time dilation by the earth’s field could be well measured. However, the atomic clocks in the GPS satellites also have unambiguously evidenced the absence of effects due to the solar gravitational field on the GPS clocks [6] [7] , showing that it is not the gravitational potential, however the velocity with respect to the QS that causes time dilation. Moreover, the small one-way anisotropy of the velocity of light of less than 8 km/sec could be measured with the help of the tightly synchronized clocks of the GPS [5] . These experiments all unambiguously show very clearly that light anisotropy and time dilation are not due to relative velocity, but is due to velocity with respect to the local QS (please see details in Section 2).
) to unambiguously detect such small effects. With the help of these precise atomic clocks the gravitational time dilation by the earth’s field could be well measured. However, the atomic clocks in the GPS satellites also have unambiguously evidenced the absence of effects due to the solar gravitational field on the GPS clocks [6] [7] , showing that it is not the gravitational potential, however the velocity with respect to the QS that causes time dilation. Moreover, the small one-way anisotropy of the velocity of light of less than 8 km/sec could be measured with the help of the tightly synchronized clocks of the GPS [5] . These experiments all unambiguously show very clearly that light anisotropy and time dilation are not due to relative velocity, but is due to velocity with respect to the local QS (please see details in Section 2).
In fact the propagation of light and of the electromagnetic oscillations in general are both ruled by velocity with respect to the QS. Hence, motion of the laboratory with respect to the QS increases the light roundtrip time and also increases in the same proportion the roundtrip time of the time standards (electromagnetic oscillators, atoms, molecules, lasers) by which the clocks count time. It also affects the inertial mass of the matter particles (oscillations of the QS). Therefore, measuring the velocity of light by the method of light roundtrip and clock, necessarily gives always the same result. Moreover, an observer monitoring the roundtrips of light along known distances within a gravitational field from outside, using his local (external) clock, will notice the distortions underlying Einstein’s space-time curvature (please see prove in Section 8.3). These effects however are clearly artifacts of the inappropriate measuring method.
If the real QS, ruling the inertial motion of matter and the propagation of light, moves in the ordinary three-dimensions, a laboratory resting in the same ordinary space, has physically genuine motion in the opposite direction. Although this motion points along an ordinary space direction, namely the one opposite to the motion of the real QS, it cannot be specified with respect to ordinary space. It is implicit and must be expressed by imaginary numbers. This motion produces real physical and well observed kinematical effects that will be shown to act independently (are orthogonal) from those of the ordinary motions (please see Section 5.2 for conclusive details). In this context the planets in the solar system and the solar system in the galaxy are very closely commoving with the real QS and hence are closely resting with respect to it, which explains the null results of the Michelson light anisotropy experiments, searching for effects of the orbital and cosmic motion of earth. This spacedynamics also will be shown to straightforwardly explain, in terms of simple and genuine physical effects, all the effects caused by the gravitational fields on the velocity of light and on time (the rate of clocks) etc.
If the real QS is moving consistently with the local main astronomical motions throughout the universe, what we call celestial mechanics in fact is mainly spacedynamics. The orbiting astronomical bodies are very closely resting with respect to the QS. No gravitational forces are needed to constrain these motions to their orbits because it is space itself, the ultimate reference that so moves. Local mechanical and electromagnetic experiments reveal no resultant motion of the earth globe because there is no motion to reveal. The effect of the very low velocity of the earth globe with respect to the QS is only about a hundred of meters per second, much too low to be detected even by the actual most sensitive instruments.
The present work is going to show that, according to recent experimental observations [5] -[7] , Einstein’s assumption of the intrinsic isotropy and constancy of light with respect to all possible inertial references effectively is false. Einstein’s interpretation of the null results of the Michelson light anisotropy experiments is not only mistaken. It also has made the obvious physical explanation of the gravitational physics unviable. It was exactly the first wrong step beginning the route toward the now century old impasse about the nature of space and the gravitational physics. The recent experimental observations show very clearly that the velocity of light is isotropic and constant, not with respect to all inertial references, but only with respect to the QS and hence with respect to all references locally commoving with the QS. As this QS is moving round the gravitational sources according to a Keplerian velocity field consistent with the local main astronomical motions, thereby generating the gravitational dynamics, the velocity of light is nearly the same and is very closely isotropic with respect to all these natural astronomical bodies throughout the universe. Moreover, clocks locally commoving with the QS run not slow as demonstrated by the GPS clocks (please see Section 2.3 for details). Such clocks run all closely synchronous and all show closely the same universal proper time throughout the universe.
Within earth based laboratories that are moving at 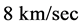 with respect to the QS in the earth’s Keplerian velocity field, clocks run a very little bit slow (
with respect to the QS in the earth’s Keplerian velocity field, clocks run a very little bit slow (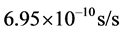 ), as precisely shown by atomic clocks. They do not display (absolute) proper time even resting in the observer’s reference. Within such laboratories physical phenomena in general evolve at a slower rate. Moreover, light anisotropy experiments, using highly sensitive Michelson interferometers, found anisotropies of closely 8 km/sec, constant the whole day and the whole year. The effects, due to motions with respect to the QS, are well described by the known formulas of the TR, however in these expressions the relative velocity with respect to the observer must be replaced by the velocity with respect to the QS, because it is the velocity with respect to the QS that rules these effects and not the relative velocity.
), as precisely shown by atomic clocks. They do not display (absolute) proper time even resting in the observer’s reference. Within such laboratories physical phenomena in general evolve at a slower rate. Moreover, light anisotropy experiments, using highly sensitive Michelson interferometers, found anisotropies of closely 8 km/sec, constant the whole day and the whole year. The effects, due to motions with respect to the QS, are well described by the known formulas of the TR, however in these expressions the relative velocity with respect to the observer must be replaced by the velocity with respect to the QS, because it is the velocity with respect to the QS that rules these effects and not the relative velocity.
If the Higgs condensate (QS) is moving along any direction in the ordinary three-dimensional space at a velocity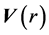 , a laboratory, fixed in the same ordinary space, will have real opposite and implicit motion with respect to the local moving Higgs condensate at a velocity
, a laboratory, fixed in the same ordinary space, will have real opposite and implicit motion with respect to the local moving Higgs condensate at a velocity . If the QS in this velocity field is rotating, the implicit velocity vectors of particles within the laboratory will rotate together with it. Although this implicit motion of the laboratory with respect to the moving QS is physically real, it cannot be expressed with respect to the ordinary space or with respect to any ordinary reference. Hence, mathematically it must be expressed as an imaginary quantity
. If the QS in this velocity field is rotating, the implicit velocity vectors of particles within the laboratory will rotate together with it. Although this implicit motion of the laboratory with respect to the moving QS is physically real, it cannot be expressed with respect to the ordinary space or with respect to any ordinary reference. Hence, mathematically it must be expressed as an imaginary quantity . Despite the velocity vector, expressing this motion, points along an ordinary direction (opposite to the velocity of the QS), it is not velocity with respect to ordinary space. It simply is physically real motion (distance
. Despite the velocity vector, expressing this motion, points along an ordinary direction (opposite to the velocity of the QS), it is not velocity with respect to ordinary space. It simply is physically real motion (distance 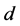 traveled as a function of time
traveled as a function of time  of the resting laboratory with respect to real QS, the locally absolute reference for rest and for motion. Clearly, Einstein’s concept of motion of the universe altogether along the time axis at the fixed velocity of light
of the resting laboratory with respect to real QS, the locally absolute reference for rest and for motion. Clearly, Einstein’s concept of motion of the universe altogether along the time axis at the fixed velocity of light 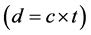 does not fit into this view because, according to the TR, a real spatial medium, ruling the propagation of light and the inertial motion of matter, does not exist and hence speaking of motions of such a medium or motions with respect to it simply does make no sense.
does not fit into this view because, according to the TR, a real spatial medium, ruling the propagation of light and the inertial motion of matter, does not exist and hence speaking of motions of such a medium or motions with respect to it simply does make no sense.
Visibly the orbital motions of the natural astronomical bodies (planetary satellites, planets in the solar system, stars in the galactic disks etc.) are very closely concentrated about the equatorial plane of the respective Keplerian velocity field, minimizing their velocity with respect to the QS and hence very closely resting all the time with respect to the moving QS. Please see in the preceding Section 2 the experimental evidence of this spacedynamics and in Section 5 its fundamental role in generating the observed gravitational dynamics. Within the context of this spacedynamics, Einstein’s gravitational (inertial) dynamics of matter bodies within the conveniently curved (four-dimensional) spacetime must be replaced by inertial dynamics within the three-dimensional QS (Higgs condensate) moving in the (flat) ordinary space according to a Keplerian velocity field round each astronomical body.
When physics is described with respect to ordinary spatial coordinates, all physical effects caused by activity (motion) of the QS itself (the local absolute reference for rest and for motion of matter) in the ordinary space must be expressed in terms of imaginary quantities. The gravitational effects, observed within the earth based laboratories, are clearly of this nature. Moreover, likewise normal matter of the superconductor does not directly perceive the dynamics of the superconducting condensate (because no interaction) but only the effects of this dynamics (magnetic field, mechanic tensions etc.), matter objects too do not perceive directly the dynamics of the QS (it seems arcane) but only its effects (gravitational pull, gravitational time dilation, gravitational light deflection, light anisotropy etc.). In reality, physical effects, caused by activity of the real QS are ubiquitous in physics, especially in quantum mechanics phenomena. If the matter particles are in their essence perturbations of QS, elementary particle phenomena necessarily and directly involve activity of QS, analogously as the ripples in the ocean involve activity of the ocean water. The explicit introduction of the activity of QS adds new degrees of freedom to the particles or system of particles that allow for implicit or intrinsic dynamical states that cannot be described with respect to ordinary space coordinates.
The new conception of space, matter and gravitation of the present work, in which the Higgs condensate (HC) plays the role of the QS, associates together the central idea of Einstein’s GR, according to which the gravitational pull is an inertial effect and the idea of QFT underlying the SEPM, according to which the HC is a QS that rules the inertial motion of matter. This is the possible unification of GR and of Quantum Mechanics (QG). However, in the new conception, gravitation is not due to inertial motion within Einstein’s curved four-dimensional spacetime. It also is not the result of a central field of gravitational forces, created by the quantum exchange interaction mediated by gravitons, as proposed in QG. In the new conception Einstein’s curved four-dimensional spacetime is replaced by a macroscopic Keplerian velocity field of the real QS in the (flat) ordinary three-dimensional space. The gravitational acceleration is the result of inertial motion of matter bodies and light within the moving and warping real QS in the ordinary three dimensions round the gravitational sources according to a Keplerian velocity field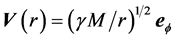 , consistent with the local main astronomical motions.
, consistent with the local main astronomical motions.
4.2. Space and Time Invariance of the Laws of Physics throughout the Universe
Many observations indicate that the laws of physics are the same throughout the universe and also with time. According to the present view the motion of the real QS is closely consistent with the astronomical motions throughout the universe. Hence, this universality of the laws of physics arises straightforwardly because the astronomical bodies essentially trace out very closely the motion of the QS itself (Higgs condensate) creating the respective gravitational fields. Hence, each astronomical body very closely rests with respect to the local moving QS that rules the propagation of light and the inertial motion of matter. Therefore the velocity of light is the same and is isotropic with respect to all these bodies, which explains the null results of the Michelson experiments and also implies that clocks commoving with these bodies run all closely synchronous and show all closely the universal proper time. This must have been so since the formation of the first stars and galaxies. The universality of the laws of physics thus is a straightforward consequence of the fact that the physical phenomena taking place on Earth and in all these worlds evolve locally under closely the same kinematical circumstances (rest) with respect to the local QS. This spatial invariance of the laws of physics is clearly not the same thing as Lorentz invariance. In order to unambiguously verify the Lorentz invariance, the laws of physics must be exactly the same in all the different inertial references at the same place.
The superconducting condensate is physically anchored to the superconducting material. It is not Lorentz invariant because it has a preferred reference that is the superconducting material. The Higgs condensate, the QS has no such preferred reference. Moreover, if all the elementary particles are in their essence local dynamical states (phase perturbations) of the Higgs condensate and get their mechanical properties from it, they cannot represent a reference for the local motion of the Higgs condensate. Contrarily, the moving Higgs condensate, the QS is the local ultimate reference for rest and for motion of matter and light. Along its motions this QS carries with it all the ultimate and locally absolute reference for rest and for motion of matter and for all the material phenomena. This will say that the locally moving Higgs condensate, the QS is necessarily itself the local preferred reference for rest and or motion of matter. Hence, its motion is completely innocuous to the local physical phenomena within a laboratory commoving with the QS, its velocity is a gauge invariant. This assures the close sameness of the laws of physics on all natural astronomical bodies throughout the universe because they all very nearly rest with respect to the QS. On the other hand, the expansion of the universe is expansion of the QS itself that however does not expand bound systems like galaxies. The observed Hubble spectral redshifts of radiation from galaxies show that on the overall the galaxies are reseeding from each other. However, these redshifts are not usual Doppler shifts. They are due to stretching of the wavelengths of radiation as a function of time, due to expansion of the QS their medium of propagation.
Now several experimental observations prove that within gravitational fields the QS moves round the astronomical bodies according to a Keplerian velocity field, consistent with the local main astronomical motions (please see details in Section 2), thereby creating the gravitational fields. Hence, within gravitational fields, the preferred reference is a different one at each point of space. Each natural satellite, each planet of the solar system, each star in the galactic disk and each galaxy represent very closely the local preferred reference. All these bodies very closely rest with respect to the local moving QS. On observing that physical events on Mars or on very distant galaxies evolve the same rate as on Earth, one could naively see prove in this that the laws of physics are Lorentz invariant, that is, are not affected by the visible relative velocity of all these bodies in the ordinary space. However, from the viewpoint of the present work, these observations do not support the Lorentz invariance. The laws of physics are the same because the kinematical circumstances with respect to the local moving QS, the locally absolute reference for rest and motion of matter and light, are closely the same in all these worlds.
The remaining sections of this article work out the practical consequences and predictions of the spacedynamic gravitational mechanism, showing that it systematically matches the experimental observations.
5. The Spacedynamic Origin of the Gravitational Dynamics
5.1. Origin of the Gravitational Dynamics on Earth and in the Solar System
Consider the system of orthogonal non-rotating (XYZ) axes, with origin at the gravitational center and the Z axis pointing respectively along the rotation axis of earth and of the solar system and let  be the usual spherical coordinates. The Keplerian velocity field
be the usual spherical coordinates. The Keplerian velocity field 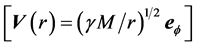 of the real QS [Equation (1)] round the earth and round the sun will be shown to correctly induce the gravitational dynamics, observed within the earth’s field and within the solar system, in terms of inertial motions with respect to the local inertial references (IRs). Of course, due to the spherical symmetry of the magnitude of the velocity of the QS in the Keplerian velocity field, a specific local rotating IR corresponds to each point of space. Hence, ordinary motion of a matter body within a gravitational field is in fact motion through an infinite sequence of local rotating inertial references (IRs). As affirmed in the introduction, if the free-fall and the curved motion of free particles within gravitational fields is not caused by real gravitational forces, but is ruled by inertia (Einstein’s Principle of Equivalence), then these relatively very slow motions must be ruled by inertia and are congruent with Galilean relativity. It will be seen that the velocity components of the slow motions of force-free bodies with respect to the moving QS undergo homogeneous linear transformations totally analogous to those of 4-vectors in the theory of relativity. However, this rotation takes place in the three-dimensional space and the parameter gauging the transformation is not relative velocity but the local characteristic angular velocity of the local IRs, that increases for decreasing distance from the gravitational source.
of the real QS [Equation (1)] round the earth and round the sun will be shown to correctly induce the gravitational dynamics, observed within the earth’s field and within the solar system, in terms of inertial motions with respect to the local inertial references (IRs). Of course, due to the spherical symmetry of the magnitude of the velocity of the QS in the Keplerian velocity field, a specific local rotating IR corresponds to each point of space. Hence, ordinary motion of a matter body within a gravitational field is in fact motion through an infinite sequence of local rotating inertial references (IRs). As affirmed in the introduction, if the free-fall and the curved motion of free particles within gravitational fields is not caused by real gravitational forces, but is ruled by inertia (Einstein’s Principle of Equivalence), then these relatively very slow motions must be ruled by inertia and are congruent with Galilean relativity. It will be seen that the velocity components of the slow motions of force-free bodies with respect to the moving QS undergo homogeneous linear transformations totally analogous to those of 4-vectors in the theory of relativity. However, this rotation takes place in the three-dimensional space and the parameter gauging the transformation is not relative velocity but the local characteristic angular velocity of the local IRs, that increases for decreasing distance from the gravitational source.
As asserted previously, the orbital motion of bodies in the gravitational field is the combination of the Keplerian velocity field of the QS and of the usual very slow inertial motion of the bodies with respect to this moving QS. Observations consistently show that the orbital motions of the planets in the solar system concentrate them closely within the equatorial plane of the solar Keplerian velocity field and follow closely the circulation of the QS. Hence, by moving along circular orbits, the planets very closely rest with respect to the moving QS and this circular motion needs not to be explained anymore because it is space itself, the ultimate reference for rest and for motions, that so moves. The planets have only very low velocities (hundreds of meters per second) with respect to the QS, which causes the small ellipticity of the orbits and this ellipticity needs to be explained.
A particle, fixed with respect to the (X, Y, Z) axes at any fixed point [ ,
, 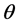 ,
, ] within this Keplerian velocity field above the surface of the gravitational source will be moving with respect to the QS with the implicit velocity:
] within this Keplerian velocity field above the surface of the gravitational source will be moving with respect to the QS with the implicit velocity:
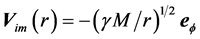 (3)
(3)
This velocity of the particle is implicit and cannot be specified with respect to the [X, Y, Z] axes. It is due to the motion of the QS, the locally ultimate reference for rest and for motion of matter and may be represented as an imaginary quantity. The fact that the velocity of QS along the  coordinate increases for decreasing
coordinate increases for decreasing , the local velocity distribution, seen by the resting particle, corresponds to rotation of the QS and of the local IR round an overhead axis with an angular velocity
, the local velocity distribution, seen by the resting particle, corresponds to rotation of the QS and of the local IR round an overhead axis with an angular velocity  pointing along the
pointing along the  spherical coordinate. This will say that the resting particle is implicitly moving within the local rotating IR oppositely along a circular path about this same overhead axis under a real upward
spherical coordinate. This will say that the resting particle is implicitly moving within the local rotating IR oppositely along a circular path about this same overhead axis under a real upward  centripetal force.
centripetal force.
However, the QS is of course not rotating round an overhead axis, but circulates round the gravitational center. In the view of the present work, a particle, resting in the ordinary space, is propagating in the QS as a de Broglie matter wave with an implicit velocity pointing along the 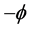 coordinate, whose wave fronts lie in the
coordinate, whose wave fronts lie in the 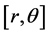 plane. From the viewpoint of these wave fronts the local velocity distribution of the QS corresponds to rotation round an overhead axis, because the velocity of the QS along
plane. From the viewpoint of these wave fronts the local velocity distribution of the QS corresponds to rotation round an overhead axis, because the velocity of the QS along 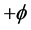 in the Keplerian velocity field increases for decreasing
in the Keplerian velocity field increases for decreasing 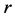 coordinate. Nevertheless, wave fronts of a particle having velocity with respect to the QS along the
coordinate. Nevertheless, wave fronts of a particle having velocity with respect to the QS along the 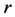 coordinate, whose wave fronts lie in the
coordinate, whose wave fronts lie in the 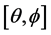 plane, do not see this rotation, but see the opposite rotation round the gravitational center (please see Figure 2 and Equations (4) for details). This rotation of the
plane, do not see this rotation, but see the opposite rotation round the gravitational center (please see Figure 2 and Equations (4) for details). This rotation of the 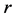 velocity component remembers the (acoustical) wave propagation within a medium in rigid-body rotation. Totally similar refraction effects also occur with sound waves propagating through whirlwind [19] . The opposite rotations of the implicit
velocity component remembers the (acoustical) wave propagation within a medium in rigid-body rotation. Totally similar refraction effects also occur with sound waves propagating through whirlwind [19] . The opposite rotations of the implicit 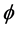 and of the ordinary
and of the ordinary  velocity components of the particle characterizes a hyperbolic rotation. Finally the wave fronts of a particle moving in a polar orbit, that lie in the
velocity components of the particle characterizes a hyperbolic rotation. Finally the wave fronts of a particle moving in a polar orbit, that lie in the  plane see no
plane see no
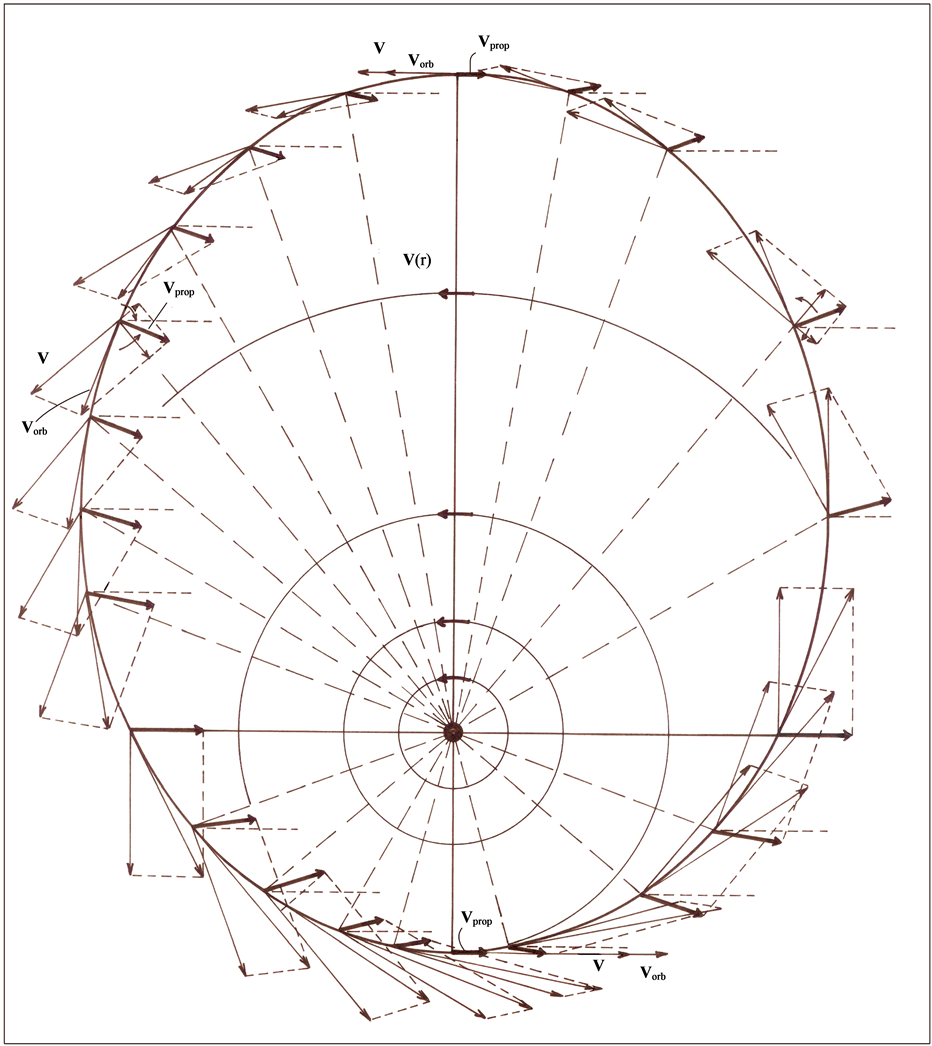
Figure 2. The figure is a very precise graphical representation. It displays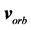 ,
, 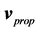 and
and 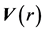 for a large number of points along an elliptical orbit with eccentricity
for a large number of points along an elliptical orbit with eccentricity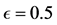 . The rotation rate of
. The rotation rate of  can be read precisely enough in the figure. Specifically the rotation rate of the
can be read precisely enough in the figure. Specifically the rotation rate of the 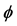 velocity component can be read at the top of the figure, while that of the
velocity component can be read at the top of the figure, while that of the 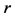 component can be read at the left hand side (please see Equations (4)).
component can be read at the left hand side (please see Equations (4)).
rotation at all because the Keplerian velocity field has no velocity gradient in the 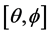 plane and so cannot rotate the wave fronts in the
plane and so cannot rotate the wave fronts in the 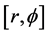 plane. Note that the QS in the Keplerian velocity field contracts along certain directions and stretches along others, thereby changing the wavelengths of the particles along these directions and their velocity with respect to the QS according to de Broglie’s equation
plane. Note that the QS in the Keplerian velocity field contracts along certain directions and stretches along others, thereby changing the wavelengths of the particles along these directions and their velocity with respect to the QS according to de Broglie’s equation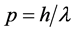 . However, along the
. However, along the  and
and  directions no such deformations occur and hence, if the effects of the velocity field on the motion of the particles are expressed in terms of the effective rotation rates of the
directions no such deformations occur and hence, if the effects of the velocity field on the motion of the particles are expressed in terms of the effective rotation rates of the 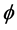 and
and 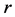 velocity components these effects on the wavelength are automatically included in the effective rotation rates and need not to be included explicitly.
velocity components these effects on the wavelength are automatically included in the effective rotation rates and need not to be included explicitly.
In order to describe the motion of a free particle within the velocity field Equation (1), there is need knowing precisely the effective rotation rates of the 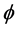 and the
and the  velocity components of the particle. A careful analysis of the velocity of a small test body with respect to the QS in an elliptic orbit round a large gravitational source
velocity components of the particle. A careful analysis of the velocity of a small test body with respect to the QS in an elliptic orbit round a large gravitational source 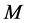 allows reading the effective refraction rates and the angular velocities with which the
allows reading the effective refraction rates and the angular velocities with which the 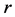 and
and  velocity components are rotated. Figure 2 is a very precise graphical representation of the velocity of the QS in the Keplerian velocity field
velocity components are rotated. Figure 2 is a very precise graphical representation of the velocity of the QS in the Keplerian velocity field 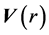 of a source
of a source , of the orbital velocity
, of the orbital velocity 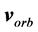 and of the velocity of the orbiting particle
and of the velocity of the orbiting particle 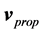 with respect to the QS at a number of points along an elliptical orbit with eccentricity
with respect to the QS at a number of points along an elliptical orbit with eccentricity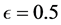 . These velocities are related through the vector equation
. These velocities are related through the vector equation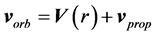 . The rotation rates
. The rotation rates 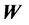 of the velocity components of
of the velocity components of 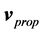 along the
along the 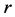 and
and 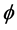 coordinates can be read precisely enough respectively at the left hand side and on top of Figure 2. The corresponding rotation rates are:
coordinates can be read precisely enough respectively at the left hand side and on top of Figure 2. The corresponding rotation rates are:
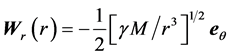 (4a)
(4a)
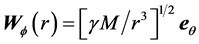 (4b)
(4b)
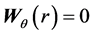 (4c)
(4c)
It is important to note that Equations (4) express exactly what we expect intuitively and the fact that the sign of Equation (4a) is opposite to that of Equation (4b) shows that the rotation is not a trigonometric rotation, but a hyperbolic one. Moreover, the fact that the rate Equation (4a) of the  velocity component is only one half the rate Equation (4b) of the
velocity component is only one half the rate Equation (4b) of the  component shows that this hyperbolic rotation is asymmetric, which is fundamental to assure conservation of the total mechanical energy (se details at the end of this section) and to accomplish the Virial theorem. Equation (4a) shows that the refraction rate of the
component shows that this hyperbolic rotation is asymmetric, which is fundamental to assure conservation of the total mechanical energy (se details at the end of this section) and to accomplish the Virial theorem. Equation (4a) shows that the refraction rate of the 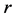 velocity component just compensates for the variation of the velocity field as a function of
velocity component just compensates for the variation of the velocity field as a function of . This assures conservation of the angular momentum round the center of mass and that the path of the free-falling particle from initial rest is strictly along the radial coordinate, as observed.
. This assures conservation of the angular momentum round the center of mass and that the path of the free-falling particle from initial rest is strictly along the radial coordinate, as observed.
In terms of Equation (4b), the instantaneous rate at which vertical downward velocity is generated during free-fall from initial rest within a laboratory fixed with respect to the  axes and thus moving with respect to the QS with the implicit velocity Equation (3) is given by the vector product:
axes and thus moving with respect to the QS with the implicit velocity Equation (3) is given by the vector product:
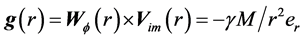 (5)
(5)
Equation (5) shows that, while in GR the gravitational acceleration results mainly from the very slow rotation of the huge timelike component of the 4-velocity, in the present spacedynamics it results from the much larger and position dependent rotation rate of the also position dependent implicit velocity vector. The instantaneous acceleration field [Equation (5)] points from any point toward the gravitational center from the equator to the poles. It does not depend on the angular coordinates and is spherically symmetric. From the viewpoint of the non-inertial laboratory observer, it is the instantaneous rate at which vertical downward velocity of free particles is created with respect to the fixed laboratory, due to the refraction rate Equation (4b) of the local implicit velocity vector Equation (3) of the particle. In reality, from the viewpoint of the local inertial reference (IR) that is rotating with an angular velocity given by Equation (4b) round an overhead axis that can be found to be located at , this acceleration is apparent (centrifugal). The free particle simply tends to move instantaneously along a straight line within the local IR. The judgment of the non-inertial laboratory observer comes from the fact that his laboratory reference, apparently resting in the ordinary space, is implicitly moving within the rotating local IR round the same overhead axis under an upward centripetal force acted on it by the ground. Equation (5) does not contain the angular coordinates because the implicit velocity
, this acceleration is apparent (centrifugal). The free particle simply tends to move instantaneously along a straight line within the local IR. The judgment of the non-inertial laboratory observer comes from the fact that his laboratory reference, apparently resting in the ordinary space, is implicitly moving within the rotating local IR round the same overhead axis under an upward centripetal force acted on it by the ground. Equation (5) does not contain the angular coordinates because the implicit velocity , given by Equation (3), as well as the refraction rate
, given by Equation (3), as well as the refraction rate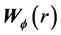 , given by Equation (4b), do not depend on the angular coordinates
, given by Equation (4b), do not depend on the angular coordinates  and
and . Neglecting the rotation and the slightly non-spherical form of earth, Equation (5) has the same value for all
. Neglecting the rotation and the slightly non-spherical form of earth, Equation (5) has the same value for all  and
and . Hence
. Hence 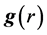 is a central spherically symmetric field of centrifugal accelerations toward the gravitational center.
is a central spherically symmetric field of centrifugal accelerations toward the gravitational center.
In case of two interacting masses 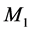 and
and , Equation (5) must be written for both
, Equation (5) must be written for both 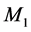 as well as for
as well as for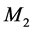 . On inserting the other mass into each equation, it is verified that the (apparently) attractive forces are equal and opposite, pointing toward the center of mass. In fact the mutual acceleration occurs not because of gravitational forces, however is due to the mutual influence of the local inertial references.
. On inserting the other mass into each equation, it is verified that the (apparently) attractive forces are equal and opposite, pointing toward the center of mass. In fact the mutual acceleration occurs not because of gravitational forces, however is due to the mutual influence of the local inertial references.
Equation (5) is suitable only for free-fall along short distances. In order to describe the free-fall along large radial distances, it is necessary to take into account the refraction rate of the radial velocity component  of the particle too. Note that the refraction rate of this component is opposite to that of the
of the particle too. Note that the refraction rate of this component is opposite to that of the 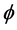 component [see Equations (4)].
component [see Equations (4)].
Such free-fall along large distances is governed by the elementary homogeneous linear differential equation:
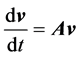 (6)
(6)
where  is the column matrix of the
is the column matrix of the  and the
and the 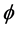 velocity components of the free-falling particle:
velocity components of the free-falling particle:
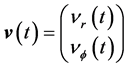 (7)
(7)
and  is the hyperbolic infinitesimal rotation matrix:
is the hyperbolic infinitesimal rotation matrix:
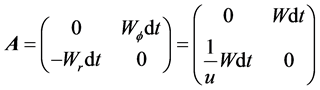 (8)
(8)
Here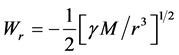 ,
, 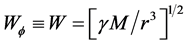 are from Equations (4). For
are from Equations (4). For ,
, 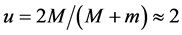
and for ,
, . This expression for
. This expression for  is obtained from conservation of energy and linear momentum and accounts for the asymmetric distribution of kinetic energy between
is obtained from conservation of energy and linear momentum and accounts for the asymmetric distribution of kinetic energy between 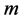 and
and 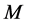 as well as for the explicit time dependence of the velocity field
as well as for the explicit time dependence of the velocity field 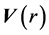 due to motions of the source
due to motions of the source  with respect to the center of mass under the field of
with respect to the center of mass under the field of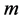 .
.
Note that the successive infinitesimal rotations by the Matrix A about the same axis are commutative. The solution of Equation (6) is a homogeneous linear transformation of velocity components analogous to that of 4-vectors in the TR. If 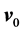 is the initial velocity, then the solution of Equation (6) is:
is the initial velocity, then the solution of Equation (6) is:
 (9)
(9)
where  is the integrated angular displacement:
is the integrated angular displacement:
 (10)
(10)
Here use has been made of . The superscripts CM define quantities taken with respect to the center of mass. An expression for
. The superscripts CM define quantities taken with respect to the center of mass. An expression for  can be found equating the total kinetic energy of the system in the CM reference to the total variation of the potential energy and using the definition of the factor
can be found equating the total kinetic energy of the system in the CM reference to the total variation of the potential energy and using the definition of the factor 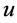 to relate coordinates and velocities of
to relate coordinates and velocities of 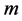 and
and .
.
Equation (9) is a linear transformation of the 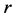 and
and 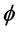 velocity components of free-falling particles on going from one local rotating inertial reference to the other. This hyperbolic rotation is completely analogous to the one of 4-vectors in the theory of relativity. However, here the parameter gauging the transformation is the characteristic local angular velocity
velocity components of free-falling particles on going from one local rotating inertial reference to the other. This hyperbolic rotation is completely analogous to the one of 4-vectors in the theory of relativity. However, here the parameter gauging the transformation is the characteristic local angular velocity 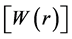 of the local IRs, defined by the Keplerian velocity field of the QS and not the relative velocity between inertial reference frames.
of the local IRs, defined by the Keplerian velocity field of the QS and not the relative velocity between inertial reference frames.
Inversion of Equation (10) leads to:
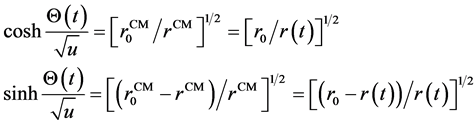 (11)
(11)
where the last equality is easily proved. With this result Equation (9) becomes:
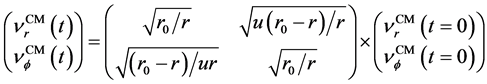 (12)
(12)
For free fall on from 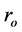 and initial rest [
and initial rest [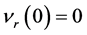 , which means
, which means ], the solution of Equation (6) is:
], the solution of Equation (6) is:
 (13a)
(13a)
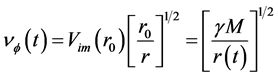 (13b)
(13b)
Equation (13a) is just the well known expression for the observed vertical free-fall on from rest at  and Equation (13b) is just the implicit (imaginary) velocity as a function of the radial position
and Equation (13b) is just the implicit (imaginary) velocity as a function of the radial position , which shows that the refraction of the radial velocity component just compensates for the increase of the velocity field as a function of the decrease of the radial coordinate. This assures that the particle falls on from rest along a perfectly vertical (radial) path and hence assures conservation of the angular momentum about the gravitational center.
, which shows that the refraction of the radial velocity component just compensates for the increase of the velocity field as a function of the decrease of the radial coordinate. This assures that the particle falls on from rest along a perfectly vertical (radial) path and hence assures conservation of the angular momentum about the gravitational center.
From the viewpoint of the ordinary space coordinates, the implicit velocity of a matter body , falling in the field of
, falling in the field of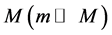 , given by (13b), is an imaginary quantity
, given by (13b), is an imaginary quantity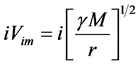 . The corresponding implicit kinetic energy
. The corresponding implicit kinetic energy 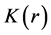 is:
is:
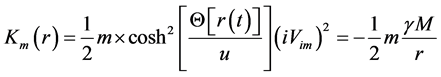 (14)
(14)
Obviously this negative quantity cannot be usual kinetic energy. It must be interpreted as the potential energy associated with the initially resting and free-falling body 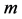 in the field of
in the field of . Potential energy in physics is an emergency concept to explain the ability of certain systems and fields to absorb, store, conserve and give back work. Here the gravitational potential energy appears as implicit kinetic energy of the resting body
. Potential energy in physics is an emergency concept to explain the ability of certain systems and fields to absorb, store, conserve and give back work. Here the gravitational potential energy appears as implicit kinetic energy of the resting body 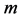 due to its imaginary velocity with respect to the moving quantum space (QS). This imaginary velocity cannot be described with respect to ordinary space coordinates. This mechanism explains why and how the gravitational field absorbs, stores and gives back the same amount of work. In reality, potential energy always involves a system of two or more interacting bodies. In the case of two gravitationally interacting bodies
due to its imaginary velocity with respect to the moving quantum space (QS). This imaginary velocity cannot be described with respect to ordinary space coordinates. This mechanism explains why and how the gravitational field absorbs, stores and gives back the same amount of work. In reality, potential energy always involves a system of two or more interacting bodies. In the case of two gravitationally interacting bodies 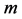 and
and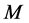 ,
,  too is free-falling in the field of
too is free-falling in the field of 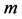 and the corresponding (implicit kinetic) potential energy is:
and the corresponding (implicit kinetic) potential energy is:
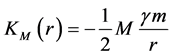 (15)
(15)
Adding Equations (14) and (15), which are identical in value, gives the total potential (implicit kinetic) energy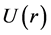 :
:
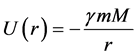 (16)
(16)
From the viewpoint of spacedynamics, that is, from the viewpoint of the local inertial references, the gravitational potential 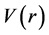 is really a centrifugal potential integrated from infinity to a given radial position
is really a centrifugal potential integrated from infinity to a given radial position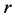 . The angular velocity of a mass
. The angular velocity of a mass , resting at
, resting at , round the overhead rotation axis of the local rotating IR within the gravitational field of a mass
, round the overhead rotation axis of the local rotating IR within the gravitational field of a mass 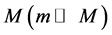 is:
is:
 (17)
(17)
Integration of the real upward centripetal force per unit mass 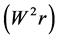 for motion from
for motion from  to
to  gives:
gives:
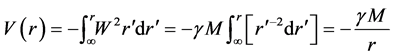 (18)
(18)
This variation of the centrifugal potential depends only on the radial coordinate and hence is a spherically symmetric scalar potential field. It essentially measures the mechanical work realized per unit mass along a uniform motion from  to
to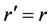 .
.
The corresponding real kinetic energy of the free-falling body is expressed in terms of the hyperbolic  function [please see Equation (9)]. Conservation of the total mechanical energy
function [please see Equation (9)]. Conservation of the total mechanical energy 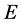 of a free-falling body
of a free-falling body 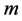 in the gravitational field of
in the gravitational field of 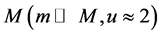 may be expressed in terms of the hyperbolic
may be expressed in terms of the hyperbolic  and
and  as:
as:
 (19)
(19)
where the  term is related with the potential energy and the
term is related with the potential energy and the  term is related with the kinetic energy as a function of time.
term is related with the kinetic energy as a function of time.
5.2. Symmetry of the Gravitational Fields with Orbital Motions
Obviously, from the viewpoint of spacedynamics, the orbital motion of the planets round the sun can certainly not be looked anymore as motion within a usual inertial reference, valid in the whole region, under a central field of gravitational forces because, within the gravitational field, each local IR is valid rigorously only within an infinitesimal region of space. However, on analyzing the motion of bodies for different orbital velocities within the velocity field of the QS Equation (1), it will be found that the spacedynamic gravitational mechanism is perfectly symmetric with direct and retrograde orbital motions and that the orbital motion of bodies round a gravitational source works identically as motions within an extended inertial reference under a central field of fictitious gravitational forces exactly as conceived in Newtonian gravity.
Consider free-fall experiments within a laboratory on the surface of a spherical planet of radius  that rotates about the
that rotates about the  axis (the axis of the velocity field of the real QS) at an angular velocity
axis (the axis of the velocity field of the real QS) at an angular velocity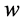 . A body within the laboratory will be moving with respect to the QS at a velocity of propagation:
. A body within the laboratory will be moving with respect to the QS at a velocity of propagation:
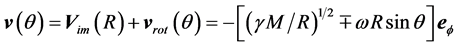 (20)
(20)
where  is the implicit velocity Equation (3) on the planet’s surface,
is the implicit velocity Equation (3) on the planet’s surface,  is the local ordinary velocity of the laboratory along the
is the local ordinary velocity of the laboratory along the  coordinate due to the planet’s rotation, which depends on the latitude via
coordinate due to the planet’s rotation, which depends on the latitude via  and the upper and lower signs are respectively for direct and retrograde rotation of the planet with respect to that of the velocity field of the QS.
and the upper and lower signs are respectively for direct and retrograde rotation of the planet with respect to that of the velocity field of the QS.
However, the orbital motion along the  coordinate also affects the direction of
coordinate also affects the direction of  with respect to the gravitational center by a usual trigonometric rotation rate. Hence, the effective angular velocity is:
with respect to the gravitational center by a usual trigonometric rotation rate. Hence, the effective angular velocity is:
 (21)
(21)
where the same convention for the upper and the lower signs as in Equation (20) is used.
Considering the effective velocity and the effective angular velocity, respectively Equations (20) and (21), the effective gravitational acceleration on the planet’s surface is:
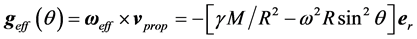 (22)
(22)
Equation (22) shows that  is perfectly symmetric for direct or retrograde rotation of the planet (orbital motion of a body). The first term in the right hand side describes acceleration toward the gravitational center [see Equation (5)], while the second term seems to describe an outward centrifugal acceleration. However, this is only the viewpoint of the local non-inertial laboratory observer. From the viewpoint of the local-IR, the first term is a centrifugal effect toward the gravitational center. The second term describes simply the decrease of this centrifugal acceleration, due to the tangential velocity of the body and the laboratory along the
is perfectly symmetric for direct or retrograde rotation of the planet (orbital motion of a body). The first term in the right hand side describes acceleration toward the gravitational center [see Equation (5)], while the second term seems to describe an outward centrifugal acceleration. However, this is only the viewpoint of the local non-inertial laboratory observer. From the viewpoint of the local-IR, the first term is a centrifugal effect toward the gravitational center. The second term describes simply the decrease of this centrifugal acceleration, due to the tangential velocity of the body and the laboratory along the  coordinate, as consequence of the planet’s rotation. This result lets clear that the spacedynamic gravitational mechanism is symmetric for direct or retrograde equatorial orbital motions, as effectively observed.
coordinate, as consequence of the planet’s rotation. This result lets clear that the spacedynamic gravitational mechanism is symmetric for direct or retrograde equatorial orbital motions, as effectively observed.
For strictly circular polar orbits of radius ,
, 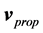 has a component
has a component 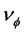 along
along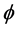 :
:
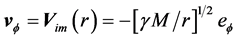 (23)
(23)
as well as a component  along
along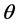 :
:
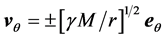 (24)
(24)
while 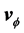 generates the gravitational acceleration field
generates the gravitational acceleration field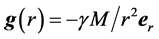 , see Equation (5), the
, see Equation (5), the 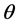 component is not affected directly by spacedynamics because the velocity field Equation (1) has no velocity gradient in the
component is not affected directly by spacedynamics because the velocity field Equation (1) has no velocity gradient in the 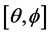 plane. Hence, the effective gravitational acceleration is:
plane. Hence, the effective gravitational acceleration is:
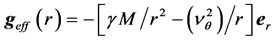 (25)
(25)
Depending on the magnitude of the 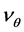 velocity component, the effect of the
velocity component, the effect of the 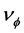 component enforces the particle into a parabolic (downward elliptic), circular or (upward) elliptic path. The curved motion along the
component enforces the particle into a parabolic (downward elliptic), circular or (upward) elliptic path. The curved motion along the 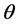 coordinate gives rise to a usual centrifugal effect. More general motions combine the effects expressed by Equations (22) and (25). Although an analytical solution of Equation (6) for such general motions is not at all simple, numerical methods may be quite effective.
coordinate gives rise to a usual centrifugal effect. More general motions combine the effects expressed by Equations (22) and (25). Although an analytical solution of Equation (6) for such general motions is not at all simple, numerical methods may be quite effective.
The results expressed by Equations (5), (13), (22) and (25) are indeed remarkable. Although the local-IR changes from point to point within the velocity field Equation (1), the spherical symmetry of the velocity field ends up by creating a central spherically symmetric field of centrifugal accelerations toward the gravitational center. In the view of the observer in the non-inertial earth-based laboratory, this inward centrifugal acceleration field seems to be a gravitational acceleration that manifests it as a gravitational pull on the objects, simulating a central field of Newtonian gravitational forces. On the other hand, the ordinary orbital motion of bodies with respect to the 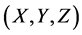 axes simulate outward centrifugal forces likewise circular motions within an extended inertial reference exactly as conceived in Newtonian mechanics. This explains why Newtonian gravitation works so well.
axes simulate outward centrifugal forces likewise circular motions within an extended inertial reference exactly as conceived in Newtonian mechanics. This explains why Newtonian gravitation works so well.
However, what is really auspicious in this spacedynamic gravitational mechanism is that within the velocity field of the real QS Equation (1), in which each local IR can be valid at only one geometrical point, ends up in such a simple solution in which the orbital motions of the planets can be described as usual motions in a well defined (extended) inertial reference under a hypothetical central force field. This shows that the effects of spacedynamics and of the ordinary motions are independent, which means that the implicit (imaginary) dynamics created by the velocity field Equation (1) and the ordinary dynamics due to the ordinary motions behave as functionally orthogonal. Effectively, while the implicit velocity Equation (3) and the implicit rotation rate of the earth based laboratories about axes overhead have no meaning from the viewpoint of the 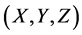 coordinate axes, the ordinary motions have no meaning from the viewpoint of the local rotating IRs, because each local-IR is valid at only one geometrical point. While a body, resting all the time at the same point within the
coordinate axes, the ordinary motions have no meaning from the viewpoint of the local rotating IRs, because each local-IR is valid at only one geometrical point. While a body, resting all the time at the same point within the  axes, is implicitly moving along a circular paths round the overhead axis of the local-IR, another body resting with respect to a given local-IR, necessarily will be orbiting and moving through numberless local-IRs, that is, moving in a circular equatorial orbit. Hence, the effects of spacedynamics and the effects of the dynamics in the ordinary space manifest them independently and functionally behave as orthogonal. If we choose to describe this gravitational dynamics from the viewpoint of the
axes, is implicitly moving along a circular paths round the overhead axis of the local-IR, another body resting with respect to a given local-IR, necessarily will be orbiting and moving through numberless local-IRs, that is, moving in a circular equatorial orbit. Hence, the effects of spacedynamics and the effects of the dynamics in the ordinary space manifest them independently and functionally behave as orthogonal. If we choose to describe this gravitational dynamics from the viewpoint of the  coordinate axes of the ordinary space, we may express the ordinary motions of bodies as purely real quantities, while the implicit velocity Equation (3) and the rotation rate of the earth based laboratories, as purely imaginary quantities as described in the end of Section 5.1.
coordinate axes of the ordinary space, we may express the ordinary motions of bodies as purely real quantities, while the implicit velocity Equation (3) and the rotation rate of the earth based laboratories, as purely imaginary quantities as described in the end of Section 5.1.
5.3. Spacedynamics Predicts the Observed Galactic Gravitational Dynamics without the Need of Dark Matter
The rotation of galaxies is known since decades to strongly discord from the predictions of the current theories of space and gravitation. Figure 3 displays the observed velocity profile of the stars in our Milky Way galaxy [20] [21] .
Instead of looking for flaws in the current theories of space and of gravitation, people have blamed experimental observations and introduced the hypothesis of an exotic, unseen (dark) non-baryonic matter that acts gravity but does not scatter, absorb or emit photons [22] [23] . Awkwardly however, there must be 5 times more dark matter than the whole of visible matter in the universe. Actually a variety of very massive exotic hypothetical particles (MACHOS, WIMPS etc.) that interact with gravity, but practically do not interact otherwise with ordinary matter are being proposed as candidates for dark matter. However, if these exotic particles act gravity, they are expected to be concentrated within the astronomical bodies likewise ordinary matter. Though in order to explain the gravitational dynamics of galaxies, their density had to remain well away from the galactic center and increase as a function of distance. In reality dark matter seems to be an emergency resort to preserve a mistaken theoretical view. Despite the enormous theoretical and experimental efforts, to present date no suitable candidate for dark matter or experimental evidence has been found.
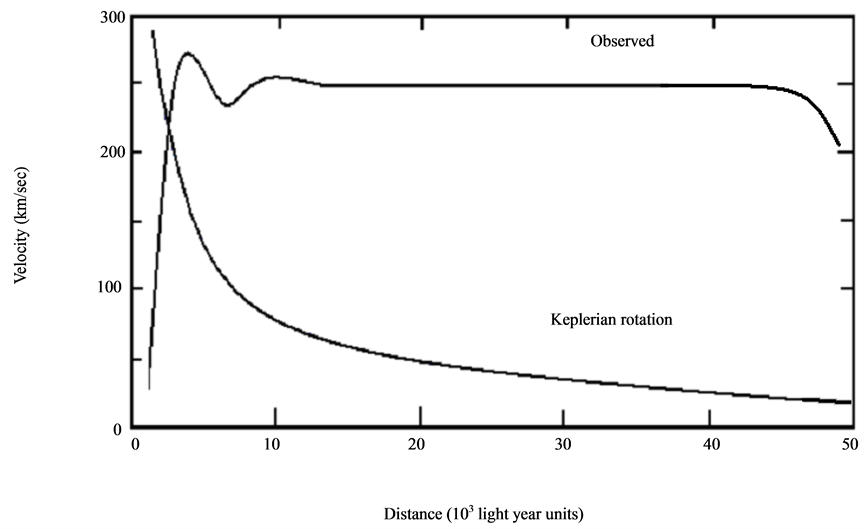
Figure 3. Profiles of the observed rotation rate of the Milky Way galaxy as a function of distance from the galactic center and the Keplerian rotation rate.
The present work, instead of mistrusting the experimental observations, blames the current theories of space and of gravitation for the impasse. According to spacedynamics, what is especially relevant in the galactic gravitational dynamics is the fact that almost the whole matter, creating the galactic velocity (gravitational) field of the QS, is moving within the galactic disk in nearly circular orbits round the galactic nucleus. Obviously each orbiting star carries with it its Keplerian velocity (gravitational) field given by Equation (1). The axes of the stellar velocity fields of the QS, likewise in the solar system, are fairly well polarized and rotate all in the same sense. This determines the form of the galactic velocity field of the QS ruling the galactic gravitational dynamics. In order to highlight the relevance of the effect of motion of the gravitational sources on the collective velocity field of the QS of a system of bodies gravitating in their self-consistent field, let us begin with the simple gravitational dynamics of a binary system of two large masses depicted in Figure 4.
The dynamics of such a system from the viewpoint of the non-rotating orthogonal XY coordinate axes is fairly well described by Newtonian mechanics. Balance of the Newtonian gravitational forces 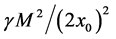 and of the centripetal forces
and of the centripetal forces 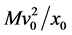 on each star, due to the orbital motion, define the orbital velocity
on each star, due to the orbital motion, define the orbital velocity 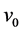 round the CM:
round the CM:
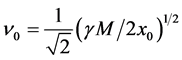 (26)
(26)
On the other hand, the velocity of a small test particle, orbiting round an equal isolated resting mass M in a circular equatorial orbit at the same distance 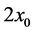 from the mass
from the mass , is considerably larger:
, is considerably larger:
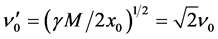 (27)
(27)
Obviously, from the viewpoint of the current gravitational theories there is nothing wrong with Equation (26) and Equation (27). However, from the viewpoint of spacedynamics, Equations (26) and (27) unveil a key feature that discloses the effect of motion of the gravitational sources on the velocity fields of the QS. This is an essential ingredient in the gravitational dynamics of a system of gravitating bodies in their collective velocity (spacedynamic gravitational) field. From the viewpoint of spacedynamics, Equation (27) describes the velocity of the QS in the Keplerian velocity field round the resting isolated mass  at the radial distance of the orbiting particle m. However, Equation (26) too is the velocity of the QS at the position of
at the radial distance of the orbiting particle m. However, Equation (26) too is the velocity of the QS at the position of  and
and  in the combined
in the combined

Figure 4. Two equal masses  =
=  = M moving in the same sense round the center of mass (CM) within the equatorial plane of the combined velocity field. Note that the velocity fields of the QS round each individual mass of the binary are symmetric from the viewpoint of the non-rotating references attached to each moving mass. However, from the viewpoint of the non-rotating [X,Y] coordinate axes with origin fixed to the CM, the velocity of the QS in the velocity fields of
= M moving in the same sense round the center of mass (CM) within the equatorial plane of the combined velocity field. Note that the velocity fields of the QS round each individual mass of the binary are symmetric from the viewpoint of the non-rotating references attached to each moving mass. However, from the viewpoint of the non-rotating [X,Y] coordinate axes with origin fixed to the CM, the velocity of the QS in the velocity fields of  and
and  are larger outside than inside the binary orbit due to the orbital motion of the sources round the CM.
are larger outside than inside the binary orbit due to the orbital motion of the sources round the CM.
velocity field of the binary system. Hence, both Equations (26) and (27) represent the velocity of the QS in the respective fields. However, why are these velocities so different The only possible reason for the reduced velocity of the QS due to 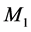 at the position of
at the position of 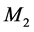 and that of
and that of  at the position of
at the position of  in the binary system is the orbital motion of respectively the sources
in the binary system is the orbital motion of respectively the sources 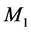 and
and  round the center of mass. The orbital velocity of the binary system reduces the velocity in the velocity field
round the center of mass. The orbital velocity of the binary system reduces the velocity in the velocity field 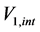 of
of 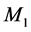 at the right-hand side of
at the right-hand side of 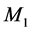 and also reduces
and also reduces 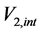 of
of 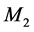 toward the left-hand side of
toward the left-hand side of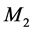 , as given by Equation (26) and as depicted in Figure 4. In the case of Equation (27) the CM of the system practically coincides with
, as given by Equation (26) and as depicted in Figure 4. In the case of Equation (27) the CM of the system practically coincides with , and therefore the velocity field of the QS is not affected at all and its velocity field is exactly given by Equation (1).
, and therefore the velocity field of the QS is not affected at all and its velocity field is exactly given by Equation (1).
Consider now in addition a small test particle moving in the collective velocity field round the binary system within the orbital plane of the binary, however sufficiently far away in order to minimize the asymmetries of the binary field. The orbital velocity 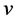 of such a test particle is of course:
of such a test particle is of course:
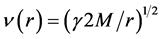 (28)
(28)
This expression for  represents the velocity of the QS in the collective velocity field
represents the velocity of the QS in the collective velocity field  round the binary system:
round the binary system:
 (29)
(29)
In order to reconcile the addition of the velocity fields of 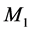 and
and 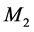 outside the binary with the collective velocity field
outside the binary with the collective velocity field 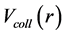 given by Equation (29), the same orbital velocity that reduces the velocity fields toward the inner side must enhance the velocity fields outward the binary. It must increase
given by Equation (29), the same orbital velocity that reduces the velocity fields toward the inner side must enhance the velocity fields outward the binary. It must increase 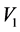 toward the left-hand side of
toward the left-hand side of 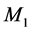 and
and 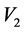 toward the right-hand side of
toward the right-hand side of 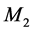 in Figure 4. At distances
in Figure 4. At distances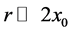 , the addition of the velocity fields of
, the addition of the velocity fields of 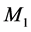 and
and 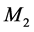 must reproduce the value given by Equation (29). Note that addition of velocity fields on the X axis obeys the sum rule:
must reproduce the value given by Equation (29). Note that addition of velocity fields on the X axis obeys the sum rule:
 (30)
(30)
This rule arises because in the expression for the velocity field Equation (1) only the square root of the source mass is effective. Accordingly, addition of the velocity fields as a function of 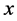 along the X axis outside of the binary in Figure 4 conforms to the equation:
along the X axis outside of the binary in Figure 4 conforms to the equation:
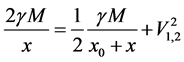 (31)
(31)
Solving for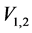 , along the
, along the  axis for large
axis for large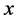 , which means large
, which means large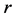 , the velocity fields of
, the velocity fields of  to the left of
to the left of  as well as of
as well as of  to the right of
to the right of 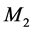 are given by:
are given by:
 (32)
(32)
This shows that effectively the same orbital velocity that reduces the velocity field of 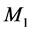 [Equation (26)] by a factor
[Equation (26)] by a factor  toward the right-hand side of
toward the right-hand side of 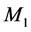 in Figure 4 and the velocity field of
in Figure 4 and the velocity field of  toward the left-hand side of
toward the left-hand side of , enhances the velocity field of
, enhances the velocity field of 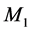 and
and 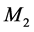 by a factor
by a factor  outside the binary. This is of course not for nothing. The reason for this is clearly the orbital motion of the sources. However, from the viewpoint of spacedynamics, the individual sources are locally resting with respect to the moving QS in the collective velocity field, thereby closely preserving the local spherical symmetry of their velocity fields.
outside the binary. This is of course not for nothing. The reason for this is clearly the orbital motion of the sources. However, from the viewpoint of spacedynamics, the individual sources are locally resting with respect to the moving QS in the collective velocity field, thereby closely preserving the local spherical symmetry of their velocity fields.
According to Equation (30), taking into account Equations (26) and (32), the collective velocity field of the QS as a function of  on the X axis outside the binary is given by:
on the X axis outside the binary is given by:
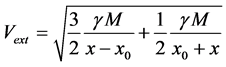 (33)
(33)
which for large , becomes more and more spherically symmetric and the value tends to meet that given by Equation (29).
, becomes more and more spherically symmetric and the value tends to meet that given by Equation (29).
In-between the orbiting bodies of the binary, the velocity fields of  and
and , are reduced by their orbital velocity and are opposite to each other and opposite to the external velocity field. Close to
, are reduced by their orbital velocity and are opposite to each other and opposite to the external velocity field. Close to  the velocity field of
the velocity field of  dominates and close to
dominates and close to 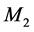 the velocity field of
the velocity field of  is dominant. The resultant collective internal velocity field as a function of
is dominant. The resultant collective internal velocity field as a function of  on the X axis is given by:
on the X axis is given by:
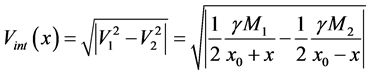 (34)
(34)
For  = 0
= 0 , while for
, while for 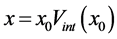 points downwards in Figure 4 and is large near
points downwards in Figure 4 and is large near , for
, for 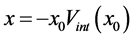 points upwards and is large near
points upwards and is large near . For other directions,
. For other directions, 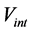 must be found by adequate vector composition, taking into account Equation (30).
must be found by adequate vector composition, taking into account Equation (30).
Note that within the binary orbit the rotation of the velocity field round the CM is opposite to the orbital motion of the binary as well as to the external velocity field. Note also that this internal velocity field is strongly reduced and that a stagnation point exists at the CM where the velocity of the QS falls to zero. The formation of such an opposite internal velocity field becomes even more evident if on the same circular orbit there are four or more equally spaced bodies of mass  orbiting in the same sense round the CM under their self-consistent velocity (gravitational) field and having their velocity fields well polarized as shown in Figure 5.
orbiting in the same sense round the CM under their self-consistent velocity (gravitational) field and having their velocity fields well polarized as shown in Figure 5.
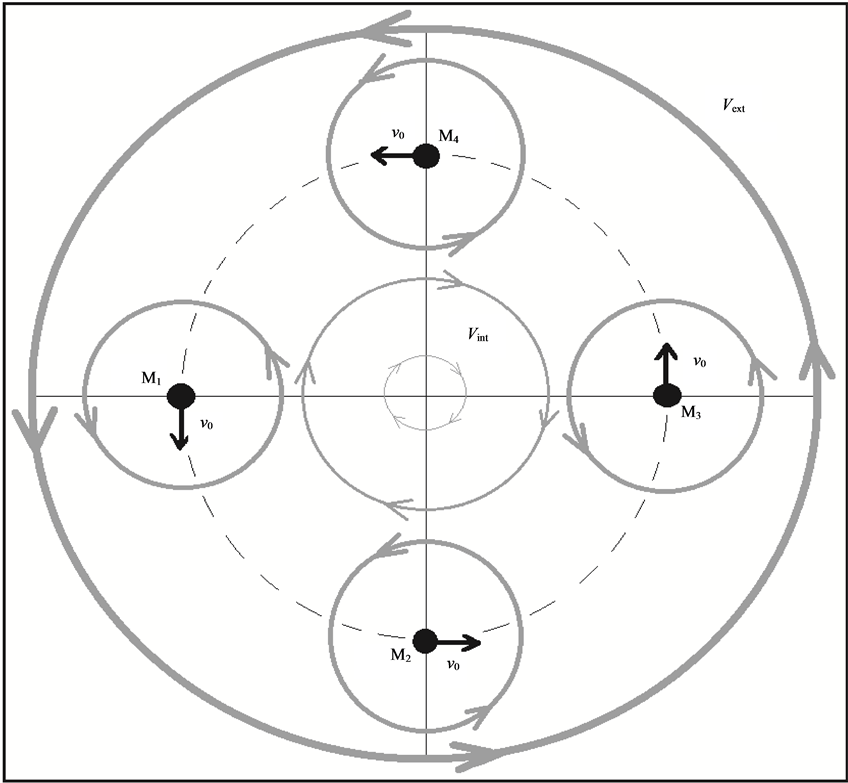
Figure 5. Sketch of the collective velocity field, generated by four equal masses moving in the same circular orbit round the center of mass. Note that the velocity 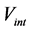 in the internal opposite velocity field is much smaller than in the external velocity field
in the internal opposite velocity field is much smaller than in the external velocity field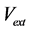 .
.
With the increase of the number of masses moving in the same sense in the same orbit, the opposite internal velocity field of the QS will remain weak but become more and more symmetric in the whole interior of the orbit, while outside the orbit the direct collective velocity field will become more symmetric and be reinforced by more and more sources. In order to advance closer toward the realistic situation in a galactic disk, consider now multiple concentric orbits with increasing radii, each one containing a very large number of stars orbiting in the same sense round the CM. Each subsequent external orbit acts in the sense of reducing the velocity field toward the inner side while enhancing the velocity field outward. If the mass density as a function of the radial distance from the galactic center is constant, the velocity of the QS necessarily increases on going outward. It hence is easy to perceive that the tangential velocity of the QS in the galactic velocity field must increase with distance from the galactic center while in the very central part a retrograde velocity field may form. In some galaxies such retrograde rotation is effectively observed. NGC 7331 is an example of a galaxy in which the bulge is rotating in the opposite sense to that of the galactic disk [24] . However, this is not an exception. Other well known examples do exist. Moderate decrease of the mass density with distance may lead to a nearly constant velocity as a function of distance from the galactic center, as observed in our Milky Way galaxy. However, beyond the border of the galactic disk the velocity field is expected to decrease according to a Keplerian rotation rate.
Although an exact model for the galactic rotation and velocity field was not accomplished here, the above analysis gives convincing evidence that spacedynamics predicts the observed galactic rotation rate without the need of dark matter and provides the basis to settle the galactic gravitational dynamics. It may be interesting to note that within the solar system the planets too are expected to induce a very weak but non-vanishing attenuation in the 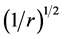 dependence of the solar Keplerian velocity (gravitational) field. Hence, the radial dependence of the velocity field becomes truly Keplerian only beyond the border of the solar system. This will say that the solar gravitational acceleration increases a little bit beyond the border of the solar system. This can explain the Pioneer anomaly, which is a very small but consistent increase in the gravitational attraction of the Pioneer 10 and Pioneer 11 spacecrafts by the sun, observed when they moved out beyond the border of the solar system [25] [26] . The local perturbation of the solar velocity field by a planet may, in principle, also cause another gravitational anomaly that is responsible for the anomalous acceleration of spacecrafts, observed during close to Earth flybys [27] .
dependence of the solar Keplerian velocity (gravitational) field. Hence, the radial dependence of the velocity field becomes truly Keplerian only beyond the border of the solar system. This will say that the solar gravitational acceleration increases a little bit beyond the border of the solar system. This can explain the Pioneer anomaly, which is a very small but consistent increase in the gravitational attraction of the Pioneer 10 and Pioneer 11 spacecrafts by the sun, observed when they moved out beyond the border of the solar system [25] [26] . The local perturbation of the solar velocity field by a planet may, in principle, also cause another gravitational anomaly that is responsible for the anomalous acceleration of spacecrafts, observed during close to Earth flybys [27] .
Within the disk of the Milky Way galaxy the stars are moving round the galactic center along nearly circular orbits. From the viewpoint of spacedynamics, these stars are commoving with the QS in the galactic velocity field of the QS. The null results of the Michelson experiments searching for light anisotropy due to the orbital and cosmic motion of Earth demonstrate that, despite the motion of the solar system at nearly  round the galactic center, its velocity with respect to the QS is closely zero. This will say that the equator of the velocity field of the QS creating the galactic velocity (gravitational) field coincides with the galactic disk and that the velocity of all stars with respect to the QS within the galactic disk is closely zero. Hence, the velocity of light is expected to be isotropic with respect to these stars and that clocks commoving with these stars may run closely at the same rate as clocks resting with respect to the QS in free space throughout the universe. Also according to spacedynamics, the stars are essentially carried around by the QS moving round the galactic nucleus, analogously as the planets are carried around the sun by the solar velocity field of the QS that creates the solar gravitational field. These orbital motions need not to be explained anymore, because it is space itself that so moves.
round the galactic center, its velocity with respect to the QS is closely zero. This will say that the equator of the velocity field of the QS creating the galactic velocity (gravitational) field coincides with the galactic disk and that the velocity of all stars with respect to the QS within the galactic disk is closely zero. Hence, the velocity of light is expected to be isotropic with respect to these stars and that clocks commoving with these stars may run closely at the same rate as clocks resting with respect to the QS in free space throughout the universe. Also according to spacedynamics, the stars are essentially carried around by the QS moving round the galactic nucleus, analogously as the planets are carried around the sun by the solar velocity field of the QS that creates the solar gravitational field. These orbital motions need not to be explained anymore, because it is space itself that so moves.
Another important parameter in the gravitational dynamics is the gravitational potential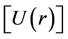 . According to the Virial Theorem, the gravitational potential has a very simple relation with the (circular) orbital velocity
. According to the Virial Theorem, the gravitational potential has a very simple relation with the (circular) orbital velocity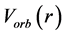 :
:
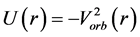 (35)
(35)
Hence, knowing the orbital velocity, the gravitational potential can be directly calculated from Equation (35) and vice-versa.
Several authors have computed the gravitational potential 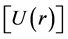 as a function of the distance from the galactic nucleus for our Milky Way galaxy as well as for other galaxies with base in the conventional theories of gravitation, taking into account the visible star density as a function of distance (see for instance reference [28] ). Systematically these gravitational potentials are all inconsistent with the observed orbital motions of the stars.
as a function of the distance from the galactic nucleus for our Milky Way galaxy as well as for other galaxies with base in the conventional theories of gravitation, taking into account the visible star density as a function of distance (see for instance reference [28] ). Systematically these gravitational potentials are all inconsistent with the observed orbital motions of the stars.
As predicted by spacedynamics, the gravitational potential determined within the galactic disk, with base in Equation (35) (please see Figure 6), is considerably more leveled than the potentials computed with base in the current gravitational theories. The velocity gradient in the galactic velocity field and hence the gravitational acceleration of a body resting within the galactic disk, predicted by spacedynamics, is very low and notwithstanding the stars move along circular orbits round the galactic center (no need of a central force field). They are carried around the galactic nucleus by the moving QS; likewise the planets are carried round the sun by the solar velocity field of the QS and need no centripetal force to move so. However, on from the galactic border, on from which the density of stars falls very fast, the velocity field of the QS falls according to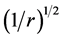 , where
, where 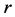 is the distance on from the galactic border (not from the galactic center). This
is the distance on from the galactic border (not from the galactic center). This  dependence of the velocity field is empirically well established, however its more fundamental reason is not clear. Beyond the galactic border, the gravitational acceleration of a resting body toward the galactic center is very large. The galactic gravitational potential is approximately a disk shaped square potential well.
dependence of the velocity field is empirically well established, however its more fundamental reason is not clear. Beyond the galactic border, the gravitational acceleration of a resting body toward the galactic center is very large. The galactic gravitational potential is approximately a disk shaped square potential well.
Although an exact determination of the galactic velocity field with base in the spacedynamic gravitational mechanism has not been worked out, the above analysis gives convincing evidence that spacedynamics predicts qualitatively and correctly even with details the observed galactic gravitational dynamics without the need of dark matter. Even the possibility of the unbelievable retrograde rotation of the inner part of galaxies, observed in many galaxies, is a natural outcome of spacedynamics. Section 6 describes the antigravitational mechanism causing expansion of the universe.
6. Dominant Anti-Gravitation between Galaxies, the Nature of Dark Energy
To now the accelerated expansion of the universe [29] [30] has no physical explanation. Usually it is imputed to a new kind of positive potential energy, simply named dark energy. The explanation of the accelerated expansion of the universe in terms of the cosmological term in Einstein’s equation for the spacetime curvature is not a physical explanation, but only a mathematical account.
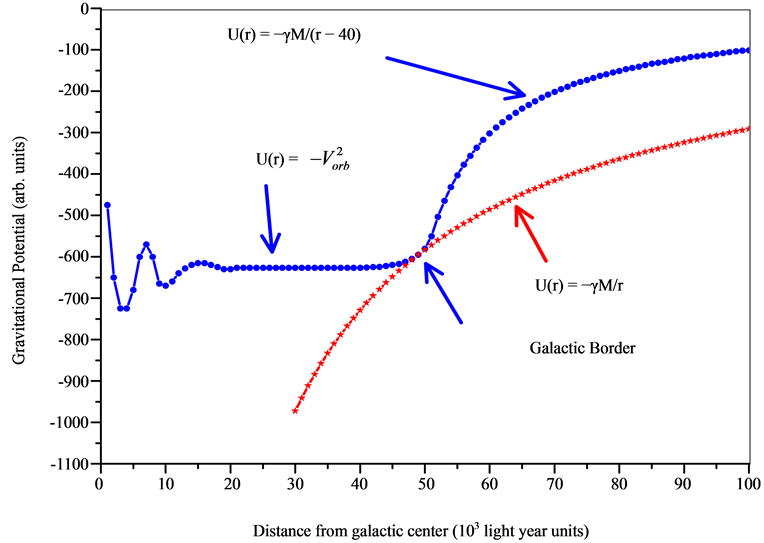
Figure 6. The figure depicts the usual gravitational potential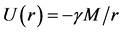 , calculated using as reference the value of
, calculated using as reference the value of  at the galactic border, where
at the galactic border, where 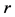 is the distance from the galactic center as well as the gravitational potential within the galactic disk, calculated using Equation (35) and assuming that beyond the galactic border it follows the
is the distance from the galactic center as well as the gravitational potential within the galactic disk, calculated using Equation (35) and assuming that beyond the galactic border it follows the 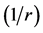 dependence, where however
dependence, where however 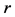 is the distance on from the galactic border.
is the distance on from the galactic border.
In spacedynamics the accelerating expansion of the universe is to be understood in terms of a dominant antigravitational interaction. In order to realize the meaning here of antigravitation, consider two well separated astronomical bodies of equal masses and the velocity fields of the QS, creating their gravitational fields, spinning round parallel axes. The crucial question to be answered is: What will happen if the two bodies approximate each-other? The view of the present work is that, in case the velocity fields are spinning in the same sense, they will add up according to Equation (30) reinforcing the total velocity (gravitational) field and the negative gravitational potential. However, in case the velocity fields are spinning in opposite senses, on approximating each other, their velocity fields will add up to zero, not reinforcing the negative gravitational potential and even gradually canceling their individual negative gravitational potentials. While the behavior in the first case fits well into the current gravitational theories, the second case is a novelty predicted by spacedynamics. Due to conservation of energy, while in the first case kinetic energy can be created by letting the two bodies approximate each-other, because this increases the negative gravitational potential energy of the system, in the second case kinetic energy can be created by letting the bodies move away from each-other because this too increases the negative gravitational potential energy of the system. While in the first case the bodies interact attractively, in the second case they repel each other, they antigravitate. Attraction between vortices rotating in the same sense and repulsion between oppositely rotating vortices in superfluids is a well known fact.
Within the solar system the rotation axes of the velocity fields of the sun, the planets and the satellites are fairly well aligned, their velocity fields spinning in the same sense as can be verified from the motions of the satellites round the planets and of the planets round the Sun. The only anomalous case is with the satellites of Uranus, which however may be due because they are captured satellites. An analogous polarization seems to be well present within each galaxy. Within these systems only attractive gravitational interaction is present. Nevertheless, the observed direction of the rotation axes of the different galaxies throughout the universe is almost random, which means that the probability of each galaxy to have oppositely rotating first nearest neighbor galaxies is considerably larger than to have galaxies rotating in the same sense. Due to the 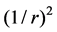 dependence of the gravitational interaction, the overall repulsion (antigravitation) between galaxies and galactic clusters is expected to be dominant. This will say that from a large scale point of view the overall gravitational potential energy has a positive value, which is what is called dark energy. This gravitational potential energy, due to dominant anti-gravitation between galaxies involves no new additional mass; it is simply an interaction term that has not been considered in the current theories.
dependence of the gravitational interaction, the overall repulsion (antigravitation) between galaxies and galactic clusters is expected to be dominant. This will say that from a large scale point of view the overall gravitational potential energy has a positive value, which is what is called dark energy. This gravitational potential energy, due to dominant anti-gravitation between galaxies involves no new additional mass; it is simply an interaction term that has not been considered in the current theories.
In the following Section 7 the effects of motions of a laboratory with respect to the QS or motion of the QS through a laboratory resting within the Keplerian velocity field generating the gravitational field are discussed.
7. The Effects of Motion of the Laboratory with Respect to the QS on the Propagation of Light and on the Rate of Clocks
Many of the troubles, actually afflicting fundamental physics, were seeded by the wrong interpretation of the Michelson light anisotropy experiments. In the view of spacedynamics, the one way velocity of light has a well defined value 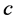 with respect to the moving QS, analogously as sound waves have a well defined velocity with respect to homogeneous, isobaric and moving atmosphere. Hence, if the laboratory moves with respect to the QS, or the QS moves through the laboratory with velocity v, the one way velocity of light with respect to this laboratory is:
with respect to the moving QS, analogously as sound waves have a well defined velocity with respect to homogeneous, isobaric and moving atmosphere. Hence, if the laboratory moves with respect to the QS, or the QS moves through the laboratory with velocity v, the one way velocity of light with respect to this laboratory is:
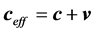 (36)
(36)
Due to this effective velocity, an EM signal in a laboratory, moving with respect to the QS , takes a longer time  to complete a go-return roundtrip between two fixed points than
to complete a go-return roundtrip between two fixed points than  in a laboratory, resting with respect to the QS:
in a laboratory, resting with respect to the QS:
 (37)
(37)
In this equation 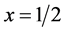 for transverse go-return roundtrips and
for transverse go-return roundtrips and 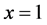 for longitudinal go-return roundtrips (all intermediate values are possible). This light roundtrip is anisotropic as shown by the light anisotropy experiments described in Section 2.1. The oscillation periods of the best time standards, by which atomic clocks count time, are the period of electromagnetic (EM) oscillations of molecules or atoms. These oscillations too are go-return roundtrips of an EM signal along a certain distance. In principle the oscillation period of these oscillators is affected by the motion of the laboratory with respect to the QS in the same proportion as the light roundtrips and hence the EM oscillation period
for longitudinal go-return roundtrips (all intermediate values are possible). This light roundtrip is anisotropic as shown by the light anisotropy experiments described in Section 2.1. The oscillation periods of the best time standards, by which atomic clocks count time, are the period of electromagnetic (EM) oscillations of molecules or atoms. These oscillations too are go-return roundtrips of an EM signal along a certain distance. In principle the oscillation period of these oscillators is affected by the motion of the laboratory with respect to the QS in the same proportion as the light roundtrips and hence the EM oscillation period  in the moving laboratory too is described by Equation (37). Certainly atomic and molecular orbitals may respond to the effects of the motion of the laboratory as evidenced by speeding Hydrogen atoms [9] . However, the energy of a given atomic orbital should not be anisotropic. To first approximation the correction to the light roundtrip time
in the moving laboratory too is described by Equation (37). Certainly atomic and molecular orbitals may respond to the effects of the motion of the laboratory as evidenced by speeding Hydrogen atoms [9] . However, the energy of a given atomic orbital should not be anisotropic. To first approximation the correction to the light roundtrip time  is given by:
is given by:
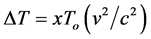 (38)
(38)
Therefore, measurements of the light velocity and or of distances by the method of light go-return roundtrip and clocks are constrained to give always the same result, regardless the velocity of the laboratory with respect to the QS.
In a laboratory within a gravitational field fixed with respect to the corresponding [X,Y,Z] axes, the QS is moving through the laboratory according to a velocity given by the Keplerian velocity field Equation (1). Hence, the fixed laboratory will be moving with respect to QS at the implicit velocity , where
, where 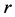 is the distance of the laboratory from the gravitational source. This velocity is implicit because it is not velocity of the laboratory with respect to a usual reference, but of QS with respect to the resting laboratory. In this case, the velocity of a light signal within the fixed laboratory will be given by:
is the distance of the laboratory from the gravitational source. This velocity is implicit because it is not velocity of the laboratory with respect to a usual reference, but of QS with respect to the resting laboratory. In this case, the velocity of a light signal within the fixed laboratory will be given by:
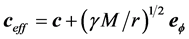 (39)
(39)
Hence, Equation (37) becomes
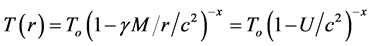 (40)
(40)
where the value of 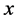 may be set to 1, which minimizes the energy of the atomic level, so that the light roundtrip takes
may be set to 1, which minimizes the energy of the atomic level, so that the light roundtrip takes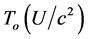 , the same predicted by GR.
, the same predicted by GR.
Due to the effective velocity of light [Equation (39] within the gravitational field, an external observer measuring distances within the gravitational field by the method of light go-return roundtrips using his local (external) clock, without taking into account the effective velocity of light given by Equation (39), will obtain the non-Euclidean metric underlying Einstein’s space time curvature (please see prove in Section 8.3). The nonEuclidean metric and the space time curvature arise because of the mistaken assumption that the velocity of light is intrinsically isotropic and constant.
The following Section 8 shows that the Keplerian velocity field, creating the a gravitational field, correctly accounts in terms of simple and genuine physical effects for all the observed effects, caused by the gravitational fields, on the propagation of light and on the rate of clocks.
8. To Conclude This Article Let Us Show That Spacedynamics Systematically Reproduces the Experimental Observations
8.1. Michelson Light Anisotropy Experiments
The large majority of the Michelson experiments searched for light anisotropy due to the orbital and cosmic motion of earth. They all found closely null results as now predicted by spacedynamics. In the view of spacedynamics, the only motion, that causes genuine anisotropy of light within the earth based laboratories, is the velocity field of the QS round the earth in the sense of the Moon’s orbital motion and creating the earth’s gravitational field. This velocity field reaches 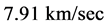 on surface and is constant the whole day and the whole year. The anisotropy experiments, searching for light anisotropy with respect to the earth based laboratories [10] , found very closely the anisotropy predicted by spacedynamics [please see Figure 1 in Section 2.1].
on surface and is constant the whole day and the whole year. The anisotropy experiments, searching for light anisotropy with respect to the earth based laboratories [10] , found very closely the anisotropy predicted by spacedynamics [please see Figure 1 in Section 2.1].
8.2. Gravitational Time Dilation and Gravitational Spectral Red Shifts
Gravitational time dilation and spectral red shifts are now well confirmed experimentally [31] -[33] . According to spacedynamics, the increase of the periods of the time standards, due to motion with respect to the QS, and the consequent decrease of the frequency of classical and quantum mechanical oscillators (molecules, atoms, nuclei etc.) arise because the matter waves (wavefunctions) need a longer time to complete an oscillation period within a laboratory moving with respect to the QS [Equation (37)] or the QS moving through a fixed laboratory within a gravitational field [Equation (40)]. The nuclear, atomic and molecular states certainly adjust them to these same time dilation effects.
8.3. Excess Time Delay of Radar Signals within the Solar System
Considering the effective velocity Equation (39) the excess time delay for the roundtrip of radar signals within the solar system, from earth to Venus and back to earth along straight lines [see Figure 7] has been precisely calculated here.
The excess time delays in Table 1 were numerically calculated using Equation (39), dividing the straight line paths for each 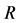 in a large number of segments (shorter segments close to the sun), calculating the time-delay and time-gain, due to the transverse and to the longitudinal components of the solar Keplerian velocity field along the signal paths and finally adding up the contributions along the whole path. The large majority of the time-delay or time-gain comes from the longitudinal component. In the calculation, the different Earth-Venus distances, due to their orbital positions as well as the different signal path due to the motion of earth during a given roundtrip, was considered. The results for the different
in a large number of segments (shorter segments close to the sun), calculating the time-delay and time-gain, due to the transverse and to the longitudinal components of the solar Keplerian velocity field along the signal paths and finally adding up the contributions along the whole path. The large majority of the time-delay or time-gain comes from the longitudinal component. In the calculation, the different Earth-Venus distances, due to their orbital positions as well as the different signal path due to the motion of earth during a given roundtrip, was considered. The results for the different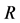 , listed in Table 1 in
, listed in Table 1 in 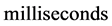 and plotted in Figure 8, show that although the excess travel times for the Earth-Venus and the Venus-Earth journeys is considerably asymmetric, the effective excess time delay for a full roundtrip (column 4 in Table 1), in
and plotted in Figure 8, show that although the excess travel times for the Earth-Venus and the Venus-Earth journeys is considerably asymmetric, the effective excess time delay for a full roundtrip (column 4 in Table 1), in 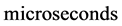 and displayed in Figure 9, practically coincide with the excess time delays measured by Shapiro, [34] displayed in Figure 10. In spacedynamics, this effective excess time delay is a genuine physical effect, due to the effective signal velocity Equation (39) within the solar velocity field Equation (1) and not to the increase of the geometrical distance due to the spacetime curvature, as asserted in GR.
and displayed in Figure 9, practically coincide with the excess time delays measured by Shapiro, [34] displayed in Figure 10. In spacedynamics, this effective excess time delay is a genuine physical effect, due to the effective signal velocity Equation (39) within the solar velocity field Equation (1) and not to the increase of the geometrical distance due to the spacetime curvature, as asserted in GR.
Other even more precise measurements of the excess time delay (Shapiro Effect) of signals passing by the sun have been made with the help of Mars landed transponders during the Mariner 6 and Mariner 7 missions as well as other spacecrafts (Cassini). However, in all of these experiments what was measured is the effective excess time delay for complete go-return signal roundtrips and hence could not detect anisotropies. The fact that spacedynamics predicts correctly the effective excess time delay (Shapiro effect) confirms that the velocity field Equation (1) simulates correctly Einstein’s space-time curvature.
8.4. The Gravitational Light Lensing Effect
A light beam propagating directly toward the sun, practically has a velocity component only along r in the solar
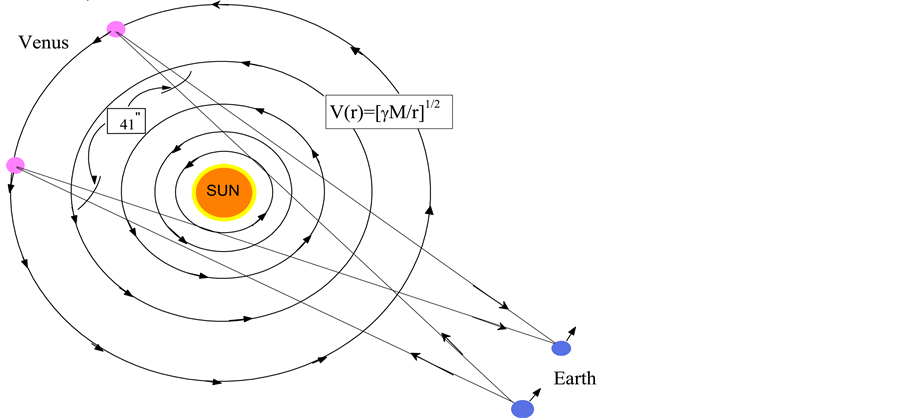
Figure 7. The path of radar signals from earth to Venus and back to earth (impact parameter R) within the velocity field of the sun, before and after superior conjunction.
Table 1. The Excess time-delays for individual go (column 2) and return (column 3) journeys and the effective excess time-delays (last column) for full go-return roundtrips of radar signals between earth and Venus for impact parameters R = 0, 2, 4, 8, 25, 50 and 100 million km from the center of the sun, before and after superior conjunction.

Figure 8. The calculated excess time delay  and the time gain
and the time gain  in
in  for one-way journeys of radar signals before and after superior conjunction in Table 1.
for one-way journeys of radar signals before and after superior conjunction in Table 1.

Figure 9. The effective time delay for a complete go-return travel as calculated from spacedynamics in , fourth column in Table 1.
, fourth column in Table 1.
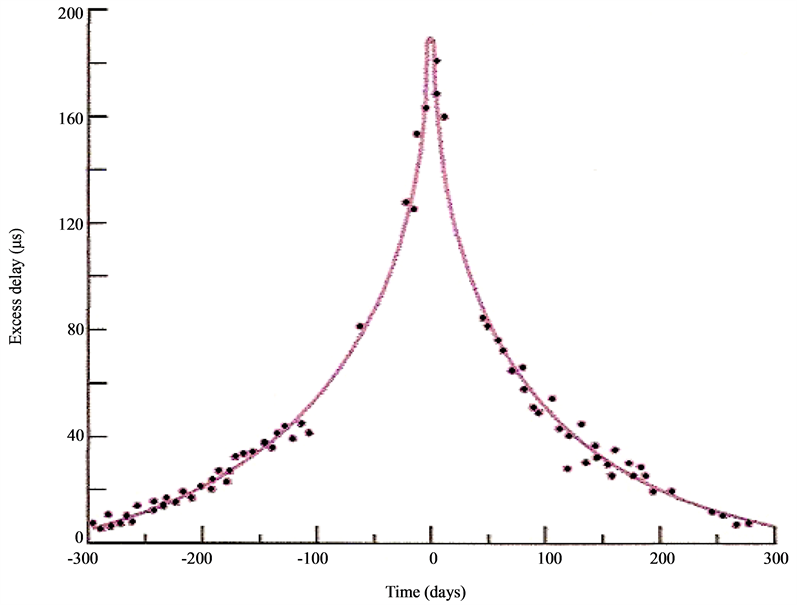
Figure 10. The effective time delay for a complete go-return travel as measured by Shapiro [34] . The value of 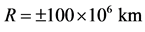 in Figure 9 corresponds to about
in Figure 9 corresponds to about 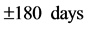 in Figure 10.
in Figure 10.
non-rotating reference. This component is refracted according to Equation (4a). Thereby it gains a velocity component along 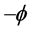 and reduces its radial velocity component to
and reduces its radial velocity component to  where
where 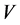 is the velocity of the QS along
is the velocity of the QS along  given by [Equation (1)]. GR attributes this reduction of the radial velocity to stretching of the radial distances due to the space-time curvature.
given by [Equation (1)]. GR attributes this reduction of the radial velocity to stretching of the radial distances due to the space-time curvature.
Consider two light beams, propagating toward the sun along initially parallel paths by equidistant and opposite sides of the sun, see Figure 11. First the wave vectors will be refracted according to Equation (4a) by a total

Figure 11. Gravitational light-lensing effect, by a heavy mass. The light-lensing results from the excessive deflection 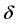 at the retrograde side and the insufficient deflection
at the retrograde side and the insufficient deflection 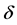 at the prograde side.
at the prograde side.
angle . Near to the sun, where the solar velocity field achieves 436 km/sec, refraction by Equation (4b) dominates and the wave vector is refracted oppositely by a total angle
. Near to the sun, where the solar velocity field achieves 436 km/sec, refraction by Equation (4b) dominates and the wave vector is refracted oppositely by a total angle . Finally, after passing by the sun and going away at the opposite side, the wave vectors are refracted back according to Equation (4a) by an angle
. Finally, after passing by the sun and going away at the opposite side, the wave vectors are refracted back according to Equation (4a) by an angle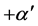 . However, near the sun, the solar velocity field is favorable to the prograde ray so that it spends less time (Table 1) near the sun and hence is deflected by a smaller angle
. However, near the sun, the solar velocity field is favorable to the prograde ray so that it spends less time (Table 1) near the sun and hence is deflected by a smaller angle . To the retrograde ray the solar velocity field is unfavorable and hence it spends a longer time near the sun and refracts by a larger angle
. To the retrograde ray the solar velocity field is unfavorable and hence it spends a longer time near the sun and refracts by a larger angle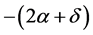 . This differentiated refraction
. This differentiated refraction 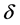 by Equation (4b) causes the convergence of the rays that is responsible for the gravitational light lensing effect.
by Equation (4b) causes the convergence of the rays that is responsible for the gravitational light lensing effect.
The effective deflection of light by the solar gravitational field can be calculated simply by multiplying the refraction rate Equation (4b) times the excess (or shortage) of time delays listed in Table 1 (Section 8.3). On the solar surface 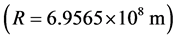 the refraction rate is
the refraction rate is 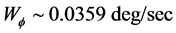 and, interpolating the value of
and, interpolating the value of  in Table 1 for light passing by the surface of the sun, the total excess time delay at the retrograde side, or shortage at the prograde side, gives about 13.5 ms. The product
in Table 1 for light passing by the surface of the sun, the total excess time delay at the retrograde side, or shortage at the prograde side, gives about 13.5 ms. The product 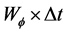 gives
gives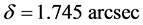 , which is very closely the observed value.
, which is very closely the observed value.
8.5. The Perihelion Precession
An analogous differentiated refraction rate of the propagation velocity 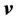 with respect to the QS of an orbiting body as in the preceding Section 8.4 must be responsible for the perihelion precession of elliptical orbits. At the aphelion the direction of the body’s velocity
with respect to the QS of an orbiting body as in the preceding Section 8.4 must be responsible for the perihelion precession of elliptical orbits. At the aphelion the direction of the body’s velocity 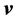 with respect to the QS is opposite to the velocity field (retrograde) as well as to the orbital motion. This increases the time of permanence in this region of the orbit and hence refracts during a longer time. At the perihelion
with respect to the QS is opposite to the velocity field (retrograde) as well as to the orbital motion. This increases the time of permanence in this region of the orbit and hence refracts during a longer time. At the perihelion 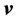 is parallel to the velocity field (prograde), which displaces it more rapidly in the orbit, so that it has not enough time to recover the tangential direction. It recovers it only somewhat beyond the ideal perihelion point. In this way the perihelion is displaced a little bit in the prograde sense in each orbital roundtrip.
is parallel to the velocity field (prograde), which displaces it more rapidly in the orbit, so that it has not enough time to recover the tangential direction. It recovers it only somewhat beyond the ideal perihelion point. In this way the perihelion is displaced a little bit in the prograde sense in each orbital roundtrip.
8.6. Anomalous Red/Blue Shifts
The so called anomalous red/blue spectral shifts of radiation of non-Doppler origin are especially clear-cut in binary stars and binary galaxies. The frequency shifts achieve values several orders of magnitude larger than can be explained by GR. [35] From the viewpoint of spacedynamics, these frequency shifts are caused by the variable excess time delay  of the radiation by interposition and motion of the velocity fields of the QS due to very massive bodies. These shifts are essentially proportional to
of the radiation by interposition and motion of the velocity fields of the QS due to very massive bodies. These shifts are essentially proportional to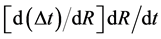 , where
, where 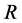 is the impact parameter of the radiation passing by the companion star or galaxy or by any other strong gravitational source. If the velocity
is the impact parameter of the radiation passing by the companion star or galaxy or by any other strong gravitational source. If the velocity 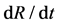 is zero, the effect vanishes as it must. Such an anomalous frequency shift also was observed when Pioneer 6, (operating at 2295 MHz) passed by the opposite side of the sun (from right to left in Figure 8) during superior conjunction [35] [36] . Spacedynamics predicts a blue shift of about (
is zero, the effect vanishes as it must. Such an anomalous frequency shift also was observed when Pioneer 6, (operating at 2295 MHz) passed by the opposite side of the sun (from right to left in Figure 8) during superior conjunction [35] [36] . Spacedynamics predicts a blue shift of about ( ), approximately the value observed.
), approximately the value observed.
8.7. Absence of Effects of the Solar Gravitational Potential on the GPS Clocks
The rate of clocks moving with respect to QS is ruled by Equations (37) and (40). The velocity of clocks, moving in direct circular equatorial orbits, with respect to the QS is:
 (41)
(41)
Such clocks rest with respect to the QS and may show no gravitational time dilation as indeed observed for the GPS clocks moving with earth round the sun. All clocks orbiting in circular equatorial orbits round an astronomical body, which normally orbits itself round a larger body and so forth, are naturally synchronous and all show closely the same proper time throughout the universe.
8.8. Effects of the Velocity Field of the QS Equation (1) on Moving Clocks
Clocks moving along polar orbits have, besides the implicit velocity 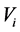 along
along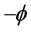 , the velocity along the polar orbit. Hence, their total velocity
, the velocity along the polar orbit. Hence, their total velocity  with respect to the QS is
with respect to the QS is 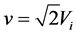 and the total time dilation is two times larger than that of identical clocks resting at the same altitude. Moreover, the velocity
and the total time dilation is two times larger than that of identical clocks resting at the same altitude. Moreover, the velocity 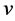 with respect to the QS of clocks in retrograde circular equatorial orbits is
with respect to the QS of clocks in retrograde circular equatorial orbits is  and their time dilation is four times larger than that of identical clocks resting in the gravitational field at the same altitude. In particular, the GPS satellites move at
and their time dilation is four times larger than that of identical clocks resting in the gravitational field at the same altitude. In particular, the GPS satellites move at  of altitude, along circular orbits inclined 55 degrees with respect to the earth’s equator and hence their clocks have velocity components with respect to real QS
of altitude, along circular orbits inclined 55 degrees with respect to the earth’s equator and hence their clocks have velocity components with respect to real QS  along
along 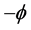 and
and 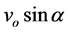 along
along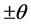 , where
, where 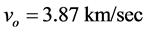 and
and 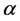 is the angle of their orbital velocity
is the angle of their orbital velocity  with respect to the equator or parallels. The effective velocity is
with respect to the equator or parallels. The effective velocity is 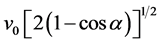 and the estimated average velocity of the GPS satellites over the entire orbit is
and the estimated average velocity of the GPS satellites over the entire orbit is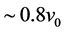 . Considering in addition the velocity of
. Considering in addition the velocity of 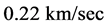 of the
of the  atoms in the atomic clocks, this makes
atoms in the atomic clocks, this makes . Analogously, for the earth based stations we find
. Analogously, for the earth based stations we find . Using these results, we find that the rate of the GPS clocks must be slowed by
. Using these results, we find that the rate of the GPS clocks must be slowed by 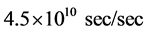 before launch in order to the GPS clocks to run synchronous with identical clocks resting on ground. This is closely the value by which NASA slows the rate of the GPS clocks before launch.
before launch in order to the GPS clocks to run synchronous with identical clocks resting on ground. This is closely the value by which NASA slows the rate of the GPS clocks before launch.
8.9. The Non-Synchronous Arrival of the Pulsar Signals to Equidistant Earth-Based Antennas along the Earths Orbital Motion
From the viewpoint of spacedynamics, the velocity vector of signals coming from a distant pulsar toward the sun are refracted toward  according to Equation 4a by a total angle
according to Equation 4a by a total angle 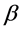 and the wave fronts are slanted so that
and the wave fronts are slanted so that 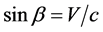 and the radial velocity is
and the radial velocity is . This is equal to the usual aberration angle of star light, please see Figure 12.
. This is equal to the usual aberration angle of star light, please see Figure 12.
In GR the lowered velocity of light along the radial coordinate is imputed to stretching of the radial coordinate due to spacetime curvature. In spacedynamics the radial velocity of light is lower because it necessarily develops an increasing orthogonal component along . According to spacedynamics, the non-synchronous arrival of the signal to the different earth based observatories along the orbital motion of earth, (please see Figure 13), is real and shows that synchronization of the clocks in the distant observatories with the help of the GPS is correct. The fact that the observed arrival of the pulsar signal [6] [7] is out of synchrony up to
. According to spacedynamics, the non-synchronous arrival of the signal to the different earth based observatories along the orbital motion of earth, (please see Figure 13), is real and shows that synchronization of the clocks in the distant observatories with the help of the GPS is correct. The fact that the observed arrival of the pulsar signal [6] [7] is out of synchrony up to 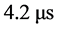 along the earth’s orbital motion and is synchronous along the direction transverse to the orbital motion exactly as dictated by Euations (4) is a spectacular confirmation of the predictions of spacedynamics.
along the earth’s orbital motion and is synchronous along the direction transverse to the orbital motion exactly as dictated by Euations (4) is a spectacular confirmation of the predictions of spacedynamics.
8.10. The Astronomical Motions Closely Track the Motion of the QS Throughout the Universe
The nearly circular planetary orbits are squeezed into the disk shaped solar system. Analogously the stellar orbits are squeezed into the galactic disk. Why? From the spacedynamics viewpoint all these bodies minimize their velocity with respect to the QS. This reduction of velocities may have taken place during the expansion of the universe that stretched the wavelengths  of the particles analogously as it stretched that of the photons, as is well known from the cosmic background microwave radiation. Stretching and shrinking of the wavelengths affects the velocity of particles with respect to the QS according to de Broglie’s equation
of the particles analogously as it stretched that of the photons, as is well known from the cosmic background microwave radiation. Stretching and shrinking of the wavelengths affects the velocity of particles with respect to the QS according to de Broglie’s equation . The light anisotropy experiments corroborate the viewpoint of spacedynamics.
. The light anisotropy experiments corroborate the viewpoint of spacedynamics.
8.11. The Conventional Relativistic Effects Can Easily Be Reinterpreted as Effects Due to Motion with Respect to the QS
If earth rests with respect to the QS, as demonstrated by so many experimental facts, then the very high velocities of elementary particles and or atoms within earth-based laboratories are almost equally high velocities with respect to the local QS. In the view of spacedynamics, the solar and galactic velocity fields are not effective within the earth-based laboratories because earth is commoving with the QS in the velocity fields generating their respective gravitational fields. The velocity field of the QS through the earth based laboratories is only the one creating the local gravitational field of earth itself. On the rotating earth this velocity varies from 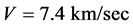 at the equator to
at the equator to 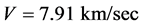 near to the poles. This is a rather low velocity compared with that in all the conventional relativistic experiments. To first approximation the effect of this velocity is proportional to
near to the poles. This is a rather low velocity compared with that in all the conventional relativistic experiments. To first approximation the effect of this velocity is proportional to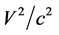 , which is in the order of
, which is in the order of , much too low to be detected by the conventional relativistic experiments. Therefore these so called relativistic effects can all easily be reinterpreted as effects due to the velocity with respect to the QS.
, much too low to be detected by the conventional relativistic experiments. Therefore these so called relativistic effects can all easily be reinterpreted as effects due to the velocity with respect to the QS.
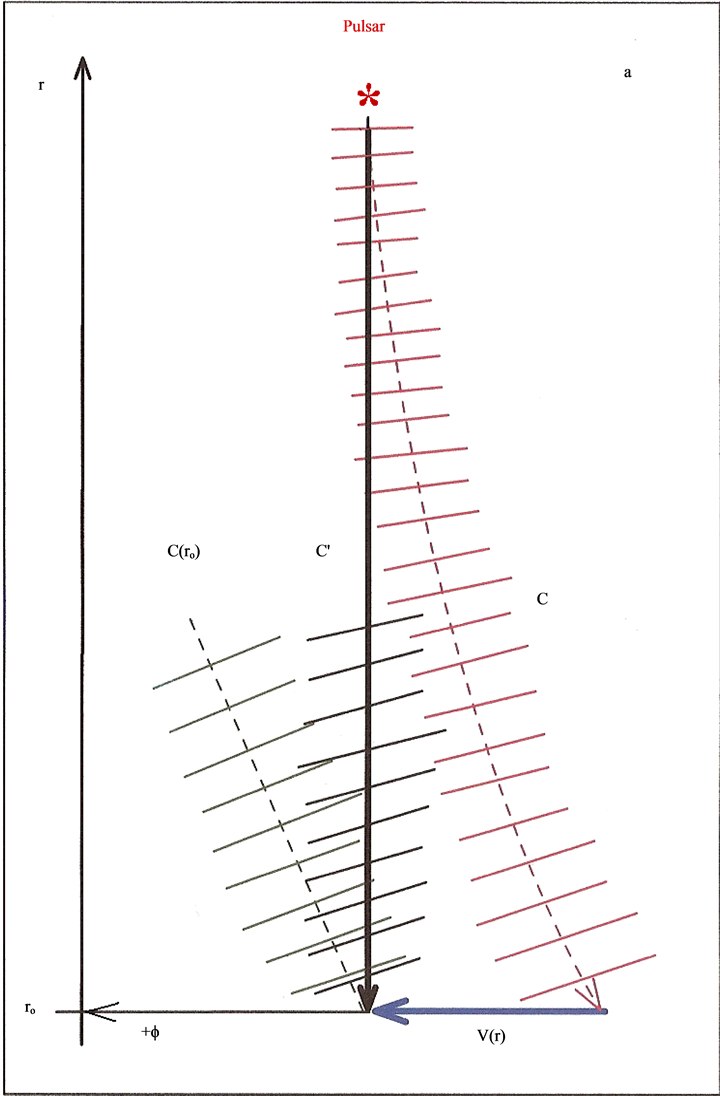
Figure 12. An  signal from distant pulsar propagating into the solar velocity field directly toward the sun. The signal under the refraction rate, given by Equation (4a), would go along the path
signal from distant pulsar propagating into the solar velocity field directly toward the sun. The signal under the refraction rate, given by Equation (4a), would go along the path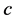 . However, drag by the solar velocity field forces the signal back to the radial path
. However, drag by the solar velocity field forces the signal back to the radial path , without changing the slope of the wave fronts. In optical (midnight) observations from earth, the telescope must point along
, without changing the slope of the wave fronts. In optical (midnight) observations from earth, the telescope must point along 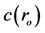 along which the wave fronts of light are perpendicular to the signal path and the velocity with respect to the telescope is exactly the usual velocity of light
along which the wave fronts of light are perpendicular to the signal path and the velocity with respect to the telescope is exactly the usual velocity of light . This is the well known aberration of stars. In the figure, the effects are largely exaggerated to make them visible.
. This is the well known aberration of stars. In the figure, the effects are largely exaggerated to make them visible.
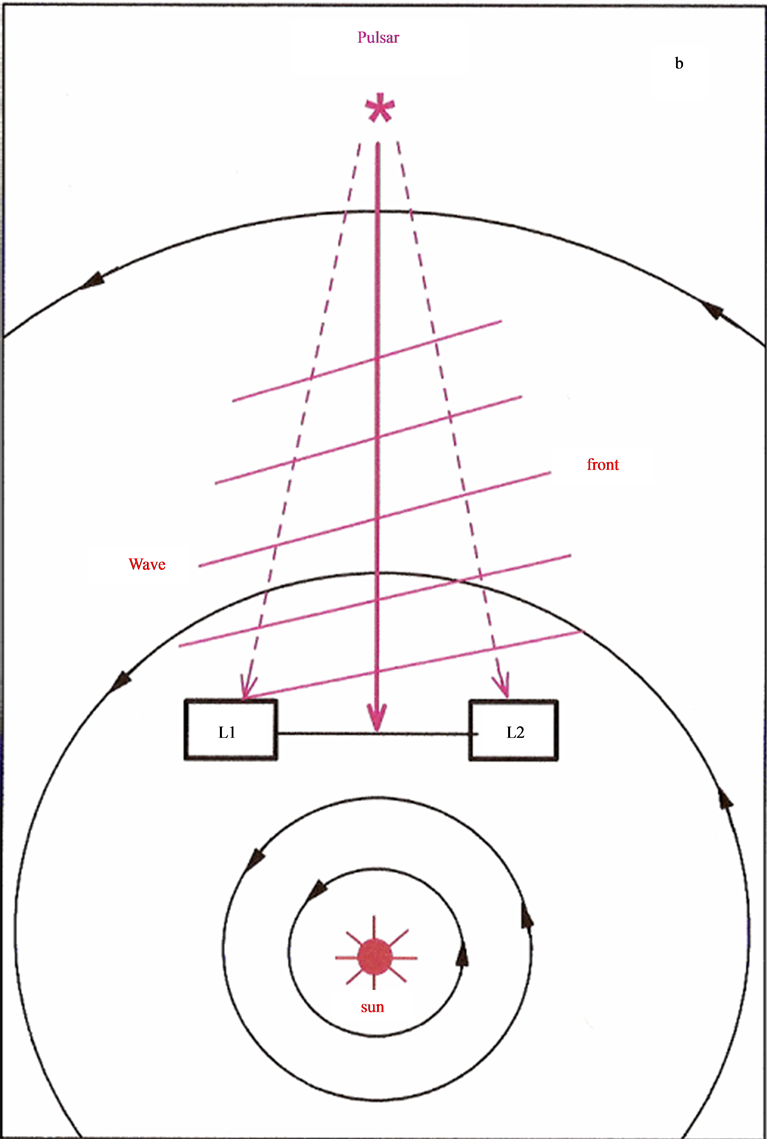
Figure 13. The wave fronts of an 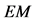 signal coming from a distant pulsar toward the sun along
signal coming from a distant pulsar toward the sun along  are slanted due to the refraction by the solar velocity field Equation (4a) as also shown in Figure 12). The signals are detected in two antennas separated by the earth’s diameter, fixed in the solar gravitational field at the earth’s orbit and equidistant from the pulsar. The wave front reaches first the antenna
are slanted due to the refraction by the solar velocity field Equation (4a) as also shown in Figure 12). The signals are detected in two antennas separated by the earth’s diameter, fixed in the solar gravitational field at the earth’s orbit and equidistant from the pulsar. The wave front reaches first the antenna 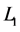 and only
and only 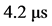 later
later 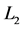 because the wave fronts are slanted according to Equation (4a). Motion of the antennas along the
because the wave fronts are slanted according to Equation (4a). Motion of the antennas along the  direction does not change the situation. All effects are largely exaggerated in the figure to make them visible.
direction does not change the situation. All effects are largely exaggerated in the figure to make them visible.
8.12. The Pioneer-10 and Pioneer-11 Anomalous Accelerations, Observed beyond the Solar System
In Section 5.3 it has been shown that the orbiting stars within the galactic disk almost completely suppress the  decay of the Keplerian velocity field of the QS with distance from the galactic center. Therefore the orbital velocity of the stars practically is constant as a function of the distance from the galactic center and the gravitational acceleration of resting free bodies is very low within the galactic disk. The stars are carried along their circular orbits by the circulating QS. The planets of the solar system (planetary disk) too cause a very weak, but consistent non-zero attenuation in the
decay of the Keplerian velocity field of the QS with distance from the galactic center. Therefore the orbital velocity of the stars practically is constant as a function of the distance from the galactic center and the gravitational acceleration of resting free bodies is very low within the galactic disk. The stars are carried along their circular orbits by the circulating QS. The planets of the solar system (planetary disk) too cause a very weak, but consistent non-zero attenuation in the  decay of the solar Keplerian velocity of the QS up to the border of the solar system. However, beyond the border the Keplerian velocity field regains its
decay of the solar Keplerian velocity of the QS up to the border of the solar system. However, beyond the border the Keplerian velocity field regains its 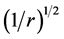 dependence and hence the gravitational acceleration increases a little bit beyond the border of the solar system as verified in the acceleration of the Pioneer 10 and 11 spacecrafts [25] [26] .
dependence and hence the gravitational acceleration increases a little bit beyond the border of the solar system as verified in the acceleration of the Pioneer 10 and 11 spacecrafts [25] [26] .
9. Conclusion
The present work introduces a completely new conception of space, matter and gravitational and shows that it straightforwardly and appropriately solves the gravitational physics. This conception is clearly suggested by several recent and trustworthy experimental observations, achieved with the help of the tightly synchronized clocks of the GPS. It also is implicit in the Quantum Field Theory (QFT), underlying the SEPM, according to which the Higgs condensate, permeating all of space, gives mass to the elementary particles and hence rules the inertial motion of matter and the propagation of light. The new conception links together the central idea of Einstein’s GR, according to which the gravitational fields act by inertial effects and the idea of QFT, according to which the Higgs condensate is a quantum space that rules the inertial motion of matter and the propagation of light. In conclusion, gravitation is an inertial dynamics, caused by the Keplerian velocity field of the QS, a residual macroscopic manifestation of the Higgs mechanism, associated with concentrations of matter. This is all the possible unification of GR and of Quantum Mechanics.
References
- Lorentz, H.A., Einstein, A., Minkowski, H. and Weyl, H. (1923) The Principle of Relativity. Dover Publications Inc., New York.
- Higgs, P.W. (1964) Physical Review Letters, 13, 508. http://dx.doi.org/10.1103/PhysRevLett.13.508
- Englert, F. and Brout, R. (1964) Physical Review Letters, 13, 321-323. http://dx.doi.org/10.1103/PhysRevLett.13.321
- Kibble, T.W.B. (2009) Scholarpedia, 4, 8741. http://dx.doi.org/10.4249/scholarpedia.8741
- Hatch, R.R. (2007) Physics Essays, 20, 83-100. http://dx.doi.org/10.4006/1.3073811
- Hatch, R.R. (2004) GPS Solutions, 8, 67-73. http://dx.doi.org/10.1007/s10291-004-0092-8
- Hatch, R.R. (2004) Foundations of Physics, 34, 1725-1739. http://dx.doi.org/10.1007/s10701-004-1313-2
- Schaff, J. (2012) Journal of Modern Physics, 3, 714-749. http://dx.doi.org/10.4236/jmp.2012.38097
- Ives, H.E. and Stilwell, G.R. (1938) Journal of the Optical Society of America, 28, 215-219. http://dx.doi.org/10.1364/JOSA.28.000215
- Miller, D.C. (1933) Reviews of Modern Physics, 5, 203-242. http://dx.doi.org/10.1103/RevModPhys.5.203
- Ashby, N. Private communication.
- Bailey, H., Borer, K., Combley, F., Drumm, H. and Krienen, F. (1977) Nature, 268, 301-305.
- Dixon, L. (1996) From Superconductors to Supercolliders. www.slac.stanford.edu/pubs/beamline/26/1/26-1-dixon.pdf
- Ginzburg, V.L. and Landau, L.D. (1950) Journal of Experimental and Theoretical Physics (JETP), 20, 1064.
- Abrikosov, A.A. (1957) Soviet Physics JETP, 5, 1174.
- Aharonov, Y. and Bohm, D. (1959) Physical Review, 115, 485. http://dx.doi.org/10.1103/PhysRev.115.485
- Varma, R.K., Punithavelu, A.M. and Banerjee, S.B. (2002) Physics Letters A, 303, 114-120. http://dx.doi.org/10.1016/S0375-9601(02)01223-9
- Dias, F.T., Pureur, P., Rodrigues Jr., P. and Obradors, X. (2004) Physical Review B, 70, 224519. http://dx.doi.org/10.1103/PhysRevB.70.224519
- Salant, R.E. (1969) The Journal of the Acoustical Society of America, 46, 1153-1167. http://dx.doi.org/10.1121/1.1911835
- Rubin, V. and Ford Jr., W.K. (1970) Astrophysical Journal, 159, 379-404. http://dx.doi.org/10.1086/150317
- Rubin, V., Thonnard, N. and Ford Jr., W.K. (1980) Astrophysical Journal, 238, 471-487. http://dx.doi.org/10.1086/158003
- Remmen, G. (2010) Journal of Undergraduate Research in Physics, 19, 1.
- Leibovitz, J. (2011) Journal of Modern Physics, 2, 1470-1479. http://dx.doi.org/10.4236/jmp.2011.212181
- Prada, F., Gutierrez, C., Peletier, R.F. and McKeith, C.D. (1996) A Counter-Rotating Bulge in the Sb Galaxy NGC 7331. arXiv:astro-ph/9602142.
- Turyshev, S.G. and Toth, V.T. (2012) The Pioneer Anomaly. arXiv:1001.3686v1 19 Aug (2010) (v2).
- Anderson, J.D., Laing, P.A., Lau, E.L., Liu, A.S., Nieto, M.M. and Turyshev, S.G. (2002) Physical Review D, 65, Article ID: 082004. http://dx.doi.org/10.1103/PhysRevD.65.082004
- Anderson, J.D., Campbell, J.K., Ekelund, J.E., Ellis, J. and Jordan, J.F. (2008) Physical Review Letters, 100, Article ID: 091102. http://dx.doi.org/10.1103/PhysRevLett.100.091102
- Barbanis, B. and Prendergast, K.H. (1966) The Astronomical Journal, 72, 215. http://dx.doi.org/10.1086/110220
- Riess, A., et al. (1998) The Astronomical Journal, 116, 1009-1038. http://dx.doi.org/10.1086/300499
- Perlmutter, S., et al. (1999) The Astrophysical Journal, 517, 565-586. http://dx.doi.org/10.1086/307221
- Pound, R.V. and Snider, J.L. (1965) Physical Review B, 140, B788-B893. http://dx.doi.org/10.1103/PhysRev.140.B788
- Brault, J.W. (1963) Bulletin of the American Physical Society, 8, 28.
- Ashby, N. (1996) Mercury, 25, 23-27.
- Shapiro, I.I., Ash, M.E., Ingals, R.P., Smith, W.B., Campbell, D.B., Dyce, R.B., Jurgens, R.F. and Pettengill, G.H. (1971) Physical Review Letters, 26, 1132-1135. http://dx.doi.org/10.1103/PhysRevLett.26.1132
- Merat, P., Pecker, J.C. and Vigier, J.P. (1974) Astronomy & Astrophysics, 30, 167.
- Goldstein, R.M. (1969) Science, 166, 598-601. http://dx.doi.org/10.1126/science.166.3905.598


