Journal of Modern Physics
Vol.4 No.3(2013), Article ID:28872,7 pages DOI:10.4236/jmp.2013.43052
Hamiltonian of Acoustic Phonons in Inhomogeneous Solids
Department of Physics, Faculty of Education, Catholic University, Ruzomberok, Slovak Republic
Email: stanislav.minarik@ku.sk
Received November 12, 2012; revised December 20, 2012; accepted January 16, 2013
Keywords: Phonons; Mass Density; Elastic Coefficient; Energy States; Inhomogeneities; 1D Ionic Chain; Hamiltonian
ABSTRACT
Theoretical solid-state physicists formulate their models usually in the form of a Hamiltonian. In quantum mechanics, the Hamilton operator 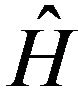 (Hamiltonian) is of fundamental importance in most formulations of quantum theory. Mentioned operator corresponds to the total energy of the system and its spectrum determines the set of possible outcomes when one measures the total energy. Interpretation of results obtained by the applying of models based on the Hamiltonian indicates very specific mechanisms of some observed phenomena that are not fully consistent with the experience. Such approach may occasionally lead to surprises when obtained results are confronted with expectations. The aim of this work is to find Hamilton operator of acoustic phonons in inhomogeneous solids. The transport of energy in the vibrating crystal consisting of ions whose properties differ over long distances is described in the work. We modeled crystal lattice by 1D “inhomogeneous” ionic chain vibrating by acoustic frequencies and found the Hamiltonian of such system in the second quantization. The influence of long-distance inhomogeneities on the acoustic phonons quantum states can be discussed on basis of our results.
(Hamiltonian) is of fundamental importance in most formulations of quantum theory. Mentioned operator corresponds to the total energy of the system and its spectrum determines the set of possible outcomes when one measures the total energy. Interpretation of results obtained by the applying of models based on the Hamiltonian indicates very specific mechanisms of some observed phenomena that are not fully consistent with the experience. Such approach may occasionally lead to surprises when obtained results are confronted with expectations. The aim of this work is to find Hamilton operator of acoustic phonons in inhomogeneous solids. The transport of energy in the vibrating crystal consisting of ions whose properties differ over long distances is described in the work. We modeled crystal lattice by 1D “inhomogeneous” ionic chain vibrating by acoustic frequencies and found the Hamiltonian of such system in the second quantization. The influence of long-distance inhomogeneities on the acoustic phonons quantum states can be discussed on basis of our results.
1. Introduction
Many authors have been studied the influence of phonons on various processes in solids. Phonons affect certain aspects of the solid structure such as electronic density distribution [1], electron correlation [2], coupling of phonon with another phonons [3], heat capacity of solid [4], splitting of exciton lines [5], etc. In recent decades a lot of phenomena in solid state were analyzed in detail and role of crystal lattice vibration (phonons) in the explaining of these phenomena was investigated (metalinsulator phase transition [6], spin excitations of high-Tc superconductors [7], paramagnetic relaxation [8], Josephson oscillations of excitonic and polaritonic condensates [9], martensitic transformation in NiTi [10], etc.). Generaly the canonical quantization method must be used in order to phonon structure of vibrational energy become apparent. The procedure of quantization of energy of acoustic waves obviously consists from next basic steps: 1) Solution of equations of the elastic wave in accordance with the proper boundary conditions and determination of the spectrum of the resulting acoustic modes; 2) Determination of phonon modes by applying the second quantization formalism to a complete orthonormal set of classical waves [11].
Procedure mentioned above is well applicable in fully homogeneous structures where phonon-mediated energy transport can be successfully introduced.
With the understanding of the importance of acoustic excitations in solids the procedure of canonical quantization attracts a significant interest. During past years some effort has been devoted to the understanding of the influence of quantization on the vibrational properties of heterostructures. Great interest has been oriented mainly on effects of acoustic-phonon quantization in restricted geometries [11]. For most geometries, the solutions of elastic wave equations are well established [12,13] and the actual studies are focused on the modification of elastic modes in systems. This modification allows to study energy dissipation, phonon-limited mobility, and other kinetic properties of electrons in solids. The behavior of an acoustic waves in a solid-state medium with spatiallydependent mass density and elastic properties can play an important role and the impact of the changing conditions on the phononic state must be evaluated.
In this paper we present a description of the long-distance structural inhomogenities influence on acoustic phonon quantum-mechanical states.
Main ideas of the work are outlined in the next sections which are organized as follows: We present motivation of the work in Section 2. Section 3 describes the dynamics of ions in the 1D model of “inhomogeneous” crystal lattice. Section 4 illustrates continuum limit for the model presented in Section 3. Section 5 examines canonical coordinates of the investigated system. Application of second quantization formalism to inhomogeneous vibrating solid is presented in Section 6. Section 7 is devoted to short discussion of our result. Finally we give a brief conclusion in Section 8.
2. Motivation
If there are a weak interatomic forces in the ideal crystal, then the Hamiltonian of vibrating crystal can be written in the one-phonon approximation:
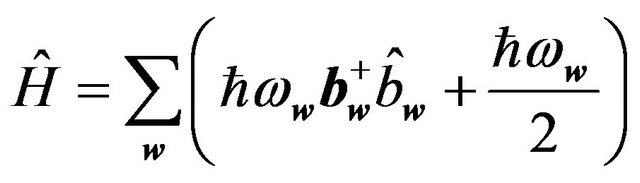 , (2.1)
, (2.1)
where 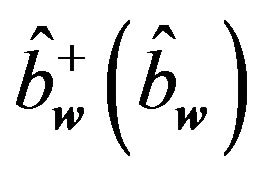 is the phonon creation (annihilation) operator for the w-th phonon mode. In the harmonic approximation, a crystal can be described in terms of noninteracting phonons. The different phonon modes are independent and do not interact with each other. However, this simple picture is only an approximation, and in the case of large atom displacements, we should take into account the higher-order terms obtained by expanding of the potential energy. Keeping the cubic term, we can describe the interaction between phonon modes and thus we explicitly consider the phonon-phonon interaction between two modes [14].
is the phonon creation (annihilation) operator for the w-th phonon mode. In the harmonic approximation, a crystal can be described in terms of noninteracting phonons. The different phonon modes are independent and do not interact with each other. However, this simple picture is only an approximation, and in the case of large atom displacements, we should take into account the higher-order terms obtained by expanding of the potential energy. Keeping the cubic term, we can describe the interaction between phonon modes and thus we explicitly consider the phonon-phonon interaction between two modes [14].
The concept of phonon mentioned above remains valid when the anharmonic contribution in crystal vibration is small compared with the harmonic. In this case, the quasi-particle approximation can be made as well. Then some of the phenomena can be explained on the basis of the idea of interaction of phonons with other elementary excitation in solid-state matter (excitons, magnons, plasmons, etc.).
The question is, what is the effect of long-distance spatial inhomogeneities of structure in solids on acoustic phonon states and how it is necessary to modify results of “phonon based” quantum mechanical models of some phenomena in the case of inhomogeneous continuum. In the modern literature, numerous investigations were, devoted to the chracter of phonon mediated interactions in solids. However, only a little work had been done about the quantum-mechanical states of phonons in inhomogeneous solids. Thus, it is very difficult to evaluate theoretical and practical importance of consideration of structure inhomogeneities in the frame of second quantization method. Next we propose the basis for the solution of this problem.
3. 1D Ion Chain Model—“Inhomogeneous” Case
Next, the 1D ion chain model is studied (Figure 1). A 1D lattice seems an appropriate model that could, in addition, allow for some mathematical treatment and thus a better theoretical understanding of the phenomena and mechanisms at play.
Consider N ions of unequal masses 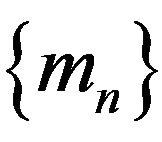 and charges
and charges  with nonlinear nearest-neighbor interactions, described by a potential energy U. The position of the n-th ion will be denoted by xn, where the ions are numbered in order of increasing value of their axial positions, so that
with nonlinear nearest-neighbor interactions, described by a potential energy U. The position of the n-th ion will be denoted by xn, where the ions are numbered in order of increasing value of their axial positions, so that 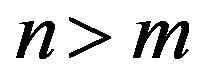 implies that
implies that  (see Figure 1). Initially, the particles are at rest at positions
(see Figure 1). Initially, the particles are at rest at positions , which is an equilibrium state for the system.
, which is an equilibrium state for the system.
Ions are bound relatively strongly in their equilibrium positions in the crystal lattice. The following analysis is based on the classical description of the dynamics of ions in the 1D crystal lattice in harmonic approximation.
We consider one-dimensional crystal represented by a linear chain of N ions (Figure 1), which is not inserted into the external field. It turns out that the results provided by the solution of such a simplified one-dimensional model can be applied in the real three-dimensional case. The total potential energy U of the chain depends on the positions of all ions. Let 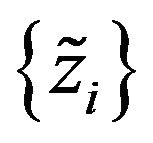 are displacements of ions from equilibrium positions, displacement of n-th ion in the chain is defined as follows:
are displacements of ions from equilibrium positions, displacement of n-th ion in the chain is defined as follows:
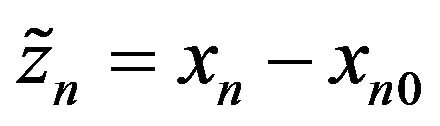 . (3.1)
. (3.1)
If displacements of ions from the equilibrium are small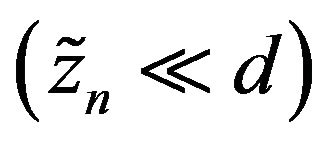 , the potential energy U can be expanded to the Taylor series. Next harmonic approximation can be applied, i.e. only the second degree polynomial function
, the potential energy U can be expanded to the Taylor series. Next harmonic approximation can be applied, i.e. only the second degree polynomial function  can be considered. Moreover is it possible to take account the fact that potential energy U has a minimum for each equilibrium positions
can be considered. Moreover is it possible to take account the fact that potential energy U has a minimum for each equilibrium positions . Therefore, the potential energy U in the harmonic approximation is given by:
. Therefore, the potential energy U in the harmonic approximation is given by:
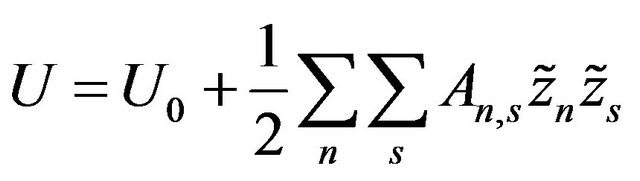 , (3.2)
, (3.2)
where:
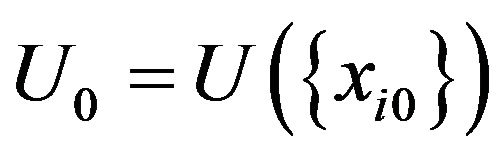 and
and . (3.3)
. (3.3)
Then the force acting on the n-th ion in chain can be written as:
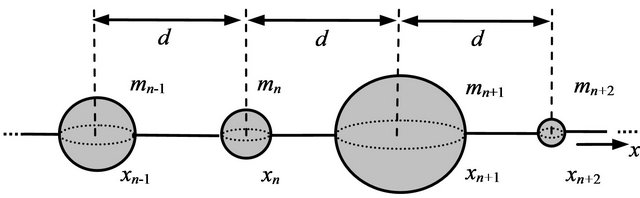
Figure 1. 1D ion chain model of the crystal lattice.
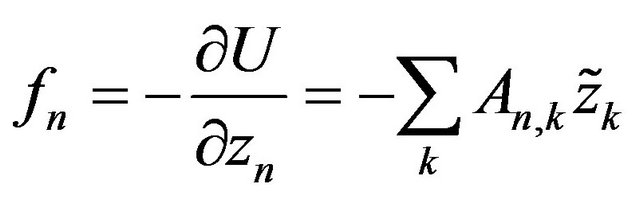 . (3.4)
. (3.4)
In case if displacements of all ions from equilibrium are the same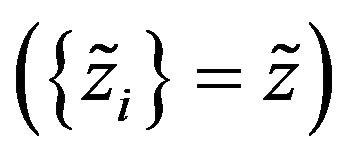 , the force (3.4) acting on any ion in chain is zero because it corresponds to the displacement of whole crystal:
, the force (3.4) acting on any ion in chain is zero because it corresponds to the displacement of whole crystal:
 . (3.5)
. (3.5)
This means that the coefficients 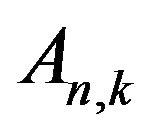 are not linearly independent. Next condition results from the relation (3.5):
are not linearly independent. Next condition results from the relation (3.5):
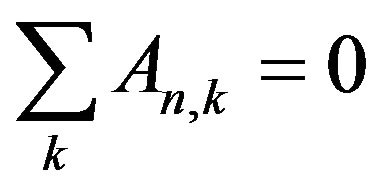 . (3.6)
. (3.6)
Assuming inhomogeneous case of 1D chain there are different masses of individual ions (see Figure 1) and also a variety of binding forces between them can be considered. Using the following notations:
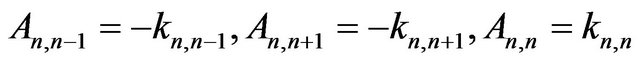 (3.7)
(3.7)
and applying the tight binding approximation the equation of motion for the n-th ion in the chain is given by:
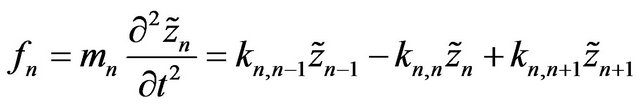 . (3.8)
. (3.8)
In addition, as can be seen from the Equation (3.6):
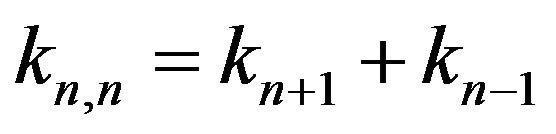 , (3.9)
, (3.9)
the Equation (3.8) can be written in the next form:
 . (3.10)
. (3.10)
System of Equations (3.10) for 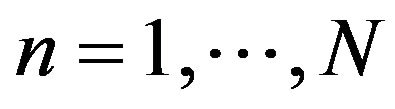 allows to describe the dynamics of ions in the frame of the proposed 1D chain model. Solution of this system is the set of functions
allows to describe the dynamics of ions in the frame of the proposed 1D chain model. Solution of this system is the set of functions , which describes time dependence of the displacements of ions from equilibrium in the chain.
, which describes time dependence of the displacements of ions from equilibrium in the chain.
4. Continuum Limit
We consider the continuum limit for model of solid presented above. The term “continuum limit” usually relates to discrete models where it means “becoming less discrete”. To make this let us consider a transitions:
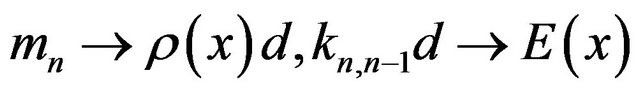 (4.1)
(4.1)
where d is the distance of neighboring ions in the chain acting oscillations.
Linear density 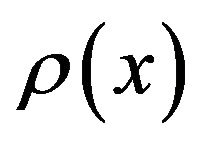 and elastic coefficient
and elastic coefficient 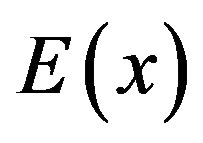 change in the inhomogeneous case along the chain. They depend on coordinate x in the 1D model (see Figure 2). We consider that formula (3.10) can be written in the form:
change in the inhomogeneous case along the chain. They depend on coordinate x in the 1D model (see Figure 2). We consider that formula (3.10) can be written in the form:

Figure 2. Continuum limit.
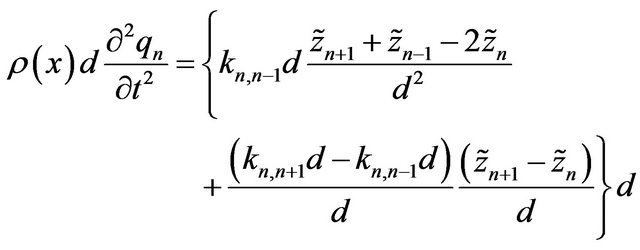 (4.2)
(4.2)
and next we suggest to replace discrete variables in the Equation (4.2) by continuous functions on the basis of (4.1), i.e.:
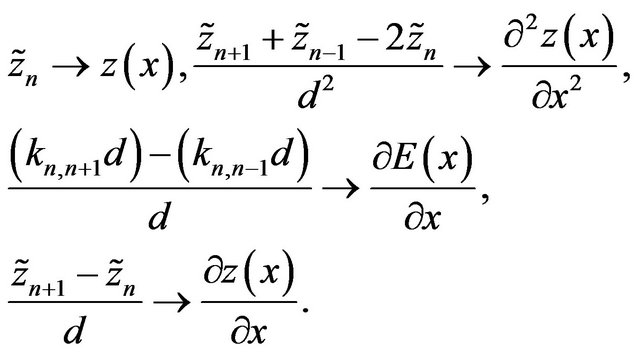 (4.3)
(4.3)
After substituting of relations (4.3) into Equation (4.2) we get:
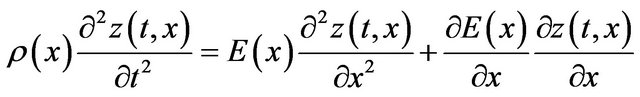 . (4.4)
. (4.4)
We believe that the Equation (4.4) describes the transport of acoustic waves in inhomogeneous continuum in 1D case.
On the basis of the result (4.4) it can be concluded that transport of acoustic waves in 3D case can be described by next equation:
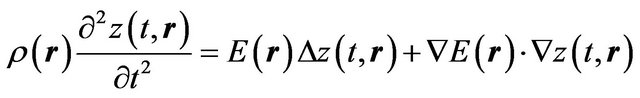 . (4.5)
. (4.5)
5. Canonical Coordinates
Lagrangian formulation of the oscillating system mechanics is based on the formal introduction of canonical variables to Equation (4.5). Firstly, it is necessary to find Lagrangian L of the oscillating system considered above. Suppose that after the substituting of the Lagrangian L into the Euler-Lagrange equation:
 (5.1)
(5.1)
this equation changes into the form (4.5). Consider the Lagrangian in an analogous form as in the homogeneous case:
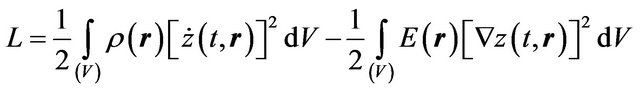 (5.2)
(5.2)
where we integrate over the entire sample volume. One can easily check that by the substituting of the relation (5.2) into Equation (5.1) this equation takes the form (4.5).
Displacement from equilibrium state 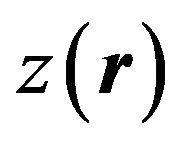 is a one of complex conjugated variables-canonical coordinate. Complex conjugated momentum
is a one of complex conjugated variables-canonical coordinate. Complex conjugated momentum 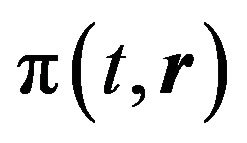 can be found using the next relationship:
can be found using the next relationship:
 . (5.3)
. (5.3)
By substituting (5.2) into (5.3) the conjugated momentum 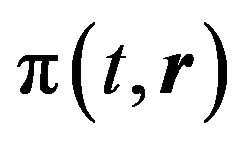 can be written in the form:
can be written in the form:
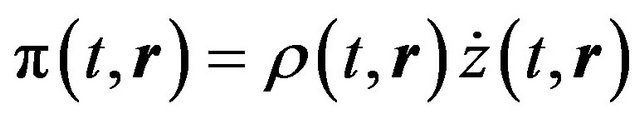 . (5.4)
. (5.4)
Then the Hamilton function of oscillating inhomogeneous continuum is determined by formula:
 . (5.5)
. (5.5)
Canonical variables of the inhomogeneous oscillating continuum can be written as:
 , (5.6)
, (5.6)
 . (5.7)
. (5.7)
We propose the canonical coordinates of the investigated system in an analogous form as in the homogeneous case. The question is, what is the impact of spatial dependence of mass density 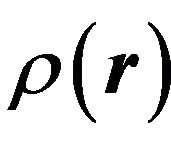 and elastic coefficient
and elastic coefficient 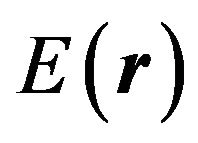 on the energy states of the system.
on the energy states of the system.
6. Quantum-Mechanical Case
For the quantization of Equation (4.5) it is necessary to define operators corresponding to physical quantities. In the considered case it is necessary to replace the canonical variables by their operators:
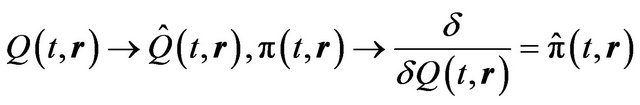 (6.1)
(6.1)
Mentioned operators satisfy well known commutation relations:
 (6.2)
(6.2)
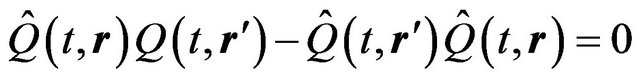 , (6.3)
, (6.3)
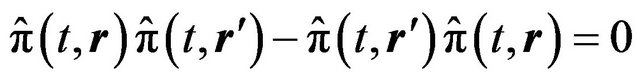 (6.4)
(6.4)
Subsequently, the coefficients in the relations (5.6) and (5.7) become operators defined by the next way:
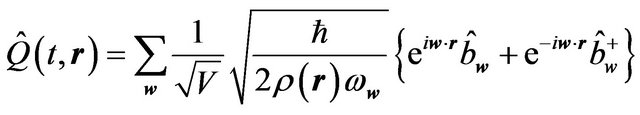 , (6.5)
, (6.5)
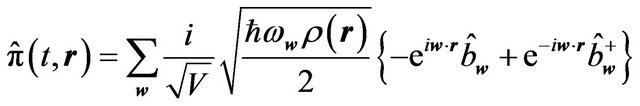 . (6.6)
. (6.6)
Formulas for the annihilation and creation operators 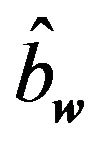 and
and  can be found by inversion of relations (6.5) and (6.6). The quantization of the elastic vibrations is made through the commutation relations:
can be found by inversion of relations (6.5) and (6.6). The quantization of the elastic vibrations is made through the commutation relations:
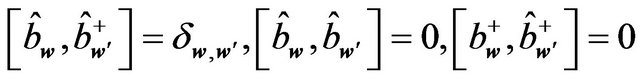 . (6.7)
. (6.7)
We assume that operators 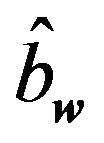 and
and 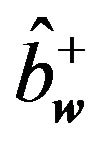 obey mentioned commutation relations even in the inhomoneneous case. Hamiltonian of the vibrating system can be obtained easily by the replacing of the canonical variables in formula (5.5) by the operators (6.5) and (6.6), i.e.:
obey mentioned commutation relations even in the inhomoneneous case. Hamiltonian of the vibrating system can be obtained easily by the replacing of the canonical variables in formula (5.5) by the operators (6.5) and (6.6), i.e.:
 . (6.8)
. (6.8)
It is necessary to substitute relations (6.5) and (6.6) into the Equation (6.8) and determine the Hamiltonian  by means of operators
by means of operators 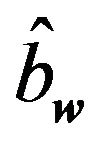 and
and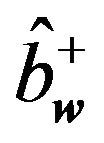 . If we raise to the second power the formula (6.6) and next we substitute it to the first integral in (6.8), we get:
. If we raise to the second power the formula (6.6) and next we substitute it to the first integral in (6.8), we get:
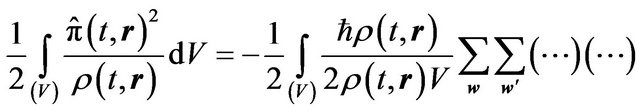
i.e.:
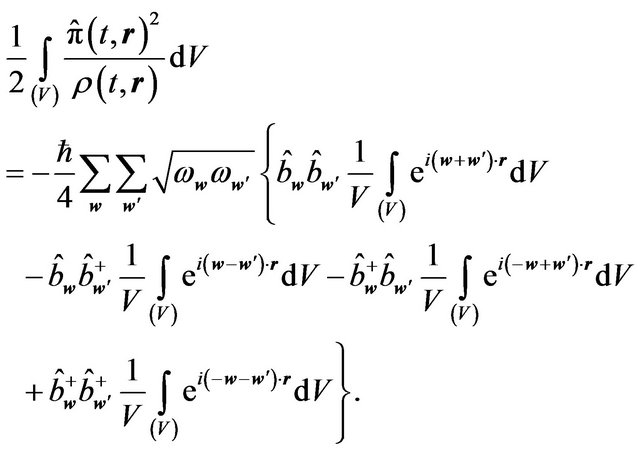 (6.9)
(6.9)
Because it holds:
 ;
;
where a = 1, 2; b = 1, 2, the Equation (6.9) goes into the next simple form:
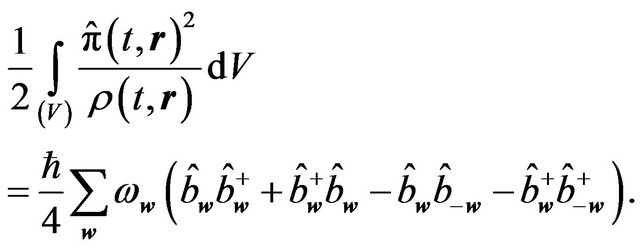 (6.10)
(6.10)
We take into account the fact that:
 . (6.11)
. (6.11)
It is necessary to find the gradient of the operator (6.5) for the calculation of the second integral in the expression (6.8). We must take into account the spatial dependence of 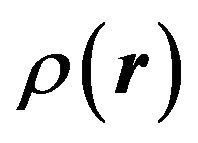 in this calculation. The gradient of operator (6.5) may be determined as follows:
in this calculation. The gradient of operator (6.5) may be determined as follows:
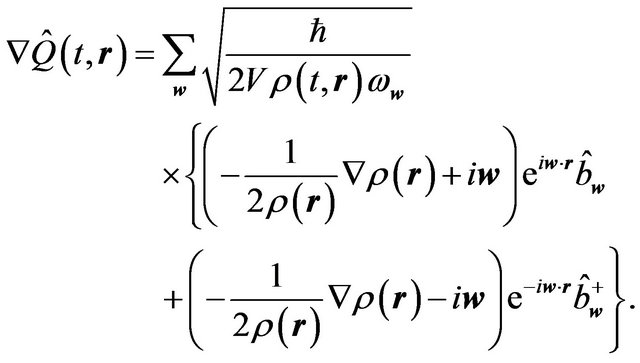 (6.12)
(6.12)
In order to find the operator  we must raise to the second power the Equation (6.12) and next substitute the obtained result into the second integral in Equation (6.8).
we must raise to the second power the Equation (6.12) and next substitute the obtained result into the second integral in Equation (6.8).
After the substituting of (6.12) to the second integral in the (6.8) it takes the form:
 (6.13)
(6.13)
where:
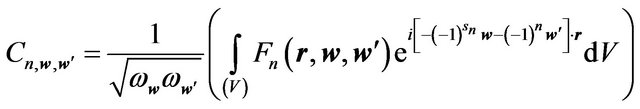 (6.14)
(6.14)
and .
.
Operator  in (6.13) is determined as follows:
in (6.13) is determined as follows:
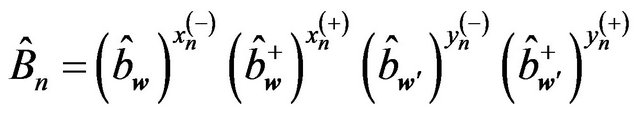 where
where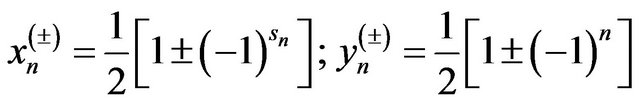 .
.
Functions  (for n = 1, 2, 3, 4) are related to spatial inhomogeneities of investigated continuum:
(for n = 1, 2, 3, 4) are related to spatial inhomogeneities of investigated continuum:
 (6.15)
(6.15)
Mentioned functions  can be expanded into the Fourier series:
can be expanded into the Fourier series:
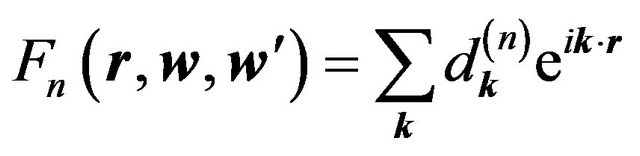 (6.16)
(6.16)
where:
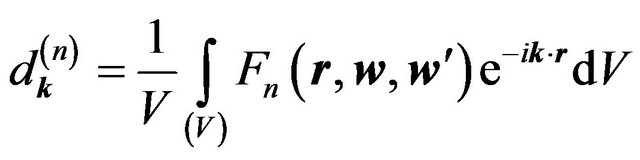 (6.17)
(6.17)
and then coefficients 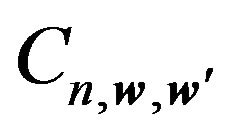 determined by formula (6.14) take the form:
determined by formula (6.14) take the form:
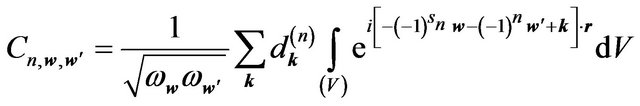 . (6.18)
. (6.18)
Next the coefficients 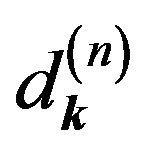 in (6.18) can be determined by means of integrals (6.17). It is necessary to substitute functions
in (6.18) can be determined by means of integrals (6.17). It is necessary to substitute functions 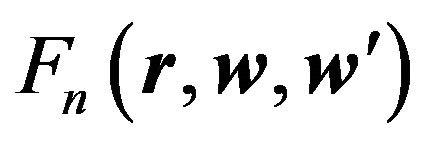 in the form (6.15) to mentioned integrals. For example:
in the form (6.15) to mentioned integrals. For example:
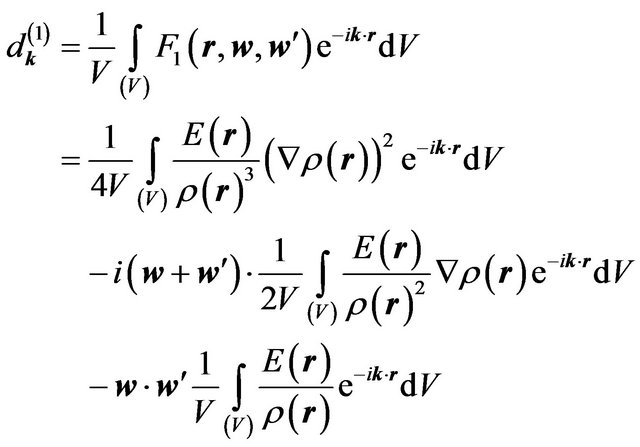 (6.19)
(6.19)
By the introduction of the:
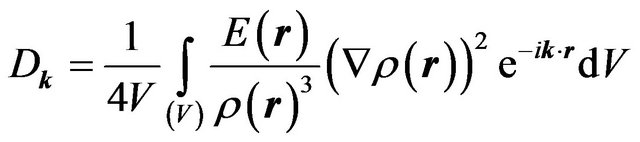 , (6.20)
, (6.20)
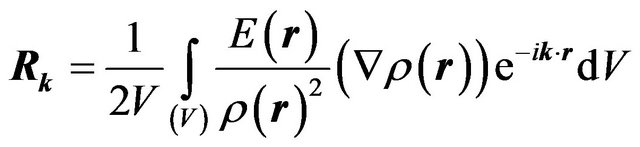 , (6.21)
, (6.21)
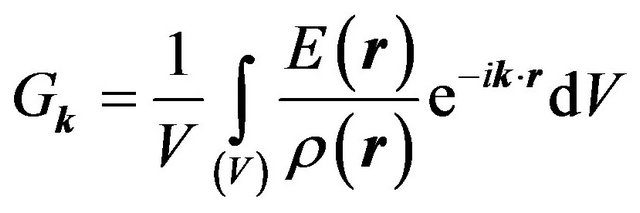 (6.22)
(6.22)
the coefficients  take the form:
take the form:
 , (6.23)
, (6.23)
 , (6.24)
, (6.24)
 , (6.25)
, (6.25)
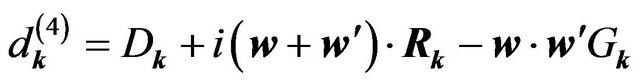 . (6.26)
. (6.26)
Then we consider:
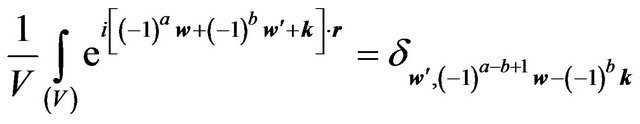 ;
;
where a = 1, 2; b = 1, 2 and the relation (6.13) can be simplified:
 (6.27)
(6.27)
Finally after the substituting of both results (6.10) and (6.27) into the Equation (6.8) the Hamilton operator of the inhomogeneous continuum vibrating by the acoustic frequencies can be written as:
 (6.28)
(6.28)
where:
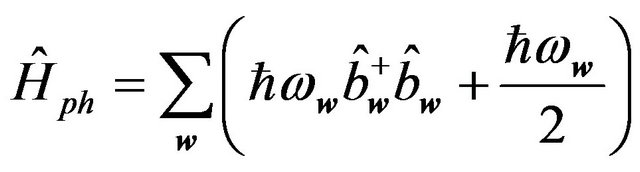 . (6.29)
. (6.29)
Operator  must be hermitian (self adjoint) and therefore can be modified to the following form:
must be hermitian (self adjoint) and therefore can be modified to the following form:
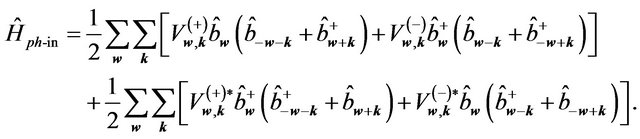 (6.30)
(6.30)
where coefficients 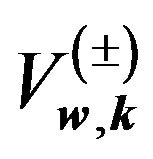 are:
are:
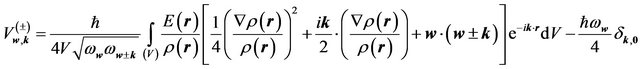 . (6.31)
. (6.31)
We believe that the second term in the Hamiltonian (6.28) determined by Equation (6.30) can make the basis for quantum-mechanical analysis of acoustic phonons scattering process in solid structure caused by long-distance spatial inhomogeneities.
7. Discussion
In this paper we presented a simple approach to the quantization of energy of acoustic waves in inhomogeneous continuum. A fully canonical quantization of mechanical energy of vibrating media was introduced in the presence of inhomogeneities of structure represented by the spatial dependencies of mass density  and elastic coefficient
and elastic coefficient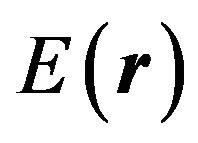 . Subsequently, the Hamilton operator of the vibrating inhomogeneous continuum was determined by standard technique of second quantization. The contribution of the work lies in the fact that our result makes it possible to estimate the impact of long-distance inhomogeneities on the energy spectrum of acoustic phonons.
. Subsequently, the Hamilton operator of the vibrating inhomogeneous continuum was determined by standard technique of second quantization. The contribution of the work lies in the fact that our result makes it possible to estimate the impact of long-distance inhomogeneities on the energy spectrum of acoustic phonons.
Hamiltonian of the inhomogeneous continuum vibrating by acoustic frequencies can be written in the form (6.28) where 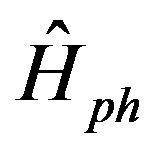 is well-known Hamiltonian of homogeneous vibrating system identical to (2.1). Operator
is well-known Hamiltonian of homogeneous vibrating system identical to (2.1). Operator  is generated by inhomogeneities. In that case the coefficients
is generated by inhomogeneities. In that case the coefficients 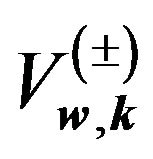 can be interpreted as phonon scattering form factors that reflect the structure of an extended energy distribution. Mentioned coefficients determined by integrals (6.31) represent non-locality of phonons scattering centre and in the case of homogenous continuum disappear
can be interpreted as phonon scattering form factors that reflect the structure of an extended energy distribution. Mentioned coefficients determined by integrals (6.31) represent non-locality of phonons scattering centre and in the case of homogenous continuum disappear .
.
8. Conclusions
Summing up the above-said, one can conclude that nonlocal changes of mechanical properties affect the mechanical energy of acoustic vibration of the continuum. This may affect the formation of acoustic excitation and cause anomalies in related phenomena. Possible influence of long-distance structural inhomogenities on acoustic phonon spectrum is expected. For example a heat capacity anomalies in some materials observed at low temperatures by many authors [15,16] could be partly caused by their structural transition, which is associated with origin of structural inhomogeneities. In our opinion the influence of these structural inhomogeneities on the low-T behavior of heat capacity of such system could be discussed on the basis of our results.
Finally, we would like to point out that the presented contribution is only intended to preliminarily obtain some aspects of second quantization in inhomogeneous cases which could be useful within other theoretical models.
REFERENCES
- V. M. Axt and A. Stahl, “Influence of Phonon Bath on the Hierarchy of Electronic Densities in a Optically Excited Semiconductor,” Physical Review B, Vol. 53, No. 7244, 1996.
- T. Hotta and Y. Takada, “Effect of Electron Correlation on Phonons in a Strongly Coupled Electron-Phonon System,” Physical Review B, Vol. 56, No. 21, 1997, pp. 13916-13926. doi:10.1103/PhysRevB.56.13916
- R. Fahrenbacher, “Coupling of Optical Phonons in OneDimensional t-J Model: Effect of Superconducting Fluctuation and Phase Separation,” Physical Review Letters, Vol. 77, No. 11, 1996, pp. 2288-2291. doi:10.1103/PhysRevLett.77.2288
- V. M. Kuznetsov and V. I. Khromov, “Fractal Representation of the Debye Theory for Studying the Heat Capacity of Macroand Nanostructures,” Technical Physics, Vol. 53, No. 11, 2008, pp. 1401-1406.
- W. C. Walker and D. M. Roesslev, “Phonon Induced Splitting of Exciton Lines in MgO and BeO,” Physical Review Letters, Vol. 20, No. 16, 1968, pp. 847-848. doi:10.1103/PhysRevLett.20.847
- D. C. Mattis and W. D. Langer, Physical Review Letters, Vol. 25, No. 6, 1970.
- S. Tajima and J. Schützmann, “Role of Phonons in Electronic and Spin Excitations of High-Tc Superconductors,” Physica B: Condensed Matter, Vol. 219-220, 1996, pp. 128-131. doi:10.1016/0921-4526(95)00672-9
- B. W. Faughnan and M. W. P. Strandberg, Journal of Physics and Chemistry of Solids, Vol. 19, No. 1-2, 1961, pp. 155- 166.
- E. B. Magnusson, H. Flayac, G. Malpuech and I. A. Shelykh, “Role of Phonons in Josephson Oscillations of Excitonic and Polaritonic Condensates,” Phyical. Review B, Vol. 82, No. 19, 2010, Article ID: 195312. doi:10.1103/PhysRevB.82.195312
- P. D. Bogdanoff and B. Fultz, “The Role of Phonons in the Thermodynamics of the Martensitic Transformation in NiTi,” Philisophical Magazine B, Vol. 81, No. 3, 2001, pp. 299-311. doi:10.1080/13642810108221985
- M. A. Stroscio, Yu. M. Sirenko, S. Yu and K. W. Kim, “Acoustic Phonon Quantization in Buried Waveguides and Resonators,” Journal of Physics: Condensed Matter, Vol. 8, No. 13, 1996, p. 2143. doi:10.1088/0953-8984/8/13/006
- M. A. Stroscio, et al., In: P. Bhattacharya, Eds., Properties of III-V Quantum Wells and Superlattices, INSPEC, London, 1996, p. 194.
- B. A. Auld, “Acoustic Fields and Waves,” Wiley, New York, 1973.
- K. Kneipp, L. T. Perelman, H. Kneipp, V. Backman, A. Jorio, G. Dresselhaus and M. S. Dresselhaus, “Coupling and Scattering Power Exchange between Phonon Modes Observed in Surface-Enhanced Raman Spectra of Single-Wall Carbon Nanotubes on Silver Colloidal Clusters,” Physical Review B, Vol. 63, No. 19, 2001, Article ID: 193411. doi:10.1103/PhysRevB.63.193411
- D. J. Safarik, R. B. Schwarz and M. F. Hundley, “Similarities in the Cp/T3 Peaks in Amorphous and Crystalline Metals,” Physical Review Letters, Vol. 96, No. 19, 2006, Article ID: 195902. doi:10.1103/PhysRevLett.96.195902
- P. Giudicelli and N. Bernhoeft, Europhysics Letters, Vol. 67, 2004, pp. 117-122.

