Journal of Modern Physics
Vol.4 No.2(2013), Article ID:28324,4 pages DOI:10.4236/jmp.2013.42033
The Propagation of Circularly Polarized Waves in Quantum Plasma
1Plasma Physics Department, N.R.C., Atomic Energy Authority, Cairo, Egypt
2Physics Department, Faculty of Science, Banha University, Banha, Egypt
Email: mohamedbahf@yahoo.co.uk
Received September 2, 2012; revised November 1, 2012; accepted November 28, 2012
Keywords: Dense Quantum Plasma; Laser Plasma Interaction; Quantum Effects
ABSTRACT
The quantum effects on the propagation circularly polarized waves have been investigated in electron magnetized quantum plasmas. We obtain the dispersion equations of the propagation of circularly polarized laser beam through cold plasma. The results show that the laser can be propagated due to the quantum effects which enhance the propagation phase velocity. For this purpose, the quantum hydrodynamic (QHD) equations with magnetic field and Maxwell’s equations system is used to derive these dispersion relations. The perturbed electron density and current due to the interaction of laser beam with quantum plasma have been investigated. It is shown that the external magnetic field which is parallel to the propagation waves has strong effect on the dispersion relation for the laser propagation in quantum model than the classical regime.
1. Introduction
The classical plasmas, in general, are characterized by high temperature and low density regimes where quantum effects are negligible. However, there are examples in nature where both plasma and quantum effect can coexist. In such situations, quantum effects are expected to play a significant role on the dynamics of plasma particles.
The quantum plasma has received much attention in recent years due to its important applications in ultrasmall electronics devices [1], quantum dots and quantum wire [2], in dense astrophysical plasma system [3,4] as well as in laser-produced plasma [5] and nonlinear optics [6].
Two well-known models are used to study quantum plasmas systems. The first one is the Wigner model which describes the statistical behavior of plasmas based on the Wigner-Poisson system. The other is Hartree model which describes the hydrodynamic behavior of plasmas based on the Schrodinger-Poisson system [7,8]. The quantum hydrodynamic (QHD) model describes the transport of charge, momentum and energy in charged particle system interacting though a self-consistent electrostatic potential.
The quantum plasma effects become important in dense plasmas, when the de Broglie wavelength of the charge carriers becomes comparable to the spatial scale of plasma system. So, the new dispersion relationship with quantum effects corrections for some types of linear waves in a uniform cold quantum plasma with nonzero external magnetic field are calculated by Ren et al. [9]. Also, the dispersion relation for the propagation of linearly polarized laser beam through cold quantum plasma has been obtained by Kumar et al. [10] using perturbation techniques.
In addition, the surface plasma waves propagating along the plasma-vacuum interface has attracted much attention since the frequency spectra have wide applications in many areas such as laser physics, Plasma spectroscopy and plasma technology [11]. Lazer et al. [12] has presented the dispersion relation for surface plasmons that can exist on a dense quantum plasma halfspace. Also, the dispersion relations of one-, two-stream and beam-plasma instabilities in uniform quantum magnetized plasmas are investigated through the new dielectric tensor [13].
In the present paper, the quantum effects on the propagation circularly polarized waves have been investigated in electron quantum plasmas. We study the dispersion equations of its propagation through cold plasma under an external magnetic field based on the (QHD) model.
2. Governing Equations
Considering a circularly polarized laser beam represented by the electric field

and the magnetic field
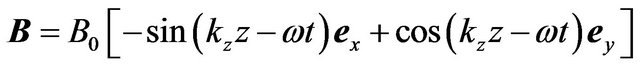
propagates through the quantum electron plasma electrons.
We assume that the plasma is immersed in an ambient static magnetic field . From QHD model, the dynamics of the electrons are governed by the following continuity equation and the momentum equation:
. From QHD model, the dynamics of the electrons are governed by the following continuity equation and the momentum equation:
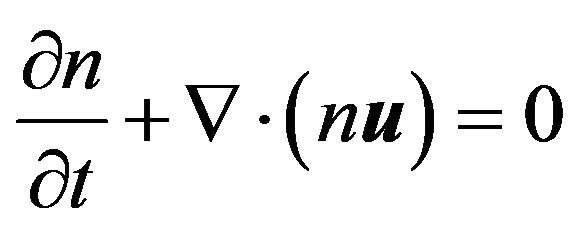 (1)
(1)
 (2)
(2)
Here n, u and m are the number density, the velocity and the mass of electron respectively and  is the Plank’s constant divided by
is the Plank’s constant divided by . The electrons obey the following pressure law which represents the equation of state in one-dimensional zero-temperature Fermi gas:
. The electrons obey the following pressure law which represents the equation of state in one-dimensional zero-temperature Fermi gas:
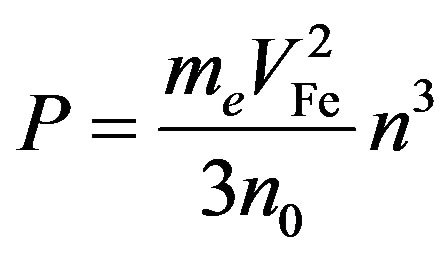
where 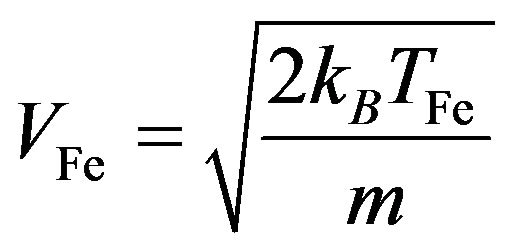 is the Fermi thermal speed,
is the Fermi thermal speed, 
is the particle Fermi temperature, KB is the Boltzmann’s constant and  is the equilibrium particle number density. We have included both the quantum statistical effects through Fermi temperature and the quantum diffraction in the
is the equilibrium particle number density. We have included both the quantum statistical effects through Fermi temperature and the quantum diffraction in the 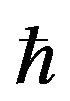 -dependent. If we set
-dependent. If we set  equal to zero and
equal to zero and 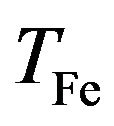 equal the temperature of electrons, we obtain the classical hydrodynamic equation.
equal the temperature of electrons, we obtain the classical hydrodynamic equation.
Using the perturbation technique, we assume any physical quantity 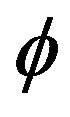 representing has the following form
representing has the following form 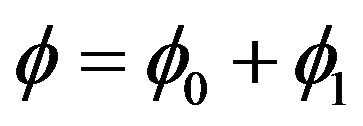 where
where  is the unperturbed value and
is the unperturbed value and  is a small perturbation
is a small perturbation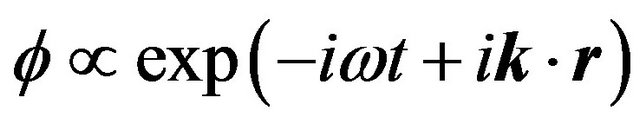 , we get:
, we get:
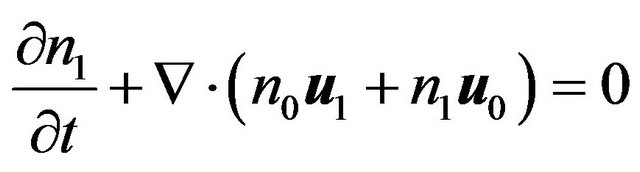 (3)
(3)
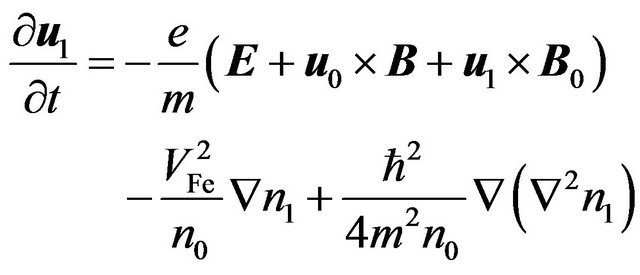 (4)
(4)
The last term in the Equation (4), which representing the Bohm potential, has been perturbatively expanded using [10]. The basic set of linearized equation in homogeneous quantum magnetized cold plasma is:
 (5)
(5)
 (6)
(6)
where,

Taking into account Equation (6) and the expression of k, the following equation is derived:
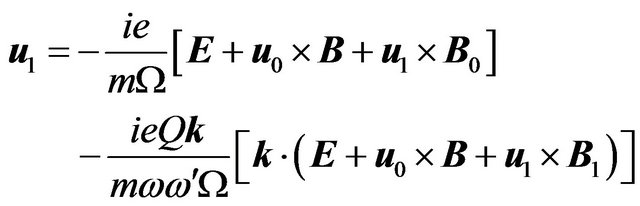 (7)
(7)
where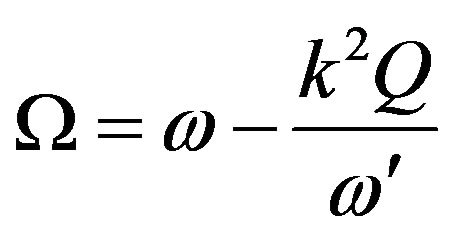 ,
, 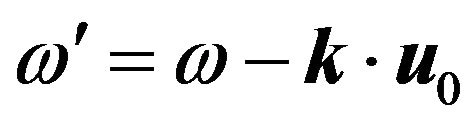 When we have
When we have
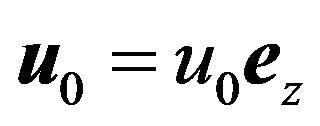 ,
, 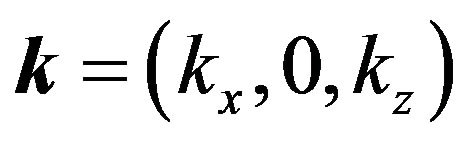 then the current density
then the current density 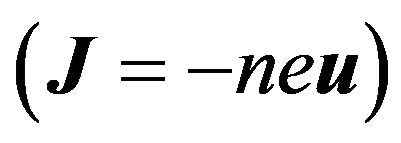 components of the plasma electrons in the plane of circularized polarized laser beam can be written as:
components of the plasma electrons in the plane of circularized polarized laser beam can be written as:
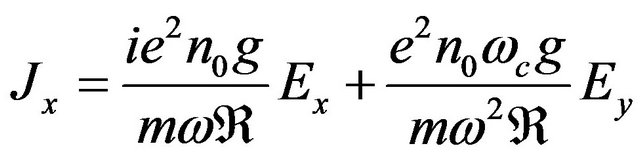 (8)
(8)
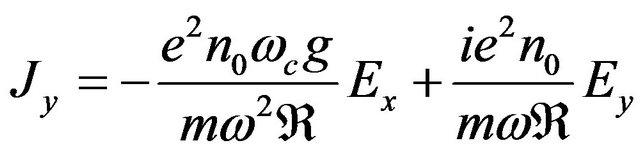 (9)
(9)
where,
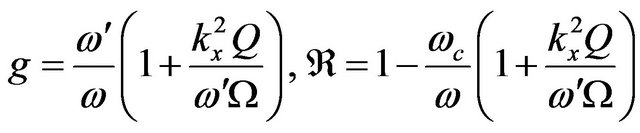
and  is the electron Larmor frequency. But at the same time the current density and the dielectric tensor
is the electron Larmor frequency. But at the same time the current density and the dielectric tensor 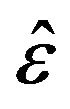 are given by:
are given by:
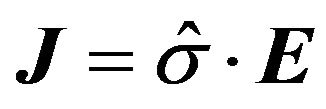 (10)
(10)
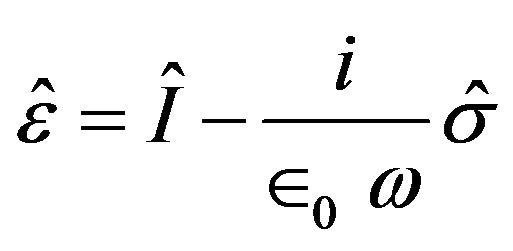 (11)
(11)
Then, according to Equations (8), (9) and (11) we obtain:
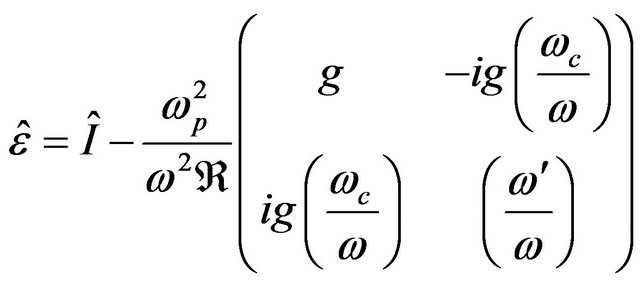 (12)
(12)
where 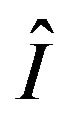 is the unit tensor and
is the unit tensor and 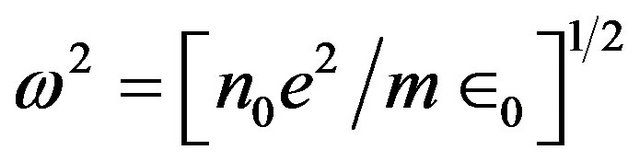 is the electron plasma frequency. Therefore, the dispersion relation can be written as
is the electron plasma frequency. Therefore, the dispersion relation can be written as
 (13)
(13)
where, 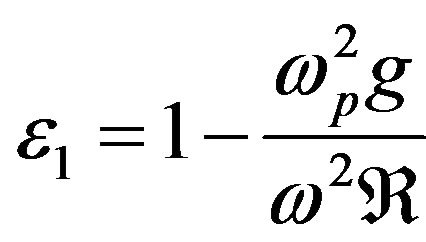 ,
, 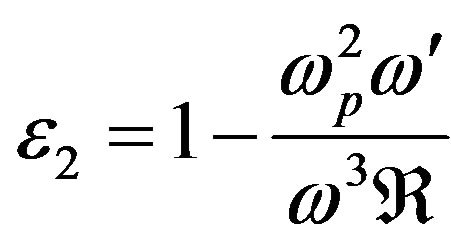 ,
, 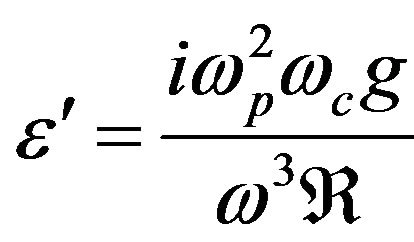 Also,
Also,
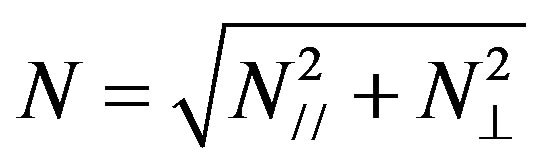 ,
, 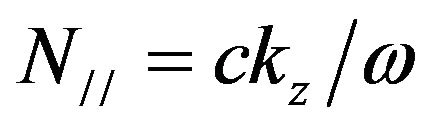 and
and 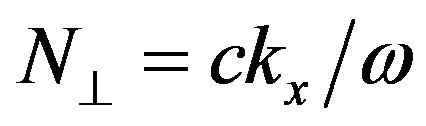
3. Discussions
In this section, we focus our attention to investigate the dispersion relationship (13) analytically and numerically in some cases for 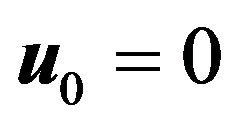 (i.e.,
(i.e.,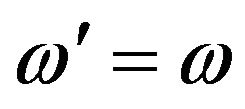 ). First, in the absence of the external magnetic field
). First, in the absence of the external magnetic field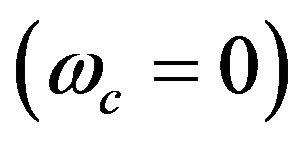 , it is reduced to the following equation:
, it is reduced to the following equation:
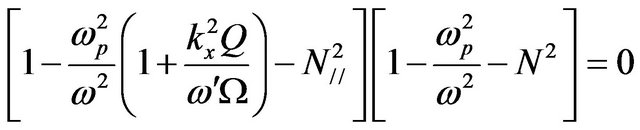 (14)
(14)
which gives two dispersion relations describe the propagation of laser beam in unmagnetized plasma. In this case
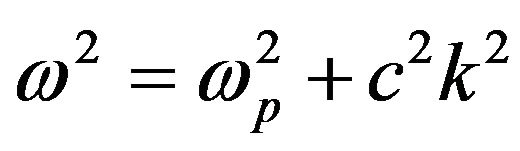 (15)
(15)
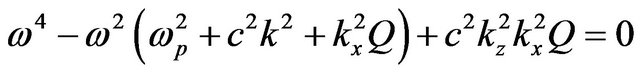 (16)
(16)
It is noticed that Equation (15) is the well known linear dispersion relation of the laser beam propagating in classical plasma  and Equation (16) agrees with Equation (8), in reference [10], which describes the propagation of the linearly polarized laser beam in unmagnetized quantum plasma.
and Equation (16) agrees with Equation (8), in reference [10], which describes the propagation of the linearly polarized laser beam in unmagnetized quantum plasma.
Second, in the case of magnetized plasma and ignoring the quantum effects caused by the Bohm potential and the quantum statistical effects through Fermi temperature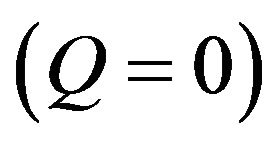 , Equation (13) becomes:
, Equation (13) becomes:
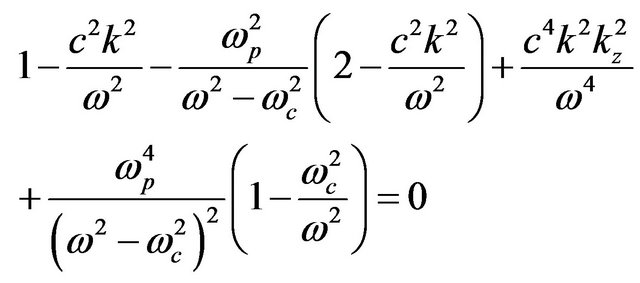 (17)
(17)
It is the dispersion relation of beam laser propagating in classical magnetized plasma which is as the earlier result [14].
Introducing the normalized quantities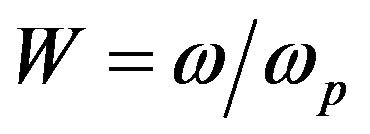 ,
, 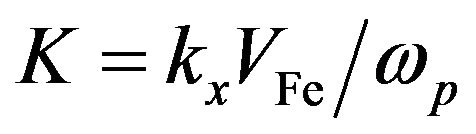 ,
, 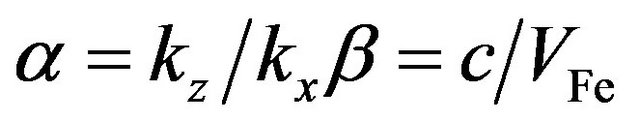 ,
, 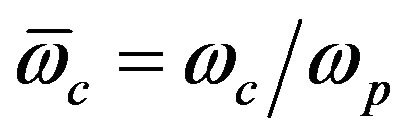 and the plasmonic coupling
and the plasmonic coupling 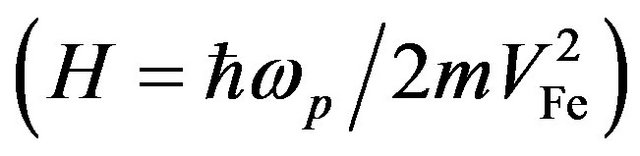 which describes the ratio of plasmonic energy density to the electron Fermi energy density, we rewrite the dispersion relation (16) as:
which describes the ratio of plasmonic energy density to the electron Fermi energy density, we rewrite the dispersion relation (16) as:
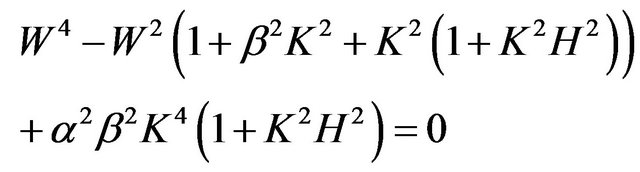 (18)
(18)
For typical parameters of the gold metallic plasma at room temperature [12], n0 = 5.9 × 1022 cm−3, ωp = 1.37 × 1016 s−3, VFe = 1.4 × 108 cm/s, Equation (18) is plotted for different H in Figure 1. It is clear that quantum effects cannot be ignored but become significant only when the wave number is large enough where the dispersion curves for different values of the parameter H = 0, 3, 5 are exactly superposed on each other’s at low wave numbers for unmagnetized plasm as shown in Figure 1. At zero wave number , the wave frequency equals the plasma frequency.
, the wave frequency equals the plasma frequency.
Again, for numerical analysis and using the normalized quantities and the above typical parameters, Equation (13) has been numerically solved to investigate the quantum and magnetic field effects on dispersion relation. Figure 2 displays the normalized frequency 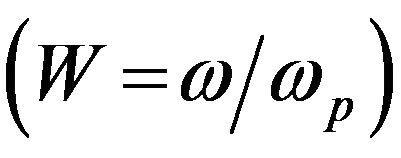 against the normalized wave number
against the normalized wave number 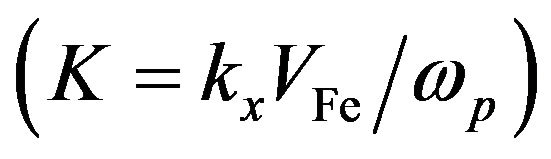 for different plasmonic parameter H = 0, 1, 3, 5. It is found that quantum effects in magnetized plasma also become significant only when the wave number is large enough for
for different plasmonic parameter H = 0, 1, 3, 5. It is found that quantum effects in magnetized plasma also become significant only when the wave number is large enough for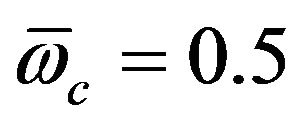 . The dispersion curves for different values of the parameter H are exactly superposed on each other’s at low wave numbers with dispersion curve
. The dispersion curves for different values of the parameter H are exactly superposed on each other’s at low wave numbers with dispersion curve  and has changed faster with larger quantum effects for high wave number.
and has changed faster with larger quantum effects for high wave number.
Besides, Figure 3 displays the effect of the magnetic field on dispersion relation of laser propagation inside

Figure 1. Normalized dispersion relation for the propagation of circularly polarized laser in unmagnetized quantum plasma with H = 0, 3, 5.

Figure 2. Normalized dispersion relation for the propagation of circularly polarized laser in magnetized quantum plasma with H = 0, 1, 3, 5 for ωc = 0.2.
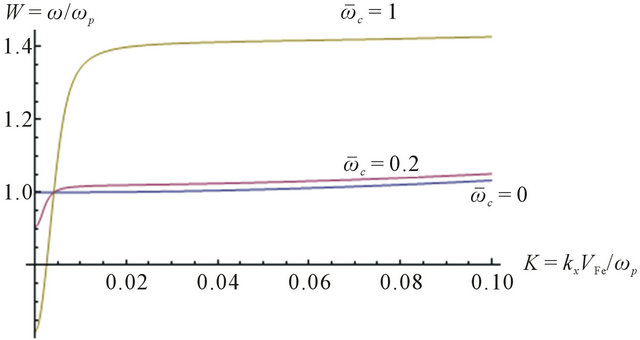
Figure 3. Normalized dispersion relation for the propagation of circularly polarized laser in magnetized quantum plasma at 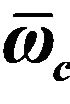 = 0, 0.2, 1 for H = 1.
= 0, 0.2, 1 for H = 1.
quantum plasma (with H = 1) for very low wave numbers. It is shown at zero wave number that wave frequency equals plasma frequency in the case of unmagnetized plasma and it is less than the plasma frequency for stronger magnetic field ( for
for 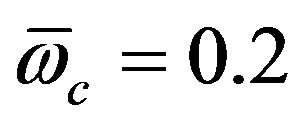 and
and 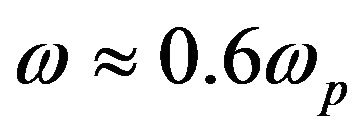 for
for ). For increasing wave number, the wave frequency increased faster with larger magnetic field.
). For increasing wave number, the wave frequency increased faster with larger magnetic field.
4. Conclusion
In this work, we have investigated the general dispersion relation for the propagation of circularized laser beam in uniform electron magnetized quantum plasma based on the (QHD) equations and Maxwell’s equations. Using perturbation technique, the perturbed electron density and current due to the interaction of laser beam with quantum plasma have been obtained. Furthermore, for numerical analysis and using the normalized parameters, the general dispersion equation has been numerically solved to investigate the quantum and magnetic field effects on dispersion relation. It is shown that the quantum effects enhance the propagation phase velocity and for increasing wave number, the wave frequency increased faster with larger magnetic field.
REFERENCES
- P. A. Markowich, C. A. Ringhofer and C. Schmeiser, “Semiconductor Equations,” Springer-Verlag, New York, 1990. doi:10.1007/978-3-7091-6961-2
- G. V. Shpatakovskaya, “Semiclassical Model of a OneDimensional Quantum Dot,” Journal of Experimental and Theoretical Physics, Vol. 102, No. 3, 2006, pp. 466-474. doi:10.1134/S1063776106030095
- M. Marklund, G. Brodin and L. Stenflo, “Electromagnetic Wave Collapse in a Radiation Background,” Physical Review Letters, Vol. 91, No. 16, 2003, 4 p. doi:10.1103/PhysRevLett.91.163601
- L. K. Ang and P. Zhang, “Ultrashort-Pulse Child-Langmuir Law in the Quantum and Relativistic Regimes,” Physical Review Letters, Vol. 98, No. 16, 2007, 4 p. doi:10.1103/PhysRevLett.98.164802
- M. M. Tskhakaya and P. K. Shukla, “Quantum Electrodynamical Shocks and Solitons in Astrophysical Plasmas,” Europhysics Letters, Vol. 72, No. 6, 2005, pp. 950-954. doi:10.1209/epl/i2005-10330-9
- C. Gardner, “The Quantum Hydrodynamic Model for Semiconductor Devices,” SIAM Journal on Applied Mathematics, Vol. 54, No. 2, 1994, pp. 409-427.
- G. Manfredi, “How to Model Quantum Plasmas,” Fields Institute Communications Series, Vol. 46, 2005, pp. 263- 287.
- G. Manfredi and F. Haas, “Self-Consistent Fluid Model for a Quantum Electron Gas,” Physical Review B, Vol. 64, No. 7, 2001, 7 p. doi:10.1103/PhysRevB.64.075316
- H. Ren, A. Wu and P. Chu, “Dispersion of Linear Waves in Quantum Plasmas,” Physics of Plasma, Vol. 14, No. 6, 2007, 6 p. doi:10.1063/1.2738848
- P. Kumar and C. Tiwari, “High Frequency Oscillations in Quantum Plasma,” Journal of Physics: Conference Series, Vol. 208, No. 1, 2010, Article ID: 012051. doi:10.1088/1742-6596/208/1/012051
- A. F. Alexandrov, L. S. Bogdankevich and A. A. Rukhodze, “Principles of Plasma Electrodynamics,” Springer, Berlin, 1984. doi:10.1007/978-3-642-69247-5
- M. Lazar, P. K. Shukla and A. Smolyakov, “Surface Waves on a Quantum Plasma Half-Space,” Physics of Plasma, Vol. 14, No. 12, 2007, Article ID: 124501. doi:10.1063/1.2825278
- H. Ren, Z. Wu, J. Cao and P. K. Chu “Dispersion of Multi-Stream Instability in Quantum Magnetized Hot Plasmas,” Physics Letters A, Vol. 372, No. 15, 2008, 2676- 2683. doi:10.1016/j.physleta.2007.12.028
- J. Lundin, J. Zamanian, M. Marklund and G. Brodin, “Short Wavelength Electromagnetic Propagation in Magnetized Quantum,” Physics of Plasma, Vol. 14, No. 6, 2007, Article ID: 062112. doi:10.1063/1.2743028

