Journal of Modern Physics
Vol.3 No.9A(2012), Article ID:23090,5 pages DOI:10.4236/jmp.2012.329156
On the Stability of Our Universe
Instituto Albert Einstein/Latinamerica, Av. Sete de Setembro 4500 # 101 80250-210, Curitiba, Brazil
Email: msberman@institutoalberteinstein.org, marsambe@yahoo.com, ncacosta@institutoalberteinstein.org, ncacosta@usp.br, ncacosta@terra.com.br
Received June 16, 2012; revised July 20, 2012; accepted July 27, 2012
Keywords: Roberston-Walker’s Universe; Rotation of the Universe; Stability
ABSTRACT
We argue that the Robertson-Walker’s Universe is a zero-energy stable one, even though it may possess a rotational state besides expansion.
1. Introduction
The first pseudo-tensorial calculation of the energy of the Universe, has been made by Berman, in 1981 [1], in his Master of Science Thesis advised by F. M. Gomide. In his three best-sellers (Hawking, in 1996 [2]; in 2001 [3]; in 2003 [4]), Hawking describes inflation (Guth, in 1981 [5]; in 1998 [6]), as an accelerated expansion of the Universe, immediately after the creation instant, while the Universe, as it expands, borrows energy from the gravitational field to create more matter. According to his description, the positive matter energy is exactly balanced by the negative gravitational energy, so that the total energy is zero, and that when the size of the Universe doubles, both the matter and gravitational energies also double, keeping the total energy zero (twice zero). Moreover, in the recent, next best-seller, Hawking and Mlodinow in 2010 [7] comment that if it were not for the gravity interaction, one could not validate a zero-energy Universe, and then, creation out of nothing would not have happened.
In a previous paper Berman (2009 [8]) has calculated the energy of the Friedman-Robertson-Walker’s Universe, by means of pseudo-tensors, and found a zero-total energy. Our main task will be to show that our possibly rotating Robertson-Walkers Universe is stable, in the sense that it has a reparametrized metric of Minkowski’s, while the latter has been shown to be the ground state of energy level among possible universal metrics (see Witten, in 1981 [9]).
The zero-total-energy of the Roberston-Walker’s Universe, and of any Machian ones, have been shown by many authors. It may be that the Universe might have originated from a vacuum quantum fluctuation. By “vacuum”, we mean the spacetime of Minkowski. In support of this view, we shall show that the pseudotensor theory (Adler et al., in 1975 [10]) points out to a null-energy for a rotating Robertson-Walker’s Universe. Some prior work is mentioned: Tryon, in 1973 [11]; Berman (in 1981 [1]; in 2006 [12,13]; in 2007 [14,15], and [16]); Rosen (in 1994 [17], 1995 [18]); York Jr. in 1980 [19]; Cooperstock in 1994 [20]; Cooperstock and Israelit in 1995 [21]; Garecki in 1995 [22]; Johri et al. [23]; Feng and Duan in 1996 [24]; Banerjee and Sen in 1997 [25]; Radinschi, in 1999 [26]; Cooperstock and Faraoni, in (2003 [27]). See also Katz in 2006 [28], and 1985 [29]); Katz and Ori, in 1990[30]; and Katz et al. 1997 [31]. Recent developments include torsion models (So and Vargas, 2006 [32]), and, a paper by Xulu, in 2000 [33].
The reason for the failure of non-Cartesian curvilinear coordinate energy calculations through pseudotensors, resides in that curvilinear coordinates carry non-null Christoffel symbols, even in Minkowski spacetime, thus introducing inertial or fictitious fields that are interpreted falsely as gravitational energy-carrying (false) fields.
2. Reparametrization of Robertson-Walker’s Metric
Consider first Robertson-Walker’s metric, added by a temporal metric coefficient which depends only on t. The line element (Gomide and Uehara, 1981 [34]), becomes:
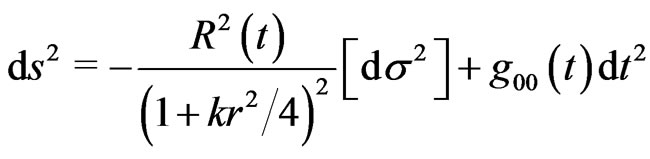 (1)
(1)
Of course, when 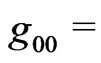 constant, the above equations reproduce conventional Robertson-Walker’s field equations.
constant, the above equations reproduce conventional Robertson-Walker’s field equations.
We must mention that the idea behind RobertsonWalker’s metric is the Gaussian coordinate system. Though the condition 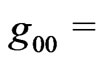 constant, is usually adopted, we must remember that, the resulting time-coordinate is meant as representing proper time. If we want to use another coordinate time, we still keep the Gaussian coordinate properties. Berman (2008 [35]) has interpreted the generalized metric as representing a rotating evolutionary model, with angular speed given by Berman (2011 [36]; 2011 [37]; 2012 [38-40]) and Berman and Gomide (2012 [41-43])
constant, is usually adopted, we must remember that, the resulting time-coordinate is meant as representing proper time. If we want to use another coordinate time, we still keep the Gaussian coordinate properties. Berman (2008 [35]) has interpreted the generalized metric as representing a rotating evolutionary model, with angular speed given by Berman (2011 [36]; 2011 [37]; 2012 [38-40]) and Berman and Gomide (2012 [41-43])
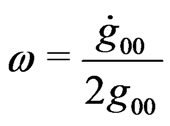
Consider the following reparametrization:
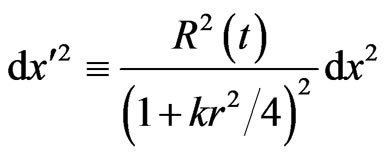 (2)
(2)
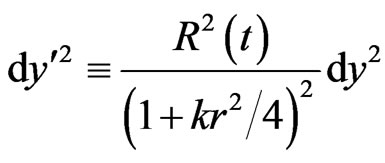 (3)
(3)
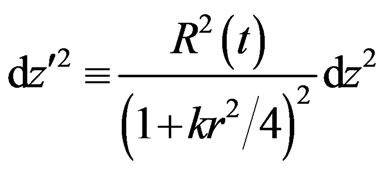 (4)
(4)
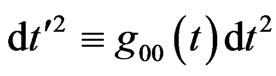 (5)
(5)
In the new coordinates, the generalized RWs metric becomes:
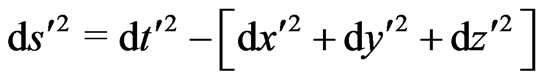 (6)
(6)
This is Minkowski’s metric.
3. Energy and Stability of the Robertson-Walker’s Metric
Even in popular Science accounts (Hawking, 1996 [2]; 2001 [3]; 2003 [4]; and Moldinow, 2010 [7]; Guth, 1981 and 1988 [5,6]), it has been generally accepted that the Universe has zero-total energy. The first such claim, seems to be due to Feynman, in years 1962-1963 [44]. Lately, Berman (2006 [12,13]) has proved this result by means of simple arguments involving Robertson-Walker’s metric for any value of the tri-curvature (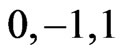 ).
).
Berman and Gomide (2012 [41-43]) has recently shown that the generalized Robertson-Walker’s metric yielded a zero-energy pseudotensorial result. The same authors showed that the result applied in case of a rotating and expanding Universe.
The equivalence principle, says that at any location, spacetime is (locally) flat, and a geodesic coordinate system may be constructed, where the Christoffel symbols are null. The pseudotensors are, then, at each point, null. But now remember that our old Cosmology requires a co-moving observer at each point. It is this co-motion that is associated with the geodesic system, and, as RWs metric is homogeneous and isotropic, for the co-moving observer, the zero-total energy density result, is repeated from point to point, all over spacetime. Cartesian coordinates are needed, too, because curvilinear coordinates are associated with fictitious or inertial forces, which would introduce inexistent accelerations that can be mistaken additional gravitational fields (i.e., that add to the real energy). Choosing Cartesian coordinates is not analogous to the use of center of mass frame in New-tonian theory, but the null results for the spatial components of the pseudo-quadrimomentum show compatibility.
Witten in 1981 [9], proved that within a semiclassical approach, Minkowski’s space was in the ground state of energy, which was zero-valued. He also showed that in Classical General Relativity, this space also was the unique space of lowest energy. This last result was obtained with spinor calculus, and thus could be extended to higher dimensions whenever spinors existed. The proof was obtained through the study of the limit 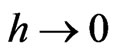 of a supergravity argument by Deser and Teitelboim, in 1977 [45], and by Grisaru, in 1978 [46], where h stands for Planck’s constant.
of a supergravity argument by Deser and Teitelboim, in 1977 [45], and by Grisaru, in 1978 [46], where h stands for Planck’s constant.
The conclusion of Witten was that Minkowski’s space was also stable, because perturbations in the form of gravitational waves should not decrease the total energy, because it is known that gravitational waves have positive energy. We now conclude that our Universe is also stable, due to the reparametrization above. But, first, let us deal with some conceptual issues.
We have three kinds of stability criteria: 1) Since a physical system shows a tendency to decay into its state of minimum energy, the criterion states that the system should not be able to collapse into a series of infinitely many possible negative levels of energy. There should be a minimum level, usually zero-valued, which is possible for the physical system; 2) The matter inside the system must not be possibly created out of nothing,or else, the bodies should have positive energy; 3) “Small” disturbances should not alter a state of equilibrium of the system (it tends to return to the original equilibrium state). In the case of the Universe, disturbances, of course, cannot be external.
According with our discussion, the rotating RobertsonWalkers Universe is locally and globally stable, whenever Classical Physics is concerned. Now, Berman and Trevisan (in 2010 [47]), have shown that Classical General Relativity can be used to describe the scalefactor of the Universe even inside Plancks zone, provided that we consider that the calculated scale-factor behaviour reflects an average of otherwise uncertain values, due to Quantum fluctuations, as Berman and Trevisan suggested in several papers at Los Alamos Archives, during the last decade, and in 2010, when it was published paper [47].
4. Final Comments and Conclusions
Berman and Gomide (2012 [41-43]) and Berman (2012 [38,39]) have obtained a zero-total energy proof for a rotating expanding Universe. The zero result for the spatial components of the energy-momentum-pseudotensor calculation, are equivalent to the choice of a center of Mass reference system in Newtonian theory, likewise the use of comoving observers in Cosmology. It is with this idea in mind, that we are led to the energy calculation, yielding zero total energy, for the Universe, as an acceptable result: we are assured that we chose the correct reference system; this is a response to the criticism made by some scientists which argue that pseudotensor calculations depend on the reference system, and thus, those calculations are devoid of physical meaning.
Related conclusions should be consulted (see all Berman’s references and references therein). As a bonus, we can assure that there was not an initial infinite energy density singularity, because attached to the zero-total energy conjecture, there is a zero-total energy-density result, as was pointed by Berman elsewhere (see, for instance, Berman, in 2009 [48,49]). The so-called total energy density of the Universe, which appears in some textbooks, corresponds only to the non-gravitational portion, and the zero-total energy density results when we subtract from the former, the opposite potential energy density (Berman, 2012 [38,39]).
As Berman (2009 [49,50]) shows, we may say that the Universe is singularity-free, and was created ab-nihilo; in particular, there is no zero-time infinite energy-density singularity.
Rotation of the Universe and zero-total energy were verified for Sciama’s linear theory, which has been expanded, through the analysis of radiating processes, by one of the present authors (Berman, 2008 [51]; 2009 [52]). There, Berman found Larmor’s power formula, in the gravitational version,that leads to the correct constant power relation for the Machian Universe. However, we must remember that in local Physics, General Relativity deals with quadrupole radiation, while Larmor is a dipole formula; for the Machian Universe the resultant constant power is basically the same, either for our Machian analysis or for the Larmor and general relativistic formulae.
Referring to rotation, it could be argued that cosmic microwave background radiation should show evidence of quadrupole asymmetry and it does not, but one could argue that the angular speed of the present Universe is too small to be detected; also, we must remark that CMBR deals with null geodesics, while Pioneers’ anomaly, for instance, deals with time-like geodesics. In favor of evidence on rotation, we remark neutrinos’ spin, parity violations, the asymmetry between matter and antimatter, left-handed DNA-helices, the fact that humans and animals alike have not symmetric bodies, the same happening to molluscs.
We predict that chaotic phenomena and fractals, rotations in galaxies and clusters, may provide clues on possible left handed preference through the Universe.
Berman and Trevisan (2010 [47]) have remarked that creation out-of-nothing seems to be supported by the zero-total energy calculations. Rotation was included in the derivation of the zero result by Berman and Gomide (2012 [41-43]). We could think that the Universes are created in pairs, the first one (ours), has negative spin and positive matter; the second member of the pair, would have negative matter and positive spin: for the ensemble of the two Universes, the total mass would always be zero; the total spin, too. The total energy (twice zeros) is also zero.
Hawking and Mlodinow (2010 [7]) conclude their book with a remark on the fact that the Universe is locally stable, but globally unstable because spontaneous creation is the reason why the Universe exists, and new creations like this may still happen. Of course, this is a question of interpretation.
We now want to make a conjecture related to the stability criteria of last Section.
A physical system is not “chaotic”, if small perturbations in its initial state do not originate “large” variations in its future behaviour. According to our discussion, the Robertson-Walkers Universe, with or without rotation, is locally and globally stable under the three criteria. As its total energy is zero, we conjecture that this type of Universe is not globally chaotic, and that the three criteria for stability imply that any such system cannot be globally chaotic altogether. We remark nevertheless, that because Einsteins field equations are non-linear, chaos is not forbidden in a local sense.
We regret that the name of a basic result in General Relativity Theory, is called “positive energy theorem” instead of the “non-negative energy theorem”. Experimental observational evidence on the rotation of the Universe is dealt with, in the books by Berman (2012 [38, 39]), and references therein. Seminal papers on rotation evidence were due to Paul Birch in 1982, in the wellknown Nature .
5. Acknowledgements
One of the authors (MSB) thanks Marcelo Fermann Guimarães, Nelson Suga, Mauro Tonasse, Antonio F. da F. Teixeira, and for the important incentive offered by Miss Solange Lima Kaczyk,now a brand new advocate, continued during the last five years of his research in Cosmology.
REFERENCES
- M. S. Berman, M.S. Thesis, Instituto Tecnológico de Aeronáutica, São José dos Campos, 1981. http://www.sophia.bibl.ita.br/biblioteca/index.html
- S. W. Hawking, “The Illustrated a Brief History of Time,” Bantam Books, New York, 1996, pp. 166-167.
- S. W. Hawking, “The Universe in a Nutshell,” Bantam Books, New York, 2001, pp. 90-91.
- S. W. Hawking, “The Illustrated Theory of Everything,” Phoenix Books, Beverly Hills, 2003, p. 74.
- A. Guth, Phys. Rev. D, Vol. 23, 1981, p. 347 .
- A. Guth, “The Inflationary Universe,” Vintage, New York, 1998, p. 12.
- S. W. Hawking and L. Mlodinow, “The Grand Design,” Bantam Books, New York, 2010.
- M. S. Berman, “On the Zero-Energy Universe,” International Journal of Theoretical Physics, Vol. 48, No. 11, 2009, pp. 3278-3296. HUdoi:10.1007/s10773-009-0125-8U
- E. Witten, “A New Proof of the Positive Energy Theorem,” Communications in Mathematical Physics, Vol. 80, No. 3, 1981, pp. 381-402. HUdoi:10.1007/BF01208277U
- R. J. Adler, M. Bazin and M. Schiffer, “Introduction to General Relativity,” 2nd Edition, McGraw-Hill, New York, 1975.
- E. P. Tryon, “Is the Universe a Vacuum Fluctuation?” Nature, Vol. 246, No. 5433, 1973, pp. 396-397. HUdoi:10.1038/246396a0U
- M. S. Berman, “Energy of Black-Holes and Hawkings Universe,” In: P. V. Kreitler, Ed., Trends in Black Hole Research, Nova Science, New York, 2006.
- M. S. Berman, “Energy, Brief History of Black-Holes, and Hawkings Universe,” In: P. V. Kreitler, Ed., New Developments in Black Hole Research, Nova Science, New York, 2006.
- M. S. Berman, “Introduction to General Relativity and the Cosmological Constant Problem,” Nova Science, New York, 2007.
- M. S. Berman, “Introduction to General Relativistic and Scalar Tensor Cosmologies,” Nova Science, New York, 2007.
- M. S. Berman, “The Pioneer Anomaly and a Machian Universe,” Astrophysics and Space Science, Vol. 312, 2007, p. 275. http://arxiv.org/abs/physics/0606117.
- N. Rosen, “The Energy of the Universe,” General Relativity and Gravitation, Vol. 26, No. 3, 1994, pp. 319-321. HUdoi:10.1007/BF02108013U
- Rosen, N. GRG, Vol. 27, 1995, p. 313.
- J. W. York Jr, “Energy and Momentum of the Gravitational Field,” In: F. J. Tipler, Ed., A Festschrift for Abraham Taub, Academic Press, New York, 1980.
- F. I. Cooperstock, - GRG Vol. 26, 1994, p. 323.
- F. I. Cooperstock and M. Israelit, “The Energy of the Universe,” Foundations of Physics, Vol. 25, No. 4, 1995, pp. 631-635. HUdoi:10.1007/BF02059009U
- J. Garecki, GRG, Vol. 27, 1995, p. 55.
- V. B. Johri, et al., GRG, Vol. 27, 1995, p. 313.
- S. Feng and Y. Duan, “About the Energy of the University,” Chinese Physics Letters, Vol. 13, No. 6, 1996, p. 409. HUdoi:10.1088/0256-307X/13/6/003U
- N. Banerjee and S. Sen, Pramana J.Phys., Vol. 49, 1997, p. 609.
- I. Radinschi, Acta Phys. Slov., Vol. 49, 1999, p. 789.
- F. I. Cooperstock and V. Faraoni, Ap.J. Vol. 587, 2003, p. 483.
- J. Katz, Private Communication, 2006.
- J. Katz, “A Note on Komar’s Anomalous Factor,” Classical and Quantum Gravity, Vol. 2, No. 3, 1985, p. 423. HUdoi:10.1088/0264-9381/2/3/018U
- J. Katz and A. Ori, “Localisation of Field Energy,” Classical and Quantum Gravity, Vol. 7, No. 5, 1990, p. 787. HUdoi:10.1088/0264-9381/7/5/009U
- J. Katz, J. Bicak and D. Lynden-Bell, Physical Review D, Vol. 55, 1997, p. 5957.
- L. L. So and T. Vargas, Los Alamos Archives, 2006.
- S. Xulu, International Jounal of Theoretical Physics, Vol. 39, 2000, p. 1153.
- F. M. Gomide and M. Uehara, Astronomy and Astrophysics, Vol. 95, 1981, p. 362.
- M. S. Berman, “A General Relativistic Rotating Evolutionary Universe,” Astrophysics and Space Science, Vol. 314, No. 4, 2008, pp. 319-321. HUdoi:10.1007/s10509-008-9772-0U
- M. S. Berman, “The Two Pioneers Anomalies and Universal Rotation,” Astrophysics and Space Science, Vol. 336, No. 2, 2011, pp. 337-339. HUdoi:10.1007/s10509-011-0825-4U
- M. S. Berman, “General Relativity with Variable Speed of Light and Pioneers Anomaly,” Astrophysics and Space Science, Vol. 336, No. 2, 2011, pp. 327-329.
- M. S. Berman, “General Relativity and the Pioneers Anomaly,” Nova Science Publishers, New York, 2012.
- M. S. Berman, “Realization of Einstein’s Machian Program,” Nova Science Publishers, New York, 2012.
- M. S. Berman, “Realization of Einsteins Machian Program: The Pioneers and Fly-By Anomalies,” Astrophysics and Space Science, Vol. 337, No. 1, 2012, pp. 477-481.
- M. S. Berman and F. M. Gomide, “General Relativistic Treatment of Pioneers Anomaly,” Journal of Modern Physics, Special Issue on Gravitation, Astrophysics and Cosmology, 2012.
- M. S. Berman and F. M. Gomide, “Relativistic Cosmology and the Pioneers Anomaly,” Journal of Modern Physics, Special Issue on Gravitation, Astrophysics and Cosmology, 2012.
- M. S. Berman and F. de M. Gomide, “On the Rotation of the Zero-Energy Expanding Universe,” In: J. R. O’Connell and A. L. Hale, Eds., The Big-Bang-Theory, Assumptions and Problems, Nova Science Publishers, New York, 2012.
- R. P. Feynman, “Lectures on Gravitation,” Addison-Wesley, Reading, 1962-1963.
- S. Deser and C. Teitelboim, Physical Review Letters, Vol. 39, 1977, p. 249. HUdoi:10.1103/PhysRevLett.39.249U
- M. Grisaru, Physical Letters, Vol. 73B, 1978, p. 207.
- M. S. Berman and L. A. Trevisan, International Journal of Modern Physics D, Vol. 19, 2010, pp. 1309-1313. http://arxiv.org/abs/gr-qc/0104060
- M. S. Berman, “General Relativistic Singularity-Free Cosmological Model,” Astrophysics and Space Science, Vol. 321, No. 3-4, 2009, pp. 157-160. HUdoi:10.1007/s10509-009-0024-8U
- M. S. Berman, “Why the Initial Infinite Singularity of the Universe Is Not There?” International Journal of Theoretical Physics, Vol. 48, No. 8, 2009, pp. 2253-2258. HUdoi:10.1007/s10773-009-0007-0U
- M. S. Berman, “General Relativistic Singularity-Free Cosmological Model,” Astrophysics and Space Science, Vol. 321, 2009, p. 157. http://arxiv.org/abs/0904.3141
- M. S. Berman, “On the Machian Origin of Inertia,” Astrophysics Space Science, Vol. 318, 2008, pp. 269-272. http://arxiv.org/abs/physics/0609026
- M. S. Berman, “On Sciama’s Machian Cosmology,” International Journal of Theoretical Physics, Vol. 48, No. 11, 2009, pp. 3257-3261. HUdoi:10.1007/s10773-009-0112-0U
- D. W. Sciama, M.N.R.A.S., Vol. 113, 1953, p. 34.
- M. S. Berman, “A Primer in Black Holes, Mach’s Principle and Gravitational Energy,” Nova Science, New York 2008.

