Journal of Modern Physics
Vol.2 No.12(2011), Article ID:16506,3 pages DOI:10.4236/jmp.2011.212188
The Ionic and Electron Stream Acceleration
Federal State Unitary Enterprise “All-Russian Electrotechnical Institute Named after V.I. Lenin” (VEI), State Science Center Russian Federation, Moscow, Russia
E-mail: churchev@mail.ru
Received October 7, 2011; revised November 11, 2011; accepted November 29, 2011
Keywords: Isentropic state, ions flow, electrons flow, ion-acoustic speed
ABSTRACT
The work deals with the steady flows of ions and electrons coinciding in quantity and direction. The onedimensional problem considers the cold ions and electrons characterized by the isentropic state. The area was defined in which the speed of ions exceeds the ion-acoustic speed. The problem may be of interest for the creation of accelerators in which the charged particles have to leave the accelerator in pairs excluding the possibility of charge accumulation in the accelerator.
1. Introduction
The solution of the fundamental problems of plasma dynamics is of interest to energy efficient thrusters and analysis of states of the plasma that forms around the spacecraft analysis of states of the plasma that forms around the spacecraft.
In Specifically, should create an conditions in which there is no charge accumulation on the spacecraft. Is commonly used “cathode-compensator” (see [1]).
The problem also is the appearance of “sound singularity” in the thruster (see [2-4]), which appears with using the quasi-neutral approach, but in [5] it is shown that the singularity appears due to an inadequate description of the system.
In the work [6] the acceleration of heavy ions with the counter flows of ions and electrons was explored, moreover the electrons were characterized by the isotherm equation of condition 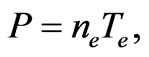 where
where 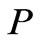 is pressure,
is pressure, 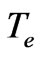 is the temperature of electrons,
is the temperature of electrons, 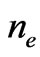 - electron density. The present work deals with the states with electrons characterized by the isentropic equation of condition considering that the flows of particles coincide in quantity and direction. It will be shown that the ions flow rate continuously passes through the value corresponding to ion-sound barrier.
- electron density. The present work deals with the states with electrons characterized by the isentropic equation of condition considering that the flows of particles coincide in quantity and direction. It will be shown that the ions flow rate continuously passes through the value corresponding to ion-sound barrier.
The electrons are considered to be the monatomic ideal gas which is described by the equation of condition:
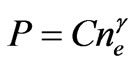 (1)
(1)
where 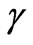 is an adiabatic index. For the monatomic gas
is an adiabatic index. For the monatomic gas . It is suitable to represent the constant C as:
. It is suitable to represent the constant C as:
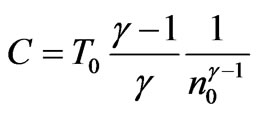 , here
, here  is a constant of the energy dimension (temperature),
is a constant of the energy dimension (temperature), 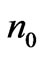 is the initial electron density.
is the initial electron density.
2. Equations
The one-dimensional hydrodynamic equation of the electron motion is as follows:
 (2)
(2)
where  is the speed of electrons,
is the speed of electrons, —the potential,
—the potential, —the electron charge and mass,
—the electron charge and mass, —the axial coordinate.
—the axial coordinate.
This equation can be integrated:
 (3)
(3)
The equation (3) is modified Bernoulli equation describing the equilibrium of the fluid in an external field (see [7]).
In (3) the quantity 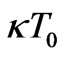 is the integration constant.
is the integration constant.
The ions are described by means of the relation:
 (4)
(4)
where —the velocity,
—the velocity, —the initial velocity of the ion flow, M—the ion mass.
—the initial velocity of the ion flow, M—the ion mass.
Let us introduce the parameter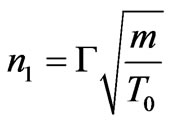 , where
, where
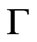 is the stream of particles. Let us denote
is the stream of particles. Let us denote
 . It is suitable to introduce the dimensionless length:
. It is suitable to introduce the dimensionless length: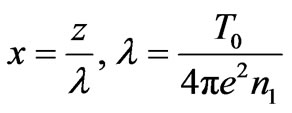 .
.
From the Poisson equation: 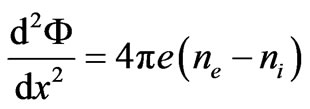 (
(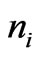
—the ion density) using (3) and (4) ( ), the equality of the ion and electron streams, we shall get:
), the equality of the ion and electron streams, we shall get:
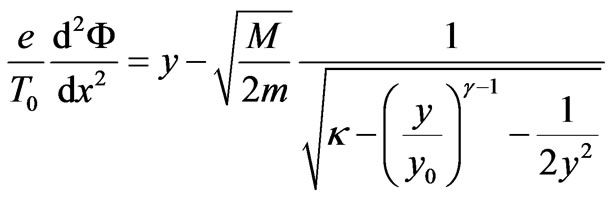 (5)
(5)
Substituting 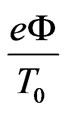 from (3) we shall get the equality:
from (3) we shall get the equality:
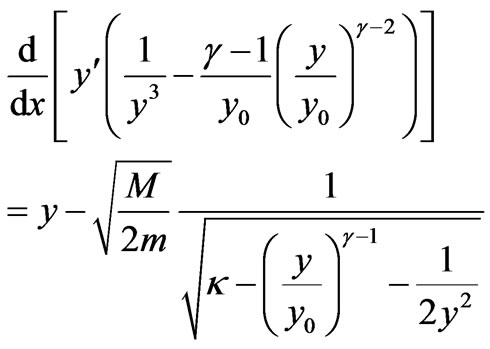 (6)
(6)
The equation (6) has the integral:
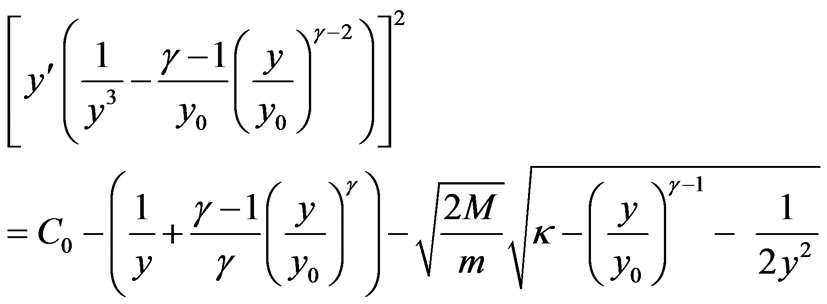 (7)
(7)
Hereinafter we will solve the Equation (7) in view of 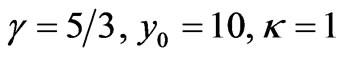 as well as assuming that
as well as assuming that
 , i.e. we will consider the plasma of the singly-ionized xenon.
, i.e. we will consider the plasma of the singly-ionized xenon.
3. The Solve of the Equations
Let us explore the behavior of the second member of the equation (7) with these parameter values. Figure 1 shows the behavior of the function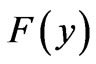 :
:
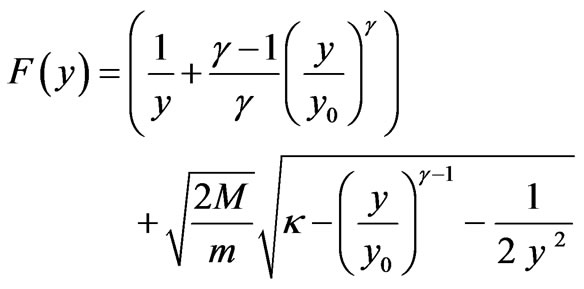
It can be seen from this figure that the equation (7) has meaning for all the values of y, if 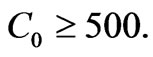 Figure 2 shows the solution of the equation (7) with
Figure 2 shows the solution of the equation (7) with  and with the initial value
and with the initial value . It was considered that
. It was considered that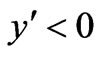 , meanwhile the electron density decreases with the rise of
, meanwhile the electron density decreases with the rise of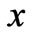 , the pressure gradient accelerates the electrons in the same direction with the electric field accelerating the ions. The pressure gradient value is sufficient for the deceleration force excess on the part of the electric field.
, the pressure gradient accelerates the electrons in the same direction with the electric field accelerating the ions. The pressure gradient value is sufficient for the deceleration force excess on the part of the electric field.
According to the equation of the ideal gas condition, the temperature of the electron stream is the function of the axial coordinate:
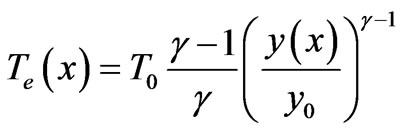
The ion flow velocity is defined by means of the expression:
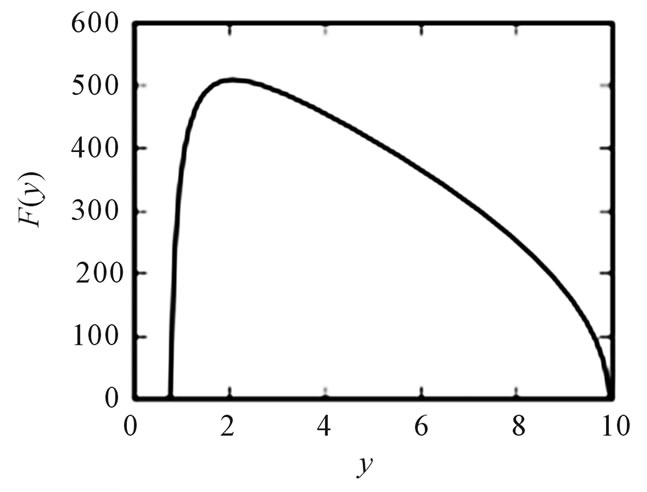
Figure 1. Graph of the function F(y), which describe the right-hand side of equation (7).

Figure 2. The solution of equation (7).
 .
.
For the comparison of the ion-acoustic speed
(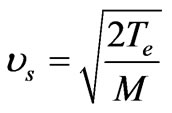 ) with the ion flow velocity the Figure 3 shows the dependance
) with the ion flow velocity the Figure 3 shows the dependance 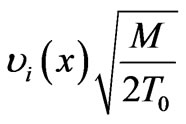 and
and
 on the longitudional coordinate.
on the longitudional coordinate.
The ion flow velocity increases and starts ranking over the value of the ion-acoustic speed even at small values of .
.
Let us calculate the density of the electron and ion charges in the acceleration gap. These values are shown in Figure 4 in logarithmic scale as the functions of the axial coordinate.
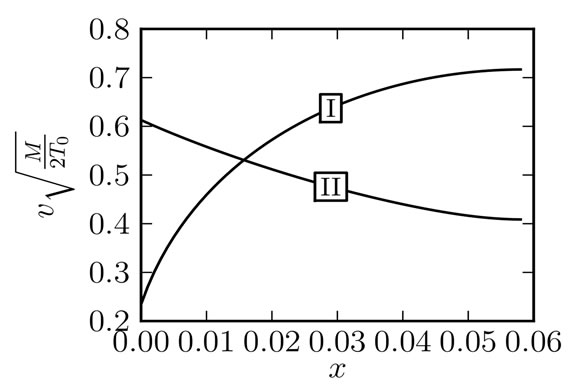
Figure 3. Dependance —curve I, and
—curve I, and 
 —curve II on the longitudional coordinate.
—curve II on the longitudional coordinate.
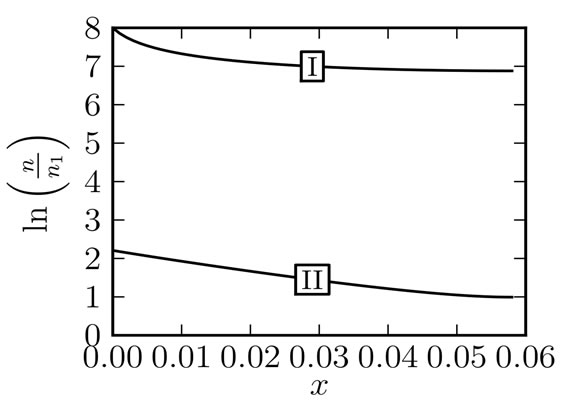
Figure 4. Dependance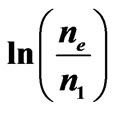 —curve I, and
—curve I, and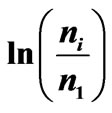 — curve II on the longitudinal coordinate.
— curve II on the longitudinal coordinate.
It can be seen from Figure 4 that the ion density in the acceleration gap (curve II) significantly exceeds the electron density (curve I). The electron density decrease has to be large in order to create the acceleration force exceeding the deceleration force on the part of the electric field which accelerates the ions.
It should be mentioned that in the considered values range of the axial coordinate the coefficient of  does not go to zero. The range related to the zero crossing of this coefficient needs the further exploration. Furthermore, the higher values the coefficient
does not go to zero. The range related to the zero crossing of this coefficient needs the further exploration. Furthermore, the higher values the coefficient  has (i.e.
has (i.e. ), the greater effect of the ion acceleration can be achieved.
), the greater effect of the ion acceleration can be achieved.
Thus, the present work shows that basically it is theoretically possible to achieve the simultaneous electron and ion acceleration with the streams of particles with the opposite charges which coincide in the quantity and the direction. This circumstance is quite significant for the electrojet engines creation—the particles with the opposite charges leave the device in pairs which enables to avoid the charge accumulation in the accelerator.
REFERENCES
- A. N. Ermilov and Yu. A. Kovalenko, et al., “Experimental Investigations of a Breadboard Model of Hall Thruster,” High Temperature, Vol. 46, No. 4, 2008, pp. 535- 541. doi:10.1134/S0018151X08040147
- J. Ashkenasy, A. Fruchtman, Y. Raitses and N. Fish, “Modelling the Behaviour of a Hall Current Plasma Accelerator,” Plasma Physics and Controlled Fusion, Vol. 41, No. 3A, 1999, pp. A357-A364. doi:10.1088/0741-3335/41/3A/029
- E. Ahedo, J. M. Gallardo and M. Martines-Sanches, “Model of the Plasma Discharge in a Hall Thruster with Heat Conduction,” Physics of Plasmas, Vol. 9, No. 9 2002, pp. 4061-4070. doi:10.1063/1.1499496
- T. M. Sapronova and A. S. Chikhachev, “An Acoustic Singularity of a Plasma Flow in a Hall Accelerator (Thruster),” Journal of Comunications Technology and Electronics, Vol. 55, No. 3, 2010, pp. 347-351. doi:10.1134/S1064226910030150
- T. V. Chernyshev, A. S. Chikhachev and A. N. Shramov, “Modelling of Dynamic of Particles in Thruster,” Applied Physics, No. 4, 2010, pp. 64-68.
- Yu. A. Kovalenko, T. V. Chernyshev and A. S. Chikhachev, “Acceleration of the Heavy Ions, When Ion and Electron Fluxes Are Equal,” Izvestiya RAN, Energetics Series, No. 4, 2011, pp. 24-28.
- L. D. Landau, E. M. Lifshits, “Teoreticheskaya Fizika,” Gidrodinamika, Moscow, 1986.

