Journal of Modern Physics
Vol. 2 No. 11 (2011) , Article ID: 8639 , 17 pages DOI:10.4236/jmp.2011.211165
Transformation of the Angular Power Spectrum of the Cosmic Microwave Background (CMB) Radiation into Reciprocal Spaces and Consequences of This Approach
Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
E-mail: L.Cervinka@icaris.cz
Received July 30, 2011; revised September 8, 2011; accepted September 20, 2011
Keywords: CMB Radiation, Analysis of CMB Spectrum, Radial Distribution Function of Objects, Early Universe Cluster Structure, Density of Ordinary Matter
ABSTRACT
A formalism of solid state physics has been applied to provide an additional tool for the research of cosmological problems. It is demonstrated how this new approach could be useful in the analysis of the Cosmic Microwave Background (CMB) data. After a transformation of the anisotropy spectrum of relict radiation into a special two-fold reciprocal space it was possible to propose a simple and general description of the interaction of relict photons with the matter by a “relict radiation factor”. This factor enabled us to process the transformed CMB anisotropy spectrum by a Fourier transform and thus arrive to a radial electron density distribution function (RDF) in a reciprocal space. As a consequence it was possible to estimate distances between Objects of the order of ~102 [m] and the density of the ordinary matter ~10–22 [kg∙m–3]. Another analysis based on a direct calculation of the CMB radiation spectrum after its transformation into a simple reciprocal space and combined with appropriate structure modelling confirmed the cluster structure. The internal structure of Objects may be formed by Clusters distant ~10 [cm], whereas the internal structure of a Cluster consisted of particles distant ~0.3 [nm]. The work points in favour of clustering processes and to a cluster-like structure of the matter and thus contributes to the understanding of the structure of density fluctuations. As a consequence it may shed more light on the structure of the universe in the moment when the universe became transparent for photons. On the basis of our quantitative considerations it was possible to derive the number of particles (protons, helium nuclei, electrons and other particles) in Objects and Clusters and the number of Clusters in an Object.
1. Introduction
The angular power spectrum (anisotropy spectrum) of the Cosmic Microwave Background (CMB) radiation ([1,2]) shows incredible similarity with X-ray or neutron scattering measured on non-crystalline materials ([3], [4]), see Figures 1 and 2.
Astronomers ascribe to various peaks of the anisotropy spectrum of the CMB radiation different processes [5]. It is the Sachs-Wolf effect, Doppler effect, Silk damping, Rees-Sciama effect, Sunyaev-Zeldovich effect, etc. In this connection it should be stated that all theoretical predictions of the standard cosmological model are in very good agreement with the course of the anisotropy spectrum of CMB radiation.
However, the formal similarity in the form of both figures initiates the tempting idea if an analysis of the anisotropy spectrum of relict radiation using an analogous approach as is common in solid state physics, i.e. in the structural analysis of disordered materials, would bring more information on the structure of the early universe.
The inspiration for this approach we found further in the nowadays situation: Although the individual disciplines in physics are highly specialized, nevertheless their methods and results are shared in areas that at the first sight may seem to be far apart. An example of this is the already established use of elementary particle physics
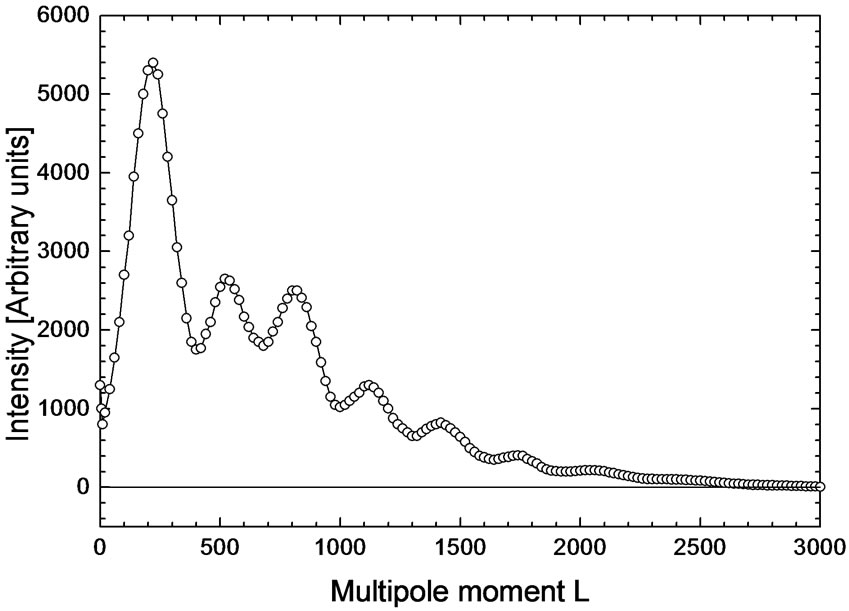
Figure 1. Anisotropy spectrum of the CMB radiation [1]. The figure describes the dependence of the magnitude of the intensity of microwave background on the multipole moment L = 180˚/α, where α is the angle between two points in which the temperature fluctuations are compared to an overall medium temperature. The description of the Y-axis is for simplicity described in [Arbitrary units]. The original description was given as L(L + 1)CL/2π in [μK2] units, where L is the multipole moment, CL is a function reflecting the width of the window measuring the temperature fluctuations.

Figure 2. X-ray scattering diagram taken on a sample of a chalcogenide glass of a composition (Ge0.19Ag0.25Se0.50) using the MoKα radiation, see [4] for detail. The reciprocal space scattering vector s is defined in Equation (A5).
in cosmology.
Similarly, we hope that it may be time now to apply the formalism of solid state physics to some special cosmological problems and in this way to provide an additional tool for their research.
First of all our new approach may be useful in the analysis of the CMB data. We will show how after the transformation of the anisotropy spectrum of relict radiation into a special two-fold reciprocal space we will be able to process the transformed CMB anisotropy spectrum by a Fourier transform and thus calculate a radial distribution function (RDF) of the matter in a reciprocal space. Because the CMB radiation reflects the fluctuations in the density of the matter, we hope that in this way our study will contribute to the understanding of the structure of these density fluctuations. Simultaneously, as a consequence, it may shed more light on the structure of the universe in the moment when the universe became transparent for photons (see Subsection 5.1.).
Moreover, in contrast to solid state physics where the atomic (coherent) and Compton (incoherent) scattering factors are describing theoretically the interaction of X-rays (or neutrons) with all kinds of atoms, this new formalism will present a general description of the interaction of relict radiation with the matter by a single “relict radiation factor”, which should unify all processes realized during the interaction of relict radiation with various kinds of particles forming the primordial matter, see Subsections 2.3.3. and 5.2.
2. Construction of the Classic and Relict Reciprocal Space
In solid state physics the principal mathematical method during the structure analysis of the matter is the Fourier transform of the intensity of X-rays (or neutrons) scattered by atoms building the material. The experimental data are collected in the reciprocal space and their Fourier transform brings the required information on the distribution of atoms in the real space. In this contribution we will try to apply this approach to the CMB spectrum (see Figure 1) and simultaneously point out the complications we have to overcome in this direction.
The necessary basic mathematical apparatus is summarized in the Appendix A, the most important basic equations for the analysis of “scattered” radiation and leading to the radial density distribution function (RDF) are Equations (A1) and (A2). The essential difference in the use of terms “scattering” and “interaction” of photons will be elucidated in the next Subsection 2.1.
2.1. The Relict Radiation Factor
During a conventional structure analysis with X-rays or neutrons, the X-ray or neutron atomic scattering factors are a precise picture of the interaction of radiation with the matter and are known precisely [6]. They enter into the calculation of the RDF in correspondence with the composition of the studied material; see Equations (A6), (A7) and (A10). Generally, for coherent scattering, the atomic scattering factor f is the ratio of the amplitude of X-rays scattered by a given atom Ea and that scattered according to the classical theory by one single electron Ee, i.e. 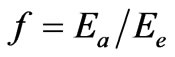 (
( ), where Z is the number of electrons in the atom.
), where Z is the number of electrons in the atom.
Moreover, there are scattering factors not only for the coherent but also for the incoherent (Compton) type of scattering, see e.g. later on Figure 6.
In our study, however, the basic obstacle is that with CMB photons we have not a classic scattering process of photons on atoms; i.e. a process described in equations of the Appendix A. There are not atoms, there are particles only (e.g. baryons, electrons, etc.), which participate in the formation of the structure of density fluctuations. Therefore we will speak throughout this article about an “interaction” instead of “scattering” in all cases when instead of the classic “atomic scattering factor” the new “relict radiation factor” will be used.
It is true that a part of the interaction of photons with electrons before the recombination may be realised as Thomson scattering (elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism)1, but the complex picture of physical processes describing the interaction of relict photons with the non uniform matter composed of various particles (electrons, ions, etc.) is not known to such an extent in order to enable a theoretical calculation of this interaction (on the basis of scattering factors).
It is therefore evident that it will not be possible to use the conventional atomic scattering factors and that a new special factor reflecting the complexity of interaction processes of photons with the primordial matter has to be constructed. We only point out that the description of these interactions is possible only in a special two-fold reciprocal space into which the CMB spectrum is transformed. This new factor will be called the relict radiation factor and substitutes all complicated processes which participate in the formation of the angular power spectrum of CMB radiation.
The construction of the relict radiation factor is presented in Subsection 2.3.3.
2.2. The Wavelength of Radiation
The wavelength of radiation is a quantity of highest importance, too. It follows from Equation (A5), that the greater the wavelength the smaller is the maximal possible value smax of the reciprocal space vector. At the same time the upper limit of the integral in Equation (A2) strongly influences the quality of the Fourier transform.
Although there is a broad distribution of wavelengths of photons (see later on the discussion in Subsection 5.3.) the calculation will be undertaken for the wavelength corresponding to the maximum of the wavelength distribution which corresponds to the temperature 2.725 K of the Universe today (see later on Figure 18), i.e. for the wavelength λ = 1.9 [mm].
That this wavelength is rational is based on three arguments. First of all photons with this wavelength bring us the information on their last several interactions with particles today, in the second place the CMB radiation spectrum is the same for all wavelengths and in the third place the wavelength corresponding to the maximum of the wavelength distribution secures the highest probability of the interaction process of photons with the matter.
2.3. Preparatory Calculations
2.3.1. The Classic Reciprocal Space
During a classic scattering experiment we measure the intensity of the scattered radiation (e.g. X-rays) as a function of the scattering angle θClassic. This scattering angle describes in real space the angle between the incident and scattered radiation. Its relation with the scattering vector in reciprocal space was described in Equation (A5).
On the other hand the angle α in the anisotropy spectrum of relict radiation (see already Figure 1) is not a scattering angle. It is an angle characterizing the distance between an arbitrary point to another—in those different points the temperature fluctuation is measured and compared with the overall medium one.
In order to overcome the incomparableness between the angles α and θ, we will construct an angle dependent reciprocal space to the angle α. The basic quantity determining this reciprocal space will be the scattering angle θClassic.
We will suppose that the maximum possible value of the classic scattering angle 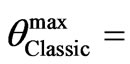 90˚, corresponds to the maximum value of the multipole moment Lmax = 3000.
90˚, corresponds to the maximum value of the multipole moment Lmax = 3000.
As a consequence we receive a transformation coefficient Q
 , (1)
, (1)
(its value in this case is Q = 0.03).
We are then able to calculate the whole set of θClassic angles
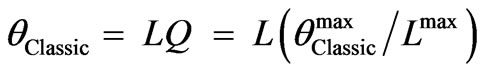 (2)
(2)
and because L = 180/α, then
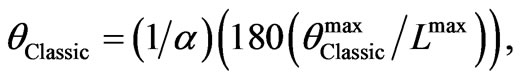 (3)
(3)
i.e.
 (4)
(4)
where
 (5)
(5)
is a coefficient enabling the transition between the space α and the space θClassic and where the angular space θClassic is reciprocal to the angular space α.
According Equation (A5) we are now able to construct the whole set of scattering vectors sClassic
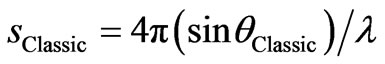 , (6)
, (6)
where λ is the wavelength of the relict radiation. It should be noted that the quantities sClassic and α are in an indirect relation. The space of the vector sClassic will be further on called a “Classic reciprocal space”.
It should be pointed out that in this construction (see Equation (6)) the scattering vector sClassic is defined in the reciprocal space (1/λ) and that this space is now dipped into the reciprocal space (1/α), see Equations (2), (4) and (6). For this “dipping” we will use further on the expression that the space sClassic is a 2-fold reciprocal space to the space α.
The recalculation of the original data presented in Figure 1 using Equations (4) and (6) is shown in Figure 3. This new intensity dependence is labelled IClassic ( ).
).
2.3.2. The Relict Reciprocal Space
There is a possibility to construct another reciprocal space which will be based directly on the angle α. For a better comparison and lucidity we will use now for the angle α the labelling θRelict. i.e.
 , (7)
, (7)
hence L = 180˚/α = 180˚/θRelict. (8)
In close analogy with Equation (A5) we now transform the anisotropy spectrum of CMB (relict) radiation into a reciprocal space (1/λ) described by the parameter SRelict
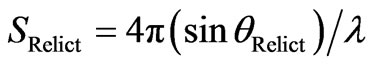 , (9)
, (9)
where λ is the wavelength of the relict radiation. The space of the vector SRelict will be further on called the “Relict reciprocal space”.
It should be noted that quantities SRelict and 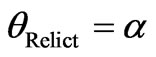 are in a direct relation. The anisotropy spectrum of the CMB radiation rescaled on the basis of Equation (9) is here labelled IRelict (SRelict) and is shown in Figure 4.
are in a direct relation. The anisotropy spectrum of the CMB radiation rescaled on the basis of Equation (9) is here labelled IRelict (SRelict) and is shown in Figure 4.
2.3.3. Construction of the Relict Radiation Factor
Generally, a correct scattering factor has to fulfil three criterions:

Figure 3. Anisotropy spectrum of the relict radiation shown in Figure 1 is recalculated as a function of sClassic, i.e. after a rescaling of the angular moment L and is labelled IClassic (sClassic). The rescaling of the angular moment L is realized on the basis of Equations (2), (4) and (6) and using the MoKα radiation wavelength λ = 0.071609 [nm].

Figure 4. Anisotropy spectrum of the relict radiation shown in Figure 1 is after a rescaling of the angular moment L, recalculated as a function of the relict reciprocal space vector SRelict and labelled IRelict (SRelict). The rescaling of the angular moment L is realized on the basis of Equations (8), (9) and (11) using the MoKα radiation wavelength λ = 0.071609 [nm]. The dashed line represents a smoothed curve.
1) the Inorm (s) curve should oscillate along the Igas (s) curve and as a consequence according Equation (A9);
2) the curve Idistr (s) should oscillate along the zero value of the intensity axis;
3) the resulting RDF must not be contaminated by parasitic fluctuations due to bad scaling (see Section A2.) as a consequence of a bad course of the scattering factor.
The mutual relation between quantities Inorm (s), Igas (s) and Idistr (s) is explained in the Appendix A, see Equations (A9), (A10) and (B1) with (B2).
In Figure 5 the calculation of the crucial curve Igas is undertaken for the relict radiation factor fRelict. The form of this factor was determined by the trial and error method and is shown in Figure 6. In this figure is the factor fRelict compared with the coherent ( ) and incoherent (
) and incoherent (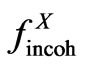 ) atomic scattering factor for X-rays corresponding to the Hydrogen atom (according the International Tables for Crystallography [6]).
) atomic scattering factor for X-rays corresponding to the Hydrogen atom (according the International Tables for Crystallography [6]).
Similarly as for X-rays we have set the relict radiation factor fRelict
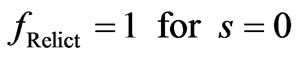 (10)
(10)
and further, we have set in Equation (A7) Z = 1 and m = 1, hence in Equation (A6) is Km = 1. From this point of view our construction of the relict radiation factor fRelict should formally correspond to a “hydrogen-like” particle.
Further we have to point out that in connection with the presentation of the quantity Igas(s) in Equation (A10) its course in Figure 5 is given now by the relation
 . (11)
. (11)
In Figure 5 we see that the function Inorm(s) is properly oscillating along the function Igas(s) and therefore the function Idistr(s) is properly oscillating along the zero line. The consequence is that we will obtain a “proper” radial distribution function, i.e. without any parasitic maxima, see the Subsection 3.1.
2.3.4. Relation between the Classic and Relict Distribution of Distances
We rewrite now the basic Equation (A2) using the scat-
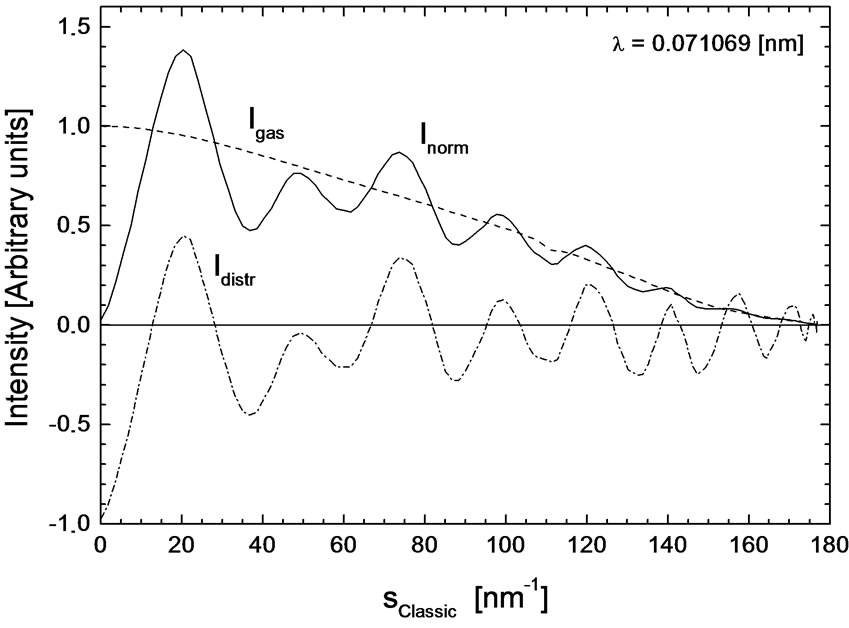
Figure 5. Calculation of quantities Inorm (s)—full line, Igas (s) —dashed line (see Equation (11)) and of Idistr (s)—dashed dotted line, according Equations (A9), (A10) and (B1), (B2) using the “artificial” relict radiation factor fRelict for the wavelength λ = 0.071069 [nm]. Oscillations of the curve Idistr (s) are along the x-axis; hence the criterions set at the beginning of this section are fulfilled. See text for details.
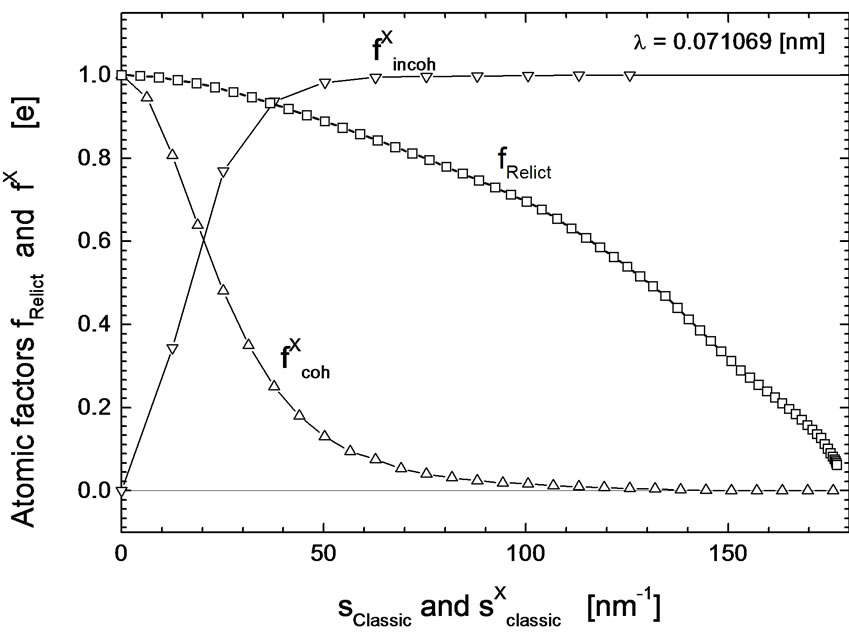
Figure 6. Behaviour of the relict radiation factor fRelict is shown. For comparison the courses of the classic coherent and incoherent X-ray atomic scattering factors 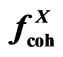 and
and 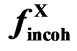 for Hydrogen are included. The parameter sClassic is defined in Equation (6), the parameter
for Hydrogen are included. The parameter sClassic is defined in Equation (6), the parameter  is described in Equation (A5). Data for
is described in Equation (A5). Data for  and
and 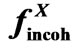 are taken from [6]. The calculation is demonstrated for the wavelength λ = 0.071069 [nm].
are taken from [6]. The calculation is demonstrated for the wavelength λ = 0.071069 [nm].
tering vector in the classic reciprocal space sClassic, see Equation (6).
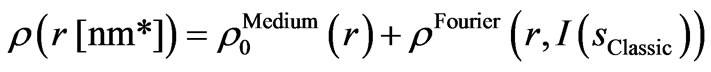 , (12)
, (12)
where  is the member which is not Fourierdependent and describes the structure-less total disorder depending on the density of the matter.
is the member which is not Fourierdependent and describes the structure-less total disorder depending on the density of the matter.
The parameter r is measured in [nm*] in order to emphasize that the calculation of the RDF ρ(r) is realized on the basis of the parameter sClassic, which is dipped in a 2-fold reciprocal space (see Subsection 2.3.1.). In other words: the calculation of the RDF ρ(r) is realized in the reciprocal space of classic distances, which have the dimension [nm*]. Here we again point out the fact, that classic distances are distances between Objects calculated on the basis of the function IClassic (sClassic), see Figure 3, which we analyze using Equation (A2) or (12).
In order to receive now the information in the real space of classic distances (characterized by the parameter R) we must calculate the reciprocal value of the parameter r, hence the relation between r and R is
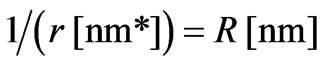 . (13)
. (13)
It would be now possible to rewrite quite formally Equation (A2) using the scattering vector in the relict reciprocal space SRelict, see Equation (9). Similarly as for Equation (12) we would receive
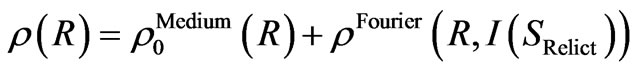 . (14)
. (14)
Quite hypothetically the RDF ρ(R) would then bring us information on the real space of relict distances, which have the dimension [nm]. Actually, however, a RDF will not be calculated in this case, because the distribution I(SRelict), see Figure 4, is not convenient for a Fourier transform. The calculation of relict distances in the real space, i.e. of distances between complex Objects (big clusters) will be done on the basis of a theoretical calculation of the function I(SRelict)) using the Debye formula (18) calculated for appropriate models, see later on Section 4.
3. Calculations in the Classic Reciprocal Space sClassic
3.1. Calculation of RDFs
In our first example we calculate in Figure 7 the RDF of Objects corresponding to the Fourier transform of intensities  for the wavelength λ = 0.071069 [nm] which is a frequently used wavelength (λMoKα) in e.g. structure analysis, see Equation (A2) andor (12). The scaling of intensities has been already demonstrated in Figure 5 on the basis of the relict radiation factor fRelict constructed in Figure 6.
for the wavelength λ = 0.071069 [nm] which is a frequently used wavelength (λMoKα) in e.g. structure analysis, see Equation (A2) andor (12). The scaling of intensities has been already demonstrated in Figure 5 on the basis of the relict radiation factor fRelict constructed in Figure 6.
The calculated RDF shows a form typical for RDFs obtained for disordered materials. It turns out that in the region from 0.1 to 0.4 [nm*] we observe peaks 0r and 1r. Moreover there is a minimum minr which separates this region from a structure-less course starting at the position 2r. Such behaviour indicates the existence of ordering in the matter. In other words, there is a distinctive separation of the matter ending its ordering at 1r = 0.312 [nm*] from the residual structure-less phase which starts at 2r = 0.395 [nm*]. For these reasons we will consider as a boarder between the ordered and disordered state the gap at minr = 0.348 [nm*].
In the same way we calculated RDFs for four more typical wavelengths, i.e. 0.110674 (λSeKα), 0.154178 (λCuKα), 0.250466 (λVKα) and 0.537334 [nm] (λSKα). From these calculations it follows that, as expected, the dependence of the magnitude of corresponding coordination spheres on the wavelength λ is linear, see Figure 8, moreover, all RDFs had the same appearance.
In this connection we have to point out, that the distances are measured in reciprocal space distances [nm*] and that, with respect to Equation (13), these distances have to be recalculated to “real space” distances, e.g. in [km]. This recalculation is realized in Table 1 only for the most important distance minr = 0.348 [nm*]. Simultaneously we review this parameter for all wavelengths (Figure 8) and simultaneously extrapolate this distance to the wavelength of relict radiation photons λ = 1.9

Figure 7. Calculation of the radial distribution function (RDF) according Equations (A2) and-or (12) for the wavelength λ = 0.071069 [nm]. The dashed-dotted line corresponds to the second member in Equation (12), the dashed line is the first member in this equation (dependent on density) and full line is the sum of both components, see text for details. Value of the density D necessary to shift the minimum at 0.348 [nm*] to positive values of the RDF is indicated in the upper right corner.

Figure 8. Dependences of most important distances, i.e. of coordination spheres 1r (squares), 2r (circles) separated by the minimum minr (down triangles) on the wavelength λ in the reciprocal space [nm*] according Figure 7 and from analogical calculations for wavelengths 0.110674, 0.154178, 0.250466 and 0.537334 [nm]. For an easier survey error bars are inserted only for the sphere 1r.
[mm].
Real space distances minR calculated in Table 1 are visualized in Figure 9. The extrapolation to the wavelength of relict photons 1.9 [mm] indicates that for this wavelength the shortest minR distances are of the order 102 meters. Later on (see Subsections 4. and 5.1.) the distance minR will be ascribed to the distance between “Objects”.
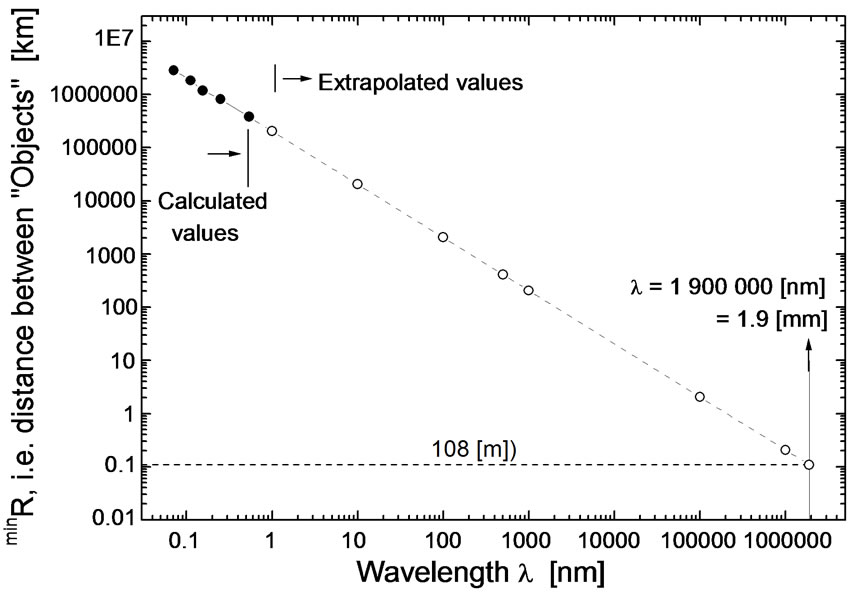
Figure 9. Dependence of the real space distances minR (full circles) on the wavelength λ (see Table 1 for details). Simultaneously an extrapolation to a distance corresponding to the wavelength of CMB (relict) photons 1.9 [mm] is visualized (empty circles). Later on (Sections 4. and 5.1.) the quantity minR will describe the distance between “Objects”.
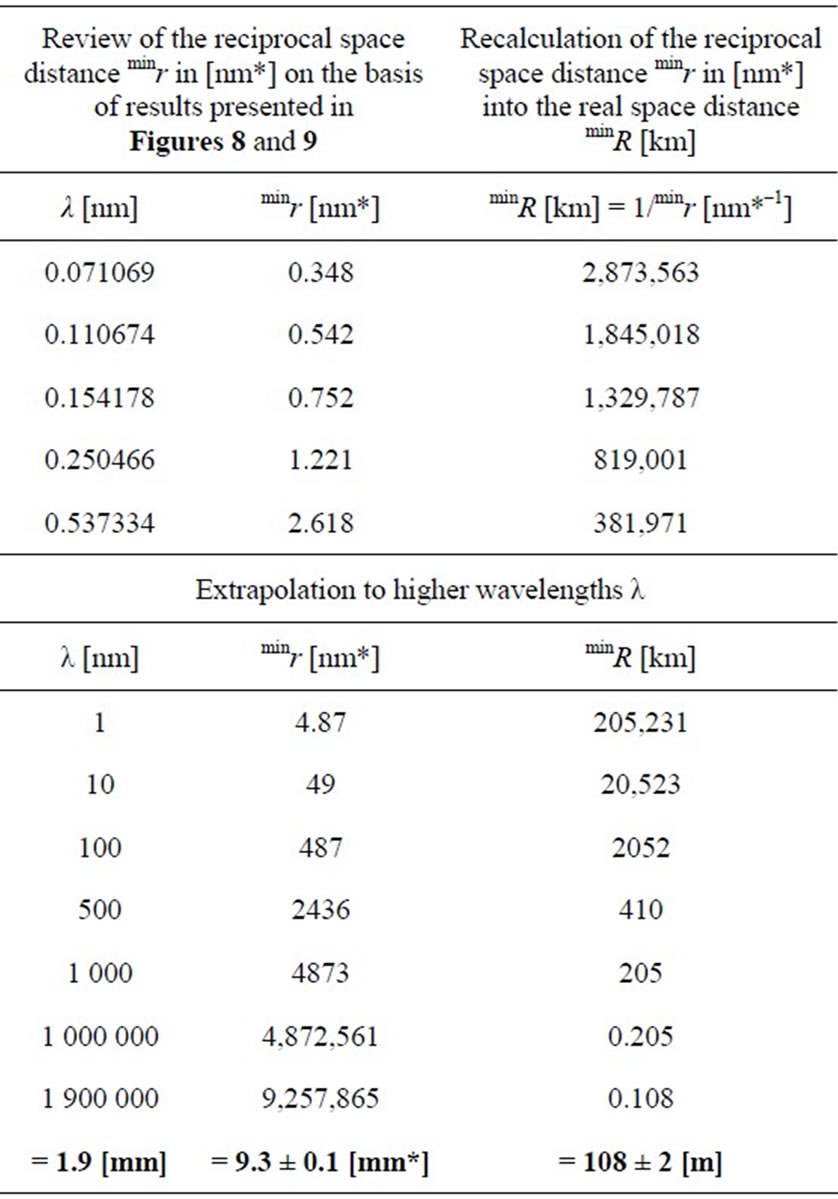
Table 1. Review of the most important distance minr characterizing the separation of the ordered region from the structure-less one on the wavelength λ (see Figure 8). Recalculation to the real space distances minR [km] is included. Extrapolation of this distance to the wavelength of relict radiation photons 1.9 [mm] is computed together with an estimate of final errors.
3.2. Calculation of the Density
The calculation presented in Figure 7 and repeated for four additional wavelengths enabled us to estimate the density of the matter, i.e. the important parameter effecting the first member ρ0Medium(r) in Equation (12). We simply supposed that the fluctuations of the RDF should not be negative. In order to shift in Figure 7 the minimum at minr = 0.348 [nm*] to positive values we had to set the density to a value D = 108.60 [kg∙m–3]. In the same way we have determined densities for the remaining four wavelengths.
The results are summarized in Figure 10 and Table 2. In the log-scale is the dependence of density on the wavelength nearly linear and therefore enables again an extrapolation to higher wavelengths. This extrapolation is presented in Table 2 and visualized in Figure 11.
It follows from Table 2 and Figure 11 that the most probable medium density of density fluctuations of the matter with which CMB (relict) photons realized their last interaction is ~9 × 10–23 [kg∙m–3]. Taking in account the limits of our calculation then the density can be formally written as 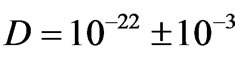 [kg∙m–3], see also Figure 11 and Table 2.
[kg∙m–3], see also Figure 11 and Table 2.
4. Modelling in the Relict Reciprocal Space SRelict
In the case when Figure 4 should be an X-ray scattering picture of a disordered material (e.g. of a glass) then such record would represent a picture typical for a material with well developed clusters. Their mutual distance should then characterize the position of the “first” massive peak. It follows from theory and experience that it is

Figure 10. Dependence of macroscopic densities on short wavelengths. In the log-scale this dependence is nearly linear. Numerical values are given in Table 2. Numbers indicate wavelengths, for which the corresponding RDF was calculated.
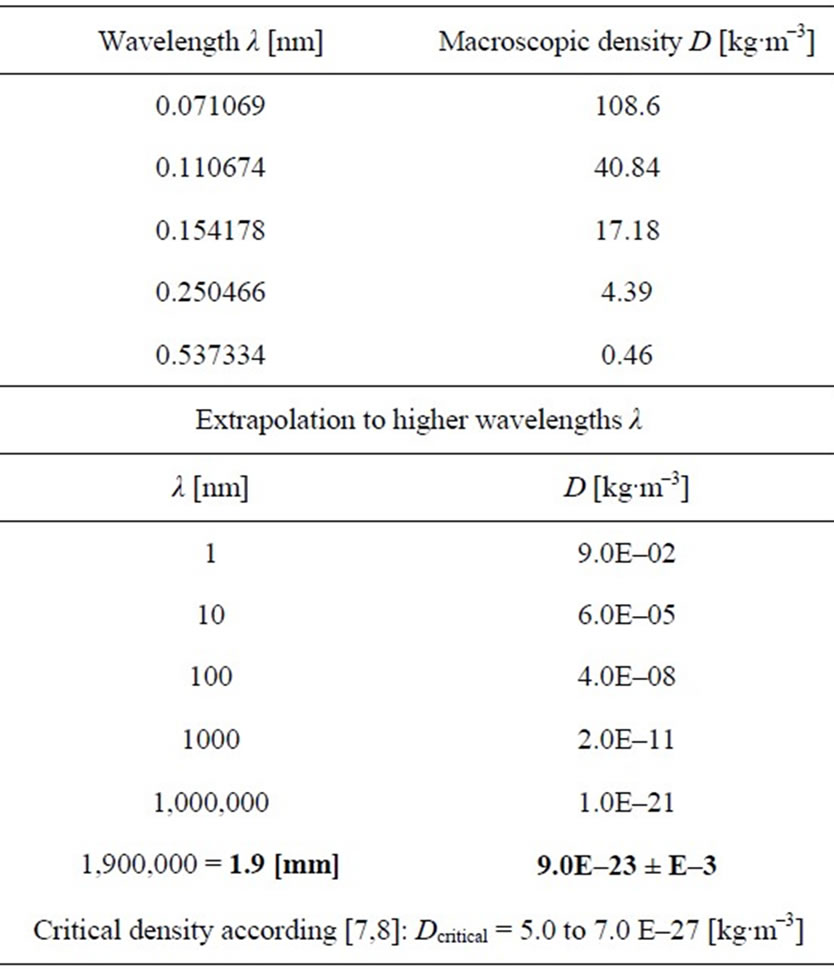
Table 2. Review of numerical values of densities according Figure 10 is presented. Extrapolation of the sequence of densities to higher wavelengths, especially to the wavelength of relict radiation photons 1.9 [mm] is shown. First five densities D were calculated following the description in Subsection 3.2. Possible final error is estimated and the values of the critical density according [7] and [8] are given.
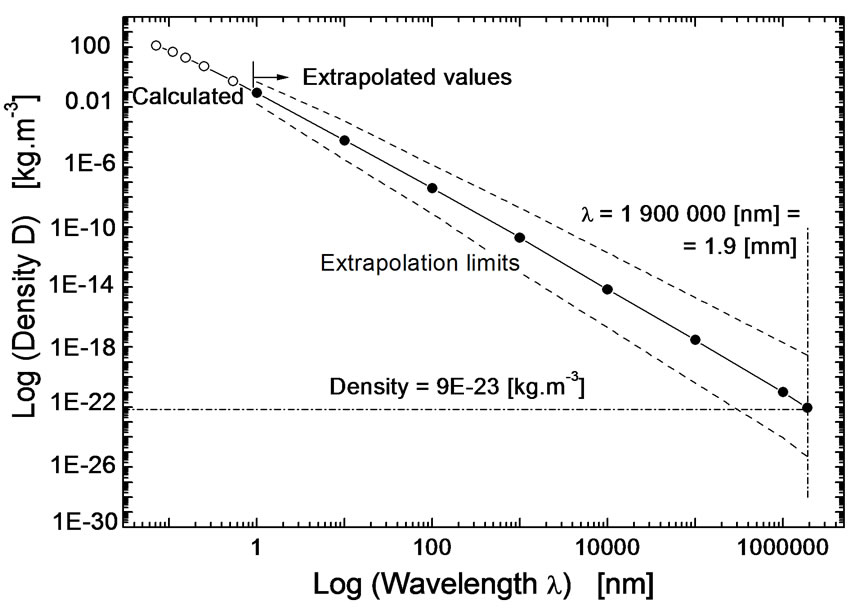
Figure 11. Extrapolation of the dependence of densities on wavelengths λ to the wavelength of relict (CMB) photons λ = 1.9 [mm]. Empty circles represent values shown already in Figure 10. Full circles are extrapolated values. Dashed lines show the limits of possible extrapolations.
not possible to get from this peak information on the internal structure of Clusters, only on their magnitude and mutual distance.
The method which has to be used for an analysis of this type of scattering is a direct calculation of scattered radiation on the basis of the Debye formula
 . (18)
. (18)
Here fi and fj are the scattering factors of n input particles and dij are the distances in real space between all available particles in the model and SRelict is the scattering vector in the relict reciprocal space defined in Equation (9). It should be pointed out that as scattering factors fi and fj we have used now the relict radiation factor fRelict calculated in Subsection 2.3.3. The summation is over all n particles in the model. This formula gives the average scattered intensity for an array of particles (or atoms in solid state physics) with a completely random orientation in space to the incident radiation.
Our model was quite simple: For the wavelength λ = 0.071069 [nm] the Cluster was a tetrahedron (5 particles) with an inter-particle distance 0.263 [nm] i.e. located in a cube with an edge 0.607 [nm]. In order to find the best fit with the scattering curve according Equation (18), the distance between Clusters (tetrahedrons) had to be d = 3 [nm], i.e. the tetrahedrons were located in positions of the basic skeleton, see Figure 12, characterized now by a side a = 6.93 [nm]. This model had 22 × 5 particles, i.e. a total of 110 particles. This calculation is shown in Figure 13.
For all other wavelengths (λ ≥ 0.110674 [nm]) we had to increase the dimensions of the Cluster. The Cluster had then the form of the skeleton shown in Figure 12 with an edge 0.607 [nm] and consisted of 22 particles (again with an inter-particle distance 0.263 [nm]) embedded in 8 edge-bound tetrahedrons. Only this Cluster occupied then the “positions” of the cubic basic skeleton shown in Figure 12 forming now an Object. (A more
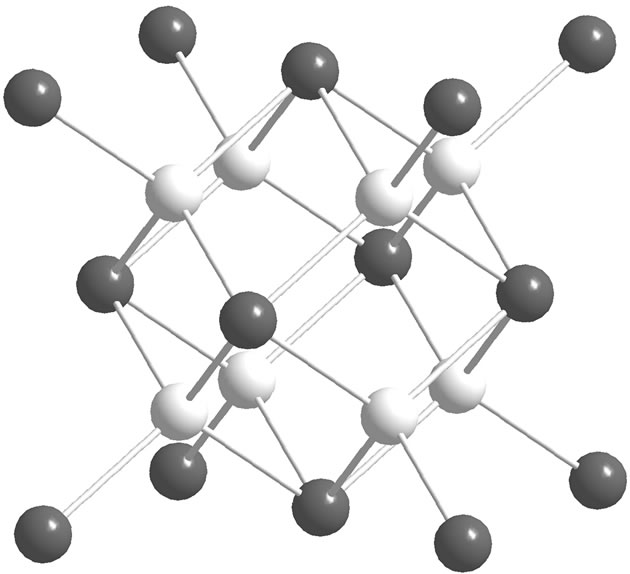
Figure 12. The basic skeleton (and-or a part of a Cluster structure) consists of 22 “positions” formed by 8 edgebound tetrahedrons. All positions are identical, for a better graphic representation are the centres of tetrahedrons drawn white. The picture has been constructed using programs [9] and [10].
instructive schematic presentation of an Object is shown in Figure 17 where Clusters are presented as small darker circles filled with “particles”.) When changing the dimension of this basic skeleton, we simultaneously changed again the distance d between Clusters. In order to reach for λ = 0.110674 [nm] the correct position of the massive peak at 1.6 [nm–1] an inter-Cluster distance d = 4.65 [nm] had to be used, i.e. the dimension of the skeleton was characterized by the side a = 10.74 [nm]. This model had then 22 × 22 particles, i.e. a total of 484 particles and simulated a part of the Object structure. The
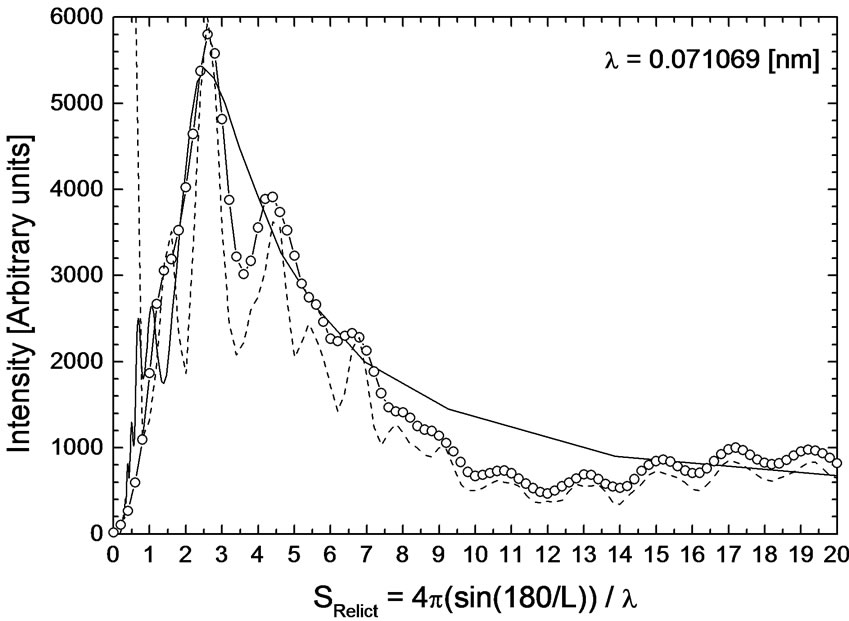
Figure 13. Calculation of the profile of the recalculated anisotropy spectrum for λ = 0.071069 [nm] based on a set of 22 Clusters with a mutual distance d = 3 [nm]. The Cluster was formed by a tetrahedron (5 particles); hence there were 110 particles in a model, see text for details. Full line - experiment, empty circles—calculated scaled and smoothed curve, dashed line—calculated scaled scattering.
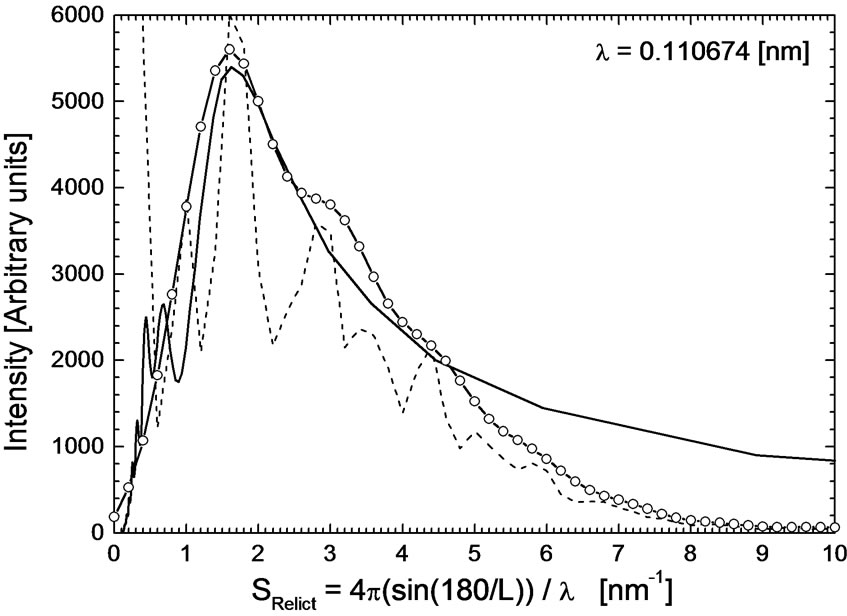
Figure 14. Calculation of the profile of the recalculated anisotropy spectrum for λ = 0.110674 [nm] and for a set of 22 Clusters with a mutual distance d = 4.65 [nm]. The Cluster consisted of 22 particles, hence there were 484 particles in the model, see text for details. Full line—experiment, empty circles—calculated scaled and smoothed curve, dashed line—calculated scaled scattering.
calculation is shown in Figure 14.
Calculations of Cluster distances for additional wavelengths (0.154178, 0.250466 and 0.537334 [nm]) have shown (see Figure 15) that the dependence of Cluster distances on the corresponding wavelength is linear. This fact enabled an extrapolation of the Cluster distance d to the wavelength of relict photons λ = 1.9 [nm], see Table 3. This extrapolated distance is 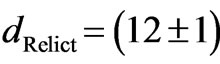 [cm]. The extrapolation is visualized in Figure 16.
[cm]. The extrapolation is visualized in Figure 16.
It should be noted that the recalculated anisotropy spectrum depends in this case directly on the angle θRelict which is equal to the angle α (see Equation (8)) and therefore a recalculation of the inter-Cluster distance d into real space distances is not necessary because the Debye formula analyzes the relict reciprocal space represented by the vector SRelict directly in real space distances, see the quantity dij in Equation (18).
5. Discussion
In the following discussion we will concentrate on several important ideas which may arise when reading this paper.
In particular this contribution should demonstrate how the formalism imported from solid state physics could be useful in solving specific cosmological problems: It may shed some new light on the physical processes taking place in the primordial plasma.
First of all, according our opinion, this work points in favour of clustering processes and consequently to a cluster-like structure of the matter in the moment when

Figure 15. Dependence of distances d between Clusters on the wavelength λ (numerical values are shown). With exception of the “0.071 case” models consisted of 22 Clusters with 22 particles in each Cluster, i.e. a model included 484 particles. Inter-Cluster distances characterize the position of the massive peak, see Figures 13 and 14 and the text for details.
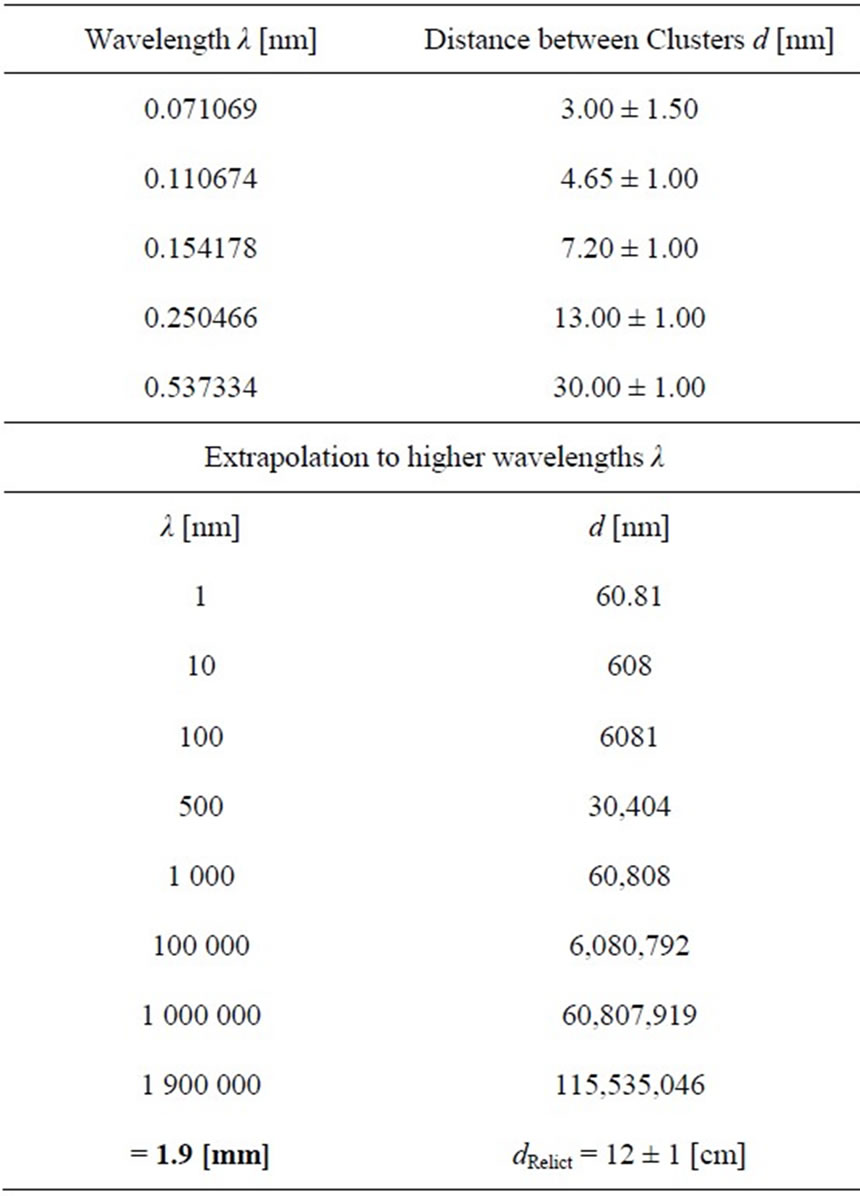
Table 3. Extrapolation of distances d between Clusters to the wavelength of relict photons λ = 1.9 [nm]. These distances influence the position of the massive peak, see Figures 14, 15 and 16. The estimate of the final error is based on errors given in Figure 15.
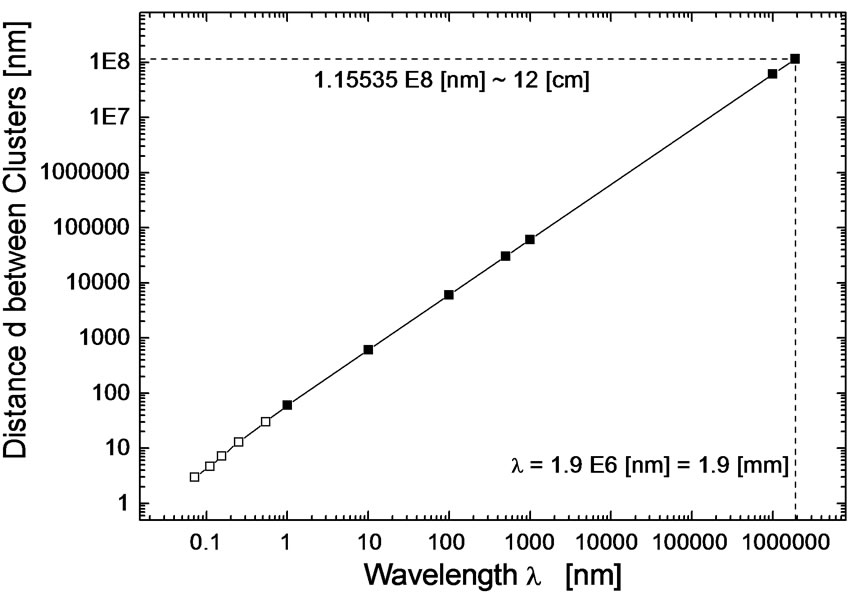
Figure 16. Extrapolation of distances d between Clusters to the wavelength λ = 1.9 [mm]—full squares; calculated values—empty squares (see Figure 15 and Table 3).
the universe became transparent for photons (see Subsection 5.1.).
In the second place the new formalism enabled us a simple and general description of the interaction of relict radiation with the matter and may help in an improvement of the theoretical predictions of the CMB pattern (see Subsection 5.2.).
Finally this new approach may be useful in the analysis of the CMB data. We have shown that the transformation of the anisotropy spectrum of relict radiation into a special two-fold reciprocal space and into a simple reciprocal space was able to bring quantitative data in real space. Problems with the transformation into reciprocal spaces, mainly with the use of the proper wavelength of relict photons will be discussed in Subsection 5.3.
5.1. The Cluster-Like Structure of the Primordial Matter
The most important consequence of our quantitative results obtained in Sections 3 and 4 is, according our opinion, the idea of clustering processes taking part in the formation of the primordial matter. There we have arrived to three distances, which we interpret in a following way: The first distance ~102 [m], (Table 1) should indicate the distance between Objects (big clusters), the second one ~10–1 [m], (Table 3) should indicate the distance between smaller Clusters, while the internal struc-
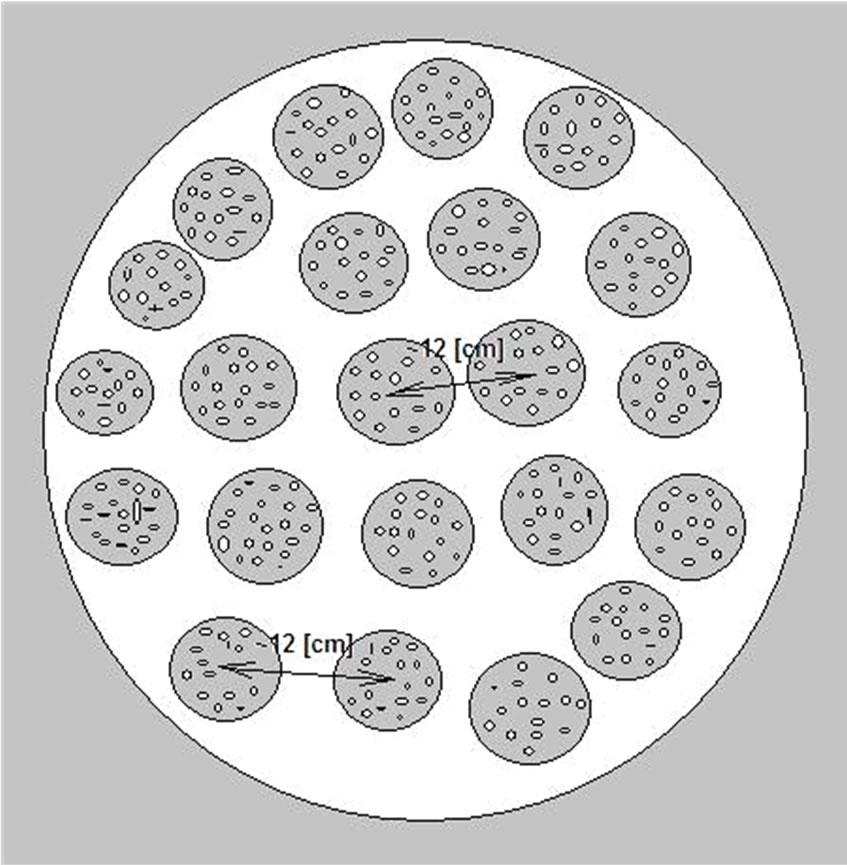
Figure 17. A schematic arrangement of Clusters (darker regions) with particles (small white points) in an Object (white region). In our model the distance between Objects is ~102 [m], see Table 1. A detailed structure of a Cluster and of an Object in this model is presented in Figure 12. The most probable model distance between Clusters is ~10–1 [m], see Table 3. The distance between particles in the model is 0.26 [nm]. We estimate that there are ~1011 particles in one Object and ~102 particles in one Cluster (see Appendix C1 and C2) and ~109 Clusters in one Object, see Appendix C3.
ture of a single Cluster was formed in the model by 22 particles with a medium particle distance 0.26 [nm], see Section 4.
In Figure 17 we show a schematic picture of this cluster model. The big circle represents an Object. An Object is a clump of Clusters, where only a part of this clump was simulated in the model (the model of an Object had 22 Clusters each consisting of 22 particles, i.e. it consisted of a total of 484 particles).
Although this model gave a sufficiently well agreement with the width of the massive peak, as demonstrated in Figure 14, our estimates (see Appendix C) show that the number of Clusters as well as the number of particles in one Cluster is greater, i.e. that there may be as far as 1011 particles in one Object and 102 particles in one Cluster. That the density plays an important role in these calculations will be discussed in Subsection 5.4.
Even when the cluster model gave a good profile of the massive peak at e.g. 1.62 [nm], than such a model of internal structure of Clusters cannot be a unique one, because the calculation of the profile is not sensitive to the internal cluster structure, nevertheless the cluster-like character of the modelling process has to be maintained.
5.2. The Relict Radiation Factor
We have already pointed out in Subsection 2.1. why during the analysis of the CMB spectrum it has not been possible to apply conventional atomic scattering factors used in solid state physics and why a new special factor reflecting the complexity of interaction processes of photons with the primordial matter has to be constructed. It is important to have on mind that the description of these interactions is possible only in a special two-fold reciprocal space into which the CMB spectrum was transformed. We have called this new factor the relict radiation factor and it had to substitute all complicated processes which participate in the formation of the angular power spectrum of CMB radiation.
Because relict photons realize their interaction with various kinds of particles and we have generated only one radiation factor, this factor represents, as a matter of fact, a medium from all possible individual relict radiation factors. In this way this new formalism offers a general description of the interaction of relict radiation with the matter and simultaneously reflects the complexity of processes which influence the anisotropy spectrum of CMB radiation from the cosmological point of view [5].
During our study we have concentrated on three important facts which may justify the attempt to interpret the anisotropy spectrum of CMB radiation as a conesquence of the interaction of photons with density fluctuations which characterize the distribution of particles before the recombination process.
The first fact is that temperature fluctuations in the CMB spectrum are related to fluctuations in the density of matter in the early universe and thus carry information about the initial conditions for the formation of cosmic structures such as galaxies, clusters or voids [11].
Secondly, it is the fact that the information on these density fluctuations in the distribution of particles (electrons, ions, etc.) has been brought by photons. Photons which we observe from the microwave background have travelled freely since the matter was highly ionized and they realized their last Thomson scattering (see already Subsection 2.1.). If there has been no significant early heat input from galaxy formation then this happened when the Universe became cool enough for the protons to capture electrons, i.e. when the recombination process started [12].
The third fact is that the anisotropy spectrum is angular dependent, see Figure 1.
Although we know that the anisotropy spectrum of CMB radiation, as presented in Figure 1, has no direct connection with a scattering process of photons, it was the transformation of the CMB spectrum into a two-fold reciprocal space, which enabled us to interpret the anisotropy spectrum of CMB radiation as a result of an interaction process of photons with density fluctuations of the matter represented by electrons, ions or other particles. This approach enabled us to reach an advantageous approximation of this process.
The process consisted of two steps: First of all we have constructed in Subsection 2.3.1. an angular reciprocal space characterized by the “scattering” angle θClassic, see Equations (2) and (4). This space is reciprocal to the space characterized by the angle α (α is the angle between two points in which the temperature fluctuations of CMB radiation are compared to an overall medium temperature).
Then, we have constructed an additional “classic” reciprocal space (1/λ) into which the first one (the θClassic space) was dipped, by defining in this new “two-fold” reciprocal space the classic scattering vector sClassic, see Equation (6). Only after these transformations we treated in this new classic reciprocal space the transformed anisotropy CMB spectrum as a scattering picture of relict photons.
It was only this space in which we simulated (in Subsection 2.3.3.) the interaction of CMB (relict) photons with density fluctuations by the relict radiation factor fRelict.
The criterion for the trial and error construction of the relict radiation factor fRelict has been that this factor had to fulfil the three requirements set at the beginning of Subsection 2.3.3. Only then it was secured that after the Fourier transform, according Equations (A2) and-or (12), there will not be any (or at least small) parasitic fluctuations on the curve ρ(r) and-or ρFourier. That we have achieved these demands is documented in Figure 7 where we do not see any parasitic fluctuations on the curve ρFourier and as a consequence on the curve ρ(r).
To summarize: It is true that in our formal analogy between scattering of e.g. short-wave radiation on disordered matter (Figure 2) and “scattering” of CMB photons on electrons, ions and other particles (Figure 1) is an essential difference, because the physical processes are completely different, e.g. the scattering process itself, length scales involved, etc., however, the difference between physical processes is reflected and simultaneously eliminated by the special relict radiation factor fRelict (Subsection 2.3.3.), which we have included into all calculations based on the classic two-fold reciprocal space (see Subsection 2.1.). Moreover, additional calculations in the relict reciprocal space (see Subsection 4.) based on the relict radiation factor were done directly for the transformed angular power spectrum of relict radiation (see IRelict (SRelict) in Figure 4) and thus present an information on distance relations between Clusters (formed by particles) in real space.
5.3. The Wavelength Problem
The problem is to which wavelength of relict photons we have to relate our calculations. One possibility may be to refer this wavelength to that time when 379.000 years after the Big Bang the Universe cooled down to 3000 K and the ionization of atoms decreased already only to 1%. Then according Wien’s law
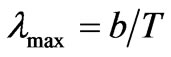 (16)
(16)
where λmax is the peak wavelength, T is the absolute temperature of the blackbody, and b is a constant of proportionality called Wien’s displacement constant, 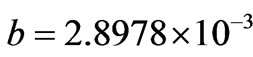 [mK], we obtain for the temperature 3000 K a wavelength value
[mK], we obtain for the temperature 3000 K a wavelength value 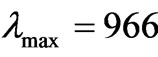 [nm], see [13].
[nm], see [13].
However, simultaneously we must be aware of the fact that we are analyzing CMB photons now when the temperature of the universe, due to its expansion, is 2.725 K. Then the wavelength of photons according the Wien’s law should be ~1 [mm].
On the other hand the COsmic Background Explorer (COBE) measured with the Far Infrared Absolute Spectrophotometer (FIRAS) the frequency spectrum of the CMB, which is very close to a blackbody with a temperature 2.725 K [11,14]. The results are shown in Figure 18 in units of intensity (see the text to Figure 18). It follows that the wavelength corresponding to the maximum is 1.9 [mm].
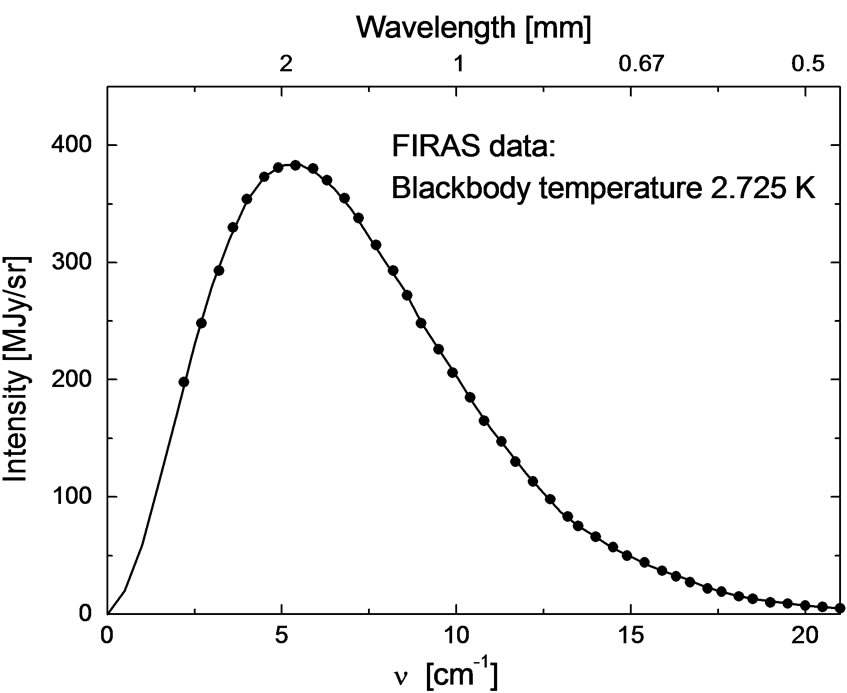
Figure 18. Dependence of the intensity of the CMB radiation on frequency as measured by the COBE Far InfraRed Absolute Spectrophotometer (FIRAS) ([11,14]). The thick curve is the experimental result; the points are theoretically calculated for an absolute black body with a temperature of 2.725 [K]. The x axis variable is the frequency in [cm–1]. The y-axis variable is the power per unit area per unit frequency per unit solid angle in MegaJanskies per steradian [sr], (1 [Jansky] is a unit of measurement of flux density used in radioastronomy, abbreviated “Jy” (1 [Jansky] is 10–26 [W∙m–2∙Hz–1]).
After all we have decided to relate our results to the wavelength of CMB photons λ = 1.9 [mm] which corresponds to the maximum of the intensity distribution. Because the distribution of the spectrum covers a relatively broad interval of wavelengths, see Figure 18, calculations based on the wavelength 1.9 [mm] should then represent the most probable estimate. Moreover, this consideration is supported by the fact that the angular distribution of CMB radiation is the same for all wavelengths.
However, on the basis of graphs in Figures 10, 12 and 16 an easy recalculation of distances and-or of the density would be possible when another CMB photons wavelength would be considered as more appropriate.
5.4. The Density of the Mass and Distances between Objects, Clusters and Particles
The way how we arrived to numbers characterizing the density of the matter was described in Subsection 3.2. In a conventional X-ray analysis the density is the macroscopic density of the material under study. Therefore we suppose that also in this case the density which influences the parabolic shape of the curve of total disorder (see the first member on the right side of Equation (A2) and-or (12) and Figure 8) should be understood as a real medium density of density fluctuations.
The dependence of the density on the wavelength as demonstrated in Figures 11 and 12 is not perfectly linear; therefore we have marked in Figure 11 the extent of possible linear dependences. This result can be formally written as
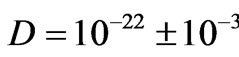 [kg∙m–3].(17)
[kg∙m–3].(17)
This medium value is about 105 times higher than the “critical density” Dcritical ~ (5 to 7) × 10–27 [kg∙m–3], see Table 2.
Further, we should have in mind that the local density in a Cluster or in an Object has to be greater. We are able to document this fact on the basis of our Cluster model. Based on particle distances dparticles = 0.263 [nm], we have simulated a part of the Cluster structure by a cube with an edge aCluster = 0.607 [nm]. There were 22 particles in this cube which can be closed in a sphere with a radius RCluster = 2dparticles = 2 × 0.263 [nm] = 0.53 [nm]. The volume of this sphere is VCluster = 0.62 [nm3] = 0.62 × 10–27 [m3]. Supposing that particles are represented according expression (C6) by their medium mass 
 [kg], we obtain for the density in the Cluster the value
[kg], we obtain for the density in the Cluster the value
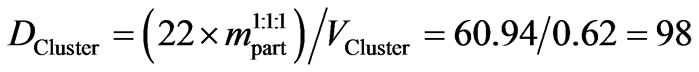 [kg∙m–3], (18)
[kg∙m–3], (18)
i.e. a value approaching density values known from solid state physics (i.e. values lying between the densities of gases and liquids).
At the same time we have to take in account that the estimates concerning the density of matter are really complicated. The microwave light seen by the Wilkinson Microwave Anisotropy Probe (WMAP), suggests that fully 72% of the matter density in the universe appears to be in the form of dark energy [15] and 23% is dark matter. Only 4.6% is ordinary matter. So less than 1 part in 20 is made out of matter we have observed experimenttally or described in the standard model of particle physics. Of the other 96%, apart from the properties just mentioned, we know “absolutely nothing” [16]. In this connection we consider the density value we have received (9 × 10–23 [kg∙m–3]) as the density of the ordinary matter.
Last remark should be given to the probability of Object interactions in the case of their apparently large mutual distances (~102 [m]). It follows from the Maxwell speed distribution that the root mean square particle velocity v corresponding to the temperature T = 3000 [K], is
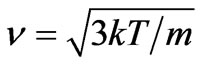 , (19)
, (19)
where k is the Boltzmann constant (k = 1.38 × 10–23 [Joule∙K–1]) and m is the mass of the particle, which may be here for example the mass of the proton m = 1.67 × 10–27 [kg]. Then we obtain
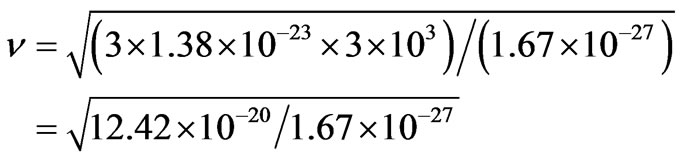
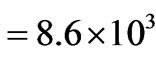 [m∙s–1]
[m∙s–1]
This is already a velocity, which should make possible an intensive interaction of Objects formed by Clusters consisting of particles.
6. Conclusions
A formalism of solid state physics has been applied to provide an additional tool for the research of cosmological problems. It was demonstrated how this new approach could be useful in the analysis of the CMB data. After a transformation of the anisotropy spectrum of relict radiation into a special two-fold reciprocal space it was possible to propose a simple and general description of the interaction of relict photons with the matter 380.000 years after the Big-Bang by a “relict radiation factor”. This factor, which may help in an improvement of the theoretical predictions of the CMB pattern, enabled us to process the transformed CMB anisotropy spectrum by a Fourier transform and thus arrive to a radial electron density distribution function (RDF) in a reciprocal space.
As a consequence it was possible to estimate distances between Objects of the order of ~102 [m] and the density of the ordinary matter ~10–22 [kg∙m–3]. Another analysis based on a direct calculation of the CMB radiation spectrum after its transformation into a simple reciprocal space and combined with appropriate structure modelling confirmed the cluster structure. It indicated that the internal structure of Objects may be formed by Clusters distant ~10–1 [m], whereas the internal structure of a Cluster consisted of particles distant ~0.3 [nm].
In this way the work points in favour of clustering processes and to a cluster-like structure of the matter and thus may contribute to the understanding of the structure of density fluctuations and hence to a refinement of parameters describing the Standard Model of Cosmology [17]. Simultaneously, the work sheds more light on the structure of the universe in the moment when the universe became transparent for photons. On the basis of quantitative considerations it was possible to estimate the number of particles (protons, helium nuclei, electrons and other particles) in Objects and Clusters and the number of Clusters in an Object.
7. Acknowledgements
My thanks are due to Prof. Richard Gerber (University of Salford, Manchester) for discussion and proposals directed to the final presentation of this paper, to Mgr. Radomír Šmída, PhD (Institute of Physics, Acad. Sci. of the Czech Republic) for comments, proposals and discussion concerning this article, to Prof. Karel Segeth (Institute of Mathematics, Acad. Sci. of the Czech Republic) for discussions and help in clarifying some aspects of the Fourier transform, to Prof. Jan Kratochvíl (Department of Physics, Faculty of Civil Engineering, Czech Technical University in Prague) for discussions pointing out several inconsistencies in the original conception of the article. Last acknowledgement is due to Dr. Jiří Hybler (Institute of Physics, Acad. Sci. of the Czech Republic) for help in the preparation of Figure 12 presenting a part of a Cluster skeleton.
REFERENCES
- J. L. Sievers, J. R. Bond, J. K. Cartwright, C. R. Contaldi, B. S. Mason, S. T. Myers, S. Padin, T. J. Pearson, U.-L. Pen, D. Pogosyan, S. Prunet, A. C. S. Readhead, M. C. Shepherd, P. S. Udomprasert, L. Bronfman, W. L. Holzapfel and J. May, “Cosmological Parameters from Cosmic Background Imager Observations and Comparisons with BOOMERANG, DASI, and MAXIMA,” Astrophysics Journal, Vol. 591, No. 2, 2003, pp. 599-622. doi:10.1086/375510
- G. Hinshaw, D. N. Spergel, L. Verde, R. S. Hill, S. S. Meyer, C. Barnes, C. L. Bennett, M. Halpern, N. Jarosik, A. Kogut, E. Komatsu, M. Limon, L. Page, G. S. Tucker, J. Weiland, E. Wollack and E. L. Wright, “First-Year Wilkinson Microwave Anisotropy Probe (WMAP) observations: The Angular Power Spectrum,” Astrophysical Journal, Supplement Series, Vol. 148, No. 1, 2003, pp. 135-159. doi:10.1086/377225
- L. Červinka, “Several Remarks on the Medium-Range Order in Glasses,” Journal of Non-Crystalline Solids, Vol. 1, No. 1-3, 1998, pp. 1-17. doi:10.1016/S0022-3093(98)00457-8
- L. Červinka, J. Bergerová, L. Tichý and F. Rocca, “A Contribution to the Structure of Ge-Se-Ag Glasses,” Physics and Chemistry of Glasses, Vol. 46, No. 4, 2005, pp. 444-450.
- W. Hu, D. Scott, N. Sugiyama and M. White, “The Effect of Physical Assumptions on the Calculation of Microwave Background Anisotropies,” Physical Review, Vol. D52, 1995, pp. 5498-5515.
- J. C. Wilson and E. Price (Eds.), “International Tables for Crystallography,” Volume C, Mathematical, Physical and Chemical Tables, Second Edition, Published for International Union of Crystallography, Kluwer Academic Publishers, Dordrecht, 1999.
- G. Smoot and K. Davidson, “Wrinkles in Time,” Avon, New York, 1977, p. 158.
- J. Silk, “Big Bang,” Freeman & Co. Publishers, New York, 1977, p. 299.
- V. Petříček, M. Dušek and L. Palatinus, “The Crystallographic Computing System,” Institute of Physics, Praha, Czech Republic, 2006.
- K. Brandenburg, “Program DIAMOND, Version 2.1c,” Crystal Impact GbR, Bonn, Germany, 1999.
- E. L. Wright, J. C. Mather, D. J. Fixsen, A. Kogut, R. E. Eplee, Jr., R. B. Isaacman, S. M. Read, R. A. Shafer, C. L. Bennett, N. W. Boggess, E. S. Cheng, S. Gulkis, M. G. Hauser, M. Janssen, T. Kelsall, P. M. Lubin, S. H. Moseley Jr., T. L. Murdock, R. F. Silverberg, G. F. Smoot, R. Weiss and D. T. Wilkinson, “Interpretation of the COBE FIRAS CMBR Spectrum,” Astrophysics Journal, Vol. 420, No. 2, 1994, pp. 450-456. doi:10.1086/173576
- M. White, D. Scott and J. Silk, “Anisotropies in the Cosmic Microwave Background,” Annual Review of Astronomy and Astrophysics, Vol. 32, 1994, pp. 319-370. doi:10.1146/annurev.aa.32.090194.001535
- R. Šmída, Institute of Physics, Acadamic Science of the Czech Republic, 2010 (Private Communication).
- J. C. Mather, E. S. Cheng, D. A. Cottingham, R. E. Eplee, Jr., D. J. Fixen, T. Hewagama, R. B. Isaacman, K. A. Jensen, S. S. Meyer, P. D. Noerdlinger, S. M. Read, L. P. Rosen, R. A. Shafer, E. L. Wright, C. L. Bennett, N. W. Boggess, M. G. Hauser, T. Kelsall, S. H. Moseley Jr., R. F. Silverberg, G. F. Smoot, R. Weiss and D. T. Wilkinson, “Measurement of the Cosmic Microwave Background Spectrum by the COBE FIRAS Instrument,” Astrophysics Journal, Vol. 420, No. 2, 1994, pp. 439-444. doi:10.1086/173574
- J. C. Wheeler, “Cosmic Catastrophes,” Cambridge University Press, Cambridge, 2007, p. 282.
- L. Smolin, “The Trouble with Physics,” Mariner Books, New York, 2007, p. 16.
- D. Scott, “The Standard Cosmological Model,” Canadian Journal of Physics, Vol. 84, No. 6-7, 2006, pp. 419-435. doi:10.1139/p06-066
- K. Steeb, “Springer Tracts in Modern Physics—Ergebnisse der exakten Naturwissenschaften,” Vol. 47, SpringerVerlag, Berlin, 1968, pp. 1-66.
- R. Hultgren, N. S. Gingrich and B. E. Warren, “The Atomic Distribution in Red and Black P and the Crystal Structure of Black P,” Journal of Chemical Physics, Vol. 3, 1935, p. 351. doi:10.1063/1.1749671
- J. Krogh Moe, “A Method for Converting Experimental X-Ray Intensities to an Absolute Scale,” Acta Crystallographica, Vol. 9, No. 11, 1956, pp. 951-953. doi:10.1107/S0365110X56002655
Appendix A. Basic Equations
Generally the intensity of radiation scattered2 on a matter (solid, liquid) offers us information on the structure of a material of any kind in the reciprocal space. The relation between the reciprocal and real space is mediated by the Fourier transform of the radiation intensity scattered by a disordered material.
The basic formula transforming the reciprocal space information into the real space one is in the case of non- crystalline (non-periodic) materials [18]
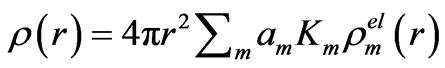 . (A1)
. (A1)
In a more detailed description the quantity ρ(r) is then expressed as
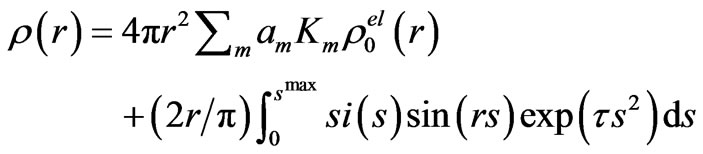 (A2)
(A2)
and describes the radial electron density distribution function (RDF) in real space in the case when the atomic scattering factor fm (see Equation (A6)) is given in electrons [e]. The parameter r is the distance of an arbitrary atom from the origin in real space units.
In Equation (A2) am are the concentrations of elements composing the matter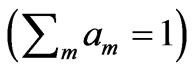 ,
,  are the elemental contributions of electron density to the overall electron density, i.e. it is the electron density around an atom of kind m, the factor exp(τs2) is an artificial temperature factor in which usually τ = –0.010,
are the elemental contributions of electron density to the overall electron density, i.e. it is the electron density around an atom of kind m, the factor exp(τs2) is an artificial temperature factor in which usually τ = –0.010, 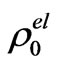 is the mean electron density in a totally disordered material, which can be deduced from the macroscopic density via the Avogadro number L
is the mean electron density in a totally disordered material, which can be deduced from the macroscopic density via the Avogadro number L
 , (A3)
, (A3)
where Zm is the atomic number of kind m, D is the macroscopic density in [g∙cm–3] and M is the molecular weight
 , (A4)
, (A4)
Wm are corresponding atomic weights. The factor 10–21 in Equation (A3) is a consequence of the fact that the parameter r is in [nm].
The parameter s is in Equation (2) related with the wavelength λ of scattered radiation by the formula
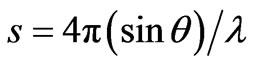 . (A5)
. (A5)
Here is s = s – s0, where s0 is the vector of the incident and s the vector of the scattered radiation in the reciprocal space.
Further, θ is the angle between the incident and scattered radiation (X-rays or neutrons) and λ is the wavelength of this radiation and Km is the effective number of electrons in an atom of kind m
 , (A6)
, (A6)
where fm is the atomic scattering factor for X-rays for an atom of the kind m (see already Subsection 2.1.) and fe is the atomic scattering power of an electron for X-rays
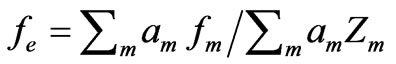 (A7)
(A7)
During a conventional experiment (e.g. see Figure 2), i.e. using MoKa radiation, we have  = 0.071069 [nm] and the maximum possible value of
= 0.071069 [nm] and the maximum possible value of  corresponding to θ = 90˚ is then according Equation (A5)
corresponding to θ = 90˚ is then according Equation (A5)
 . (A8)
. (A8)
Here we are starting to use the subscript “Classic”, which should point out that the scattering vector in the reciprocal space sClassic will be considered in the same way as in the “classic” conventional non-crystalline case.
In Equation (A2) is i(s) the experimentally obtained scattered intensity of radiation, Icorr is this intensity corrected for various factors3 and properly scaled for the absolute value of scattering, hence
 , (A9)
, (A9)
the parameter 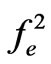 is acting here as a sharpening function.
is acting here as a sharpening function.
The general formula for the scattering on gas Igas (s) is
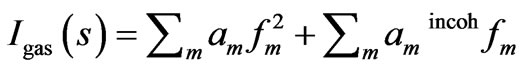 , (A10)
, (A10)
where 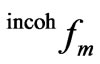 are the scattering factors for the incoherent (Compton) scattering, see Figure 6.
are the scattering factors for the incoherent (Compton) scattering, see Figure 6.
The labelling Idistr for i(s) is used in Appendix B, where the scaling methods, important for a correct Fourier transform, are reviewed.
Appendix B. The Scaling Problem
In Equation (A9) we have already introduced the quantity Icorr (s), i.e. the corrected experimental scattered intensity. However, in order to arrive to a correct RDF, Icorr (s) must be scaled to the Igas (s) function in the absolute scale of atomic scattering, see Equation (A10).
In the simplest scaling method we suppose that for high s-values there are not any scattering effects on the corrected experimental curve Icorr (s) and therefore the Icorr (s) and the Igas (s) curves should be equal. Then the scaling parameter aHSV is for 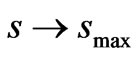 easily calculated as
easily calculated as
 . (B1)
. (B1)
As a consequence we obtain in the whole interval of s-values a scaled scattered intensity 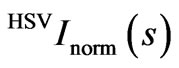 represented by the equation
represented by the equation
 . (B2)
. (B2)
The function 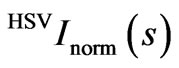 oscillates around the Igas (s) curve. Following Equation (A9), we subtract the scattering on gas and obtain the most important function Idistr, see Figure 5.
oscillates around the Igas (s) curve. Following Equation (A9), we subtract the scattering on gas and obtain the most important function Idistr, see Figure 5.
There are several other scaling methods. An integral method [19] is characterized by a scaling factor 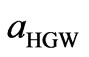 and supposes that the areas under the experimental scattering curve Icorr (s) and the structure-less Igas (s) curve should be equal. Similarly there is a quadratic integral method [20] characterized by a scaling parameter
and supposes that the areas under the experimental scattering curve Icorr (s) and the structure-less Igas (s) curve should be equal. Similarly there is a quadratic integral method [20] characterized by a scaling parameter .
.
Our long experience in the research of disordered materials documents that the better was the experiment and the better has been the application of scattering factors, the smaller was the difference (only several percent) between the scaling coefficients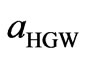 ,
, 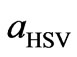 and
and  and simultaneously the smaller were the parasitic fluctuations on the RDF. In the present work we have used all three scaling methods and have kept the difference between scaling factors in the limit of 4 percent.
and simultaneously the smaller were the parasitic fluctuations on the RDF. In the present work we have used all three scaling methods and have kept the difference between scaling factors in the limit of 4 percent.
Appendix C. Quantitative Relations between Objects, Clusters and Particles Estimated on the Basis of the Cluster Model
C1. Estimates from Object Distances
In Subsection 3.1, we have defined that the nearest distance between Objects (big clusters) is ~108 [m], see Table 1. In this moment we suppose a relatively simple organization of Objects, i.e. a “cubic body-centred” arrangement, in which an Object in the centre has 8 nearest neighbour Objects distant bO = 108 [m], where bO is the half of the body diagonal in a cube with a side
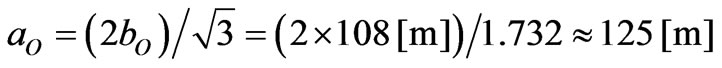 . (C1)
. (C1)
The volume VO of this cube is therefore
 . (C2)
. (C2)
Using now our result on the density of the matter, see Table 2,
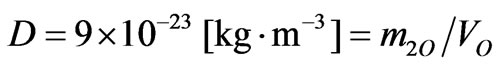 (C3)
(C3)
we are able to calculate in this model the mass m2O of Objects embedded in a cube with the volume VO.
 (C4)
(C4)
At the same time, however, we have to take in account that, as a matter of fact, there are two Objects in the space of the cube (in each cube corner there is only 1/8 of the second Object). Hence the mass mO embedded in one Object is
 . (C5)
. (C5)
1) The mass is formed by a 1:1:1 mixture of protons, helium nuclei and electrons
We may suppose now that the universe (in the time when the microwave background radiation began propagating) consisted of baryons (protons, helium nuclei, etc) and electrons, neutrinos, photons and dark matter particles. Supposing now that we have a mixture consisting of protons, helium nuclei and electrons in a relation 1:1:1, then the medium mass of a “particle” 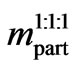 in this mixture is
in this mixture is
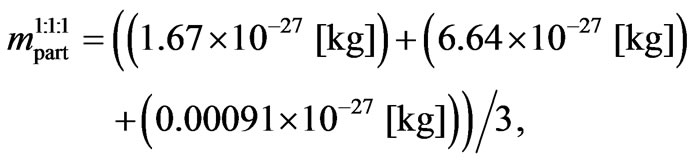
i.e.
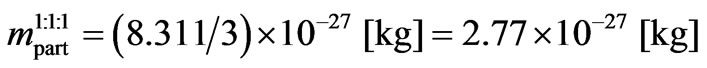 (C6)
(C6)
and the number of particles 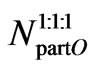 in one Object is in this case
in one Object is in this case
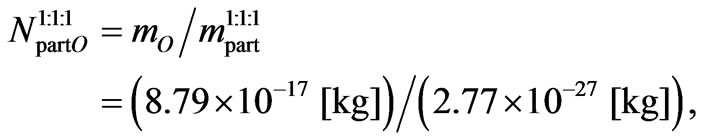
i.e.
 (C7)
(C7)
2) The mass is formed by a 1:1:10 mixture of protons, helium nuclei and electrons
Supposing now a mixture consisting of protons, helium nuclei and electrons in a relation 1:1:10, then the medium mass of a “particle” 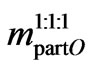 in this system is
in this system is

i.e.
 . (C8)
. (C8)
and the number of particles  in one Object is then
in one Object is then
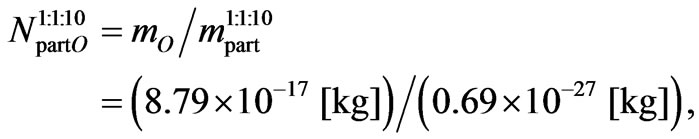
i.e.
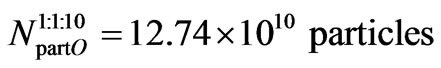 . (C9)
. (C9)
This section may be summarized by the statement that there are
 particles in one Object (C10)
particles in one Object (C10)
C2. Estimates from Cluster Distances
According our calculations the distance between Clusters is ~12 [cm] = 1.2 × 10–1 [m], see Table 3 and Figure 17. Similarly as in the previous case we suppose again a relatively simple organization of Clusters, i.e. a cubic body-centred arrangement in which a Cluster in the centre has 8 “nearest neighbour” Clusters distant 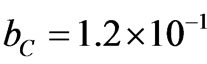 [m], where bC is the half of the body diagonal in a cube with a side
[m], where bC is the half of the body diagonal in a cube with a side
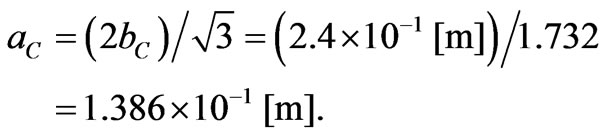 (C11)
(C11)
The volume VC of this cube is therefore
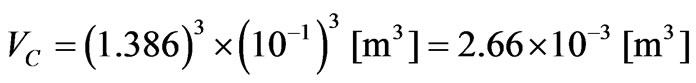 . (C12)
. (C12)
Using now our result on the density of the matter, see already Equation (C3)

we are able to calculate for this model the mass m2C of Clusters embedded in a cube having the volume VC.
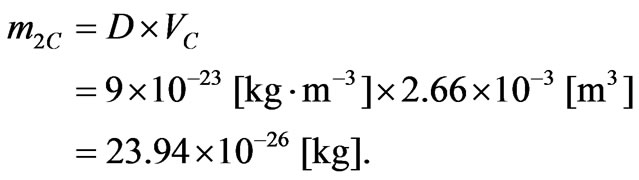 (C13)
(C13)
Here again we have to take in account that there are two Clusters in the space of the cube (in each corner there is only 1/8 of the second Cluster). Hence the mass mC embedded in one Cluster is
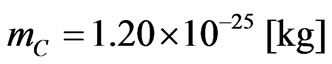 . (C14)
. (C14)
1) The mass is formed by a 1:1:1 mixture of protons, helium nuclei and electrons
Similarly as in the preceding Appendix C1 we suppose again a mixture of protons, helium nuclei and electrons in a relation 1:1:1, respectively. The medium mass of a “particle”  in this mixture is (see Equation (C6)).
in this mixture is (see Equation (C6)).

and the number of particles 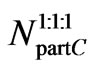 in one Cluster is then
in one Cluster is then

i.e.
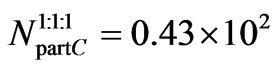 particles.(C15)
particles.(C15)
2) The mass is formed by a 1:1:10 mixture of protons, helium nuclei and electrons
Identically as in the preceding Appendix C1 the medium mass of a “particle” is in this case, see equation (C8),

and the number of particles 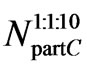 in one Cluster is then
in one Cluster is then

i.e.
 . (C16)
. (C16)
This section can be summarized by the statement that there are
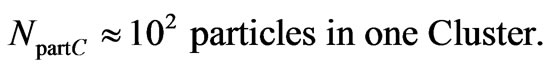 (C17)
(C17)
C3. Consequences of Previous Calculations
We are now able to calculate easily the number of Clusters in one Object. Because there are 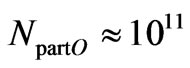 particles in one Object (Equation (C10)) and there are
particles in one Object (Equation (C10)) and there are 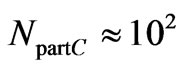 particles in one Cluster, it follows that an Object should be composed from NC Clusters, where
particles in one Cluster, it follows that an Object should be composed from NC Clusters, where
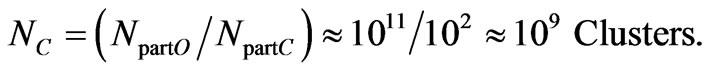 (C18)
(C18)
Supposing that densities in the Object and in the Cluster are equal then this value is independent on the value of the density and on the mass of the particle (e.g.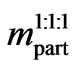 ) and depends only on the relation of the volumes VO/VC, because
) and depends only on the relation of the volumes VO/VC, because
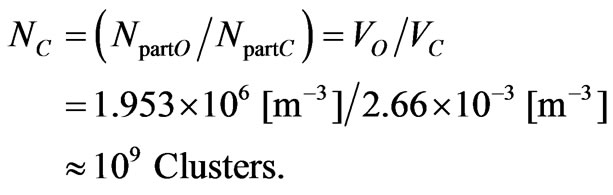 (C19)
(C19)
NOTES
1It is just the low-energy limit of Compton scattering: the particle kinetic energy and photon frequency are the same before and after the scattering, however this limit is valid as long as the photon energy is much less than the mass energy of the particle.
2The term “scattering” (e.g. of radiation) is used throughout the Appendix, however, in the moment when in the quantity fm (see equation (A6)) the atomic scattering factor is substituted by the relict radiation factor, see Subsections 2.1. and 5.2. we speak about an interaction of photons with the primordial matter.
3In a conventional experiment the scattered intensity is corrected for scattering on “air”, absorption, divergency of the X-ray beam, Lorentz and polarization factor. During our calculations we have included only the polarization factor.

