Journal of Modern Physics
Vol. 2 No. 7 (2011) , Article ID: 5837 , 22 pages DOI:10.4236/jmp.2011.27086
Detailing Coherent, Minimum Uncertainty States of Gravitons, as Semi Classical Components of Gravity Waves, and How Squeezed States Affect Upper Limits to Graviton Mass
Department of Physics, Chongqing University, Chongqing, China
E-mail: abeckwith@uh.edu
Received April 12, 2011; revised June 1, 2011; accepted June 13, 2011
Keywords: Squeezed State, Graviton, GW, Pilot Model
ABSTRACT
We present what is relevant to squeezed states of initial space time and how that affects both the composition of relic GW, and also gravitons. A side issue to consider is if gravitons can be configured as semi classical “particles”, which is akin to the Pilot model of Quantum Mechanics as embedded in a larger non linear “deterministic” background.
1. Introduction
Gravitons may be de composed via an instanton-anti instanton structure. i.e. that the structure of SO(4) gauge theory is initially broken due to the introduction of vacuum energy [1], so after a second-order phase transition, the instanton-anti-instanton structure of relic gravitons is reconstituted. This will be crucial to link graviton production with entropy, provided we have sufficiently HFGW at the origin of the big bang. The linkage to SO(4) gauge theory and gravitons was brought up by [1] Kuchiev, M. Yu, and we think it leads to a kink-anti kink pair tie in for attendant gravitons. Note that Kuchiev [1] writes that “Conventional non-Abelian SO(4) gauge theory is able to describe gravity provided the gauge field possesses a specific polarized vacuum state. In this vacuum the instantons and anti-instantons have a preferred direction of orientation”, and furthermore “Gravitons appear as the mode describing propagation of the gauge field which strongly interacts with the oriented instantons” Furthermore, as given by Ivan Andrić, Larisa Jonke and Danijel Jurman [2], what is called an n-soliton solution is shown to have an equivalence with the following, namely “semiclassical solutions corresponding to giant gravitons described by matrix models obtained in the framework of AdS/CFT correspondence”. Solitons have a kink-anti kink structure, even in low dimensions, as was worked out by Beckwith in a condensed matter application. The string theory methodology is merely extending much the same thinking up to higher than four dimensional situations.
1) Modeling of entropy, generally, as kink-anti-kinks pairs with 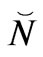 the number of the kink-anti-kink pairs. This number,
the number of the kink-anti-kink pairs. This number,  is, initially in tandem with entropy production, as will be explained later2) The tie in with entropy and gravitons is this: the two structures are related to each other in terms of kinks and anti-kinks. It is asserted that how they form and break up is due to the same phenomenon: a large insertion of vacuum energy leads to an initial breakup of both entropy levels and gravitons. When a second-order phase transition occurs, there is a burst of relic gravitons. Similarly, there is an initial breakup of net entropy levels, and after a second-order phase transition, another rapid increase in entropy.
is, initially in tandem with entropy production, as will be explained later2) The tie in with entropy and gravitons is this: the two structures are related to each other in terms of kinks and anti-kinks. It is asserted that how they form and break up is due to the same phenomenon: a large insertion of vacuum energy leads to an initial breakup of both entropy levels and gravitons. When a second-order phase transition occurs, there is a burst of relic gravitons. Similarly, there is an initial breakup of net entropy levels, and after a second-order phase transition, another rapid increase in entropy.
The supposition we are making here is that the value of N so obtained is actually proportional to a numerical graviton density we will refer to as 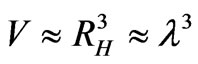 . Furthermore, structure formation arguments, as given by Perkins [3] give ample evidence that if we use an energy scale,
. Furthermore, structure formation arguments, as given by Perkins [3] give ample evidence that if we use an energy scale, 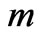 , over a Planck mass value
, over a Planck mass value , as well as contributions from field amplitude
, as well as contributions from field amplitude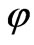 , and using the contribution of scale factor behavior
, and using the contribution of scale factor behavior

where we assume  due to inflation
due to inflation
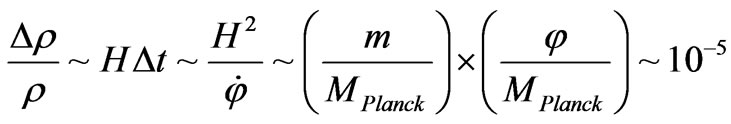 (1)
(1)
At the very onset of inflation, 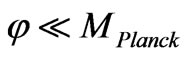 , and if
, and if 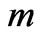 (assuming
(assuming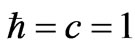 ) is due to inputs from a prior universe, we have a wide range of parameter space as to ascertain where
) is due to inputs from a prior universe, we have a wide range of parameter space as to ascertain where  comes from and plays a role as to the development of entropy in cosmological evolution In the next Chapter , we will discuss if or not it is feasible/reasonable to have data compression of prior universe “information”. It suffices to say that if
comes from and plays a role as to the development of entropy in cosmological evolution In the next Chapter , we will discuss if or not it is feasible/reasonable to have data compression of prior universe “information”. It suffices to say that if 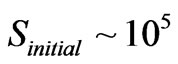 is transferred from a prior universe to our own universe at the onset of inflation, at times less than Planck time
is transferred from a prior universe to our own universe at the onset of inflation, at times less than Planck time 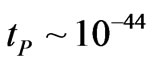 seconds, that enough information MAY exit for the preservation of the prior universe’s cosmological constants, i.e.
seconds, that enough information MAY exit for the preservation of the prior universe’s cosmological constants, i.e. 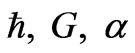 (fine structure constant) and the like. Confirmation of this hypothesis depends upon models of how much “information”
(fine structure constant) and the like. Confirmation of this hypothesis depends upon models of how much “information” 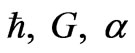 actually require to be set in place, at the onset of our universe’s inflation, a topic which we currently have no experimental way of testing at this current time.
actually require to be set in place, at the onset of our universe’s inflation, a topic which we currently have no experimental way of testing at this current time.
2. Is Each “Particle Count Unit” as Brought up by Ng, Is Equivalent to a Brane-Anti Brane Unit in Brane Treatments of Entropy? How does This Tie in with String/Brane Theory Treatments of Entropy
It is useful to state this convention for analyzing the resulting entropy calculations, because it is a way to explain how and why the number of instanton-anti instanton pairs, and their formulation and break up can be linked to the growth of entropy. If, as an example, there is a linkage between quantum energy level components of the quantum gas as brought up by Glinka [4,5] and a number of instanton-anti instanton pairs, then it is possible to ascertain a linkage between a Wheeler De Witt worm hole introduction of vacuum energy from a prior universe to our present universe, and the resulting brane-anti brane (instanton-anti instanton) units of entropy. Such an approach may permit asking how information is transferred from a prior to the present universe .What would be ideal would be to make an equivalence between a quantum number, n, say of a quantum graviton gas, as entering a worm hole, i.e. going back to the Energy (quantum gas)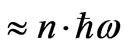 , and the number
, and the number 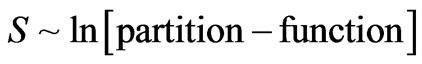 . This is a counter part as to what Asakawa et al. [7] suggested for quark-gluongases, and the 2nd order phase transition written up by Torrieri et al. [8] brought up at the nuclear physics Erice school, in discussions with the author.
. This is a counter part as to what Asakawa et al. [7] suggested for quark-gluongases, and the 2nd order phase transition written up by Torrieri et al. [8] brought up at the nuclear physics Erice school, in discussions with the author.
Furthermore, finding out if or not it is either a drop in viscosity [7,9,10], then
 or a major increase in entropy density may tell us how much information is, indeed, transferred from a prior universe to our present. If it is
or a major increase in entropy density may tell us how much information is, indeed, transferred from a prior universe to our present. If it is , for all effective purposes, at the moment after the pre big bang configuration , likely then there will be a high degree of “information” from a prior universe exchanged to our present universe. If on the other hand,
, for all effective purposes, at the moment after the pre big bang configuration , likely then there will be a high degree of “information” from a prior universe exchanged to our present universe. If on the other hand,  due to restriction of ‘information from four dimensional “geometry” to a variable fifth dimension, so as to indicate almost infinite collisions with a closure of a fourth dimensional “portal” for information flow, then it is likely that significant data compression has occurred. While stating this, it is note worthy to state that the Penrose-Hawking singularity theorems do not give precise answers as to information flow from a prior to the present universe. Hawking’s singularity theorem is for the whole universe, and works backwards-in-time: it guarantees that the big-bang has infinite density. This theorem is more restricted, it only holds when matter obeys a stronger energy condition, called the dominant energy condition, which means that the energy is bigger than the pressure. All ordinary matter, with the exception of a vacuum expectation value of a scalar field, obeys this condition.
due to restriction of ‘information from four dimensional “geometry” to a variable fifth dimension, so as to indicate almost infinite collisions with a closure of a fourth dimensional “portal” for information flow, then it is likely that significant data compression has occurred. While stating this, it is note worthy to state that the Penrose-Hawking singularity theorems do not give precise answers as to information flow from a prior to the present universe. Hawking’s singularity theorem is for the whole universe, and works backwards-in-time: it guarantees that the big-bang has infinite density. This theorem is more restricted, it only holds when matter obeys a stronger energy condition, called the dominant energy condition, which means that the energy is bigger than the pressure. All ordinary matter, with the exception of a vacuum expectation value of a scalar field, obeys this condition.
This leaves open the question of if or not there is “infinite” density of ordinary matter, or if or not there is a fifth dimensional leakage of “information” from a prior universe to our present. If there is merely infinite “density”, and possibly infinite entropy density/disorder at the origin, then perhaps no information from a prior universe is transferred to our present universe. On the other hand, having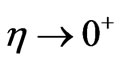 , or at least be very small may indicate that data compression is a de rigor way of treating how information for cosmological parameters, such as
, or at least be very small may indicate that data compression is a de rigor way of treating how information for cosmological parameters, such as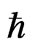 , G, and the fine structure constant.
, G, and the fine structure constant. 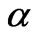 arose, and may have been recycled from a prior universe. Details about this have to be worked out, and this because that as of present one of the few tools which is left to formulation and proof of the singularity theorems is the Raychaudhuri equation, which describes the divergence θ of a congruence (family) of geodesics, which has a lot of assumptions behind it, as stated by Naresh Dadhich [11]. As indicated by Hawkings theorem, infinite density is its usual modus operandi, for a singularity, and this assumption may have to be revisited. Natário [12] has more details on the different type of singularities involved. The supposition is that the value of N is proportional to a numerical DM density referred to as
arose, and may have been recycled from a prior universe. Details about this have to be worked out, and this because that as of present one of the few tools which is left to formulation and proof of the singularity theorems is the Raychaudhuri equation, which describes the divergence θ of a congruence (family) of geodesics, which has a lot of assumptions behind it, as stated by Naresh Dadhich [11]. As indicated by Hawkings theorem, infinite density is its usual modus operandi, for a singularity, and this assumption may have to be revisited. Natário [12] has more details on the different type of singularities involved. The supposition is that the value of N is proportional to a numerical DM density referred to as 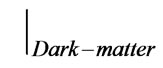 . HFGW would play a role if
. HFGW would play a role if  has each
has each 
of the order of being within an order of magnitude of the Planck length value, as implied by Beckwith [13]. Examined, and linked to modeling gravity as an effective theory, as well as giving credence to how to avoid dS/dt = ∞ at S = 0. If so, then one can look at the research results of Mathur [14]. This is part of what has been developed in the case of massless radiation, where for D space-time dimensions, and E, the general energy is
 (2)
(2)
This suggests that entropy scaling is proportional to a power of the vacuum energy, i.e., entropy ~ vacuum energy, if  is interpreted as a total net energy proportional to vacuum energy, as given below. Conventional brane theory actually enables this instanton structure analysis, as can be seen in the following. This is adapted from a lecture given at the ICGC-07 conference by Beckwith [15]
is interpreted as a total net energy proportional to vacuum energy, as given below. Conventional brane theory actually enables this instanton structure analysis, as can be seen in the following. This is adapted from a lecture given at the ICGC-07 conference by Beckwith [15]
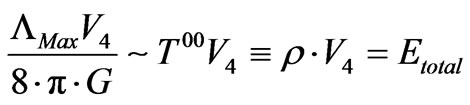 (3)
(3)
The approximation we are making, in this treatment initially is that  where we are looking at a potential energy term [15].
where we are looking at a potential energy term [15].
What we are paying attention to, here is the datum that for an exponential potential (potential energy) [16]
 (4)
(4)
De facto, what we come up with pre, and post Planckian space time regimes, when looking at consistency of the emergent structure is the following. Namely, [17]
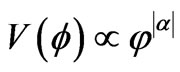 for
for 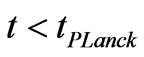 (4a)
(4a)
Also, we would have
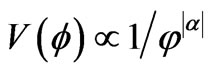 for
for 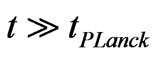 (4b)
(4b)
The switch between Equations (4a) and (4b) is not justified analytically. i.e. it breaks down. Beckwith, et al. [17] stated this as the boundary of a causal discontinuity.
Now according to Weinberg [16], if

so that one has a scale factor behaving as
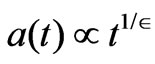 (5)
(5)
Then, if
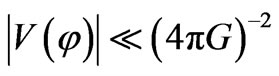 (6)
(6)
there are no quantum gravity effects worth speaking of. i.e., if one uses an exponential potential a scalar field could take the value of, when there is a drop in a field from 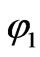 to
to 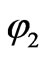 for flat space geometry and times
for flat space geometry and times 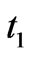 to
to 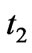 [16]
[16]
 (7)
(7)
Then the scale factors, from Planckian time scale as [16]
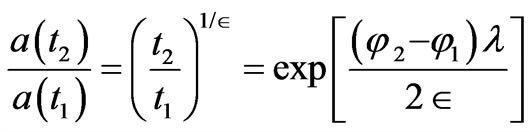 (8)
(8)
The more  then the less likely there is a tie in with quantum gravity. Note those that the way this potential is defined is for a flat, Roberson-Walker geometry, and that if and when
then the less likely there is a tie in with quantum gravity. Note those that the way this potential is defined is for a flat, Roberson-Walker geometry, and that if and when 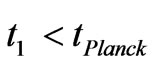 then what is done in Equation (8) no longer applies, and that one is no longer having any connection with even an octonionic Gravity regime. If so, as indicated by Beckwith, et al. [15] one may have to tie in graviton production due to photonic (“light”) inputs from a prior universe, i.e. a causal discontinuity, with consequences which will show in both GW and graviton production.
then what is done in Equation (8) no longer applies, and that one is no longer having any connection with even an octonionic Gravity regime. If so, as indicated by Beckwith, et al. [15] one may have to tie in graviton production due to photonic (“light”) inputs from a prior universe, i.e. a causal discontinuity, with consequences which will show in both GW and graviton production.
3. Linking Instaton-Anti Instaton Construction in both Entropy Generation and Gravitons
Here is a quick review of how to have an instaton-anti instanton construction for entropy, and then proposing a similar construction for gravitons. Afterwards, we will analyze squeezed states. It is the authors conviction that semi classical treatment of Gravitons, if gravitons are in an instanton-anti instanton paring is equivalent to the break down of the “thin wall approximation” used in density wave physics. In what may be by some peoples visualization, an outrageous simplication, the issue of squeezing of graviton states is similar to what happens with the break down of the purely quantum mechanical analogy done for initially non squeezed states, which when squeezed have their own non quantum mechanical flavor.
We will start first looking at entropy, as an instanton-anti instanton construction and go from there:
Traditionally, minimum length for space-time benchmarking has been via the quantum gravity modification of a minimum Planck length for a grid of space-time of Planck length, whereas this grid is changed to something bigger
 .
.
So far, we this only covers a typical string gas model for entropy.  is assigned as the as numerical density of brains and anti-branes. A brane-antibrane pair corresponds to solitons and anti-solitons in density wave physics. The branes are equivalent to instanton kinks in density wave physics, whereas the antibranes are an anti-instanton structure. First, a similar pairing in both black hole models and models of the early universe is examined, and a counting regime for the number of instanton and anti-instanton structures in both black holes and in early universe models is employed as a way to get a net entropy-information count value. One can observe this in the work of Gilad Lifschytz [18] in 2004. Lifschyztz codified thermalization equations of the black hole, which were recovered from the model of branes and antibranes and a contribution to total vacuum energy. In lieu of assuming an antibrane is merely the charge conjugate of say a Dp brane. Here,
is assigned as the as numerical density of brains and anti-branes. A brane-antibrane pair corresponds to solitons and anti-solitons in density wave physics. The branes are equivalent to instanton kinks in density wave physics, whereas the antibranes are an anti-instanton structure. First, a similar pairing in both black hole models and models of the early universe is examined, and a counting regime for the number of instanton and anti-instanton structures in both black holes and in early universe models is employed as a way to get a net entropy-information count value. One can observe this in the work of Gilad Lifschytz [18] in 2004. Lifschyztz codified thermalization equations of the black hole, which were recovered from the model of branes and antibranes and a contribution to total vacuum energy. In lieu of assuming an antibrane is merely the charge conjugate of say a Dp brane. Here,  is the number of branes in an early universe configuration, while
is the number of branes in an early universe configuration, while 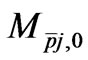 is anti-brane number. i.e., there is a kink in the given
is anti-brane number. i.e., there is a kink in the given
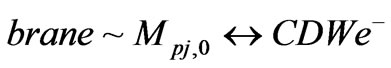
electron charge and for the corresponding anti-kink
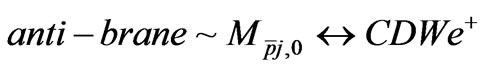
positron charge. Here, in the bottom expression, 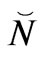 is the number of kink-anti-kink charge pairs, which is analogous to the simpler CDW structure [17].
is the number of kink-anti-kink charge pairs, which is analogous to the simpler CDW structure [17].
 (9)
(9)
This expression for entropy (based on the number of brane-anti-brane pairs) has a net energy value of  as expressed in Equation (9) above, where
as expressed in Equation (9) above, where 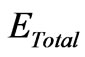 is proportional to the cosmological vacuum energy parameter; in string theory,
is proportional to the cosmological vacuum energy parameter; in string theory,  is also defined via
is also defined via
 (10)
(10)
Equation (10) can be changed and rescaled to treating the mass and the energy of the brane contribution along the lines of Mathur’s CQG article [14] where he has a string winding interpretation of energy: putting as much energy  into string windings as possible via
into string windings as possible via  , where there are
, where there are  wrappings of a string about a cycle of the torus , and
wrappings of a string about a cycle of the torus , and 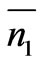 being “wrappings the other way”, with the torus having a cycle of length L, which leads to an entropy defined in terms of an energy value of mass of
being “wrappings the other way”, with the torus having a cycle of length L, which leads to an entropy defined in terms of an energy value of mass of  (
(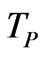
is the tension of the ith brane, and  are spatial dimensions of a complex torus structure). The toroidal structure is to first approximation equivalent dimensionally to the minimum effective length of
are spatial dimensions of a complex torus structure). The toroidal structure is to first approximation equivalent dimensionally to the minimum effective length of 
times Planck length  centimeters
centimeters
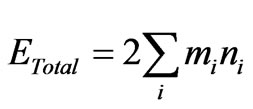 (11)
(11)
The windings of a string are given by Becker et al. [19], as the number of times the strings wrap about a circle midway in the length of a cylinder. The structure the string wraps about is a compact object construct Dp branes and anti-branes. Compactness is used to roughly represent early universe conditions, and the brane-anti brane pairs are equivalent to a bit of “information”. This leads to entropy expressed as a strict numerical count of different pairs of Dp brane-Dp anti-branes, which form a higher-dimensional equivalent to graviton production. The tie in between Equation (12) below and Jack Ng’s treatment [6] of the growth of entropy is as follows: First, look at the expression below, which has 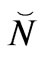 as a stated number of pairs of Dp brane-antibrane pairs: The suffix
as a stated number of pairs of Dp brane-antibrane pairs: The suffix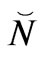 is in a 1-1 relationship with
is in a 1-1 relationship with 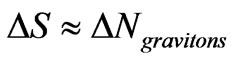
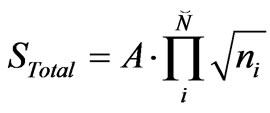 (12)
(12)
Now, how do we make sense of the following entropy values? Note the following:
As an example of present confusion, please consider the following discussion where leading cosmologists, i.e. Sean Carroll [20] asserted that there is a distinct possibility that mega black holes in the center of spiral galaxies have more entropy, in a calculated sense, i.e. up to 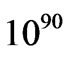 in non dimensional units. This has to be compared to Carroll’s [20] stated value of up to 1088 in non dimensional units for observable non dimensional entropy units for the observable universe. Assume that there are over one billion spiral galaxies, with massive black holes in their center, each with entropy
in non dimensional units. This has to be compared to Carroll’s [20] stated value of up to 1088 in non dimensional units for observable non dimensional entropy units for the observable universe. Assume that there are over one billion spiral galaxies, with massive black holes in their center, each with entropy , and then there is due to spiral galaxy entropy contributions
, and then there is due to spiral galaxy entropy contributions 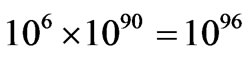 entropy units to contend with, vs.
entropy units to contend with, vs.  entropy units to contend with for the observed universe. i.e. at least a ten to the eight order difference in entropy magnitude to contend with. The author is convinced after trial and error that the standard which should be used is that of talking of information, in the Shannon sense, for entropy, and to find ways to make a relationship between quantum computing operations, and Shannon information. Making the identification of entropy as being written as
entropy units to contend with for the observed universe. i.e. at least a ten to the eight order difference in entropy magnitude to contend with. The author is convinced after trial and error that the standard which should be used is that of talking of information, in the Shannon sense, for entropy, and to find ways to make a relationship between quantum computing operations, and Shannon information. Making the identification of entropy as being written as . This is Shannon information theory with regards to entropy, and the convention will be the core of this text. What is chosen as a partition function will vary with our chosen model of how to input energy into our present universe. This idea as to an input of energy, and picking different models of how to do so leading to partition functions models is what motivated research in entropy generation. From now on, there will be an effort made to identify different procedural representations of the partiton function, and the log of the partion function with both string theory representations, i.e. the particle count algorithm of Y. Jack Ng [6], and the Wheeler De Witt version of the log of the partition function as presented by Glinka [4,5]. Doing so may enable researchers to eventually determine if or not gravity/gravitational waves are an emergent field phenomenon.
. This is Shannon information theory with regards to entropy, and the convention will be the core of this text. What is chosen as a partition function will vary with our chosen model of how to input energy into our present universe. This idea as to an input of energy, and picking different models of how to do so leading to partition functions models is what motivated research in entropy generation. From now on, there will be an effort made to identify different procedural representations of the partiton function, and the log of the partion function with both string theory representations, i.e. the particle count algorithm of Y. Jack Ng [6], and the Wheeler De Witt version of the log of the partition function as presented by Glinka [4,5]. Doing so may enable researchers to eventually determine if or not gravity/gravitational waves are an emergent field phenomenon.
A further datum to consider is that Equation (8) with its variance of density fluctuations may eventually be linkable to Kolmogrov theory as far as structure formation. If we look at R. M. S. Rosa [21], and energy cascades of the form of the “energy dissipation law”, assuming 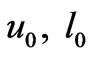 are minimum velocity and length, with velocity less than the speed of light, and the length at least as large, up to
are minimum velocity and length, with velocity less than the speed of light, and the length at least as large, up to  time larger than Planck length
time larger than Planck length 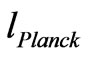
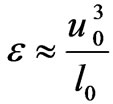 (13)
(13)
Equation (13) above can be linked to an eddy break down process, which leads to energy dissipated by viscosity. If applied appropriately to structures transmitted through a “worm hole” from a prior to a present universe, it can explain 1)How there could be a break up of “encapsulating” structure which may initially suppress additional entropy beyond , in the onset of inflation 2) Provide a “release” mechanism for [6]
, in the onset of inflation 2) Provide a “release” mechanism for [6]
 , with
, with 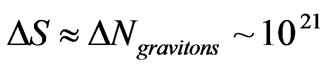
perhaps a starting point for increase in entropy in
 , rising to
, rising to 
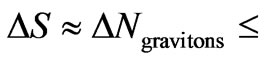 for times up to 1000 seconds after the big bang.
for times up to 1000 seconds after the big bang.
Here is, in a nutshell the template for the Gravitons which will examine, and eventually link to Gravitational waves, and entropy.
4. Different Senarios for Entropy Growth Depending upon if or Not We Have Low to High Frequency GW from the Big Bang
As mentioned above, there is a question of what frequency range of GW is dominant during the onset of the big bang. To begin with let us look at frequency range of GW from relic conditions. As given by for a peak amplitude as stated by Tina Kahniashvili [22]. Now for the amplitude of a GW, as detected today
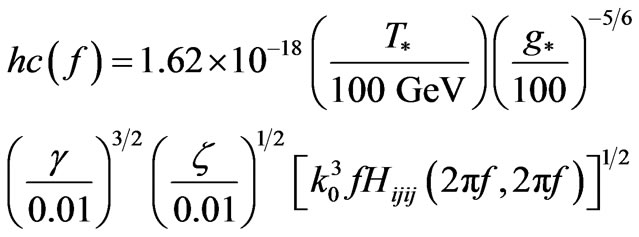 (14)
(14)
The equation, as given by Kahniashvili [22] with a frequency f given below in Equation (15) which is for todays detected GW frequency a detector would observe, whereas 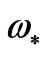 is the frequency of a process synthesizing GW during a 2nd order phase transition in the early universe. Also,
is the frequency of a process synthesizing GW during a 2nd order phase transition in the early universe. Also, 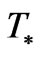 is a mean temperature during that 2nd order phase transition. If as an example
is a mean temperature during that 2nd order phase transition. If as an example 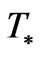 is many times larger than 100 GeV, which is the case if GW nucleation occurred at the ORIGIN of the big bang, i.e. at temperatures
is many times larger than 100 GeV, which is the case if GW nucleation occurred at the ORIGIN of the big bang, i.e. at temperatures , then it is likely that f in Equation (10) below is capable of approaching values of the order of what was predicted by Grishkuk [23] (2007), i.e. approaching 10 Giga Hertz. Equation (8) and Equation (9) above, would have either a small, or a huge
, then it is likely that f in Equation (10) below is capable of approaching values of the order of what was predicted by Grishkuk [23] (2007), i.e. approaching 10 Giga Hertz. Equation (8) and Equation (9) above, would have either a small, or a huge , which would pay a role as to how large the amplitude of a GW would be, detected today, as opposed to what it would be at the origin, say, of the big bang. The larger f is, the more likely the amplitude is, of Equation (14) would be very large. In both Equation (14) above, and Equation (15) below,
, which would pay a role as to how large the amplitude of a GW would be, detected today, as opposed to what it would be at the origin, say, of the big bang. The larger f is, the more likely the amplitude is, of Equation (14) would be very large. In both Equation (14) above, and Equation (15) below,  is a degree of freedom for spatial conditions factor, which has, according to Kolb and Turner [24] high values of the order of 100 right after the big bang, to values closer to 2 and/or 3 in the modern era. i.e. the degrees of freedom radically dropped in the evolution of space time.
is a degree of freedom for spatial conditions factor, which has, according to Kolb and Turner [24] high values of the order of 100 right after the big bang, to values closer to 2 and/or 3 in the modern era. i.e. the degrees of freedom radically dropped in the evolution of space time.
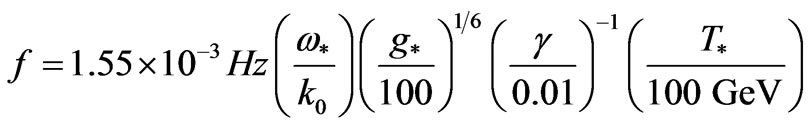 (15)
(15)
Here, in this choice of magnitude h of a GW today, and frequency f detected today, as presumed by using a factor given by Kahniashvili [22] as
 (16)
(16)
Why? The factor  is due to complicated physics which gives a tensor/scalar ratio As well as
is due to complicated physics which gives a tensor/scalar ratio As well as
 (17)
(17)
Why? Equation (17) is a two correlation point function, much in the spirit of calculations of two point correlation functions, i.e. greens functions of Quantum field theory. See [25] Peskin’s QFT reference as to how such functional calculations are to show the degree of interaction between , with each individual
, with each individual 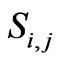 defined as part of a GR “stress tensor” contribution of
defined as part of a GR “stress tensor” contribution of
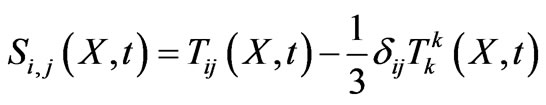 (18)
(18)
This is where, commonly, we have a way to interpret  in terms of
in terms of  via
via
 (19)
(19)
As well as a wave equation we can write as
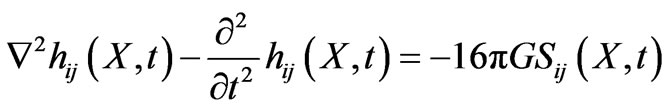 (20)
(20)
What is above, is a way for making sense of GW “density” as given by the formula
 (21)
(21)
Here, the temperature 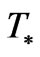 for the onset of a phase transition, i.e. usually interpreted as a 2nd order phase transition plays a major role as to if or not the frequency, f, for today is very low, or higher, and if or not energy density is high, or low, as well as the attendant amplitude of a GW, as given by Equation (19) above is important. Furthermore appropriate calculations of Equation (21) very much depend upon the correlation function as given by Equation (17) is correctly done, allowing for a minimization of sources of noise, of the sort alluded to by [26] Michelle Maggiore. Possibly though, cosmological evolution is so subtle that no simple use of correlation functions will be sufficient to screen noise by typical field theory derived methods. If temperature
for the onset of a phase transition, i.e. usually interpreted as a 2nd order phase transition plays a major role as to if or not the frequency, f, for today is very low, or higher, and if or not energy density is high, or low, as well as the attendant amplitude of a GW, as given by Equation (19) above is important. Furthermore appropriate calculations of Equation (21) very much depend upon the correlation function as given by Equation (17) is correctly done, allowing for a minimization of sources of noise, of the sort alluded to by [26] Michelle Maggiore. Possibly though, cosmological evolution is so subtle that no simple use of correlation functions will be sufficient to screen noise by typical field theory derived methods. If temperature  for the onset of a phase transition, is very high, it is almost certain that we are looking at HFGW, and relic gravitons which are severely energized, i.e. w* would be enormous. If so, then for high
for the onset of a phase transition, is very high, it is almost certain that we are looking at HFGW, and relic gravitons which are severely energized, i.e. w* would be enormous. If so, then for high 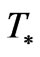 and enormous w*, at the onset of inflation, we are looking at HFGW, and that [6]
and enormous w*, at the onset of inflation, we are looking at HFGW, and that [6]
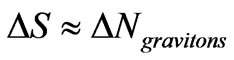 (22)
(22)
If the frequency is much lower, we will see, if the particle-wave duality has large , for DM candidates
, for DM candidates
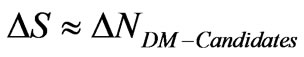 (23)
(23)
This graviton counting as given in Equation (22) will next be connected to information counting which will be a necessary and sufficient condition for information exchanged from a prior to the present universe.
5. Minimum Amount of Information Needed to Initiate Placing Values of Fundamental Cosmological Parameters
A. K. Avessian’s [27] article (2009) about alleged time variation of Planck’s constant from the early universe depends heavily upon initial starting points for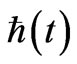 , as given below, where we pick our own values for the time parameters, for reasons we will justify in this manuscript:
, as given below, where we pick our own values for the time parameters, for reasons we will justify in this manuscript:
 (24)
(24)
The idea is that we are assuming a granular, discrete nature of space time. Futhermore, after a time we will state as t ~ tPlanck there is a transition to a present value of space time, which is then probably going to be held constant. It is easy to, in this situation, to get an inter relationship of what 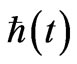 is with respect to the other physical parameters, i.e. having the values of
is with respect to the other physical parameters, i.e. having the values of  written as
written as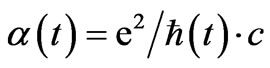 , as well as note how little the fine structure constant actually varies. Note that if we assume an unchanging Planck’s mass
, as well as note how little the fine structure constant actually varies. Note that if we assume an unchanging Planck’s mass

this means that G has a time variance, too. This leads to us asking what can be done to get a starting value of 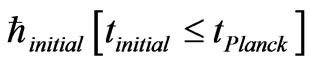 recycled from a prior universe, to our present universe value. What is the initial value, and how does one insure its existence? We obtain a minimum value as far as “information” via appealing to Hogans [28] argument where we have a maximum entropy as
recycled from a prior universe, to our present universe value. What is the initial value, and how does one insure its existence? We obtain a minimum value as far as “information” via appealing to Hogans [28] argument where we have a maximum entropy as
 (25)
(25)
and this can be compared with A. K. Avessian’s article [27] 2009 value of, where we pick 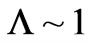
 (26)
(26)
i.e. a choice as to how 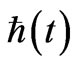 has an initial value, and entropy as scale valued by
has an initial value, and entropy as scale valued by 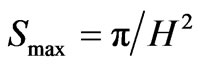 gives us an estimate as to compressed values of
gives us an estimate as to compressed values of 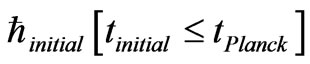 which would be transferred from a prior universe, to todays universe. If
which would be transferred from a prior universe, to todays universe. If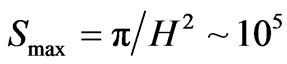 , this would mean an incredibly small value for the INITIAL H parameter, i.e. in pre inflation, we would have practically NO increase in expansion, just before the introduction vacuum energy, or emergent field energy from a prior universe, to our present universe. Typically though, the value of the Hubble parameter, during inflation itself is HUGE, i.e. H is many times larger than 1, leading to initially very small entropy values. This means that we have to assume, initially, for a minimum transfer of entropy/information from a prior universe, that H is neligible. If we look at Hogan’s holographic model, this is consistent with a non finite event horizon [28]
, this would mean an incredibly small value for the INITIAL H parameter, i.e. in pre inflation, we would have practically NO increase in expansion, just before the introduction vacuum energy, or emergent field energy from a prior universe, to our present universe. Typically though, the value of the Hubble parameter, during inflation itself is HUGE, i.e. H is many times larger than 1, leading to initially very small entropy values. This means that we have to assume, initially, for a minimum transfer of entropy/information from a prior universe, that H is neligible. If we look at Hogan’s holographic model, this is consistent with a non finite event horizon [28]
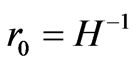 (27)
(27)
This is tied in with a temperature as given by
 (28)
(28)
Nearly infinite temperatures are associated with tiny event horizon values, which in turn are linked to huge Hubble parameters of expansion. Whereas initially nearly zero values of temperature can be arguably linked to nearly non existent H values, which in term would be consistent with 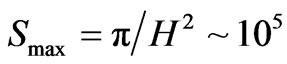 as a starting point to entropy. We next then must consider how the values of initial entropy are linkable to other physical models. i.e. can there be a transfer of entropy/information from a pre inflation state to the present universe. Doing this will require that we keep in mind, as Hogan writes, that the number of distinguishable states is writable as [28]
as a starting point to entropy. We next then must consider how the values of initial entropy are linkable to other physical models. i.e. can there be a transfer of entropy/information from a pre inflation state to the present universe. Doing this will require that we keep in mind, as Hogan writes, that the number of distinguishable states is writable as [28]
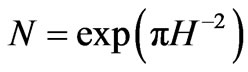 (29)
(29)
If, in this situation, that N is proportional to entropy, i.e. N as ~ number of entropy states to consider, then as H drops in size, as would happen in pre inflation conditions, we will have opportunities for N ~ 105.
6. How the CMBR Permits, via Maximum Frequency, and Maximum Wave Amplitude Values, an Upper Bound Value for Massive Graviton Mass 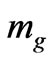
Camp and Cornish [29], as does Fangyu Li [30] use the typical transverse gravitational gauge hij with a typically traceless value summed as 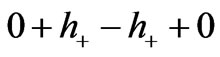 and off diagonal elements of
and off diagonal elements of  on each side of the diagnonal to mix with a value of
on each side of the diagnonal to mix with a value of
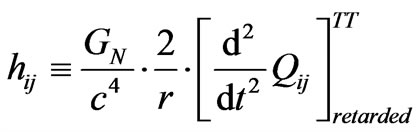 (30)
(30)
This assumes 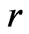 is the distance to the source of gravitational radiation, with the retarded designation on the Equation (30) denoting
is the distance to the source of gravitational radiation, with the retarded designation on the Equation (30) denoting  replaced by a retarded time derivative
replaced by a retarded time derivative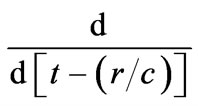 , while TT means take the transverse projections and substract the trace. Here, we call the quadrupole moment, with
, while TT means take the transverse projections and substract the trace. Here, we call the quadrupole moment, with 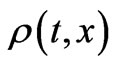 a density measurement. Now, the following value of the
a density measurement. Now, the following value of the 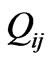 as given gives a luminosity function
as given gives a luminosity function , where
, where 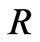 is the “characteristic size” of a gravitational wave source. Note that if
is the “characteristic size” of a gravitational wave source. Note that if 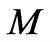 is the mass of the gravitating system
is the mass of the gravitating system
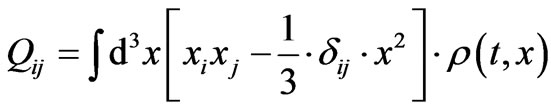 (31)
(31)
 (32)
(32)
After certain considerations reported by Camp and Cornish [29], one can recover a net GW amplitude
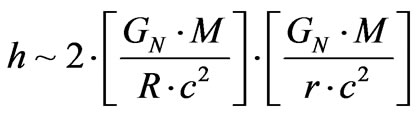 (33)
(33)
This last equation requires that
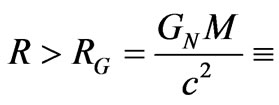 (34)
(34)
gravitational radius of a system, with a black hole resulting if one sets
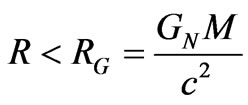 . (35)
. (35)
Note that when
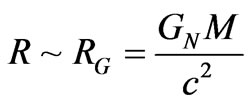 (36)
(36)
we are at an indeterminate boundary where one may pick our system as having black hole properties.
Now for stars, Camp and Cornish [29] give us that
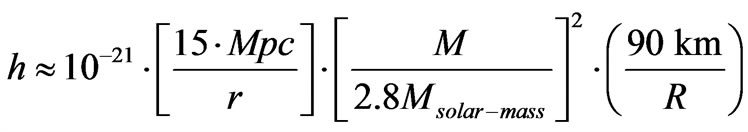 (37)
(37)
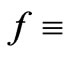 frequency
frequency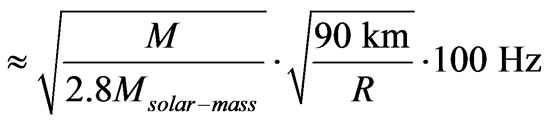 (38)
(38)
As well as a mean time  for half of gravitational wave potential energy to be radiated away as
for half of gravitational wave potential energy to be radiated away as
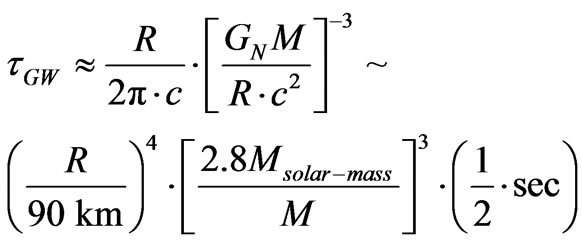 (39)
(39)
The assumption we make is that if we model
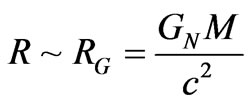 for a sufficiently well posed net mass M that the star formulas roughly hold for early universe conditions, provided that we can have a temperature T for which we can use the approximation
for a sufficiently well posed net mass M that the star formulas roughly hold for early universe conditions, provided that we can have a temperature T for which we can use the approximation
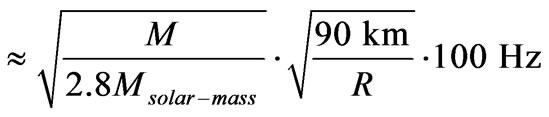 (40)
(40)
that we also have  or higher, so, that at a minimum we recover Grishchuck’s [23] value of
or higher, so, that at a minimum we recover Grishchuck’s [23] value of
 (41)
(41)
Equation (40) places, for a specified value of R, which can be done experimentally, an upper bound as far as far as what a mass M would be. Can this be exploited to answer the question of if or not there is a minimum value for the Graviton mass?
The key to the following discussion will be that
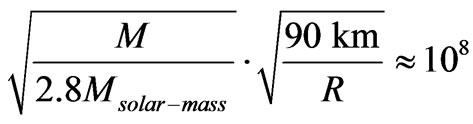 , or larger.
, or larger.
7. Inter Relationship between Graviton Mass 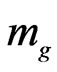 and the Problem of a Sufficient Number of Bits of
and the Problem of a Sufficient Number of Bits of 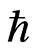 from a Prior Universe, to Preserve Continuity between Fundamental Constants from a Prior to the Present Universe
from a Prior Universe, to Preserve Continuity between Fundamental Constants from a Prior to the Present Universe
P. Tinyakov [31] gives that there is, with regards to the halo of sub structures in the local Milky Way galaxy an amplitude factor for gravitational waves of
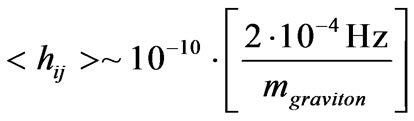 (42)
(42)
If we use LISA values for the Pulsar Gravitational wave frequencies, this may mean that the massive graviton is ruled out. On the other hand
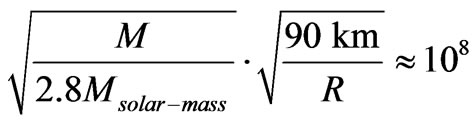 (43)
(43)
leads to looking at, if
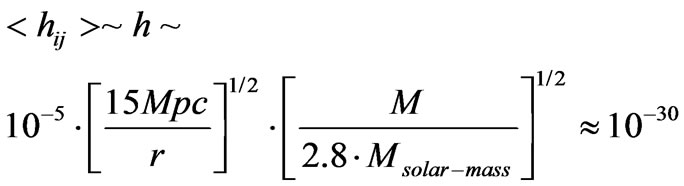 (44)
(44)
If the radius is of the order of  10 billion light-years ~4300 Mpc or much greater, so then we have, as an example
10 billion light-years ~4300 Mpc or much greater, so then we have, as an example
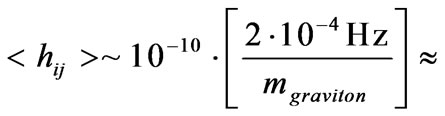
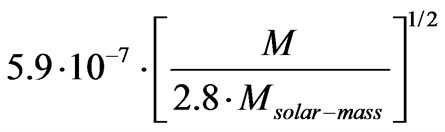
 (45)
(45)
This Equation (45) is in units where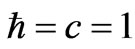 .
.
If 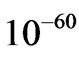 grams per graviton, and 1 electron volt is in rest mass, so
grams per graviton, and 1 electron volt is in rest mass, so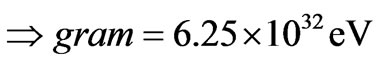
 . Then
. Then
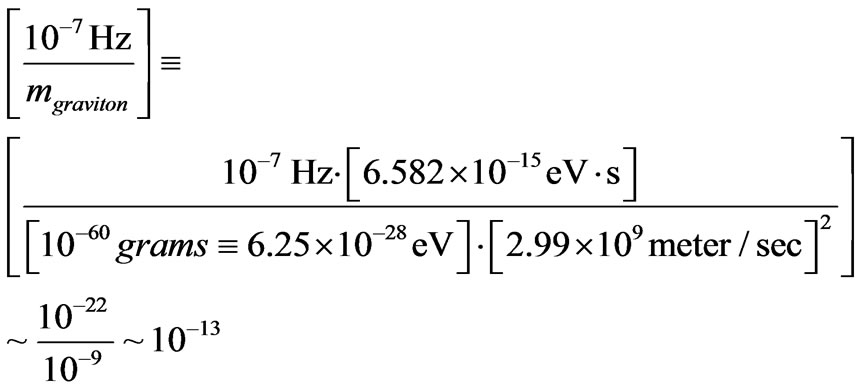 Then, exist
Then, exist
 (46)
(46)
If each photon, as stated above is 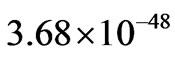 grams per photon, [32] then
grams per photon, [32] then
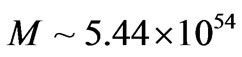 initially transmitted photons.(47)
initially transmitted photons.(47)
Futhermore, if there are, today for a back ground CMBR temperature of 2.7 degrees Kelvin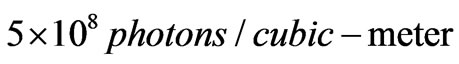 , with a wave length specified as
, with a wave length specified as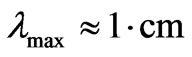 . This is for a numerical density of photons per cubic meter given by
. This is for a numerical density of photons per cubic meter given by
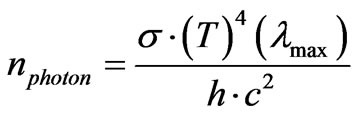 (48)
(48)
As a rough rule of thumb, if, as given by Weinberg [33] that early quantum effects , for quantum gravity take place at a temperature 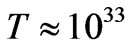 Kelvin, then, if there was that temperature for a cubic meter of space, the numerical density would be , roughly
Kelvin, then, if there was that temperature for a cubic meter of space, the numerical density would be , roughly 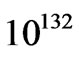 times greater than what it is today. Forget it. So what we have to do is to consider a much smaller volume area. If the radii of the volume area is
times greater than what it is today. Forget it. So what we have to do is to consider a much smaller volume area. If the radii of the volume area is
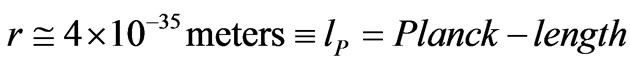
then we have to work with a de facto initial volume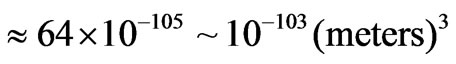 . i.e. the numerical value for the number of photons at
. i.e. the numerical value for the number of photons at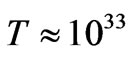 , if we have a per unit volume area based upon Planck length, in stead of meters, cubed is
, if we have a per unit volume area based upon Planck length, in stead of meters, cubed is 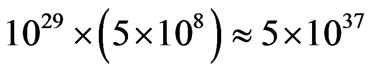 photons for a cubic area with sides
photons for a cubic area with sides 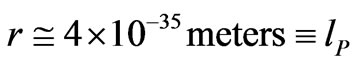 at
at 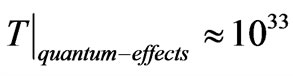 Kelvin However,
Kelvin However, 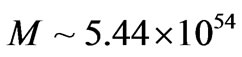
initially transmitted photons! Either the minimum distance, i.e. the grid is larger, or  Kelvin We have, now, so far linked entropy, gravitons, and also information with certain qualifications. Next, we will attempt to quantify the treatment of gravitons, as given in Figure 1 above, with thin wall (box shape) treatment of quantum mechanics rendition of a Graviton. When the thin wall approximation fails, we approach having a semi classical embedding for Gravitons. Corresponding to squeezed states, for gravitons, we will introduce coherent states of gravitons.
Kelvin We have, now, so far linked entropy, gravitons, and also information with certain qualifications. Next, we will attempt to quantify the treatment of gravitons, as given in Figure 1 above, with thin wall (box shape) treatment of quantum mechanics rendition of a Graviton. When the thin wall approximation fails, we approach having a semi classical embedding for Gravitons. Corresponding to squeezed states, for gravitons, we will introduce coherent states of gravitons.
The next part of our discussion will be in linking sequeezed states, with a break down of the purely quantum mechanical modeling of gravitons.
8. Issues about Coherent State of Gravitons (Linking Gravitons with GW)
In the quantum theory of light (quantum electrodynamics) and other bosonic quantum field theories, coherent states were introduced by the work of [34] Roy J. Glauber in 1963 Now, what is appropriate for presenting gravitons as coherent states? Coherent states, to first approximation are retrievable as minimum uncertainty states. If one takes string theory as a reference, the minimum value of uncertainty becomes part of a minimum uncertainty which can be written as given by Venziano [35] (1993)where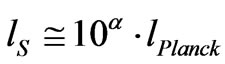 , with
, with 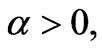 and
and 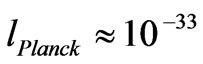 centimeters
centimeters
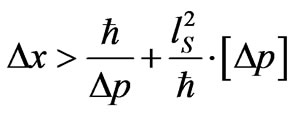 (50)
(50)
To put it mildly, if we are looking at a solution to minimize graviton position uncertainty, we will likely be out of luck if string theory is the only tool we have for early universe conditions. Mainly, the momentum will not be small, and uncertainty in momentum will not be small either. Either way, most likely,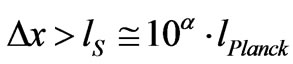 In addition, it is likely, as Klaus Kieffer [36] in the book “Quantum Gravity” on page 290 of that book that if gravitons are excitations of closed strings, then one will have to look for conditions for which a coherent state of gravitons, as stated by [37] Mohaupt occurs. What Mohaupt is referring to is a string theory way to re produce what Ford [38] gave in 1995, i.e. conditions for how Gravitons in a squeezed vacuum state, the natural result of quantum creation in the early universe will introduce metric fluctuations. Ford’s [38] treatment is to have a metric averaged retarded Green’s function for a massless field becoming a Gaussian. The condition of Gaussianity is how to obtain semi classical, minimal uncertainty wave states, in this case de rigor for coherent wave function states to form. Ford [38] uses gravitons in a so called “squeezed vacuum state” as a natural template for relic gravitons. i.e. the squeezed vacuum state (a squeezed coherent state) is any state such that the uncertainty principle is saturated: in QM coherence would be when
In addition, it is likely, as Klaus Kieffer [36] in the book “Quantum Gravity” on page 290 of that book that if gravitons are excitations of closed strings, then one will have to look for conditions for which a coherent state of gravitons, as stated by [37] Mohaupt occurs. What Mohaupt is referring to is a string theory way to re produce what Ford [38] gave in 1995, i.e. conditions for how Gravitons in a squeezed vacuum state, the natural result of quantum creation in the early universe will introduce metric fluctuations. Ford’s [38] treatment is to have a metric averaged retarded Green’s function for a massless field becoming a Gaussian. The condition of Gaussianity is how to obtain semi classical, minimal uncertainty wave states, in this case de rigor for coherent wave function states to form. Ford [38] uses gravitons in a so called “squeezed vacuum state” as a natural template for relic gravitons. i.e. the squeezed vacuum state (a squeezed coherent state) is any state such that the uncertainty principle is saturated: in QM coherence would be when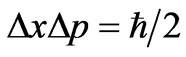 . In the case of string theory it would have to be
. In the case of string theory it would have to be
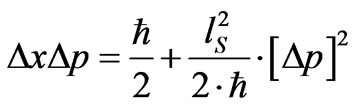 . (51)
. (51)
Putting it mildly, the string theory case is far more difficult. And that is the problem, with regards to string theory, what is an appropriate vacuum expectation value for treating a template of how to nucleate gravitons into a coherent state with respect to relic conditions [38]. Ford, in 1994 [38], wrote a squeezed state operation S( ) via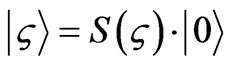 , Here, the operator.
, Here, the operator. 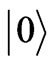 is a ground state, and frequently, as Ford did, in 1994, there is a definition of a root mean squared fluctuation of a graviton/gravitational wave state via use of an average scalar field
is a ground state, and frequently, as Ford did, in 1994, there is a definition of a root mean squared fluctuation of a graviton/gravitational wave state via use of an average scalar field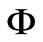 , where
, where
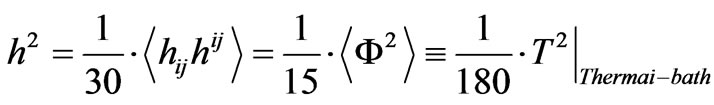 (52)
(52)
Here, the value 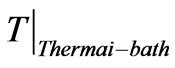 has yet to be specified, and that actually for energy values approximately of the order of
has yet to be specified, and that actually for energy values approximately of the order of  which may be the mean temperature for the expanding universe mid way, to the end of inflation, which does not equal current even smaller string theory estimates as presented by Li et al. [30]
which may be the mean temperature for the expanding universe mid way, to the end of inflation, which does not equal current even smaller string theory estimates as presented by Li et al. [30]
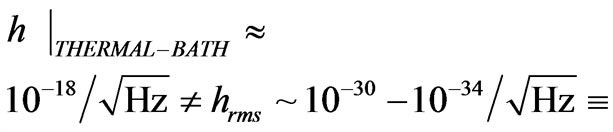
string theory values for inflationary Gravitational amplitudes. i.e. the more modern treatments are predicting almost infinitesimal GW fluctuations. It is not clear from Ford’s [38] treatmentof gravitons, and fluctuations, if he is visualizing fluctuation of gravitons/GW, but if one takes literally Equation (53) as a base line, and then considering what would be the optimal way to obtain a way to obtain coherent states of gravitons, going to the Li [30] stated value of 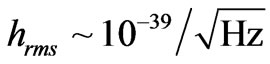 for solar plasma from the sun as a graviton source, would be a way of obtaining fluctuations
for solar plasma from the sun as a graviton source, would be a way of obtaining fluctuations 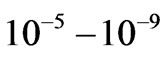 times weaker, i.e. going to
times weaker, i.e. going to 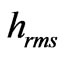 values so small that the requirement for a minimum fluctuation , in line with not contradicting
values so small that the requirement for a minimum fluctuation , in line with not contradicting
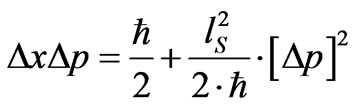 , (53)
, (53)
if we consider experimental conditions for obtaining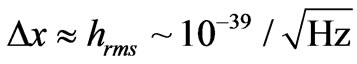 . Note that this would put severe restrictions upon the variations in momentum. A subject which will be referenced in whether or not the Li-Baker detector can suitably obtain such small values of
. Note that this would put severe restrictions upon the variations in momentum. A subject which will be referenced in whether or not the Li-Baker detector can suitably obtain such small values of 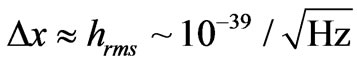 in detection capacity. To do so will require an investigation into extreme sensitivity requirements, for this very low value of
in detection capacity. To do so will require an investigation into extreme sensitivity requirements, for this very low value of . Fanguy Li. et al. [30] reports in their PRD document
. Fanguy Li. et al. [30] reports in their PRD document
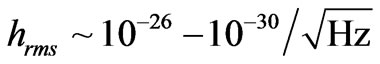 (54)
(54)
would require up to 105 seconds in evaluative time for a clean signal, for GW. What will be asked in further sections is if or not the 105 seconds in evaluative time for a clean signal can evaluate additional data. i.e. what if one would have to do to distinguish if or not coherent states of gravitons which merge to form GW may be measured via the protocols brought up by Li et al. [30] for relic GW. Now what could be said about forming states close to classical representations of gravitons? Venkatartnam, and Suresh [39], built up a coherent state via use of a displacement operator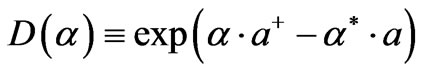 , applied to a vacuum state , where
, applied to a vacuum state , where 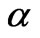 is a complex number, and
is a complex number, and 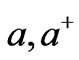 as annihilation, and creation operations
as annihilation, and creation operations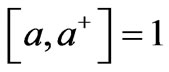 , where one has
, where one has
 (55)
(55)
However, what one sees in string theory, is a situation where a vacuum state as a template for graviton nucleation is built out of an initial vacuum state,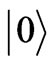 . To do this though, as Venkatartnam, and Suresh [39] did, involved using a squeezing operator
. To do this though, as Venkatartnam, and Suresh [39] did, involved using a squeezing operator 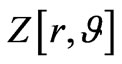 defining via use of a squeezing parameter r as a strength of squeezing interaction term, with
defining via use of a squeezing parameter r as a strength of squeezing interaction term, with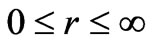 , and also an angle of squeezing,
, and also an angle of squeezing,  as used in
as used in
 where combining the
where combining the 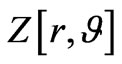 with (55) leads to a single mode squeezed coherent state, as they [39] define it via
with (55) leads to a single mode squeezed coherent state, as they [39] define it via
 (56)
(56)
The right hand side of Equation (56) given above becomes a highly non classical operator, i.e. in the limit that the super position of states 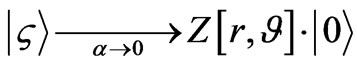 occurs, there is a many particle version of a “vacuum state” which has highly non classical properties. Squeezed states, for what it is worth, are thought to occur at the onset of vacuum nucleation, but what is noted for
occurs, there is a many particle version of a “vacuum state” which has highly non classical properties. Squeezed states, for what it is worth, are thought to occur at the onset of vacuum nucleation, but what is noted for 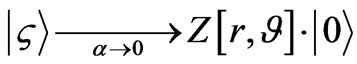 being a super position of vacuum states, means that classical analog is extremely difficult to recover in the case of squeezing, and general non classical behavior of squeezed states. Can one, in any case, faced with
being a super position of vacuum states, means that classical analog is extremely difficult to recover in the case of squeezing, and general non classical behavior of squeezed states. Can one, in any case, faced with 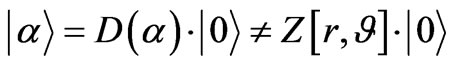 do a better job of constructing coherent graviton states, in relic conditions, which may not involve squeezing? Note L. Grishchuk [40] wrote in “On the quantum state of relic gravitons”, where he claimed in his abstract that “It is shown that relic gravitons created from zero-point quantum fluctuations in the course of cosmological expansion should now exist in the squeezed quantum state. The authors have determined the parameters of the squeezed state generated in a simple cosmological model which includes a stage of inflationary expansion. It is pointed out that, in principle, these parameters can be measured experimentally”. Grishchuk [40], et al., (1989) reference their version of a cosmological perturbation
do a better job of constructing coherent graviton states, in relic conditions, which may not involve squeezing? Note L. Grishchuk [40] wrote in “On the quantum state of relic gravitons”, where he claimed in his abstract that “It is shown that relic gravitons created from zero-point quantum fluctuations in the course of cosmological expansion should now exist in the squeezed quantum state. The authors have determined the parameters of the squeezed state generated in a simple cosmological model which includes a stage of inflationary expansion. It is pointed out that, in principle, these parameters can be measured experimentally”. Grishchuk [40], et al., (1989) reference their version of a cosmological perturbation 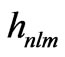 via the following argument. How we work with the argument will affect what is said about the necessity, or lack of, of squeezed states in early universe cosmology. From [40], where
via the following argument. How we work with the argument will affect what is said about the necessity, or lack of, of squeezed states in early universe cosmology. From [40], where  has a component
has a component 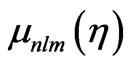 obeying a parametric oscillator equation, where K is a measure of curvature which is
obeying a parametric oscillator equation, where K is a measure of curvature which is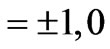 ,
, 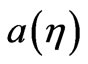 is a scale factor of a FRW metric, and
is a scale factor of a FRW metric, and 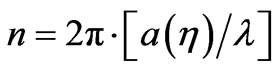 is a way to scale a wavelength,
is a way to scale a wavelength, 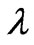 , with n, and with
, with n, and with 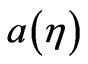
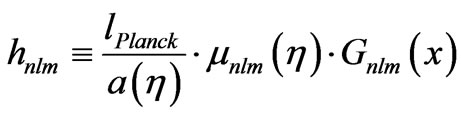 (57)
(57)
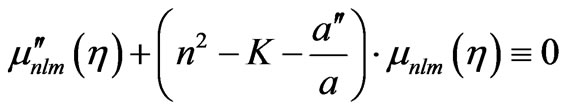 (58)
(58)
If 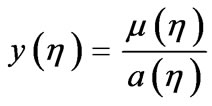 is picked, and a Schrodinger equation is made out of the Lagrangian used to formulate Equation (50) above, with
is picked, and a Schrodinger equation is made out of the Lagrangian used to formulate Equation (50) above, with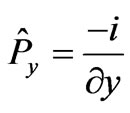 , and
, and ,
,
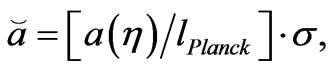

and 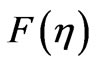 an arbitrary function.
an arbitrary function.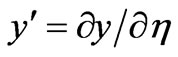 . Also, we have a finite volume
. Also, we have a finite volume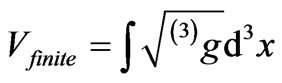 .
.
Then the Lagrangian for deriving Equation (58) is (and leads to a Hamiltonian which can be also derived from the Wheeler De Witt equation), with 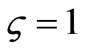 for zero point subtraction of energy
for zero point subtraction of energy
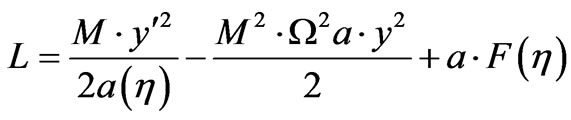 (59)
(59)
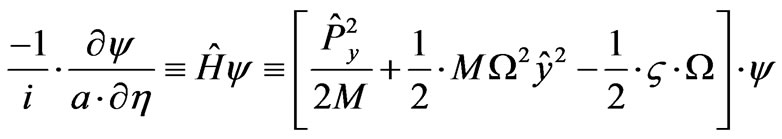 (60)
(60)
then there are two possible solutions to the S. E. Grushchuk [40] created in 1989, one a non squeezed state, and another a squeezed state. So in general we work with
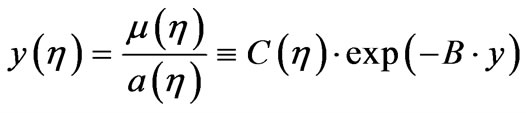 (61)
(61)
The non squeezed state has a parameter
 (62)
(62)
where 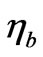 is an initial time, for which the Hamiltonian given in Equation (60) in terms of raising/lowering operators is “diagnonal”, and then the rest of the time for
is an initial time, for which the Hamiltonian given in Equation (60) in terms of raising/lowering operators is “diagnonal”, and then the rest of the time for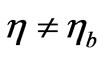 , the squeezed state for
, the squeezed state for 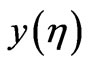 is given via a parameter B for squeezing which when looking at a squeeze parameter r, for which
is given via a parameter B for squeezing which when looking at a squeeze parameter r, for which , then Equation (53) has, instead of
, then Equation (53) has, instead of 
 (63)
(63)
Taking Grishchuck’s formalism [40] literally, a state for a graviton/GW is not affected by squeezing when we are looking at an initial frequency, so that 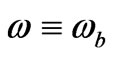 initially corresponds to a non squeezed state which may have coherence, but then right afterwards, if
initially corresponds to a non squeezed state which may have coherence, but then right afterwards, if 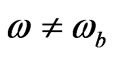 which appears to occur whenever the time evolution,
which appears to occur whenever the time evolution,
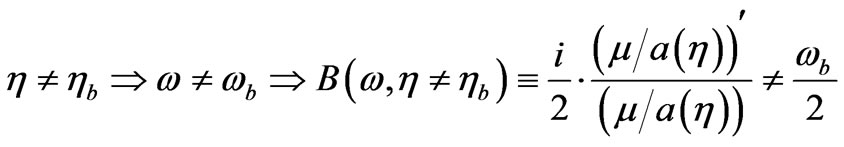
A reasonable research task would be to determine, whether or not
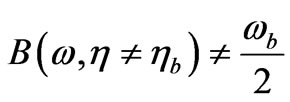 (64)
(64)
would correspond to a vacuum state being initially formed right after the point of nucleation, with 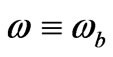 at time
at time  with an initial cosmological time some order of magnitude of a Planck interval of time
with an initial cosmological time some order of magnitude of a Planck interval of time 
seconds The next section will be to answer whether or not there could be a point of no squeezing, as Grishchuck implied, for initial times, and initial frequencies, and an immediate transition to times, and frequencies afterwards, where squeezing was mandatory. Note that Grischchuk [40] further extended his analysis, with respect to the same point of departure, i.e. what to do with when
 .
.
Having 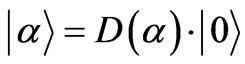 with
with 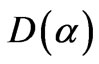 a possible displacement operator, seems to be in common with
a possible displacement operator, seems to be in common with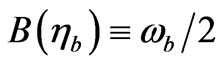 , whereas
, whereas  which is highly non classical seems to be in common with a solution for which
which is highly non classical seems to be in common with a solution for which 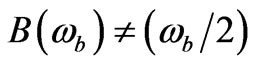 This leads us to the next section, i.e. does
This leads us to the next section, i.e. does 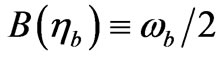 when of time
when of time 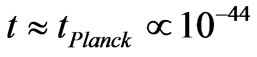 seconds, and then what are the initial conditions for forming “frequency”
seconds, and then what are the initial conditions for forming “frequency” ?
?
9. Necessary and Sufficient Conditions for String/Brane Theory Graviton Coherent States?
A curved spacetime is a coherent background of gravitons, and therefore in string theory is a coherent state Joseph Gerard Polchinski [41] starting with the typical small deviation from flat space times as can be written up by , with
, with 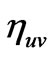 flat space time, and the Polyakov action, is generalized as follows, the
flat space time, and the Polyakov action, is generalized as follows, the 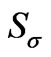 Polyakov action is computed and compared with exponentiated values
Polyakov action is computed and compared with exponentiated values
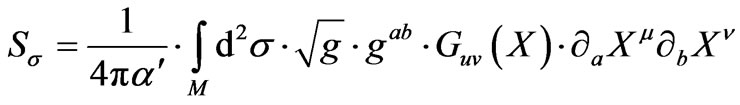 (65)
(65)
becomes
 (66)
(66)
Polochinski [41] writes that the term of order 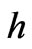 in Equation (65) is the vertex operator for the graviton state of the string, with
in Equation (65) is the vertex operator for the graviton state of the string, with , and the action of
, and the action of  a coherent state of a graviton. Now the important question to ask, is if this coherent state of a graviton, as mentioned by Polochinski [41] can hold up in relic, early universe conditions. R. Dick [42] argued as stating that the “graviton multiplet as one particular dark matter source in heterotic string theory. In particular, it is pointed out that an appreciable fraction of dark matter from the graviton multiplet requires a mass generating phase transition around Tc
a coherent state of a graviton. Now the important question to ask, is if this coherent state of a graviton, as mentioned by Polochinski [41] can hold up in relic, early universe conditions. R. Dick [42] argued as stating that the “graviton multiplet as one particular dark matter source in heterotic string theory. In particular, it is pointed out that an appreciable fraction of dark matter from the graviton multiplet requires a mass generating phase transition around Tc 108 GeV, where the symmetry partners of the graviton would evolve from an ultrahard fluid to pressureless dark matter. indicates m
108 GeV, where the symmetry partners of the graviton would evolve from an ultrahard fluid to pressureless dark matter. indicates m 10 MeV for the massive components of the graviton multiplet”. This has a counter part in a presentation made by Berkenstein [43] with regards to BPS states, and SHO models for
10 MeV for the massive components of the graviton multiplet”. This has a counter part in a presentation made by Berkenstein [43] with regards to BPS states, and SHO models for 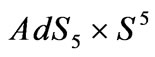 geometry. The upshot is that string theory appears to construct coherent graviton states, but it has no answer to the problem that Ford [38], wrote on if the existing graviton coherent states would be squeezed into non classical configurations in relic conditions.
geometry. The upshot is that string theory appears to construct coherent graviton states, but it has no answer to the problem that Ford [38], wrote on if the existing graviton coherent states would be squeezed into non classical configurations in relic conditions.
10. Does LQG Give Us More Direct Arguments as to Coherent States, Squeezed States, and the Break down of Classical Behavior at the Onset of Inflation?
Carlo Rovelli [44], in a PRL article states that a vertex amplitude that contributes to a coherent graviton state is the exponential of the Regge action: the other terms, that have raised doubts on the physical viability of the model, are suppressed by the phase of the vacuum state, and Rovelli writes a coherent vacuum state as given by a Gaussian peaked on parts of the boundary 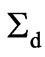 of a four dimensional sphere.
of a four dimensional sphere.

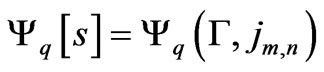 (67)
(67)
Rovelli [44] states that “bad” contributions to the behavior of Equation (67) are cancelled out by an appropriate (Gaussian?) vacuum wave functional which has “appropriately” chosen contributions from the boundary 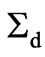 of a four dimensional sphere. This is to avoid trouble with “bad terms” from what is known as the Barret-Crane vertex amplitude contributions, which are can be iminized by an appropriate choice of vacuum state amplitude being picked. Rovelli [44] calculated some components of the graviton two-point function and found that the Barrett-Crane vertex yields a wrong long-distance limit. A problem, as stated by Lubos Motel (2007) [45], that there are infinitely many other components of the correlators in the LQG that are guaranteed not to work unless an infinite number of adjustments are made. The criticism is harsh, but until one really knows admissible early universe geometry one cannot rule out the Rovelli approach, or confirm it. In addition, Jakub Mielczarek [46] considered tensor gravitational perturbations produced at a bounce phase in presence of the holonomy corrections. Here bounce phase and holonomy corrections originate from Loop Quantum Cosmology. What comes to the fore are corrections due to what is called quantum holonomy, l. A comment about the quantum bounce. i.e. what is given by Dah-Wei Chiou, Li-Fang Li [47], is that there is a branch match up between a prior to a present set of Wheeler De Witt equations for a prior to present universe, as far as modeling how the quantum bounce links the two Wheeler De Witt solution branches, i.e. one Wheeler De Witt wave function for a prior univers, and another wave function for a present universe. Furthermore, Abhay Ashtekar [48] wrote a simple treatment of the Bounce causing Wheeler De Witt equation along the lines of, for
of a four dimensional sphere. This is to avoid trouble with “bad terms” from what is known as the Barret-Crane vertex amplitude contributions, which are can be iminized by an appropriate choice of vacuum state amplitude being picked. Rovelli [44] calculated some components of the graviton two-point function and found that the Barrett-Crane vertex yields a wrong long-distance limit. A problem, as stated by Lubos Motel (2007) [45], that there are infinitely many other components of the correlators in the LQG that are guaranteed not to work unless an infinite number of adjustments are made. The criticism is harsh, but until one really knows admissible early universe geometry one cannot rule out the Rovelli approach, or confirm it. In addition, Jakub Mielczarek [46] considered tensor gravitational perturbations produced at a bounce phase in presence of the holonomy corrections. Here bounce phase and holonomy corrections originate from Loop Quantum Cosmology. What comes to the fore are corrections due to what is called quantum holonomy, l. A comment about the quantum bounce. i.e. what is given by Dah-Wei Chiou, Li-Fang Li [47], is that there is a branch match up between a prior to a present set of Wheeler De Witt equations for a prior to present universe, as far as modeling how the quantum bounce links the two Wheeler De Witt solution branches, i.e. one Wheeler De Witt wave function for a prior univers, and another wave function for a present universe. Furthermore, Abhay Ashtekar [48] wrote a simple treatment of the Bounce causing Wheeler De Witt equation along the lines of, for 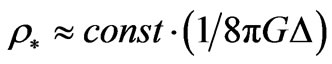 as a critical density, and
as a critical density, and  the eignvalue of a minimum area operator. Small values of
the eignvalue of a minimum area operator. Small values of  imply that gravity is a repulsive force, leading to a bounce effect [48,49].
imply that gravity is a repulsive force, leading to a bounce effect [48,49].
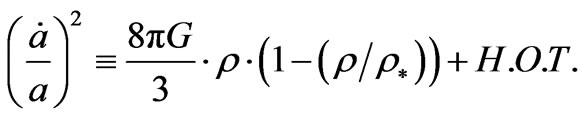 (68)
(68)
Furthermore, Bojowald [49,50] specified a criteria as to how to use an updated version of  and
and 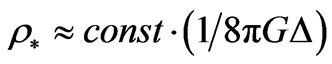 in his GRG manuscript on what could constitute grounds for the existence of generalized squeezed initial (graviton?) states. Bojowald [50] was referring to the existence of squeezed states, as either being necessarily, or NOT necessarily a consequence of the quantum bounce. As Bojowald [50,51] wrote it up, in both his Equation (26) which has a quantum Hamiltonian
in his GRG manuscript on what could constitute grounds for the existence of generalized squeezed initial (graviton?) states. Bojowald [50] was referring to the existence of squeezed states, as either being necessarily, or NOT necessarily a consequence of the quantum bounce. As Bojowald [50,51] wrote it up, in both his Equation (26) which has a quantum Hamiltonian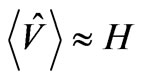 , with
, with
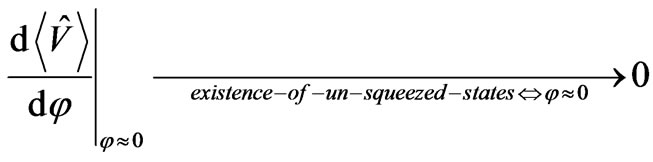 (69)
(69)
and 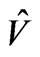 is a “volume” operator where the “ volume” is set as
is a “volume” operator where the “ volume” is set as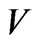 , Note also, that Bojowald has, in his initial Friedman equation, density values
, Note also, that Bojowald has, in his initial Friedman equation, density values
 , (70)
, (70)
so that when the Friedman equation is quantized, with an initial internal time given by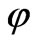 , with
, with 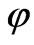 becoming a more general evolution of state variable than “internal time”. If so, Bojowald writes, when there are squeezed states [50,51]
becoming a more general evolution of state variable than “internal time”. If so, Bojowald writes, when there are squeezed states [50,51]
 (71)
(71)
for his Equation (26), which is incidently when links to classical behavior break down, and when the bounce from a universe contracting goes to an expanding present universe. Bojowald [51] also writes that if one is looking at an isotropic universe, that as the large matter “H” increases, that in certain cases, one observes more classical behavior, and a reduction in the strength of a quantum bounce. Bojowalds [51] states that “Especially the role of squeezed states is highlighted. The presence of a bounce is proven for uncorrelated states, but as squeezing is a dynamical property and may change in time”. The upshot is that although it is likely in a quantum bounce state that the states should be squeezed, it is not a pre requisite for the states to always start off as being squeezed states. So a physics researcher can, look at if an embedding of the present universe in a higher dimensional structure which could have lead to a worm hole from a prior universe to our present for re introduction of inflationary growth.
11. Other Models. Do Worm Hole Bridges between Different Universes Allow for Initial un Squeezed States? Wheeler de Witt Solution with Pseudo time Component Added in
This discussion is to present a not so well known but useful derivation of how instanton structure from a prior universe may be transferred from a prior to the present universe. This discussion is partly rendered in [15], but is reproduced here due to the relatively unknown feature of a pseudo time component to the Wheeler de Witt equation
1) The solution as taken from L. Crowell’s [52] book, and re produced has many similarities with the WKB method. i.e. it is semi classical.
2) Left unsaid is what embedding structure is assumed.
3) A final exercise for the reader. Would a WKB style solution as far as transfer of “material” from a prior to a present universe constitute procedural injection of non compressed states from a prior to a present universe? Also if uncompressed, coherent states are possible, how long would they last in introduction to a new universe?
This is the Wheeler-de-Witt equation with pseudo time component added. From Crowell [52]
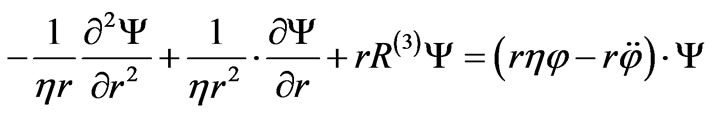 (72)
(72)
This has when we do it , and frequently
, and frequently 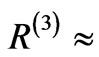 constant, so then we can consider
constant, so then we can consider
 (73)
(73)
In order to do this, we can write out the following for the solutions to Equation (72) above.
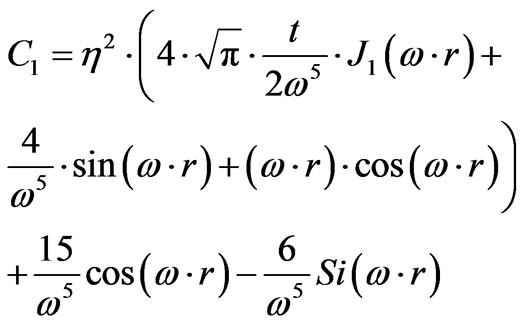 (74)
(74)
and
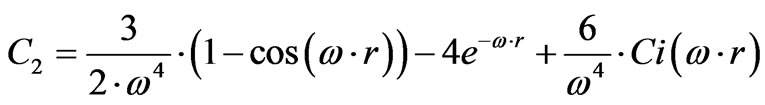 (75)
(75)
This is where 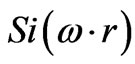 and
and 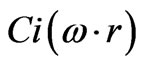 refer to inte grals of the form
refer to inte grals of the form
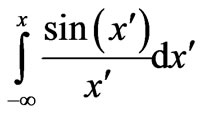 and
and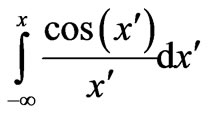 .
.
Next, we should consider whether or not the instanton so formed is stable under evolution of space-time leading up to inflation. To model this, we use results from Crowell [52] on quantum fluctuations in space-time, which gives a model from a pseudo time component version of the Wheeler-De-Witt equation, with use of the Reinssner-Nordstrom metric to help us obtain a solution that passes through a thin shell separating two space-times. The radius of the shell 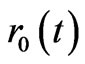 separating the two space-times is of length
separating the two space-times is of length 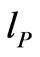 in approximate magnitude, leading to a domination of the time component for the Reissner-Nordstrom metric
in approximate magnitude, leading to a domination of the time component for the Reissner-Nordstrom metric
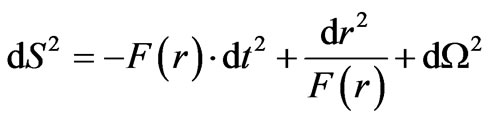 (76)
(76)
This has:
 (77)
(77)
This assumes that the cosmological vacuum energy parameter has a temperature dependence, leading to
 (78)
(78)
as a wave functional solution to a Wheeler-de-Witt equation bridging two space-times, similar to two space-times with “instantaneous” transfer of thermal heat, as given by Crowell [52]
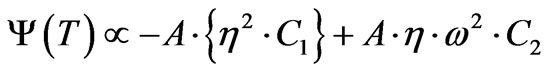 (79)
(79)
This has 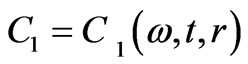 as a pseudo cyclic and evolving function in terms of frequency, time, and spatial function. This also applies to the second cyclical wave function
as a pseudo cyclic and evolving function in terms of frequency, time, and spatial function. This also applies to the second cyclical wave function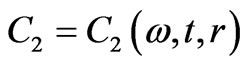 , where
, where  Equation (74) and
Equation (74) and  Equation (75) then we get that Equation (79) is a solution to the pseudo time WDM equation.
Equation (75) then we get that Equation (79) is a solution to the pseudo time WDM equation.
The question which will be investigated is if Equation (79) is a way to present either a squeezed or un squeezed state. A way forward is to note that Prado Martin-Moruno, Pedro F. Gonzalez-Diaz in July [53] wrote up about thermal phantom-like radiation process coming from the wormhole throat. Note that the Crowell construction of a worm hole bridge is in some ways similar to Carco Cavaglià’s [54] treatment of use of conjugate momentum  of
of  generalized momentum variables, also known as conjugate momenta
generalized momentum variables, also known as conjugate momenta
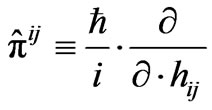 , (80)
, (80)
leading to the sort of formalism as attributed to Luis J. Garay’s [55] article, of
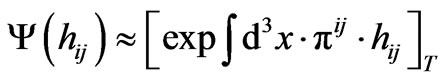 (81)
(81)
Now in the case of what can be done with the worm hole used by Crowell [52], with, if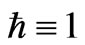 ,
,
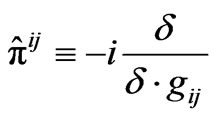 ,
,  ,
, 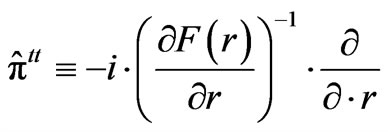 and a kinetic energy value as given of the form
and a kinetic energy value as given of the form 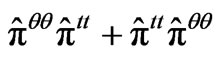 . The supposition which we have the worm hole wave functional may be like, so, use the wave functional looking like
. The supposition which we have the worm hole wave functional may be like, so, use the wave functional looking like
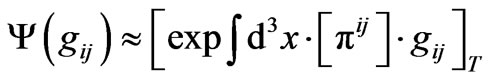 (82)
(82)
where the  for the WeinerNordstrom metric will be
for the WeinerNordstrom metric will be
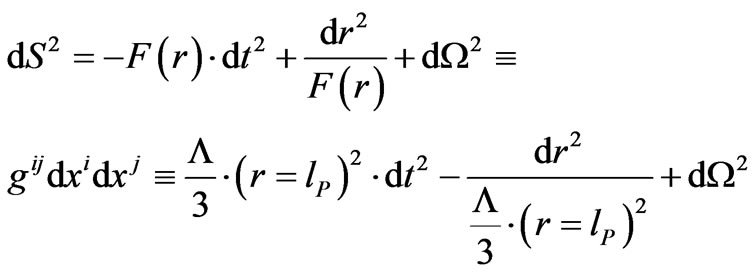 (83)
(83)
12. Unanswered Questions, and What This Suggests for Future Research Endeavors
As far back as 1982, Linde [56], when analyzing a potential of the form
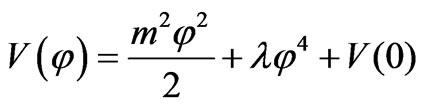 (84)
(84)
This is when the “mass” has the form, (here M is the bare mass term of the field 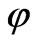 in de Sitter space, which does not take into account quantum fluctuations)
in de Sitter space, which does not take into account quantum fluctuations)
 (85)
(85)
Specified non linearity of  at a time from the big bang, of the form
at a time from the big bang, of the form
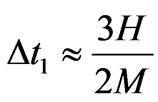 (86)
(86)
The question raised repeatedly in whether or not 1) if higher dimensions are necessary, and whether or not 2) mass gravitons are playing a role as far as the introduction of DE speed up of cosmological expansion may lead to an improvement over what was specified for density fluctuations and structure formation (the galaxy hierarchy problem) of density fluctuations given as
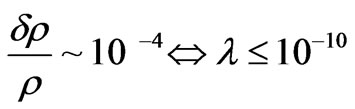 (87)
(87)
Equation (74) is for four space, a defining moment as to what sort of model would lead to density fluctuations. It totally fails as to give useful information as to the galaxy hierarchy problem as given in Figure 1, above. Secondly, to what degree is the relative speed up of the q(z) function is impacted by various inter plays between , say a modified version of, say a KK DM model, using a modified mass hierarchy to get suitable DM masses of the order of 100 GeV or more. Giving a suitable definition as to q(z) as well as the inter play between DM values, 4 Dim Graviton mass issues, and/or what really contributes to the speed up of the universe will in the end dramatically improve the very crude estimate given by Equation (84) above which says next to nothing about how the problems illustrated by the break down of the galaxy mass formation/hierarchy can be fixed. Furthermore is considering the spectral index problem, where the spectral index is
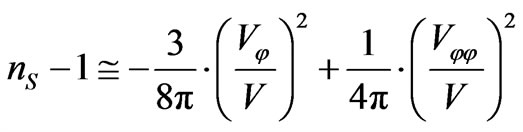 (88)
(88)
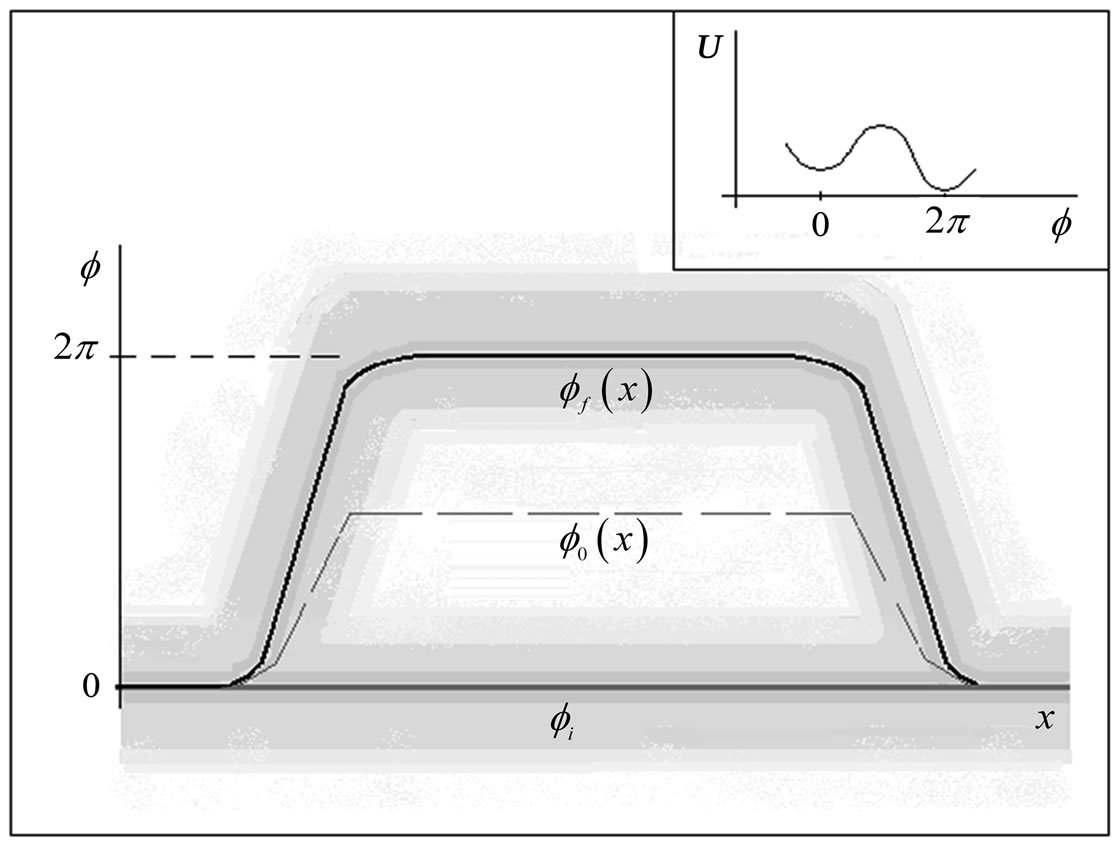
Figure 1. Here, the left hand side corresponds to a soliton, the right hand side is an anti soliton [57,58].
Usual experimental values of density fluctuations experimentally are
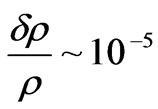 , instead of
, instead of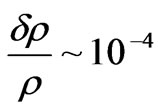 ,(89)
,(89)
and this is assuming that 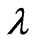 is extremely small. In addition, Linde [56] had
is extremely small. In addition, Linde [56] had
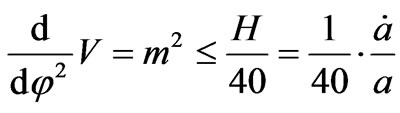 (90)
(90)
inside a false vacuum bubble. If something other than the Klein Gordon relationship

occurs, then different models of how density fluctuation may have to be devised. A popular model of density fluctuations with regards to the horizon is
 (91)
(91)
where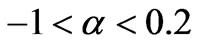 , and
, and  and to first order,
and to first order,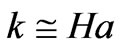 . The values, typically of
. The values, typically of 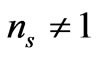 If working with
If working with
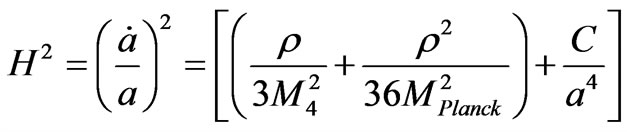 , (92)
, (92)
and with a density value
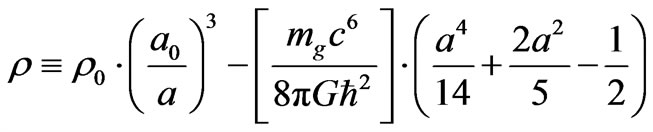 (93)
(93)
where 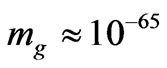 grams, and
grams, and  is usually picked to avoid over production of black holes, a very complex picture emerges. Furthermore, if working with
is usually picked to avoid over production of black holes, a very complex picture emerges. Furthermore, if working with 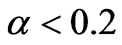 and
and 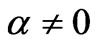
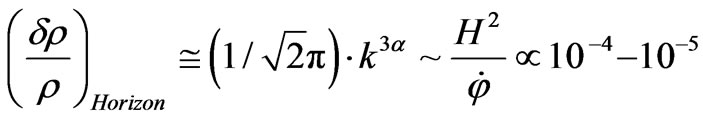 (94)
(94)
The above equation gives inter relationships between the time evolution of a pop up inflaton field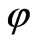 , and a Hubble expansion parameter H, and a wave length parameter
, and a Hubble expansion parameter H, and a wave length parameter 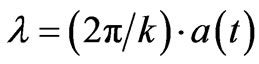 for a mode given as
for a mode given as . What should be considered is the inter relation ship of the constituent components of Equation (94) and
. What should be considered is the inter relation ship of the constituent components of Equation (94) and . What the author thinks is of particular import is to look at whether or not the more general expression, as given by the below equation also holds [59].
. What the author thinks is of particular import is to look at whether or not the more general expression, as given by the below equation also holds [59].
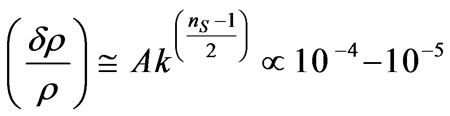 (95)
(95)
To first order, variations of 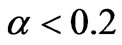 and
and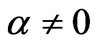 , should be compared with admissible values of
, should be compared with admissible values of
 which would closely correspond to
which would closely correspond to 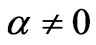
and . i.e. the precise values of this may help us out in determining how to unravel what is going on in the galaxy formation i.e. how can we have earlier than expected galaxy formation?
. i.e. the precise values of this may help us out in determining how to unravel what is going on in the galaxy formation i.e. how can we have earlier than expected galaxy formation?
13. Conclusions, as to How to Look at Early Universe Topology and Later Flat Space
One of the aspects of early universe topology we need to consider is how to introduce a de facto break down of quantization in curved space time geometries, and this is a problem which would permit a curved space treatment of . i.e. as R gets of the order of
. i.e. as R gets of the order of
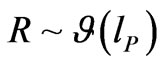 , say that the spatial geometry of early universe expansion is within a few orders of magnitude of Planck length, then how can we recover a field theory quantization condition for
, say that the spatial geometry of early universe expansion is within a few orders of magnitude of Planck length, then how can we recover a field theory quantization condition for 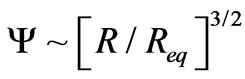 in terms of path integrals. We claim that deformation quantization, if applied successfully will eventually lead to a great refinement of the above Wheeler De Witt wave functional value, as well as allow a more through match up of a time independent solution of the Wheeler de Witt equation, with the more subtle pseudo time dependent evolution of the wave functional as Crowell wrote up. i.e. the linkage between time independent treatments of the wave functional of the universe, with what Lawrence Crowell [52] wrote will be made more explicit. This will, in addition allow us to understand better how graviton production in relic conditions may add to entropy, as well as how to link the number of gravitons, say
in terms of path integrals. We claim that deformation quantization, if applied successfully will eventually lead to a great refinement of the above Wheeler De Witt wave functional value, as well as allow a more through match up of a time independent solution of the Wheeler de Witt equation, with the more subtle pseudo time dependent evolution of the wave functional as Crowell wrote up. i.e. the linkage between time independent treatments of the wave functional of the universe, with what Lawrence Crowell [52] wrote will be made more explicit. This will, in addition allow us to understand better how graviton production in relic conditions may add to entropy, as well as how to link the number of gravitons, say 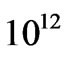 gravitons per photon, as information as a way to preserve the continuity of
gravitons per photon, as information as a way to preserve the continuity of 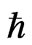 values from a prior universe to the present universe.
values from a prior universe to the present universe.
14. The Author Claims that in Order to Do This Rigorously, That Use of the Material in [60] Gutt, and Waldmann Will Be Necessary, Especially to Investigate if Quantization of Severely Curved Space Time Conditions Is Possible. We Claim that It Is Not [15]
Resolution of which add more detail to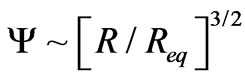 . Having said this, it is now important to consider what can be said about how relic gravitons/ information can pass through minimum vales of
. Having said this, it is now important to consider what can be said about how relic gravitons/ information can pass through minimum vales of .
.
We shall reference what A. W. Beckwith presented [61], which we think still has current validity for reasons we will elucidate upon in this document. We use a power law relationship first presented by Fontana [62], who used Park’s earlier [63] derivation: when

 (96)
(96)
This expression of power should be compared with the one presented by Giovannini on averaging of the energy-momentum pseudo tensor to get his version of a gravitational power energy density expression, namely [64]
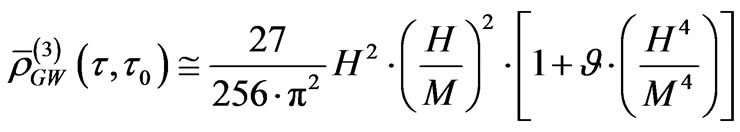 (97)
(97)
Giovannini states that should the mass scale be picked such that , that there are doubts that we could even have inflation. However, it is clear that gravitational wave density is faint, even if we make the approximation that
, that there are doubts that we could even have inflation. However, it is clear that gravitational wave density is faint, even if we make the approximation that
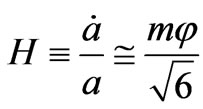 (98)
(98)
as stated by [65] by Linde, where we are following 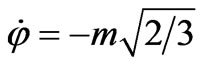 in evolution, so we have to use different procedures to come up with relic gravitational wave detection schemes to get quantifiable experimental measurements so we can start predicting relic gravitational waves. This is especially true if we make use of the following formula for gravitational radiation, as given by. Kofman [66], with
in evolution, so we have to use different procedures to come up with relic gravitational wave detection schemes to get quantifiable experimental measurements so we can start predicting relic gravitational waves. This is especially true if we make use of the following formula for gravitational radiation, as given by. Kofman [66], with 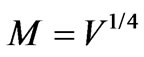 as the energy scale, with a stated initial inflationary potential V. This leads to an initial approximation of the emission frequency, using present-day gravitational wave detectors.
as the energy scale, with a stated initial inflationary potential V. This leads to an initial approximation of the emission frequency, using present-day gravitational wave detectors.
 (99)
(99)
What we would like to do for future development of entropy would be to consider a way to ascertain if or not the following is really true, and to quantify it by an improvement of a supposition advanced by [67] Kiefer, Polarski, and Starobinsky. i.e. the author, Beckwith, has in this document presented a general question of how to avoid having dS/dt = ∞ at S = 01) Removes any chance that early universe nucleation is a quantum based emergent field phenomena.
2) Goldstone gravitons would arise in the beginning due to a violation of Lorentz invariance. i.e. we have a causal break, and merely having the above condition does not qualify for a Lorentz invariance breakdown Kiefer, Polarski, and Starobinsky [67] presented the idea of presenting the evolution of relic entropy via the evolution of phase spaces, with 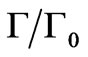 being the ratio of “final (future)”/“initial” phase space volume, for k modes of secondary GW background.
being the ratio of “final (future)”/“initial” phase space volume, for k modes of secondary GW background.
 (100)
(100)
If the phase spaces can be quantified, as a starting point of say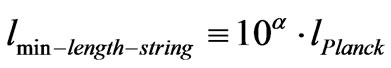 , with
, with 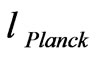 being part of how to form the “dimensions” of
being part of how to form the “dimensions” of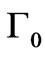 , and
, and
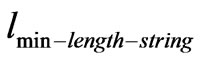 part of how to form the dimensions of
part of how to form the dimensions of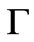 and
and 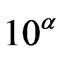 being, for a given
being, for a given , and in certain cases
, and in certain cases , then avoiding having dS/dt = ∞ at S = 0 will be straight forward We hope to come up with an emergent structure for gravitational fields which is congruent with obtaining
, then avoiding having dS/dt = ∞ at S = 0 will be straight forward We hope to come up with an emergent structure for gravitational fields which is congruent with obtaining 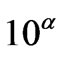 naturally, so this sort of procedure is non controversial, and linked to falsifiable experimental measurement protocol, so quantum gravity becomes a de facto experimental science. This will mean looking at Appendix B, fully. Appendix C, and Appendix D give further issues we describe later on. In future publications. We give them as pertinent information for the future development of this project.
naturally, so this sort of procedure is non controversial, and linked to falsifiable experimental measurement protocol, so quantum gravity becomes a de facto experimental science. This will mean looking at Appendix B, fully. Appendix C, and Appendix D give further issues we describe later on. In future publications. We give them as pertinent information for the future development of this project.
15. Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11075224. The author thanks Dr. Fangyu Li for conversations as to the physics of GW and Graviton physics, and also has a debt of gratitude to Stuart Allen, CEO for his efforts to permit the author to do physics work
REFERENCES
- M. Y. Kuchiev, “Can Gravity Appear Due to Polarization of Instantons in SO(4) Gauge Theory?” Classical and Quantum Gravity, Vol. 15, No. 7, 1998, pp. 1895-1913. doi:10.1088/0264-9381/15/7/008
- I. Andrić, L. Jonke and D. Jurman, “Solitons and Giants in Matrix Models,” Progress of Physics, Vol. 56, No. 4-5, 2008, pp. 324-329.
- D. Perkins, “Particle Astrophysics,” Oxford University press, Oxford, 2003.
- L. Glinka, “Preliminaries in Many-Particle Quantum Gravity. Einstein-FriedmannSpacetime,” http://arxiv.org/PS_cache/arxiv/pdf/0711/0711.1380v4.pdf;
- L. Glinka, “Quantum Information from Graviton-Matter Gas,” Symmetry, Integrability and Geometry: Methods and Applications, Vol. 3, No. 087, 2007, pp. 1-13.
- Y. J. Ng, “Spacetime Foam: From Entropy and Holography to Infinite Statistics and Nonlocality,” Entropy, Vol. 10, No. 4, 2008, pp. 441-461. doi:10.3390/e10040441
- M. Asakawa, T. Hatsuda and Y. Nakahara, “Maximum Entropy Analysis of the Spectral Functions in Lattice QCD,” Progress in Particle and Nuclear Physics, Vol. 46, No. 2, 2001, pp. 459-508. doi:10.1016/S0146-6410(01)00150-8
- M. Asakawa, S. A. Bass and B. Müller, “Anomalous Viscosity of an Expanding Quark-Gluon Plasma,” Physical Review Letters, Vol. 96, No. 25, 2006, Article ID: 252301. doi:10.1103/PhysRevLett.96.252301
- G. Torrieri and I. Mushuntin, “Instability of Boost-Invariant Hydrodynamics with a QCD Inspired Bulk Viscosity,” Physical Review C, Vol. 78, No. 2, 2008, Article ID: 021901.doi:10.1103/PhysRevC.78.021901
- N. Dadhich, “Derivation of the Raychaudhuri Equation,” General Relativity and Quantum Cosmology, 2005. http://arxiv.org/abs/gr-qc/0511123
- J. Natário, “Relativity and Singularities—A Short Introduction for Mathematicians,” March 2006. http://arxiv.org/abs/math.DG/0603190.
- A. Beckwith, “Relic High Frequency Gravitational Wavesfrom the Big Bang, and How to Detect them,” AIP Conference Proceedings, Vol. 1103, 2009, pp. 571-581. http://arxv.org/abs/0809.1454 doi:10.1063/1.3115567
- S. Mathur and B. Chowdhury, “Fractional Brane States in the Early Universe,” Classical and Quantum Gravity, Vol. 24, No. 10, 2007, pp. 2689-2720. doi:10.1088/0264-9381/24/10/014
- A. Beckwith, “Instanton Formation of Vacuum Energy via the Reissner-Nordstrom Geometry of a Wormhole Bridge between a Prior to Our Present Universe,” October 2007. arXiv:0710.3788
- S. Weinberg, “Cosmology,” Oxford University Press, Oxford, 2008
- G. Lifschytz, “Black Hole Thermalization Rate from Brane Antibrane Model,” 2004. http://arxiv.org/abs/hep-th/0406203
- A. Beckwith, F. Y. Li, et al., “Is Octonionic Quantum Gravity Relevant near the Planck Scale? If Gravity Waves Are Generated by Changes in the Geometry of the Early Universe, How Can We Measure Them?” 2011. http://vixra.org/abs/1101.0017
- K. Becker, M. Becker and J. Schwarz, “String Thetheory and M theory, a Modern Introduction,” Cambridge University Press, Cambridge, 2007
- S. Carroll, “An Introduction to General Relativity Space Time and Geometry,” Addison Wesley Publishing House, San Francisco, 2004
- C. Foias, O. Manley, et al., “Estimates for the Energy Cascade in Three-Dimensional Turbulent Flows,” Comptes Rendus de l’Académie des Sciences—Series I— Mathematics, Vol. 333, No. 5, 2001, pp. 499-504. doi:10.1016/S0764-4442(01)02008-0
- R. Rosa and R. M. S. Rosa, “Turbulence Theories,” In: J.-P. Franchioise, G. Naber and T.-T. Sheung, Eds., Encyclopedia of Mathematical Physics, Vol. 2, 2006, pp. 253-261.
- A. Beckwith, “A New Soliton-Anti Soliton Pair Creation Rate Expression Improving Upon Zener Curve Fitting for I-E Plots,” Modern Physics Letters B, Vol. 20, No. 5, 2006, pp. 849-861. doi:10.1142/S0217984906011219
- A. Beckwith, “Classical and Quantum Models of Density Wave Transport, a comparative study,” PhD Dissertation, University of Houston, Houston, December 2001
- T. Kahniashvili, “Relic Gravitational Waves as a Test of the Early Universe,” 2007. arXiv:0705.1733[astro-ph]
- L. Grishkuk, “Discovering Relic Gravitational Waves in Cosmic Microwave Background Radiation,” General Relativity and John Archibald Wheeler, Vol. 367, Part 3, 2008, pp. 151-199.
- E. Kolb and S. Turner, “The Early Universe,” Westview Press, Chicago, 1994
- M. Peskin and D. Schroeder, “An Introduction to Quantum Field Theory,” Westview Press, Chicago, 1995.
- M. Maggiore, “Gravitational Waves, Volume 1: Theory and Experiment,” Oxford University Press, Oxford, 2008.
- A. Avessian, “Plancks Constant Evolution as a Cosmological Evolution Test for the Early Universe,” Gravitation and Cosmology, Vol. 15, No. 1, 2009, pp. 10-12. doi:10.1134/S0202289309010034
- C. Hogan, “Holographic Discreteness of Inflationary Pe turbations,” 2002. arXIV astro-ph/0201020 v 2
- J. Camp and N. Cornish, “Gravitational Wave Astronomy,” In: B. Kayser, B. Holstein and A. Jawahery, Eds., Annual Review of Nuclear and Particle Science, Vol. 54, Menlo Park, 2004, pp. 525-577.
- F. Li, R. Baker, et al., “Perturbative Photon Fluxes Generated by High-Frequency Gravitational Waves and Their Physical Effects,” European Physical Journal C, Vol. 56, No. 3, 2008, pp. 407-423. doi:10.1140/epjc/s10052-008-0656-9
- H. B. J. Koers and P. Tinyakov, “Testing Large-Scale (An) isotropy of Ultra-High Energy Cosmic Rays,” Journal of Cosmology and Astroparticle Physics, Vol. 2009, No. 4, 2009. [arXiv:0812.0860 [astro-ph]].
- W. Honig, “A Minimum Photon ‘Rest Mass’—Using Planck’s Constant and Discontinuous Electromagnetic Waves,” Foundations of Physics, Vol. 4, No. 3, 1974, pp. 367-380. doi:10.1007/BF00708542
- S. Weinberg, “Gravitation,” Freeman, San Francisco, 1973.
- R. Glauber, “Coherent and Incoherent States of the Radiation Field”, Physical Review, Vol. 131, No. 6, 1963, pp. 2766-2788. doi:10.1103/PhysRev.131.2766
- M. Gasperini and G. Veneziano, “Inflation, Deflation, and Frame-Independence in String Cosmology,” Modern Physics Letters A, Vol. 8, No. 39, 1993, pp. 3701-3713.
- K. Kieffer, “Quantum Gravity,” International Series of Monographs on Physics, Oxford Science Pulications, Oxford University Press, Oxford, 2007. doi:10.1093/acprof:oso/9780199212521.001.0001
- T. Mohaupt, “Introduction to String Theory,” 2003. (hepth_0207249)(78s).pdf
- L. H. Ford, “Gravitons and Lightcone Fluctuations,” Physical Review D, Vol. 54, No. 4, 1996, pp. 2640-2646. doi:10.1103/PhysRevD.54.2640
- F. Li, N. Yang, et al., “Signal Photon Flux and Background Noise in a Coupling Electromagnetic Detecting System for High Frequency Gravitational Waves,” Physical Review D, Vol. 80, No. 6, 2009, Article ID: 064013. doi:10.1103/PhysRevD.80.064013
- K. K. Venkatartnam and P. K. Suresh, “Density Fluctuations in the Oscillatory Phase of Nonclassical Inflaton in FRW Universe,” International Journal of Modern Physics D, Vol. 17, No. 11, 2008, pp. 1991-2005. doi:10.1142/S0218271808013662
- L. Grishchuk and Y. Sidorov, “On the Quantum State of Relic Gravitons,” Classical and Quantum Gravity, Vol. 6, No. 9, 1989, pp. L161-L165. doi:10.1088/0264-9381/6/9/002
- L Grishchuk, “Quantum Effects in Cosmology,” Classical and Quantum Gravity, Vol. 10, 1993, pp. 2449-2478. doi:10.1088/0264-9381/10/12/006
- J. Polchinski, “String Theory: An introduction to the Bo-Sonic String,” Cambridge University Press, Cambridge, 1999.
- R. Dick, “Standard Cosmology in the DGP Brane Model,” Acta Physica Polonica B, Vol. 32, No. 11, 2001, pp. 3669-3682.
- Berkestein, 2004. http://uw.physics.wisc.edu/~strings/group/slides.04.fall/berenstein.pdf
- C. Rovelli, “Graviton Propagator from Background Indpendent Quantum Gravity,” Physical Review Letters, Vol. 97, No. 15, 2006, Article ID: 151301. doi:10.1103/PhysRevLett.97.151301
- L. Motl, 2007. http://motls.blogspot.com/2007/08/thiemann-dittrich-discreteness-of-lqg.html
- J. Mielchrek, “Tensor Power Spectrum with Holonomy Corrections in LQC,” Physical Review D, Vol. 79, 2009, Article ID: 123520.
- D.-W. Chiu and F. Li, “Loop Quantum Cosmology with Higher Order Holonomy Corrections,” Physical Review D, Vol. 80, No. 4, 2009, Article ID: 043512.
- A. Ashtekar, 2006. solvaynet.pdf
- M. Bojowald, “Comment on ‘Quantum Bounce and Cosmic Recall’,” Physical Review Letters, Vol. 101, No. 20, 2008, Article ID: 209001.
- M. Bojowald, “Quantum Nature of Cosmological Bounces,” General Relativity and Gravitation, Vol. 40, No. 12, 2008, pp. 2659-2683. doi:10.1007/s10714-008-0645-1
- L. Crowell, “Quantum Fluctuations of Space Time,” World Scientific Series in Contemporary Chemical Phyics, World Scientific, Singapore, Vol. 25, 2005.
- P. Martin-Moruno and P. F. Gonzalez-Diaz, “Thermal Radiation from Lorentzian Traversable Wormholes,” Physical Review D, Vol. 80, No. 16, 2009, Article ID: 024007.
- M. Cavaglià, “Quantum Electromagnetic Wormholes and Geometrical Description of the Electric Charge,” Physical Review D, Vol. 50, No. 8, 1994, pp. 5087-5092.
- L. J. Garay, “Quantum State of Wormholes and Path Integral,” Physical Review D, Vol. 44, No. 4, 1991, pp. 1059-1066. doi:10.1103/PhysRevD.44.1059
- A. Linde, “The New Inflationary Universe Scenario,” In: C. Gibbons, S. Hawking and S. Siklos, Eds., The Very Early Universe, Cambridge University Press, Cambridge, 1982, pp. 205-249.
- J. Lehners, P. McFadden, N. Turok and P. Steinhardt, “Generating Ekpyrotic Curvature Perturbations Before the Big Bang,” Physical Review D, Vol. 76, No. 10, 2007, Article ID: 103501.doi:10.1103/PhysRevD.76.103501
- S. Gutt, S. Waldmann, “Deformations of the Poisson Bracket on a Sympletic Manifold,” In: J. P. Frnachoise, G. L Naber and S. Tsuou, Eds., Encyclopedia of Mathematical Physics, Elsevier, Oxford, Vol. 2, 2006, p. 24. doi:10.1016/B0-12-512666-2/00366-7
- G. Fontana, “Gravitational Wave Propulsion,” In: M. El-Genk, Ed., Proceedings of (STAIF-05), AIP Conference Proceedings, Vol. 746, Melville, 2005. doi:10.1063/1.1867262
- D. Park, “Radiations from a Spinning Rod,” Physical Review, Vol. 99, No. 4, 1955, pp. 1324-1325. doi:10.1103/PhysRev.99.1324
- M. Giovannini, “A Primer on the Physics of the Cosmic Microwave Background,” World Press Science, Singapore, 2008.
- A. D. Linde, “Inflationary Cosmology,” In: M. Lemione, J. Martin and P. Peters, Eds., Lecture Notes in Physics 738, Inflationary Cosmology, Springer Verlag, Berlin, 2008, pp. 1-54.
- L. Kofman, “Preheating after Inflation,” In: M. Lemoine, J. Martin and P. Peter, Eds., Lecture Notes in Physics 738, Inflationary Cosmology, Springer Verlag, Berlin, 2008, pp. 50-79.
- C. Kiefer, D. Polariski and A. Starobinsky, “Entropy of Gravitons Produced in the Early Universe,” Physical Review D, Vol. 62, No. 4, 2000, Article ID: 043518.
- C. M. Will, “The Confrontation between General Relativity and Experiment,” 2001. http://mathnet.preprints.org/EMIS/journals/LRG/Articles/Irr-2006-3/
- M. Visser, “Mass for the Graviton,” General Relativity Gravity, Vol. 30, No. 12, 1998, pp. 1717-1728. doi:10.1023/A:1026611026766
- A. Beckwith, “Energy Content of Graviton as a Way to Quantify Both Entropy and Information Generation in the Early Universe,” Journal of Modern Physics, Vol. 2, 2011, pp. 58-61. doi:10.4236/jmp.2011.22010
- P. Chen, “Resonant Phton-Graviton Conversion in EM Fields: From Earth to Heaven,” 1994. http://www.slac.stanford.edu/cgi-gedoc/slac-pub-6666.pdf
- T. Rothman and S. Boughn, “Can Gravitons be Detected?” Foundations of Physics, Vol. 36, No. 12, 2006, pp. 1801-1825. doi:10.1007/s10701-006-9081-9
- D. Samtleben, S. Staggs and B. Witnstein, “The Cosmic Microwave Background for Pedestrians, a review for Particle and Nuclear Physicists,” Annual Review of Nuclear and Particle Science, Vol. 57, 2007, pp. 245-283. doi:10.1146/annurev.nucl.54.070103.181232
- R. Durrer, “Cosmological Perturbation Theory,” In: E. Papantonopoulous, Ed., Physics of the Early Universe, Lecture Notes in Physics 653, Springer-Verlag, Berlin, 2004.
- S. Capozziello, A. Feoli, et al., “Thin Shell Quantization in Weyl Spacetime,” Physics Letters A, Vol. 273, No. 1, 2000, pp. 25-30. doi:10.1016/S0375-9601(00)00478-3
Appendix A:
Bounds upon Graviton Mass, and Making Use of the Difference between Graviton Propagation Speed and HFGW Transit Speed to Observe Post Newtonian Corrections to Gravitational Potential Fields
The author presents a post Newtonian approximation based upon an earlier argument/paper by Clifford Will as to Yukawa revisions of gravitational potentials in part initiated by gravitons with explicit mass dependence in their Compton wave length.
Introduction
Post Newtonian approximations to General relativity have given physicists a view as to how and why inflationary dynamics can be measured via deviation from simple gravitational potentials. One of the simplest deviations from the Newtonian inverse power law gravitational potential being a Yukawa potential modification of gravitational potentials. So happens that the mass of a graviton would factor directly into the Yukawa exponential term modification of gravity. This appendix indicates how a smart experimentalist could use the Li-Baker detector as a way to obtain more realistic upper bounds as to the mass of a graviton and to use it as a template to investigate modifications of gravity along the lines of a Yukawa potential modification as given by Will [68].
Giving an Upper Bound to the Mass of a Graviton
The easiest way to ascertain the mass of a graviton is to investigate if or not there is a slight difference in the speed of graviton ‘particle’ propagation and of HFGW in transit from a “source” to the detector. Visser’s [69] mass of a graviton paper presents a theory which passes the equivalence test, but which has problem with depending upon a non-dynamical background metric. I.e. gravitons are assumed by both him, and also Will’s [68] write up of experimental G.R. to have mass. This document accepts that there is a small graviton mass, which the author has estimated to be on the order of 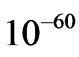 kilograms. Small enough so the following approximation is valid. Here,
kilograms. Small enough so the following approximation is valid. Here, 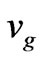 is the speed of graviton “propagation”,
is the speed of graviton “propagation”, 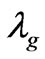 is the Compton wavelength of a graviton with
is the Compton wavelength of a graviton with
 , and
, and 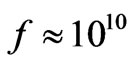 Hertz in line with L. Grischuck’s treatment of relic HFGW’s [23]. In addition, the high value of relic HFGW’s leads to naturally fulfilling
Hertz in line with L. Grischuck’s treatment of relic HFGW’s [23]. In addition, the high value of relic HFGW’s leads to naturally fulfilling  so that [68]
so that [68]
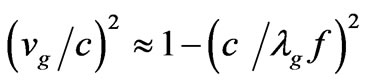 (A1)
(A1)
But Equation (1) above is an approximation of a much more general result which may be rendered as
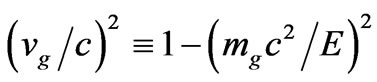 (A2)
(A2)
The terms 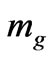 and E refers to the graviton rest mass and energy, respectively. Now specifically in line with applying the Li Baker detector, [30] physics researchers can ascertain what E is, with experimental data from the Li Baker detector, and then the next question needs to be addressed, namely if D is the distance between a detector, and the source of a HFGW/Graviton emitter source
and E refers to the graviton rest mass and energy, respectively. Now specifically in line with applying the Li Baker detector, [30] physics researchers can ascertain what E is, with experimental data from the Li Baker detector, and then the next question needs to be addressed, namely if D is the distance between a detector, and the source of a HFGW/Graviton emitter source
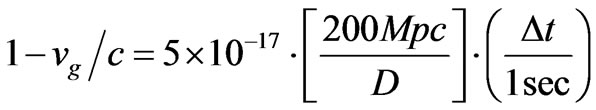 (A3)
(A3)
The above formula depends upon
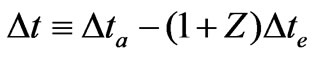 , with where
, with where 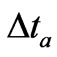 and
and  are the differences in arrival time and emission time of the two signals (HFGW and Graviton propagation ), respectively, and Z is the redshift of the source. Z is meant to be the red shift. Specifically, the situation for HFGW is that for early universe conditions, that
are the differences in arrival time and emission time of the two signals (HFGW and Graviton propagation ), respectively, and Z is the redshift of the source. Z is meant to be the red shift. Specifically, the situation for HFGW is that for early universe conditions, that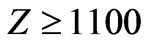 , in fact for very early universe conditions in the first few mili seconds after the big bang, that
, in fact for very early universe conditions in the first few mili seconds after the big bang, that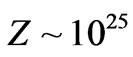 . An enormous number.
. An enormous number.
The first question which needs to be asked is, if or not the Visser [69] non-dynamical background metric correct, for early universe conditions so as to avoid the problem of the limit of small graviton mass does not coincide with pure GR, and the predicted perihelion advance, for example, violates experiment. A way forward would be to configure data sets so in the case of early universe conditions that one is examining appropriate  but with extremely small
but with extremely small 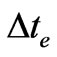 times, which would reflect upon generation of HFGW before the electro weak transition, and after the INITIAL onset of inflation. i.e. the Li-Baker detector system should be employed [42] as to pin point experimental conditions so to high accuracy, the following is an adequate presentation of the difference in times,
times, which would reflect upon generation of HFGW before the electro weak transition, and after the INITIAL onset of inflation. i.e. the Li-Baker detector system should be employed [42] as to pin point experimental conditions so to high accuracy, the following is an adequate presentation of the difference in times, . i.e.
. i.e.

 ](A4)
](A4)
The closer the emission times for production of the HFGW and Gravitons are to the time of the initial nucleation of vacuum energy of the big bang, the closer we can be to experimentally using Equation (4) above as to give experimental criteria for stating to very high accuracy the following.
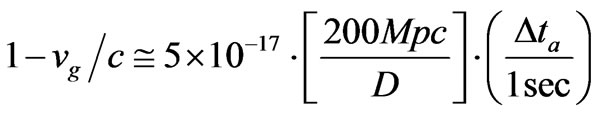 (A5)
(A5)
More exactly this will lead to the following relationship which will be used to ascertain a value for the mass of a graviton. By necessity, this will push the speed of graviton propagation very close to the speed of light. In this, we are assuming an enormous value for D
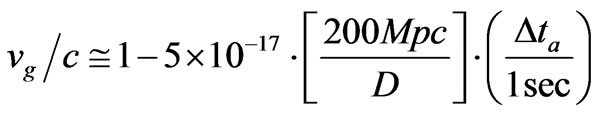 (A6)
(A6)
This Equation (A6) relationship should be placed into 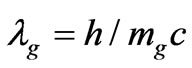 with a way to relate this above value of
with a way to relate this above value of
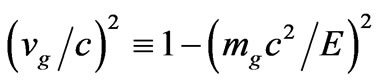 with an estimated value of E coming from the LiBaker detector [30] and field theory calculations, as well as to make the following argument rigorous, namely
with an estimated value of E coming from the LiBaker detector [30] and field theory calculations, as well as to make the following argument rigorous, namely
 (A7)
(A7)
A suitable numerical treatment of this above equation, with data sets could lead to a range of bounds for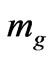 , as a refinement of the result given by Will [68] for graviton Compton wavelength bounded behavior for a lower bound to the graviton mass, assuming that
, as a refinement of the result given by Will [68] for graviton Compton wavelength bounded behavior for a lower bound to the graviton mass, assuming that 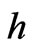 is the Planck’s constant.
is the Planck’s constant.
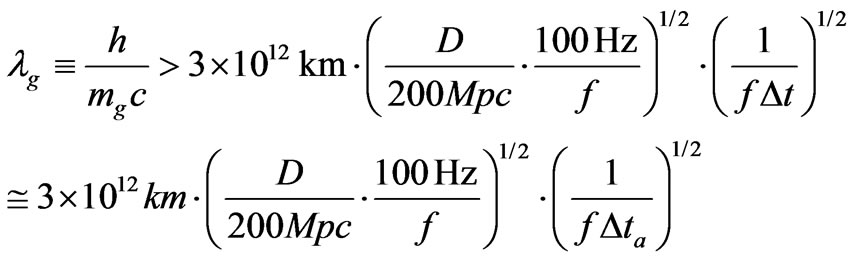 (A8)
(A8)
The above Equation (A8) gives an upper bound to the mass 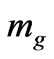 as given by
as given by
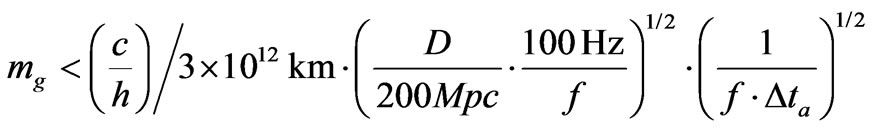 (A9)
(A9)
Needless to say that an estimation of the bound for the graviton mass , and the resulting Compton wavelength
, and the resulting Compton wavelength 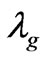 would be important to get values of the following formula, namely
would be important to get values of the following formula, namely
 (A10)
(A10)
Clifford Will [68] gave for values of frequency 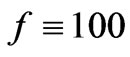 Hertz enormous values for the Compton wave length, i.e. values like
Hertz enormous values for the Compton wave length, i.e. values like 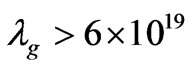 kilometers. Such enormous values for the Compton wave length make experimental tests of Equation (A10) practically infeasible. Values of
kilometers. Such enormous values for the Compton wave length make experimental tests of Equation (A10) practically infeasible. Values of  centimeters or less for very high HFGW data makes investigation of Equation (A10) above far more tractable. The above is consistent with work Beckwith [70] has reported on earlier.
centimeters or less for very high HFGW data makes investigation of Equation (A10) above far more tractable. The above is consistent with work Beckwith [70] has reported on earlier.
Application to Gravitational Synchrotron Radiation, in Accelerator Physics
Eric Davis, quoting Pisen Chen’s article [71] estimates that a typical storage ring for an accelerator will be able to give approximately  gravitons per second. Quoting Pisen Chen’s [71] 1994 article, the following for graviton emission values for a circular accelerator system, with m the mass of a graviton, and
gravitons per second. Quoting Pisen Chen’s [71] 1994 article, the following for graviton emission values for a circular accelerator system, with m the mass of a graviton, and 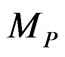 being Planck mass. N as mentioned below is the number of ‘particles’ in a ring for an accelerator system, and
being Planck mass. N as mentioned below is the number of ‘particles’ in a ring for an accelerator system, and 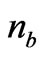 is an accelerator physics parameter for bunches of particles which for the LHC is set by Pisen Chen [71] as of the value 2800, and N for the LHC is about
is an accelerator physics parameter for bunches of particles which for the LHC is set by Pisen Chen [71] as of the value 2800, and N for the LHC is about . And, for the LHC Pisen Chen sets
. And, for the LHC Pisen Chen sets 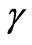 as
as , with
, with 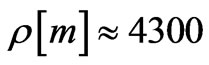 . Here,
. Here, 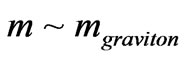 acts as a mass charge.
acts as a mass charge.
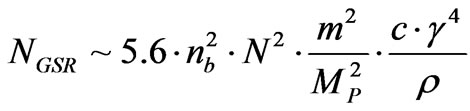 (A11)
(A11)
The immediate consequence of the prior discussion would be to obtain a more realistic set of bounds for the graviton mass, which could considerably refine the estimate of  gravitons produced per year at the LHC, with realistically 365 × 86400 seconds = 31536000 seconds in a year, leading to
gravitons produced per year at the LHC, with realistically 365 × 86400 seconds = 31536000 seconds in a year, leading to 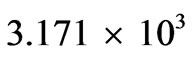 gravitons produced per second. Refining an actual permitted value of bounds for the accepted graviton mass, m, as given above, while keeping
gravitons produced per second. Refining an actual permitted value of bounds for the accepted graviton mass, m, as given above, while keeping 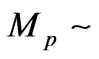 1.2209 × 1019 GeV/c2 would allow for a more precise set of gravitons per second which would significantly enhance the chance of actual detection, since right now for the LHC there is too much general uncertainty as to the likelihood of where to place a detector for actually capturing/detecting a graviton.
1.2209 × 1019 GeV/c2 would allow for a more precise set of gravitons per second which would significantly enhance the chance of actual detection, since right now for the LHC there is too much general uncertainty as to the likelihood of where to place a detector for actually capturing/detecting a graviton.
Conclusions, Falsifiable Tests for the Graviton Are Closer than the Physics Community Thinks
The physics community now has an opportunity to experimentally infer the existence of gravitons as a knowable and verifiable experimental datum with the onset of the LHC as an operating system. Even if the LHC is not used, Pisen Chens parameterization of inputs from his table [71] right after his Equation (8) as inputs into Equation (A11) above will permit the physics community to make progress as to detection of Gravitons for, say the Brookhaven site circular ring accelerator system. Tony Rothman’s [72] predictions as to needing a detector the size of Jupiter to obtain a single experimentally falsifiable set of procedures is defensible only if the wave-particle duality induces so much uncertainty as to the mass of the purported graviton, that worst case model building and extraordinarily robust parameters for a Rothman style graviton detector have to be put in place.
The Li-Baker detector [30] can help with bracketing a range of masses for the graviton, as a physical entity subject to measurements. Such an effort requires obtaining rigorous verification of the approximation used to the effect that 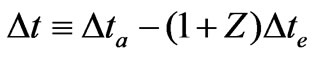
 is a defensible approximation. Furthermore, obtaining realistic inputs for distance
is a defensible approximation. Furthermore, obtaining realistic inputs for distance 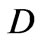 for inputs into Equation (A9) above is essential. The expected pay offs of making such an investment would be to determine the range of validity of Equation (A10), i.e. to what degree is gravitation as a force is amendable to post Newtonian approximations. The author asserts that Equation (10) can only be realistically be tested and vetted for sub atomic systems, and that with the massive Compton wavelength specified by Clifford Will cannot be done with low frequency gravitational waves.Furthermore, a realistic bounding of the graviton mass would permit a far more precise calibration of Equation (A11) as given by Pisen Chen in his 1994 article [71].
for inputs into Equation (A9) above is essential. The expected pay offs of making such an investment would be to determine the range of validity of Equation (A10), i.e. to what degree is gravitation as a force is amendable to post Newtonian approximations. The author asserts that Equation (10) can only be realistically be tested and vetted for sub atomic systems, and that with the massive Compton wavelength specified by Clifford Will cannot be done with low frequency gravitational waves.Furthermore, a realistic bounding of the graviton mass would permit a far more precise calibration of Equation (A11) as given by Pisen Chen in his 1994 article [71].
Appendix B: Basic Physics of Achieving Minimum 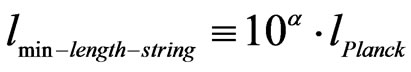 Precision in CMBR Power Spectra Measurements
Precision in CMBR Power Spectra Measurements
Begin first of all looking at
 (B1)
(B1)
This leads to consider what to do with
 (B2)
(B2)
Samtleben et al. [73] consider then what the experimental variance in this power spectrum, to the tune of an achievable precision given by
 (B3)
(B3)
 is the fraction of the sky covered in the measurement , and
is the fraction of the sky covered in the measurement , and  is a measurement of the total experimental sensitivity of the apparatus used. Also
is a measurement of the total experimental sensitivity of the apparatus used. Also 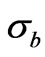 is the width of a beam, while we have a minimum value of
is the width of a beam, while we have a minimum value of 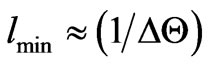 which is one over the fluctuation of the angular extent of the experimental survey.
which is one over the fluctuation of the angular extent of the experimental survey.
i.e. contributions to 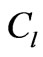 uncertainty from sample variance is equal to contributions to
uncertainty from sample variance is equal to contributions to 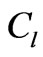 uncertainty from noise. The end result is
uncertainty from noise. The end result is
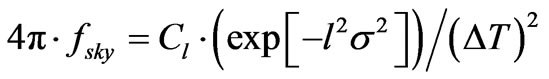 (B4)
(B4)
Appendix C: Cosmological Perturbation Theory and Tensor Fluctuations (Gravity Waves)
Durrer [74] reviews how to interpret 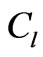 in the region where we have
in the region where we have , roughly in the region of the Sachs-Wolf contributions due to gravity waves. We begin first of all by looking at an initial perturbation, using a scalar field treatment of the “Bardeen potential”
, roughly in the region of the Sachs-Wolf contributions due to gravity waves. We begin first of all by looking at an initial perturbation, using a scalar field treatment of the “Bardeen potential”  This can lead us to put up, if
This can lead us to put up, if 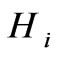 is the initial value of the Hubble expansion parameter
is the initial value of the Hubble expansion parameter
 (C1)
(C1)
and
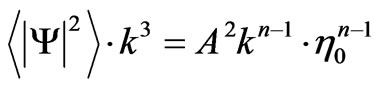 (C2)
(C2)
Here we are interpreting 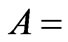 amplitude of metric perturbations at horizon scale, and we set
amplitude of metric perturbations at horizon scale, and we set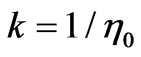 , where
, where 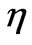 is the conformal time, according to
is the conformal time, according to 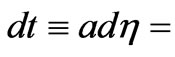 physical time, where we have
physical time, where we have 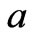 as the scale factor. Then for
as the scale factor. Then for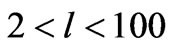 , and
, and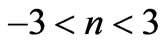 , and a pure power law given by
, and a pure power law given by
 (C3)
(C3)
We get for tensor fluctuation, i.e. gravity waves and a scale invariant spectrum with 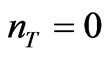
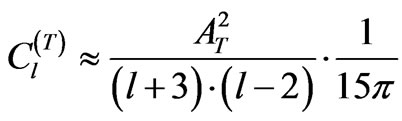 (C4)
(C4)
Appendix D: Linking the Thin Shell Approximation, Weyl Quantization, and the Wheeler de Witt Equation
This is a re capitulation of what is written by S. Capoziello, et al. [75] for physical review A, which is assuming a generally spherically symmetric line element. The upshot is that we obtain a dynamical evolution equation, similar in part to the Wheeler De Witt equation which can be quantified as 
Which in turn will lead to, with qualifications, for thin shell approximations ,
,
 (D1)
(D1)
so that 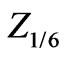 is a spherical Bessel equation for which we can write
is a spherical Bessel equation for which we can write
 (D2)
(D2)
Similarly,  leads to
leads to
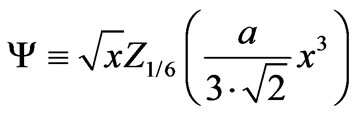 (D3)
(D3)
Also, when 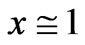
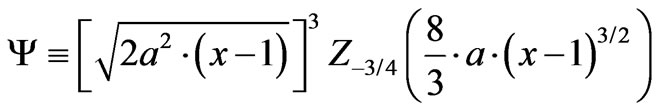 (D4)
(D4)
Realistically, in terms of applications, we will be considering very small  values, consistent with conditions near a singularity/worm hole bridge between a prior to our present universe. This is for
values, consistent with conditions near a singularity/worm hole bridge between a prior to our present universe. This is for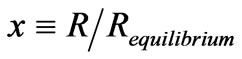 .
.

