Received 5 June 2016; accepted 23 August 2016; published 26 August 2016

ABSTRACT

We formulate efficient polynomial expansion methods and obtain the exact traveling wave solutions for the generalized Camassa-Holm Equation. By the methods, we obtain three types traveling wave solutions for the generalized Camassa-Holm Equation: hyperbolic function traveling wave solutions, trigonometric function traveling wave solutions, and rational function traveling wave solutions. At the same time, we have shown graphical behavior of the traveling wave solutions.

Keywords:

Camassa-Holm Equation, Partial Differential Equation, Polynomial Expansion Methods, Traveling Wave Solutions

1. Introduction

The study of dispersive waves originated from the study of water waves. To find the exact solutions of nonlinear evolution equation arising in mathematical physics plays an important role in the study of nonlinear physical phenomena. There exists an important class of solutions of nonlinear evolution equations is called traveling wave solutions which attract the interest of many mathematicians and physicists. The traveling wave solutions reduce the two variables, namely, the space variable x and the time variable t, of a partial differential equation (PDE) to an ordinary differential equation (ODE) with one independent variable where is the wave speed with which the wave travels either to the right or to the left. There are many classical methods proposed to find exact traveling wave solutions of PDE. For example, the homogeneous balance method [1] , the tanh method [2] [3] , the Jacobi elliptic function expansion [4] - [14] , differential quadrature method [15] , the truncated Painleve expansion [16] , Lie classical method [17] , Hirota bilinear method [18] , Darboux transformation [19] , the trial Equation method [20] . Recently, more and more methods to find traveling wave solutions

are made. In [21] - [26] introduced a method called the 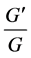-expansion method and obtained traveling solution for

the four well established nonlinear evolution equation; Seadawy et al. [27] proposed sech-tanh method to solve the Olver equation and the fifth-order KdV equation and obtained traveling wave solutions. Those methods are very efficient, reliable, simple in solving many PDEs.

In 1993, Camassa and Holm used Hamiltonian method to derive a new completely integrable shallow water wave equation

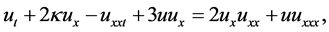(1)

where u is the fluid velocity in the x direction (or equivalently the height of the water’s free surface above a flat bottom), is a constant related to the critical shallow water wave speed, and subscripts denote partial derivatives. This equation retains higher order terms (the right hand of) (1) in a small amplitude expansion of incompressible Euler’s equations for unidirectional motion of wave at the free surface under the influence of gravity. Now, Equation (1) is called Camassa-Holm (CH) equation. In [28] , the authors showed the smoothness of periodic traveling wave solution of the CH equation with the wave length, where the periodic traveling wave solution is a special solution we obtained. In recently years, CH Equation has been generalized to the following generalized Camassa-Holm (GCH) equation

(2)

where is a function of u. In 2001, Dulin et al. considered a generalized CH equation

(3)

which is called CH-g equation. Here 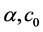and g are constants, and. The CH-g equation becomes the CH equation when 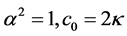and. In [11] [12] , the authors discussed the bifurcations of traveling wave solutions for the generalized Camassa-Holm Equation (2) and corresponding traveling wave system with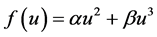, i.e.,

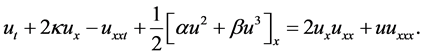(4)

In [13] , the authors discussed the bifurcations of smooth and non-smooth traveling wave solutions for the generalized Camassa-Holm Equation (2). In [14] , the author obtained the numerical solution of fuzzy Camassa- Holm equation by using homtopy analysis methods. We look for the traveling wave solutions of (4) in the form of, where c is the wave speed and. In this paper, we pay attention to solve the (4) and get the traveling wave solutions for the Equation (4).

This paper is organized as follows. In Section 1, an introduction is presented. In Section 2, a description of the polynomial expansion method is formulated. In Section 3, the traveling wave solutions of the GCH are obtained. Finally, the paper ends with a conclusion in the Section 4.

2. Analysis of the Polynomial Expansion Methods

In this section we describe the polynomial expansion methods for finding the traveling wave solutions of nonlinear evolution equation. Suppose a nonlinear equation which has independent space variable x and time variable t is given by

(5)

where is an unknown function, P is a polynomial of u and its partial derivatives and the polynomial P includes the highest order derivatives and the nonlinear terms. In following, we will describe the polynomial expansion methods.

Suppose that, where c is the wave speed and. The Equation (5) can be reduced to an ODE with variable

(6)

where “'” is the derivative with respect to.

2.1. Analysis of -Polynomial Expansion Methods

Step 1. Suppose the solution of Equation (6) can be expressed by a polynomial in as follows,

(7)

where are real constants with to be determined, N is a positive integer to be determined. The function is the solutions of the auxiliary linear ODE

(8)

where and are real constants to be determined.

Step 2. Substituting (7) into (6). At first, balancing two highest-order, get the value of N. Then separate all

terms with same order of together, the left hand of (6) is converted into anther polynomial of, where

is the solution of (8). Equating each coefficient of polynomial to zero. Then we obtain algebraic equations of, , c, and are solved by using Maple.

Step 3. Since we can get the general solutions of Equation (8), then substituting and the general solutions of (8) into (7). Thus, we obtain more traveling wave solutions of nonlinear partial differential Equation (5).

2.2. Analysis of Sech-Tanh Polynomial Expansion Methods

Step 1. Suppose the solution of Equation (6) can be expressed by a polynomial in as follows,

(9)

where and are constants to be determined.

Step 2. Equating two highest-order terms in the ODE (6) and getting the value of N.

Step 3. Let the coefficients of where and equate to zero. We have algebraic equations about the unknowns and.

Step 4. By using Maple, we can solve the algebraic equations in step 2 and we obtain the traveling wave solutions of (5).

3. The Traveling Wave Solutions of GCH

In this section, we will employ the proposed polynomial expansion methods to solve the generalized Camassa- Holm Equation (4). Substituting into (4), we have

(10)

where “'” is the derivative with respect to.

3.1. Application of -Polynomial Expansion Method

In this section, we apply the -polynomial expansion method to solve the Equation (10).

Balancing the terms with, we obtain. Therefore, we can write the solution of Equation (10) in the form

(11)

where and. From Equation (8) and (11), we obtain

(12)

(13)

(14)

Substituting (11), (12), (13), and (14) into Equation (10), let the coefficients of

be zero, we obtain the algebraic equation system for and as follows:

Solving the algebraic equation system by Maple we obtained six types of solutions:

(15)

where and are arbitrary constants.

(16)

where and are arbitrary constants.

(17)

where and are arbitrary constants.

(18)

where and are arbitrary constants.

(19)

where and are arbitrary constants.

(20)

where and are arbitrary constants.

Next, we use the solution sets from I to VI and the solutions of (8) to obtain the solutions of (10).

For I, substituting the solution set (15) and the corresponding solutions of (8) into (11), we obtain the hyperbolic function traveling wave solutions of (10) as follows:

(21)

where and are arbitrary constants. When the figure of I is like to Figure 1.

For II, substituting the solution set (16) and the corresponding solutions of (8) into (11), we obtain the rational function traveling wave solutions of (10) as follows:

(22)

where and are arbitrary constants. When, the figure of II is like to Figure 2.

For III, substituting the solution set (17) and the corresponding solutions of (8) into (11), we obtain the traveling wave solutions of (10) as follows:

When, we have the hyperbolic function traveling wave solutions

(23)

where and are arbitrary constants. When, the figure of III is like to Figure 3.

When, we have the trigonometric function traveling wave solutions

(24)

where and are arbitrary constants. When, the figure of III is like to Figure 3.

For IV, when, we have the hyperbolic function traveling wave solutions of (10) like the solution (23).

When, we have the trigonometric function traveling wave solutions of (10) like the solution (24).

For V and VI, we have the rational function traveling wave solutions of (10) like (22).

In addition, the figures of IV are similar to the figures of III, and the figures of V and VI are similar to the figure of II.

3.2. Application of Sinh-Tanh Polynomial Expansion Method

In this section, we apply the sinh-tanh polynomial expansion method to solve the Equation (10).

Balancing the terms with, we obtain. Therefore, we can write the solution of Equation (10) in the form

(25)

where are constants to be determined, and at least one is not zero. From (25), we have

(26)

(27)

(28)

Substituting (25), (26), (27), and (28) into Equation (10), let the coefficients of be zero, we obtain the algebraic equation system with the unknowns and c. Like above section, we solve the algebraic equation system by Maple, we get four types of solutions as follows:

(29)

where and are arbitrary constants;

(30)

where c and are arbitrary constants;

(31)

where and are arbitrary constants;

(32)

where and are arbitrary constants.

Therefore, we obtain the solutions of (10) by the solution sets from case 1 to case 4.

For i, substituting the solution set (29) into (11), we obtain the hyperbolic function traveling wave solutions of (10) as follows:

(33)

where and are arbitrary constants. When, the figure of i is like to Figure 4.

For ii, substituting the solution set (30) into (11), we obtain the hyperbolic function traveling wave solutions of (10) as follows:

(34)

where and c are arbitrary constants. When, the figure of ii is like to Figure 5.

For iii, substituting the solution set (31) into (11), we obtain the hyperbolic function traveling wave solutions of (10) as follows:

(35)

where and c are arbitrary constants. When, the figure of iii is like to Figure 6.

For iv, substituting the solution set (32) into (11), we obtain the hyperbolic function traveling wave solutions

of (10) as follows:

(36)

where and are arbitrary constants. When, the figure of iv is like to Figure 7.

4. Conclusions and Remarks

We proposed efficient polynomial expansion methods and obtained the exact traveling wave solutions of generalized Camassa-Holm equation. By polynomial expansion method we obtain hyperbolic function traveling wave solutions, trigonometric function traveling wave solutions, and rational function traveling wave solutions. On comparing with the polynomial expansion methods and other methods to find out the traveling wave for PDEs, the polynomial expansion methods are more effective, powerful and convenient. Moreover, the polynomial expansion methods can be used to solve any high-order degree PDEs.

Acknowledgements

The research is supported in part by the Science and Research Foundation of Yunnan Province Department of Education under grant No. 2015Y277, in part by the Natural Science Foundation of China under grant No. 11161038 and in part by Yunnan Province and Shanghai University of Finance and Economics Education Cooperation consulting Project under grant No. 42111217003.

Cite this paper

Junliang Lu,Xiaochun Hong, (2016) Exact Traveling Wave Solutions for Generalized Camassa-Holm Equation by Polynomial Expansion Methods. Applied Mathematics,07,1599-1611. doi: 10.4236/am.2016.714138

References