Applied Mathematics
Vol.07 No.10(2016), Article ID:67673,6 pages
10.4236/am.2016.710101
The Effect of Variations in Ionic Conductance Values on the Suppression of Repetitive Spiking in a Mathematical Model of Type-A Medial Vestibular Nucleus Neurons
Takaaki Shirahata
Institute of Neuroscience and Kagawa School of Pharmaceutical Sciences, Tokushima Bunri University, Sanuki, Japan

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 April 2016; accepted 21 June 2016; published 24 June 2016
ABSTRACT
A previous study has proposed a mathematical model of type-A medial vestibular nucleus neurons (mVNn). This model is described by a system of nonlinear ordinary differential equations, which is based on the Hodgkin-Huxley formalism. The type-A mVNn model contains several ionic conductances, such as the sodium conductance, calcium conductance, delayed-rectifier potassium conductance, transient potassium conductance, and calcium-dependent potassium conductance. The previous study revealed that spontaneous repetitive spiking in the type-A mVNn model can be suppressed by hyperpolarizing stimulation. However, how this suppression is affected by the ionic conductances has not been clarified in the previous study. The present study performed numerical simulation analysis of the type-A mVNn model to clarify how variations in the different ionic conductance values affect the suppression of repetitive spiking. The present study revealed that the threshold for the transition from a repetitive spiking state to a quiescent state is differentially sensitive to variations in the ionic conductances among the different types of ionic conductance.
Keywords:
Mathematical Model, Numerical Simulation, Type-A Medial Vestibular Nucleus Neurons, Ionic Conductance

1. Introduction
Type-A medial vestibular nucleus neurons (mVNn) can show spontaneous repetitive spiking without stimulation in vitro. A mathematical model, which reproduces the spiking, has been proposed based on the Hodgkin-Huxley formulation [1] . This model, which is described by a system of nonlinear ordinary differential equations (ODEs), contains several ionic conductances such as the sodium conductance, calcium conductance, delayed-rectifier potassium conductance, transient potassium conductance, and calcium-dependent potassium conductance. The study that proposed this model also indicated that the spontaneous spiking activity of the type-A mVNn model can be suppressed by hyperpolarizing stimulation [1] . However, it is important to conduct detailed analysis of the ionic conductances of excitable cells [2] . Thus, it is important to clarify how the different ionic conductances in the type-A mVNn model each affect the suppression of spiking. However, this issue was not been investigated in the previous study [1] .
Several studies have investigated the characteristics of the ionic conductances of various excitable cell models. For example, various studies have investigated the effect of co-variation of ionic conductances on the dynamics of excitable cell models [3] - [12] . In addition, studies have investigated the effect of variation of ionic conductances on the electrical stimulation-induced changes in the dynamical states [13] - [16] . The above studies have contributed to an understanding of the differences between the characteristics among different ionic conductances. Although analysis of ionic conductances has been extensively performed as described above, analysis of the ionic conductances of the type-A mVNn model has not been performed. Investigation of the type-A mVNn model will contribute to an understanding of the difference in the characteristics among ionic conductances of the type-A mVNn model in more detail. Therefore, the present study performed numerical simulation of the type-A mVNn model to clarify how the suppression of the spiking is dependent on the different ionic conductances.
2. Materials and Methods
The present study performed numerical simulations of a mathematical model of type-A mVNn, which was developed in a previous study [1] . The model is described by a system of nonlinear ODEs, which consists of the following five state variables: the membrane potential of the mVNn [V (mV)], three gating variables of ionic currents (n, x, and b), and calcium concentration {[Ca] (mM)}. The time evolution of the state variables is described as follows:

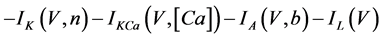 (1)
(1)
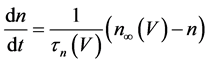 (2)
(2)
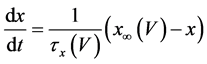 (3)
(3)
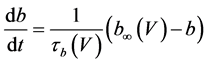 (4)
(4)
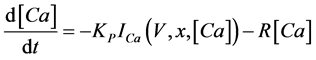 (5)
(5)
where Cm(1 mF/cm2) is the membrane capacitance; Iapp is the externally injected current of constant amplitude; INa(V, n), ICa(V, x, [Ca]), IK(V, n), IKCa(V, [Ca]), IA(V, b), and IL(V) are the sodium current, calcium current, delayed-rectifier potassium current, calcium-dependent potassium current, transient potassium current, and leak current, respectively, which are defined in Equations (6)-(11) below;tX(V) (ms) (X = n, x, b) and X∞(V) (X = n, x, b) are the time constants of activation/inactivation and the steady-state activation/inactivation functions, respectively, which are defined in Equations (12)-(17) below; Kp (=1) is the calcium influx parameter; and R (=5) is the parameter that regulates calcium removal through calcium transport and mitochondrial uptake.
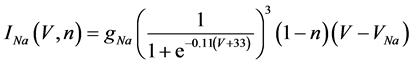 (6)
(6)
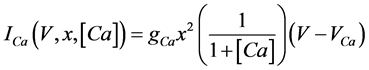 (7)
(7)
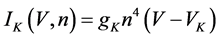 (8)
(8)
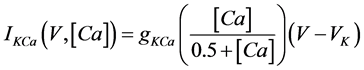 (9)
(9)
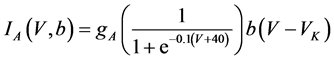 (10)
(10)
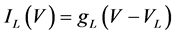 (11)
(11)
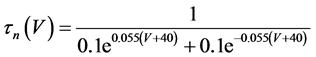 (12)
(12)
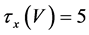 (13)
(13)
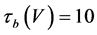 (14)
(14)



where gNa, gCa, gK, gKCa, gA, and gL (=0.3 mS/cm2) are the maximal conductances of INa(V, n), ICa(V, x, [Ca]), IK(V, n), IKCa(V, [Ca]), IA(V, b), and IL(V), respectively, and VNa(=55 mV), VCa(=124 mV), VK(=−80 mV), and VL(=−50 mV) are the reversal potentials of INa(V, n), ICa(V, x, [Ca]), three types of potassium currents {IK(V, n), IKCa(V, [Ca]), and IA(V, b)}, and IL(V), respectively. Refer to [1] for detailed explanations of the equations.
The free and open source software, Scilab (http://www.scilab.org/), was used to numerically solve the above ODEs (initial conditions: V = −60 mV, n = 0.1, x = 0.1, b = 0.9, and [Ca] = 0.1 mM). The total simulation time was 0.6 s in all the simulations. System parameters whose values were varied were Iapp, gNa, gCa, gK, gKCa, and gA. Iapp between 0.2 s and 0.6 s was varied from −2.0 mA/cm2 to 2.5 mA/cm2 at an interval of 0.5 mA/cm2, whereas Iapp between 0.0 s and 0.2 s was set to zero. Default values of gNa, gCa, gK, gKCa, and gA were 20 mS/cm2, 1 mS/cm2, 2 mS/cm2, 1 mS/cm2, and 4 mS/cm2, respectively. Each of gNa, gCa, gK, gKCa, and gA was varied to 50% or 150% of each default value.
3. Results
The previous study had indicated that a hyperpolarizing stimulation of −3 mA/cm2 suppressed spontaneous repetitive spiking [1] . To determine the effect of the hyperpolarizing stimulation on spiking activity in more detail, the present study first investigated the response of the model to hyperpolarizing stimulations of smaller amplitudes under conditions in which all the ionic conductances were set to default values. When a stimulation of −0.5 mA/cm2 was applied to the model, it showed a repetitive spiking behavior, but the frequency of spiking became smaller than that before the stimulation (Figure 1(a)). In contrast, when a stimulation of −1.0 mA/cm2 was applied to the model, it did not show a repetitive spiking behavior, but showed a quiescent state (Figure 1(b)). Based on these results, the present study defined −1.0 mA/cm2 as the stimulation threshold for suppressing repetitive spiking (we hereafter referred to this threshold as the “suppression threshold”). To reveal the relationship between the ionic conductances and the dynamics of the model, the present study next investigated how the suppression threshold changed in response to variations of each ionic conductance.
The effects of variations in the ionic conductance values on the dynamics of the model are shown in Figure 2. Under conditions in which gNa was 50% of the default value with other conductance values being set at the de-
Figure 1. Time courses of the membrane potential of the type-A mVNn model. (a) Iapp = −0.5 mA/cm2. (b) Iapp = −1.0 mA/cm2. Horizontal bars in (a) and (b) indicate the period of the hyperpolarizing stimulation.
Figure 2. The dependence of the dynamical states of the type-A mVNn model on Iapp and gx (x = Na, Ca, A, KCa, and K). ○ indicates the quiescent state, whereas ● indicates the repetitive spiking state.
fault values, the model showed a quiescent state in response to stimulation from −2.0 mA/cm2 to 2.0 mA/cm2, whereas it showed a repetitive spiking state in response to stimulation of 2.5 mA/cm2 (Figure 2(a)). Therefore, the suppression threshold at 50% gNa was 2.0 mA/cm2. Figure 2(a) also shows that the suppression thresholds at 100% gNa and 150% gNa were −1.0 mA/cm2 and −2.0 mA/cm2, respectively. Similarly, the suppression thresholds under conditions in which other ionic conductance values were varied were calculated. The suppression threshold at 50% gCa, 100% gCa, and 150% gCa was −1.5 mA/cm2, −1.0 mA/cm2, and −0.5 mA/cm2, respectively (Figure 2(b)). The suppression threshold at 50% gA, 100% gA, and 150% gA was −1.5 mA/cm2, −1.0 mA/cm2, and −0.5 mA/cm2, respectively (Figure 2(c)). The suppression threshold at 50% gKCa, 100% gKCa, and 150% gKCa was −1.5 mA/cm2, −1.0 mA/cm2, and 0.0 mA/cm2, respectively (Figure 2(d)). Finally, the suppression threshold at 50%, 100%, and 150% gK was −1.0 mA/cm2 for all three conditions (Figure 2(e)).
4. Discussion
The present study performed numerical simulation of the type-A mVNn model and revealed the differential sensitivity of the threshold for the transition from a repetitive spiking state to a quiescent state to variations in the different ionic conductance values. The present study revealed the difference in modulation of the threshold among the ionic conductances. An increase in gNa lowered the threshold, whereas an increase in gCa, gA, or gKCaraised the threshold. Finally, an increase in gK had no effect on the threshold. The sensitivity of the threshold to variations in the ionic conductance values decreased in the following order: gNa > gKCa > gCa = gA > gK. Although the previous study had investigated the response of the type-A mVNn model to hyperpolarizing and depolarizing stimulation [1] , the relationship between the ionic conductances and the threshold for the transition from a repetitive spiking state to a quiescent state had not been clarified prior to the present study.
It is important to determine whether or not variations in system parameters affect mathematical models of neurons linearly. For example, analysis of the ghostbursting model has reported that changes in the dendritic potassium conductance kinetics induce anonlinear effect on the dynamical states in a two-dimensional parameter space of the ghostbursting model [17] . In contrast, in the ghostbursting model, the threshold for the transition from a repetitive spiking state to a bursting state is influenced linearly by several ionic conductances [16] . In addition, one report has indicated that whether or not variations in ionic conductance values affect a certain type of neuron model linearly depends on the type of ionic conductance: in a vibrissa motoneuron model, the threshold for the transition between a subthreshold oscillation state and a tonic firing state changes nonlinearly in response to variations in the M-type potassium and the persistent sodium conductances [15] , whereas the threshold for the transition between a subthreshold oscillation state and a mixed-mode oscillation state changes linearly in response to variations in the cationic h conductance [15] . The study that developed the type-A mVNn model had not investigated the effect of variations in the ionic conductance values on the dynamics of the type-A mVNn model in detail [1] ; thus, whether or not variations in the ionic conductance values affect the type-A mVNn model linearly was unclear. The present study resolved this problem: in the type-A mVNn model, the threshold for the transition from a repetitive spiking state to a quiescent state changed linearly in response to variations in gCa and gA, whereas the threshold changed highly nonlinearly in response to variations in gNa (the threshold changed slightly nonlinearly in response to variations in gKCa). In particular, the present study clarified that the dynamics of the type-A mVNn model was affected linearly in response to variations in the calcium conductance. However, because neither the ghostbursting model nor the vibrissa motoneuron model contains the calcium conductance variable [15] [16] , whether or not variations in the calcium conductance affects the dynamics of these two models linearly cannot be studied.
5. Conclusion
The present study performed numerical simulation of the type-A mVNn model to reveal that the threshold for the transition from a repetitive spiking state to a quiescent state was differentially sensitive to variations in the ionic conductance values among the different types of the ionic conductances, which had not been reported in the previous study of the type-A mVNn model. The present study contributes to a more detailed understanding of the difference among the ionic conductances of the type-A mVNn model.
Acknowledgements
The author would like to thank Enago (www.enago.jp) for their review of the English language.
Cite this paper
Takaaki Shirahata, (2016) The Effect of Variations in Ionic Conductance Values on the Suppression of Repetitive Spiking in a Mathematical Model of Type-A Medial Vestibular Nucleus Neurons. Applied Mathematics,07,1134-1139. doi: 10.4236/am.2016.710101
References
- 1. Av-Ron, E. and Vidal, P.P. (1999) Intrinsic Membrane Properties and Dynamics of Medial Vestibular Neurons: A Simulation. Biological Cybernetics, 80, 383-392.
http://dx.doi.org/10.1007/s004220050533 - 2. Ashrafuzzaman, M. and Tuszynski, J. (2012) Membrane Biophysics. Springer, Heidelberg.
- 3. Prinz, A.A., Billimoria, C.P. and Marder, E. (2003) Alternative to Hand-Tuning Conductance-Based Models: Construction and Analysis of Databases of Model Neurons. Journal of Neurophysiology, 90, 3998-4015.
http://dx.doi.org/10.1152/jn.00641.2003 - 4. Drion, G., Massotte, L., Sepulchre, R. and Seutin, V. (2011) How Modeling Can Reconcile Apparently Discrepant Experimental Results: The Case of Pacemaking in Dopaminergic Neurons. PLoS Computational Biology, 7, Article ID: e1002050.
http://dx.doi.org/10.1371/journal.pcbi.1002050 - 5. Shirahata, T. (2011) The Effect of Variations in Sodium Conductances on Pacemaking in a Dopaminergic Retinal Neuron Model. Acta Biologica Hungarica, 62, 211-214.
http://dx.doi.org/10.1556/ABiol.62.2011.2.11 - 6. Soofi, W., Archila, S. and Prinz, A.A. (2012) Co-Variation of Ionic Conductances Supports Phase Maintenance in Stomatogastric Neurons. Journal of Computational Neuroscience, 33, 77-95.
http://dx.doi.org/10.1007/s10827-011-0375-3 - 7. Vo, T., Bertram, R. and Wechselberger, M. (2013) Multiple Geometric Viewpoints of Mixed Mode Dynamics Associated with Pseudo-Plateau Bursting. SIAM Journal on Applied Dynamical Systems, 12, 789-830.
http://dx.doi.org/10.1137/120892842 - 8. Shirahata, T. (2014) Effect of Sodium Conductance Variations on Electrical Behavior of a Neocortical Neuron Model. Acta Biologica Hungarica, 65, 379-384.
http://dx.doi.org/10.1556/ABiol.65.2014.4.2 - 9. Drion, G., O’Leary, T. and Marder, E. (2015) Ion Channel Degeneracy Enables Robust and Tunable Neuronal Firing Rates. Proceedings of National Academy of Sciences, 112, E5361-E5370.
http://dx.doi.org/10.1073/pnas.1516400112 - 10. Shirahata, T. (2015) Numerical Study of a Mathematical Model of Vibrissa Motoneurons: The Relationship between Repetitive Spiking and Two Types of Sodium Conductance. International Journal of Theoretical and Mathematical Physics, 5, 48-52.
- 11. Shirahata, T. (2015) Numerical Simulation Analysis of a Mathematical Model of Circadian Pacemaker Neurons. Applied Mathematics, 6, 1214-1219.
http://dx.doi.org/10.4236/am.2015.68113 - 12. Shirahata, T. (2016) Quantitative Evaluations of the Contribution of the Excitatory Ionic Conductance to Repetitive Spiking in a Mathematical Model of Medial Vestibular Nucleus Neurons. Acta Biologica Hungarica, 67, 215-219.
http://dx.doi.org/10.1556/018.67.2016.2.9 - 13. Doiron, B., Laing, C., Longtin, A. and Maler, L. (2002) Ghostbursting: A Novel Neuronal Burst Mechanism. Journal of Computational Neuroscience, 12, 5-25.
http://dx.doi.org/10.1023/A:1014921628797 - 14. Fernandez, F.R., Mehaffey, W.H. and Turner, R.W. (2005) Dendritic Na+ Current Inactivation Can Increase Cell Excitability By Delaying a Somatic Depolarizing Afterpotential. Journal of Neurophysiology, 94, 3836-3848.
http://dx.doi.org/10.1152/jn.00653.2005 - 15. Golomb, D. (2014) Mechanism and Function of Mixed-Mode Oscillations in Vibrissa Motoneurons. PLoS ONE, 9, Article ID: e109205.
http://dx.doi.org/10.1371/journal.pone.0109205 - 16. Shirahata, T. (2016) The Relationship of Sodium and Potassium Conductances with Dynamic States of a Mathematical Model of Electrosensory Pyramidal Neurons. Applied Mathematics, 7, 819-823.
http://dx.doi.org/10.4236/am.2016.79072 - 17. Shirahata, T. (2015) Evaluation of Kinetic Properties of Dendritic Potassium Current in Ghostbursting Model of Electrosensory Neurons. Applied Mathematics, 6, 128-135.
http://dx.doi.org/10.4236/am.2015.61013



