Received 202 February 2016; accepted 25 April 2016; published 28 April 2016

ABSTRACT

We study the problem of a diffusing particle confined in a large sphere in the n-dimensional space being absorbed into a small sphere at the center. We first non-dimensionalize the problem using the radius of large confining sphere as the spatial scale and the square of the spatial scale divided by the diffusion coefficient as the time scale. The non-dimensional normalized absorption rate is the product of the physical absorption rate and the time scale. We derive asymptotic expansions for the normalized absorption rate using the inverse iteration method. The small parameter in the asymptotic expansions is the ratio of the small sphere radius to the large sphere radius. In particular, we observe that, to the leading order, the normalized absorption rate is proportional to the (n − 2)-th power of the small parameter for.

Keywords:

Diffusion Equation, Brownian Diffusion, Asymptotic Solutions, Absorption Rate

1. Introduction

Search theory represents the birth of operations analysis [1] - [4] . One of the classical search problems involves a searcher equipped with a cookie-cutter sensor looking for a single moving target. A cookie-cutter sensor can detect a target instantly when the target gets within distance R to the searcher and there is no deteciton when the target range is larger than R. One interesting mathematical challenge is to find the probability of a diffusing target avoiding detection by a stationary cookie-cutter sensor. This problem has been addressed by Eagle [5] where the search region is a two-dimensional disk. Recently we have revisited this problem and have derived a unified asymptotic expression for the decay-rate of the non-detection problability which is valid for the cases where the search region is either a disk or a square [6] .

In this paper, we would like to extend our earlier work [6] to high dimensions. More specifically, we investigate the absorption rate into a small sphere such as a cookie-cutter sensor for a difusing particle (i.e. target) confined in a large sphere (i.e. search region).

From the next section, the paper is outlined as follows. We first present the mathematical formulation of the problem in Section 2. Then we consider the special case of the three dimensions in Section 3 and derive the exact solution for this case in Section 4. Section 5 and Section 6 describe the solutions for dimension four and dimension five, respectively. These asymptotic solutions are validated against the accurate numerical solutions of a Sturm-Liouville problem in Section 7. Finally, Section 8 summarizes the paper.

2. Mathematical Formulation

We consider a particle in the n-dimensional space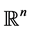, undergoing a Brownian diffusion with diffusion coefficient D. Let 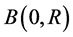denote the ball in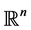, of radius R and centered at the origin

Let 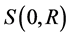denote the sphere in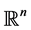, of radius R and centered at the origin. 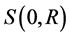is the boundary of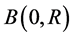. We consider the situation where the diffusing particle is confined from outside by a large sphere 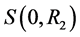and is absorbed near the origin by a a small sphe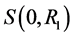re where. Figure 1 shows the geometry of the problem setpup in the three dimensional space ().

Let 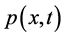be the probability of the particle being at position 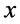at time. is governed by the diffusion equation with boundary and initial conditions:

(1)

where denotes the Laplace operator and represents the directional derivative of p along the

normal vector of.

We first perform non-dimensionalization to make the problem dimensionless. Let

The function has the meaning of probability density with respect to. It satisfies the initial boundary value problem below (we drop the subscript “” for simplicity):

(2)

where. After non-dimensionalization, the outside confining sphere has radius 1 and the inside absorbing sphere has radius.

The solution of initial boundary value problem (2) can be expressed in terms of exponentially decays of eigenfunctions.

(3)

Here are the eigenvalues and are the associated eigenfunc- tions of the Sturm-Liouville problem

(4)

In (3), the slowest decaying term is. Over long time, the dominant term is the one with the slowest decay and probability density has the approximate expression

(5)

We consider the survival probability:. Over long time, the decay of survival

probability is described by the smallest eigenvalue

(6)

Quantity corresponds to the time scale of the particle being absorbed by sphere. For small, time scale is large. In contrast, is approximately determined by the time scale of probability density relaxing to equilibrium within the region. As a result, , approximately independent of. This separation of time scales makes it possible to derive asymptotic expressions for the smallest eigenvalue.

The normalized decay rate of survival probability is, which is dimensionless. The physical decay rate (before non-dimensionalization) of survival probability is related to the normalized decay rate as

(7)

In the two-dimensional case (), we showed that for small the smallest eigenvalue has the expansion (Wang and Zhou, 2016)

(8)

In this study, we derive asymptotic expansions for the smallest eigenvalue in the cases of, and. For simplicity, we drop the subscript “”, and use to denote the smallest eigenvalue and to denote a corresponding eigenfunction. Since an eigenfunction for the smallest eigenvalue is axisymmetric, function depends only on. We write as. The axisymmetric Sturm-Liouville problem for the eigenpair (and) has the form

(9)

We use the inverse iteration method to derive an asymptotic expansion for, starting with an initial guess for eigenfunction:

Specifically, we solve the linear differential equation with boundary conditions below to update the approximation from to.

(10)

In the first iteration (), the delta function on the right hand side can be conveniently incorporated into the boundary condition at. For, Equation (10) becomes

(11)

An approximation to the smallest eigenvalue is calculated as

(12)

In the subsequent sections, we show that

(13)

(14)

(15)

3. The Three Dimensional Case: n = 3

For the three dimensional case (), the differential equation in (10) has the form

(16)

We first solve for two independent solutions of (16) in the case of without any boundary condition

Next we solve

(17)

For, the solution is

(18)

For, the solution is

(19)

For, the solution is

(20)

For, the solution is

(21)

With these results, we start the inverse iteration. For the first iteration (), the solution of (11) is a linear

combination of two independent solutions and 1.

The corresponding approxomation for using (12) is

In the second iteration (), the right hand side of (10) is and the solution of (10) is

formed using and described above.

The corresponding approxomation for using (12) is

In the third iteration (), the right hand side of (10) is

The solution of (10) is constructed using, , and.

The corresponding approxomation for using (12) is

Therefore, in the three dimensional case, has the expansion

(22)

For the three dimensional case, the smallest eigenvalue can be written as the exact solution of a transcendental equation, which provides an alternative way of deriving the asymptotic expansion. This is carried out in the next section.

4. Exact Solution for the Special Case of n = 3

For the special case of, we write as

(23)

Substituting it into (9) for, we derive the differential equation for:

The boundary condition for at is

The boundary condition for at is

Thus, satisfies the Sturm-Liouville problem

(24)

A general solution of the differential equation has the expression

Enforcing the boundary condition, we have and

(25)

Here we have set because an eigenfunction must be non-trivial and can be multiplied by any non-zero constant. Enforcing the boundary condition yields

(26)

The smallest eigenvalue is the smallest (positive) solution of Equation (26). The corresponding eigen- function is given by (25).

This exact solution specified by Equation (26) provides an alternative derivation for the asymptotic expansion of. Let. Substituting it into Equation (26) gives us an equation for.

(27)

Using the Taylor expansion of

and subtracting 1 from both sides of (27), we get

(28)

Based on (28), we construct an iterative formula for expanding

(29)

The iterative formula gives us

Going from back to, we obtain

(30)

which is the same as the asymptotic expnsion derived using inverse iteration method.

5. The Four Dimensional Case: n = 4

For the four dimensional case (), the differential equation in (10) has the form

(31)

We first solve for two independent solutions of (31) in the case of without any boundary condition:

Next we solve

(32)

For, the solution is

(33)

For, the solution is

(34)

With these results, we start the inverse iteration. For the first iteration (), the solution of (11) is a linear

combination of two independent solutions and 1.

The corresponding approxomation for using (12) is

In the second iteration (), the right hand side of (10) is and the solution of (10) is

formed using and described above.

The corresponding approxomation for using (12) is

Therefore, in the four dimensional case, has the expansion

(35)

6. The Five Dimensional Case: n = 5

For the five dimensional case (), the differential equation in (10) has the form

(36)

We first solve for two independent solutions of (36) in the case of without any boundary con- dition

Next we solve

(37)

For, the solution is

(38)

For, the solution is

(39)

With these results, we start the inverse iteration. For the first iteration (), the solution of (11) is a linear

combination of two independent solutions and 1.

The corresponding approxomation for using (12) is

In the second iteration (), the right hand side of (10) is and the solution of (10) is

formed using and described above.

The corresponding approxomation for using (12) is

Therefore, in the four dimensional case, has the expansion

(40)

7. Accuracy of Asymptotic Solutions

To demonstrate the accuracy of asymptotic expansions we obtained above, we solve numerically Sturm- Liouville problem (9). Instead of using a uniform grid in variable r, we use a uniform grid in variable, which provides a more uniform numerical resolution for the whole region even when is small. Let

In variable, Sturm-Liouville problem (9) becomes

(41)

We use the central difference with points to discretize Sturm-Liouville problem (41). The discrete version of (41) is an eigenvalue problem of a tridiagonal matrix. The smallest eigenvalue of this sparse matrix provides a very accurate appriximation to, the smallest eigenvalue of Sturm-Liouville problem (9). Below we treat this very accurate numerical solution as the true solution and use it to judge the performance of asymptotic solutions.

Figure 2 compares 3 asymptotic solutions and a very accurate numerical solution in the three dimensional case (). Solutions are compared for in the interval of. The one-term asymptotic solution is not very good in this range of. Nevertheless, as is reduced, the one-term asymptotic solution converges slowly to the true solution, which is represented by the accurate numerical solution in Figure 2. The two-term asymptotic solution is better than the one-term solution. The three-term asymptotic solution is even better. For, the three-term asymptotic solution is indistinguishable from the true solution.

Figure 3 compares 2 asymptotic solutions and a very accurate numerical solution in the four dimensional case (). The one-term asymptotic solution in the four dimensional case (Figure 3) is much more accurate than that in the three dimensional case (Figure 2). In Figure 3, the one-term solution is very close to the true solution for. This indicates that as n is increased, the leading order asymptotic solution becomes more accurate. The two-term asymptotic solution in Figure 3 coincides with the true solution for.

Figure 4 compares 2 asymptotic solutions and a very accurate numerical solution in the five dimensional case (). The one-term asymptotic solution in Figure 4 is already very close to the true solution for, confirming the trend that in higher dimensional space (larger n), the leading order asymptotic solution is more

accurate than that in lower dimensional space (smaller n). The two-term asymptotic solution in Figure 4 is indistinguishable from the true solution even at.

In each case (, , or), the most accurate asymptotic solution coincides with the true solution, at least, for.

8. Concluding Remarks

The focus of this paper was to calculate the absorption rate into a small sphere for a diffusing particle which was confined in a large sphere. Under the assumption that the ratio of the small sphere radius to the large sphere radius was small, we derived asymptotic expansions for the normalized absorption rate with the inverse iteration method.

Acknowledgements

Hong Zhou would like to thank Naval Postgraduate School Center for Multi-INT Studies for supporting this work. The views expressed in this document are those of the authors and do not reflect the official policy or position of the Department of Defense or the U.S. Government.

Cite this paper

Hongyun Wang,Hong Zhou, (2016) Absorption Rate into a Small Sphere for a Diffusing Particle Confined in a Large Sphere. Applied Mathematics,07,709-720. doi: 10.4236/am.2016.77065

References