Received 3 November 2015; accepted 28 December 2015; published 31 December 2015

ABSTRACT

The existence condition of the solution of special nonlinear penalized equation of the linear complementarity problems is obtained by the relationship between penalized equations and an absolute value equation. Newton method is used to solve penalized equation, and then the solution of the linear complementarity problems is obtained. We show that the proposed method is globally and superlinearly convergent when the matrix of complementarity problems of its singular values exceeds 0; numerical results show that our proposed method is very effective and efficient.

Keywords:

Linear Complementarity Problem, Nonlinear Penalized Equation, Newton Method, Singular Values

1. Introduction

Given a matrix 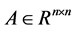and a vector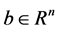, the problem of finding vectors 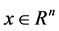such that

(1.1)

is called the linear complementarity problem (LCP). We call the problem the LCP (A, b). It is well known that several problems in optimization and engineering can be expressed as LCPs. Cottle, Pang, and Stone [1] [2] provide a thorough discussion of the problem and its applications, as well as providing solution techniques.

There are a large number of general purpose methods for solving linear complementarity problems. We can divide these methods into essentially two categories: direct methods, such as pivoting techniques [1] [2] , and iterative methods, such as Newton iteration [2] [3] and interior point algorithms [4] .

The penalty method has been used an LCP (or, equivalently, a variational inequality) [5] [6] . The paper [7] [8] constructed a nonlinear penalized Equation (1.2) corresponding to variational inequality.

Find 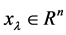such that

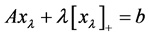(1.2)

where 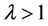is the penalized parameter,.

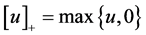The nonlinear penalized problems (1.2) corresponding to the linear complementarity problem (1.1), which its research has achieved good results. Wang [9] [10] , Yang [11] and Li [12] [13] was extended to a general form of (1.2) to present a power penalty function

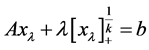(1.3)

approach to the linear complementarity problem. For the penalty Equation (1.2) Li [14] proved the solution to this equation converges to that of the linear complementarity problem when the singular values of A exceed 1 and Han [15] the interval matrix 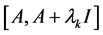is regular. It is worth mentioning that the penalty technique has been widely used solving nonlinear programming, but it seems that there is a limited study for LCP.

Some words about our notation: I refers to the identity matrix, and 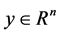are column vectors, y^T refers to the transpose of the y, we denote by 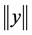the Euclidian norm.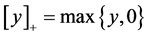, that generalized Jacobian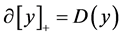, where 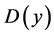denotes diagonal matrix, On the diagonal elements with component 1, 0 or corresponding to the component of y which is positive , negative or zero, respectively.

2. Generalized Newton Method

In this section, we will propose that a new generalized Newton method based on the nonlinear penalized Equation (1.2) for solving the linear complementarity problem.

Proposition 1 [15] . equivalent to, where

Proposition 2. has a unique solution if the singular values of A exceed 0.

Proof: Since the singular values of A exceed 0, then A is a positive definite matrix，and is positive definite, then is positive definite, then has a unique solution. □

Let us note

(2.1)

Thus, nonlinear penalized Equation (1.2) is equivalent to the equation.

A generalized Jacobian of is given by

.

where is a diagonal matrix whose diagonal entries are equal 1, 0 or a real number depending on whether the corresponding component of is positive, negative, or zero. The generalized Newton method for finding a solution of the equation consists of the following iteration:

equavelently

(2.2)

Algorithm 1

Step 1: Choose an arbitrary initial point, and given, , , let;

Step 2: for the, computer by solving (2.2).

Step 3: If, terminate. Otherwise, go to step 2.

Step4: If, terminate, is solution of LCP. Otherwise let, let, go to 2.

3. The Convergence of the Algorithm

We will show that the sequence generated by generalized Newton iteration (2.2) converges to an ac-

cumulation point associated with. First, we establish boundness of the sequence for any generated by the Newton iterates (2.2) and hence the existence of accumulation point at each generalized Newton iteration.

Theorem 1: Suppose the singular values of M exceed 0. Then, the sequence generated by Algorithm 1 is bounded. Consequently, there exits an accumulation points such that.

Proof. Suppose that sequence is unbounded, Thus, there exists an infinite nonzero subsequence such that

, and

where is main diagonal element of diagonal matrix which is.

We know subsequence is bounded. Hence, exists convergence subsequence and assume that convergence point is, and satisfy

.

Letting yields

Since the singular values of A exceed 0, then A is regular, and is regular, we know that is exists and hence, contradicting to the fact that. Consequently, the sequence is bounded and there exists an accumulation point of such that

. □

Under a somewhat restrictive assumption we can establish finite termination of the generalized Newton iteration at a penalized equation solution as follows.

Theorem 2: Suppose the singular values of A exceed 0 and holds for all suffi-

ciently large, then the generalized Newton iteration (2.2) linearly converges from any starting point to a solution of the nonlinear penalized Equation (1.2).

Proof. Similar to the proof of Theorem 4 in [15] . □

Theorem 3: Suppose the singular values of A exceed 0 and holds, then Algorithm

1 linearly converges from any starting point to a solution of the (1.1).

Proof. Similar to the proof of Theorem 5 in [15] . □

4. Numerical Experiments

In this section, we give some numerical results in order to show the practical performance of Algorithm 2.1 Numerical results were obtained by using Matlab R2007(b) on a 1G RAM, 1.86 Ghz Intel Core 2 processor. Throughout the computational experiments, the parameters were set as, ,.

Example 1: The matrix A of linear complementarity problem of as follows (This example appears in the Geiger and Kanzow [16] , Jiang and Qi [17] , YONG Long-quan, DENG Fang-an, CHEN Tao [18] and Han [15] ):

,

The computational results are shown in Table 1. This is initial point, k is number of inner iterations, the outer iteration number is m, is iteration results.

Example 2: The matrix A of linear complementarity problem of as follows:

,

Optimal solution of this problem is. The computational results are shown in Table 2. This is initial point, k is number of inner iterations, the outer iteration number is m, is iteration results.

Example 3: The matrix A of linear complementarity problem of as follows (This example appears in the Geiger and Kanzow [16] , Jiang and Qi [17] , YONG Long-quan, DENG Fang-an, CHEN Tao [18] and Han [15] ):

,

The computational results are shown in Table 3. This is initial point, k is number of inner iterations, the outer iteration number is m, is iteration results.

Cite this paper

HaishanHan,YuanLi, (2015) A Singular Values Based Newton Method for Linear Complementarity Problems. Applied Mathematics,06,2354-2359. doi: 10.4236/am.2015.614207

References

NOTES

^*This work supported by the Science Foundation of Inner Mongolia in China (2011MS0114).