Received 18 July 2015; accepted 22 August 2015; published 25 August 2015

ABSTRACT

In the present paper the definition of invexity for continuous functions is extended to invexity of order m which is further generalized to r-pseudoinvexity type I of order m, r-pseudoinvexity type II of order m, as well as r-quasi invexity type I of order m and r-quasiinvexity type II of order m. The central objective of the paper is to study variational problem where the functionals involved satisfy the above stated generalized r-invexity assumptions of order m. Wolfe type and Mond Weir type of duals are formulated. Sufficient optimality conditions and duality results are proved. It is demonstrated with the help of an example that the class of r-invex functionals of order m is more general than the class of r-invex functionals. Further, it may be noted that the results presented in this paper are more powerful than the existing results as this new class of functions defined here satisfies m^th derivative test.

Keywords:

Optimality, Variational Problem, Higher Order r-Invexity, Duality

1. Introduction

Calculus of variations is a powerful technique to find solutions of various problems appearing in dynamics of rigid bodies, optimization of orbits, theory of vibrations and many other fields. The subjects whose importance is fast growing in science and engineering primarily concern with finding optimal value of a definite integral involving certain functions subject to fixed boundary value conditions. In [1] Courant and Hilbert quoted an earlier work of Friedrichs [2] and gave a dual relationship for a simple type of unconstrained variational problem. Subsequently, Hanson [3] pointed out that some of the duality results of mathematical programming have analogues in variational calculus. Exploring this relationship between mathematical programming and the classical calculus of variation, Mond and Hanson [4] formulated a constrained variational problem as a mathematical programming problem and proved optimality and duality results under the assumption of convexity. To weaken this notion of convexity, Hanson [5] defined Invex (invariably convex) functions.

Invexity plays a vital role in many aspects of mathematical programming and hence in calculus of variation. Invexity was extended to variational problems by Mond, Chandra and Husain [6] . To relax invexity assumption imposed on the functions involved, various generalized notions have been proposed. One of the useful generalizations was r-invexity given by Bhatia and Kumar [7] . Another generalization of invexity namely B-vexity for variational problems was also given by Bhatia and Kumar [8] . Concept of higher order derivative for variational problems was studied by Husain and Jabeen [9] while generalized type-1 invexity and duality were explored by Kim and Kim [10] . Bhatia and Sahay [11] introduced higher order strong invexity for multiobjective optimization problem for static case. In this paper we extend the notion of r-invexity for continuous functions to higher order r-invexity and utilize this to establish sufficient optimality conditions for variational problem. Wolfe and Mond-Weir type duals are also formulated and various duality theorems are proved under the assumption of generalized r-invexity of higher order. The present concepts of invexity in the continuous case lead to four types of generalizations of invexity whereas normally only two types of generalizations are presented in literature. The significance of this new notion of invexity allows us to relax the notion of invexity associated with optimality and duality results for the variational problem.

2. Preliminaries and Definitions

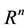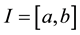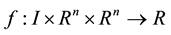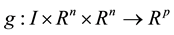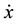Let denote n-dimensional Euclidean space and be a real interval. Let and be functions with continuous derivative up to and including second order with respect to each of their arguments. Let X be the space of continuously differentiable state functions, with its derivative such that 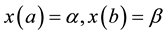and it is equipped with the norm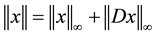, where the

differential operator D is given by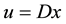, and is a given boundary value. Thus,

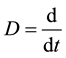except at discontinuities.

No notational distinction is made between row and column vectors. Subscripts 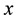and 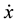denote partial derivatives with respect to second and third component respectively, of the function involved.

Consider the determination of piecewise smooth extremal 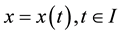for the following Variational Problem (P):

(P) Minimize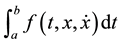

Subject to

(1)

(2)

Let G, denote the set of feasible solutions of the variational problem (P).

The following assumptions are required for the subsequent definitions: Let there exist a function with, a continuous function and a real number.

Definition 2.1. The functional is said to be r-invex (strictly r-invex) of order m (m > 1) at

with respect to and, if for all

Definition 2.2. The functional is said to be r-invex (strictly r-invex) at with respect to and, if for all

That is the functional is r-invex (strictly r-invex) of order 2.

Remark 2.1.

(1) If, the definition 2.1 reduces to the classical definition of invexity.

(2) If, the definition 2.1 reduces to the definition of r-convexity of order m.

(3) Definition of invexity of order m given by Bhatia and Sahay [11] is a particular case of definition 2.1.

(4) “r-invex functional” defined by Bhatia and Kumar [7] restricts the value of “t”, whereas in the present definition “t” is released from this restriction and hence makes it more viable.

Definition 2.3. The functional is said to be r-pseudo invex (strictly r-pseudo invex) type I of order m (m > 1) at with respect to and, if for all

Definition 2.4. The functional is said to be r-quasi invex (strictly r-quasi invex) type I of order m (m > 1) at with respect to and, if for all

Definition 2.5. The functional is said to be r-pseudo invex (strictly r-pseudo invex) type II of order m (m > 1) at with respect to and, if for all

Definition 2.6. The functional is said to be r-quasi invex (strictly r-quasi invex) type II of order m (m > 1) at with respect to and, if for all

Remark 2.2. Every r-invex functional of order m (m > 1) at with respect to and, is r-pseudo invex type I functional of order m (m > 1) as well as r-quasi invex type I functional of order m (m > 1) at with respect to same and.

Remark 2.3. It can be easily proved that every r-invex functional is a r-invex functional of order m (m > 1) with respect to same and but the converse may not be true which is shown in the following example. This illustrates the fact that the class of r-invex functionals of order m is larger than the class of r-invex functionals.

Example 2.1. Let and,

Claim: is r-invex functional of order m at, with respect to, , and, but it is not r-invex functional at, with respect to same and.

Applying the definition of r-invexity of the functional, we obtain

At, the above inequality reduces to

Integrating both sides and putting limits, we obtain, This is not true.

Hence the functional is not r-invex.

Now, the definition of r-invexity of order m = 4 of the functional yields

, and this is true.

Hence the functional is r-invex of order.

In fact the functional is r-invex of order m for any m ≥ 4.

3. Sufficient Optimality Conditions

In this section, we establish various sufficient optimality conditions for the variational problem (P) using higher order r-invexity assumptions (for notational convenience, we write y in place of).

Theorem 3.1. Let be feasible for (P) and let there exists piecewise smooth function such that, for all

(3)

(4)

(5)

(6)

Let either of the following conditions hold

(a) is r-invex functional of order m at with respect to η and ξ and is

-invex functional of order m for all, at with respect to same η and ξ, where

(7)

(b) is r-invex functional of order m at with respect to η and ξ and is r'-invex functional of order m at with respect to same η and ξ where, ,

Then is an optimal solution for (P).

Proof (a). Let x be any feasible solution of (P). Since is -invex functional of order m at with respect to and,

Multiplying each of the above inequality by −1 and taking summation over i yields

(8)

Since is r-invex functional of order m at w.r.t. to η and ξ, therefore for x Î G,

Equations (3) and (4) along with the above inequality yields

.

Hence is an optimal solution for (P).

(b). Proof of this part follows on the lines of part (a) and is hence omitted.

Theorem 3.2. Let be feasible for (P) and let there exists piece wise smooth function such that for all, conditions (3)-(6) are satisfied. Let either of the following conditions hold

(a) is r-pseudo-invex type II functional of order m at with respect to η and ξ, where

and are -quasi-invex type II functional of order m, for all at

with respect to same η and ξ where.

(b) is r-pseudo-invex type II functional of order m at with respect to η and ξ, and

is -quasi-invex type II functional of order m at with respect to same η and ξ, where

, for all.

Then is an optimal solution for (P).

Proof (a). Let x be any feasible solution of (P). Feasibility of x along with Equation (6) implies.

Since satisfies Equation (5), we get, for all which

implies, for all

Since is -quasi-invex type II functional of order m at with respect to and, for all

Multiplying each of the above inequality by −1 and taking summation over i yields

(9)

Using Equations (3) and (4) in (9) we get

Since is strictly r-pseudo-invex type II functional of order m at with respect to and, therefore

Hence is an optimal solution for (P).

(b). Proof of this part follows on the same lines as that of part (a) and is hence omitted.

4. Duality

4.1. The Wolfe Dual

The Wolfe type dual problem (WD) associated with (P) is given by

(WD) Maximize

Subject to

(10)

(11)

(12)

Here, is continuous except possibly for the values of corresponding to the corners of. For such values of, Equation (11) must be satisfied for right and left hand limits.

We now establish duality results between (P) and (WD) using higher order generalized r-invexity assumptions.

Theorem 4.1. (Weak Duality) Let be a feasible solution for (P) and be a feasible solution for (WD). If the functional is r-pseudo invex type I of order m at u with respect to η and ξ where, then

.

Proof. Since x is a feasible solution for (P) and is a feasible solution for (WD), from (11) it follows that

(13)

Now integrating by parts the following function and applying boundary conditions (1) and (10), we get

(14)

It follows from (13) and (14) that

Since the functional is r-pseudo invex type I of order m at u with respect to η and ξ, the above equation yields

(15)

Now, contrary to the result, assume that

Using Equations (2) and (12) we get

Since the above inequality yields

But this contradicts (15). Hence the result follows.

The following theorem by Mond and Hanson is required to prove the strong duality theorem.

Theorem 4.2. (Mond and Hanson [4] ) For every minimizing arc of (P) there exists a function of the form

such that

(16)

(17)

(18)

holds throughout I (except at the corners of, where (16) holds for unique right and left hand limits). Here is constant and y is continuous except possibly for values of t corresponding to corners of. Further cannot vanish for any. If is normal, can be taken equal to 1.

Theorem 4.3. (Strong Duality) Let minimizes the primal problem (P) and assume that is

normal, then there exists such that is feasible for (WD). Further if conditions of weak

duality (Theorem 4.1) are satisfied then maximizes (WD) and extreme values of (P) and (WD) are equal.

Proof. Since minimizes (P) and is normal, it follows from theorem 4.2, that there exists satisfying

(19)

(20)

(21)

It follows from (19) and (21) that is feasible for (WD). Result now follows directly from Equation (20) and weak duality theorem (4.1).

Theorem 4.4. (Strict Converse Duality) Let be an optimal solution of (P) and be an optimal solution of (WD) such that

Assume that the functional is strictly r-pseudo invex type I of order m on X with respect to η

and ξ, where. Then, and is an optimal solution of (P).

Proof. Since

It follows from Equations (2) and (12) that

(22)

Now, if, it follows from Equation (11) that

Using Equation (14), we get

Since is strict r-pseudo invex type I functional of order m with respect to η and ξ, therefore the above equation yields

This contradicts Equation (22). Hence implying there by that is an optimal solution of (P).

4.2. Mond-Weir Dual

The Mond-Weir dual problem (MD) associated with (P) is given by

(MD) Maximize

Subject to

(23)

(24)

(25)

(26)

Here, is continuous except possibly for the values of corresponding to the corners of. For such values of, Equation (24) must be satisfied for right and left hand limits.

Theorem 4.5. (Weak Duality) Let x be a feasible solution for (P) and be a feasible solution for (MD), if is r-pseudo invex type I functional of order m at u with respect to η and ξ where and

is r'-quasi invex type I functional of order m at u with respect to the same η and ξ where

, then

Proof. Since is feasible solution for (P) and is feasible solution for (MD), it follows from (2), (12) and (25) that

Now implies that

As is r'-quasi invex type I functional of order m with respect to η and ξ, above inequality yields

(27)

Integrating by parts the followings functions and using boundary conditions (1) and (23), we get

(28)

Using (28) in (27)

Now, dual feasibility constraint (24) yields

(29)

Again, integrating by parts the followings functions and using boundary conditions (1) and (23), we get

(30)

Equations (29) and (30) yield

As is r-pseudo invex type I functional of order m with respect to η and ξ, the above inequality yields

Since the above inequality yields

Hence the result follows.

Theorem 4.6. (Weak Duality) Let x be a feasible solution for (P) and be a feasible solution for (MD), if is strictly r-pseudo invex type I functional of order m at u with respect to η and ξ, where, then

.

Proof. Proceeding on the similar lines as in theorem 4.1, we arrive at the following inequality

where x is feasible for (P) and is feasible for (MD).

Now, using the dual feasibility condition (25) we get

,

this proves the theorem.

Theorem 4.7. (Strong Duality) Assume that is optimal for (P) and is normal, then there exists

such that is feasible for (MD). Further if conditions of weak duality (Theorem 4.5 or 4.6) are satisfied,

then is optimal for (MD) and extreme value of (P) and (MD) are equal.

Proof: Proof runs on the similar lines as that of theorem 4.3 and is hence omitted.

Theorem 4.8. (Strict Converse Duality) Let be optimal for (P) and be optimal for (MD) such that

.

If is strictly r-pseudo invex type I functional of order m with respect to η and ξ, then, and is an optimal solution of (P).

Proof. Since

It follows from (2), (25) and (26) that

Now proceeding on the similar lines as in theorem 4.4, we get the result.

5. Conclusions

In this paper definition of invexity for continuous functions was extended to r-invexity of order m. Four types of generalizations of r-invexity of order m are presented and they are:

(a) r-pseudoinvex type I functionals of order m,

(b) r-pseudoinvex type II functionals of order m,

(c) r-quasi invex type I functionals of order m and,

(d) r-quasi invex type II functionals of order m.

An example was presented to establish that the class of r-invex functionals of order m is more general than the class of r-invex functionals. Sufficient optimality conditions were established for the variational problem under r-invexity assumptions. Wolfe dual as well as Mond Weir duals was constructed. Weak, strong and converse duality results were proved using generalized r-invexity assumptions. The significance of this new notion of invexity allows us to relax the notion of invexity associated with optimality and duality results for variational problem. Further, it may be noted that the results presented in this paper are more powerful than the existing results as the class of functions deliberated here satisfies m^th derivative test.

Cite this paper

PromilaKumar,Jyoti , (2015) Generalized Invexity of Higher Order and Its Applications in Variational Problems. Applied Mathematics,06,1638-1648. doi: 10.4236/am.2015.69146

References