Applied Mathematics
Vol.06 No.08(2015), Article ID:58154,4 pages
10.4236/am.2015.68120
Modeling Radon Diffusion across Some Areas of Southern Jordan
Hussam Alrabaiah
Department of Mathematics, Tafila Technical University, Tafila, Jordan
Email: hussam89@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 March 2015; accepted 19 July 2015; published 22 July 2015
ABSTRACT
A numerical has been developed for the transport of radon gas in the soil-rocks of Afrahotsprings, southern of Jordan using a one-dimensional model diffusion formula. Model Result shows a consistent relation between distance from radiation source and radon concentration. Data model output were in the range of data collected from previous studies.
Keywords:
Modeling, Radioactive, Radon, Diffusion

1. Introduction
Naturally Occurring Radioactive Material occurs in most soil and rocks, and is some areas of hotsprings, some of the radionuclides are significantly enhanced. An in-situ gamma-ray detector has been used to produce a map of relative activity concentrations in Afrahotsprings in Tafila, Jordan. The activity concentrations are used with global positioning data (GPS) to produce the concentration maps. A hyper-pure germanium gamma-ray detector (HPGe) was used to measure γ-rays from the naturally occurring nuclides for soil and rock samples taken at different points on the site. The purpose of the study is also to review and develop a mathematical model for radon activity concentration predictions in areas of study.
This paper describes an idealized mathematical model that has been used to examine the diffusion of radon into our area of study. Some typical results of the application of the model are presented, together with details of the numerical technique used to produce them.
2. Methods
This investigation describes the modeling of a distance profile with respect to the radon activity concentration to understand from what distance radon might be migrating along the surface. The study was performed on a hot spring location in the province of Tafila in South of Jordan.
The Afra hot springs are a potentially Normal source of radon, since the soil and rocks in the area contains radium activity concentrations of typically 200 - 300 Bq∙kg−1. A study of the diffusion of the radon will give us a better understanding of its possible pathways through the soil into the air surrounding the hot springs. The conventional [1] mathematical model used to evaluate the transport of radon through a barrier of soil usually treats the problem as one dimensional steady-state molecular diffusion given by Fick’s law [2] .
Numerical modeling of 222Rn is complex and involves a few important physical processes. The core of the hotsprings are considered to be sources of radon since they largely contain the predecessor of radon; 226Ra. Some factor may be considered when assessing Radon diffusion such as 1) emanation from the soil grains, 2) generation of radon itself, 3) transport of the radon through the hot spring waters and rocks and 4) the pressure variations in the soil and ambient air.
3. Model Development
There are two main transport processes that dictate radon release from soil. The two processes are diffusion and advection. Advection will not be considered in this study, since its role depends on small pressure changes that tend to average out. In general, the 3D advection-diffusion equation is given by
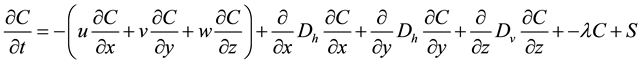
where C is the activity concentration of radon, λ is the radon decay constant, Dh, Dv are, respectively, horizontal and vertical diffusion coefficient which is adopted to include all external forces that may impact transport and S is the source rate of radon [3] [4] . Due to the nature of the location of study and the physical nature of radioactive material, the advection terms could be neglected and the modeling in y and z direction could also be dropped. Hence, our model may have the form of

On the right hand side of the equation the first term relates to the change of radon atoms due to diffusion while the second and third terms relate to the decay of radon atoms and the creation of radon respectively. The boundary conditions are: C ® Cmin as x ® ∞ where the x -axis is chosen horizontally and C ® Cmax as x ® 0 at the core area of the hotsprings. The radon concentration at the infinity (C0) will be close to zero. Assume steady state diffusion as well as no pressure changes. The solution to the above equation is then
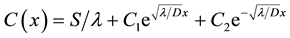
The boundary conditions lead to
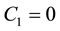 ,
,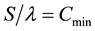 ,
, 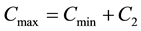 and
and
thus
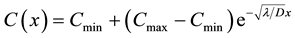
If
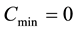 then
then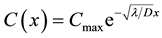 , this formula was used to calibrate our parameters using some values found in the literature [3] [5] [6] , and hence model results is shown in the next section, another result are the best-fit model is also shown.
, this formula was used to calibrate our parameters using some values found in the literature [3] [5] [6] , and hence model results is shown in the next section, another result are the best-fit model is also shown.
4. Radon Gas Measurements
Our measurements can be listed in the following Table 1 with the corresponding distance from the core of the hotsprings, alongside with model results.
5. Results and Discussions
5.1. One-Dimensional Diffusion Equation
The one-dimensional diffusion equation was solved (within certain boundary conditions) and last equation yields the results plotted in Figure 1.
Table 1. Measured and modeled data of Afrahotsprings.
Figure 1. Measured and modeled data of Afrahotsprings.
The radon concentrations are presented as a function of depth for different (diffusion lengths) values. These predictions assume that only diffusion is considered to have an effect on the radon soil-gas. It is clear from the graph that a very short diffusion length (l) would cause a very rapid increase in the radon soil-gas with increasing depth. One limitation with this analytical model is that it does not explain the radon concentrations at depths closer to the surface of the tailings. One of the possible reasons is that at these depths, pressure changes on the surface of the mine dump could influence the radon soil-gas close to the surface. The model predicts radon concentrations that tend to the maximum radon concentration assumed in the model round about 200 kBq∙m−3 as indicated in Figure.
It has been suggested that a significant contribution to the amount of radon gas in rocks and air of Afra could be due to the ingress of radon through cracks in the floor [5] . Here, the radon is assumed to be produced by the soil, or the rocks contained within it. This introduces radon into the interstitial areas of Afra soils and its soil gas system. The destitution of radon concentration into our area of study and based on our results, shows that the driving mechanism for transport of radon along our 1-dimension area of study. A possible interpretation of the result is that the movement is dominated by diffusion. Radon could diffuse through the air-pore system in soil-rock environment, where the soil gas is assumed to be relatively stationary. The radon is preferentially drawn to the boundary between soil and atmospheric air, this is because atmospheric air moves more freely than the soil gas. Further, the atmosphere does not contain a soured of radon. Another view of the results is the soil gas velocity contributes of the transport of radon. This mainly comes from the (small) difference in pressure between Afra selected locations of measurements. Air velocity is proportional to this pressure gradient (difference).
Figure 2. Coefficients, goodness measures, and results of the exponential decay model.
As we assumed before, this pressure factor is neglected.
A best-fit model is developed for the data using an exponential decay model of the form:
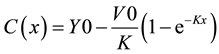
with model coefficients, goodness measures, and results show in Figure 2.
5.2. Conclusion and Future Work
The measurements of radon concentration in the longitude of our area of study have shown the existence of a good longitude-dependence [6] [7] . The radon concentration tends to decrease as distance from source is increased. Further investigations might be needed for soil type and relating it for the developed model or more proposed sophisticated modeling efforts. Some work might also be needed in incorporating pressure effects. Collecting two dimensional data is a bit challenging, in particular in that rugged or bumpy area.
Cite this paper
HussamAlrabaiah, (2015) Modeling Radon Diffusion across Some Areas of Southern Jordan. Applied Mathematics,06,1271-1275. doi: 10.4236/am.2015.68120
References
- 1. Sasaki, T., Gunji, Y. and Ocuda, T. (2006) Transient-Diffusion Measurement of Radon in Japanese Soils from a Mathematical Viewpoint. Journal of Nuclear Science and Technology, 43, 806-810.
http://dx.doi.org/10.1080/18811248.2006.9711163 - 2. Kaikwarf, D.R., Nielson, K.K., Rich, D.C. and Rogers, V.C. (1982) Comparison of Radon Diffusion Coefficients Measured by Transient-Diffusion and Steady-State Laboratory Methods, NUREG/CR-2875.
- 3. Daoud, W.Z. and Renken, K.J. (1999) Laboratory Measurements of the Radon Gas Diffusion Coefficient for a Fractured Concrete Sample and Radon Gas Barrier Systems. Proceedings of International Radon Symposium, American Association of Radon Scientists and Technologists (AARST), Las Vegas.
- 4. Willis, G.E. and Deardorf, J.W. (1981) A Laboratory Study of Dispersion from a Source in the Middle of the Convectively Mixed Layer. Atmospheric Environment, 15, 109-117.
http://dx.doi.org/10.1016/0004-6981(81)90001-9 - 5. Arvela, H. (1995) Seasonal Variation in Radon Concentration of 3000 Dwellings with Model Comparisons. Radiation Protection Dosimetry, 59, 33-42.
- 6. Ryzhakova, N.K. (2012) Parameters of Modeling Radon Transfer through Soil and Methods of Their Determination. Journal of Applied Geophysics, 80, 151-157.
http://dx.doi.org/10.1016/j.jappgeo.2012.01.010 - 7. Andersen, C.E. (1999) Numerical Modelling of Radon-222 Entry into Houses: An Outline of Techniques and Results. Radon in the Living Environment, Athens, 19-23.




