ABSTRACT

In this work, we study an analytical procedure for evaluation of the displacement and stresses in fibre-reinforced anisotropic elastic media under effects of rotation and initial magnetic field, and due to the application of the rotation and initial magnetic field. Effects of rotation and initial magnetic field are analyzed theoretically and computed numerically. Numerical results have been given and illustrated graphically. Comparison was made with the results obtained in the presence of rotation and initial magnetic field in fibre-reinforced anisotropic and isotropic elastic media. The results indicate the effect of rotation and initial magnetic field.

Keywords:

Fibre-Reinforced Medium, Harmonic Vibrations, Initial Magnetic Field, Rotation, Anisotropic

1. Introduction

The linear theory of elasticity of paramount importance in the stress analysis of steel is the commonest engineering structural material. To a lesser extent, linear elasticity describes the mechanical behavior of the other common solid materials, e.g. concrete, wood and coal. The problem of rotating disks or cylinders has its application in high-speed cameras, steam and gas turbines, planetary landings and in many other domains. Various authors have formulated these generalized theories on different grounds. Lord and Shulman [1] have developed a theory on the basis of a modified heat conduction law which involves heat-flux rate. Green and Lindsay [2] have developed a theory by including temperature-rate among the constitutive variables. Lebon [3] has formulated a theory by considering heat-flux as an independent variable. Also some problems in thermoelastic rotating media are due to Roychoudhuri and Debnath [4] [5] . These problems are based on more realistic elastic model since earth, moon and other planets have angular velocity. Abd-Alla et al. [6] study effects of the rotation on an

infinite generalized magneto-thermoelastic diffusion body with a spherical cavity. Effects of rotation and initial stress on generalized-thermoelastic problem in an infinite circular cylinder are due to Abd-Alla et al. [7] . Bayones [8] studied effects of rotation and hydrostatic initial stress on propagation of Raylegh in waves in an elastic solide half-space under the GN theory. The solution to the problems of homogeneous isotropic rotating cylinders may be found in Love [9] and Sokolnikoff [10] . Abd-Alla and Abo-Dahab [11] and Sharma et al. [12] studied the effect of the time-harmonic source in a generalized thermoelasticity. Chandrasekharaiah [13] , Green and Naghdi [14] , and Hossen and Mallet [15] discussed the problem of thermoelasticity without energy dissipation. Abd-Alla et al. [16] studied M. I. Helmy’s Propagation of S-Wave in a Non-Homogeneous Anisotropic Incompressible and Initially Stressed Medium under Influence of Gravity Field. Effects of the rotation on a non-homogeneous infinite cylinder of orthotropic material are due to Abd-Alla et al. [17] .

Fibre-reinforced composites are used in a variety of structures due to their low weight and high strength. The mechanical behavior of many fibre-reinforced composite materials is adequately modeled by the theory of linear elasticity for transversely isotropic materials, with the preferred direction coinciding with the fibre direction. In such composites, the fibres are usually arranged in parallel straight lines. The characteristic property of a reinforced composite is that its components act together as a single anisotropic unit as long as they remain in the elastic condition.

The idea of introducing a continuous self-reinforcement at every point of an elastic solid was discussed by Belfied et al. [18] . The model was later applied to the rotation of a tube as discussed by Verma and Rana [19] . The problem of surface waves in fiber-reinforced anisotropic elastic media was discussed by Sengupta and Nath [20] . The elastic moduli for fiber-reinforced materials was given by Hashin and Rosen [21] . The problem of reflection of plane waves at the free surface of a fiber-reinforced elastic half-space was discussed by Singh and Singh [22] . The dispersion of Loves waves in a self-reinforced layer over an elastic non-homogeneous half-space was studied by Pradhan et al. [23] . The propagation of plane waves in a fiber-reinforced media was discussed by Chattopadhyay et al. [24] . The problem of wave propagation in thermally conducting linear fiber-reinforced composite materials was discussed by Singh [25] . Recently, the effect of rotation on plane waves at the free surface of a fiber-reinforced thermoelastic half-space using the finite element method was studied by Othman and Abbas [26] .

In this paper, we studied an analytical procedure for evaluation of the displacement, and stresses in fibre-reinforced anisotropic elastic media under effect of rotation and initial magnetic field. Using the harmonic vibrations, we found the general solution, determining the displacements and stress components. The special case was studied in isotropic generalized elastic medium with rotation and initial magnetic field. Finally, we represented this case graphically.

2. Formulation of the Problem (Figure 1)

The propagation of general surface waves is examined here for a fiber-reinforced elastic solid semi-infinite medium 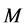covered by another fiber-reinforced elastic medium 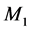(above 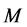and mechanical properties different from 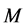and which is welded in contact with 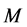to prevent any relative motion or sliding during disturbance). We consider an orthogonal Cartesian coordinate system 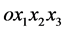with origin 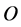at the common plane boundary surface and 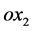directed normally into M. The elastic medium is rotating uniformly with angular velocity 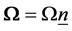where 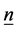is a unite vector representing the direction of the axis of rotation.

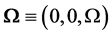Both media are under the primary magnetic field 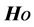acting on Z-axis,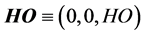. The displacement equation of motion in the rotating frame has two additional terms is The centripetal acceleration due to time varying motion only, and 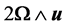is the Coriolis acceleration.

The electromagnetic field is governed by Maxwell equations , under the consideration that the medium is a perfect electric conductor taking into account the absence of the displacement current (see work of Mukhopadhyay [27] ):

(1)

where

(2)

where is the perturbed magnetic field over the primary magnetic field vector, is the electric intensity, is the electric current density, is the magnetic permeability, is the constant primary magnetic field vector, the displacement vector.

The constitutive equation for the fiber reinforced linearly elastic anisotropic medium with respect to preferred direction is Belfied et al. [28]

(3)

where are components of stress,

(4)

Are the components of strain, are elastic parameter; are reinforced anisotropic elastic parameters; are the displacement vector components and where if a has components the are (1,0,0) so that the preferred direction is -axis, (3) simplifies as given below:

(5)

The equations of motion are:

(6)

(7)

(8)

where,

where is the density of the elastic medium. Using (5)-(8) and assuming all derivatives with respect to vanish, the equations of motion become

(9)

(10(

(11)

To examine dilatational and rotational disturbances, we introduce two displacement potentials and by the relations:

(12)

The component is associated with purely distortional movement. Using (12) in (9) we obtain the following equation in satisfied by and as:

(13)

(14)

And for medium:

(15)

(16)

3. Boundary Conditions

The boundary conditions for the titled problem are:

a) The component of displacement at the boundary surface between the media and must be continues at all times and places.

b) The stress components and must be continuous a crass the interface of and at all times and place s.

where and can be written in terms of and in medium from (5) to (12)

(17)

(18)

(19)

where is the two dimensional Laplaci an operator given by

Similar relations in:

(20)

(21)

(22)

4. Solution of the Problem

We seek harmonic solutions for (11), (13) and (14) in the form (see Bullen [29] )

(23)

where is a complex frequency. In M and similar relations in M₁ with the factions, , being replaced by

, ,. This leads us to a particular solution corresponding to group of wavelength traveling forward

with speed C. It is convenient to introduce where

(24)

And similar expressions, and for the medium. The positive value of the square root being taken in each case.

Now substituting from (23) into (11), (13) and (14), we obtain for the medium

(25)

Equation (25) has solutions:

(26)

And for the medium

(27)

In the above, for the effect to be essentially a surface one ,each expression must diminish indefinitely with increasing distance from the boundary this with be the case if each expression contains an exponential factor in with the exponent is teal and negative. Hence, and similarly are taken to be imaginary. From (12), we have

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

Similar relations in with are replaced by.

By using the boundary conditions a and b, we can determined the constants, , and.

We can study the components of displacement and stresses in fibre-reinforced anisotropic elastic media under effect of rotation and initial magnetic field from Equations (28)-(35) by using Maple program, is clear up from Figures 2-9.

5. Particular Case: Isotropic Generalized Elastic Medium with Rotation and Initial Magnetic Field

In this case, substituting and in Equations (28)-(35), we obtain the corresponding expressions of displacement and stress in isotropic generalized elastic medium with rotation and initial magnetic field, is clear up from Figures 10-17.

6. Numerical Results and Discussions

To study the surface waves in fibre-reinforced we use the following physical constants for anisotropic elastic media under the in influence of rotation and initial magnetic field, are considered [18] [19] , for mediums and respectively.

The numerical technique outlined above was used to obtain of the displacement, stresses in fibre-reinforced anisotropic and isotropic elastic media under effect of rotation and initial magnetic field. These distributions are shown in Figures 2-17. For the sake of brevity some computational results are being presented here.

6.1. Effect of Rotation and Initial Magnetic Field in Fibre-Reinforced Anisotropic Elastic Media

Figure 2 shows that the components of displacement in fibre-reinforced anisotropic elastic media under effect of rotation, we find that in medium, the components of displacement and are decreasing with increasing values of the rotation, put in medium, decreasing and increasing with increasing values of respectively.

Figure 3 shows that the components of displacement in fibre-reinforced anisotropic elastic media under effect of initial magnetic field, we find that in medium, the components of displacement increasing and decreasing with increasing values of initial magnetic field respectively, put decreasing and increasing with increasing values of.

Figure 4 shows that the components of stresses in fibre-reinforced anisotropic elastic media under effect of

rotation, we find in medium the components of stresses, and are increasing with increasing values of the rotation, put decreasing with increasing values of. While, in medium the components of stresses, , and are decreasing with increasing values of.

Figure 5 shows that the components of stresses in fibre-reinforced anisotropic elastic media under effect of initial magnetic field, we find in medium the components of stresses, , and are decreasing with increasing values of initial magnetic field. While, in medium the components of stresses and are decreasing with increasing values of initial magnetic field, put and are increasing with increasing values of values of.

Figure 6 shows that the displacements distribution with change values of rotation and complex frequency in fibre-reinforced anisotropic elastic media, we find in medium the components of displacement and are decreasing with increasing values of the rotation, put in medium, decreasing and increasing with increasing values of respectively.

Figure 7 shows that the displacements distribution with change values of initial magnetic field and complex frequency in fibre-reinforced anisotropic elastic media, we find we find that that in medium, the components of displacement increasing and decreasing with increasing values of initial magnetic field, put in medium, decreasing and increasing with increasing values of, respectively.

Figure 8 shows that Stresses distribution with change values of rotation and complex frequency Ω in fibre-reinforced anisotropic elastic media under effect of rotation, we find for the medium the components of stresses, , and are increasing with increasing values of the rotation. While, for the medium the components of stresses and are increasing with increasing values of, put the components of stresses and are decreasing with increasing values of.

Figure 9 shows that Stresses distribution with change values of initial magnetic field and complex frequency Ω in fibre-reinforced anisotropic elastic media under effect of rotation, we find in the medium the components of stresses, and are increasing with increasing values of the initial magnetic field, put decreasing with increasing values of. While, in the medium the components of stresses, and are increasing with increasing values of, put decreasing with increasing values of.

6.2. Effect of Rotation and Initial Magnetic Field in Fibre-Reinforced Isotropic Elastic Media

Figure 10 shows that the components of displacement in fibre-reinforced isotropic elastic media under effect of rotation, we find in tow medium and, all components of displacement are increasing with increasing values of the rotation.

Figure 11 shows that the components of displacement in fibre-reinforced anisotropic elastic media under effect of initial magnetic field, we find that in the medium the components of displacement and are decreasing and increasing with increasing values of initial magnetic field, put and are decreasing and increasing with increasing values of, respectively .

Figure 12 shows that the components of stresses in fibre-reinforced isotropic elastic media under effect of rotation, we find in tow medium and all components of stresses are increasing with increasing values of the rotation.

Figure 13 shows that the components of stresses in fibre-reinforced isotropic elastic media under effect of initial magnetic field, we find for the medium the components of stresses, , and are increasing with increasing values of initial magnetic field. While, for the medium the components of stresses increasing with increasing values of initial magnetic field, put, ans are decreasing with increasing values of values of.

Figure 14 shows that the displacements distribution with change values of rotation and complex frequency in fibre-reinforced isotropic elastic media, we find in tow medium and, all components of displacement are increasing with increasing values of.

Figure 15 shows that the displacements distribution with change values of initial magnetic field and complex frequency in fibre-reinforced isotropic elastic media, we find the components of displacement, and are decreasing with increasing values of the initial magnetic field, put increasing with increasing values of.

Figure 16 shows that stresses distribution with change values of rotation and complex frequency in fibre-reinforced isotropic elastic media, we find in tow medium and, all components of stresses are increasing with increasing values of the rotation.

Figure 17 shows that stresses distribution with change values of initial magnetic field and complex frequency in fibre-reinforced isotropic elastic media, we find in medium, all components of stresses are increasing with increasing values of, put in medium, and are increasing with increasing values of and and are decreasing with increasing values of.

7. Conclusions

In the light of the above analysis, the following conclusions may be made:

- Effects of rotation and initial magnetic field are cleared on the components of displacement and stresses;

- Effect of complex frequency is cleared on the components of displacement and stresses;

- There is a clear difference in the two cases, anisotropic and isotropic elastic media;

- Deformation of a body depends on the nature of the forces applied as well as the type of boundary conditions.

Cite this paper

F. S. Bayones, (2015) Effect of Rotation and Initial Magnetic Field in Fibre-Reinforced Anisotropic Elastic Media. Applied Mathematics,06,877-898. doi: 10.4236/am.2015.65081

References