Applied Mathematics
Vol.06 No.02(2015), Article ID:53895,13 pages
10.4236/am.2015.62033
Homotopy Approach to Fractional Quantum Hall Effect
Janusz Jacak, Patrycja Łydżba, Lucjan Jacak
Institute of Physics, Wroclaw University of Technology, Wrocław, Poland
Email: lucjan.jacak@pwr.edu.pl
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 January 2015; accepted 6 February 2015; published 10 February 2015
ABSTRACT
The topology-based explanation of the origin of the fractional quantum Hall effect is summarized. The cyclotron braid subgroups crucial for this approach are introduced in order to identify the origin of Laughlin correlations in 2D Hall systems. The so-called composite fermions are explained in terms of the homotopy cyclotron braids. Some new concept for fractional Chern insulator states is formulated in terms of the homotopy condition applied to the Berry field flux quantization.
Keywords:
Quantum Hall Effects, Braid Groups, Homotopy Methods

1. Introduction
Topology plays increasing role in the development of current understanding of fundamentals in physics [1] . The field theory employs homotopy methods, even the classical electro-magnetics by Maxwell is formulated in terms of topological defects for vector fields in 3D. The notion of the spin is also closely related with the topological concepts visible in related covering symmetry groups or in the odd manifestation of the time reversion for spin expressed by 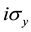 operator with the square −1 and not identity. The homotopy methods [2] [3] have found application in condensed matter structures with multicomponent phase parameters, as for superfluid He3 or for liquid crystals [4] . Recently, the strong increase of the interest in topological methods is related with so-called topological insulators [5] -[7] . The topological insight starts to be dominant in current understanding of Integer Quantum Hall Effect (IQHE) [8] and in rich applications of geometrical phase by Berry in various condensed matter problems [9] [10] . Application of the simple methods of the topological algebra in two dimensional spaces and also in locally two dimensional ones, like a sphere or torus, is linked with the exceptional richness of the topological structure for multiparticle planar systems which is expressed by the π1 group of the related configuration spaces, called the braid groups [11] . For the indistinguishable N-particle planar systems the braid groups are infinite in contrary to 3D systems where the full braid groups are finite permutation groups. The fundamental role of one dimensional unitary representations (1DURs) of the related full braid groups is noticeable in using of the path integrals by Feynman to determine statistics of quantum particles [12] . In the present paper we summarize the topological approach to Fractional Quantum Hall Effect (FQHE) via introduction of so-called cyclotron braid subgroups which help us in understanding of the Laughlin correlations specific for FQHE [13] [14] .
operator with the square −1 and not identity. The homotopy methods [2] [3] have found application in condensed matter structures with multicomponent phase parameters, as for superfluid He3 or for liquid crystals [4] . Recently, the strong increase of the interest in topological methods is related with so-called topological insulators [5] -[7] . The topological insight starts to be dominant in current understanding of Integer Quantum Hall Effect (IQHE) [8] and in rich applications of geometrical phase by Berry in various condensed matter problems [9] [10] . Application of the simple methods of the topological algebra in two dimensional spaces and also in locally two dimensional ones, like a sphere or torus, is linked with the exceptional richness of the topological structure for multiparticle planar systems which is expressed by the π1 group of the related configuration spaces, called the braid groups [11] . For the indistinguishable N-particle planar systems the braid groups are infinite in contrary to 3D systems where the full braid groups are finite permutation groups. The fundamental role of one dimensional unitary representations (1DURs) of the related full braid groups is noticeable in using of the path integrals by Feynman to determine statistics of quantum particles [12] . In the present paper we summarize the topological approach to Fractional Quantum Hall Effect (FQHE) via introduction of so-called cyclotron braid subgroups which help us in understanding of the Laughlin correlations specific for FQHE [13] [14] .
2. FQHE Revisted
Shortly after discovery of the integer quantum Hall effect (IQHE) in two dimensional electron system (2DEG) upon strong magnetic fields corresponding to complete fillings of succeeding Landau levels (LLs), the surprising observation of the fractional quantum Hall effect (FQHE) was reported at stronger magnetic fields resulting in the fractional fillings of the lowest Landau level (LLL). Both discoveries were awarded with Nobel prizes, with regard to IQHE for K. von Klitzing (1985) and to FQHE for D. Tsui, H. Störmer and R. Laughlin (1989). While IQHE can be understood within single particle approach including topology arguments [16] , the FQHE is a collective phenomenon regarded as a manifestation of strong interparticle correlations. The crucial prerequisite for FQHE is the flat band with quenched kinetic energy, as in the almost degenerated LLL in the presence of interaction (and massively degenerated without the interaction). Reducing of the kinetic energy allows for the subtle interaction effects resulting in the organization of correlated multiparticle states. The special role plays the very special 2D topology, what is convincingly supported by the absence of FQHE in 3D samples.
In order to describe correlations in 2D charged multi-particle systems in the presence of strong perpendicular
magnetic field corresponding to fractional LLL fillings  (q odd integer), the famous Laughlin wave-function
(q odd integer), the famous Laughlin wave-function
(LF) was introduced [16] . The representation of the Coulomb interaction of particles in terms of the so-called Haldane pseudopotential allowed then for an observation [17] -[19] that the LF describes exactly the ground state
for N charged 2D particles at the LLL filling , if one neglects the long-range part of the Coulomb forces. Di-
, if one neglects the long-range part of the Coulomb forces. Di-
vision of the interaction for the near- and long-range parts is expressed by the projection of the interaction onto the relative angular momenta of particle pairs and for chosen q the values of relative angular momenta greater than  correspond to the long-range tail of interaction, whereas lower than
correspond to the long-range tail of interaction, whereas lower than , to the near-range part of the field. It has been proved that the long-range part of the interaction only weekly influences the exact ground state given by LF for the near-range interaction only. The LF was a generalization of the Slater function for N noninteracting electrons completely filling LLL, written in this case in the form of the Vandermonde determinant multiplied by the Gaussian factor [20] . The LF has the same structure but with the Vandermonde determinant substituted by the Jastrow polynomial [16] ,
, to the near-range part of the field. It has been proved that the long-range part of the interaction only weekly influences the exact ground state given by LF for the near-range interaction only. The LF was a generalization of the Slater function for N noninteracting electrons completely filling LLL, written in this case in the form of the Vandermonde determinant multiplied by the Gaussian factor [20] . The LF has the same structure but with the Vandermonde determinant substituted by the Jastrow polynomial [16] ,
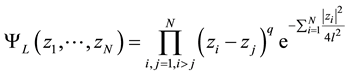 , (1)
, (1)
where,  is the complex representation of the position of i-th particle on a plane,
is the complex representation of the position of i-th particle on a plane,  is a
is a
“magnetic” distance scale (magnetic length). For 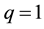 the above function is the Slater function with the Vandermonde determinant. This function (1) expresses correlations in the system, called Laughlin correlations. The main property is here the phase shift acquired by the LF if two particles interchange on the plane. This phase shift is qπ for interchange of two neighboring particles, which differentiates Laughlin correlations from ordinary fermion correlations corresponding to the phase shift π when these particles interchange. Note that a simple permutation of indices coincides with algebraic properties of the multi-argument wave function and corresponds to the fact, that in 3D (and in higher dimensions) the full braid group is the permutation group. For 2D manifolds association of the algebraic properties of multi-argument functions with exchanges of particles described by these functions may be misleading and exchanges of function arguments must be referred as to the braid group distinct than the permutation group. The unitary factor
the above function is the Slater function with the Vandermonde determinant. This function (1) expresses correlations in the system, called Laughlin correlations. The main property is here the phase shift acquired by the LF if two particles interchange on the plane. This phase shift is qπ for interchange of two neighboring particles, which differentiates Laughlin correlations from ordinary fermion correlations corresponding to the phase shift π when these particles interchange. Note that a simple permutation of indices coincides with algebraic properties of the multi-argument wave function and corresponds to the fact, that in 3D (and in higher dimensions) the full braid group is the permutation group. For 2D manifolds association of the algebraic properties of multi-argument functions with exchanges of particles described by these functions may be misleading and exchanges of function arguments must be referred as to the braid group distinct than the permutation group. The unitary factor 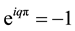 equals, however, to
equals, however, to 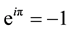 and this property does not allow for distinguishing of Laughlin correlated particles from the ordinary fermions though they are distinguished with the phase shift. This coincidence of exponential factors masks to some extent the topological difference between 2D and 3D and lies in foundations of using simplified and confusing analogies from 3D case to 2D one. Of that type is an assertion that the particles creating the correlated Laughlin state can be modeled as ordinary electrons dressed with the Coulomb interaction in analogy to quasiparticles common in solids [21] . Along this line the Laughlin correlations were modeled by so-called composite fermions (CFs) [22] , i.e., by electrons dressed with quantized magnetic field flux-tubes attached to particles as the result of the Coulomb interaction. By virtue of the Aharonov-Bohm effect, these flux-tubes, of
and this property does not allow for distinguishing of Laughlin correlated particles from the ordinary fermions though they are distinguished with the phase shift. This coincidence of exponential factors masks to some extent the topological difference between 2D and 3D and lies in foundations of using simplified and confusing analogies from 3D case to 2D one. Of that type is an assertion that the particles creating the correlated Laughlin state can be modeled as ordinary electrons dressed with the Coulomb interaction in analogy to quasiparticles common in solids [21] . Along this line the Laughlin correlations were modeled by so-called composite fermions (CFs) [22] , i.e., by electrons dressed with quantized magnetic field flux-tubes attached to particles as the result of the Coulomb interaction. By virtue of the Aharonov-Bohm effect, these flux-tubes, of 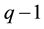 flux quanta each, attached to particles produce the required by the LF phase shift when the composite particles interchange. The advantage of the CF construction was recognized in possibility of interpretation of the FQHE in an external magnetic field as IQHE in resultant field diminished by the averaged field of the auxiliary field flux-tubes [22] . However, neither the origin of the auxiliary magnetic field nor the mechanism of fixing flux-tubes to particles were not explained and the assertion that magnetic flux tubes are result of the Coulomb interaction was not demonstrated. Moreover the hierarchy of LLL fractional fillings obtained by mapping of FQHE on IGHE in resultant magnetic field does not cover all fractional states, cf. Figure 1.
flux quanta each, attached to particles produce the required by the LF phase shift when the composite particles interchange. The advantage of the CF construction was recognized in possibility of interpretation of the FQHE in an external magnetic field as IQHE in resultant field diminished by the averaged field of the auxiliary field flux-tubes [22] . However, neither the origin of the auxiliary magnetic field nor the mechanism of fixing flux-tubes to particles were not explained and the assertion that magnetic flux tubes are result of the Coulomb interaction was not demonstrated. Moreover the hierarchy of LLL fractional fillings obtained by mapping of FQHE on IGHE in resultant magnetic field does not cover all fractional states, cf. Figure 1.
The role of topology in creation of the strongly correlated state of FQHE was noticed [23] -[25] in the context of exceptional topological properties of 2D plane or of locally 2D manifolds like sphere or torus. This special topology of planar systems is linked with the exceptionally rich structure of the braid groups for 2D manifolds (R2, or sphere and torus) in comparison to braid groups for higher dimensional spaces (Rd, d > 2) [11] . The full braid group is defined as π1 homotopy group of the configuration space for N indistinguishable particles, i.e., the group of multi-particle closed trajectory classes, disjoint and topologically nonequivalent (trajectories from various classes cannot be continuously deformed one into another one). The full braid group is infinite for 2D case while this group is finite (and equal to the ordinary permutation group SN) in higher dimensions of the manifold on which particles can be located [11] . This property makes two dimensional systems exceptional in geometry- topology sense which inherently lies in foundations of FQHE.
For matching the topological properties with quantum system properties, the quantization according to the Feynman path integral method is useful [12] [23] [24] . Due to a fundamental ideas of path integral quantization in the case of not simply-connected configuration spaces (distinguished by the nontrivial π1 groups), like for the multi-particle systems, additional phase factors―the weights of nonequivalent (nonhomotopic) trajectory classes and summation over these classes must be included in the path integral definition. It means that a measure in the trajectory space is distributed over separated disjoint homotopy classes of π1 because in general this measure cannot be defined uniformly over the domain consisting of disjoint pieces owing to the continuity requirements. As it was proved [12] , these weight factors form a one-dimensional unitary representation (1DUR) of the related braid group. Different 1DURs of the full braid group give rise to distinct types of quantum particles corresponding to the same classical ones. In this manner one can get fermions and bosons corresponding
Figure 1. FQHE features in a quantum well GaAs/AlGaAs with electron density of 1011 1/cm−2; Rxx for 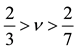 at the temperature equal T ~ 35 mK (after Ref. [15] ); the fractions outside the standard CF hierarchy are indicated in color.
at the temperature equal T ~ 35 mK (after Ref. [15] ); the fractions outside the standard CF hierarchy are indicated in color.
to only possible 1DURs of the permutation group SN, 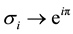 and
and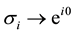 , respectively (the permutation group SN is the full braid group in 3D and in higher dimensions,
, respectively (the permutation group SN is the full braid group in 3D and in higher dimensions, 




We will develop the topological approach to Hall systems and recover Laughlin correlations by employing geometry properties of the so-called cyclotron braids [13] [14] in the framework of formal braid group approach and without invoking to any auxiliary elements inherent to the CF concepts. We will demonstrate that particles with statistics properties familiar in the CF model are 2D quantum particles characterized by appropriate 1DURs of the cyclotron braid subgroups.
3. Too-Short for Interchanges Cyclotron Trajectories in FQHE
3.1. 2D Full Braid Group without Magnetic Field―Anyons
One-dimensional unitary representations (1DURs) of the full braid group [11] , i.e., of π1 homotopy group of the configuration space for indistinguishable N particles define weights for the path integral summation over trajectories [12] [24] . All trajectories fall into separated homotopy classes that are distinguished by non-equivalent closed loops (from π1) attached to open trajectories 



where π1 stands for the full braid group and the index l enumerates π1 group elements, 






Nevertheless, it is impossible to relate CFs with the 1DURs of the full braid group in 2D, because 1DURs are periodic with a period of 2π, whereas the CFs require the statistics phase shift qπ, q-odd integer. In order to solve this problem, we propose to associate CFs with the appropriately constructed braid subgroups instead of the full braid group and in this way to distinguish CFs from the ordinary fermions.
Figure 2. The geometrical presentation of the generator 


3.2. Cyclotron Structure of Braid Group in 2D Charged Systems at Strong Magnetic Field Presence
The full braid group contains all accessible closed multi-particle classical trajectories, i.e., braids (with initial and final orderings of particles that may differ by permutation as is admitted for indistinguishable particles). One can, however, notice that inclusion of a strong magnetic field may substantially change trajectories―a classical cyclotron motion may confine a variety of accessible braids if magnetic field is strong enough and the manifold is two-dimensional. When the separation of particles is greater than twice the cyclotron radius, which situation occurs at fractional LLL fillings, the exchanges of particles along single-looped cyclotron trajectories are precluded, because the cyclotron orbits are too short for particle interchanges in this case. Interaction cannot enhance cyclotron orbit size in the uniform multiparticle system.
Particles must, however, interchange in the braid picture for the reason of defining the statistics and creation of the collective correlated state. Therefore, in order to allow exchanges again, the cyclotron radius must somehow be enhanced. This can be achieved by screening the external field, like in the construction of the CFs with flux tubes oppositely oriented with respect to the external field [22] . We suppose that the natural way to enhance the range of cyclotronic movement is to exclude inaccessible braids from the full braid group. We will show that remaining braids would be sufficiently large in size for particle exchanges realization [13] [14] . We will demonstrate below that at high magnetic fields in 2D charged N-particle systems, the multi-looped braids allow for the effective enlargement of cyclotron orbits, thus restoring particle exchanges in a natural way.
4. Cyclotron Braid Subgroups―Restitution of Particle Interchanges in 2D
The multi-looped braids form the cyclotron braid subgroups which are generated by the following generators:

where each q corresponds to a different type of the cyclotron subgroup and 
braid group. The group element 
loops, which is clear by virtue of the definition of the single interchange 
Figure 3. The generator σi of the full braid group and the corresponding relative trajectory of the ith and (i + 1)th particles exchange (upper); the generator of the cyclotron braid subgroup, 

deals with elementary particle exchange braid with one additional loop). It is clear that 

The 1DURs of the full group confined to the cyclotron subgroup (they do not depend on i as 1DURs of the full braid group do not depend on i by virtue of the 



where q is an odd integer and



In agreement with the general rules of quantization [25] , the N-particle wave function must transform according to the 1DUR of an appropriate element of the braid group, when the particles traverse, in classical terms, a closed loop in the configuration space corresponding to this particular braid element. In this way the wave function acquires an appropriate phase shift due to particle interchanges (i.e., due to exchanges of its positions as arguments of the wave function, according to the prescription given by braids in 2D configuration space). Using 1DURs as given by (4), the Aharonov-Bohm phase of CFs fictitious fluxes is replaced by the contribution of additional loops (each loop adds 2π to the total phase shift, if one considers 1DUR with 



Each additional loop of a relative trajectory for the particle pair interchange (as defined by the generators
ries, one can conclude only about the number, 




of a cyclotron braid corresponding to particle interchange, results in two additional flux quanta piercing the individual particle cyclotron trajectories. This rule follows immediately from the definition of the cyclotron trajectory, which must be a closed individual particle trajectory related to a double interchange of the particle pair (cf. Figure 5). In this way, the cyclotron trajectories of both interchanging particles are closed, just like the closed relative trajectory for the double interchange (the braid trajectory for the elementary exchange of the indistinguishable particles is open in the geometrical presentation, and therefore the double interchange is needed to close this trajectory in this presentation). If the interchange is simple, i.e., without any additional loops, the corresponding individual particle cyclotron trajectories are also simple, i.e., single-looped. Nevertheless, when the interchange of particles is multi-looped, as associated with the q-type cyclotron subgroup
double interchange relative trajectory has 
In 2D additional loops cannot enhance the total surface of the system. In this regard, it is important to emphasize the basic difference between the circumvolutions of a 3D winding (e.g., of a wire) and of multi-looped 2D cyclotron trajectories. 2D multi-looped trajectories do not enhance the surface of the system and therefore do
Figure 4. Half of the individual particle cyclotron trajectories of the ith and (i + 1)th particles (top) and the corresponding relative trajectories (bottom) for interchanges of the ith and (i + 1)th 2D-particles under a strong magnetic field, for 

Figure 5. Cyclotron trajectories of individual particles must be closed, therefore they correspond to double exchange braids, for both, simple exchanges (upper) and exchanges with additional loops (lower), in the right part, quantization of flux per particle, for 

not enhance the total magnetic field flux BS piercing the system, in opposition to 3D case. In 3D case, each circumvolution of the winding adds a new portion of the flux, just as a new circumvolution adds a new surface, which is, however, impossible in 2D. Thus in 2D all loops must share the same total flux, which results in diminishing flux-portion per a single loop and, effectively, in longer cyclotron radius (allowing again particle interchanges).
The additional loops in 2D take away the flux-portions (equal to 

multaneously diminishing the effective field; this gives an explanation for Jain’s auxiliary fluxes screening the external field B. Thus, it is clear that the CFs are actually not compositions of particles with flux-tubes, but are rightful particles in 2D corresponding to 1DURs of the cyclotron subgroups instead of the full braid group, which is unavoidably forced by too short ordinary single-looped cyclotron trajectories. The original name “composite fermions” can be, however, still used for history reason. Moreover, one can use a similar name, “composite anyons”, for particles associated with fractional 1DURs (i.e., with fractional
How Additional Loops Enhance the Cyclotron Radius in 2D Hall System
It is important to emphasize that braid group approach in terms of trajectories does not describe detailed classical trajectories of particles in the system but only determines classes of trajectories which are available upon topological constraints. Thus, if one considers physical factors which restrict availability of particular classes of trajectories (e.g., specific topology of configuration space of N particles system located on specified manifold), one should describe a condition upon which one can determine whether a specific trajectory class is possible or not. In the case of N particles system on 2D plane in the presence of a perpendicular strong magnetic field such a condition can be based on the cyclotron radius. Although cyclotron radius is properly defined for free particles one can still consider some kind of focusing of charged particle motion on the cyclotron radius scale even in the presence of interaction, especially in homogeneous planar system with isotropic interaction. One can also observe that for noninteracting fermions we have in the case of completely filled LLL exactly one external field
flux quantum 
Here must be emphasized that in the case of the degenerated LLL all particles have the same cyclotron radius. Even though the velocity is not well determined in the LLL (their coordinates do not commute as the operators), all particles have, however, the same kinetic energy, thus all particles have the same averaged velocity and the same cyclotron radius. In order to determine whether a trajectory class is available for particles in the system can be brought to comparison of cyclotron orbit size with distance between particles, which for homogeneous system is defined from density and blocked by Coulomb repulsion preventing approaching one particle onto another one. The distance between particles in homogeneous system is protected by the short-range part of the Coulomb interaction. Thus potentially available trajectory must ensure reaching neighboring particles, i.e., the trajectory must fit to the minimal distance between particles. The rigorous requirement to keep minimal distance intact leads to the observation that in too strong magnetic field (when the cyclotron radius is smaller than half of the minimal distance) some trajectory classes are unavailable for particles―as shown in Figure 6.
In 2D charged system in the presence of the perpendicular magnetic field only cyclotron trajectories are available for particles. Thus if one increases the magnetic field magnitude then the cyclotron radius will decrease causing the trajectory of particles exchange impossible. The simplest exchange was the implementation
Figure 6. Schematic presentation of effective growth of cyclotron radius in 2D case for multi-looped cyclotron trajectory in comparison to single-looped trajectory (length A − B means uniform separation between particles in the system).
of the generators of the full braid group and now they cannot be defined. If one excludes unavailable trajectories too short for exchanges, the rest of the full braid group occurs a subgroup generated by new generators describing in 2D multi-looped braids and corresponding to multi-looped cyclotron trajectories. These multi-looped cyclotron trajectories have the larger effective size allowing to match neighboring particles at strong magnetic field presence. This subgroup we call cyclotron braid group (or subgroup).
The exchange trajectories of neighboring particles―the generators of braid group―are open trajectories i the geometrical presentation (in fact for indistinguishable particles the initial and final particle ordering are bound despite remunerations, but for geometrical presentation of braid group some selected, arbitrary ordering of particles is assumed). Nevertheless, the cyclotron trajectories are closed trajectories despite the enumeration of particles (only for closed trajectories one can define the piercing flux of the magnetic field). Thus, one must consider closed cyclotron trajectories. The smallest closed trajectory is a double exchange (two semicircles create closed circle in the simplest case of single-looped exchanges). If now one considers multi-looped exchanges (for









Those multi-looped closed trajectories in case of 2D have enhanced effective cyclotron radius which allows particles to exchange and to define the statistics. Each additional loop cannot add any new surface in 2D space. For e.g., 



The Coulomb interaction plays a central role in the collective state with Laughlin correlations [17] -[19] protecting the uniform equidistant distribution of particles. Nevertheless, in 2D systems upon the quantized magnetic field, the interaction of charges cannot be accounted for in a manner of the standard dressing of particles with the interaction as it was typical for quasiparticles in solids, because in 2D Hall regime this interaction does not have a continuous spectrum with respect to particle separation expressed by relative angular momentum projection [17] [18] . This non-continuous character of the interaction contribution in 2D charged systems upon sufficiently strong magnetic fields precludes the continuity of the mass operator which prevents the quasiparticle definition (as a pole of the retarded single-particle Green function).
5. Topological Chern Insulators
Investigation of IQHE and then of FQHE in 2D charged systems opened a broad area of topologically conditioned effects [26] . Especially deeply developed with this regard is the present understanding of IQHE treated in single-particle and topological terms [7] . This is based on the observation that the IQHE states protected by Landau quantization gaps are not connected with symmetry breaking as many other condensed matter phases in scenario of ordinary phase transitions, but rather with some topological invariants associated to a particular geometry and matter organization [6] [27] . These invariants are better and better recognized currently in terms of homotopy groups related to specially defined multidimensional transformations of physically conditioned objects like Green functions and their derivatives [28] [29] , previously developed for description of topology of textures in multicomponent condensed matter states with rich matrix order parameter, including superfluid He3 or liquid crystals [4] . The role of various factors protecting gaps separating flat bands (almost degenerated, as LLs at the interaction presence, and massively degenerated in the absence of the interaction) are of particular interest in view of the role of the magnetic field breaking time reversion or other effects like spin-orbit interaction or special type (time-reversion breaking) traversing around the closed loop inside an elementary cell with complex hopping constants. Generalization of the familiar in mathematics Chern invariants [5] is developed in order to grasp the essential topology of various multiparticle structures [5] -[7] . The mappings of the Brillouin zone into the state related objects can be in that manner classified by disjoint classes corresponding to topologically nonequivalent band organizations protected by energy gaps conditioned by various physical factors and leading to distinct incompressible states in analogy to their prototype in the form of IQHE. The distinctive character of 2D space is linked in the latter case with the magnetic field flux quantization.
Topological notions allow for definition of a new state of crystal called topological insulator. Despite of the local similarity between the gapped states of the ordinary and the topological insulator, the global arrangement of the band, noticeable only non-locally (on the Brillouin zone as a whole), induces different overall behavior of the system. In the case of topological insulator one deals with insulating state inside the sample, whereas with conducting non-dissipative state on the sample edge, protected topologically, what is, however, no case for ordinary insulating state. This surprising phenomenon was confirmed experimentally, which was a strong stimulus to the rapid and enormous great growth of the interest.
The topological insulators from point of view of band organization must be characterized by flat bands which meet in summits of locally cone shaped valleys resembling Dirac points in graphene. These Dirac points changes the topology and allow Chern-type invariant to attain nonzero value, indicating the emergence of the different global state. Spin degrees of freedom are of high significance with regard to topological arrangement and related spin-type topological insulators are referred as to spin IQHE.
Commonly accepted definition of the topological insulator emphasizes the robust metallic character of the edge or surface states and extended bulk insulating states that are also robust against disorder. This is an extraordinary behavior, especially in two-dimensional models―when an edge or a surface is cut in a sample of topological insulator, the emerging edge states seem to be connected to these bulk states. The edge states can be viewed as these extended bulk states terminating at the boundary. For this reason, the bulk and the edge properties of the topological insulators are equally important and mutually dependent. This is the development of the interpretation of IQHE revealed a spectacular emergence of non-dissipative charge currents flowing around the edges of any finite IQHE sample. The IQHE was observed only in the presence of an externally applied magnetic field.
In 1988 Haldane presented a model of a condensed matter phase that exhibits IQHE without the need of a macroscopic magnetic field [30] . The general idea of this effect can be sketched by writing a model Hamiltonian, for the system of spinless particles occupying a honeycomb-type planar lattice with one state 

where 



The difference between a quantum Hall state and an ordinary insulator is a matter of topology [8] . A 2D band structure consists of a mapping from the momentum k defined on a torus of the Brillouin zone to the Bloch Hamiltonian



Figure 7. The honeycomb structure (similar as in graphene) for the Haldane model [30] ; e1, e2 are Bravais lattice vectors, nonequivalent site positions in the unit cell are indicated by

C is integer for reasons analogous to the quantization of the Dirac magnetic monopole. The Chern number, C, is a topological invariant in the sense that it cannot change when the Hamiltonian varies smoothly and this explains the quantization of conductivity in IQHE [8] . Helpful would be here a simple analogy. Rather than maps from the Brillouin zone to a Hilbert space, one can consider maps from two to three dimensions, which describe surfaces. 2D surfaces can be topologically classified by their genus g, which counts the number of holes. For instance, a sphere has g = 0, while a torus has g = 1. A theorem in mathematics states that the integral of the Gaussian curvature over a closed surface is a quantized topological invariant, and its value is related to g. The Chern number is an integral of a related curvature.
Change of the Chern number requires closing the insulating gap. This happens for the Hamiltonian (5) in the Dirac-like points when the locally cone shaped valleys of conduction and valence bands touch together. This allows for the change of the Chern number and for the metallic boundary states protected by still insulating phase inside the sample [6] [7] .
The systems that behave like the one described by Haldane are now called Chern insulators. The time reversal symmetry in these systems is broken like in the IQHE, but it is broken by the presence of a net magnetic moment in each unit cell rather than by an external magnetic field, as it was the case for IQHE. The Chern insulators were never found experimentally as of yet.
Fractional Chern Insulators
Recently grew up a new field related to IQHE and its fractional version, namely Chern insulators and fractional Chern insulators, respectively. There is linked with development of Haldane model of IQHE effect without Landau levels, but with time-braking imaginary part of hopping factors for carries on planar lattice instead of the external magnetic field. The quantization of carrier orbit along elementary cell is given in this case by the quantization of the Berry field flux which can be expressed by the Chern numbers. Even though neither Chern insulator nor its fractional state is not observed experimentally, the theoretical studies are currently extensively developing [31] [32] . From exact diagonalization of corresponding Hamiltonians, provided they give sufficiently flat bends, it follows that the interaction causes collective state analogous to FQHE, though without any magnetic field and with the dynamics assigned by nontrivial Chern number. What is especially challenging, the frac-
tional Chern insulator is predicted for fractional (
gously to ordinary FQHE. Again arises a question of how single particle trajectories ranged by Berry field flux quantization to the elementary cell can match every third cell (for 1/3 filling). The concept of CFs with auxiliary field flux-tubes is not useful here, due to absence of the magnetic field. The trajectories must be, however, enlarged somehow to allow organization of the collective state with the determined statistics via particle interchanges.
Again here the multi-looped braid subgroup might be the solution of the problem with too short orbits, especially in this case which is without any other conceptual competition (composite fermions are associated with magnetic field flux tubes, but here no magnetic field presents). This supports the topological attitude to fractional correlated 2D states which is robust against details of quantized field flux and explains the occurrence of such states only at specific fractions for fillings, surprisingly coinciding for FQHE and for fractional Chern insulators.
To be more specific with this regard, the recent analyzes of FQHE in model systems without Landau levels [33] [34] are worth emphasizing also. In the paper [33] there is constructed a class of model Hamiltonians on 2D lattice which give nearly-flat bands with nontrivial topology. This property is regarded as a required prerequisite for organization of FQHE-like states when interaction would be next included. For flat band the kinetic energy is frozen which allows the interaction to dominate and create strongly correlated state of FQHE type. This has been theoretically verified in the paper [34] for a checkerboard lattice including nearest and next-nearest interaction in model Hamiltonian of the form,

where H0 is a two-band checkerboard lattice model with nonzero Chern number implemented by complex hopping factors of the type,

and H1 describes ordinary real-number-assigned hopping between next and next-next nearest neighbors [33] . Some attributes characteristic for FQHE have been indicated within this model for fractional fillings 1/3 and 1/5 (in the latter case repulsion V was required above a certain threshold value, unless U enhances strongly) [34] . This observation supports an idea of multi-looped structure of quasiclassical wave packets which in this way can reach equidistantly separated 2D particles (in every third cell for
6. Conclusions
By means of braid group approach it is possible to select appropriate braid subgroups of the full braid group of which one dimensional unitary representations (1DURs) define effective particles in the correlated states referred to FQHE. The argumentation is linked with the simple observation that at fractional fillings of the LLL the cyclotron trajectories which build braids in equidistantly distributed 2D charged system are too short in comparison to particle separation when the magnetic field is sufficiently strong. This precludes particle exchanges which is, however, necessary for organization of the collective multiparticle state with the determined statistics according to 1DURs of related braid group. One can observe that only at these filling fractions at which FQHE occurs the multi-looped braid structure recover exchanges along enhanced cyclotron trajectories. This enhancement is an exclusive property of 2D system when additional loops of cyclotron trajectory cannot add a surface (oppositely to 3D multi-looped trajectory), but must share the same total external magnetic field flux, which leads to effective enlargement of cyclotron orbits. For 
Acknowledgements
The support from the NCN Project UMO-2011/02/A/ST3/00116 is acknowledged.
References
- Ryder, L.H. (1996) Quantum Field Theory. 2nd Edition, Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511813900
- Spanier, E. (1966) Algebraic Topology. Springer-Verlag, Berlin.
- Hatcher, A. (2002) Algebraic Topology. Cambridge University Press, Cambridge.
- Mermin, N. (1979) The Topological Theory of Defects in Ordered Media. Reviews of Modern Physics, 51, 591. http://dx.doi.org/10.1103/RevModPhys.51.591
- Prodan, E. (2011) Disordered Topological Insulators: A Non-Commutative Geometry Perspective. Journal of Physics A: Mathematical and Theoretical, 44, Article ID: 113001. http://dx.doi.org/10.1088/1751-8113/44/11/113001
- Hasan, M.Z. and Kane, C.L. (2010) Colloquium: Topological Insulators. Reviews of Modern Physics, 82, 3045-3067.
- Qi, X.L. and Zhang, S.C. (2011) Topological Insulators and Superconductors. Reviews of Modern Physics, 83, 1057. http://dx.doi.org/10.1103/RevModPhys.83.1057
- Thouless, D.J., Kohmoto, M., Nightingale, M.P. and den Nijs, M. (1982) Quantized Hall Conductance in a Two- Dimensional Periodic Potential. Physical Review Letters, 49, 405. http://dx.doi.org/10.1103/PhysRevLett.49.405
- Berry, M.V. (1984) Quantal Phase Factors Accompanying Adiabatic Changes. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 392, 45-57.
- Nakahara, M. (1990) Geometry, Topology and Physics. Adam Hilger, Bristol.
- Birman, J.S. (1974) Braids, Links and Mapping Class Groups. Princeton University Press, Princeton.
- Laidlaw, M.G. and DeWitt, C.M. (1971) Feynman Functional Integrals for Systems of Indistinguishable Particles. Physical Review D, 3, 1375-1378. http://dx.doi.org/10.1103/PhysRevD.3.1375
- Jacak, J., Jóźwiak, I. and Jacak, L. (2009) New Implementation of Composite Fermions in Terms of Subgroups of a Braid Group. Physics Letters A, 374, 346-350. http://dx.doi.org/10.1016/j.physleta.2009.10.075
- Jacak, J., Jóźwiak, I., Jacak, L. and Wieczorek, K. (2010) Cyclotron Braid Group Structure for Composite Fermions. Journal of Physics: Condensed Matter, 22, Article ID: 355602. http://dx.doi.org/10.1088/0953-8984/22/35/355602
- Pan, W., Störmer, H.L., Tsui, D.C., Pfeiffer, L.N., Baldwin, K.W. and West, K.W. (2003) Fractional Quantum Hall Effect of Composite Fermions. Physical Review Letters, 90, Article ID: 016801. http://dx.doi.org/10.1103/PhysRevLett.90.016801
- Laughlin, R.B. (1983) Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations. Physical Review Letters, 50, 1395-1398. http://dx.doi.org/10.1103/PhysRevLett.50.1395
- Haldane, F.D.M. (1983) Fractional Quantization of the Hall Effect: A Hierarchy of Incompressible Quantum Fluid States. Physical Review Letters, 51, 605-608. http://dx.doi.org/10.1103/PhysRevLett.51.605
- Prange, R.E. and Girvin, S.M. (1990) The Quantum Hall Effect. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-3350-3
- Laughlin, R.B. (1983) Quantized Motion of Three Two-Dimensional Electrons in a Strong Magnetic Field. Physical Review B, 27, 3383-3389. http://dx.doi.org/10.1103/PhysRevB.27.3383
- Landau, L.D. and Lifshitz, E.M. (1972) Quantum Mechanics: Non-Relativistic Theory. Nauka, Moscow.
- Abrikosov, A.A., Gorkov, L.P. and Dzialoshinskii, I.E. (1975) Methods of Quantum Field Theory in Statistical Physics. Dover Publications Inc., Dover.
- Jain, J.K. (1989) Composite-Fermion Approach for the Fractional Quantum Hall Effect. Physical Review Letters, 63, 199-202. http://dx.doi.org/10.1103/PhysRevLett.63.199
- Wilczek, F. (1990) Fractional Statistics and Anyon Superconductivity. World Scientific, Singapore City. http://dx.doi.org/10.1142/0961
- Wu, Y.S. (1984) General Theory for Quantum Statistics in Two Dimensions. Physical Review Letters, 52, 2103-2106. http://dx.doi.org/10.1103/PhysRevLett.52.2103
- Sudarshan, E.C.G., Imbo, T.D. and Govindarajan, T.R. (1988) Configuration Space Topology and Quantum Internal Symmetries. Physics Letters B, 213, 471-476. http://dx.doi.org/10.1016/0370-2693(88)91294-4
- Avron, J.E., Osadchy, D. and Seiler, R. (2003) A Topological Look at the Quantum Hall Effect. Physics Today, 56, 38- 42.
- Qi, X.L. and Zhang, S.C. (2010) The Quantum Spin Hall Effect and Topological Insulators. arXiv:1001.1602v1 [cond-mat.mtrl-sci]
- Wang, Z., Qi, X.L. and Zhang, S.C. (2010) Topological Order Parameters for Interacting Topological Insulators. Physical Review Letters, 105, Article ID: 256803. http://dx.doi.org/10.1103/PhysRevLett.105.256803
- Qi, X.L. (2011) Generic Wave-Function Description of Fractional Quantum Anomalous Hall States and Fractional Topological Insulators. Physical Review Letters, 107, Article ID: 126803. http://dx.doi.org/10.1103/PhysRevLett.107.126803
- Haldane, F.D.M. (1988) Model of Quantum Hall Effect without Landau Levels: Condensed Matter Realization of the “Parity Anomaly”. Physical Review Letters, 61, 2015-2018. http://dx.doi.org/10.1103/PhysRevLett.61.2015
- Kourtis, S., Venderbos, J.W.F. and Daghofer, M. (2012) Fractional Chern Insulator on a Triangular Lattice of Strongly Correlated t2g Electrons. Physical Review B, 86, Article ID: 235118. http://dx.doi.org/10.1103/PhysRevB.86.235118
- Parameswaran, S.A., Roy, R. and Sondhi, S.L. (2013) Fractional Quantum Hall Physics in Topological Flat Bands. Comptes Rendus Physique, 14, 816-839. http://dx.doi.org/10.1016/j.crhy.2013.04.003
- Sun, K., Gu, Z., Katsura, H. and Das Sarma, S. (2011) Nearly Flatbands with Nontrivial Topology. Physical Review Letters, 106, Article ID: 236803. http://dx.doi.org/10.1103/PhysRevLett.106.236803
- Sheng, D.N., Gu, Z.C., Sun, K. and Sheng, L. (2011) Fractional Quantum Hall Effect in the Absence of Landau Levels. arXiv:1102.2658v1 [cond-mat.str-el]









