Applied Mathematics
Vol.06 No.01(2015), Article ID:53104,7 pages
10.4236/am.2015.61013
Evaluation of Kinetic Properties of Dendritic Potassium Current in Ghostbursting Model of Electrosensory Neurons
Takaaki Shirahata
Kagawa School of Pharmaceutical Sciences, Tokushima Bunri University, Sanuki, Japan
Email: tshi@kph.bunri-u.ac.jp
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 October 2014; revised 20 November 2014; accepted 10 December 2014
ABSTRACT
A ghostbursting model is a mathematical model (a system of coupled nonlinear ordinary differential equations) that is based on the Hodgkin-Huxley formalism. The ghostbursting model describes bursting similar to the in vitro bursting of electrosensory neurons of weakly electric fish. Doiron and coworkers have focused on two system parameters of the model: maximal conductance of the dendritic potassium current 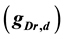 and the current injected into the somatic compartment
and the current injected into the somatic compartment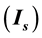 . They performed bifurcation analysis and revealed that the
. They performed bifurcation analysis and revealed that the 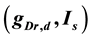 -parameter space was divided into three dynamical states: quiescence, periodic tonic spiking, and bursting. The present study focused on a third system parameter: the time constant of dendritic potassium current inactivation
-parameter space was divided into three dynamical states: quiescence, periodic tonic spiking, and bursting. The present study focused on a third system parameter: the time constant of dendritic potassium current inactivation . A computer simulation of the model revealed how the dynamical states of the
. A computer simulation of the model revealed how the dynamical states of the 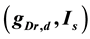 -parameter space changed in response to variations of
-parameter space changed in response to variations of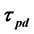 .
.
Keywords:
Mathematical Model, Bifurcation, Ghostbursting, Time Constant

1. Introduction
Hodgkin and Huxley [1] proposed a mathematical model that is composed of a system of four-coupled nonlinear ordinary differential equations (page 518 in [1] ) and that describes the action potential regeneration of the squid giant axon and the biophysical mechanisms underlying the action potential generation. Various types of mathematical models describing the electrical excitability of neurons and endocrine cells have been developed on the basis of the concepts proposed by Hodgkin and Huxley [1] , and analyses of these models, including the RPeD1 neuron model in [2] , various bursting models in Chapter 5 of [3] , and pituitary lactotroph bursting model in [4] , are important research areas in the field of applied mathematics. The concepts proposed by Hodgkin and Huxley [1] are also important in the fields of theoretical physics [5] and mathematical physics [6] . The Hodgkin-Huxley model is also used in drug-disease modeling (see Chapter 5.2.2 in [7] ).
A ghostbursting model [8] , which is a mathematical model based on the concepts proposed by Hodgkin and Huxley [1] , describes a system of six-coupled nonlinear ordinary differential equations [see Equations (1) to (6) in Section 2]. This model exhibits bursting similar to that observed in in vitro recordings of pyramidal cells in the electrosensory lateral line lobe (ELL) of the weakly electric fish Apteronotus leptorhynchus. This model consists of two compartments: the somatic compartment [see Equations (1) and (2) in Section 2] and the dendritic compartment [see Equations (3) to (6) in Section 2]. Doiron et al. have focused on two system parameters of the model: maximal conductance of the delayed-rectifying potassium current in the dendritic compartment 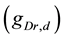 [see Equation (3)] and the current injected into the somatic compartment
[see Equation (3)] and the current injected into the somatic compartment 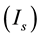 [see Equation (1)]. They performed
[see Equation (1)]. They performed 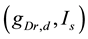 -parameter bifurcation analysis of the model (see Figure 6 in [8] ). This figure indicates that the organizing center of the
-parameter bifurcation analysis of the model (see Figure 6 in [8] ). This figure indicates that the organizing center of the 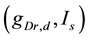 -parameter bifurcation diagram is a codimension-two bifurcation point and that unfolding the codimension-two bifurcation point yields two types of bifurcation manifolds: a curve for a saddle-node bifurcation of fixed points (SNFP curve) and a curve for a saddle-node bifurcation of limit cycles (SNLC curve). The SNFP and SNLC curves divide the
-parameter bifurcation diagram is a codimension-two bifurcation point and that unfolding the codimension-two bifurcation point yields two types of bifurcation manifolds: a curve for a saddle-node bifurcation of fixed points (SNFP curve) and a curve for a saddle-node bifurcation of limit cycles (SNLC curve). The SNFP and SNLC curves divide the 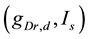 -parameter space into three dynamical states: quiescence, periodic tonic spiking, and bursting. When crossing the SNFP curve with an increase in
-parameter space into three dynamical states: quiescence, periodic tonic spiking, and bursting. When crossing the SNFP curve with an increase in 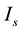 under a condition in which
under a condition in which  is fixed to a certain value smaller than the
is fixed to a certain value smaller than the 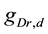 value at the codimension-two bifurcation point, the dynamical state changes from quiescence to bursting. When crossing the SNFP curve with an increase in
value at the codimension-two bifurcation point, the dynamical state changes from quiescence to bursting. When crossing the SNFP curve with an increase in  under a condition in which
under a condition in which  is fixed to a certain value larger than the
is fixed to a certain value larger than the 

Vo et al. have indicated that it is important to investigate the kinetic properties of ionic conductance for understanding the dynamics of pituitary cell models [10] . In other words, variations in the time constant values of ionic conductance can change the dynamical states of the cell model (Figure 4 in [10] ). Doiron et al. have also suggested that the appropriate setting of the time constant value in dendritic potassium current inactivation is important for bursting dynamics (see the last paragraph of Section 3.3 in [8] ). However, how variations in the time constant values affect the 

2. Materials and Methods
The ghostbursting model [Equations (1)-(6)] contains the following six state variables: the somatic membrane potential











where the definitions and values of the above-mentioned parameters are listed in Table 1. Equation (1) indicates that the time evolution of the somatic membrane potential 
Table 1. Values of the parameters in Equations (1)-(6) from [8] .
(the 2nd term), outward delayed-rectifying potassium current (the 3rd term), leak current (the 4th term), and electrotonic diffusive current between the somatic and dendritic compartments (the 5th term). Similarly, Equation (3) indicates that the time evolution of the dendritic membrane potential 



For detailed explanations of the model, see [8] .
The free and open source software Scilab (http://www.scilab.org/) was used to numerically solve equations (1)-(6) under the following initial conditions:








3. Results
3.1. Reproduction of Previous Results
The ghostbursting model can show the three dynamical states: quiescence (Figure 1(a)), periodic tonic spiking (Figure 1(b)), and bursting (Figure 1(c)). The present study shows that the regions of these dynamical states in the 















Based on the previous results (Figure 6 in [8] ), SNFP was thought to occur at certain 



3.2. Effects of Changes in 

The simulation results under conditions in which the 




At high 


Figure 1. Examples of the time courses of the simulated somatic membrane potential 





spiking (○ in Figure 2(a) and Figure 2(c)) at smaller 











4. Discussion
In the field of dynamical systems, it is important to investigate the dependence of the solutions of ordinary differential equations on system parameters. The present study illustrates the dependence of the qualitative nature of the solutions of ordinary differential equations on the following system parameters:








Figure 2. The effects of variations in the 




study, which was not reported in the previous study [8] , is that there was a nonlinear relationship between 

Other examples that illustrate how the dynamical states of two-dimensional parameter space change in response to variations in the third parameter are (1) a model of CA1 pyramidal neuron spiking dynamics (Figure 12 in [11] ) and (2) a compartmental model of Cheyne-Stokes respiration (Figure 5 in [12] ). In analysis of the CA1 model, Bianchi et al. have focused on the following three parameters: the injected current











Study [13] proposed an algorithm for the visualization of the bifurcation manifolds in the three-dimensional parameter space. In the three-dimensional parameter space, the parameter sets at which codimension one-bifur- cation occurs are visualized as bifurcation surfaces. Higher codimension bifurcations are located at intersections of the bifurcation surfaces. For example, analyses of a socioeconomic model have revealed codimension-one bifurcation surfaces: a Hopf bifurcation surface and a saddle-node bifurcation surface (Figure 5 in [13] ). In addition, the following codimension-two bifurcation curves were visualized: a Gavrilov-Guckenheimer bifurcation curve and a Takens-Bogdanov bifurcation curve. In contrast to the findings of the previous study [13] , in the present study, we did not visualize bifurcation manifolds in the three-dimensional 








5. Conclusion
In conclusion, the novelty of this paper is that it reveals in detail the influence of 

Acknowledgements
The author would like to thank Enago (www.enago.jp) for the English language review.
References
- Hodgkin, A.L. and Huxley, A.F. (1952) A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve. Journal of Physiology, 117, 500-544. http://dx.doi.org/10.1113/jphysiol.1952.sp004764
- Bungay, S.D. and Campbell, S.A. (2009) Modelling a Respiratory Central Pattern Generator Neuron in Lymnaea stagnalis. Canadian Applied Mathematics Quarterly, 17, 283-291.
- Ermentrout, G.B. and Terman, D. (2010) Mathematical Foundations of Neuroscience. Springer, New York. http://dx.doi.org/10.1007/978-0-387-87708-2
- Teka, W., Tabak, J., Vo, T., Wechselberger, M. and Bertram, R. (2011) The Dynamics Underlying Pseudo-Plateau Bursting in a Pituitary Cell Model. Journal of Mathematical Neuroscience, 1, 12. http://dx.doi.org/10.1186/2190-8567-1-12
- Blagoev, K.B., Shukla, K. and Levine, H. (2013) We Need Theoretical Physics Approaches to Study Living Systems. Physical Biology, 10, Article ID: 040201. http://dx.doi.org/10.1088/1478-3975/10/4/040201
- Holmes, P., Eckhoff, P., Wong-Lin, K.F., Bogacz, R., Zacksenhouse, M. and Cohen, J.D. (2010) The Physics of Decision Making: Stochastic Differential Equations as Models for Neural Dynamics and Evidence Accumulation in Cortical Circuits. Exner, P., Ed., XVIth International Congress on Mathematical Physics: Prague, 3-8 August 2009, 123-142. http://dx.doi.org/10.1142/9789814304634_0006
- Gieschke, R. and Serafin, D. (2014) Development of Innovative Drugs via Modeling with MATLAB: A Practical Guide. Springer, Heidelberg. http://dx.doi.org/10.1007/978-3-642-39765-3
- Doiron, B., Laing, C., Longtin, A. and Maler, L. (2002) Ghostbursting: A Novel Neuronal Burst Mechanism. Journal of Computational Neuroscience, 12, 5-25. http://dx.doi.org/10.1023/A:1014921628797
- Shirahata, T. (2012) Analysis of the Electrosensory Pyramidal Cell Bursting Model for Weakly Electric Fish: Model Prediction under Low Levels of Dendritic Potassium Conductance. Acta Biologica Hungarica, 63, 313-320. http://dx.doi.org/10.1556/ABiol.63.2012.3.1
- Vo, T., Tabak, J., Bertram, R. and Wechselberger, M. (2014) A Geometric Understanding of How Fast Activating Potassium Channels Promote Bursting in Pituitary Cells. Journal of Computational Neuroscience, 36, 259-278. http://dx.doi.org/10.1007/s10827-013-0470-8
- Bianchi, D., Marasco, A., Limongiello, A., Marchetti, C., Marie, H., Tirozzi, B. and Migliore, M. (2012) On the Mechanisms Underlying the Depolarization Block in the Spiking Dynamics of CA1 Pyramidal Neurons. Journal of Computational Neuroscience, 33, 20-225. http://dx.doi.org/10.1007/s10827-012-0383-y
- Atamanyk, J. and Langford, W.F. (2003) A Compartmental Model of Cheyne-Stokes Respiration. In: Ruan, S., Wolkowicz, G.S.K. and Wu, J., Eds., Dynamical Systems and Their Applications in Biology (Fields Institute Communications Volume 36), American Mathematical Society, Providence, 1-16.
- Stiefs, D., Gross, T., Steuer, R. and Feudel, U. (2008) Computation and Visualization of Bifurcation Surfaces. International Journal of Bifurcation and Chaos, 18, 2191-2206. http://dx.doi.org/10.1142/S0218127408021658





