ABSTRACT

We investigated the natural oscillations of dissipative inhomogeneous plate mechanical systems with point connections. Based on the principle of virtual displacements, we equate to zero the sum of all active work force, including the force of inertia which obtain equations vibrations of mechanical systems. Frequency equation is solved numerically by the method of Muller. According to the result of numerical analysis we established nonmonotonic dependence damping coefficients of the system parameters.

Keywords:

Plate, Viscoelastic Properties, Natural Frequencies, Damping Ratios, Structurally Homogeneous and Structurally Heterogeneous

1. Introduction

Studies related to the definition of inherent characteristics of plates with attached masses are discussed in [1] - [3] . In these studies, to determine the main forms and vibration frequencies a variational principle of Hamilton- Ostrogradskii is applied. In [1] , in the derivation of the frequency approach, AS Gershgorin is used [4] . Various mounting and mass concentration of the plate limits the scope of application of this approach. In [5] - [7] the authors take into account the viscoelastic (dissipative) material property records and deformable elements. Free oscillations of dissipative systems are damped. The amplitude of vibration modes decreases with time, so this process is not strictly periodic. But the frequency of the corresponding forms at the same time remain constant [7] , and in this sense the dissipative system can be studied as a system that has its own vibrations. In this paper we consider the linear problem of natural vibrations of viscoelastic rectangular plates (or package of rectangular plates) having a connection point.

2. Statement of the Problem and Their Solutions

We will consider the mechanical system consisting of N isotropic viscoelastic plates, occupying volume 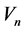and limited by surfaces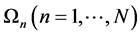. It is assumed that one linear dimension of each plate is much less than the other two. At each n on part of a surface of n-th plate uniform 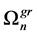boundary conditions are set, on other free surface 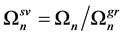in final number of points communications of kinematic and dynamic character are imposed: dot rigid, elastic and (or) viscoelastic hinged type of a support (rigid support can be jammed), the rigid elastic and (or) viscoelastic shock-absorbers connecting bodies (at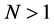), the concentrated masses 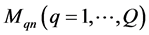. The arrangement of communications and masses on surfaces is any. Generally dissipative properties of elements of system are various. Special case of such structurally non-uniform viscoelastic system is the system with elastic and viscoelastic elements. For the last case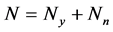, where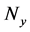?quantity of elastic elements of system,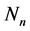?quantity of viscoelastic elements. For N = 1 the rack available. Required to determine the natural frequency of the viscoelastic system, as well as to evaluate its damping capacity.

Mathematically, the viscoelastic problem is as follows. Let all the n-th point of the body are subject to a harmonic law fluctuations, i.e.

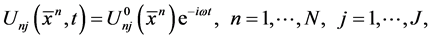(1)

where 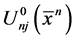j-th component of the displacement vector of n-th body, J?number of components of the displacement vector, 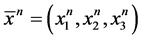the radius vector of the n-th body,?desired complex frequency of the system, and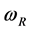?the natural frequency,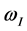?damping coefficient. As everyone a component of a vector of movements already has an index n, the last for designation a component radius vector isn’t used further.

For rectangular plates and

,

where x, y?coordinate. Proceeding from the principle of possible movements, we will equate to zero sum of works of all active forces, including inertia forces on possible movements:

(2)

where?virtual works of internal forces of bodies of springs, and also inertia forces taking into account the concentrated masses. These works can be presented the following ratios:

(3)

where?density and volume of the n-th body,?q-th accessions the mass of n-th bodies with coordinates ?number of springs (shock-absorbers) between n-th and (n + 1)-th bodies,?number of the concentrated masses on n-th body,?number of elastic (viscoelastic) support on n-th body,?components of tensors of tension and deformations according of n-th body, l-th of a spring (shock-absorber) and -th elastic (viscoelastic) support.

We will determine physical ratios for n-th viscoelastic body of system by equality [6]

(4)

where?Volterra’s having the following appearance the operators:

(5)

here?a dilatation,?Kronecker’s symbol,?the instant module of elasticity, and?a relaxation kernel. Poisson’s coefficient in an offered problem definition is accepted to constants. It means that for structurally uniform viscoelastic system of a form of own fluctuations will be equal to own vectors of the corresponding elastic task [7] [8] .

Considering (1), time function in equality (5) will be with slowly changing amplitude. Assuming a little integral, by means of a method of freezing we will replace a ratio (5) confidants:

(6)

where

Time allows to exclude it from the variation equation integrated members and, finally. In a symbolical look it can be presented in a look

(7)

We will write out concrete representation of functionality of G, for example, for a package of rectangular plates with dot communications:

where?thickness and the linear sizes of n-th plate,?coordinates of l-th concentrated weight,?coordinates of l-th spring (shock-absorber),?coordinates of l'-th elastic (viscoelastic) support. If n-th plate and l-th spring and lʹ-th support are viscoelastic, then are represented by the following formulas:

where?the complex function, the numerical coefficients which depend on the parameters of relaxation kernel corresponding viscoelastic elements,?generalized

instant rigidity according to of n-th plate, of l-th shock-absorber, of l'-th support. In an elastic case where?generalized rigidity according to of n-th plate, of l-th spring, of l'-th support.

The similar functionality can be written down for system of covers of rotation.

Components of a vector of movements are required functions of the variation Equation (7) and have to meet boundary conditions on surfaces, i.e.

(8)

It was necessary to impose rigid dot communications which don’t make work at fluctuations on system. Terms of hard hinged support the n-th body in point supports can be written as

(9)

where?coordinates of s-th support of n-th body.

If the part of support has jamming, conditions will be added

(10)

where?the direction of a single vector along which in a point the rigid jamming of a body is carried out.

Existence of rigid racks between n-th and (n + 1)-th body at is considered by ratios

(11)

where?the coordinate of r-th are resistant,?number of racks between n-th and (n + 1)-th bodies. In case of N = 1 conditions (11) are absent.

Thus, on a vector of movements restrictions of types (8)-(11) are in addition imposed. On system dot communications we will consider imposing by means the method of Lagrange multipliers. Then the variational Equation (10) will correspond in a look

(12)

where?Lagrange’s multipliers.

It is necessary to find a range of complex own frequencies, where?frequencies, and?coefficients of damping own attenuations of fluctuations.

3. Algorithm of Realization of a Variation Method at the Solution of a Viscoelastic Task on Own Fluctuations

Approach the solution of the variational Equation (12), as well as in case of an elastic task, we look for in the form of the approximating form made of fundamental functions, satisfying both to the equation, and the set geometrical boundary conditions on surfaces of each body. It is offered that functions for such bodies are known. Then approximating forms can be built in the form of final decomposition on these known functions:

, (13)

where?required complex coefficients.

Previously it is possible to normalize. On the sum (13) meets regional conditions automatically, owing to a choice of the composed. Variation on the generalized coordinates, the Equation (12) we will receive uniform system of the linear equations. Dimension of this system, where

?number component of a vector of movements.

Without providing concrete calculations, we will write down this system in a matrix look:

(14)

where?a vector column of the generalized coordinates?number of viscoelastic bodies of system; B?symmetric singular matrix generalized mass of the system;?the square matrixes of dimension consisting of zero, consisting of zeros, except the stiffness matrices of instantaneous n-th viscoelastic body, of l-th shock-absorber and of l'-th viscoelastic support, respectively; A?a symmetric matrix (its submatrix of A⁰ of dimension represents the generalized total rigidity of elastic elements of system, and submatrixes consider kinematic conditions of the rigid dot communications imposed on system);?the complex function characterizing viscosity of a viscoelastic element (its coefficients depend on relaxation parameters).

Structurally matrixes A and B are similar described in work [6] . Generally they differ from each other parameters of kernel relaxation. If all elements of the viscoelastic rheological properties are the same, then and so the second, third and fourth terms in Equation (14) are replaced by a matrix of total instantaneous stiffness of viscoelastic elements (in the case of structural homogeneous viscoelastic system).

The degeneracy of the matrix B as a resilient problem is caused in the introduction of additional point connections (rigid supports and pillars). The transformed matrixes will have dimension where

. Equating to define systems to zero, we will receive the frequency equation

which, unlike a case of an elastic task, will be complex. The most effective way of the solution of the similar equations, apparently, is the method of Müller [7] which and here was used. Without opening frequency to define, and calculating on each step only its value for the fixed value, the specified method are own complex frequencies. Coefficients of damping allow to judge damping properties of considered system. In equipment for an assessment of speed of attenuation of oscillatory processes other characteristic, namely, logarithmic decrement of attenuation of fluctuations is used. It is connected with damping coefficient by the following formula [6] :

Systems of rectangular plates and with dot communications are considered. We will consider the design representing a package from two parallel square elastic plates with the shock-absorber and the attached weight. The relaxation kernel for the shock-absorber is chosen in a look

where?parameters of a kernel [9] . Two elastic plates identical on mechanical properties (E = 28; ρ = 4; v = 0.3) are connected in the center of one spring. Mass of a spring М₀ = 0.05. Plates square(a = b = 1), supported on a contour, thickness of the bottom plate h₁ = 0.1, and of the top plate h₂ = 0.046, on the bottom plate in the center dot weight is attached. Viscosity of the shock-absorber is accepted such that its deformation of creep at quasistatic process made a small share from the general (~12%). For this case kernel parameters following: [9] . Unlike an elastic task, dependence of two lowest frequencies and the corresponding coefficients of damping from the size of instant rigidity of the shock-absorber here was investigated. The last changed from 10⁻⁴ to 10⁻¹. On the right this range is limited by the size since at C = C₂ there is a change of the second form. On Figure 1 dependence of the first two frequencies and the corresponding coefficients of damping from the size of instant rigidity of the shock-absorber C is shown. From the analysis of the figures that the dissipative properties of the system as a whole are determined not only the rheology of its elements, but depend strongly on the interaction of the vibrations of their own forms. This effect is reflected in the fact that under certain conditions (of which below), and to a certain value of the damping energy higher capacity (in this case, the second) shape dissipates less energy, less energy-intensive than the form. Then, since some value of instant rigidity of the shock-absorber (in this case), process of dissipation of energy by own forms is normalized and proceeds according to power hierarchy of forms.

Real illustration of this effect is existence of a point of intersection of schedules of damping coefficients and at. And one more feature: in this point the difference of speeds of attenuation of two forms of fluctuations of a design changes a sign, if a spring viscoelastic (i.e. system structurally non-uniform). As well as in an elastic task [6] , own frequencies which it is slightly less, than in this point approach. The analysis of tasks of this kind showed that the effect of interaction of own forms is observed only in structurally non-uniform systems (in this case with elastic and viscoelastic elements) and at noticeable rapprochement of own frequencies. Absence at least one of these conditions excludes effect manifestation. The physical explanation for observed effect should be looked for in the nature of dynamic redistribution of energy of system between two forms possessing properties described above. We will consider now, what distinctions exist between structurally uniform and non-uniform viscoelastic systems. Structurally uniform viscoelastic system (all elements viscoelastic with identical rheological properties) is characterized by that in a formula (14), first, there is no matrix A (submatrixes of A_H and A_b can be transferred to the following matrix) and, secondly, all functions are identical. Then the system of the Equation (14) in a matrix look can be copied so:

(15)

where Aⁿ?a numerical matrix of the total instantaneous stiffness of viscoelastic elements of the system.After an exception linearly dependent the component from system also can be written down (15) transformed matrixes of the generalized instant, in an initial form, i.e. special transformation of the generalized coordinates to lead these matrixes to a diagonal look. And it means that the mechanical system represents as though set of partial systems independent with one degree of freedom. In other words, own forms of such system are independent and they can be considered and calculated separately from each other. Other situation develops for structurally non-uniform viscoelastic system. In a formula (15) the matrix of the generalized of elastic elements A will increase and then (15) will look so:

where. Generally for two matrixes and В (one of which functional), after a preliminary exception linearly dependent a component, it is impossible to pick up at the same time the nondegenerate transformation of coordinates bringing them to a canonical form. And it means that own forms of such mechanical system can’t be considered separately from each other, i.e. they are dependent. Therefore, at free fluctuations between forms there is an exchange of energy. Especially strongly it is shown if forms have close own frequencies. In a point of intersection of schedules of coefficients of damping and both forms equally disseminate energy, though are excellent from each other (to within a phase). To С = С^* point * thereisenergy “transfer”. Consequently, for free oscillations between forms of energy is exchanged. This is especially true if the forms have similar natural frequencies. At the point of intersection of the graphs of damping factors and, both forms are equally dissipate energy, although different from each other (up to a phase). To the point C = C^*, the “pumping” of energy from the second form to the first, so the latter most intensively dissipates energy. After the point of intersection of the difference between the first natural frequency increases, the appropriate forms of interaction decreases and their dissipative properties take a regular character. The practical conclusion is that the damping capacity of the structure is mainly determined by the absolute value of the minimum damping factor (in this case the latest damped oscillations precisely this form); global (determining) the damping factor of the system is the first to the intersection, and then. Optimal in the sense of decay mode vibrations of the structure will be at the C = C^*, when the damping factor of the global maximum.

The second example provides the mechanical system consisting of two parallel identical mechanical properties and geometry of the elastic plat in

connected by a weightless viscoelastic damper. The parameters of its core relaxation, and instantaneous stiffness. Square plate, simply supported along the contour, each one has added mass. The purpose of the study identifies nature of dependence of the damping capacity of the structure on the location of the mass and damper on the area of the plates.

In this problem, we investigate the following variant: shock absorber is located in the center of the plates, the masses are the central axis of the structure, and М₁ is fixed to the first (bottom) plate at a distance of 0.04 m from the absorber, and the position of the mass М₂ to the second (upper) plate was varied along the central axis of the structure.

Figure 2 shows plots of the first two natural frequencies and damping coefficients of the position of the mass М₂. Calculation showed a strong dependence of the damping of the first global form on the coordinate supply М₂. Eigenfrequencies and damping ratio of the second form are practically unaffected. Having two points on the x-axis, where the first global form of construction not be damped because the waveforms of the plates in this case are indistinguishable. At the location of mass М₂ of the plate at those points become identical as to the rigidity, and on the inertial characteristics. If the mass М₂ to mix in other areas on the top plate, then there is also the point at which the damping factor is zero. Thus, for a mass М₂ there are an infinite number of positions (at fixed positions of the shock absorber, and М₁, in which no attenuation of the first global shape. These points form a closed curve (close to a circle) on the second plate. Analysis of Figure 2 shows the attenuation of the first global form; it is necessary to disrupt the symmetry of the plate, for example a

suitable arrangement of added mass. Symmetry of the left and right branches of the graph provides an opportunity to obtain the maximum (and equal) the effectiveness of the shock absorber arrangement as cargo on either side of him (left leg), and on one side (right branch).

Described effect shows that the energy of the system depends not only on the rheological properties of the damping material, but also on the geometry of the structure as a whole. Similar effect was observed for the system with finite number of degrees of freedom [10] [11] . This effect does not occur if the system is structurally homogeneous viscoelastic.

Cite this paper

Safarov Ismail Ibrahimovich,Teshaev Muhsin Hudoyberdievich,Madjidov Maqsud, (2014) Natural Oscillations of Viscoelastic Lamellar Mechanical Systems with Point Communications. Applied Mathematics,05,3018-3025. doi: 10.4236/am.2014.519289

References