Received 15 August 2014; revised 2 September 2014; accepted 9 September 2014

ABSTRACT

In this paper, we present a new algorithm of the time-dependent shortest path problem with time windows. Give a directed graph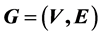, where V is a set of nodes, E is a set of edges with a non-negative transit-time function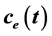. For each node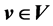, a time window 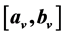within which the node may be visited and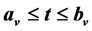, 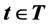is non-negative of the service and leaving time of the node. A source node s, a destination node d and a departure time t₀, the time- dependent shortest path problem with time windows asks to find an s, d-path that leaves a source node s at a departure time t₀; and minimizes the total arrival time at a destination node d. This formulation generalizes the classical shortest path problem in which c_e are constants. Our algorithm of the time windows gave the generalization of the ALT algorithm and A^* algorithm for the classical problem according to Goldberg and Harrelson [1] , Dreyfus [2] and Hart et al. [3] .

Keywords:

Shortest Path, Time-Dependent Shortest Path, ALT Algorithm, A^* Algorithm, Time Windows

1. Introduction

The shortest path problem on graphs is a problem with many real-life applications such as: route planning in an internet, car navigation system, traffic simulation or logistic optimization. The shortest path problem is a classical combinatorial optimization problem. It has countless applications and so far numerous algorithms have been proposed (see Ahuja et al. [4] ) including the well-known Dijkstra’s algorithm. Recently, because some of the new improvement becomes fairly difficult, researchers began to study variants of this problem which include the time-dependent and the time windows generalization.

Give a directed graph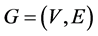, where V is a set of nodes, E is a set of edges, 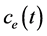is a non-negative transit-time function. For each node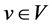, a time window 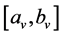within which the node may be visited and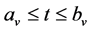, 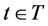is non-negative of the service and leaving time of the node. A source node 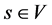with time window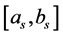, a destination node 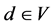with time window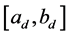, and a departure time. The time-dependent shortest path problem with time windows asks to find an s, d-path that leaves a source node s at time and minimizes the total arrival time at a destination node d which satisfies the set of all constraints (see El-Sherbeny [5] , El-Sherbeny and Tuyttens [6] , Tuyttens et al. [7] and El-Sherbeny [8] ). One can notice that the undirected graphs can be treated by replacing each undirected edge with two reverse directed edges. Without losing of the generalization, we suppose that a destination node d is reachable from a source node s. For simplicity, we suppose that the domain of the definition for all is, but our algorithms work for the discrete version too. We also assume the time complexity to calculate a which is bounded by some constant. This formulation generalizes the classical shortest path problem with constant and. It can further handle time-variable edge costs, thus it has more application than the classical one, which is also referred to as the static problem in contrast.

In Cook and Halsey [9] , it has considered and given a dynamic programming algorithm which is not polynomial-time at all. Dreyfus [2] suggested a polynomial-time straightforward generalization of the Dijkstra’s algorithm. However, he did not notice that it works correctly only for instances satisfying the First-In First-Out (FIFO) property, i.e., for any edge and, it holds that. In other words, the arrival-time function is non-decreasing. With this property, we can ensure that there is no cycle of negative transit-time, hence a simple optimal solution exists. This was pointed out and discussed later (see Halpern [10] , Kaufman and Smith [11] and Orda and Rom [12] ).

On the other hand, the general problem without the FIFO constraint is NP-hard if the waiting at nodes is not allowed (see Sherali et al. [13] ). In Orda and Rom [12] , it showed that, if the waiting at nodes is allowed, which is natural in transportation systems, any instance can be converted to an equivalent instance that satisfies the FIFO property; hence, no waiting is needed, and that can be done in polynomial time (if can be calculated in polynomial time). Thus, in the following, we will only consider instances that satisfy the FIFO property.

Even with the FIFO constraint, unlike the static case, studies are not rich. Dreyfus’s proposal of the generalized Dijkstra’s algorithm, despite of many studies (see Dean [14] , Ding et al. [15] , Halpern [10] , Kanoulas et al. [16] , Kaufman and Smith [11] and Orda and Rom [12] ), there was no significant advancement in solving the problem more efficiently.

In this paper, we give a new algorithm of the time-dependent shortest path problem with time windows that generalizes the ALT algorithm (see Goldberg and Harralson [1] ) and A^* algorithm for the static problem, unlike the generalized Dijkstra’s algorithm, which uses a function h to estimate the distances between nodes in the graph in Section 2. In Section 3, we give an application instance of our algorithm and a generalization of the ALT algorithm (see Goldberg and Harralson [1] , Dreyfus [2] and Hart et al. [3] ) that is based on the static A^* algorithm and is faster than the Dijkstra’s algorithm using preprocessing. Thus, we have found the first algorithm for the time-dependent shortest path problem with time windows that speeds up the calculation using preprocessing and we have observed that it is several time faster than the generalized Dijkstra’s algorithm. Finally, the conclusion is given in Section 4.

2. The Algorithm of the Time-Dependent Shortest Path Problem with Time Windows

We start from the classical and well-known Dijkstra’s algorithm. For each edge, we suppose that is a constant. The service and leaving time to node is and a time window where,. If, the Dijkstra’s algorithm tries to find a shortest -path in greedy manner. Let denote the precedent node of a node ν of the shortest s, ν-path found so far. The Dijkstra’s algorithm maintains for each node ν a status {“unlabeled”, “labeled”, “finished”} and a distance label. At the beginning, is the set to 0 and all status is initialized to “unlabeled” except that s is “labeled”. Then it repeatedly find a “labeled” node ν with the smallest (such ν is called the active node) until; then it tries to relax all non “finished” neighbors w of ν, i.e., if status “unlabeled” then the set it to “labeled” and let,; otherwise status “labeled”. The time window of the node is, where,. Let, if; after all these have done, set status to “finished” and continue. See Table 1 for the pseudo-code.

The our algorithm of the A^* algorithm given in (Table 2) follows the same fashion except that it employs an estimator for all with the time window and chooses the active node by the smallest. A good estimator for all can be used to reduce the search space (i.e. the set of nodes that have to be explored before the solution is found) of the shortest path queries effectively. Notice that how to determine is not part of the algorithm. It must be obtained by some other method, and the choice of h determines the correctness and the efficiency of the A^* algorithm (a good lower-bound on the -dis- tance is preferred). Clearly the Dijkstra’s algorithm is a special case with.

Remark: The Dijkstra’s algorithm is a special case of. For general, however, the correctness is not guaranteed.

Now we are ready to describe our generalized A^* algorithm. It generalizes by the time dependent version with is the time windows of a node ν where, is the service and leaving time of the node. Thus in Table 3, we use to replace. Notice the rule for choosing the active node (Line 2) has been changed in addition.

Definition 2.1. Given a directed graph, a non-negative transit-time function of each edge, and, is a time windows, , is the service and leaving time to node ν,

then for all edges is called a triangle condition.

In a directed graph, a non-negative transit-time function of each edge, with is a time windows, , is the service and leaving time to node ν, a source node, a destination node and a departure time at a source node s of the time-dependent shortest path problem with time windows such that the FIFO properly is satisfies and is reachable from, the generalized of A^* algorithm in Table 3 finds an optimal solution if h satisfies the three conditions:

· For all vertices and, is the FIFO time windows condition (2.1).

· For all edges and, is a triangle condition (2.2).

· For all vertices and, is the time windows condition (2.3).

The triangle condition (2.2) (see Figure 1) is a natural generalization from the classical A^* algorithm whereas the FIFO condition is only available in the time-dependent and time windows case. The generalized Dijkstra’s algorithm is nothing but the simplest case with, and the generalization of Kanoulas et al. [16] , on the other hand, simply uses a constant function, with the time windows and, is the service and leaving time to a node thus, it also a simple special-case of our algorithm.

Roughly speaking, it says the supposed transit-time from ν to d is no more than, i.e. the supposed transit-time of the -path. Notice that, is the supposed transit-time from w to d by leaving w at time with the time windows and,.

Theorem 2.1. Let be a path with the time windows and, is

the service and leaving time at node. Define and be the transit-time from

to. Then it holds that.

Proof. By the above conditions (2.1), (2.2) and (2.3). We show by the induction that, every active node ν must get the optimal distance label (the induction variable is the number of nodes in the shortest path), i.e., the earliest arrival time at node ν for leaving at time.

Let ν be an active node satisfies the time windows and, is the service and leaving time of this node. If, we are done. Otherwise, let be a simple optimal -path (it exists) and be the first node on such that status “finished”. Clearly must exist and (it can be ν) see Figure 2.

Let denote the optimal distance (i.e. the earliest arrival time). It is obvious that because was relaxed when the precedent node of was active and at that time by the induction hypothesis. Let be the shortest transit-time from to ν at departure time (notice). By applying the above conditions (2.1), (2.2) and (2.3) to the -path with time windows on with we have

(2.4)

That is equivalent to

(2.5)

Then, since ν is the active node with the time windows (thus has the smallest) we have

(2.6)

On the other hand, by the FIFO condition and (the optimality of), we have

(2.7)

Therefore we get the next fact by combining (2.6) and (2.7), we get

(2.8)

This means the equalities hold, hence Then by our choice of the active node, must hold. Thus hence

Remark: The analogously to the static version, an h with implies where ν satisfies the time windows and, is a lower bound on the shortest transit-time from ν to with leaving time (by Theorem 2.1). Moreover, it is not difficult to show that with an h satisfying and, the search space (the set of active nodes) of the generalized A^* algorithm is no longer than that the generalized Dijkstra’s algorithm. Using this observation, we will give our algorithm in the next section that is practically faster than the generalized Dijkstra’s algorithm.

3. Application Instance

The time complexity of the generalized Dijkstra’s algorithm is by using a Fibonacci heap (we note it was in (Ding et al. [15] ), where are the number of edges, the number of nodes, and the time complexity to calculate, respectively. While we cannot improve this theoretical bound, let us give a practically faster algorithm that is based on our A^* algorithm and generalizes the static landmark-based ALT algorithm (Goldberg and Harrelsin [1] , Dreyfus [2] , and Hart et al. [3] ).

The ALT algorithm is such as an algorithm that is supposed to answer the shortest-path queries for a known graph. This means we can preprocess the graph beforehand and use it to answer a query faster than a normal calculation by the Dijkstra’s algorithm. Of course there is a trivial method of saving solutions for all possible queries and answers a query in time, but the order (for the static case) is big (if not impossible) for large graphs, usually a road network is spares (i.e., for some small) and has several millions of nodes. So researchers are seeking efficient algorithm that uses storage, see Wagnar and Willhalm [17] for a review. While this is an extremely hot topic for the static problem of these several years, for the time-de- pendent case, as far as we know, there was no proposal before our work.

Now let us describe the detail of our generalized ALT algorithm. Let denote the shortest transit-time from a node ν with the time windows to anther node with a time windows, a service and leaving time, hence we want to find an -path of transit-time Suppose we have a node with time windows and the values for all nodes and all (is called a landmark). Also, suppose we can calculate a (if exists) that

(3.1)

In other words, is the latest leaving time in order to get ν before (from). Define h by:

if exists, 0 otherwise (i.e., does not exist) (3.2)

It is clear that and Actually this definition is a generalization from the static case, i.e., is an estimation (a lower bound) on the transit-time, which is no shorter than the right side of (3.2) (by the triangle inequality due to the optimality of). Moreover, we can show that satisfies the FIFO condition, the triangle condition and the time windows condition at the same time, too. The proof is not trivial nor difficult, but due to the page limit, we omit it in this work. We note it is important to choose to be the maximum.

We still have to show how to calculate, which usually is difficult if there is no explicit expression for Moreover, in general it is difficult to hold all values of Fortunately, however, we can show that sampling of time works, i.e., we can calculate and hold values only for some and define, if it exists, by

(3.3)

Again, we can show the function defined by (3.2) with the above satisfies the FIFO conditions, the triangle condition, the time windows condition, and,. Moreover, we can employ more than one land marks to get a better estimation (notice the maximum of all works). Applying this generalized ALT algorithm to a number of US road networks (obtained from the web site of the 9^th DIMACS implementation challenge http://www.dis.uniromal.it/~challenge9/, where and with periodic piecewise-linear transit-time functions (with 9 samples a day), we have noticed that it ran at an average of about 4 times faster than the generalized Dijkstra’s algorithm with 16 landmarks and 2 time samplings.

A comparison example of the search space between the generalized Dijkstra’s algorithm and the generalized ALT algorithm for the time dependent shortest path problem time windows and our ALT algorithm for an instance with the number of nodes are 321,270 and the number of edges are 800,172. The number of landmarks is 16 and the number of time samplings is 2. The search space of the ALT algorithm is 0.055 smaller and the running time is 7.4 times faster.

4. Conclusion

In this paper, we present a new algorithm framework of A^* algorithm for the time-dependent shortest path problem with time windows. By constructing some appropriate estimator h, it is possible to get an algorithm that is faster than a normal generalized Dijkstra’s algorithm. As an example, we have generalized the landmark based ALT algorithm, which we believe is the first algorithm that uses preprocessing to speed up the calculation of time-dependent shortest paths problem with time windows. Our experimental result shows that it is several times faster than a normal generalized Dijkstra’s algorithm for large road networks.

Acknowledgements

The author would like to thank an anonymous referee for some useful comments.

References