Applied Mathematics
Vol.5 No.4(2014), Article ID:43580,16 pages DOI:10.4236/am.2014.54067
A Consecutive Quasilinearization Method for the Optimal Boundary Control of Semilinear Parabolic Equations
Mohammad Dehghan Nayyeri*, Ali Vahidian Kamyad
Applied Mathematics Department, Ferdowsi University of Mashhad, Mashhad, Iran
Email: *mu_de324@stu-mail.um.ac.ir, mudenayyeri@gmail.com, kamyad@math.um.ac.ir
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 December 2013; revised 15 January 2014; accepted 23 January 2014
ABSTRACT
Optimal boundary control of semilinear parabolic equations requires efficient solution methods in applications. Solution methods bypass the nonlinearity in different approaches. One approach can be quasilinearization (QL) but its applicability is locally in time. Nonetheless, consecutive applications of it can form a new method which is applicable globally in time. Dividing the control problem equivalently into many finite consecutive control subproblems they can be solved consecutively by a QL method. The proposed QL method for each subproblem constructs an infinite sequence of linear-quadratic optimal boundary control problems. These problems have solutions which converge to any optimal solutions of the subproblem. This implies the uniqueness of optimal solution to the subproblem. By merging solutions to the subproblems, the solution of original control problem is obtained and its uniqueness is concluded. This uniqueness result is new. The proposed consecutive quasilinearization method is numerically stable with convergence order at least linear. Its consecutive feature prevents large scale computations and increases machine applicability. Its applicability for globalization of locally convergent methods makes it attractive for designing fast hybrid solution methods with global convergence.
Keywords:Quasilinearization; Optimal Boundary Control; SQP Methods; Semilinear Parabolic PDE’s

1. Introduction
The solution methods for the optimal control of nonlinear systems pass from nonlinearity to linearity in different approaches. For example the gradient methods modify iteratively the previous approximate solution by linearly seeking a suitable direction thorough solving a linear problem [1] . The SQP methods seek the optimal solution by linearizing the optimality systems using some version of Newton’s method [1] [2] . Our approach in this respect is to linearize the state equation through a quasilinearization method.
Quasilinearization method for nonlinear equations has its origin in the theory of dynamic programming and has important features in common with Newton’s method especially its form [3] . For a formal explanation let Y and Z be ordered Banach spaces, 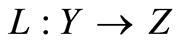 be a bounded linear operator and
be a bounded linear operator and 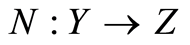 be a nonlinear differentiable operator. Consider the equation
be a nonlinear differentiable operator. Consider the equation
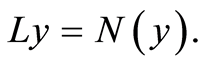 (1.1)
(1.1)
In the convex case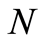 , Equation (1.1) can be written as
, Equation (1.1) can be written as
 (1.2)
(1.2)
where the right hand side is quasilinear. Then starting from 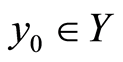 thorough the quasilinearization method, a sequence of linear equations is defined
thorough the quasilinearization method, a sequence of linear equations is defined
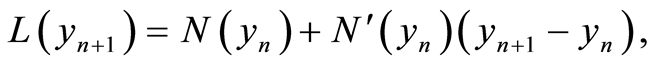 (1.3)
(1.3)
which produces the sequence of approximate solutions 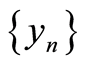 in
in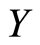 , converging to
, converging to , the solution of (1.2) or (1.1); see [3] [4] . This method has the following features. 1)
, the solution of (1.2) or (1.1); see [3] [4] . This method has the following features. 1)  is monotonic. This stems from positivity and inverse positivity of
is monotonic. This stems from positivity and inverse positivity of 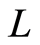 and
and . 2) the convergence is globally in the sense that
. 2) the convergence is globally in the sense that 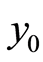 can be any lower solution of (1.1), i.e.
can be any lower solution of (1.1), i.e.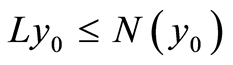 . 3) The rate of convergence is quadratic. For details on these features refer to [3] [5] . There are some extensions, refinements and generalizations to the quasilinearization method which preserve the above features but relax the convexity assumption on
. 3) The rate of convergence is quadratic. For details on these features refer to [3] [5] . There are some extensions, refinements and generalizations to the quasilinearization method which preserve the above features but relax the convexity assumption on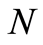 ; for a complete survey see [5] -[7] . Quasilinearization method has intimate connection with the theory of positive and monotone operators, maximum operation and differential inequalities; confer [8] , Sec. 4.33; [4] [9] .
; for a complete survey see [5] -[7] . Quasilinearization method has intimate connection with the theory of positive and monotone operators, maximum operation and differential inequalities; confer [8] , Sec. 4.33; [4] [9] .
In order to introduce the proposed consecutive quasilinearization method for optimal control problems let 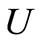 be a Banach space,
be a Banach space, 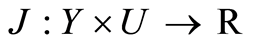 be a functional and
be a functional and 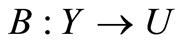 be a bounded linear boundary operator. Consider the following optimal boundary control problem:
be a bounded linear boundary operator. Consider the following optimal boundary control problem:
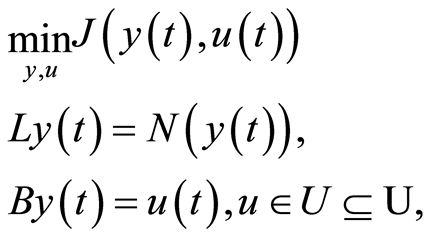 (1.4)
(1.4)
where 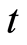 belongs to a time interval
belongs to a time interval . For
. For 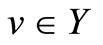 consider the following approximation to (1.4):
consider the following approximation to (1.4):
 (1.5)
(1.5)
Starting from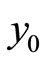 , let
, let 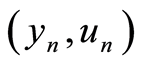 be the optimal solution of (1.5) with
be the optimal solution of (1.5) with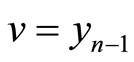 . Then the sequence
. Then the sequence 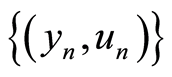 converges to the solution of (1.4) with the following features: 1) The convergence is occurred for
converges to the solution of (1.4) with the following features: 1) The convergence is occurred for , for some
, for some . 2) The convergence is globally in the sense that
. 2) The convergence is globally in the sense that 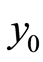 can be chosen any element in a subspace of
can be chosen any element in a subspace of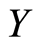 . 3) The rate of convergence is at least linear but it is not necessarily super-linear or quadratic. Here the sequence
. 3) The rate of convergence is at least linear but it is not necessarily super-linear or quadratic. Here the sequence 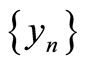 or
or 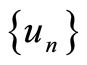 is not necessarily monotonic even when
is not necessarily monotonic even when  is convex or concave. For the case
is convex or concave. For the case  the optimal control problem is decomposed into many finite optimal control subproblems each on a time interval with length less than some
the optimal control problem is decomposed into many finite optimal control subproblems each on a time interval with length less than some 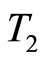 and then the above method be applied to each of them consecutively. Here
and then the above method be applied to each of them consecutively. Here 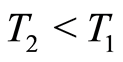 is such that the stability is preserved.
is such that the stability is preserved.
The optimal boundary control problem which is investigated has the standard quadratic objective of tracking type and a state constraint comprised of a semilinear parabolic equation with mixed boundary type. For such control problems, due to lack of convexity of the solution set, there is no general uniqueness result based on the optimality theory of optimal control problems [1] [2] [10] . However, a uniqueness result for such problems is obtained here as a by-product of the convergence of proposed consecutive quasilinearization method.
The organization of paper is as follows. Section 2 introduces the state equation and some estimates concerning solution of linear initial-boundary value problems. Section 3 proves the existence of an optimal solution. Section 4 introduces the quasilinearization method and proves its convergence for . Section 5 explains how to apply the quasilinearization method consecutively to the optimal boundary control problem when
. Section 5 explains how to apply the quasilinearization method consecutively to the optimal boundary control problem when . Also the uniqueness of optimal solution is stated there. In Section 6 the error and stability analysis of consecutive quasilinearization method is investigated. Section 7 presents a numerical example concerning the obtained results.
. Also the uniqueness of optimal solution is stated there. In Section 6 the error and stability analysis of consecutive quasilinearization method is investigated. Section 7 presents a numerical example concerning the obtained results.
2. The State Equation
Let 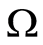 be an open bounded domain in
be an open bounded domain in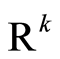 ,
, 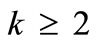 , with boundary
, with boundary 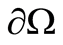 of class
of class 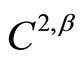 for some
for some . Let
. Let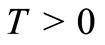 ,
, 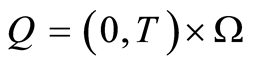 and
and . Consider the control system described by the semilinear parabolic initial-boundary value problem:
. Consider the control system described by the semilinear parabolic initial-boundary value problem:
 (1.6)
(1.6)
where  and
and 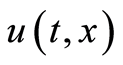 are, respectively, the state and the distributed control of system,
are, respectively, the state and the distributed control of system, 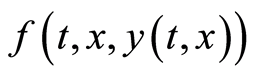 is the system nonlinearity and
is the system nonlinearity and
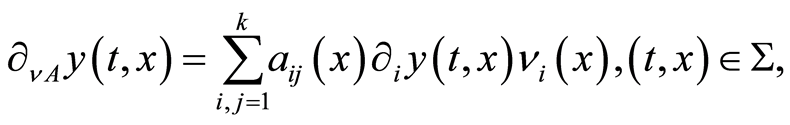
is the normal derivative of  associated with
associated with  wherein
wherein  is the outward unit normal to
is the outward unit normal to .
.
The following assumptions are imposed on the system and data:
• (A1) 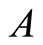 is a secod order differential operator in divergence form:
is a secod order differential operator in divergence form:
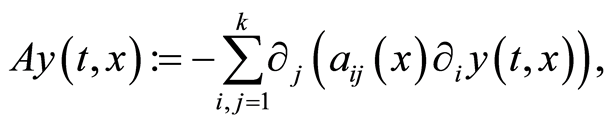 (1.7)
(1.7)
where  and
and 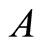 is uniformly elliptic, i.e. for every
is uniformly elliptic, i.e. for every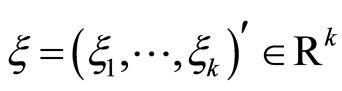 ,
,
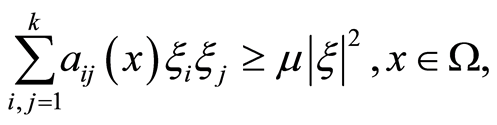 (1.8)
(1.8)
for some . Also it is considered
. Also it is considered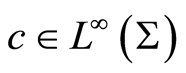 .
.
• (A2) 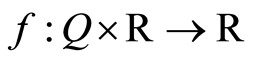 satisfies Caratheodory’s condition, i.e.
satisfies Caratheodory’s condition, i.e. 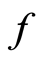 is measurable on
is measurable on 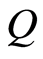 and continuous on
and continuous on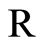 , and the Nemytskii’s operator
, and the Nemytskii’s operator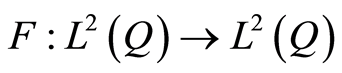 , defined by
, defined by 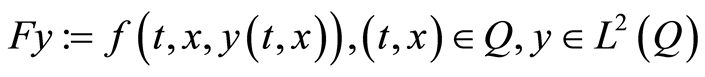 , is bounded and continuous. A sufficient condition for that is
, is bounded and continuous. A sufficient condition for that is
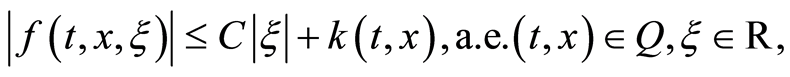 (1.9)
(1.9)
for some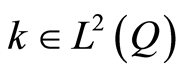 , Theorem 3.2 in [11] .
, Theorem 3.2 in [11] .
• (A3) 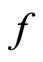 is twice continously differentiable with respect to
is twice continously differentiable with respect to  and
and
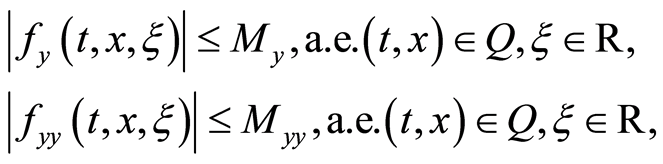
for constants ,
, .
.
The standard function spaces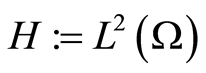 ,
, 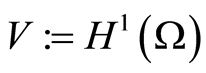 and
and 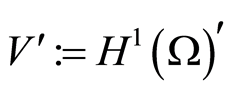 are used in the paper. Identifying
are used in the paper. Identifying 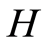 with its dual
with its dual 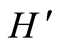 results in the evolution triples
results in the evolution triples  , where the embeddings are dense, continuous and compact. The standard solution space of parabolic problems and its norm is defined as
, where the embeddings are dense, continuous and compact. The standard solution space of parabolic problems and its norm is defined as
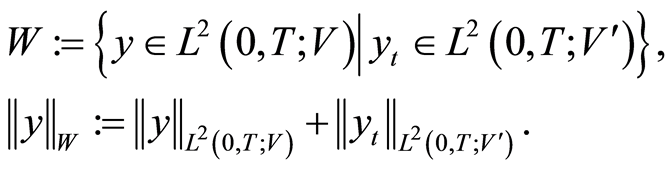
The continuous embeddings  and
and  are well-known and the latter is compact. For detailed definitions and properties of the above spaces refer to [11] -[14] .
are well-known and the latter is compact. For detailed definitions and properties of the above spaces refer to [11] -[14] .
The bilinear form associated with Equation (1.6) is defined as follows:
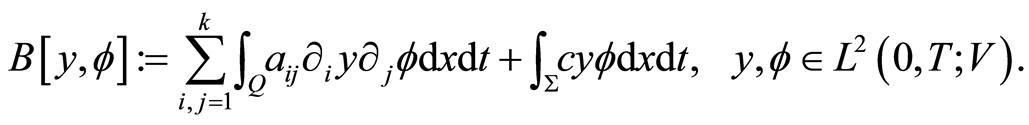 (1.10)
(1.10)
By Assumption (A1) the coefficients in (0.10) are bounded. This results in the boundedness of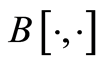 . Let
. Let 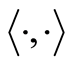 denotes the duality pairing between
denotes the duality pairing between 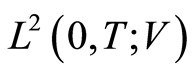 and its dual
and its dual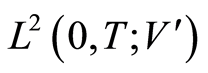 , and
, and 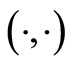 and
and 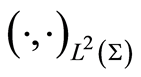 denote respectively the inner product of
denote respectively the inner product of 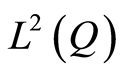 and
and . Then Definition 1 Let
. Then Definition 1 Let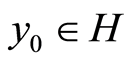 . For
. For 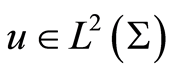 a function
a function 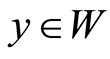 is called a weak solution of (0.6) if
is called a weak solution of (0.6) if 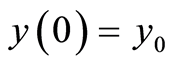 and
and
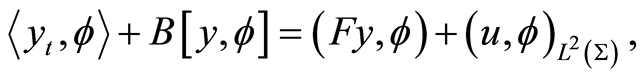
for all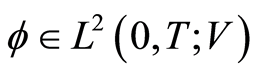 .
.
Next theorem under weaker assumptions is proved in Theorem 3.1 of [10] .
Theorem 1 Let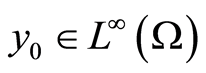 . Then under Assumptions (A1)-(A3) for every
. Then under Assumptions (A1)-(A3) for every 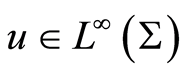 problem (0.6) admits a unique weak solution
problem (0.6) admits a unique weak solution .
.
In the following sections the linear initial-boundary value problems of the type below are used:
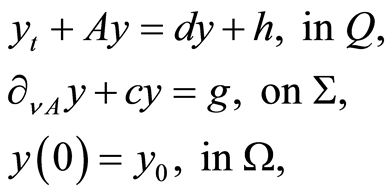 (1.11)
(1.11)
where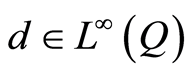 ,
, 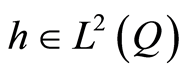 ,
, 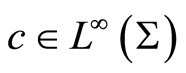 ,
, 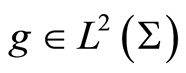 and
and . Define the family of bilinear forms
. Define the family of bilinear forms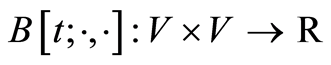 , a.e.
, a.e.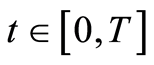 , by
, by
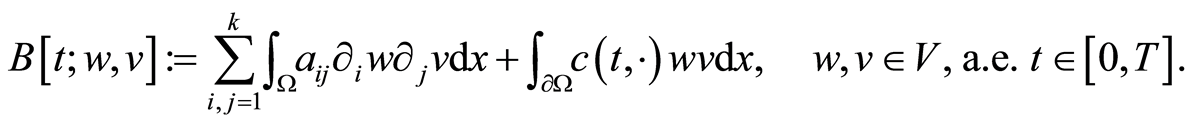 (1.12)
(1.12)
By Assumption (A1) the coefficients in (0.12) are bounded for a.e. . Thus
. Thus  is bounded on
is bounded on 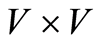 for a.e.
for a.e.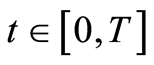 . Let
. Let 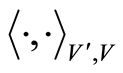 be the duality pairing between
be the duality pairing between 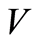 and its dual
and its dual , and
, and 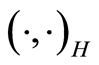 and
and 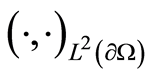 be the inner product of
be the inner product of 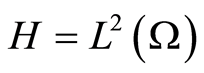 and
and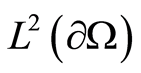 .
.
Definition 2 A function 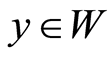 is called a weak solution of (0.11) if
is called a weak solution of (0.11) if 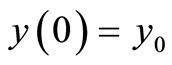 and
and
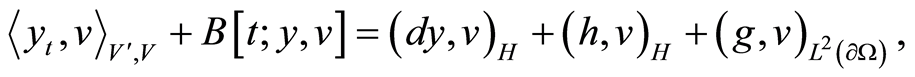
for all  and a.e.
and a.e. .
.
Norm estimates concerning solution of problem (1.11) are common in the literature of linear initial-boundary value problems [12] -[14] . Next theorem states some of them clarifying the time dependency quality of their constants. Its proof has been included due to lack of suitable reference, on the best of our knowledge, for the form stated here.
Theorem 2 The initial-boundary value problem (0.11) has a unique weak solution 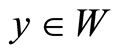 with norm estimates
with norm estimates
 (1.13)
(1.13)
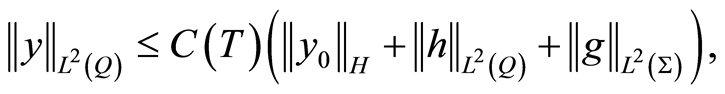 (1.14)
(1.14)
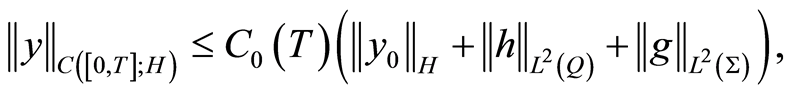 (1.15)
(1.15)
where 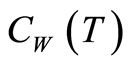 and
and 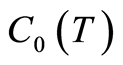 are bounded when
are bounded when  varies boundedly and
varies boundedly and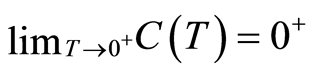 . If
. If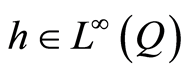 ,
, 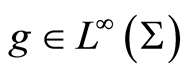 and
and 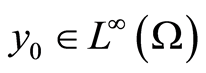 then
then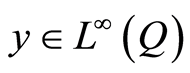 .
.
Proof 1 By Theorem 5.3 in Ch. III of [15] for some 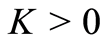 the following estimate exists:
the following estimate exists:
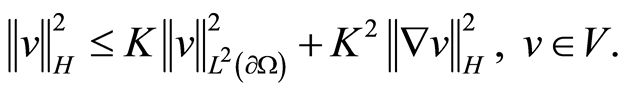
Using the Garding inequality (Proposition 22.45 in [14] ) or the elliptic energy estimates (Sec. 6.2.2, Theorem 2 in [12] ) it is obtained
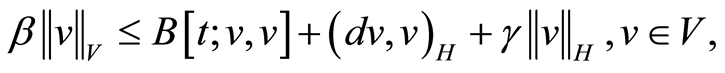 (1.16)
(1.16)
for a.e. , where
, where  and
and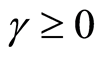 . Then the existence of a unique weak solution
. Then the existence of a unique weak solution 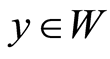 of (1.11) which satisfies the estimate (1.13) is deduced using a Galerkin procedure (Proposition 23.30 in [14] ).
of (1.11) which satisfies the estimate (1.13) is deduced using a Galerkin procedure (Proposition 23.30 in [14] ).
To obtain estimates (1.14) and (1.15) let 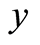 be the weak solution of (1.11). Then Definition 2 with
be the weak solution of (1.11). Then Definition 2 with 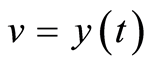 yields
yields
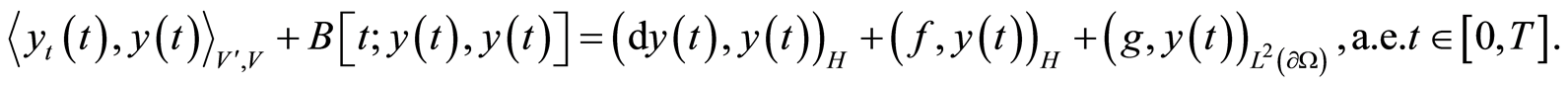 (1.17)
(1.17)
Furthermore,
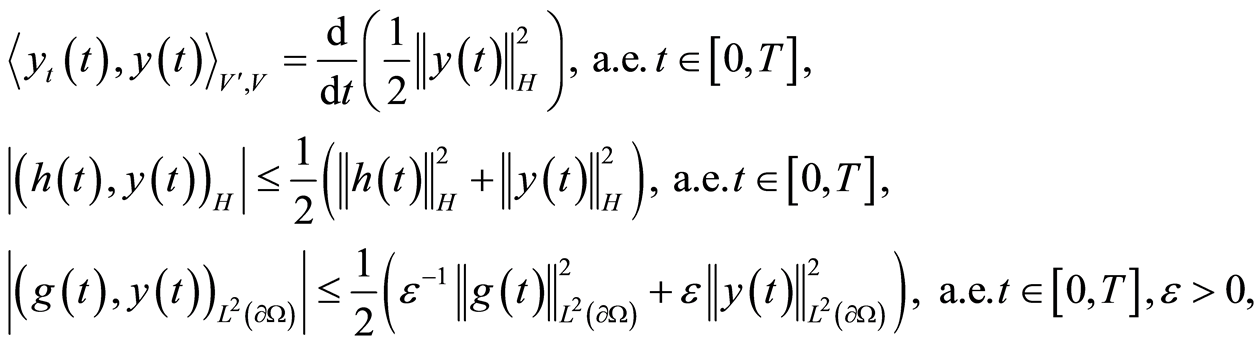 (1.18)
(1.18)
where the equation is proved in Ch. III, Proposition 2.1 [11] and the inequalities are obtained by Cauchy’s inequality. The continuous embedding  yields
yields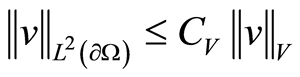 ,
, 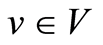 , for some
, for some , Ch. II, Theorem 3.3 in [11] .
, Ch. II, Theorem 3.3 in [11] .
Consequently, (0.16)-(0.18) with 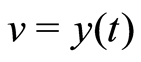 yield
yield
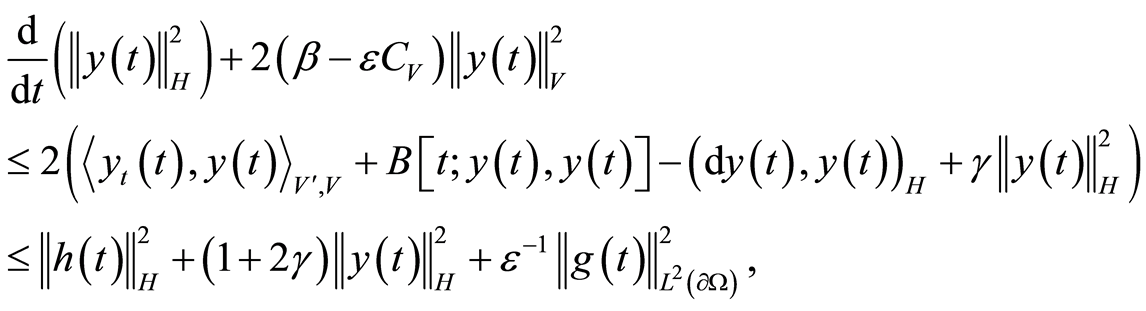 (1.19)
(1.19)
for a.e. . Now let
. Now let 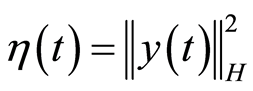 and
and . Then (1.19) implies
. Then (1.19) implies
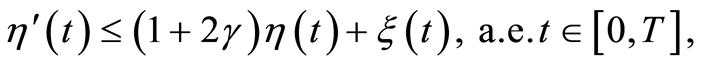
and the differential form of Gronwall’s inequality (Appendix B2 [12] ) yields
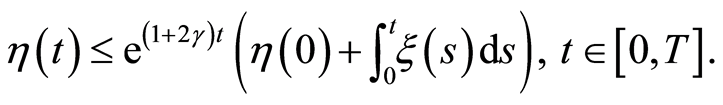
Since 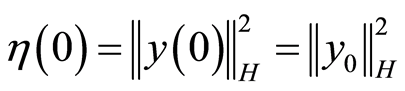 it is obtained
it is obtained
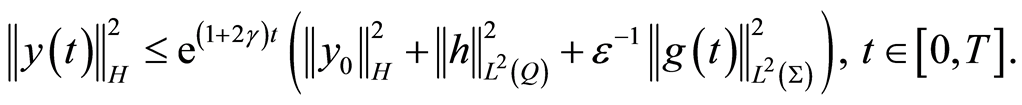 (1.20)
(1.20)
Integrating (1.20) from  to
to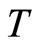 , results
, results

By employing the inequality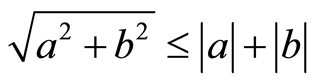 , the estimate (1.14) with
, the estimate (1.14) with  is concluded and
is concluded and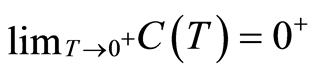 .
.
The estimate (1.15) is a consequence of (1.20) with . The last assertion of Theorem is proved in Proposition 3.3 of [10] .
. The last assertion of Theorem is proved in Proposition 3.3 of [10] .
We also meet the backward form of problem (1.11), i.e. the linear final-boundary value problem,
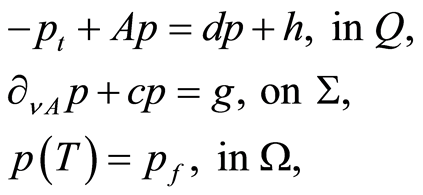 (1.21)
(1.21)
with ,
, 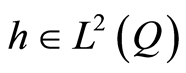 ,
, 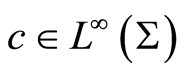 ,
,  and
and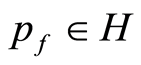 . All results of Theorem 2 are valid for (0.21).
. All results of Theorem 2 are valid for (0.21).
Theorem 3 The initial-boundary value problem (1.21) has a unique weak solution 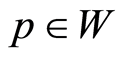 with norm estimates
with norm estimates
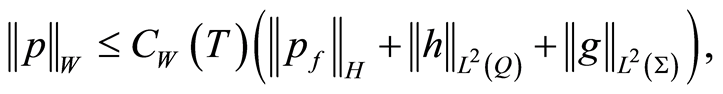 (1.22)
(1.22)
 (1.23)
(1.23)
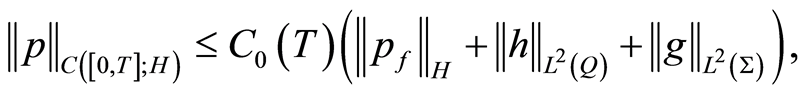 (1.24)
(1.24)
where 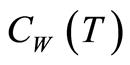 and
and 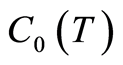 are bounded when
are bounded when  varies boundedly and
varies boundedly and 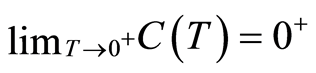 . If
. If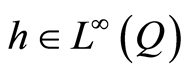 ,
, 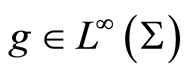 and
and  then
then .
.
Proof 2 The substitution 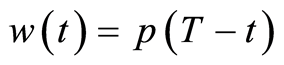 in (0.21) yields the following equivalent problem to the problem (0.11) in the forward form
in (0.21) yields the following equivalent problem to the problem (0.11) in the forward form
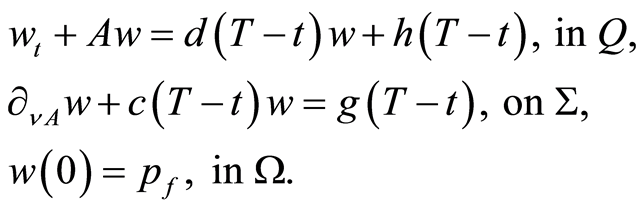 (1.25)
(1.25)
Problem (1.25) satisfies all the assumptions which problem (1.11) satisfies. Therefore the assertions of Theorem 2 and the estimates (1.13)-(1.15) are valid for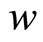 . Since
. Since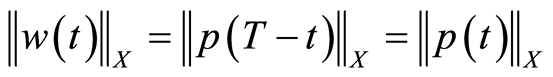 , when
, when 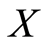 is one of spaces
is one of spaces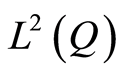 ,
, 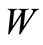 ,
, 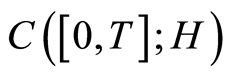 or
or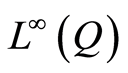 , the assertions of theorem and the estimates (1.22)-(1.24) are verified.
, the assertions of theorem and the estimates (1.22)-(1.24) are verified.
3. The Optimality System
Let 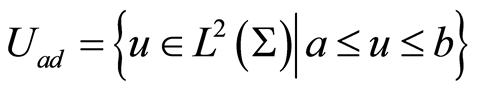 with
with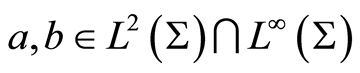 . Consider the following control problem
. Consider the following control problem
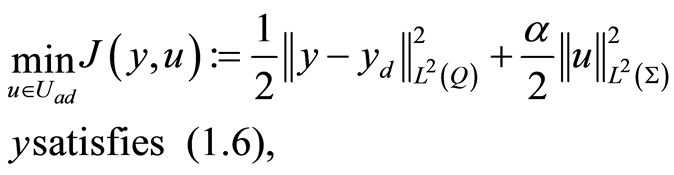 (1.26)
(1.26)
where 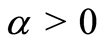 and
and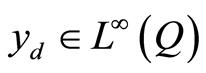 .
.
Theorem 4 Under Assumptions (A1)-(A3) the optimal control problem (0.26) has an optimal solution 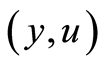 in
in .
.
Proof 3 By Theorem 1 the optimal control problem (0.26) is feasible. Also the Nemytskii operator
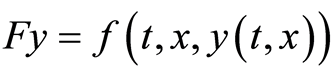 ,
, 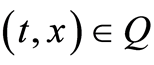 , as an operator from
, as an operator from  into
into 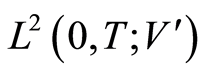 is completely continuous. Because, when
is completely continuous. Because, when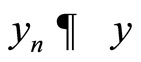 , weakly in
, weakly in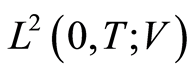 , the compact embedding
, the compact embedding  yields
yields , strongly in
, strongly in . Consequently, the continuity of
. Consequently, the continuity of  and the continuous embedding
and the continuous embedding  results in
results in 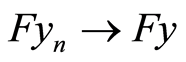 , strongly in
, strongly in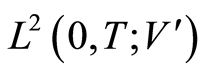 , (confer Assumption (A2)).
, (confer Assumption (A2)).
Thus, the existence of an optimal solution 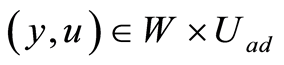 for the problem (1.26) can be deduced from Theorem 1.45 of [1] .
for the problem (1.26) can be deduced from Theorem 1.45 of [1] .
Theorem 5 A necessary condition for 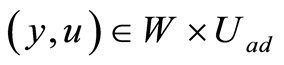 be a local solution (or an optimal solution) of problem (0.26) is that there exists
be a local solution (or an optimal solution) of problem (0.26) is that there exists 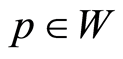 such that
such that
 (1.27)
(1.27)
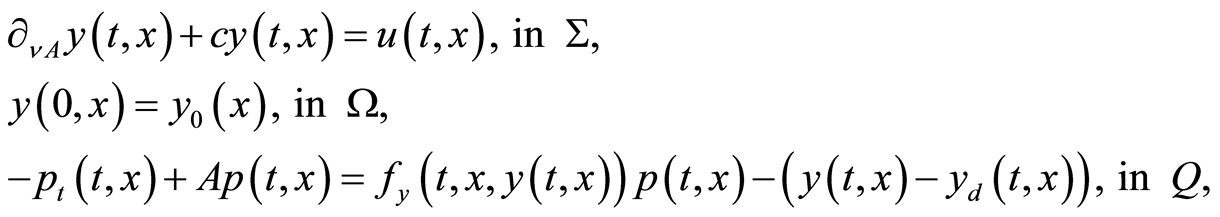 (1.28)
(1.28)
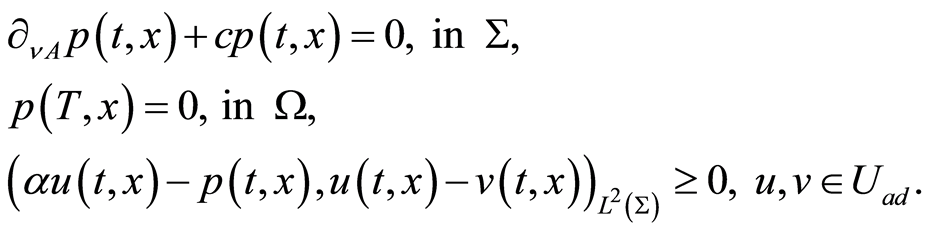 (1.29)
(1.29)
Proof 4 Corollary 1.3 in [1] (or Theorem 1.48 in [1] ).
Theorem 6 Any solution 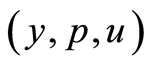 of the optimality system (1.27)-(1.29) belongs to
of the optimality system (1.27)-(1.29) belongs to
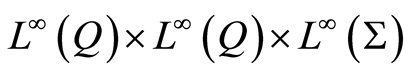 .
.
Proof 5 As 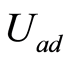 is bounded, utilizing Theorem 2.1 (or Theorem 3.1 in [10] ) it is deduced
is bounded, utilizing Theorem 2.1 (or Theorem 3.1 in [10] ) it is deduced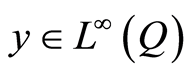 . Then Theorem 2.1 in [10] yields
. Then Theorem 2.1 in [10] yields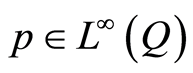 .
.
Lemma 1 The optimality condition (0.29) can be written in the equivalent form bellow:
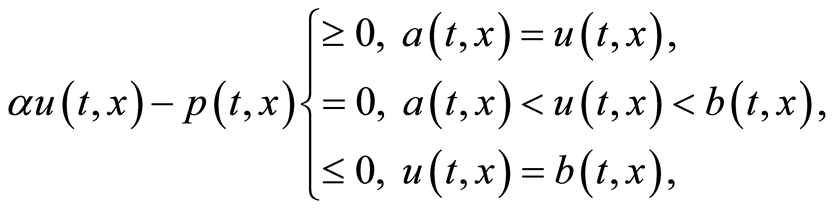 (1.30)
(1.30)
for a.e. .
.
Proof 6 Refer to Lemma 1.12 in [1] .
Corollary 1 Let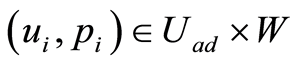 ,
, 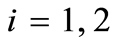 , satisfy (0.30). Then
, satisfy (0.30). Then
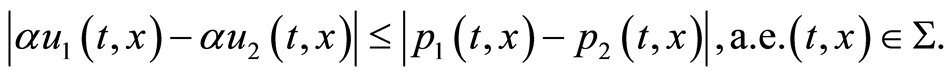 (1.31)
(1.31)
(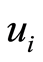 ’s and
’s and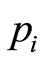 ’s do not necessarily satisfy an optimality system).
’s do not necessarily satisfy an optimality system).
Proof 7 Let  and
and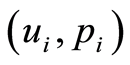 ,
,  , satisfy (0.30) at
, satisfy (0.30) at . Then one of the three cases below occurs for
. Then one of the three cases below occurs for 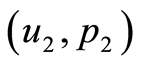 at
at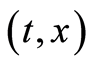 ,
,
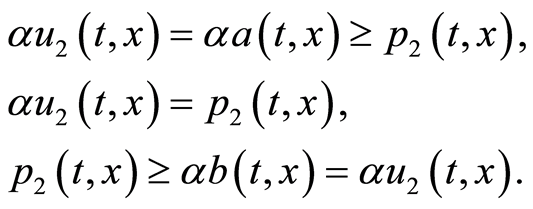
Similarly one of the three such cases occurs for 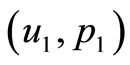 at
at . Let the first case be occurred for
. Let the first case be occurred for  at
at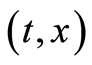 . Then one of the three cases below must be considered for
. Then one of the three cases below must be considered for  at
at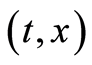 ,
,
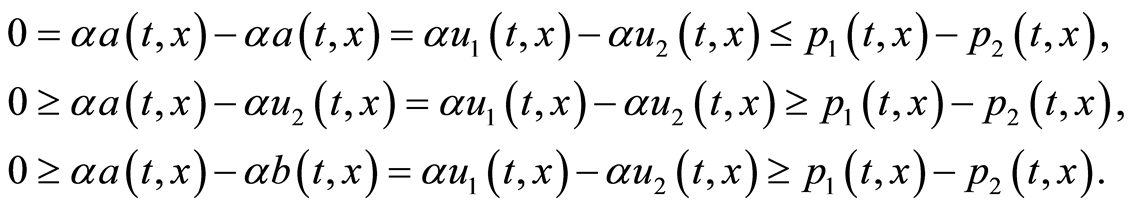
As you see each of the three cases above satisfies (0.31) at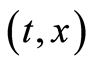 . In a similar argument for each of the two other cases of
. In a similar argument for each of the two other cases of 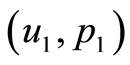 at
at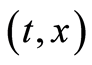 , three relations as the above can be written proving that each of them satisfy (0.31) at
, three relations as the above can be written proving that each of them satisfy (0.31) at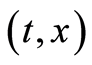 .
.
4. The Quasilinearization Method
Consider problem (1.26) under Assumptions (A1)-(A3). We investigate instead of the optimality system (1.27)- (1.29) the following one wherein the optimality condition (1.29) has been replaced by its equivalent form (1.30), confer Lemma 1:
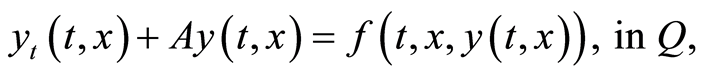 (1.32)
(1.32)
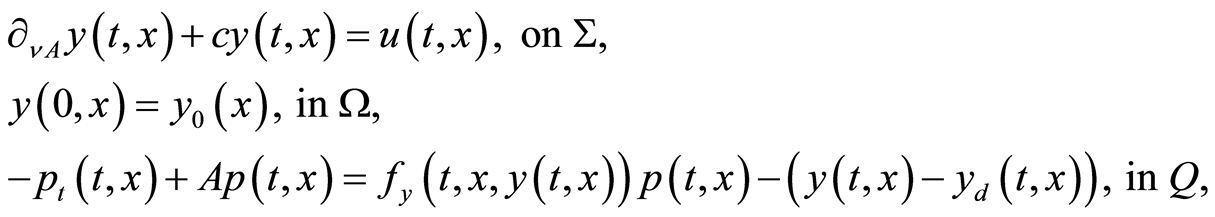 (1.33)
(1.33)
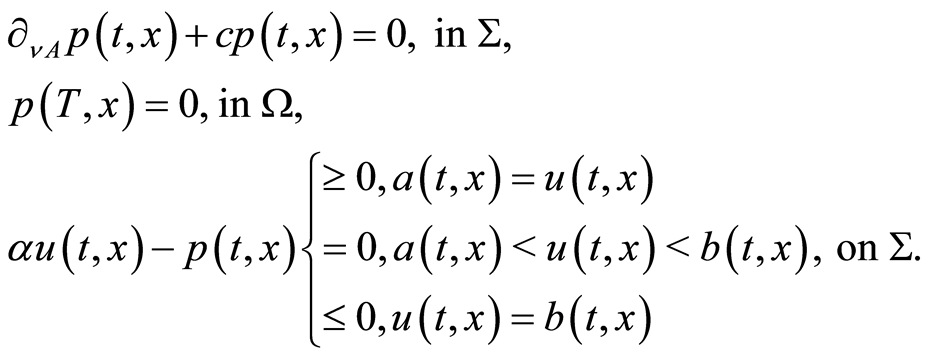 (1.34)
(1.34)
By Theorem 5 and Theorem 4 optimality system (1.32)-(1.34) has at least one solution.
Theorem 7 Let 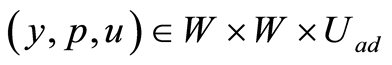 be a solution of optimality system (0.32)-(0.34). Then there exists a sequence
be a solution of optimality system (0.32)-(0.34). Then there exists a sequence 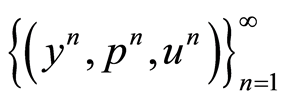 in
in 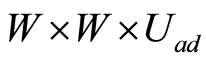 whose elements are the unique solution of the following linear optimality systems and there exists
whose elements are the unique solution of the following linear optimality systems and there exists  such that this sequence converges, at least linearly, to
such that this sequence converges, at least linearly, to 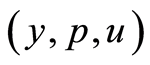 when
when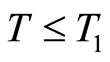 . As a consequence when
. As a consequence when 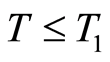 optimality system (1.32)-(1.34) has a unique solution.
optimality system (1.32)-(1.34) has a unique solution.
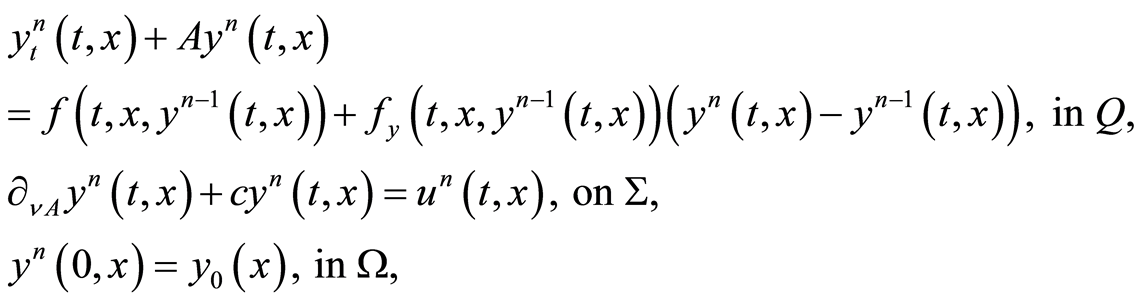 (1.35)
(1.35)
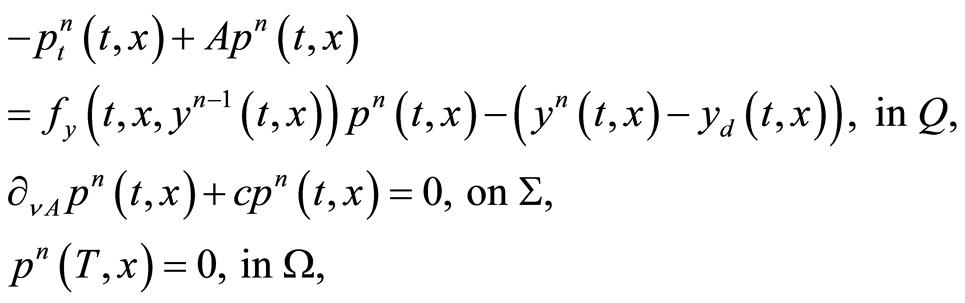 (1.36)
(1.36)
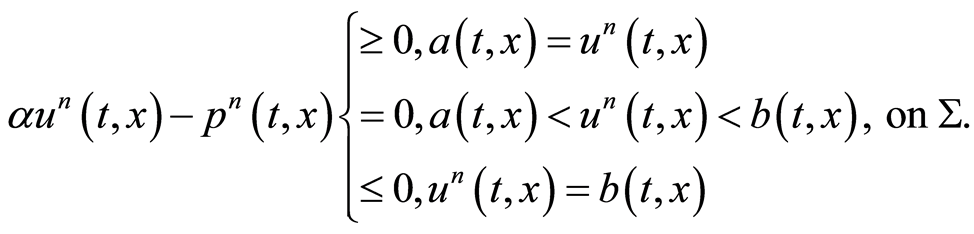 (1.37)
(1.37)
Proof 8 About the existence of sequence 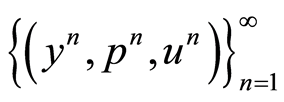 in
in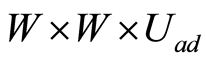 , note that (0.35)-(0.37) is the optimality system of following linear-quadratic optimal control problem
, note that (0.35)-(0.37) is the optimality system of following linear-quadratic optimal control problem
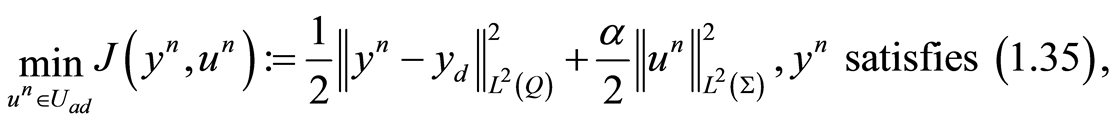 (1.38)
(1.38)
which has a unique optimal solution (Theorem 1.43 [1] ). Then the optimality theory for linear-quadratic optimal control problems yields the existence of a unique solution 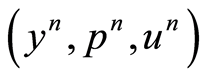 in
in 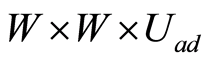 of the system (1.35)- (1.37) when
of the system (1.35)- (1.37) when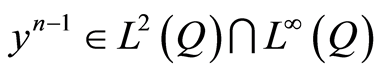 , confer Sections 1.5-1.7 in [1] . Referring to Theorems 2 and 3 it is deduced
, confer Sections 1.5-1.7 in [1] . Referring to Theorems 2 and 3 it is deduced  and
and .
.
Now let  be a solutions of the optimality systems (1.32)-(1.34). Define
be a solutions of the optimality systems (1.32)-(1.34). Define
 (1.39)
(1.39)
Then (1.32) and (1.35) and the mean value theorem yield
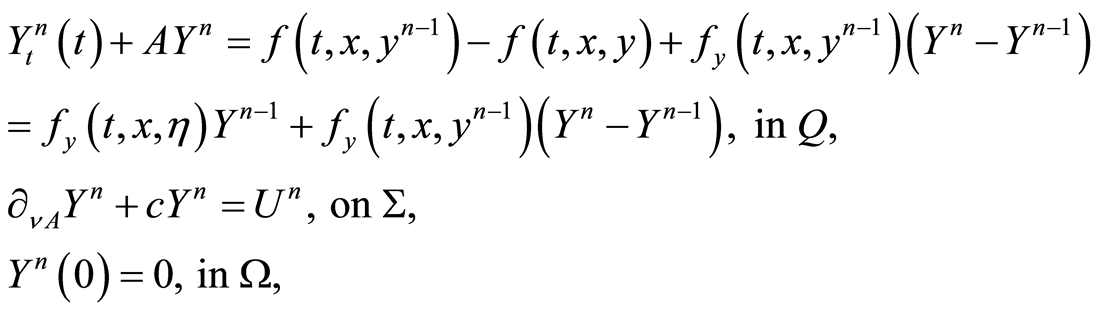 (1.40)
(1.40)
where 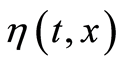 lies between
lies between 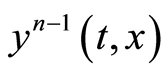 and
and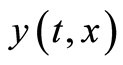 ,
,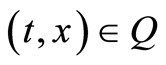 . By Assumption (A3),
. By Assumption (A3),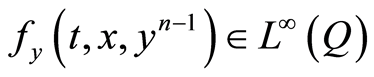 . Thus considering (1.40) as the linear problem (1.11) with
. Thus considering (1.40) as the linear problem (1.11) with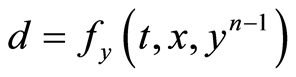 , it is concluded by Theorem 2,
, it is concluded by Theorem 2,
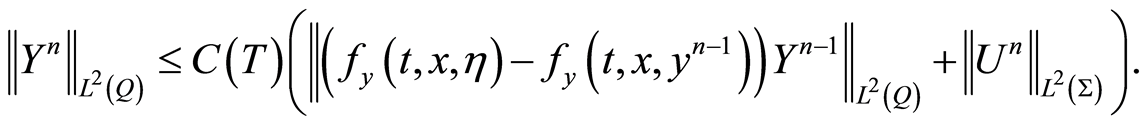 (1.41)
(1.41)
Also (1.33) and (1.36) yield
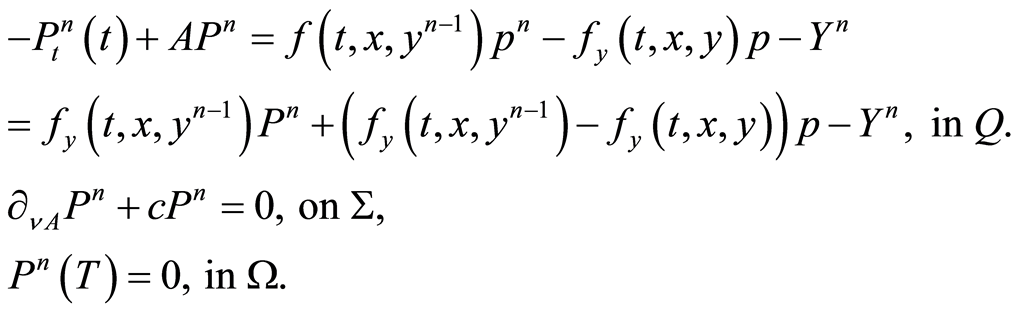 (1.42)
(1.42)
Since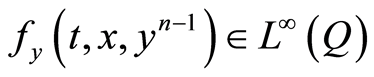 , considering (1.42) as the linear problem (1.21) with
, considering (1.42) as the linear problem (1.21) with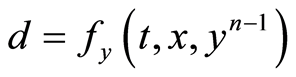 , it is concluded by Theorem 3,
, it is concluded by Theorem 3,
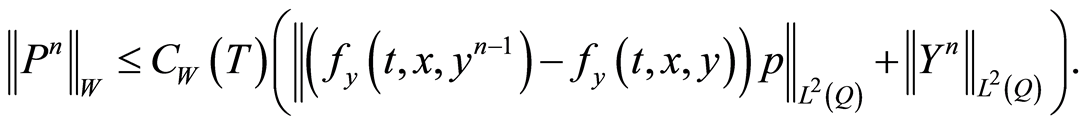 (1.43)
(1.43)
Referring to Theorem 4, 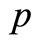 belongs to
belongs to . Consequently employing Assumption (A3) and the mean value theorem, it is obtained
. Consequently employing Assumption (A3) and the mean value theorem, it is obtained
 (1.44)
(1.44)
where 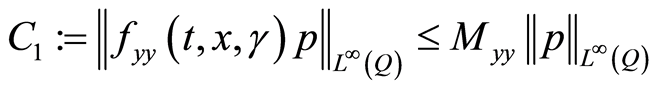 in which
in which  lies between
lies between 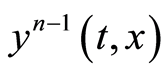 and
and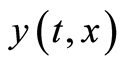 ,
,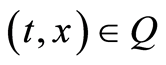 . Therefore (1.43) yields
. Therefore (1.43) yields
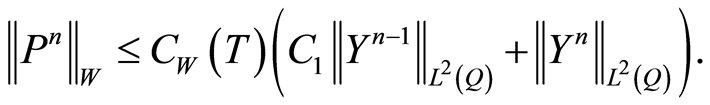 (1.45)
(1.45)
Owing to Corollary 1 and the continuous embeddings 
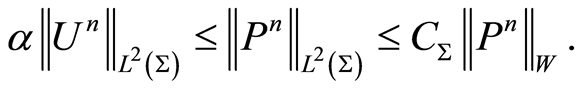 (1.46)
(1.46)
Now combining (1.41), (1.45) and (1.46) results in

Consequently, it is obtained
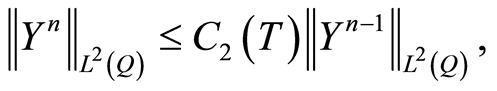 (1.47)
(1.47)
wherein
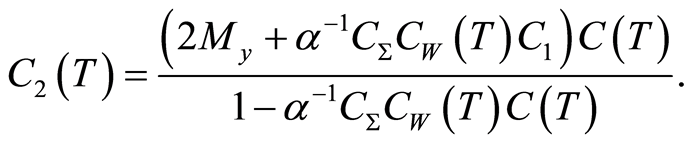 (1.48)
(1.48)
Referring to Theorem 2, 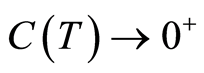 when
when 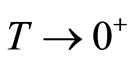 and
and  is bounded. Consequently, there exists
is bounded. Consequently, there exists  such that for
such that for 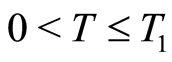 the denumerator in (1.48) be positive and
the denumerator in (1.48) be positive and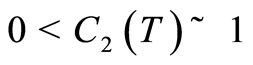 . This yields the convergence of
. This yields the convergence of 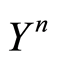 to zero in
to zero in 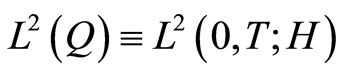 for
for , thereby the convergence of
, thereby the convergence of 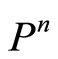 to zero in
to zero in  for
for 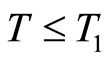 via (1.45) and the convergence of
via (1.45) and the convergence of  to zero in
to zero in  for
for 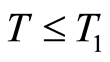 via (1.46). The estimate (1.13) in Theorem 2 for the initial boundary value problem (1.40) yields
via (1.46). The estimate (1.13) in Theorem 2 for the initial boundary value problem (1.40) yields
 (1.49)
(1.49)
where the second inequality is obtained using the mean value theorem. Consequently, the convergence of 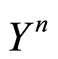 to zero in
to zero in 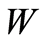 for
for 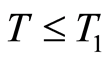 is obtained. Referring to (0.47), the convergence of
is obtained. Referring to (0.47), the convergence of 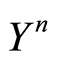 in
in 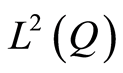 is at least linear whereby the convergence of
is at least linear whereby the convergence of 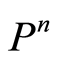 in
in 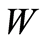 and
and 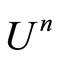 in
in 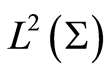 will be at least linear for
will be at least linear for , confer (1.45) and (1.46). Then it is concluded from the estimates (1.49) that the convergence rate of
, confer (1.45) and (1.46). Then it is concluded from the estimates (1.49) that the convergence rate of 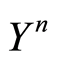 to zero in
to zero in 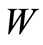 is at least linear for
is at least linear for .
.
The sequence 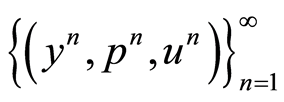 produced by (1.35)-(1.37) is independent from
produced by (1.35)-(1.37) is independent from 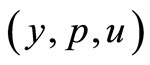 and converges to it in
and converges to it in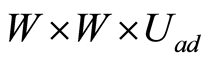 . As
. As 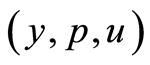 can be any solution of optimality system (1.32)-(1.34) this is impossible except optimality system (1.32)-(1.34) has only one solution.
can be any solution of optimality system (1.32)-(1.34) this is impossible except optimality system (1.32)-(1.34) has only one solution.
The next two corollaries are used in the error analysis in Section 6.
Corollary 2 Under assumptions of Theorem 7 there exists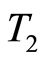 ,
,  , such that for
, such that for 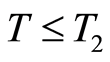 the following estimate is valid
the following estimate is valid
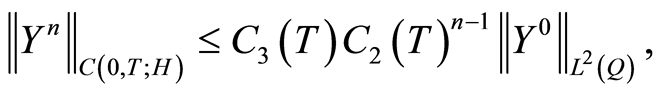 (1.50)
(1.50)
where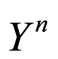 ,
,  and
and 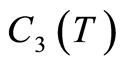 are as in (1.39), (1.48) and (1.53), respectively.
are as in (1.39), (1.48) and (1.53), respectively.
Proof 9 The proof follows the lines of proof of Theorem 7. As 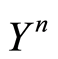 satisfies (0.40) the estimate (0.15) in Theorem 2 yields
satisfies (0.40) the estimate (0.15) in Theorem 2 yields
 (1.51)
(1.51)
Next employing the estimates (1.45) and (1.46) result in
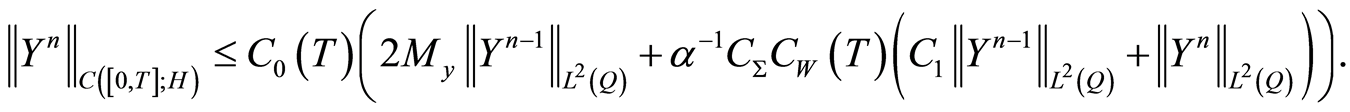
As 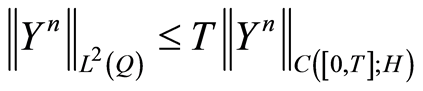 it is deduced from the above inequality
it is deduced from the above inequality
 (1.52)
(1.52)
wherein
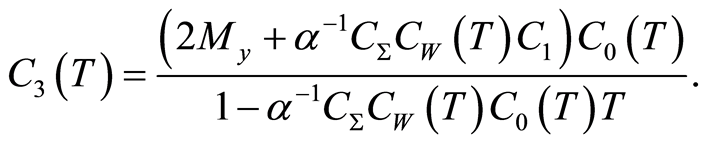 (1.53)
(1.53)
Referring to Theorem 2, 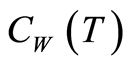 and
and 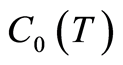 are bounded when
are bounded when 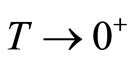 whereby there exists
whereby there exists 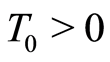 such that the denumerator in (1.53) is positive for
such that the denumerator in (1.53) is positive for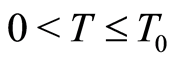 . Set
. Set 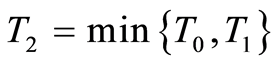 with
with 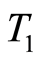 being determined in Theorem 7. Then (1.50) is obtained from (1.52) by repeatedly employing the estimate (1.47).
being determined in Theorem 7. Then (1.50) is obtained from (1.52) by repeatedly employing the estimate (1.47).
Corollary 3 Suppose in the quasilinearization method in Theorem 7 instead of the accurate initial value 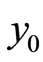 the approximate initial value
the approximate initial value 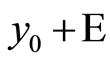 is used. Let
is used. Let  be as in Corollary 2. Then for
be as in Corollary 2. Then for 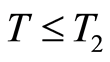 the following estimate is valid
the following estimate is valid
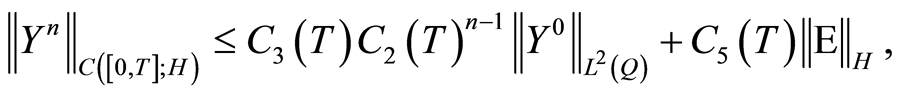 (1.54)
(1.54)
where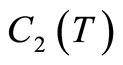 ,
,  and
and 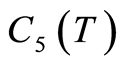 are as in (1.48), (1.53) and (1.59), respectively.
are as in (1.48), (1.53) and (1.59), respectively.
Proof 10 The proof follows the lines of proof of Theorem 7. As 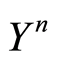 satisfies (1.40) in
satisfies (1.40) in  with
with 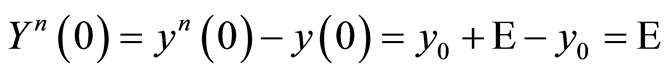 the estimate (1.15) in Theorem 2 yields
the estimate (1.15) in Theorem 2 yields
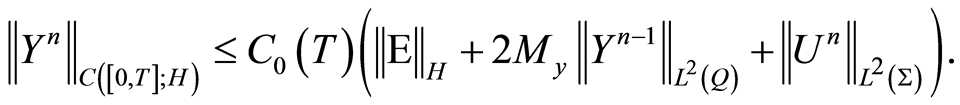 (1.55)
(1.55)
Next employing the estimate (1.45) and (1.46) result in
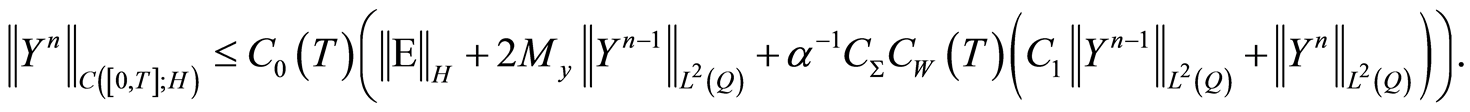
As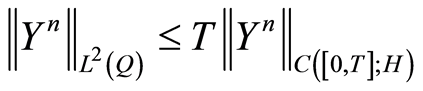 , choosing
, choosing 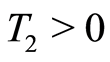 as in Corollary 2, (0.55) for
as in Corollary 2, (0.55) for  yields
yields
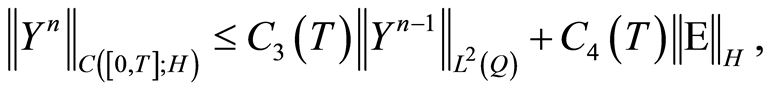 (1.56)
(1.56)
where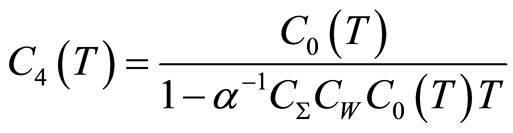 .
.
Now in order to conclude (0.54) we need an estimate like (1.47). (1.47) is for the case 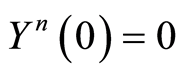 here
here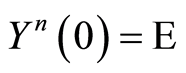 . Such an estimate is obtained following the lines which (1.47) obtained. As
. Such an estimate is obtained following the lines which (1.47) obtained. As 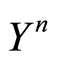 satisfies (1.40) with
satisfies (1.40) with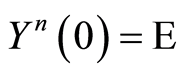 , the estimate (1.14) in Theorem 2 yields
, the estimate (1.14) in Theorem 2 yields
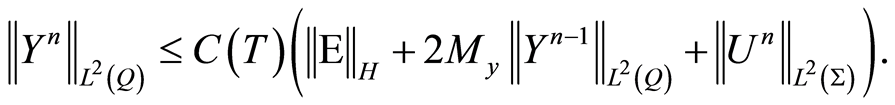
Then employing the estimates (1.45) and (1.46) result in
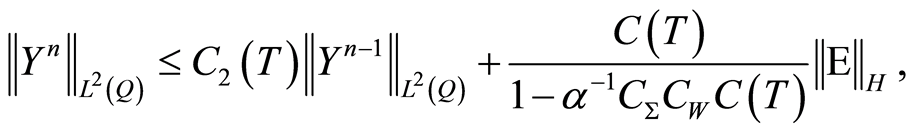
where ,
,  being determined after (1.48). Referring to (1.48), without loss of generality, it is considered
being determined after (1.48). Referring to (1.48), without loss of generality, it is considered  whereby it is obtained
whereby it is obtained
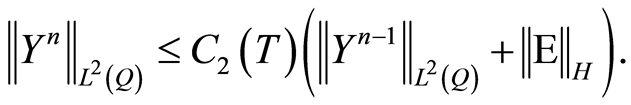 (1.57)
(1.57)
Employing repeatedly (0.57) yields
 (1.58)
(1.58)
where the last inequality is obtained from 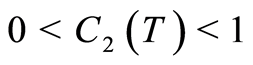 for
for . Now utilizing (1.58) in (1.56) results in (1.54) with
. Now utilizing (1.58) in (1.56) results in (1.54) with
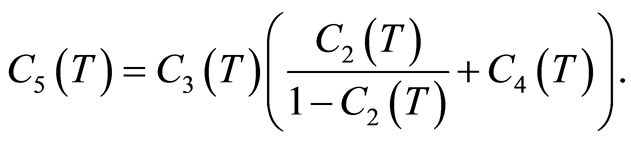 (1.59)
(1.59)
5. Application to the Optimal Boundary Control Problems and the Uniqueness
The proposed quasilinearization method in Theorem 7 is convergent on the time intervals 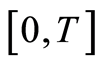 for
for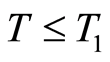 ,
, 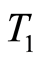 being determined in Theorem 7. In order to apply the quasilinearization method to the optimal control problem (1.26) up to an arbitrary final time
being determined in Theorem 7. In order to apply the quasilinearization method to the optimal control problem (1.26) up to an arbitrary final time  it is possible to decompose the problem into many finite optimal control problems each on an interval with length less than
it is possible to decompose the problem into many finite optimal control problems each on an interval with length less than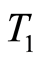 . In order to follow such an approach let
. In order to follow such an approach let  1
1
and 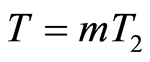 for some
for some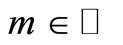 . Let
. Let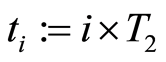 ,
, 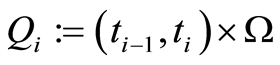 and
and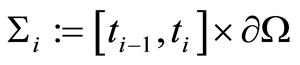 ,
, . Let
. Let 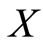 be a Banach space. Then
be a Banach space. Then 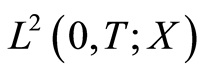 is normisomorphic to
is normisomorphic to 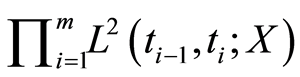 through the isomorphism
through the isomorphism
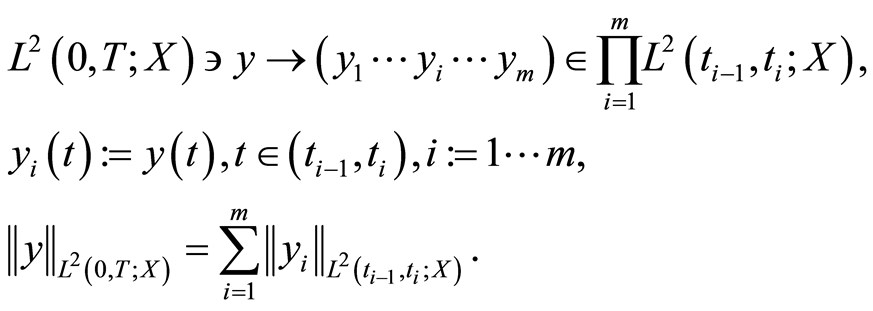
Replacing 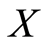 by
by 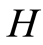 yields that
yields that  be normisomorphic to
be normisomorphic to  with the norm identity
with the norm identity , and replacing
, and replacing  by
by 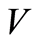 yields that
yields that 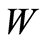 be normisomorphic to the closed subspace
be normisomorphic to the closed subspace 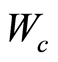 of
of 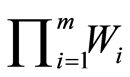 with the norm identity
with the norm identity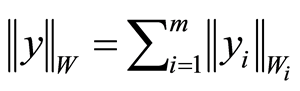 , where
, where
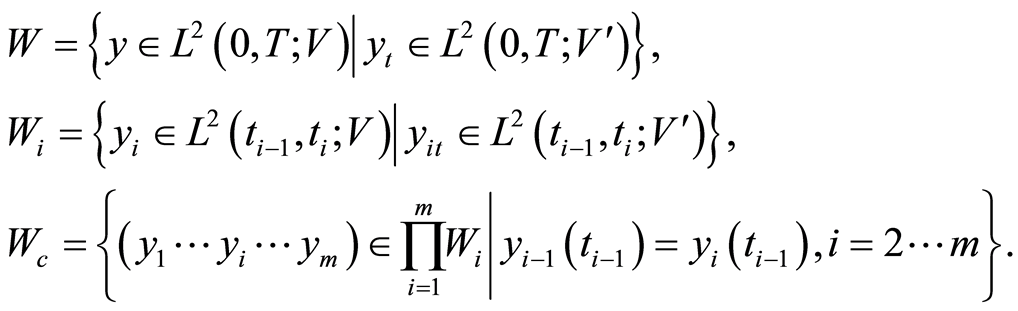
Thus, if 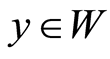 satisfies the initial-boundary value problem (0.6) then
satisfies the initial-boundary value problem (0.6) then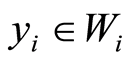 ,
, 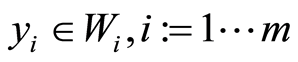 , satisfy consecutively the following initial-boundary value problems and vice versa:
, satisfy consecutively the following initial-boundary value problems and vice versa:
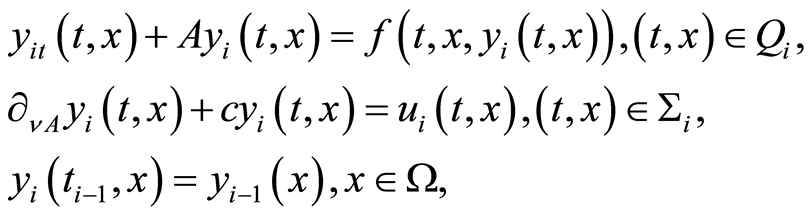 (1.60)
(1.60)
wherein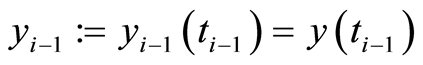 . Consequently, the optimal control problem (1.26) is equivalent to the consecutive optimal control subproblems
. Consequently, the optimal control problem (1.26) is equivalent to the consecutive optimal control subproblems
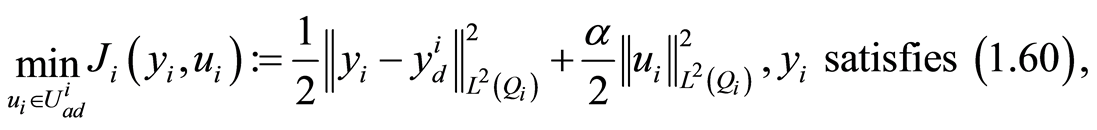 (1.61)
(1.61)
wherein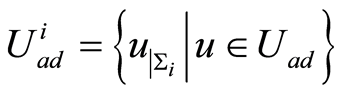 . Therefore, solving the optimal control problem (1.26) is equivalent to consecutively solving the optimal control subproblems (1.61). Furthermore, the proposed quasilinearization method in Theorem 7 is applicable to each optimal control subproblem in (1.61). In fact the substitution
. Therefore, solving the optimal control problem (1.26) is equivalent to consecutively solving the optimal control subproblems (1.61). Furthermore, the proposed quasilinearization method in Theorem 7 is applicable to each optimal control subproblem in (1.61). In fact the substitution 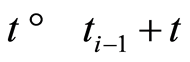 in the
in the 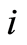 -th subproblem in (1.61) transforms it into an equivalent problem on the time interval
-th subproblem in (1.61) transforms it into an equivalent problem on the time interval 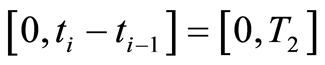 whereby the quasilinearization method will be applicable to it.
whereby the quasilinearization method will be applicable to it.
Moreover, as a consequence of Theorem 7 the solution of optimality system of  -th subproblem in (1.61) is unique. Thus, in view of Theorem’s 4 and 5, each subproblem in (1.61) has a unique optimal solution. Consequently by the equivalence between problem (1.26) and consecutive subproblems (1.61) it can be stated Theorem 8 Optimal boundary control problem (1.26) under Assumptions (A1)-(A3) has unique optimal boundary control solution and optimal state solution.
-th subproblem in (1.61) is unique. Thus, in view of Theorem’s 4 and 5, each subproblem in (1.61) has a unique optimal solution. Consequently by the equivalence between problem (1.26) and consecutive subproblems (1.61) it can be stated Theorem 8 Optimal boundary control problem (1.26) under Assumptions (A1)-(A3) has unique optimal boundary control solution and optimal state solution.
Note that the uniqueness could not be established thorough the optimality theory of optimal control problems which was used for stating the existence in Section 3. This is due to lack of convexity of the solution set of problem (1.26).
An issue concerning the above consecutive process is the relation between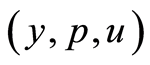 , the solution of optimality system of problem (1.26), and
, the solution of optimality system of problem (1.26), and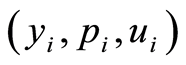 , the solution of optimality system of
, the solution of optimality system of 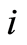 -th subproblem in (1.61).
-th subproblem in (1.61). 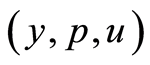 satisfies (1.27)-(1.29) on
satisfies (1.27)-(1.29) on 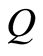 and
and 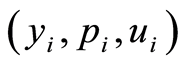 satisfies
satisfies
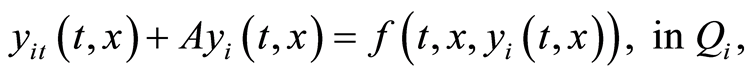 (1.62)
(1.62)
 (1.63)
(1.63)
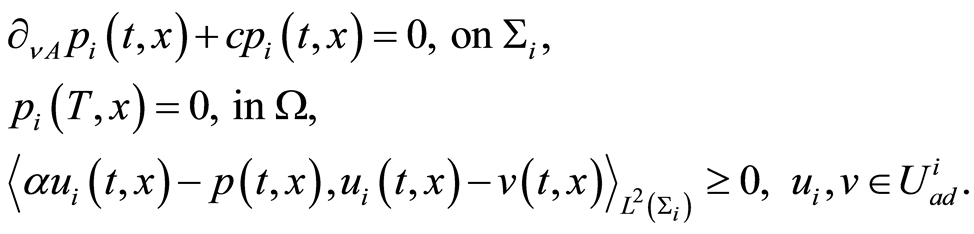 (1.64)
(1.64)
In view of Theorem’s 8, 4 and 5 optimality system of problem (1.26) has a unique solution. Consequenty comparing (1.61)-(1.64) with (1.26)-(1.29) it is concluded that 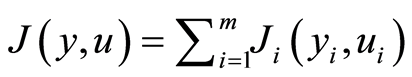 and
and ,
, 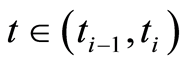 , and
, and ,
,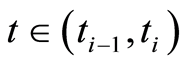 . But there is not a similar relation between the costates
. But there is not a similar relation between the costates 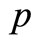 and
and
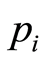 ’s, since
’s, since  satisfies (1.63) and
satisfies (1.63) and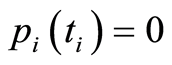 , but
, but  is not necessarily zero; confer (1.28). Also it is not possible in general to construct
is not necessarily zero; confer (1.28). Also it is not possible in general to construct 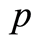 from
from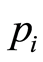 ’s; however, after obtaining
’s; however, after obtaining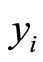 ’s,
’s,  can be computed from (1.28).
can be computed from (1.28).
6. Error Analysis
By the consecutive quasilinearization method in Section 5, the optimal control problem (1.26) is solved through m consecutive optimal control subproblems (1.61). Each subproblem is solved by the quasilinearization method in Theorem 7 which is an iterative method with infinite iterations. In applications it is implemented up to a finite iterations, thereby producing error. Consequently, during solving each subproblem there exists an error production and an error propagation.
Let 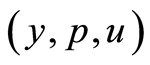 be the solution of optimality system (1.32)-(1.34),
be the solution of optimality system (1.32)-(1.34), 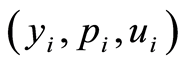 be the solution of i-th optimality system (0.62)-(0.64) and
be the solution of i-th optimality system (0.62)-(0.64) and 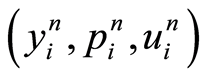 be the solution provided by the quasilinearization method at iteration n for the i-th optimality system, i.e. one which satisfies (1.35)-(1.37) on
be the solution provided by the quasilinearization method at iteration n for the i-th optimality system, i.e. one which satisfies (1.35)-(1.37) on . For the first subproblem the quasilinearization method starts with the accurate initial value
. For the first subproblem the quasilinearization method starts with the accurate initial value 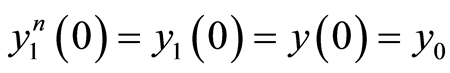 and it is terminated after N iteration with the final value
and it is terminated after N iteration with the final value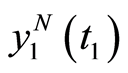 . The error equals to
. The error equals to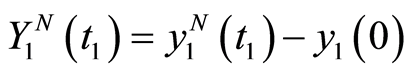 . As
. As 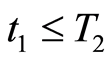 and the initial value is accurate, Corollary 2 with
and the initial value is accurate, Corollary 2 with  yields
yields
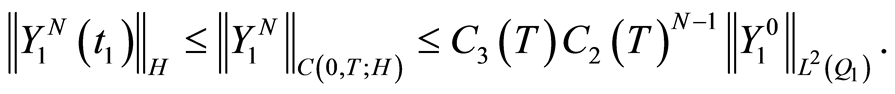 (1.65)
(1.65)
For the i-th subproblem on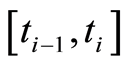 ,
, 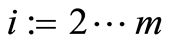 , the quasilinearization method starts with the approximate initial value
, the quasilinearization method starts with the approximate initial value  and it is terminated after N iteration with final value
and it is terminated after N iteration with final value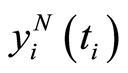 . The error of final value equals to
. The error of final value equals to . Next, we estimate this error.
. Next, we estimate this error.
The substitution  in the i-th subproblem in (1.61) transforms it into an equivalent problem on the time interval
in the i-th subproblem in (1.61) transforms it into an equivalent problem on the time interval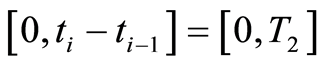 . Setting
. Setting 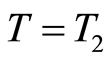 and utilizing Corollary 3 for the equivalent problem, yields the estimate (1.54) with
and utilizing Corollary 3 for the equivalent problem, yields the estimate (1.54) with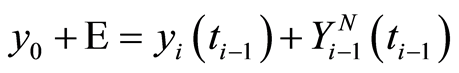 . Then utilizing the reverse substitution
. Then utilizing the reverse substitution 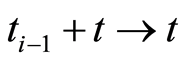 results in the estimate
results in the estimate
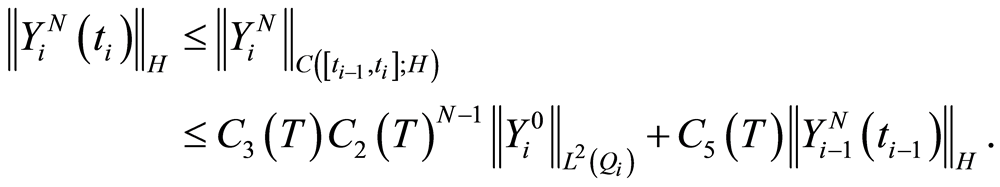 (1.66)
(1.66)
Now beginning from 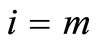 down to
down to , repeatedly employing (1.66) results in
, repeatedly employing (1.66) results in
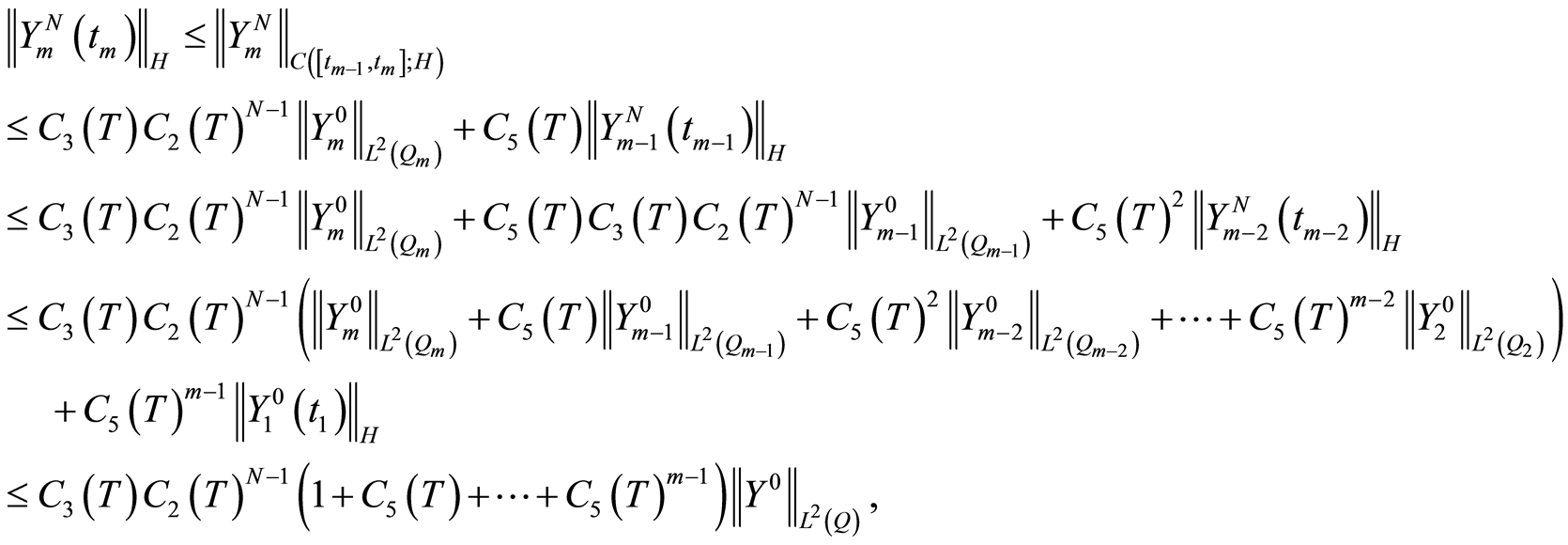
where the last inequality is obtained by 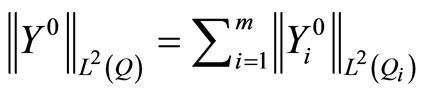 and the estimate (1.65). Consequently,
and the estimate (1.65). Consequently,
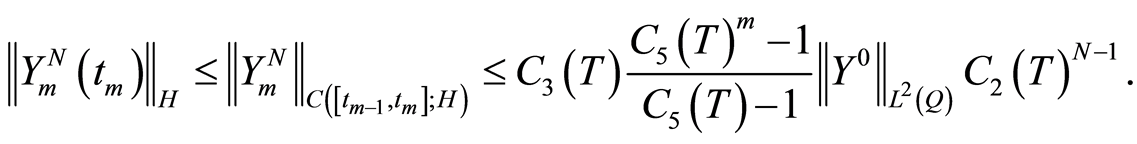 (1.67)
(1.67)
Note that  presents the accumulated error consists of the production errors and the propagation errors in the consecutive implementation of m quasilinearization method, when the implementation is up to N iteration on each subproblem. In the estimate (1.67) the term
presents the accumulated error consists of the production errors and the propagation errors in the consecutive implementation of m quasilinearization method, when the implementation is up to N iteration on each subproblem. In the estimate (1.67) the term 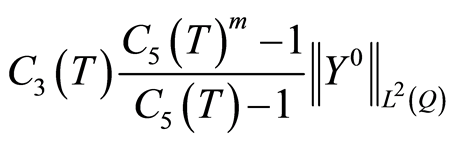 is independent from N and
is independent from N and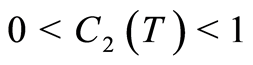 ; confer (1.48) and thereafter. Since m is fixed, by increasing the number of iterations N, the total accumulated error
; confer (1.48) and thereafter. Since m is fixed, by increasing the number of iterations N, the total accumulated error 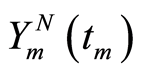 tends to zero in H. Therefore, the proposed consecutive quasilinearization method in Section 5 is stable. Furthermore,
tends to zero in H. Therefore, the proposed consecutive quasilinearization method in Section 5 is stable. Furthermore, 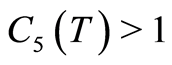 for
for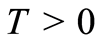 , although
, although  and
and 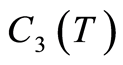 decrease when T decrease (or m increase). Consequently it may a trade off be necessary between size of m (the number of subproblems) and N (the number of required iterations in the implementation of quasilinearization method) in order to have the desired total error in the consecutive quasilinearization method.
decrease when T decrease (or m increase). Consequently it may a trade off be necessary between size of m (the number of subproblems) and N (the number of required iterations in the implementation of quasilinearization method) in order to have the desired total error in the consecutive quasilinearization method.
7. Numerical Example
A typical example is presented reflecting the obtained results in the previous sections in applications. Consider the optimal control problem (1.26) with the following data: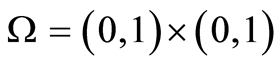 ,
, 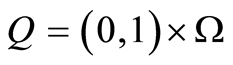 ,
, 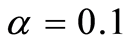 ,
,
 ,
, 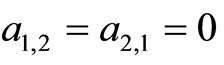 ,
, 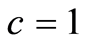 ,
, 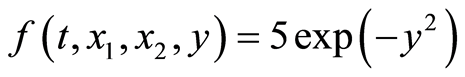 ,
, 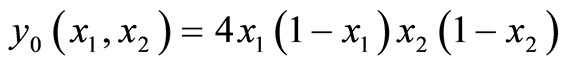 ,
, 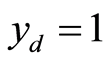 ,
,
 ,
,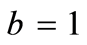 . Setting
. Setting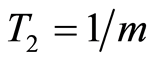 , the consecutive quasilinearization method is implemented on the m consecutive subproblems (1.61) with the optimality systems (1.62)-(1.64). The corresponding states
, the consecutive quasilinearization method is implemented on the m consecutive subproblems (1.61) with the optimality systems (1.62)-(1.64). The corresponding states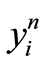 , costates
, costates 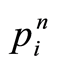 and controls
and controls  are approximated by the elements and boundary elements of continuous linear finite element spaces on
are approximated by the elements and boundary elements of continuous linear finite element spaces on 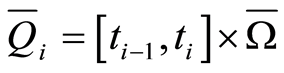 with
with 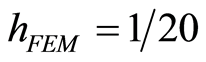 and
and , i.e. without discretization of time. The linear optimality systems (1.62)-(1.64) are solved by the semismooth Newton’s method [16] or Section 2.5 in [1] , and the implementation is done with MATLAB software. Table 1 presents the values of
, i.e. without discretization of time. The linear optimality systems (1.62)-(1.64) are solved by the semismooth Newton’s method [16] or Section 2.5 in [1] , and the implementation is done with MATLAB software. Table 1 presents the values of
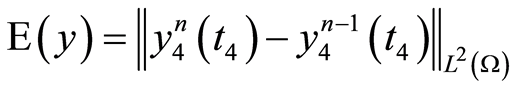 ,
,
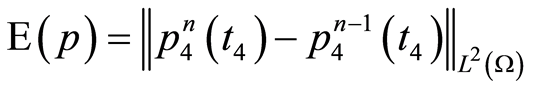
and
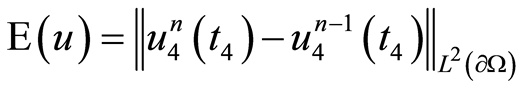 .
.
These values present at least a linear rate of convergence in the quasilinearization method as it was deduced from (1.45)-(1.47).
Table 2 presents the optimal objective values of problem when the consecutive quasilinearization method is implemented with different number of subproblems but fixed number of iterations in each quasilinearization
Table 1. The difference between iterations in the quasilineariztion method for the forth subproblem at t = t4 when m = 15 and the number of iterations is N = 10.
Table 2. The optimal objective values with different number of subproblems, m, but fixed number of iterations in the quasilinearization method, i.e. N = 5.
method, i.e. with different m’s and fixed N. As 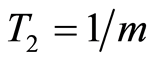 is in some sense the step size of time discretization, its increment yields more accurate approximation to the optimal objective value.
is in some sense the step size of time discretization, its increment yields more accurate approximation to the optimal objective value.
8. Conclusions
A consecutive quasilinearization method was proposed for the optimal boundary control problems with quadratic objective of tracking type and a semilinear parabolic equation with mixed boundary as the state constraint; cf.
(1.26) and (1.32). The proposed method divides the control problem equivalently into many finite consecutive subproblems through partitioning the time interval into subintervals; cf. Section 5 and (1.61). Then subproblems are solved consecutively by a quasilinearization method (hence the name of proposed method). Finally the optimal solution of control problem is obtained by consecutively merging optimal solutions of subproblems. The quasilinearization method for each subproblem constructs an infinite sequence of linear-quadratic optimal boundary control problems of form (1.38). The sequence of solutions to the optimality systems of these linear problems converges to any solutions of the optimality system of subproblem; confer Theorem 7 and Section 5. This implies the uniqueness of solution to the optimality system of a subproblem, hence the uniqueness of optimal solution to the original control problem; confer Theorem 8. This uniqueness result is new, on the best of our knowledge, in the class of optimal control problems with state constraint of semilinear parabolic equation type.
The convergence of quasilinearization method for each subproblem depends on the time interval length of the subproblem, 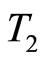 , and there is a bound on
, and there is a bound on 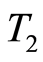 which the convergence occurs,
which the convergence occurs, 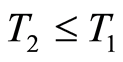 ,
, 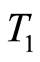 being determined in Theorem 7. In comparison with methods which require the fully discretization of original control problem, cf. Chapter 2 in [1] , [2] and [17] ,
being determined in Theorem 7. In comparison with methods which require the fully discretization of original control problem, cf. Chapter 2 in [1] , [2] and [17] , 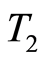 can be considered as the time discretization step length. In this view the consecutive feature of proposed method replaces the large scale computations in fully discrete methods by the consecutive small scale computations in the subproblems, hence increasing the machine applicability of method. Specially in quasilinearization method in solving the sequence of linear-quadratic control problems the time discretization can be avoided by choosing
can be considered as the time discretization step length. In this view the consecutive feature of proposed method replaces the large scale computations in fully discrete methods by the consecutive small scale computations in the subproblems, hence increasing the machine applicability of method. Specially in quasilinearization method in solving the sequence of linear-quadratic control problems the time discretization can be avoided by choosing  enough small , cf. Section 7.
enough small , cf. Section 7.
In comparison with superlinear methods which are locally convergent, as different versions of Newton’s method and/or Lagrange-SQP methods (Chapter 2 in [1] , and [2] ), the consecutive quasilinearization method is globally convergent and its convergence order is at least linear, cf. Theorem 7. For example Table 1 of Section 7 presents a cubic convergence rate. Thereby the consecutive quasilinearization method is very suitable for the globalization of locally convergent methods by applying it to find a starting solution for those methods.
The quasilinearization method for subproblems has infinite iterations, but in applications it is implemented up to a finite iteration. Therefore its consecutive application on the subproblems produces and propagates errors. However choosing 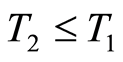 guarantees the numerical stability, cf. Section 6.
guarantees the numerical stability, cf. Section 6.
The imposed boundedness assumptions on the nonlinearity of problem and the admissible controls are necessary for the convergence proof, cf. Assumption (A3), Section 3 and proof of Theorem 7. As the investigated control problem here also has optimal solution with much weaker boundedness assumptions, cf. [10] , application of consecutive quasilinearization method in this case requires new convergence proof.
References
- Hinze, M., Pinnau, R., Ulbrich, M. and Ulbrich, S. (2009) Optimization with PDE Constraints. Springer, Berlin.
- Trötzsch, F. (1999) On the Lagrange-Newton-SQP Method for the Optimal Control of Semilinear Parabolic Equations. SIAM Journal on Control and Optimization, 38, 294-312. http://dx.doi.org/10.1137/S0363012998341423
- Bellman, R. and Kalaba, R. (1965) Quasilinearization and Nonlinear Boundary-Value Problems. American Elsevier Publishing Company, New York.
- Bellman, R. (1955) Functional Equations in the Theory of Dynamic Programming. V. Positivity and Quasi-Linearity. Proceedings of the National Academy of Sciences of the United States of America, 41, 743-746. http://dx.doi.org/10.1073/pnas.41.10.743
- Buica, A. and Precup, R. (2002) Abstract Generalized Quasilinearization Method for Coincidences. Nonlinear Studies, 9, 371-386.
- Lakshmikantham, V. and Vatsala, A.S. (1995) Generalized Quasilinearization for Nonlinear Problems. Kluwer Academic Publishers, Dordrecht.
- Carl, S. and Lakshmikantham, V. (2002) Generalized Quasilinearization and Semilinear Parabolic Problems. Nonlinear Analysis, 48, 947-960. http://dx.doi.org/10.1016/S0362-546X(00)00225-X
- Beckenbach, E.F. and Bellman, R. (1961) Inequalities. Springer-Verlag, Berlin.
- Kalaba, R. (1959) On Nonlinear Differential Equations, the Maximum Operation, and Monotone Convergence. Journal of Mathematics and Mechanics, 8, 519-574.
- Raymond, J.P. and Zidani, H. (1999) Hamiltonian Pontryagin’s Principles for Control Problems Governed by Semilinear Parabolic Equations. Applied Mathematics and Optimization, 39, 143-177. http://dx.doi.org/10.1007/s002459900102
- Showalter, R.E. (1997) Monotone Operators in Banach Spaces and Nonlinear Partial Differential Equations. American Mathematical Society, Providence.
- Evans, L.C. (1998) Partial Differential Equations. American Mathematical Society, Providence.
- Ladyzenskaja, O.A., Solonnikov, V.A. and Ural’ceva, N.N. (1968) Linear and Quasi-Linear Equations of Parabolic Type. American Mathematical Society, Providence.
- Zeidler, E. (1990) Nonlinear Functional Analysis and Its Applications Vol II/A: Linear Monotone Operators. Springer, Berlin.
- Showalter, R.E. (1994) Hilbert Space Methods for Partial Differential Equations. Electronic Journal of Differential Equations, Monograph 01, Dover Publications, Mineola.
- Ulbrich, M. (2011) Semismooth Newton Methods for Variational Inequalities and Constrained Optimization Problems in Function Spaces. SIAM. http://dx.doi.org/10.1137/1.9781611970692
NOTES
*Corresponding author.
1In order to preserve the stability, T2 is chosen as in Corollary 2 (also confer Section 6).


