Applied Mathematics
Vol.4 No.10C(2013), Article ID:38417,22 pages DOI:10.4236/am.2013.410A3013
Hidden Symmetries of Lax Integrable Nonlinear Systems
1Department of Mathematical Sciences, New Jersey Institute of Technology, Newark, USA
2Department of Mathematics, Agriculture University, Krakow, Poland
3Department of Applied Mathematics, AGH University of Science and Technology, Krakow, Poland
Email: deblac@m.njit.edu, yarpry@gmail.com, golenia@agh.edu.pl, prykanat@ua.fm
Copyright © 2013 Denis Blackmore et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 29, 2013; revised May 29, 2013; accepted June 7, 2013
Keywords: Lie-Algebraic Approach; Marsden-Weinstein Reduction Method; R-Matrix Structure; Poissonian Manifold; Differential-Algebraic Methods; Gradient Holonomic Algorithm; Lax Integrability; Symplectic Structures; Compatible Poissonian Structures; Lax Representation
ABSTRACT
Recently devised new symplectic and differential-algebraic approaches to studying hidden symmetry properties of nonlinear dynamical systems on functional manifolds and their relationships to Lax integrability are reviewed. A new symplectic approach to constructing nonlinear Lax integrable dynamical systems by means of Lie-algebraic tools and based upon the Marsden-Weinstein reduction method on canonically symplectic manifolds with group symmetry, is described. Its natural relationship with the well-known Adler-Kostant-Souriau-Berezin-Kirillov method and the associated R-matrix method [1,2] is analyzed in detail. A new modified differential-algebraic approach to analyzing the Lax integrability of generalized Riemann and Ostrovsky-Vakhnenko type hydrodynamic equations is suggested and the corresponding Lax representations are constructed in exact form. The related bi-Hamiltonian integrability and compatible Poissonian structures of these generalized Riemann type hierarchies are discussed by means of the symplectic, gradientholonomic and geometric methods.
1. Introduction
It is well known that hidden symmetry properties, related to symplectic, differential-geometric, differential-algebraic (D-A) or analytical structures of nonlinear Hamiltonian dynamical systems on functional manifolds, such as an infinite hierarchy of conservation laws and compatible Poissonian structures, often give rise to their Lax integrability. This fact was extensively worked out by many researchers during the past half century and a very powerful so called inverse Lie-algebraic orbit method [1,3-6] of constructing hierarchies of a priori Lax integrable nonlinear dynamical systems was devised. A related direct problem of retrieving these hidden intrinsic symmetries for a priori given well posed nonlinear dynamical system, which are suspected to be Lax integrable, proved to be a very complicated task, whose solution is still far from being solved. Among different approaches to coping with it one can mention, for instance, the classical Kowalewskaya-Painlevé method and its modifications, the Mikhaylov-Shabat [7] recursion operator method, based on analyzing the Lie-Backlund symmetries and some other techniques, which appeared to be reasonably effective in diverse applications, especially for classifying nonlinear integrable dynamical systems possessing special structure. Recently, when studying integrability properties of infinite so called Riemann type hydrodynamical hierarchies, a new direct approach to testing the Lax integrability of a priori given nonlinear dynamical systems with special structure, based on treating the related symplectic and differential-algebraic structures of differentiations, was suggested [8] and devised in [9]. By means of this technique the direct integrability problem was effectively reduced to the classical one of finding the corresponding compatible representations in suitably constructed differential rings.
Concerning the inverse Lie-algebraic orbit method, as its name suggests, it consists [1,3,6,10-12] in studying invariant orbits of the coadjoint group 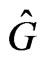 action on a specially chosen element
action on a specially chosen element 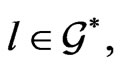 where
where 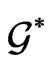 is the conjugate space to the Lie algebra
is the conjugate space to the Lie algebra 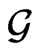 of a suitably chosen, in general formal, group
of a suitably chosen, in general formal, group  In other words, the main Lie-algebraic essence of this approach consists in considering functional invariance and related symplectic properties of these extended orbits in
In other words, the main Lie-algebraic essence of this approach consists in considering functional invariance and related symplectic properties of these extended orbits in 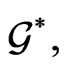 generated by the given element
generated by the given element 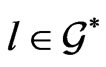 and inherited from the standard Lie algebra structure of
and inherited from the standard Lie algebra structure of 
From this point of view, subject to this extension scheme of constructing a priori Lax integrable dynamical systems, it was natural to search for another way of constructing such systems, but based on a suitably chosen reduction construction of the corresponding coadjoint group 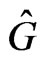 action on the general element
action on the general element 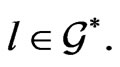 Happily, in modern symplectic geometry such a reduction method was well developed many years ago by Marsden and Weinstein [13,14] and effectively applied to studying integrability properties of some nonlinear dynamical systems [15,16] on finite-dimensional symplectic manifolds. Thus, a next step, consisting in developing this Marsden-Weinstein reduction method and applying it to the case of infinite-dimensional dynamical systems on functional manifolds, was quite natural and effectively realized in [17]. The latter, in particular, made it possible to substantially generalize results of [18] and apply them to studying a new physically feasible and important model in modern quantum physics. As all of the topics, mentioned above and recently studied in our publications, are closely connected to each other, we tried in this work to review those main essentially used analytical, Lie-algebraic and differential-algebraic structures which proved to be algorithmically effective for studying Lax integrability of nonlinear dynamical systems on functional manifolds.
Happily, in modern symplectic geometry such a reduction method was well developed many years ago by Marsden and Weinstein [13,14] and effectively applied to studying integrability properties of some nonlinear dynamical systems [15,16] on finite-dimensional symplectic manifolds. Thus, a next step, consisting in developing this Marsden-Weinstein reduction method and applying it to the case of infinite-dimensional dynamical systems on functional manifolds, was quite natural and effectively realized in [17]. The latter, in particular, made it possible to substantially generalize results of [18] and apply them to studying a new physically feasible and important model in modern quantum physics. As all of the topics, mentioned above and recently studied in our publications, are closely connected to each other, we tried in this work to review those main essentially used analytical, Lie-algebraic and differential-algebraic structures which proved to be algorithmically effective for studying Lax integrability of nonlinear dynamical systems on functional manifolds.
As an important example of applying these recently devised techniques, a new generalized Riemann type hydrodynamic system is studied by means of a novel combination of symplectic and differential-algebraic tools. A compatible pair of polynomial Poissonian structures, a Lax representation and a related infinite hierarchy of conservation laws are constructed. Also analyzed is the complete Lax integrability of the important (for applications) Ostrovsky-Vakhnenko Equation, studied by means of symplectic, gradient-holonomic and differential-algebraic tools. A compatible pair of polynomial Poissonian structures, Lax representations and related infinite hierarchies of conservation laws are also presented.
2. Lax Integrability via Marsden-Weinstein Reduction and the AKS-BK and R-Matrix Approaches
Loop Group, Canonically Symplectic Manifold and Hamiltonian Action
As it is well-known [1,6,13,14], the most popular canonically symplectic manifolds are supplied by cotangent spaces 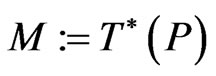 to some “coordinates” phase spaces
to some “coordinates” phase spaces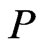 , which can often possess additional symmetry properties. If this symmetry can be identified with a Lie group
, which can often possess additional symmetry properties. If this symmetry can be identified with a Lie group
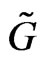 action on the phase space
action on the phase space  and its natural extension on the whole manifold
and its natural extension on the whole manifold  proves to be symplectic and even more, Hamiltonian, the Marsden-Weinstein reduction method [10,13] makes it possible to construct new Hamiltonian flows on the smaller invariant reduced phase space
proves to be symplectic and even more, Hamiltonian, the Marsden-Weinstein reduction method [10,13] makes it possible to construct new Hamiltonian flows on the smaller invariant reduced phase space 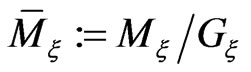 subject to the group invariant constraint
subject to the group invariant constraint 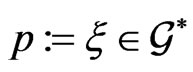 for some specially chosen element
for some specially chosen element , where
, where 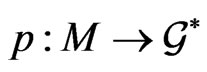 is the related momentum mapping on the symplectic manifold
is the related momentum mapping on the symplectic manifold  and
and  is the adjoint space to the Lie algebra
is the adjoint space to the Lie algebra  of the group Lie
of the group Lie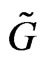 .
.
As the corresponding Hamiltonian flows on the reduced phase space 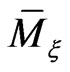 often possess very interesting properties important for applications in many branches of mathematics and physics, they were topics of many investigations during the past decades. As a result of our interest in the mathematical properties of the Lax integrable flows, we observed that their modern Lie algebraic description by means of the Hamiltonian group action classical Lie-Poisson-Adler-Kostant-Berezin-Kirillov scheme on the adjoint space
often possess very interesting properties important for applications in many branches of mathematics and physics, they were topics of many investigations during the past decades. As a result of our interest in the mathematical properties of the Lax integrable flows, we observed that their modern Lie algebraic description by means of the Hamiltonian group action classical Lie-Poisson-Adler-Kostant-Berezin-Kirillov scheme on the adjoint space 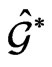 to the Lie algebra
to the Lie algebra 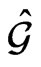 of a suitably chosen group
of a suitably chosen group 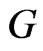 is a natural consequence of applying the Marsden-Weinstein reduction method to the canonical symplectic phase space
is a natural consequence of applying the Marsden-Weinstein reduction method to the canonical symplectic phase space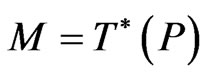 . The basis space
. The basis space , has to be a specially chosen Lie algebra
, has to be a specially chosen Lie algebra  with the naturally related Hamiltonian group
with the naturally related Hamiltonian group 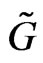 action on the symplectic phase space
action on the symplectic phase space 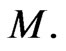 Moreover, such classical integrability theory ingredients as
Moreover, such classical integrability theory ingredients as 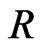 -structures [19] and the related commutation properties of the related transfer matrices are also naturally retrieved from the Marsden-Weinstein reduction method via the scheme specified above.
-structures [19] and the related commutation properties of the related transfer matrices are also naturally retrieved from the Marsden-Weinstein reduction method via the scheme specified above.
Consider a complex matrix Lie group 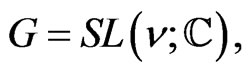
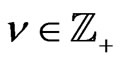 , its Lie algebra
, its Lie algebra , and a related [1,4,6] formal loop group
, and a related [1,4,6] formal loop group 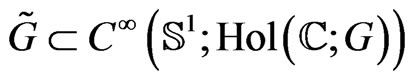 of G-valued functions on the circle
of G-valued functions on the circle , meromorphically depending on the complex parameter
, meromorphically depending on the complex parameter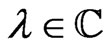 . Its Lie algebra
. Its Lie algebra  can be viewed as the completion
can be viewed as the completion
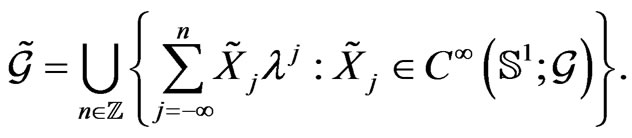 (1)
(1)
By the standard procedure [1,10] one can construct the centrally extended current algebra , on which the adjoint loop group
, on which the adjoint loop group  -action is defined: for any
-action is defined: for any 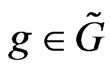
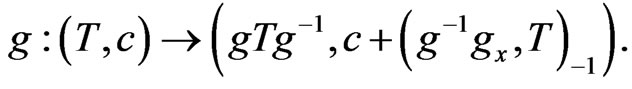 (2)
(2)
Here 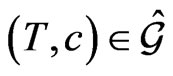 and
and  is the following nondegenerate symmetric scalar product on
is the following nondegenerate symmetric scalar product on :
:
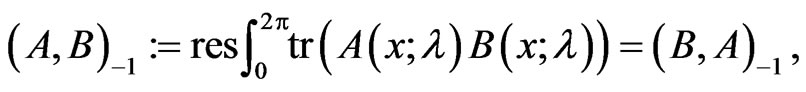 (3)
(3)
for any . The scalar product (3) is ad-invariant, that is
. The scalar product (3) is ad-invariant, that is
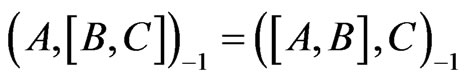 (4)
(4)
for any elements 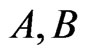 and
and 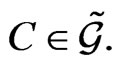
Define now the canonically symplectic phase space
 with the corresponding Liouville 1-form on
with the corresponding Liouville 1-form on 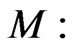
 (5)
(5)
whose exterior derivative gives the symplectic structure on the functional manifold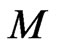 :
:
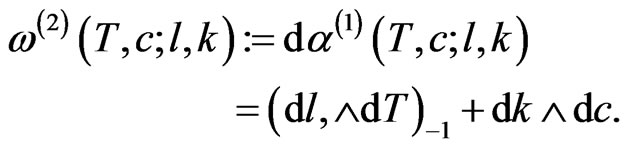 (6)
(6)
Similarly to (2) one can naturally extend the group  -action on the whole phase space
-action on the whole phase space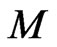 , having
, having
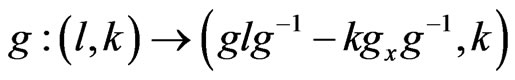 (7)
(7)
for any  and
and 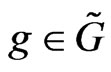 as the corresponding co-adjoint action of the current group
as the corresponding co-adjoint action of the current group  to the adjoint linear space
to the adjoint linear space 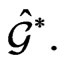 The following lemma is almost selfevident.
The following lemma is almost selfevident.
Lemma 1 The 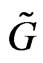 -group action (2) and (7) on the symplectic phase space
-group action (2) and (7) on the symplectic phase space 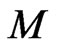 is symplectic and Hamiltonian.
is symplectic and Hamiltonian.
It is easy to check that the canonical Liouville 1-form (5) on the manifold 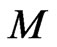 is
is 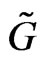 -invariant:
-invariant:
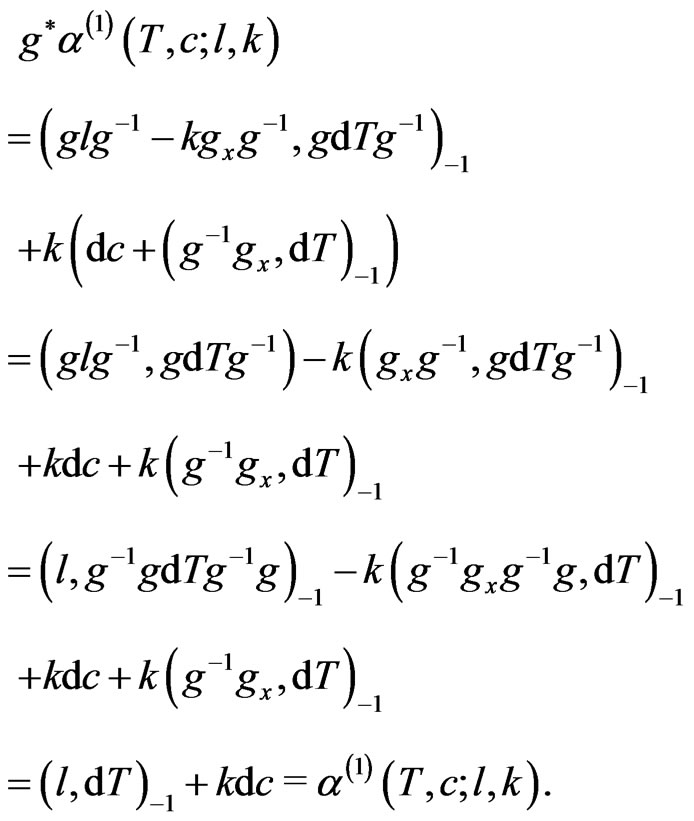 (8)
(8)
From (8), owing to the expression (6), one obtains the symplectic form invariance
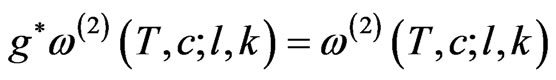 (9)
(9)
for any element 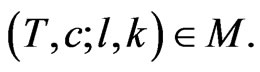
To define the Hamiltonian G-action on the symplectic manifold M we take the group flow 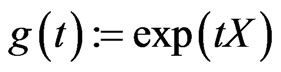 for
for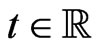 ,
, 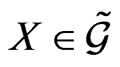 , and find the generated vector field
, and find the generated vector field  on the phase space
on the phase space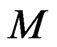 :
:
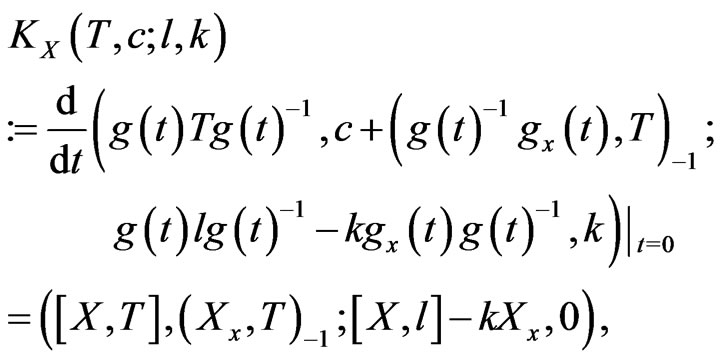 (10)
(10)
by a Hamiltonian function 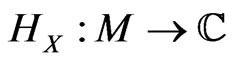 owing to the canonical relationship
owing to the canonical relationship 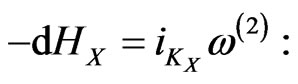
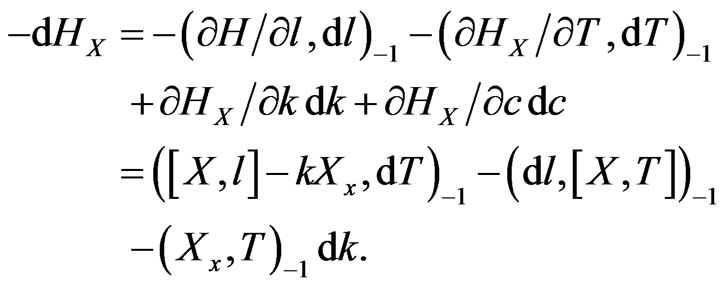 (11)
(11)
As a consequence of (11), one obtains
 (12)
(12)
for any point 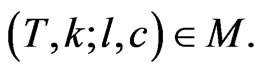 From (12) it follows that
From (12) it follows that
 (13)
(13)
is linear with respect to the generator element 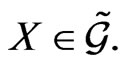 This means that the loop group
This means that the loop group  action on the symplectic manifold
action on the symplectic manifold 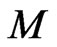 is Hamiltonian by definition [12,13].
is Hamiltonian by definition [12,13].
The corresponding mapping 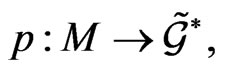 where
where
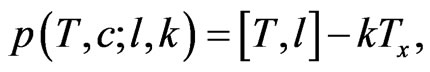 (14)
(14)
is called the momentum mapping [10,12,13] which can be constrained to be fixed for further applications to the phase space 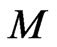 in the Marsden-Weinstein reduction procedure [13].
in the Marsden-Weinstein reduction procedure [13].
Let us describe in detail the related symplectic structure on the 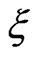 -level submanifold
-level submanifold
 (15)
(15)
for a fixed element  As a more natural case we take that
As a more natural case we take that  The corresponding isotropy group
The corresponding isotropy group
 , as
, as  holds for any element
holds for any element 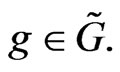
To proceed further, we need some additional properties of the submanifold  which we describe next.
which we describe next.
3. Marsden-Weinstein Reduction and Poisson Brackets
In this section we shall be interested in describing the submanifold 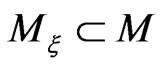 parameterized by the points of the reduced phase space
parameterized by the points of the reduced phase space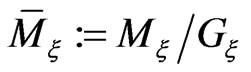 . It is known [13,14] that this parametrization uniquely determines the points
. It is known [13,14] that this parametrization uniquely determines the points  which are invariant with respect to the appropriate loop group
which are invariant with respect to the appropriate loop group  action (2) and (7). The last property makes it possible [10,13,14,20] to define on the phase space
action (2) and (7). The last property makes it possible [10,13,14,20] to define on the phase space  the reduced nondegenerate symplectic structure on the phase space
the reduced nondegenerate symplectic structure on the phase space 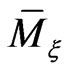 by means of the appropriate symplectic structure on the submanifold
by means of the appropriate symplectic structure on the submanifold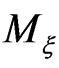 . Let us consider the point
. Let us consider the point 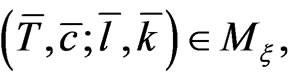
where the elements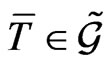 ,
, 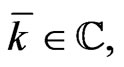 according to the definition (15), satisfy the differential expressions:
according to the definition (15), satisfy the differential expressions:
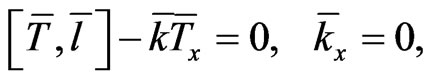 (16)
(16)
for all  Consider now a Hamiltonian vector field
Consider now a Hamiltonian vector field  on the submanifold
on the submanifold 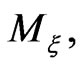 generated by the element
generated by the element 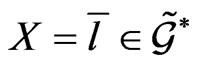 owing to the expressions
owing to the expressions
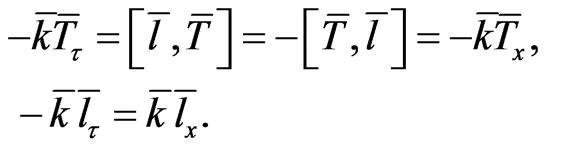 (17)
(17)
From (17) it follows that the equality 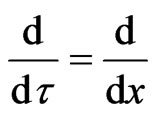 holds on the reduced phase space
holds on the reduced phase space 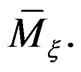 Let us also compute the evolution of the element
Let us also compute the evolution of the element 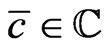 with respect to this vector field
with respect to this vector field 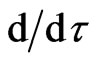 on
on 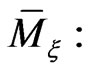
 (18)
(18)
coinciding with the a priori assumed condition 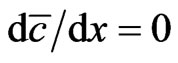 for any
for any 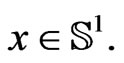
Define similarly a vector field 
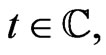 on the reduced phase space
on the reduced phase space 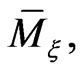 generated by the Lie algebra element
generated by the Lie algebra element 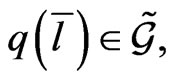 depending on the basis element
depending on the basis element 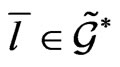 such that
such that
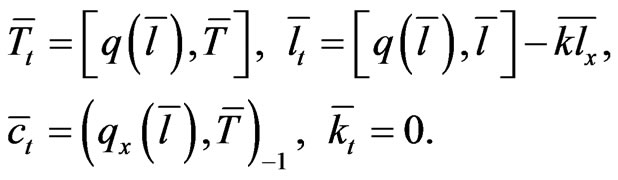 (19)
(19)
This, in particular, means that the flows  and
and  on the reduced phase space
on the reduced phase space  possess the countable set
possess the countable set 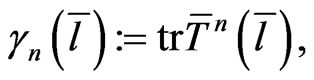
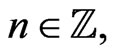 of conservation lows, where by definition, the element
of conservation lows, where by definition, the element 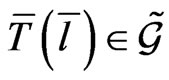 satisfies for a given element
satisfies for a given element 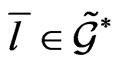 the determining equation
the determining equation
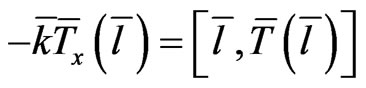 (20)
(20)
for all 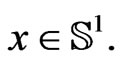 From the Equation (20) one easily finds that upon the reduced phase space
From the Equation (20) one easily finds that upon the reduced phase space 
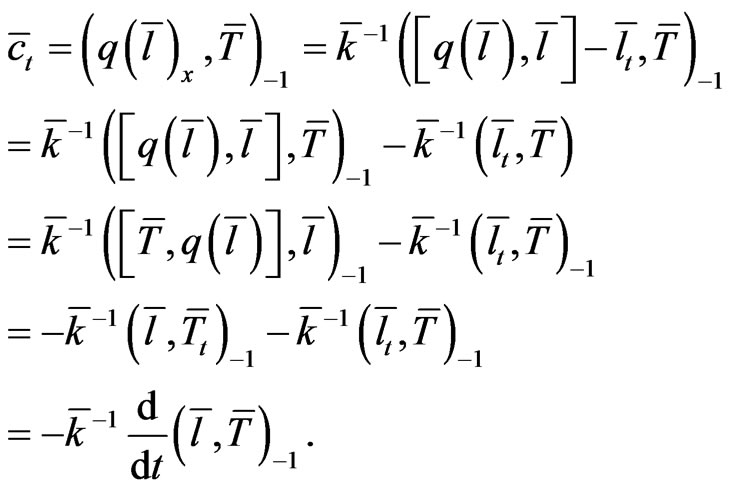 (21)
(21)
Thus, from the  -evolution (21) of the parameter
-evolution (21) of the parameter 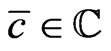 one finds that the constraint
one finds that the constraint
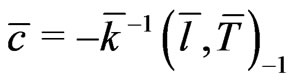 (22)
(22)
holds on the reduced phase space 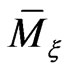 subject to the vector field
subject to the vector field 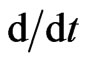 generated by the element
generated by the element  Moreover, as it is easy to observe, these two vector fields
Moreover, as it is easy to observe, these two vector fields 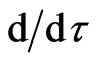 and
and  on the reduced phase space
on the reduced phase space  commute:
commute:
 (23)
(23)
This is very promising, since the condition (23) results in a differential relationships on the components of the reduced matrix 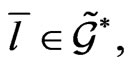 for which the related evolution equation
for which the related evolution equation
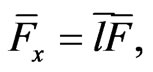 (24)
(24)
and the differential Equation
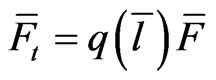 (25)
(25)
for the matrix 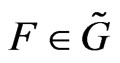 are compatible. These Equations (24) and (25) realize the well-known [1,4-6,10,12] generalized Lax spectral problem, allowing to integrate the above differential relationships by means of either the inverse scattering or the spectral transform methods [1,4,5,21] and algebraic geometry methods [4,5], or their modern generalizations [6].
are compatible. These Equations (24) and (25) realize the well-known [1,4-6,10,12] generalized Lax spectral problem, allowing to integrate the above differential relationships by means of either the inverse scattering or the spectral transform methods [1,4,5,21] and algebraic geometry methods [4,5], or their modern generalizations [6].
To make this aim more constructive, it is necessary to describe the evolution of the vector field 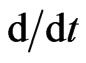 on the reduced phase space
on the reduced phase space  in more detail subject to its dependence on the phase space element
in more detail subject to its dependence on the phase space element  Taking into account that the vector fields
Taking into account that the vector fields 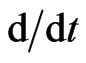 and
and  satisfy the commutation condition (23) on the reduced manifold
satisfy the commutation condition (23) on the reduced manifold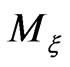 , we will apply Marsden-Weinstein reduction theory to our symplectic manifold
, we will apply Marsden-Weinstein reduction theory to our symplectic manifold  with the fixed value of the moment mapping
with the fixed value of the moment mapping  for computing the Poisson bracket
for computing the Poisson bracket
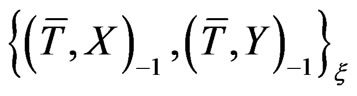 (26)
(26)
of the functions 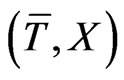 and
and  on the reduced phase space
on the reduced phase space  for arbitrary
for arbitrary  It can be shown [10,20,22] that this Poisson bracket on
It can be shown [10,20,22] that this Poisson bracket on 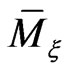 in general is
in general is
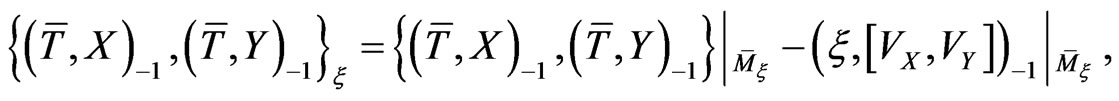 (27)
(27)
where, by definition, the mappings 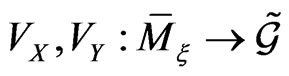 denote the solutions to the relationship
denote the solutions to the relationship
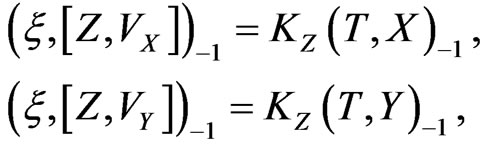 (28)
(28)
which holds for all 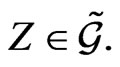 The functions
The functions 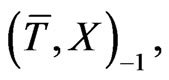
 should be extended to the whole phase space
should be extended to the whole phase space  in such a way that their restrictions on the submanifold
in such a way that their restrictions on the submanifold  are
are  -invariant.
-invariant.
To apply the Marsden-Weinstein reduction, we will take into account that, by definition, there exists a group element 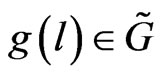 such that for arbitrarily chosen
such that for arbitrarily chosen  the expression
the expression
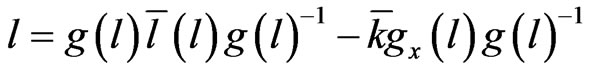 (29)
(29)
holds and satisfies the normalization condition 
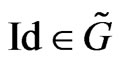 . By considering the function
. By considering the function
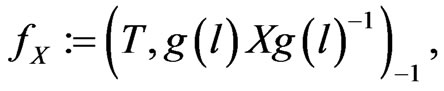 (30)
(30)
one can observe that 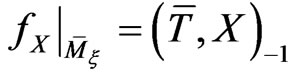 and, by construction, it is
and, by construction, it is 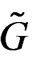 -invariant. This means that
-invariant. This means that 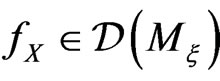 for any
for any 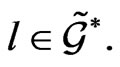 In fact, for any
In fact, for any 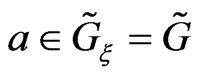
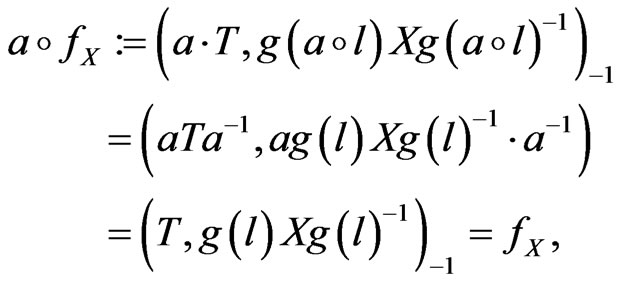 (31)
(31)
where we made use of the property 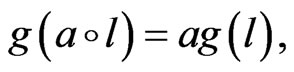
 This holds owing to the definitions (29) and (7):
This holds owing to the definitions (29) and (7):
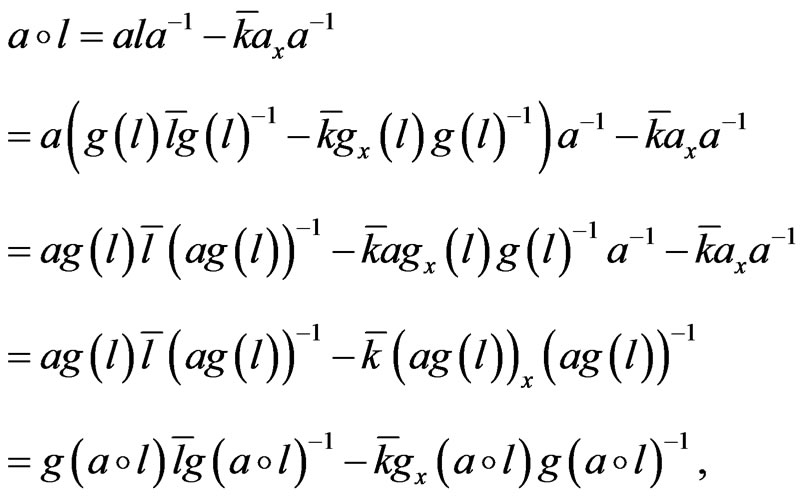 (32)
(32)
giving rise to relationship 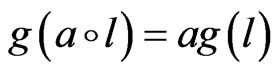 for any
for any  and
and 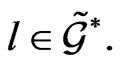
Returning to the Poisson bracket (27), we can replace the functions 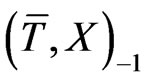 and
and  with their
with their
 -invariant extensions
-invariant extensions  Before calculating the corresponding Poisson bracket
Before calculating the corresponding Poisson bracket
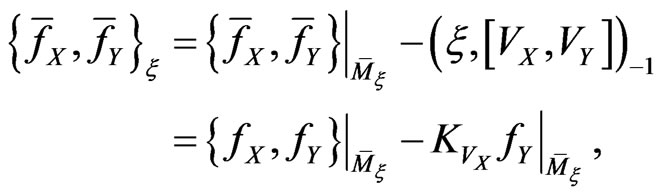 (33)
(33)
where  is the vector field generated on
is the vector field generated on 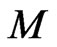 by the element
by the element 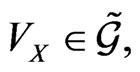 we need to calculate the action
we need to calculate the action 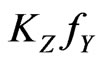 for any element
for any element 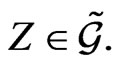 Just as with the calculations from [22], one finds that on the submanifold
Just as with the calculations from [22], one finds that on the submanifold 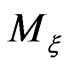
 (34)
(34)
Thus, on the reduced phase space 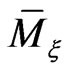 the general expression (34) implies
the general expression (34) implies
 (35)
(35)
Therefore, the Poisson bracket (33), in view of the relationships 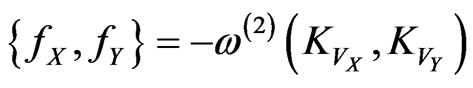 and (35), becomes
and (35), becomes
 (36)
(36)
where we take into account that owing to (28) and (35), the expression
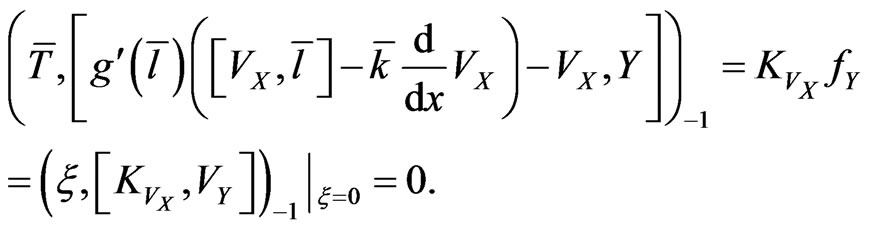
Now one can rewrite the Poisson bracket (36) as
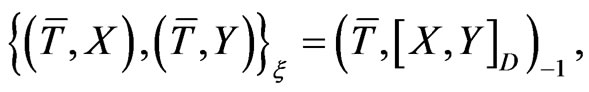 (37)
(37)
where, by definition, we have introduced the classical  -matrix structure in the Lie algebra
-matrix structure in the Lie algebra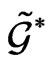 :
:
 (38)
(38)
where 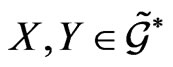 and the linear homomorphism
and the linear homomorphism 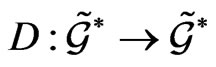 is defined as
is defined as
 (39)
(39)
The mapping (39) should satisfy [23] the well-known condition
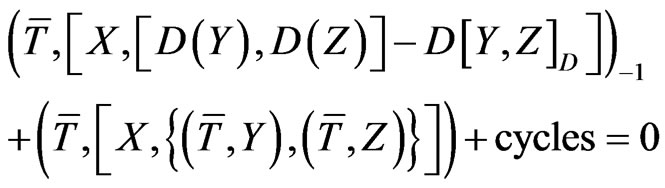 (40)
(40)
for any 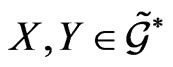 and
and 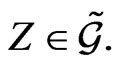
Now it is useful to recall that the mapping 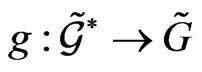 satisfies the relationship (29), which implies [24] the following differential expression
satisfies the relationship (29), which implies [24] the following differential expression
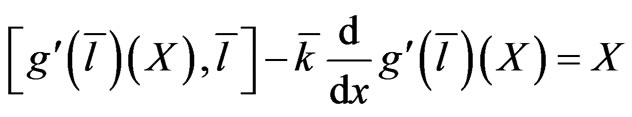 (41)
(41)
for any 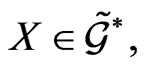 where
where  is the derivative mapping depending on the chosen reduction
is the derivative mapping depending on the chosen reduction 
The mapping (39) satisfies an additional relationship, which can be obtained from the group 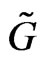 -action on the element
-action on the element 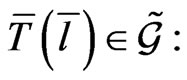
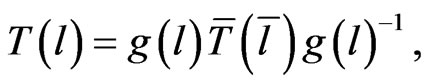 (42)
(42)
following naturally from (29). Differentiation of (42) with respect to 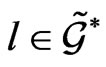 at the point
at the point  gives rise to
gives rise to
 (43)
(43)
for an arbitrary 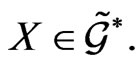 Moreover, since the matrix (42) satisfies the relationship (20), its differentiation with respect to
Moreover, since the matrix (42) satisfies the relationship (20), its differentiation with respect to 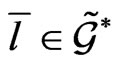 yields the differential expression:
yields the differential expression:
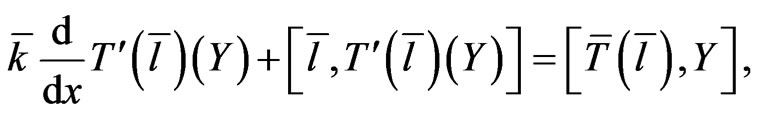 (44)
(44)
which holds for any . The above results can be formulated as the following proposition.
. The above results can be formulated as the following proposition.
Proposition 1 The Poisson bracket (26) on the reduced phase space  represented as a
represented as a 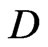 -structure (37) on the linear space
-structure (37) on the linear space , naturally generated by the gauge transformation (29), which reduces the arbitrary element
, naturally generated by the gauge transformation (29), which reduces the arbitrary element 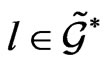 to the element
to the element 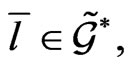 is uniquely defined on
is uniquely defined on 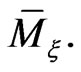
As a consequence of representation (37) we find that there exists an another infinite hierarchy of mutually commuting functionals with respect to the Poisson bracket on the phase space . The latter follows from the tensor form of the Poisson bracket (26) in the space
. The latter follows from the tensor form of the Poisson bracket (26) in the space 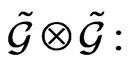
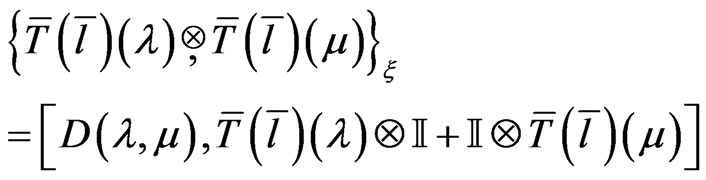 (45)
(45)
which holds for arbitrary 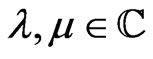 and where
and where 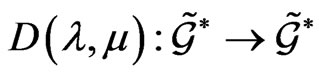 denotes the tensor form of the
denotes the tensor form of the  - structure
- structure 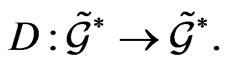 The trace operation in (45) causes the Poisson bracket to vanish on the phase space
The trace operation in (45) causes the Poisson bracket to vanish on the phase space  for the functionals
for the functionals 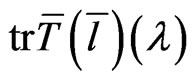 and
and 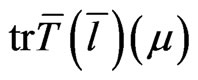 for arbitrary
for arbitrary 
4. Monodromy, R-Structure and Lie-Poisson Brackets
Next we analyze possible forms of the 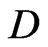 -mapping (39) as a function on the reduced phase space
-mapping (39) as a function on the reduced phase space 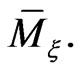 Since
Since 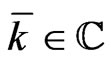 is constant, its value for convenience is set at
is constant, its value for convenience is set at 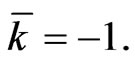 Thus, taking into account the definition (39), the determining
Thus, taking into account the definition (39), the determining  -structure Equation (41) takes the form:
-structure Equation (41) takes the form:
 (46)
(46)
for any element 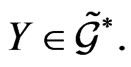
Let us consider the linear matrix Equation
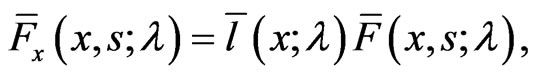 (47)
(47)
where 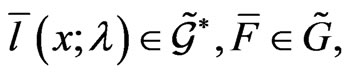 with Cauchy data at a point
with Cauchy data at a point 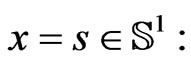
 (48)
(48)
The corresponding normalized monodromy matrix
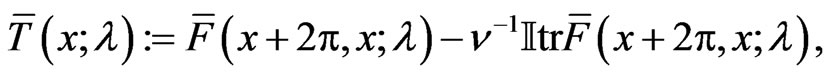 (49)
(49)
for 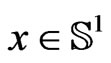 and arbitrary
and arbitrary 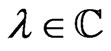 satisfies
satisfies
 (50)
(50)
exactly coinciding with (20). Thus, if by the co-adjoint transformation (7) this chosen matrix  is transformed into the matrix
is transformed into the matrix 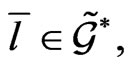 then the corresponding monodromy matrix of (24) transforms into the monodromy matrix of (47), which satisfies (50).
then the corresponding monodromy matrix of (24) transforms into the monodromy matrix of (47), which satisfies (50).
In view of the relationships (47), (48) and (50), one can recalculate the Poisson bracket (37) as
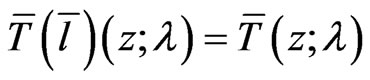 (51)
(51)
for arbitrary 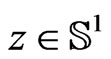 and
and 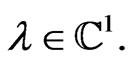 It yields the following tensor expression for the reduced phase space
It yields the following tensor expression for the reduced phase space 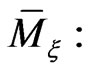
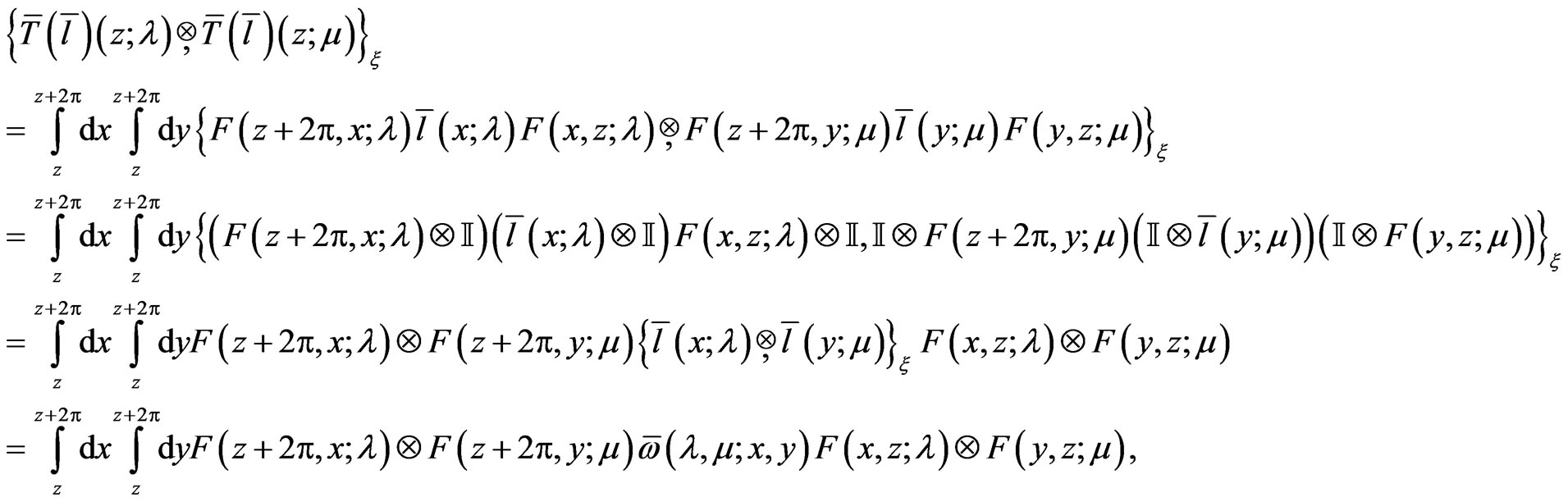 (52)
(52)
where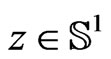 ,
, 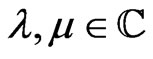 and, by definition,
and, by definition,
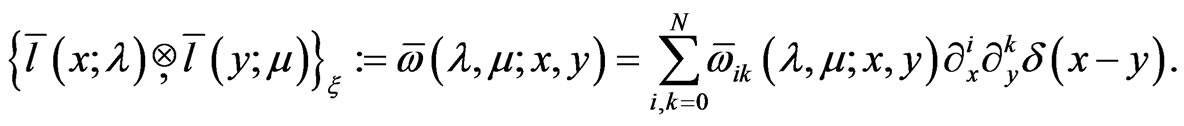 (53)
(53)
The local functional matrices
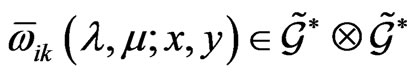
satisfy the antisymmetry property:
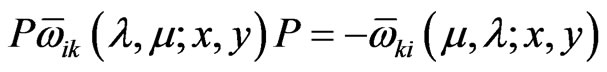 (54)
(54)
for all 
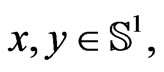
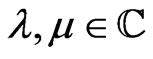 and the permutation operator
and the permutation operator  acts as
acts as  for any
for any 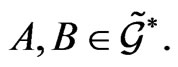 Just as in the calculation from [1,25,26] one obtains from (53) that
Just as in the calculation from [1,25,26] one obtains from (53) that
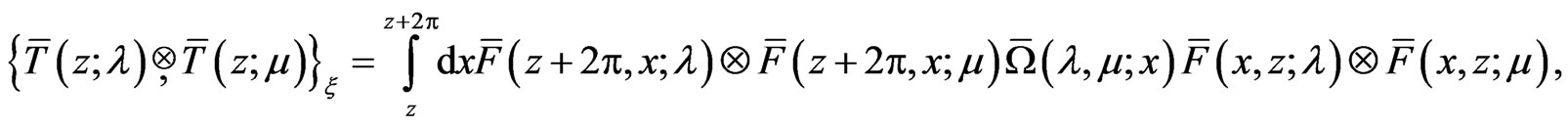 (55)
(55)
where the matrix 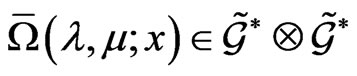 for all
for all  depends only on
depends only on  The expression (55) allows the very compact representation
The expression (55) allows the very compact representation
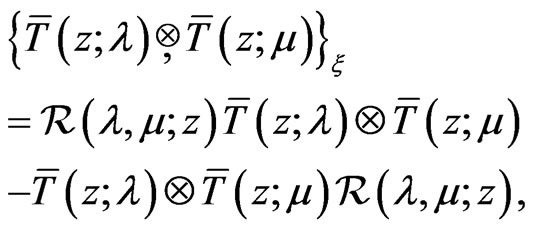 (56)
(56)
if the tensor  -matrix
-matrix 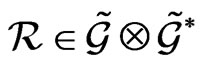 satisfies for
satisfies for 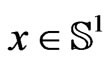 and
and  the differential relationship
the differential relationship
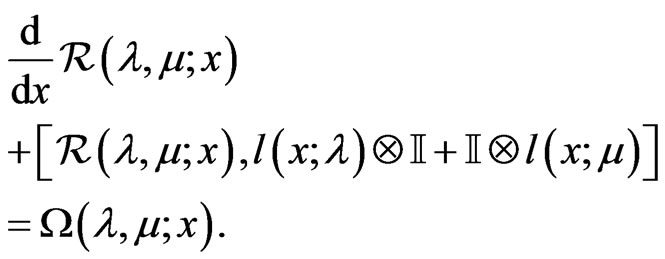 (57)
(57)
If we define the mapping 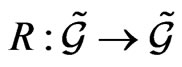 as
as
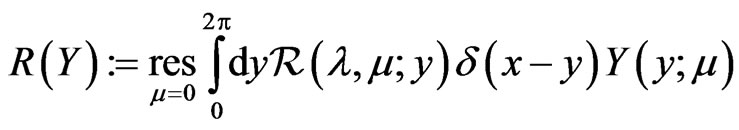 (58)
(58)
for any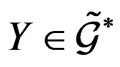 , then the relationship (57) can be easily presented in the following operator form:
, then the relationship (57) can be easily presented in the following operator form:
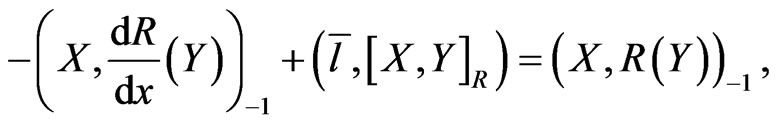 (59)
(59)
which holds for any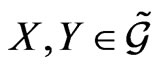 , where we denoted
, where we denoted
 (60)
(60)
The result (59) can be used for rewriting the Poisson bracket (56) as
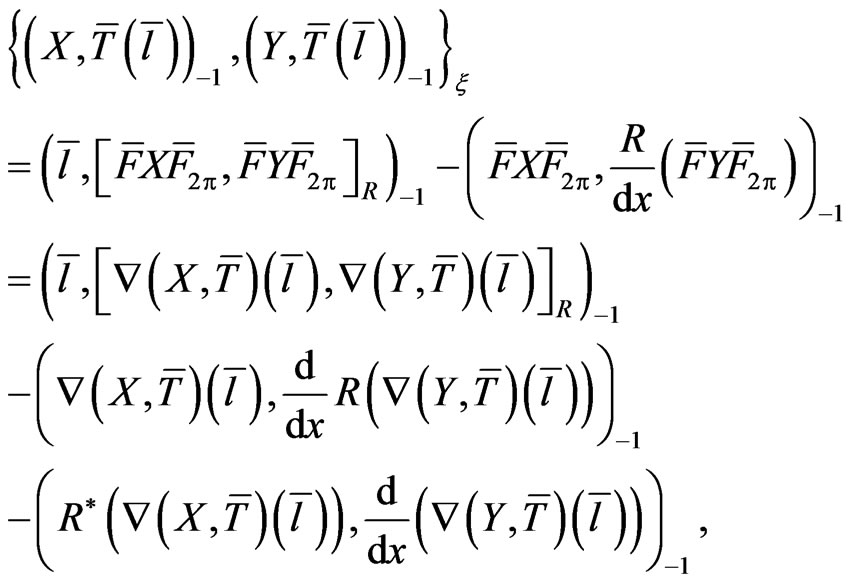 (61)
(61)
where
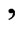
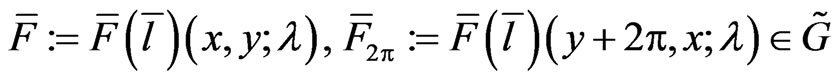
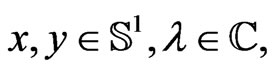 and we defined the gradients
and we defined the gradients  and
and  in the standard way as
in the standard way as
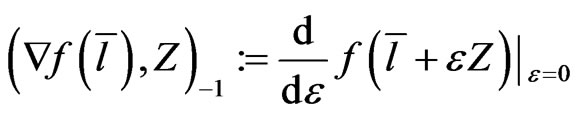 (62)
(62)
for any smooth functional 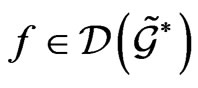 and
and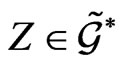 .
.
It is easy to observe that under the antisymmetry condition 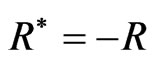 the right-hand side of (61) equals the Lie-Poisson bracket [1,2,4,6,10] for the functionals
the right-hand side of (61) equals the Lie-Poisson bracket [1,2,4,6,10] for the functionals
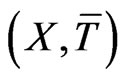 and
and 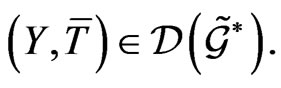 Here the adjoint space
Here the adjoint space
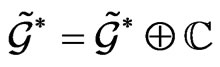 is with respect to a new commutator structure
is with respect to a new commutator structure 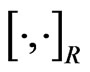 on the centrally extended Lie algebra
on the centrally extended Lie algebra 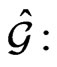 for any
for any  with commutator
with commutator
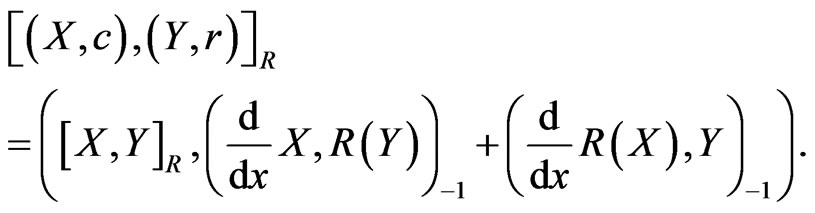 (63)
(63)
In (63) the classical  -structure on the Lie algebra
-structure on the Lie algebra
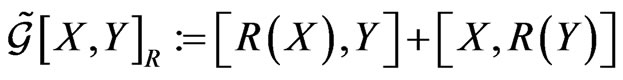 under some conditions on the mapping
under some conditions on the mapping 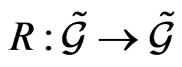 can generate on
can generate on 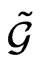 a new Lie structure (which it must not).
a new Lie structure (which it must not).
The above results can be formulated as follows.
Proposition 2 The Marsden-Weinstein reduced canonical Poisson structure on the phase space 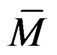 for the monodromy matrix
for the monodromy matrix 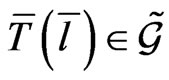 exactly coincides with the corresponding classical Lie-Poisson AKS-bracket on the centrally extended basis Lie algebra
exactly coincides with the corresponding classical Lie-Poisson AKS-bracket on the centrally extended basis Lie algebra 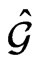 subject to the
subject to the 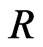 -structure (63) when it is antisymmetric.
-structure (63) when it is antisymmetric.
If the antisymmetry property for the mapping 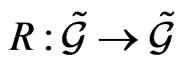 does not hold, the generated Lie-Poisson type bracket on the functional space
does not hold, the generated Lie-Poisson type bracket on the functional space  can be, owing to (61), defined as follows: for any
can be, owing to (61), defined as follows: for any 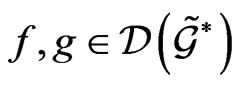 the bracket
the bracket
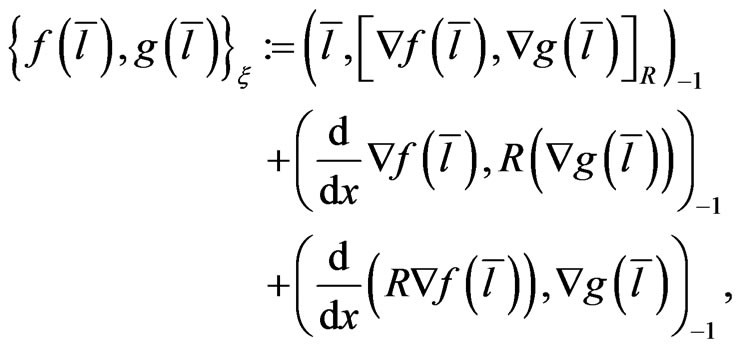 (64)
(64)
where the generalized 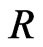 -structure
-structure 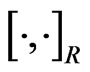 on
on  is given by the expression (60).
is given by the expression (60).
5. D-Structure and Generalized R-Structure
As stated above, the reduced Poisson bracket on the phase space 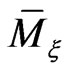 is
is
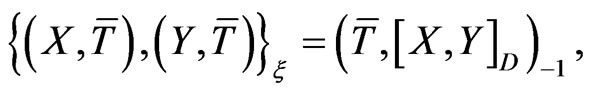 (65)
(65)
where for any  the corresponding
the corresponding 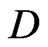 -structure on the Lie algebra
-structure on the Lie algebra 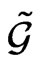 is defined by the classical expression (38) and the mapping (39). It is natural to assume that there exists a relationship between the D-structure
is defined by the classical expression (38) and the mapping (39). It is natural to assume that there exists a relationship between the D-structure 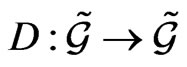 and the R-structure
and the R-structure 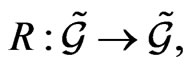 described above in Section 3.
described above in Section 3.
Assume, for brevity, that the 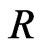 -structure (58) is antisymmetric, that is
-structure (58) is antisymmetric, that is 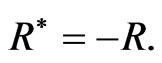 Then it is easy to check that the following algebraic relationship
Then it is easy to check that the following algebraic relationship
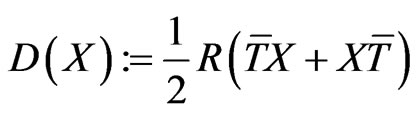 (66)
(66)
holds for any  In fact, (56) is equivalent to
In fact, (56) is equivalent to
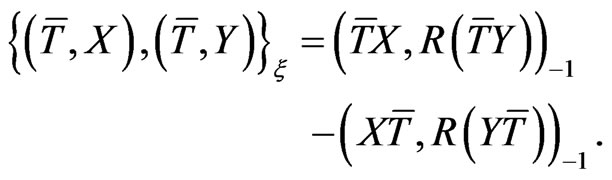 (67)
(67)
Now, substituting (66) into (37), one obtains that
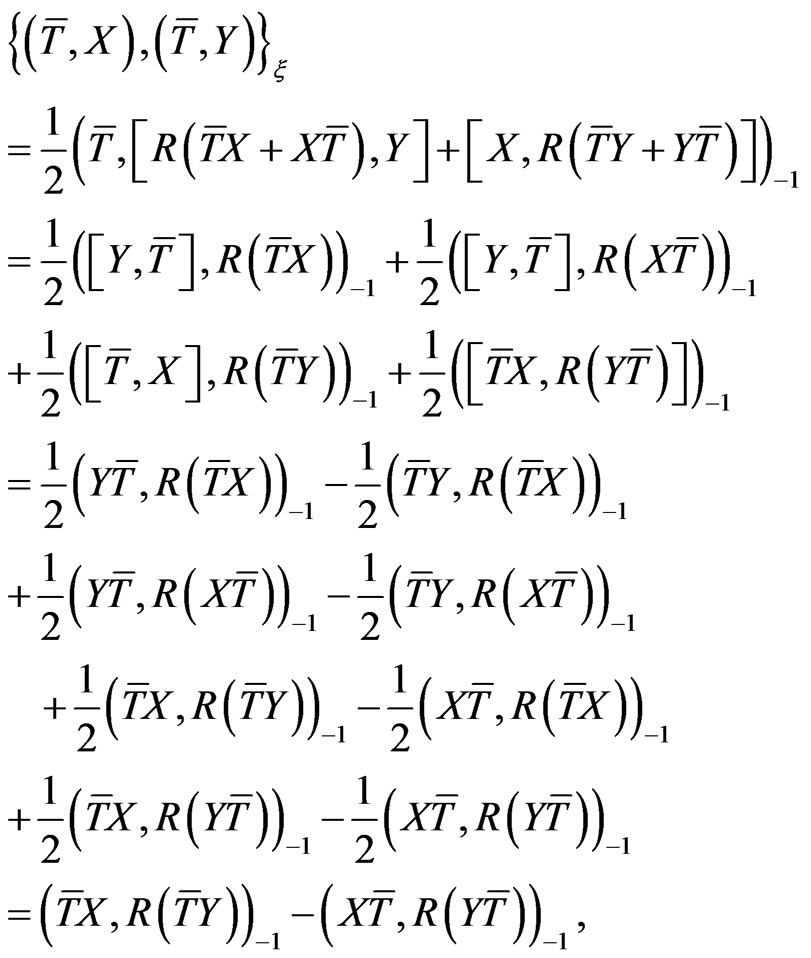 (68)
(68)
which coincides exactly with (67).
It is convenient to rewrite the operator relationship (46) in the tensor form as
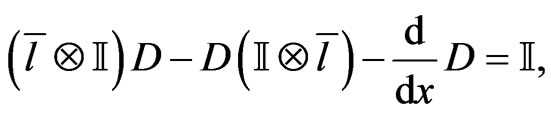 (69)
(69)
where the tensor , owing to the action (66), equals
, owing to the action (66), equals
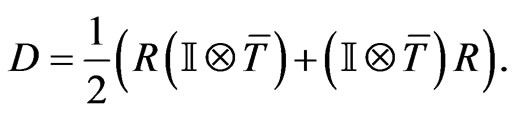 (70)
(70)
Substituting the expression (70) into the Equation (69) and taking into account the determining Equation (57)
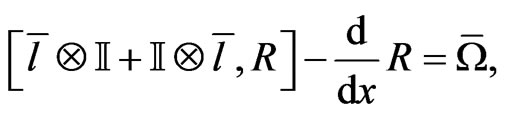 (71)
(71)
one obtains the relationship for the tensor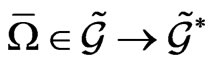 :
:
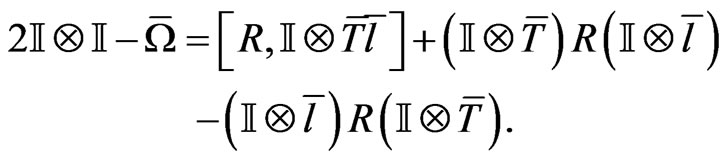 (72)
(72)
This makes two 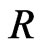 - and
- and 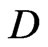 -structures on the Lie algebra
-structures on the Lie algebra  compatible. Observe that the
compatible. Observe that the 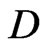 -structure (66) is not antisymmetric even though the
-structure (66) is not antisymmetric even though the  -structure was assumed to be antisymmetric. Concerning the
-structure was assumed to be antisymmetric. Concerning the  -structure determining Equation (69) one can anticipate that a study of its solutions would describe a set of nonlinear dynamical systems on the reduced phase space
-structure determining Equation (69) one can anticipate that a study of its solutions would describe a set of nonlinear dynamical systems on the reduced phase space 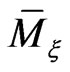 possessing an infinite hierarchy of mutually commuting conservation laws.
possessing an infinite hierarchy of mutually commuting conservation laws.
6. Generalized Riemann Systems: Lax Integrability and D-A Structures
6.1. Setting the Problem
Recently, new mathematical approaches based on differential-algebraic [27-31] and differential geometric methods and techniques, were applied in [8,32,33] for studying the Lax integrability of nonlinear differential equations of the Korteweg-de Vries and Riemann type. In particular, many analytical studies [32,34-40] have been devoted to finding the corresponding Lax representations of the infinite Riemann type hydrodynamical hierarchy, suggested recently by M. Pavlov and D. Holm in the form
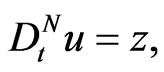 (73)
(73)
where the differentiation 
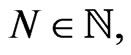
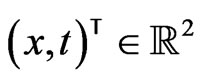 and
and  It was found that the related dynamical system
It was found that the related dynamical system
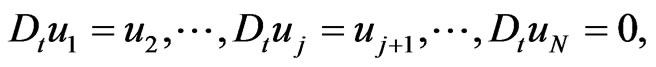 (74)
(74)
defined on a  -periodic infinite-dimensional smooth functional manifold
-periodic infinite-dimensional smooth functional manifold 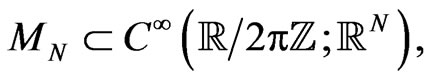 possesses [8,37] for an arbitrary integer
possesses [8,37] for an arbitrary integer 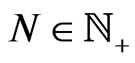 a suitable Lax representation
a suitable Lax representation
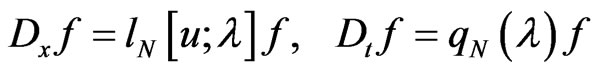 (75)
(75)
with  being a complex spectral parameter and
being a complex spectral parameter and 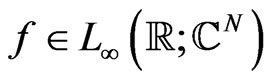 and matrices
and matrices
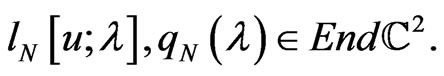
Here, by definition, 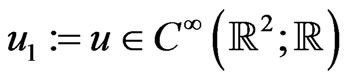 and the differentiations
and the differentiations
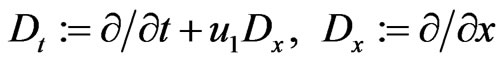 (76)
(76)
satisfy on the manifold  the following commutation relationship:
the following commutation relationship:
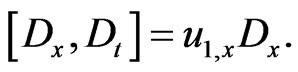 (77)
(77)
In particular, for 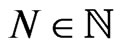 the following result [8,41] was recently obtained.
the following result [8,41] was recently obtained.
Proposition 3 The Lax representation for the generalized Riemann type hydrodynamical system
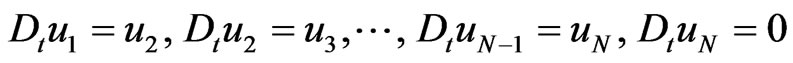 (78)
(78)
is given for any arbitrary 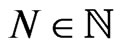 by a set of linear compatibility equations (see Equation (79))where
by a set of linear compatibility equations (see Equation (79))where 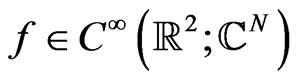 and
and 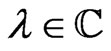 is an arbitrary complex parameter. Moreover, the relationships (79) realize a linear matrix representation of the commutator condition (77).
is an arbitrary complex parameter. Moreover, the relationships (79) realize a linear matrix representation of the commutator condition (77).
In our work we study the complete integrability of a new dispersive Riemann type hydrodynamic flow
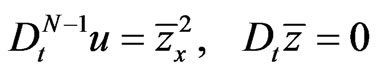 (80)
(80)
on a 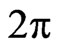 -periodic functional manifold
-periodic functional manifold
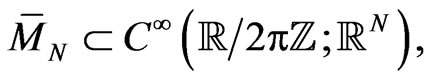
where 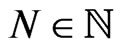 is an arbitrary natural number, the vector
is an arbitrary natural number, the vector

the differentiations
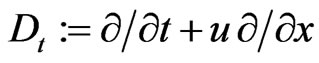
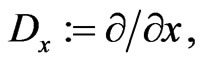
 (79)
(79)
satisfy as above the Lie-algebraic commutator relationship (77) and  is an evolution parameter. This system can be considered as a slight generalization of the dispersive Riemann hydrodynamic system (73), extensively studied by means of different mathematical tools in [8,9,32,35,37,41]. For the case
is an evolution parameter. This system can be considered as a slight generalization of the dispersive Riemann hydrodynamic system (73), extensively studied by means of different mathematical tools in [8,9,32,35,37,41]. For the case 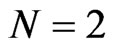 it is well known [10,12] that the system (80) is a smooth Lax integrable bi-Hamiltonian flow on the
it is well known [10,12] that the system (80) is a smooth Lax integrable bi-Hamiltonian flow on the 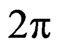 -periodic functional manifold
-periodic functional manifold  whose Lax representation is given by the compatible linear system
whose Lax representation is given by the compatible linear system
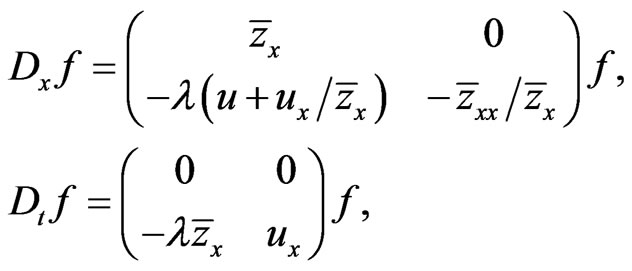 (81)
(81)
where 
 and
and  is an arbitrary spectral parameter.
is an arbitrary spectral parameter.
For 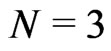 the dynamical system (80) is equivalent to that on a
the dynamical system (80) is equivalent to that on a  -periodic functional manifold
-periodic functional manifold
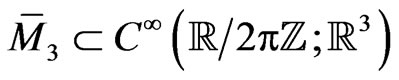
for a vector 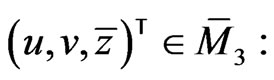
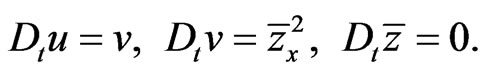 (82)
(82)
This can be easily rewritten by means of the change of variables 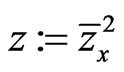 as that on a
as that on a  -periodic functional manifold
-periodic functional manifold

for a vector 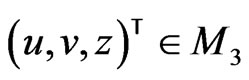
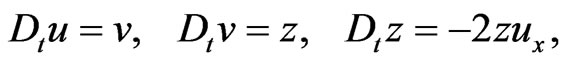 (83)
(83)
or in the form of the flow
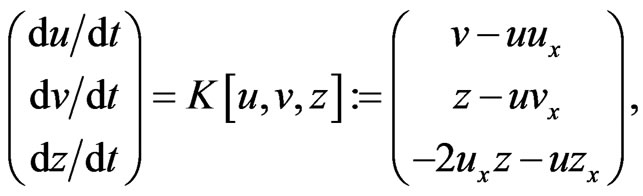 (84)
(84)
defining a standard smooth dynamical system on the infinite-dimensional functional manifold  where
where  is the corresponding vector field on
is the corresponding vector field on 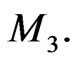 We succeeded in proving the following result based on symplectic gradient-holonomic and differential algebraic tools.
We succeeded in proving the following result based on symplectic gradient-holonomic and differential algebraic tools.
Proposition 4 The Riemann type hydrodynamic flow (97) is a bi-Hamiltonian dynamical system on the functional manifold  with respect to two compatible Poissonian structures
with respect to two compatible Poissonian structures 
 (85)
(85)
possessing an infinite hierarchy of mutually commuting conservation laws and a non-autonomous Lax representation of the form (see Equation (86)).
where 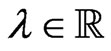 is an arbitrary spectral parameter and
is an arbitrary spectral parameter and 
We demonstrate the effectiveness of the devised differential-algebraic tools and methods by means of application to the very interesting [42-47] nonlinear Ostrovsky-Vakhnenko hydrodynamic equation
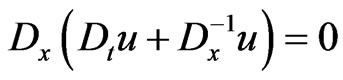 (87)
(87)
on the 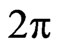 -periodic functional manifold
-periodic functional manifold
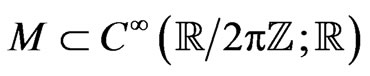
subject to which the following proposition is proved.
Proposition 5 The Ostrovsky-Vakhnenko dynamical system (79) allows the standard differential Lax representation and defines on the functional manifold 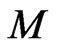 an integrable bi-Hamiltonian flow with two compatible Poisson structures. In particular, this dynamical system possesses an infinite hierarchy of mutually commuting nonlocal conservation laws.
an integrable bi-Hamiltonian flow with two compatible Poisson structures. In particular, this dynamical system possesses an infinite hierarchy of mutually commuting nonlocal conservation laws.
In particular, we construct by means of the differential-algebraic tools a differential Lax representation, coinciding with that found in [43], and given in the equivalent matrix Zakharov-Shabat form as
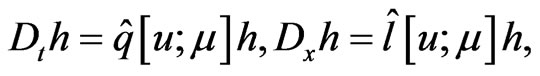 (88)
(88)
where matrices (see Equation (89))
 (86)
(86)
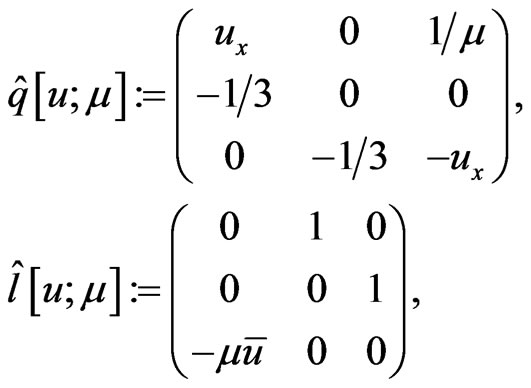 (89)
(89)
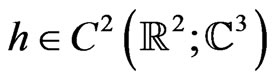 and
and 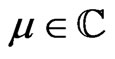 is an arbitrary spectral parameter. We also find a related pair of compatible polynomial Poissonian structures
is an arbitrary spectral parameter. We also find a related pair of compatible polynomial Poissonian structures
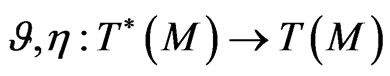
 (90)
(90)
with 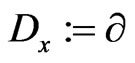 and
and  with respect to which the Ostrovsky-Vakhnenko hydrodynamic equation (87) is equivalent to a suitable bi-Hamiltonian flow on the functional manifold
with respect to which the Ostrovsky-Vakhnenko hydrodynamic equation (87) is equivalent to a suitable bi-Hamiltonian flow on the functional manifold  Also analyzed by means of the devised differential-algebraic tools is the Lax integrability of the interesting generalized Ostrovsky-Vakhnenko type system of evolution equations
Also analyzed by means of the devised differential-algebraic tools is the Lax integrability of the interesting generalized Ostrovsky-Vakhnenko type system of evolution equations
 (91)
(91)
on a  -periodic functional manifold
-periodic functional manifold
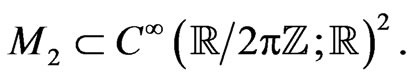
6.2. Integrability of a Generalized Riemann Hydrodynamic System
6.2.1. New Generalization of the Riemann Hydrodynamic Hierarchy
In this section we shall study the complete integrability of the dispersiveness Riemann type hydrodynamic flow (80)
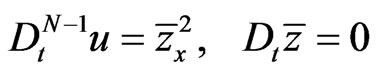 (92)
(92)
on a  -periodic functional manifold
-periodic functional manifold
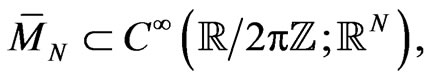
where  is an arbitrary natural number, the vector
is an arbitrary natural number, the vector
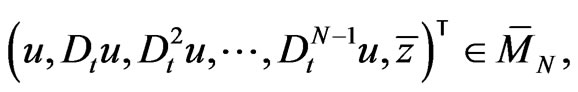 the differentiations
the differentiations
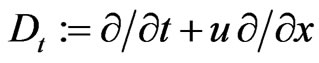
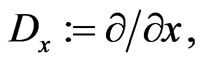 satisfy, as above, the Lie-algebraic commutator relationship (77) and
satisfy, as above, the Lie-algebraic commutator relationship (77) and 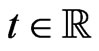 is an evolution parameter. The system can be considered as a slight generalization of the dispersiveness Riemann hydrodynamic system suggested recently by M. Pavlov and D. Holm in the form
is an evolution parameter. The system can be considered as a slight generalization of the dispersiveness Riemann hydrodynamic system suggested recently by M. Pavlov and D. Holm in the form
 (93)
(93)
for 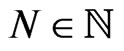 and extensively studied in [8,9,32,35,37,41], where it was proved that it is a Lax integrable bi-Hamiltonian flow on the manifold
and extensively studied in [8,9,32,35,37,41], where it was proved that it is a Lax integrable bi-Hamiltonian flow on the manifold  and possesses an infinite hierarchy of mutually commuting dispersive Lax integrable Hamiltonian flows.
and possesses an infinite hierarchy of mutually commuting dispersive Lax integrable Hamiltonian flows.
For 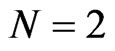 it is well known [10,12] that the system (92) is a smooth Lax integrable bi-Hamiltonian flow on the
it is well known [10,12] that the system (92) is a smooth Lax integrable bi-Hamiltonian flow on the 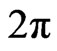 -periodic functional manifold
-periodic functional manifold 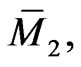 whose Lax representation is given by the compatible linear system
whose Lax representation is given by the compatible linear system
 (94)
(94)
where 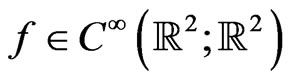 and
and  is an arbitrary spectral parameter.
is an arbitrary spectral parameter.
Our focus here is an investigation of the Lax integrability of the Riemann type hydrodynamic system (92) for 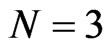 on a
on a 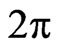 -periodic functional manifold
-periodic functional manifold 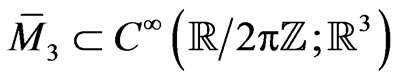 for a vector
for a vector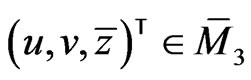 . We treat this problem in the following extended form:
. We treat this problem in the following extended form:
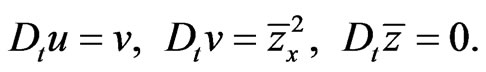 (95)
(95)
The flow (95) can be recast as a one on a 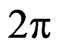 -periodic functional manifold
-periodic functional manifold 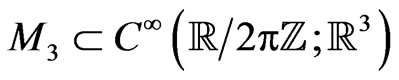 for a vector
for a vector 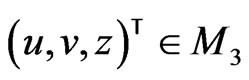 as
as
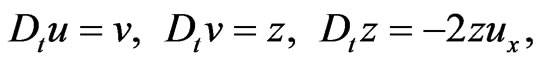 (96)
(96)
where, for further convenience, we have made the change of variables:  We will also use the form of the flow (96):
We will also use the form of the flow (96):
 (97)
(97)
defining a standard smooth dynamical system on the infinite-dimensional functional manifold 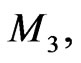 where
where 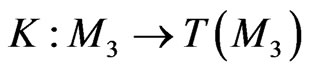 is the corresponding vector field on
is the corresponding vector field on 
In the sequel, we shall prove by means of gradientholonomic and differential algebraic tools Proposition 4, stating the Lax integrability of the dynamical system (97), in particular, we will devise an effective approach for constructing its exact Lax representation and related compatible Poissonian structures.
6.2.2. Symplectic Gradient-Holonomic Integrability Analysis: Poissonian Structure on M3
Our first steps in proving Proposition 4 are fashioned using the symplectic gradient-holonomic method, which takes us a long way towards the desired result.
By employing the symplectic gradient-holonomic approach [10,12,48] to study the integrability of smooth nonlinear dynamical systems on functional manifolds, one can find a set of conservation laws for (97) by constructing analytical solutions 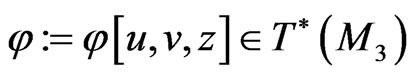 to the functional Lax gradient Equation:
to the functional Lax gradient Equation:
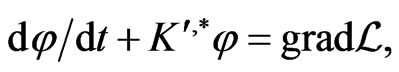 (98)
(98)
where 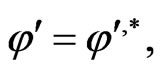
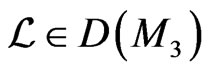 is a suitable Lagrangian functional and the linear operator
is a suitable Lagrangian functional and the linear operator
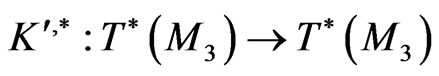
is the adjoint with respect to the standard convolution 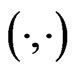 on
on 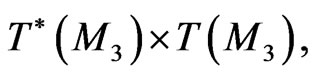 of the Fréchet derivative of a nonlinear mapping
of the Fréchet derivative of a nonlinear mapping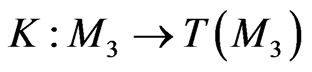 ; namely,
; namely,
 (99)
(99)
The Lax gradient Equation (98) can be, owing to (80), rewritten as
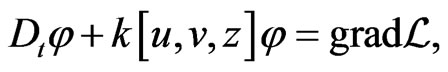 (100)
(100)
where the matrix operator is
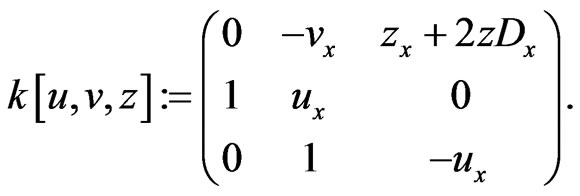 (101)
(101)
The first vector elements
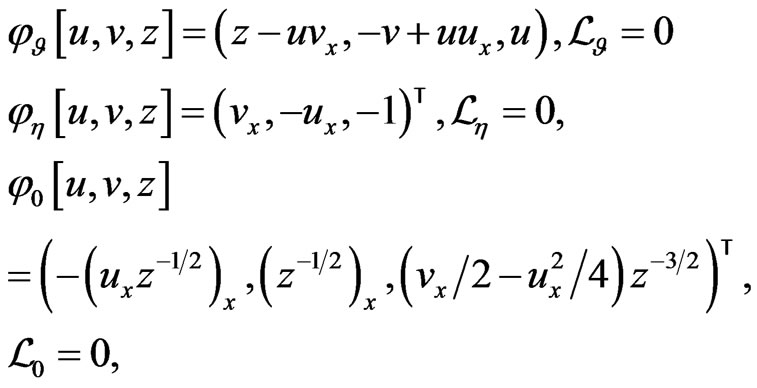 (102)
(102)
as can be easily checked, are solutions of the functional Equation (100). From an application of the standard Volterra homotopy formula
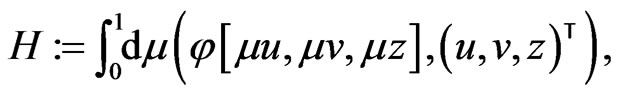 (103)
(103)
one finds the conservation laws for (80); namely,
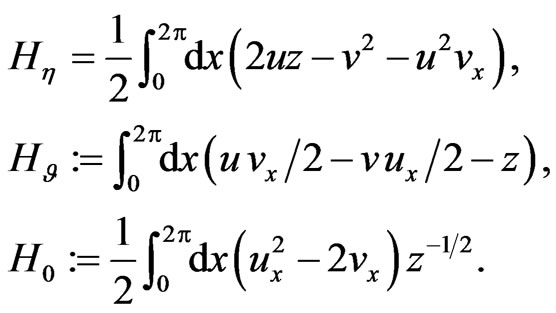 (104)
(104)
It is now quite easy, making use of the conservation laws (104), to construct a Poissonian structure  for the dynamical system (97). If we use the representations
for the dynamical system (97). If we use the representations
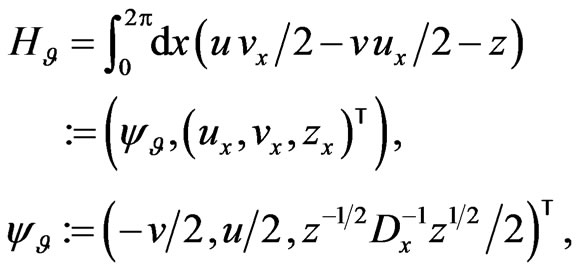 (105)
(105)
it follows that the vector  satisfies the Lax gradient Equation (100):
satisfies the Lax gradient Equation (100):
 (106)
(106)
where the Lagrangian function 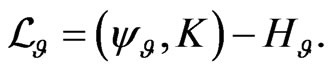 Thus, based on the inverse co-symplectic functional expression
Thus, based on the inverse co-symplectic functional expression
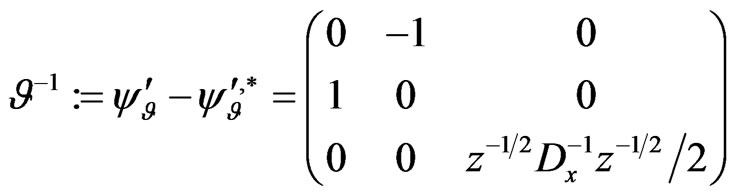 (107)
(107)
one readily obtains the linear co-symplectic operator on the manifold 
 (108)
(108)
which is the corresponding Poissonian operator for the dynamical system (80). It is also important to observe that the dynamical system (80) is a Hamiltonian flow on the functional manifold 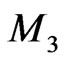 with respect to the Poissonian structure (108).
with respect to the Poissonian structure (108).
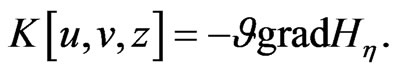 (109)
(109)
6.2.3. Poissonian Structure on 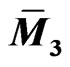
In what follows, we shall find it convenient to construct other Poissonian structures for dynamical system (95) on the manifold  rewritten in the equivalent form
rewritten in the equivalent form
 (110)
(110)
where 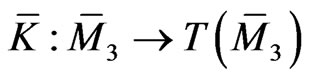 is the corresponding vector field on
is the corresponding vector field on 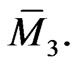 To proceed, we need to obtain additional solutions to the Lax gradient Equation (100) on the functional manifold
To proceed, we need to obtain additional solutions to the Lax gradient Equation (100) on the functional manifold 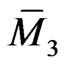
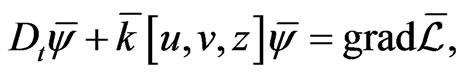 (111)
(111)
where the matrix operator is
 (112)
(112)
and which we may rewrite in the component form
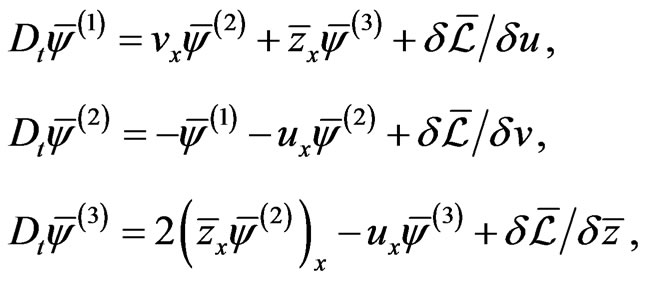 (113)
(113)
where the vector
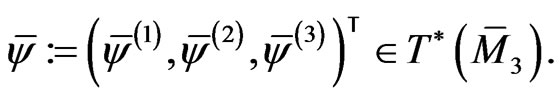
As a simple consequence of (113), one obtains the following system of differential relationships:
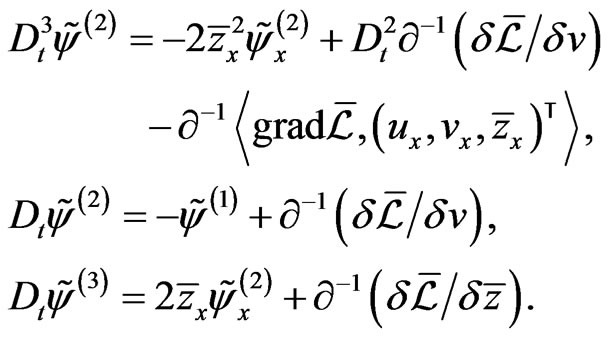 (114)
(114)
Here we have defined

and made use of the commutator relationship for differentiations 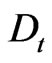 and
and 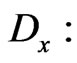
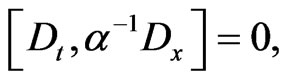 (115)
(115)
which holds for the function 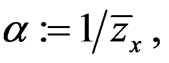 where
where  It therefore follows that after solving the first equation of system (114), and one can recursively solve the remaining two equations. In particular, it is easy to see that the three vector elements
It therefore follows that after solving the first equation of system (114), and one can recursively solve the remaining two equations. In particular, it is easy to see that the three vector elements
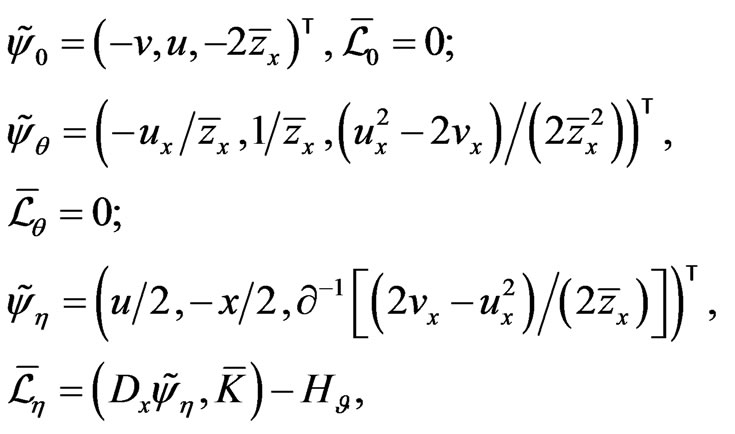 (116)
(116)
are solutions of the system (114). The first two elements of (116) lead to the Volterra symmetric vectors

entailing the trivial conservation laws

The third element of (116) gives rise to the Volterra asymmetric vector 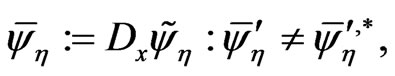 entailing the following inverse co-symplectic functional expression:
entailing the following inverse co-symplectic functional expression:
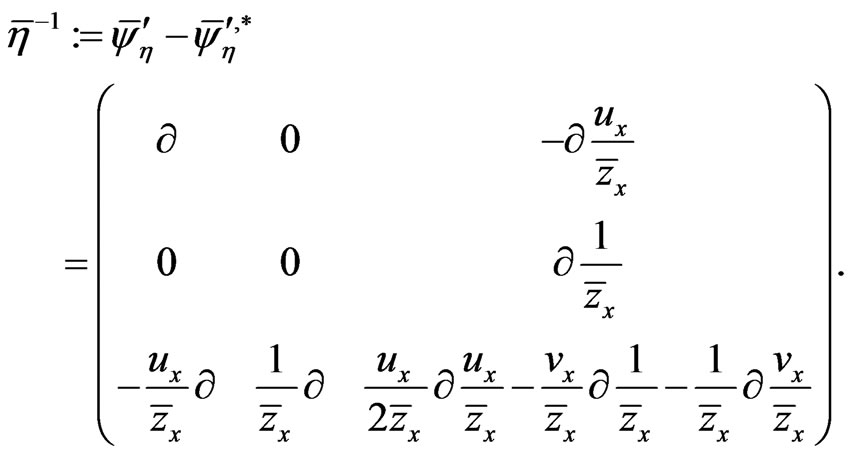 (117)
(117)
Correspondingly, the Poissonian operator
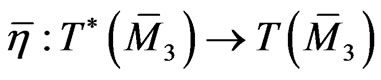
is
 (118)
(118)
subject to which the following Hamiltonian representation
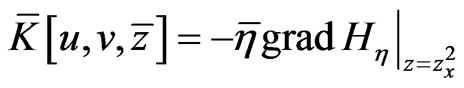 (119)
(119)
holds on the manifold .
.
6.2.4. Hamiltonian Integrability Analysis
Next, we return to our integrability analysis of the dynamical system (97) on the functional manifold 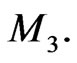 It is easy to recalculate the form of the Poissonian operator (118) on the manifold
It is easy to recalculate the form of the Poissonian operator (118) on the manifold 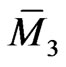 to that acting on the manifold
to that acting on the manifold 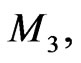 giving rise to the second Hamiltonian representation of (97):
giving rise to the second Hamiltonian representation of (97):
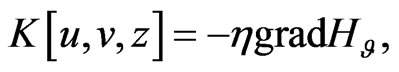 (120)
(120)
where 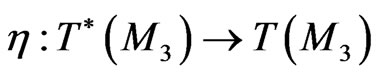 is the corresponding Poissonian operator. As a next important point, the Poissonian operators (108) and (118) are compatible [1,3,10,12] on the manifold
is the corresponding Poissonian operator. As a next important point, the Poissonian operators (108) and (118) are compatible [1,3,10,12] on the manifold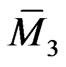 ; that is, the operator pencil
; that is, the operator pencil 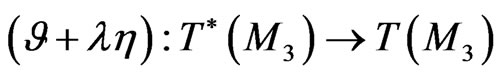 is also Poissonian for arbitrary
is also Poissonian for arbitrary  As a consequence, any operator of the form
As a consequence, any operator of the form
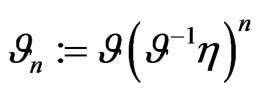 (121)
(121)
for all  is Poissonian on the manifold
is Poissonian on the manifold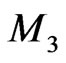 . Using now the homotopy formula (103) and recursion property of the Poissonian pair (109) and (118), it is easy to construct the related infinite hierarchy of mutually commuting conservation laws
. Using now the homotopy formula (103) and recursion property of the Poissonian pair (109) and (118), it is easy to construct the related infinite hierarchy of mutually commuting conservation laws
 (122)
(122)
for the dynamical system (97), where  and
and
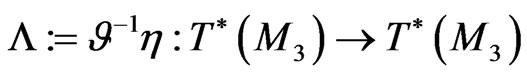
is the corresponding recursion operator, which satisfies the so called associated Lax commutator relationship
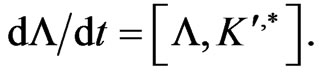 (123)
(123)
In the course of the above analysis and observations, we have proved the following result.
Proposition 6 The Riemann hydrodynamic system (97) is a bi-Hamiltonian dynamical system on the functional manifold  with respect to the compatible Poissonian structures
with respect to the compatible Poissonian structures 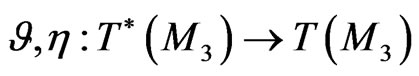
 (124)
(124)
and possesses an infinite hierarchy of mutually commuting conservation laws (122).
Concerning the existence of an additional infinite and parametrically 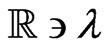 -ordered hierarchy of conservation laws for the dynamical system (92), it is instructive to consider the dispersive nonlinear dynamical system
-ordered hierarchy of conservation laws for the dynamical system (92), it is instructive to consider the dispersive nonlinear dynamical system
 (125)
(125)
By solving the corresponding Lax equation
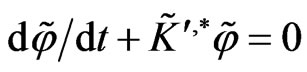 (126)
(126)
for an element 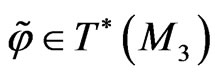 in a suitably chosen asymptotic form, one can construct an infinite ordered hierarchy of conservation laws for (92), which we will not delve into here. This hierarchy and the existence of an infinite and parametrically
in a suitably chosen asymptotic form, one can construct an infinite ordered hierarchy of conservation laws for (92), which we will not delve into here. This hierarchy and the existence of an infinite and parametrically 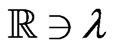 -ordered hierarchy of conservation laws for the Riemann type dynamical system (92) provided compelling indications that it is completely integrable in the sense of Lax on the functional manifold
-ordered hierarchy of conservation laws for the Riemann type dynamical system (92) provided compelling indications that it is completely integrable in the sense of Lax on the functional manifold . We shall study the complete integrability in the next section using rather powerful differentialalgebraic tools that were devised recently in [8,9,37].
. We shall study the complete integrability in the next section using rather powerful differentialalgebraic tools that were devised recently in [8,9,37].
6.3. D-A Integrability Analysis for 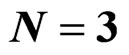
Consider a polynomial differential ring
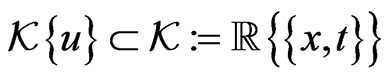
generated by a fixed functional variable 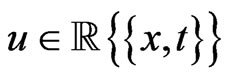 and invariant with respect to two differentiations
and invariant with respect to two differentiations 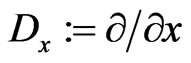 and
and 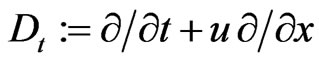 that satisfy the Lie-algebraic commutator relationship (77) together with the constraint (96) expressed in the differential-algebraic functional form
that satisfy the Lie-algebraic commutator relationship (77) together with the constraint (96) expressed in the differential-algebraic functional form
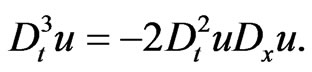 (127)
(127)
Since the Lax representation for the dynamical system (97) can be interpreted [8,10] as the existence of a finite-dimensional invariant ideal  realizing the corresponding finite-dimensional representation of the Lie-algebraic commutator relationship (127), this ideal can be constructed as
realizing the corresponding finite-dimensional representation of the Lie-algebraic commutator relationship (127), this ideal can be constructed as
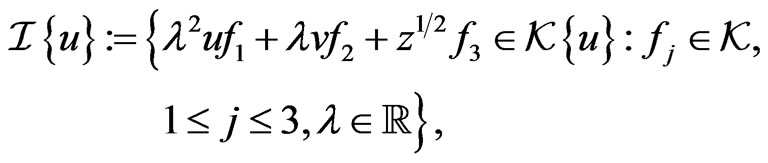 (128)
(128)
where 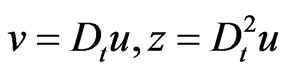 and
and 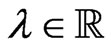 is an arbitrary real parameter. To find finite-dimensional representations of the
is an arbitrary real parameter. To find finite-dimensional representations of the 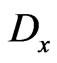 - and
- and 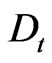 -differentiations, it is necessary [8] first to find the
-differentiations, it is necessary [8] first to find the  -invariant kernel
-invariant kernel  and next to check its invariance with respect to the
and next to check its invariance with respect to the 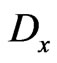 -differentiation. It is easy to show that
-differentiation. It is easy to show that
 (129)
(129)
where the matrix  is given as
is given as
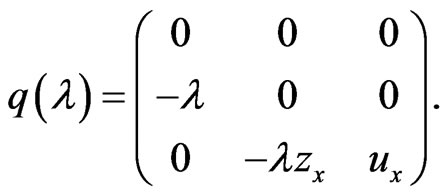 (130)
(130)
To obtain the corresponding representation of the 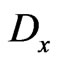 -differentiation in the space
-differentiation in the space 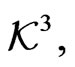 it suffices to find a matrix
it suffices to find a matrix 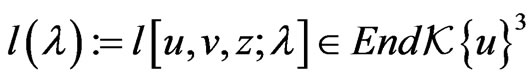 that
that
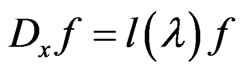 (131)
(131)
for 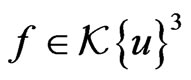 and the related ideal
and the related ideal
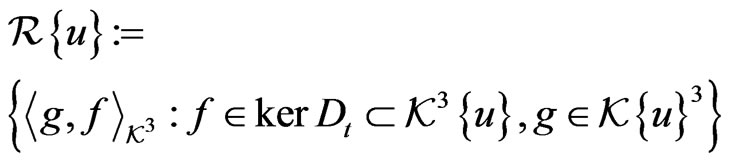 (132)
(132)
is 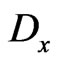 -invariant with respect to the differentiation (131). Straightforward calculations using this invariance condition then yield the following matrix
-invariant with respect to the differentiation (131). Straightforward calculations using this invariance condition then yield the following matrix
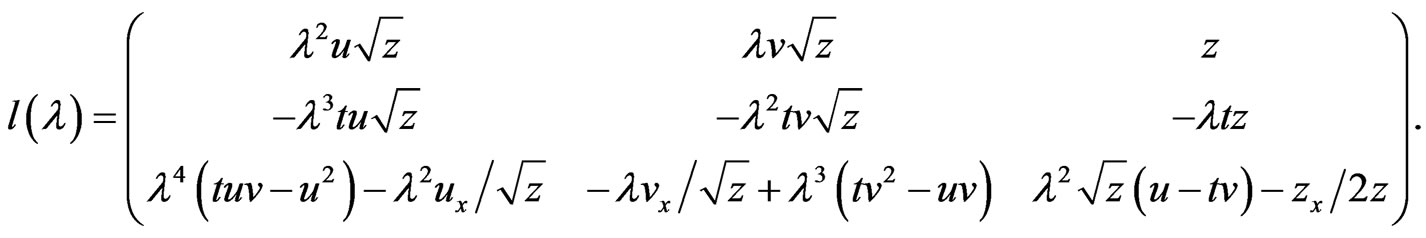 (133)
(133)
Remark 1 Simple analogs of the above differentialalgebraic calculations for the case 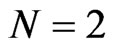 lead readily to the corresponding Riemann type hydrodynamic system
lead readily to the corresponding Riemann type hydrodynamic system
 (134)
(134)
on the functional manifold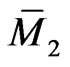 , which possesses the following matrix Lax representation:
, which possesses the following matrix Lax representation:
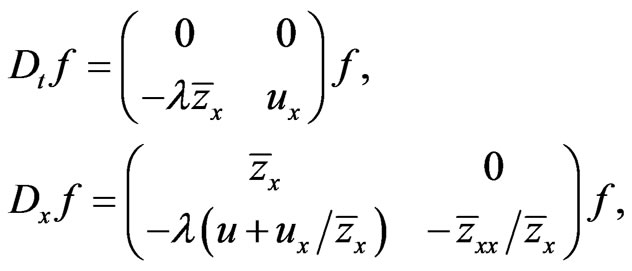 (135)
(135)
where 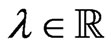 is an arbitrary spectral parameter and
is an arbitrary spectral parameter and 
As one can readily see, these differential-algebraic results provide a direct proof of Proposition 4 describing the integrability of system (97) for 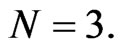 The matrices (133) are not of standard form since they depend explicitly on the temporal evolution parameter
The matrices (133) are not of standard form since they depend explicitly on the temporal evolution parameter 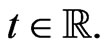 Nonetheless, the matrices (130) and (133) satisfy for all
Nonetheless, the matrices (130) and (133) satisfy for all 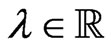 the well-known Zakharov-Shabat type compatibility condition
the well-known Zakharov-Shabat type compatibility condition
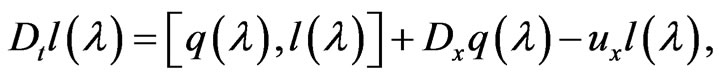 (136)
(136)
which follows from the Lax type relationships (129) and (131)
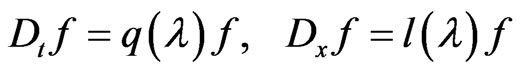 (137)
(137)
and the commutator condition (127). Moreover, taking into account that the dynamical system (97) has a compatible Poissonian pair (108) and (118) depending only on the variables 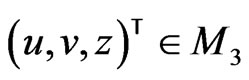 and not depending on the temporal variable
and not depending on the temporal variable 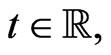 one can certainly assume that it also possesses a standard autonomous Lax representation, which can possibly be found by means of a suitable gauge transformation of (137). We plan to pursue this line of analysis in a forthcoming paper.
one can certainly assume that it also possesses a standard autonomous Lax representation, which can possibly be found by means of a suitable gauge transformation of (137). We plan to pursue this line of analysis in a forthcoming paper.
6.4. Integrability of Ostrovsky-Vakhnenko Equation
6.4.1. An Introduction and Problem Description
In 1998 V. O. Vakhnenko investigated high-frequency perturbations in a relaxing barotropic medium. He discovered that this phenomenon is described by a new non-linear evolution equation. Later it was proved that this equation is equivalent to the reduced Ostrovsky equation [44], which describes long internal waves in a rotating ocean. The nonlinear integro-differential Ostrovsky-Vakhnenko equation
 (138)
(138)
on the real axis  for a smooth function
for a smooth function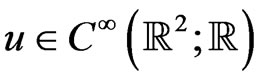 , where
, where 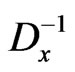 is the inverse-differential operator to
is the inverse-differential operator to 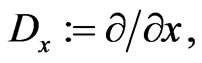 can be derived [45] as a special case of the Whitham type equation
can be derived [45] as a special case of the Whitham type equation
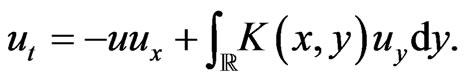 (139)
(139)
Here the generalized kernel
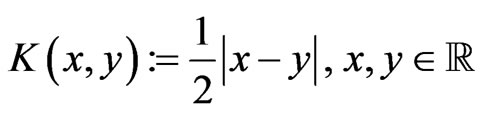
and  is an evolution parameter. Various analytical properties of (138) and related Equations were analyzed in articles [44-46,49], the corresponding Lax integrability was proved in [43].
is an evolution parameter. Various analytical properties of (138) and related Equations were analyzed in articles [44-46,49], the corresponding Lax integrability was proved in [43].
Recently, J. C. Brunelli and S. Sakovich [42] demonstrated that the Ostrovsky-Vakhnenko Equation is a reduction of the well known Camassa-Holm Equation making it possible to construct the corresponding compatible Poisson structures for (138), but in a complicated nonpolynomial form.
In the present work we will reanalyze the integrability of Equation (138) from the gradient-holonomic [10,12,48], symplectic and formal differential-algebraic points of view. As a result, we will re-derive the Lax representation for the Ostrovsky-Vakhnenko Equation (138) and construct the related simple compatible polynomial Poisson structures and an infinite hierarchy of conservation laws.
6.4.2. Gradient-Holonomic Integrability Analysis
Consider the nonlinear Ostrovsky-Vakhnenko Equation (138) as a a nonlinear dynamical system
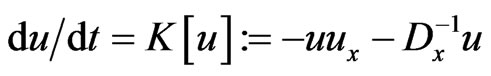 (140)
(140)
on the smooth  -periodic functional manifold
-periodic functional manifold
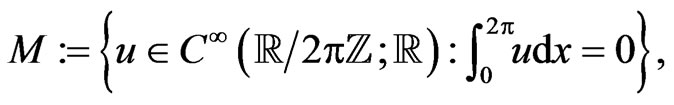 (141)
(141)
where 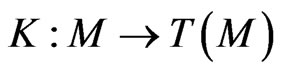 is the corresponding well-defined smooth vector field on
is the corresponding well-defined smooth vector field on 
We shall first show that the dynamical system (140) on manifold  possesses an infinite hierarchy of conservation laws as a necessary condition for its integrability. For this we need to construct a solution to the Lax gradient equation
possesses an infinite hierarchy of conservation laws as a necessary condition for its integrability. For this we need to construct a solution to the Lax gradient equation
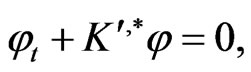 (142)
(142)
in the special asymptotic form
 (143)
(143)
where, by definition, a linear operator
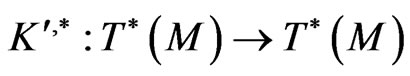
is adjoint with respect to the standard convolution 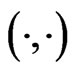 on
on 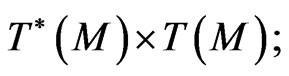 the Fréchet-derivative of a nonlinear mapping
the Fréchet-derivative of a nonlinear mapping 
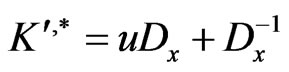 (144)
(144)
and, respectively,
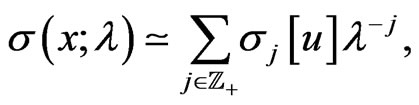 (145)
(145)
as 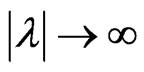 with some local functionals
with some local functionals

on  for all
for all 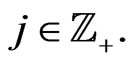
By substituting (143) into (142), one easily obtains the following recurrent sequence of functional relationships
 (146)
(146)
for all 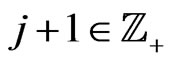 modulo the Equation (140). By means of standard calculations one finds that this recurrent sequence is solvable and
modulo the Equation (140). By means of standard calculations one finds that this recurrent sequence is solvable and
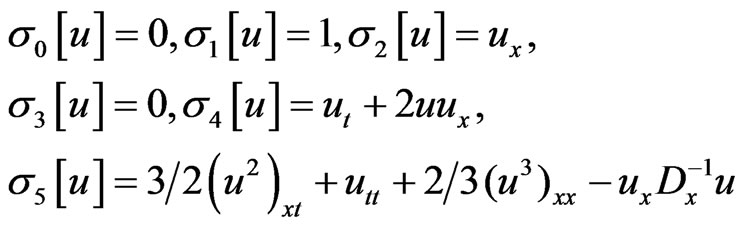 (147)
(147)
and so on. It is easy check that all of functionals
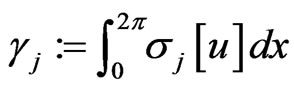 (148)
(148)
are conservation laws on the manifold , that is
, that is  for
for 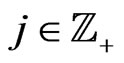 with respect to the dynamical system (140). For instance, if
with respect to the dynamical system (140). For instance, if 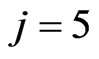 one obtains:
one obtains:
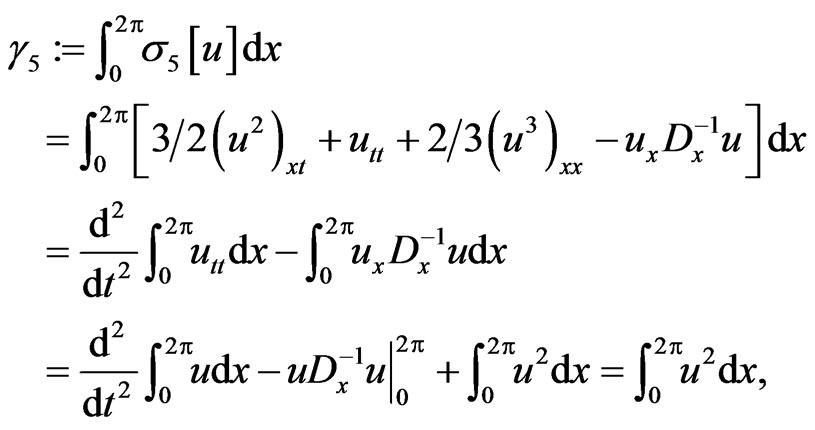 (149)
(149)
and
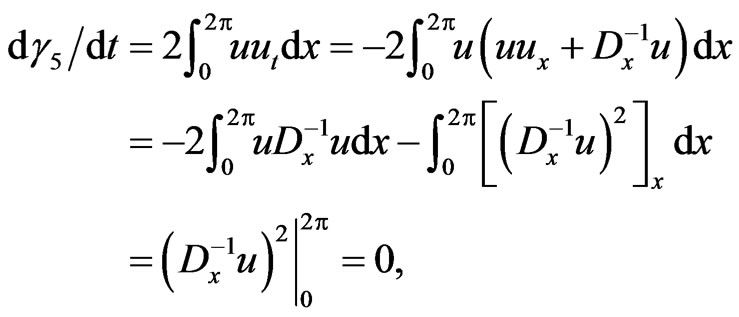 (150)
(150)
since, owing to the constraint (141), the integrals
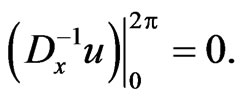
The result above suggests that the dynamical system (140) on the functional manifold  is an integrable Hamiltonian system.
is an integrable Hamiltonian system.
First, we will show that this dynamical system is a Hamiltonian flow
 (151)
(151)
with respect to some Poisson structure
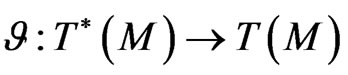
and a Hamiltonian function 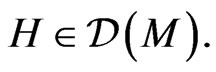 Using on the standard symplectic techniques [1,3,10,12], consider the conservation law (149) and present it in the scalar “momentum” form
Using on the standard symplectic techniques [1,3,10,12], consider the conservation law (149) and present it in the scalar “momentum” form
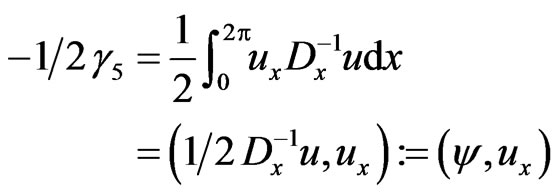 (152)
(152)
with the co-vector 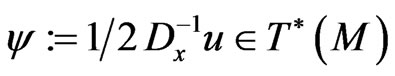 and calculate the corresponding co-Poissonian structure
and calculate the corresponding co-Poissonian structure
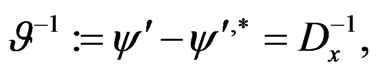 (153)
(153)
or the Poissonian structure
 (154)
(154)
This operator  is really Poissonian for (140) since the following determining symplectic condition
is really Poissonian for (140) since the following determining symplectic condition
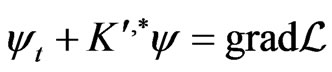 (155)
(155)
holds for the Lagrangian function
 (156)
(156)
As a result of (155), one readily infers that
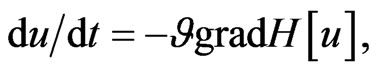 (157)
(157)
where the Hamiltonian function
 (158)
(158)
is an additional conservation law of the dynamical system (140). Thus, one can formulate the following proposition.
Proposition 7 The Ostrovsky-Vakhnenko dynamical system (140) possesses an infinite hierarchy of nonlocal, in general, conservation laws (148) and is a Hamiltonian flow (157) on the manifold 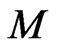 with respect to the Poissonian structure (154).
with respect to the Poissonian structure (154).
Remark 2 It is useful to remark here that the existence of an infinite ordered (by 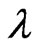 -powers) hierarchy of conservations laws (148) is a typical property [1,3,10,12] of Lax integrable Hamiltonian systems that are simultaneously bi-Hamiltonian flows with respect to a corresponding pair of compatible Poissonian structures (cf. [50]).
-powers) hierarchy of conservations laws (148) is a typical property [1,3,10,12] of Lax integrable Hamiltonian systems that are simultaneously bi-Hamiltonian flows with respect to a corresponding pair of compatible Poissonian structures (cf. [50]).
As is well known [1,3,10,12], the second Poissonian structure 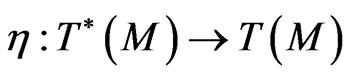 on the manifold
on the manifold 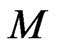 for (140), if it exists, can be calculated as
for (140), if it exists, can be calculated as
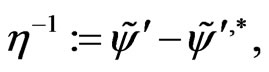 (159)
(159)
where a covector 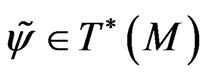 is a second solution to the determining Equation (155):
is a second solution to the determining Equation (155):
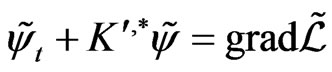 (160)
(160)
for some Lagrangian functional 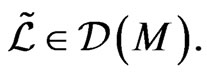 It can be easily shown by means of simple but cumbersome analytical calculations based, for example, on the asymptotic small parameter method [10,12,48] and on which we will not dwell upon here.
It can be easily shown by means of simple but cumbersome analytical calculations based, for example, on the asymptotic small parameter method [10,12,48] and on which we will not dwell upon here.
Instead of this, we shall apply the direct differential-algebraic approach to dynamical system (140) and reveal its Lax representation both in the differential scalar and canonical matrix Zakharov-Shabat forms. Moreover, we will construct the naturally related compatible polynomial Poissonian structures for the OstrovskyVakhnenko dynamical system (140) and generate an infinite hierarchy of mutually commuting nonlocal conservation laws.
6.5. Lax Representation and Poisson Structures: A D-A Approach
We will start by constructing of the polynomial differential ring 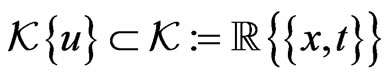 generated by a fixed functional variable
generated by a fixed functional variable 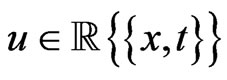 and invariant with respect to two differentiations
and invariant with respect to two differentiations
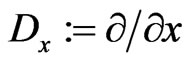 and
and 
satisfying the Lie-algebraic commutator relationship (77). Since the Lax representation for the dynamical system (140) can be interpreted [8,10] as the existence of a finitedimensional invariant differential ideal 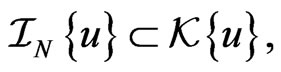 realizing the corresponding finite-dimensional representation of the Lie-algebraic commutator relationship (77), this ideal can be presented as
realizing the corresponding finite-dimensional representation of the Lie-algebraic commutator relationship (77), this ideal can be presented as
 (161)
(161)
where an element 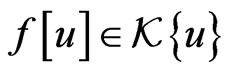 and
and 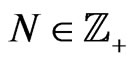 are fixed. The
are fixed. The  -invariance of ideal (161) will be a priori evident, if the function
-invariance of ideal (161) will be a priori evident, if the function  satisfies the linear differential relationship
satisfies the linear differential relationship
 (162)
(162)
for some coefficients 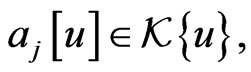
 but its
but its 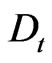 -invariance strongly depends on the element
-invariance strongly depends on the element 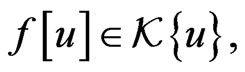 which can be found from the functional relationship (142) on the element
which can be found from the functional relationship (142) on the element
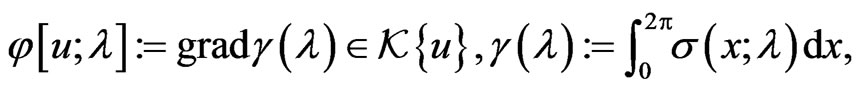
rewritten in the following form:
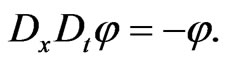 (163)
(163)
From the right-hand side it follows that there exists an element 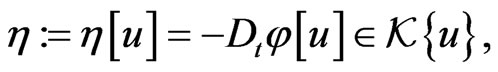 such that
such that
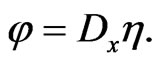 (164)
(164)
Upon substituting (164) into the left hand side of (163) one finds that
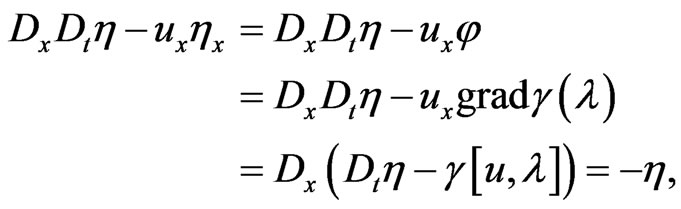 (165)
(165)
where  for a suitably chosen density element
for a suitably chosen density element 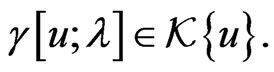 As an evident result of (165) one concludes that there exists an element
As an evident result of (165) one concludes that there exists an element 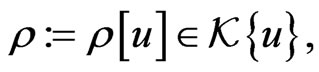 such that
such that
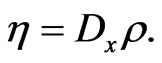 (166)
(166)
Turning back to the relationships (164) and (166), one concludes that the differential representation
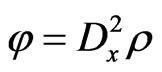 (167)
(167)
holds.
As a further step, we can try to realize the differential ideal (161) by means of the generating element  defined by the relationship (167). But, as it is easy to check, this differential ideal is not finite-dimensional. So, for future calculating convenience, we will represent the element
defined by the relationship (167). But, as it is easy to check, this differential ideal is not finite-dimensional. So, for future calculating convenience, we will represent the element 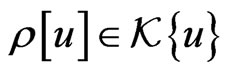 in the following natural factorized form:
in the following natural factorized form:
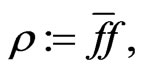 (168)
(168)
where elements 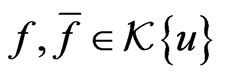 satisfy the adjoint pairs of the following differential relationships:
satisfy the adjoint pairs of the following differential relationships:
 (169)
(169)
and
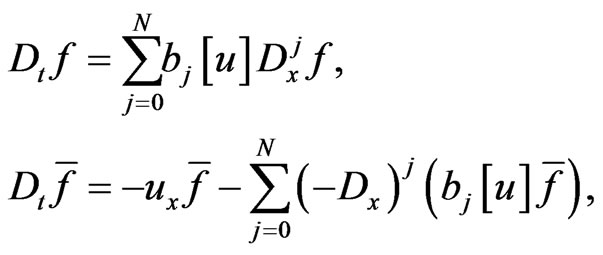 (170)
(170)
for some elements 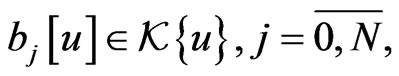 and check the finite-dimensional
and check the finite-dimensional  - and
- and 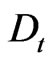 -invariance of the corresponding ideal (161) generated by the element
-invariance of the corresponding ideal (161) generated by the element 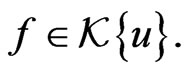
Now it is easy to check by means of straightforward calculations, based on the relationship (163) and (167), that the following differential equalities
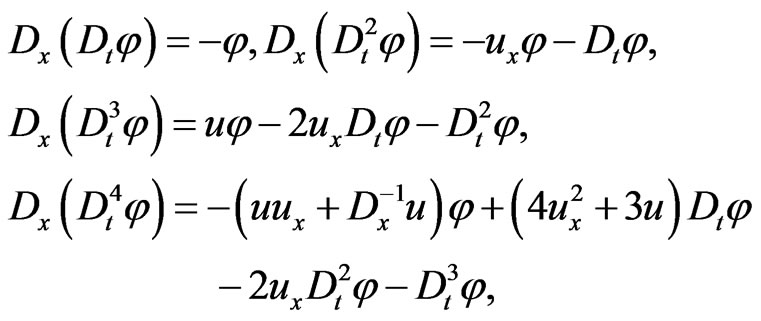 (171)
(171)
and their consequences
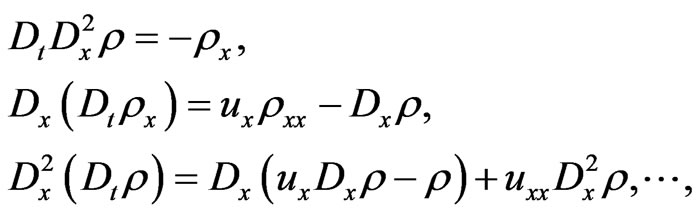 (172)
(172)
hold. Taking into account the independence of the sets of functional elements
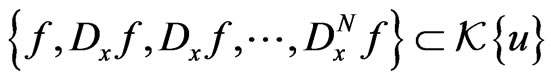
and

the relationships (172) together with (168), (169) and (170) make it possible to state the following lemma.
Lemma 2 The set (161) represents a  - and
- and 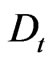 -invariant differential ideal in the ring
-invariant differential ideal in the ring 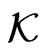 for all
for all 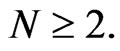
Proof 1 This result easily follows from the fact that for 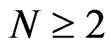 all of the relationships (172) are compatible upon taking into account the differential expressions (168) and (170). However, for
all of the relationships (172) are compatible upon taking into account the differential expressions (168) and (170). However, for  they are not compatible.
they are not compatible.
As a corollary of Lemma 2, in light of (161) and (170), for  one readily finds by means of elementary calculations that the related differential ideal
one readily finds by means of elementary calculations that the related differential ideal  is to be invariant if the following differential Lax relationships hold:
is to be invariant if the following differential Lax relationships hold:
 (173)
(173)
and
 (174)
(174)
where  is an arbitrary complex parameter. Moreover, they exactly coincide with those found before in [43]. The above differential relationships (173) and (174) can be equivalently rewritten in the following matrix Zakharov-Shabat type form:
is an arbitrary complex parameter. Moreover, they exactly coincide with those found before in [43]. The above differential relationships (173) and (174) can be equivalently rewritten in the following matrix Zakharov-Shabat type form:
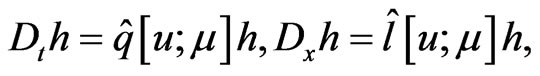 (175)
(175)
where the matrices
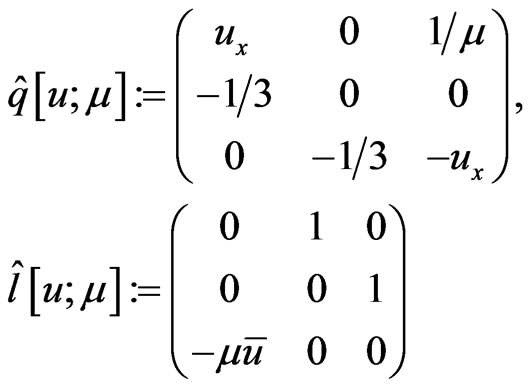 (176)
(176)
and 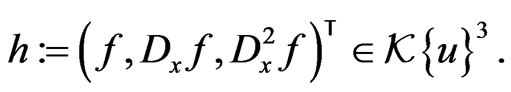
Furthermore, it follows from the differential relationships (173) and (174) that the compatibility condition (163) gives rise to the following important relationship
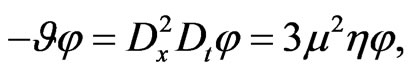 (177)
(177)
where the polynomial integro-differential operator
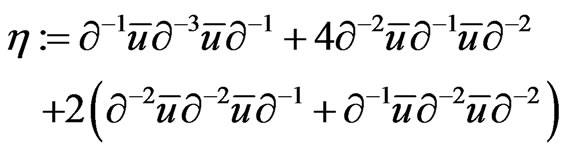 (178)
(178)
is skew-symmetric on the functional manifold  and comprises the second compatible Poisson structure for the Ostrovsky-Vakhnenko dynamical system (140).
and comprises the second compatible Poisson structure for the Ostrovsky-Vakhnenko dynamical system (140).
Now by virtue of the recurrent relationships following from substitution of the asymptotic expansion
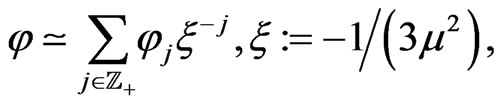 (179)
(179)
into (177), one can determine a new infinite hierarchy of conservations laws for dynamical system (140):
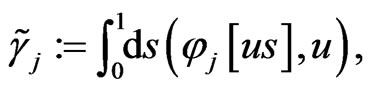 (180)
(180)
for 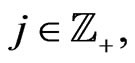 where
where
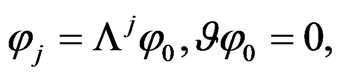 (181)
(181)
and the recursion operator 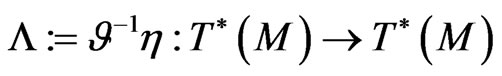 satisfies the standard Lax representation:
satisfies the standard Lax representation:
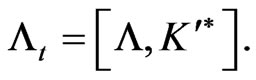 (182)
(182)
The above results can be formulated as follows.
Proposition 8 The Ostrovsky-Vakhnenko dynamical system (140) allows the standard differential Lax representation (173), (174) and defines on the functional manifold 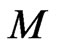 an integrable bi-Hamiltonian flow with compatible Poisson structures (154) and (178). In particular, this dynamical system possesses an infinite hierarchy of nonlocal conservation laws (180) defined by the gradient elements (181).
an integrable bi-Hamiltonian flow with compatible Poisson structures (154) and (178). In particular, this dynamical system possesses an infinite hierarchy of nonlocal conservation laws (180) defined by the gradient elements (181).
Remark 3 It should be noted that the existence of an infinite 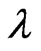 -powers ordered hierarchy of conservations laws (148) is a typical property [1,3,10,12] of the Lax integrable Hamiltonian systems, which are simultaneously bi-Hamiltonian flows with respect to corresponding compatible Poissonian structures.
-powers ordered hierarchy of conservations laws (148) is a typical property [1,3,10,12] of the Lax integrable Hamiltonian systems, which are simultaneously bi-Hamiltonian flows with respect to corresponding compatible Poissonian structures.
Remark 4 It is interesting to observe that our second polynomial Poisson structure (178) differs from that obtained recently in [42], which contains rational power factors.
Making use of the differential Expressions (173) and (174), it is easy to construct a slightly different from (175) matrix Lax representation of the Zakharov-Shabat form for the dynamical system (138).
In fact, if one defines the “spectral” parameter  and new basis elements of the invariant differential ideal (161):
and new basis elements of the invariant differential ideal (161):
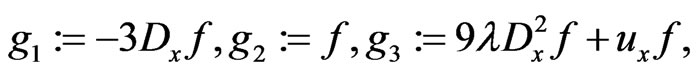 (183)
(183)
then relationships (173) and (174) can be rewritten as follows:
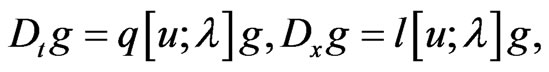 (184)
(184)
where the matrices
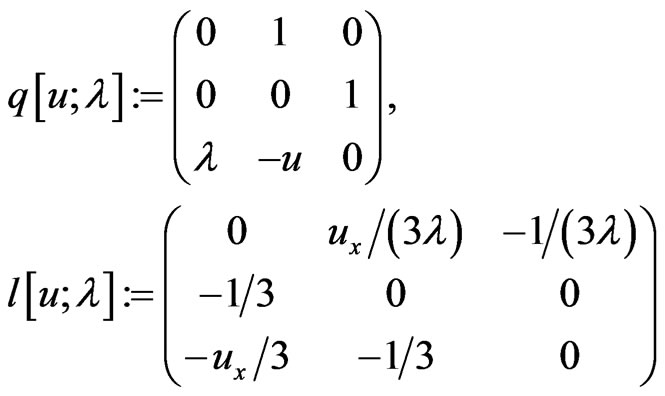 (185)
(185)
coincide with those of [42,43] and satisfy the Zakharov-Shabat type compatibility condition:
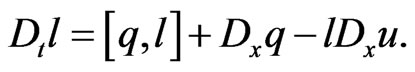 (186)
(186)
Remark 5 As already mentioned above, the Lax representation (185) of the Ostrovsky-Vakhnenko dynamical system (138) was obtained in [43] by means of a suitable limiting reduction of the Degasperis-Processi equation
 (187)
(187)
For convenience, let us rewrite this in the following form:
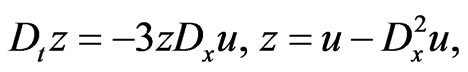 (188)
(188)
where differentiations
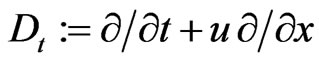 and
and 
satisfy the Lie-algebraic relationship (77). It is impressive that Equation (187) is itself a special reduction of a new Lax integrable Riemann type hydrodynamic system, proposed and studied (for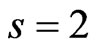 ) recently in [51]:
) recently in [51]:
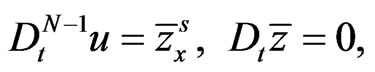 (189)
(189)
where 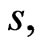
 are arbitrary natural numbers. Actually, defining
are arbitrary natural numbers. Actually, defining  and
and  from (189) one easily obtains the following dynamical system:
from (189) one easily obtains the following dynamical system:
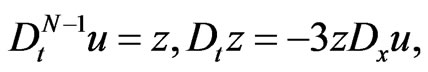 (190)
(190)
coinciding with the Degasperis-Processi Equation (188) if one makes the identification  As a resultwe have proved that a function
As a resultwe have proved that a function 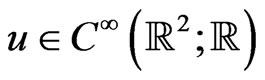 that satisfies, for an arbitrary
that satisfies, for an arbitrary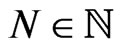 , the generalized Riemann type hydrodynamical equation
, the generalized Riemann type hydrodynamical equation
 (191)
(191)
simultaneously solves the Degasperis-Processi equation (187). In particular, for 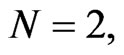 we find that solutions to the Burgers type equation
we find that solutions to the Burgers type equation
 (192)
(192)
are also solutions to the Degasperis-Processi Equation (187). This means, in particular, that the reduction procedure in [43] can also be applied to the Lax integrable Riemann type hydrodynamic system (189), giving rise to a related Lax representation for the Ostrovsky-Vakhnenko dynamical system (138).
7. Conclusions
We have considered the standard canonically symplectic phase space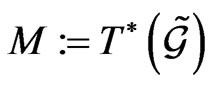 , generated by the centrally extended basis manifold to be an affine loop Lie algebra
, generated by the centrally extended basis manifold to be an affine loop Lie algebra 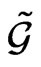 on the circle
on the circle  Subject to the standard Hamiltonian Lie algebra
Subject to the standard Hamiltonian Lie algebra 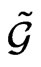 -action on
-action on 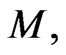 with respect which the symplectic structure on
with respect which the symplectic structure on 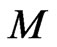 is invariant, we have constructed the corresponding momentum mapping and carried out the standard Marsden-Weinstein reduction of the manifold
is invariant, we have constructed the corresponding momentum mapping and carried out the standard Marsden-Weinstein reduction of the manifold 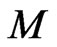 upon the reduced phase space
upon the reduced phase space 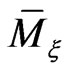 endowed with the reduced Poisson bracket
endowed with the reduced Poisson bracket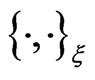 . This allows to construct on the phase space
. This allows to construct on the phase space 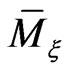 mutually commuting vector fields which are equivalent to nonlinear dynamical systems possessing an infinite hierarchy of commuting conservation laws. Moreover, these commuting vector fields on
mutually commuting vector fields which are equivalent to nonlinear dynamical systems possessing an infinite hierarchy of commuting conservation laws. Moreover, these commuting vector fields on 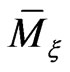 realize exactly their corresponding Lax representations.
realize exactly their corresponding Lax representations.
In addition, we have detailed analysis of commutation properties for the related flows on the basis manifold making it possible to define a suitable  -structure on the Lie algebra
-structure on the Lie algebra 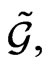 intimately related to the corresponding classical
intimately related to the corresponding classical  -structure on
-structure on , generated by the reduced Poisson bracket on the phase space
, generated by the reduced Poisson bracket on the phase space . As a by-product of our analysis we proved that these
. As a by-product of our analysis we proved that these 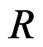 - and
- and 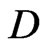 -structures are completely equivalent to a suitably generalized classical Lie-Poisson-Adler-Kostant-SymesKirillov-Berezin structure on the adjoint space
-structures are completely equivalent to a suitably generalized classical Lie-Poisson-Adler-Kostant-SymesKirillov-Berezin structure on the adjoint space . We also derived the determining Equation for the
. We also derived the determining Equation for the 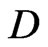 -structure, classifying the generalized Lax integrable nonlinear dynamical systems on the reduced phase space
-structure, classifying the generalized Lax integrable nonlinear dynamical systems on the reduced phase space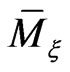 , whose respectively defined R-structures are not necessary both antisymmetric and local, as shown in [22,24] by means of another approach. It is also worth mentioning that the reduction scheme devised in this work can be applied to the centrally extended algebra of pseudo-differential operators and affine loop algebras on the circle
, whose respectively defined R-structures are not necessary both antisymmetric and local, as shown in [22,24] by means of another approach. It is also worth mentioning that the reduction scheme devised in this work can be applied to the centrally extended algebra of pseudo-differential operators and affine loop algebras on the circle 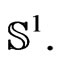
A new differential-algebraic approach, elaborated in [9] for revisiting the integrability analysis of generalized Riemann type hydrodynamical Equation (73), made it possible to prove the Lax integrability of new nonlinear Hamiltonian dynamical systems representing Riemann type hydrodynamic Equations (80), (87) and (91). In particular, the integrability prerequisites of these dynamical system, such as compatible Poissonian structures, an infinite hierarchy of conservation laws and related Lax representation have been constructed by means of both the symplectic gradient-holonomic approach [10,12,48] and innovative differential-algebraic tools devised recently [8,9,35] for analyzing the integrability of a special infinite hierarchy of Riemann type hydrodynamic systems. It is also quite clear from recent research in this area and our work in this paper that the dynamical system (80) is a Lax integrable bi-Hamiltonian flow for arbitrary integers . This is perhaps most readily verified by means of the differential-algebraic approach, which was devised and successfully applied here for the cases
. This is perhaps most readily verified by means of the differential-algebraic approach, which was devised and successfully applied here for the cases 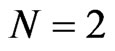 and 3.
and 3.
Making use of the differential-algebraic approach, we have also re-derived the Lax representation for the Ostrovsky-Vakhnenko Equation (138) and constructed the related simple compatible polynomial Poisson structures.
As we have seen in the course of this investigation, perhaps the most important lesson that one can derive from this approach is the following: If an investigation of a given nonlinear Hamiltonian dynamical system via the gradient-holonomic method indicates (but does not necessarily prove) that the system is Lax integrable, then its Lax representation can often be shown to exist and then successfully derived by means of a suitably constructed invariant differential ideal 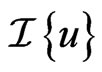 of the ring
of the ring 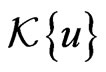 in accordance with the differential-algebraic approach developed here for the integrability analysis of the Riemann hydrodynamical system. Consequently, when it comes applying this lesson to the investigation of other nonlinear dynamical systems, it is natural to start with systems that are known to be Lax integrable and to try to identify and characterize those algebraic structures responsible for the existence of a related finite-dimensional matrix representation for the basic
in accordance with the differential-algebraic approach developed here for the integrability analysis of the Riemann hydrodynamical system. Consequently, when it comes applying this lesson to the investigation of other nonlinear dynamical systems, it is natural to start with systems that are known to be Lax integrable and to try to identify and characterize those algebraic structures responsible for the existence of a related finite-dimensional matrix representation for the basic 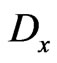 - and
- and 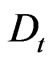 -differentiations in a vector space
-differentiations in a vector space  for some finite
for some finite 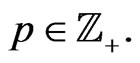
It seems plausible that if one could do this for several classes of Lax integrable dynamical systems, certain patterns in the algebraic structures may be detected that can be used to assemble a more extensive array of symplectic and differential-algebraic tools capable of resolving the question of complete integrability for many other types of nonlinear Hamiltonian dynamical systems. Moreover, if the integrability is established in this manner, the approach should also serve as a means of constructing associated artifacts of the integrability such as Lax representations and hierarchies of mutually commuting invariants. As a particular differential-algebraic problem of interest concerning these matrix representations, one can seek to develop a scheme for the effective construction of functional generators of the corresponding invariant finite-dimensional ideals 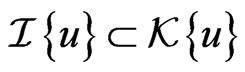 under given differential-algebraic constraints imposed on the
under given differential-algebraic constraints imposed on the 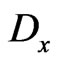 - and
- and 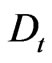 -differentiations.
-differentiations.
We have also demonstrated here that an approach combining the gradient-holonomic method with some recently devised differential-algebraic techniques can be a very effective and efficient way of investigating integrability for a particular class of infinite-dimensional Hamiltonian dynamical systems (generalized Riemann hydrodynamical systems). But a closer look at the specific details of the approach employed here reveals, we believe, that this combination of methods can be adapted to perform effective integrability analysis of a much wider range of dynamical systems.
8. Acknowledgements
D.B. acknowledges the National Science Foundation (Grant CMMI-1029809) and A.P. and Y.P. acknowledge the Scientific and Technological Research Council of Turkey (TUBITAK/NASU-111T558 Project) for partial support of their research.
REFERENCES
- L. D. Faddeev and L. A. Takhtadjan, “Hamiltonian Methods in the Theory of Solitons,” Springer, Berlin, 2000.
- A. G. Reyman and M. A. Semenov-Tyan-Shansky, “Reduction of Hamiltonian Systems, Affine Lie Algebras, and Lax Equations, I, II,” Invent. Math, Vol. 54, No. 1, 1979, pp. 81-100 and Vol. 63, No. 3, 1981, pp. 423-432.
- M. Blaszak, “Multi-Hamiltonian Theory of Dynamical Systems,” Springer, Berlin, 1998.
- A. Newell, “Solitons in Mathematics and Physics,” SIAM, Philadelphia, 1985. http://dx.doi.org/10.1137/1.9781611970227
- S. P. Novikov, “Theory of Solitons,” Springer, Berlin, 1984.
- A. G. Reyman and M. A. Semenov-Tian-Shansky, “Integrable Systems,” The Computer Research Institute Publishing, Moscow-Izhvek, 2003. (in Russian)
- A. M. Mikhaylov, A. B. Shabat and R. I. Yamilov, “Extension of the Module of Invertible Transformations. Classification of Integrable Systems,” Communications in Mathematical Physics, Vol. 115, No. 1, 1988, pp. 1-19. http://dx.doi.org/10.1007/BF01238850
- A. K. Prykarpatsky, O. D. Artemovych, Z. Popowicz and M. V. Pavlov, “Differential-Algebraic Integrability Analysis of the Generalized Riemann Type and Korteweg-de Vries Hydrodynamical,” Journal of Physics A: Mathematical and Theoretical, Vol. 43, No. 29, 2010, Article ID: 295205.
- Y. A. Prykarpatsky, O. D. Artemovych, M. Pavlov and A. K. Prykarpatsky, “The Differential-Algebraic and Bi-Hamiltonian Integrability Analysis of the Riemann Type Hierarchy Revisited,” Journal of Mathematical Physics, Vol. 53, 2012, Article ID: 103521.
- D. Blackmore, A. K. Prykarpatsky and V. Hr Samoylenko, “Nonlinear Dynamical Systems of Mathematical Physics: Spectral and Differential-Geometrical Integrability Analysis,” World Scientific, New Jersey, 2011.
- Y. Mitropolsky, N. Bogolubov Jr., A. Prykarpatsky and V. Samoylenko, “Integrable Dynamical System: Spectral and Differential-Geometric Aspects,” Naukova Dunka, Kiev, 1987. (in Russian)
- A. Prykarpatsky and I. Mykytyuk, “Algebraic Integrability of Nonlinear Dynamical Systems on Manifolds: Classical and Quantum Aspects,” Kluwer Academic Publishers, Dordrecht, The Netherlands, 1998. http://dx.doi.org/10.1007/978-94-011-4994-5
- R. Abraham and J. E. Marsden, “Foundations of Mechanics,” Benjamin/Cummins Publisher, San Francisco, 1978.
- V. I. Arnold, “Mathematical Methods of Classical Mechanics,” Springer, Berlin, 1989. http://dx.doi.org/10.1007/978-1-4757-2063-1
- M. Adler, “Completely Integrable Systems and Symplectic Action,” Journal of Mathematical Physics, Vol. 20, No. 1, 1979, pp. 60-67. http://dx.doi.org/10.1063/1.523963
- A. M. Perelomov, “Integrable Systems of Classical Mechanics and Lie Algebras,” Nauka Publishing, Moscow, 1990. (in Russian)
- N. N. Bogolubov Jr. and Y. A. Prykarpatsky, “The Marsden-Weinstein Reduction Structure of Integrable Dynamical Systems and a Generalized Exactly Solvable Quantum Superradiance Model,” International Journal of Modern Physics B, Vol. 28, No. 1, 2012, pp. 237-245.
- R. V. Samulyak, “Generalized Dicke Type Dynamical System as the Inverse Nonlinear Schrödinger Equation,” Ukrainian Mathematical Journal, Vol. 47, No. 1, 1995, pp. 149-151. http://dx.doi.org/10.1007/BF01058807
- M. A. Semenov-Tian-Shansky, “What Is an R-Matrix?” Functional Analysis and Its Applications, Vol. 17, No. 4, 1983, pp. 259-272. http://dx.doi.org/10.1007/BF01076717
- Y. A. Prykarpatsky, A. M. Samoilenko and A. K. Prykarpatsky, “The Geometric Properties of Canonically Reduced Symplectic Spaces with Symmetry, Their Relationship with Structures on Associated Principal Fiber Bundles and Some Applications,” Opuscula Mathematica, Vol. 25, No. 2, 2005, pp. 287-298.
- F. Calogero and A. Degasperis, “Spectral Transform and Solitons,” North-Holland, Amsterdam, 1982.
- J. Avan, O. Babelon and M. Talon, “Construction of Classical
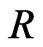 -Matrices for the Toda and Calogero Models,” Algebra and Analysis, Vol. 6, No. 2, 1994, p. 67.
-Matrices for the Toda and Calogero Models,” Algebra and Analysis, Vol. 6, No. 2, 1994, p. 67. - O. Babelon and C.-M. Viallet, “Hamiltonian Structures and Lax Equations,” Physics Letter B, Vol. 237, No. 3-4, 1990, pp. 411-416.
- G. E. Arutyunov and P. B. Medvedev, “Generating Equation for
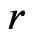 -Matrices Related to the Dynamical Systems of Calogero Type,” Physics Letter A, Vol. 223, No. 1-2, 1996, pp. 66-74. http://dx.doi.org/10.1016/S0375-9601(96)00719-0
-Matrices Related to the Dynamical Systems of Calogero Type,” Physics Letter A, Vol. 223, No. 1-2, 1996, pp. 66-74. http://dx.doi.org/10.1016/S0375-9601(96)00719-0 - E. K. Sklyanin, “Quantum Variant of the Inverse Scattering Transform Method,” Proceedings of LOMI 95, Leningrad, 15-20 January 1980, pp. 55-128. (in Russian)
- S. A. Tsyplyaev, “Commutation Relations for Transition Matrix in Classical and Quantum Inverse Scattering Method,” Theoretical and Mathematical Physics, Vol. 48, No. 1, 1981, pp. 24-33. (in Russian) http://dx.doi.org/10.1007/BF01037981
- T. Crespo and Z. Hajto, “Algebraic Groups and Differential Galois Theory. Graduate Studies in Mathematics Series,” American Mathematical Society Publisher, Providence, 2011.
- I. Kaplanski, “Introduction to Differential Algebra,” Hermann, Paris, 1957.
- E. R. Kolchin, “Differential Algebra and Algebraic Groups,” Academic Press, New York, 1973.
- J. F. Ritt, “Differential Algebra,” AMS-Colloqium Publications, New York, 1966.
- J.-A. Weil, “Introduction to Differential Algebra and Differential Galois Theory,” CIMPA-UNESCO-Vietnam Lectures, Hanoi, 2001.
- J. Golenia, M. Pavlov, Z. Popowicz and A. Prykarpatsky, “On a Nonlocal Ostrovsky-Whitham Type Dynamical System, Its Riemann Type Inhomogenious Regularizations and Their Integrability,” SIGMA 6, 2010, pp. 1-13.
- G. Wilson, “On the Quasi-Hamiltonian Formalism of the KdV Equation,” Physics Letter, Vol. 132, No. 8-9, 1988, pp. 445-450.
- L. Brunelli and A. Das, “On an Integrable Hierarchy Derived from the Isentropic Gas Dynamics,” Journal of Mathematical Physics, Vol. 45, No. 7, 2004, p. 2633. http://dx.doi.org/10.1063/1.1756699
- J. Golenia, N. N. Bogolubov Jr., Z. Popowicz, M. V. Pavlov and A. K. Prykarpatsky, “A New Riemann Type Hydrodynamical Hierarchy and Its Integrability Analysis,” 2009. http://publications.ictp.it
- M. Pavlov, “The Gurevich-Zybin System,” Journal of Physics A: Mathematical and General, Vol. 38, No. 17, 2005, pp. 3823-3840. http://dx.doi.org/10.1088/0305-4470/38/17/008
- Z. Popowicz and A. K. Prykarpatsky, “The Non-Polynomial Conservation Laws and Integrability Analysis of Generalized Riemann Type Hydrodynamical Equations,” Nonlinearity, Vol. 23, No. 10, 2010, pp. 2517-2537. http://dx.doi.org/10.1088/0951-7715/23/10/010
- Y. Prykarpatsky, “Finite Dimensional Local and Nonlocal Reductions of One Type Hydrodynamic Systems,” Reports on Mathematical Physics, Vol. 50, No. 3, 2002, pp. 349-360. http://dx.doi.org/10.1016/S0034-4877(02)80065-9
- A. K. Prykarpatsky and M. M. Prytula, “The GradientHolonomic Integrability Analysis of a Whitham-Type Nonlinear Dynamical Model for a Relaxing Medium with Spatial Memory,” Nonlinearity, Vol. 19, No. 9, 2006, pp. 2115-2122. http://dx.doi.org/10.1088/0951-7715/19/9/007
- J. P. Wang, “The Hunter-Saxton Equation: Remarkable Structures of Symmetries and Conserved Densities,” Nonlinearity, Vol. 23, No. 8, 2010, pp. 2009-2028. http://dx.doi.org/10.1088/0951-7715/23/8/011
- Z. Popowicz, “The Matrix Lax Representation of the Generalized Riemann Equations and Its Conservation Laws,” Physics Letter A, Vol. 375, No. 37, 2011, pp. 3268-3272.
- J. C. Brunelli and S. Sakovich, “Hamiltonian Structures for the Ostrovsky-Vakhnenko Equation,” Communications in Nonlinear Science and Numerical Simulation, Vol. 18, No. 1, 2013, pp. 56-62.
- A. Degasperis, D. D. Holm and A. N. W Hone, “A New Integrable Equation with Peakon Solutions,” Theoretical and Mathematical Physics, Vol. 133, No. 2, 2002, pp. 1463-1474. http://dx.doi.org/10.1023/A:1021186408422
- L. A. Ostrovsky, “Nonlinear Internal Waves in a Rotating Ocean,” Okeanologia, Vol. 18, No. 2, 1978, pp. 181-191.
- A. A. Vakhnenko, “Solitons in a Nonlinear Model Medium,” Journal of Physics A, Vol. 25, No. 15, 1992, pp. 4181-4187.
- Y. Wang and Y. Chen, “Integrability of the Modified Generalized Vakhnenko Equation,” Journal of Mathematical Physics, Vol. 53, No. 12, 2012, Article ID: 123504. http://dx.doi.org/10.1063/1.4764845
- G. B. Whitham, “Linear and Nonlinear Waves,” WileyInterscience, New York, 1974.
- O. Hentosh, M. Prytula and A. Prykarpatsky, “Differential-Geometric and Lie-Algebraic Foundations of Investigating Nonlinear Dynamical Systems on Functional Manifolds,” 2nd Edition, Lviv University Publishing, Lviv, 2006. (in Ukrainian)
- E. J. Parkes, “The Stability of Solutions of Vakhnenko’s Equation,” Journal of Physics A, Vol. 26, No. 22, 1993, pp. 6469-6475.
- A. G. Reyman and M. A. Semenov-Tian-Shansky, “The Hamiltonian Structure of Kadomtsev-Petviashvili Type Equations,” LOMI Proceedings, Leningrad, 12-17 January 1987, pp. 212-227. (in Russian)
- D. Blackmore, Y. A. Prykarpatsky, O. D. Artemowych, D. Orest and A. K. Prykarpatsky, “On the Complete Integrability of a One Generalized Riemann Type Hydrodynamic System,” arXiv:1204.0251v1.

