Applied Mathematics
Vol.4 No.7(2013), Article ID:34322,5 pages DOI:10.4236/am.2013.47145
Tail Dependence Study of SSE Composite Index and SZSE Component Index Based on the Copula*
College of Science, Guilin University of Technology, Guilin, China
Email: 296231428@qq.com
Copyright © 2013 Guohua Sun et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 17, 2013; revised May 17, 2013; accepted May 24, 2013
Keywords: Rank; Copula; Nonparametric Estimation; Tail Dependence
ABSTRACT
With the rapid development of financial industry, copula methods are more and more widely used for the study of financial fields. By selecting the appropriate copulas, the tail dependence of financial variables can be measured easily. Using the nonparametric estimation method to select A12 copula from Archimedean copulas, and do tail dependence study of SSE composite index and SESE component index. The results show that the SSE composite index and SESE component index simultaneously have the upper tail dependence and lower tail dependence, and the upper tail dependence coefficient is less than the lower tail dependence coefficient, which is consistent with the real financial market rule.
1. Introduction
With the continuous development of the financial markets, the relationship of interior financial markets is more and more complex, it will promote the study of dependence between financial market structure. In the quantitative analysis of related financial market structure, dependence study is very important, a series of financial problems involve the dependence studies, such as risk management, portfolio selection, asset pricing and so on. Using multivariate distribution function to depict the dependence between each component is the most common method in mathematics; However traditional multivariate distribution function exists some problems in practical application, when the analysis formulas of multivariate distribution function contain many variables, it will be difficult to handle, and it requires the type of marginal distribution function to fit the type of multivariate distribution function. In financial analysis, marginal distribution often do not have the same type of distribution, this makes the traditional multivariate distribution functions can not be widely used in the dependence analysis of financial markets. By Sklar theorem [1], using the copula function to structure flexible multivariate distribution function, so as to grasp the real dependence between financial markets. Therefore, in this paper we use copula functions to study the tail dependence between SSE composite index and SZSE component index.
At present, using copula function to study the dependence of the financial market already had many achievements, but also in many domestic and foreign literatures, most of them used parameter estimation method to estimate parameters of copula functions. The innovation of this paper is to use a parameter estimation method for parameter estimation, to determine copula functions, and then to do the test of tail dependence.
2. Tail Dependence Based on Copula
Tail dependence can be used to represent extreme events of the interaction between the variables, for example, when the random variable X increased or decreased significantly, the probability of the random variable Y increased or decreased significantly [2]. We use the tail dependence coefficient of copula to research the relationship between SSE composite index and SZSE component index. Let X and Y be continuous random variables with distribution functions F and G respectively, and whose copula is C, and then, based on the copula function we define the upper tail dependence coefficient  and the lower tail dependence coefficient
and the lower tail dependence coefficient  as follows [3]:
as follows [3]:
 (1)
(1)
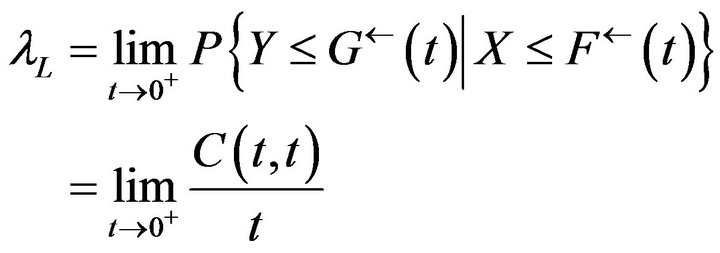 (2)
(2)
where , when
, when , we think the upper (lower) tail of X and Y be asymptotic dependence; when
, we think the upper (lower) tail of X and Y be asymptotic dependence; when , we think the upper (lower) tail of X and Y be asymptotic independence; where
, we think the upper (lower) tail of X and Y be asymptotic independence; where  and
and  are the t quantile functions of distribution functions
are the t quantile functions of distribution functions  and
and  respectively [4].
respectively [4].
3. Selecting Copulas and Estimating Parameters
There are many kinds of copula functions, Elliptic copulas and Archimedean copulas are used commonly, and each group has many specific copula functions. Different copula functions have different properties, in the actual application, choosing the right copula functions need to follow two principles: one is that the established model of copulas should be easy to operate and understand, to avoid the phenomenon of unknown parameters [5]; second is to choose the appropriate copula functions which are suitable for the sample datas. Elliptical copula functions are with a symmetrical tail dependence, this will be conflicted with fat-tailed distribution of financial datas. Archimedean copulas are the most widely used in the financial field, and it is easy to build and calculate them. The bivariate normal copula with symmetry and asymptotic tail independence is applied widely, but it is unable to capture the asymmetric dependence and tail dependence between the variables. Here we select copulas which have obvious tail features. Because the log return correlation is accorded with the Archimedean copula distribution, so we choose the Clayton copula with obvious lower tail features, the Gumbel copulas with obvious upper tail features, and the A12 copula with both upper and lower tail features from Archimedean copulas on the financial data fitting [6]. Moreover Archimedean copulas have a feature that Kendall’s tau is the analytic function of . By Sklar theorem, when marginal distribution function is continuous, the copulas function will be uniquely identified.
. By Sklar theorem, when marginal distribution function is continuous, the copulas function will be uniquely identified.
For the parameter estimation of a specific copula function, parametric approach and nonparametric approach are common methods: 1) strict maximum likelihood approach (EML) and marginal distribution extrapolation approach (IFM) are more frequently used in the parameter method. Maximum likelihood approach estimates marginal distribution and parameters of copula function at the same time; Marginal distribution extrapolation approach divide estimation process into two steps, first to estimate the parameters of the marginal distribution function, and then estimate the parameters of copula function. 2) Genest and Rivest approachs are commonly used in the nonparametric approach [7]. As we know, for a copula function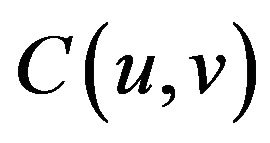 , it is related to the Kendall’s tau as following:
, it is related to the Kendall’s tau as following:

So for most of the single parameter Archimedean copula functions, because of its generating element 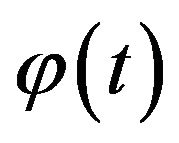 is a function of the parameter
is a function of the parameter  and the relationship between
and the relationship between 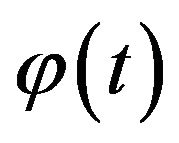 and the Kendall’s tau as follows:
and the Kendall’s tau as follows:
 (3)
(3)
By solving the formula above, we can get the estimate value of . The deficiency of EML and IFM approaches lie in the parameter estimation of copula function is affected by the marginal distribution function, if the assumptive model of marginal distribution function were wrong, it will lead to a biased estimate to the copula function. Therefore, in this article we use nonparametric estimation method in view of the features of the Archimedean copulas, to calculate the estimate value of
. The deficiency of EML and IFM approaches lie in the parameter estimation of copula function is affected by the marginal distribution function, if the assumptive model of marginal distribution function were wrong, it will lead to a biased estimate to the copula function. Therefore, in this article we use nonparametric estimation method in view of the features of the Archimedean copulas, to calculate the estimate value of  by the estimate value of the Kendall’s tau, further to estimate the parameters of copula functions.
by the estimate value of the Kendall’s tau, further to estimate the parameters of copula functions.
3.1. The Introduction of Three Types of Copulas
1) Gumbel copula
 (4)
(4)
Gumbel copula function is very sensitive to the change of variables at the upper tail of the distribution, so it can quickly capture the changes of upper tail dependence, and it can be used to represent the relations between financial variables which have upper tail dependence. Its parameter  represent the degree of correlation, when
represent the degree of correlation, when , the variables are independent; when
, the variables are independent; when , the variables are completely related. By formula (1) and (4), we can get the upper tail dependence coefficient of Gumbel copula function, namely
, the variables are completely related. By formula (1) and (4), we can get the upper tail dependence coefficient of Gumbel copula function, namely , by its generating element
, by its generating element  and formula (3), the Kendall’s tau is the analytic function of
and formula (3), the Kendall’s tau is the analytic function of :
:

Then, 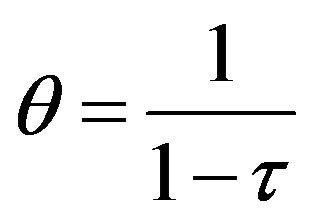 , accordingly,
, accordingly,
 (5)
(5)
In addition, by the formula

We can get  under different levels of
under different levels of .
.
2) Clayton copula
 (6)
(6)
Clayton Copula function is very sensitive to the change of variables at the lower tail of the distribution, so it can quickly capture the changes of lower tail dependence, and it can be used to represent the relations between financial variables which have lower tail dependence. Its parameter  also represent the degree of correlation, when
also represent the degree of correlation, when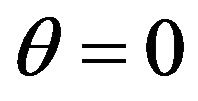 , the variables are independent; when
, the variables are independent; when , the variables are completely related. By formula (2) and (6), we can get the lower tail dependence coefficient of Clayton copula function, namely
, the variables are completely related. By formula (2) and (6), we can get the lower tail dependence coefficient of Clayton copula function, namely , by its generating element
, by its generating element  and formula (3), the Kendall’s tau is the analytic function of
and formula (3), the Kendall’s tau is the analytic function of :
:

Then,  , accordingly,
, accordingly,
 (7)
(7)
In addition, by the formula

We can get  under different levels of
under different levels of .
.
3) A12 copula of Archimedean copulas
 (8)
(8)
Gumbel copula function has only the feature of the upper tail dependence, and Clayton copula function has only the feature of the lower tail dependence, while the A12 copula of Archimedean copulas has both upper tail and lower tail dependence, by formula (1) and (8), the upper tail dependence coefficient can be expressed with the formula , and by formula (2) and (8), the lower tail dependence coefficient can be expressed with the formula
, and by formula (2) and (8), the lower tail dependence coefficient can be expressed with the formula , then by its generating element
, then by its generating element
 and formula (3), the Kendall’s tau is the analytic function of
and formula (3), the Kendall’s tau is the analytic function of :
:

Then,  , accordingly,
, accordingly,
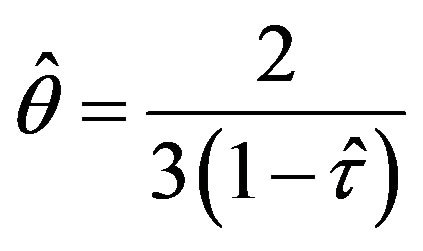 (9)
(9)
3.2. Estimating  with Nonparametric Estimation
with Nonparametric Estimation
In order to estimate the parameters, firstly we need to know the estimated value of the Kendall’s tau, originally the Kendall’s tau was not defined by the copula function , it was defined by the consistent probability of the random variable
, it was defined by the consistent probability of the random variable  minus the non-uniform probability of the random variable
minus the non-uniform probability of the random variable , that is
, that is

where  and
and  are independent identically distributed samples of the random variable
are independent identically distributed samples of the random variable .
.
If  are independent identically distributed samples which come from joint distribution function
are independent identically distributed samples which come from joint distribution function  of random variable
of random variable  and its copula function is
and its copula function is  are the ranks of these samples,
are the ranks of these samples,  represent the rank of
represent the rank of ;
;  represent the rank of
represent the rank of ; then the Kendall’s tau for the sample is defined as
; then the Kendall’s tau for the sample is defined as
 (10)
(10)
So we can work out  on the basis of
on the basis of , and the copula function can be determined solely; then according to the next two formulas to calculate the estimated values of the upper tail dependence coefficient and the lower tail dependence coefficient.
, and the copula function can be determined solely; then according to the next two formulas to calculate the estimated values of the upper tail dependence coefficient and the lower tail dependence coefficient.
 (11)
(11)
 (12)
(12)
4. Computing Steps and Results
4.1. Calculating the Parameter 
We select day’s closing price , of SSE composite index and SZSE component index from January 4, 2007 to March 21, 2011. Logarithmic yield
, of SSE composite index and SZSE component index from January 4, 2007 to March 21, 2011. Logarithmic yield
 .
.
We define , and by formula (10), we can get
, and by formula (10), we can get . Then by formula (5), formula (7) and formula (9) respectively; we get estimated values of parameters of different copulas in Table 1.
. Then by formula (5), formula (7) and formula (9) respectively; we get estimated values of parameters of different copulas in Table 1.
From Table 1, the parameters of three kinds of copulas are in their respective domains, this explain that there exist both upper tail dependence and lower tail dependence between SSE composite index and SZSE component index. Because the A12 copula of Archimedean copulas has both upper tail and lower tail dependence, we choose A12 copula to study for tail dependence, then we should do the test for the selected copula functions.
4.2. Testing for Copulas
In order to further illustrate A12 copula function can describe the tail dependence between SSE composite index and SZSE component index, we do test for the datas. In order to avoid the fault of hypothetical marginal distribution of copula function, we estimate parameters with the Kendall’s tau directly, so we don’t know the marginal distribution function. We use the empirical distribution and 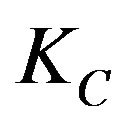 to structure and test variables which obey uniform distribution on inspection. Firstly we use geometric method to test copula distribution, then use K-S statistics to do the test of goodness of fit.
to structure and test variables which obey uniform distribution on inspection. Firstly we use geometric method to test copula distribution, then use K-S statistics to do the test of goodness of fit.
Univariate distribution function  is defined as
is defined as

where,  is the generating element of copula functions [8],
is the generating element of copula functions [8],  obeys the standard uniform distribution. Setting variables X and Y to obey the empirical distribution, then we can wok out the
obeys the standard uniform distribution. Setting variables X and Y to obey the empirical distribution, then we can wok out the 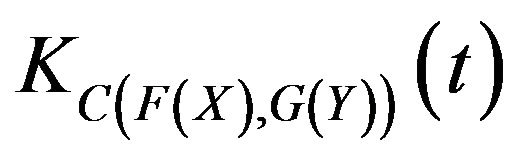 by means of
by means of .
.
For A12 copula function,
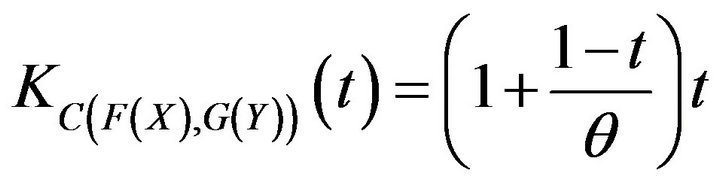 (13)
(13)
Follow the steps to calculate1) To solve the distribution function  and
and 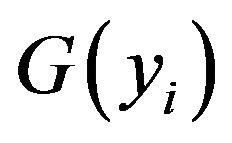 of logarithm yield
of logarithm yield  (both F and G are empirical distribution function);
(both F and G are empirical distribution function);
2) To solve  by formula (8);
by formula (8);
3) Putting the  which was calculated in step 2) into formula (13);
which was calculated in step 2) into formula (13);
4) , to do test with a Q-Q figure of the uniform distribution.
, to do test with a Q-Q figure of the uniform distribution.
So we use these steps to get the Q-Q test which is shown in Figure 1.
In Figure 1, the  of A12 copula distribute uniformly on the oblique diagonal line and two sides, so it obey uniform distribution; Table 2 can also explain the
of A12 copula distribute uniformly on the oblique diagonal line and two sides, so it obey uniform distribution; Table 2 can also explain the  of A12 copula obeys uniform distribution. Therefore, we think that the A12 copula function is appropriate for describing the relationship between SSE composite index and SZSE component index, namely, A12 copula function is feasible to study the tail dependence of SSE composite index and SZSE component index.
of A12 copula obeys uniform distribution. Therefore, we think that the A12 copula function is appropriate for describing the relationship between SSE composite index and SZSE component index, namely, A12 copula function is feasible to study the tail dependence of SSE composite index and SZSE component index.
4.3. Studying Tail Dependence
By formula (11) and formula (12), we can work out the upper tail dependence coefficient and the lower tail dependence coefficient, the results are shown in Table 3.
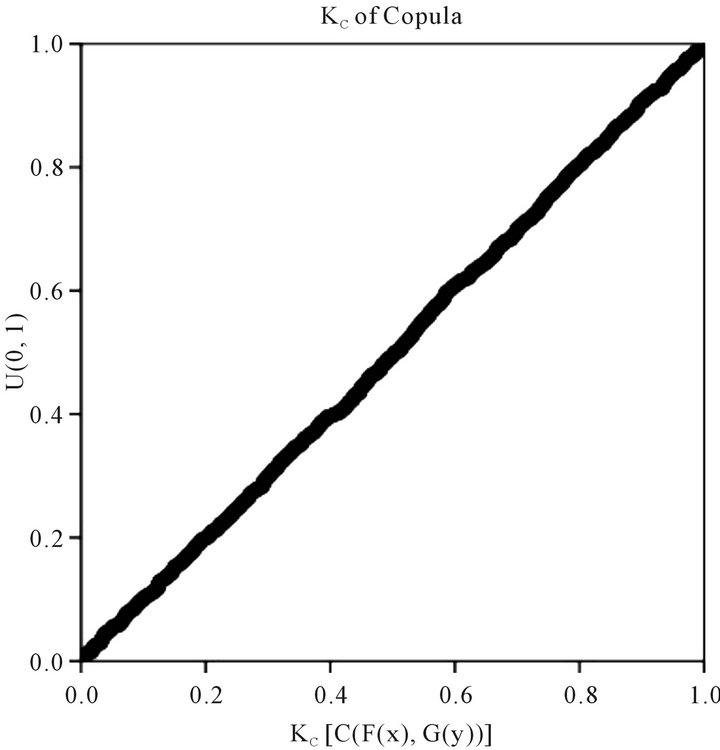
Figure 1. Q-Q figure of KC function of A12 copula.

Table 1. Parameter estimation of copulas.

Table 2. K-S test.

Table 3. The values of  and
and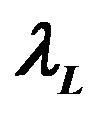 .
.
The Table 3 shows that the upper tail dependence coefficient is 0.7343, the lower tail dependence coefficient is 0.7901. It indicates that there exists both upper tail dependence and lower tail dependence between SSE composite index and SZSE component index, what’s more, the upper tail dependence is less than the lower tail dependence. The tail dependence between logarithmic yield of SSE composite index and logarithmic yield of SZSE component index demonstrated the consistency of both two extremums; it also demonstrated that whether the price rise or fall, there would be different degrees of dependence between two indices.
5. Conclusion
We select Gumbel copula, Clayton copula and A12 copula from Archimedean copulas, all of which have features of tail dependence. We use the nonparametric estimation approach to estimate parameters of copula functions, and find that there exists both upper tail dependence and lower tail dependence between SSE composite index and SZSE component index, therefore, we select A12 copula to do the empirical analysis about the tail dependence between SSE composite index and SZSE component index. The results show that the upper tail dependence coefficient is less than the lower tail dependence coefficient between SSE composite index and SZSE component index, that is to say, the dependence between SSE composite index and SZSE component index during the downturn of the stock market is higher than the active period, which is consistent with the real financial market rule [9].
REFERENCES
- R. B. Nelsen, “An Introduction to Copulas,” SpringerVerlag, New York, 2006, pp. 17-23.
- A. Juri and M. V. Wutrich, “Copula Convergence Theorems for Tail Events,” Insurance Mathematics and Economics, Vol. 30, No. 3, 2002, pp. 405-420. doi:10.1016/S0167-6687(02)00121-X
- H. Joe, “Multivariate Models and Dependence Concepts,” Chapman & Hall, London, 1997, pp. 186-198. doi:10.1201/b13150
- A. J. McNeil, R. Frey and P. Embrechts, “Quantitative Risk Management: Concepts, Techniques and Tools,” Princeton University Press, Princeton, 2005, pp. 201-208.
- J. V. Rosenberg and T. Schuermann, “A General Approach to Integrated Risk Management with Skewed, FatTailed Risks,” Journal of Financial Economics, Vol. 79, No. 3, 2006, pp. 569-614. doi:10.1016/j.jfineco.2005.03.001
- Y. Li and X. J. Cheng, “Tail Dependence Analysis of SZI & HSI Based on Copula Method,” Systems Engineering, Vol. 24, No. 5, 2006, pp. 88-92.
- C. Genest and L. P. Rivest, “Statistical Inference Procedures for Bivariate Archimedean Copula,” Journal of the American Statistical Association, Vol. 88, No. 423, 1993, pp. 1034-1043. doi:10.1080/01621459.1993.10476372
- V. Durrleman, A. Nikeghbali and T. Roncalli, “Which Copula Is the Right One?” Groupe de Recherche Operationelle, Credit Lyonnais, France, 2000, pp. 13-15.
- X. L. Ren and S. Y. Zhang, “Tail Dependence Analysis of Financial Market Based on the Copula,” Statistics & Information Forum, Vol. 23, No. 6, 2008, pp. 66-71.
NOTES
*This study was supported by the National Natural Science Foundation of China under the Grant No. 11061012. It was also supported by Guangxi Key Laboratory of Spatial Information and Geomatics (1103108-20) and Guilin Technology Projects (20110120-5).

