Applied Mathematics
Vol.4 No.6(2013), Article ID:33174,5 pages DOI:10.4236/am.2013.46130
Reconnection of Vortex Bundles Lines with Sinusoidally
Department of Applied Mathematics, College of Applied Science, Taibah University, Al-Madinah Al-Munawarah, KSA
Email: *szalamri@hotmail.com
Copyright © 2013 Sultan Z. Alamri, Abeer A. Alenezi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 26, 2013; revised April 8, 2013; accepted April 15, 2013
Keywords: Numerical Simulation; Superfluid Turbulence; Vortex Filament; Vortex; Reconnection
ABSTRACT
Using the vortex filament model with the full Biot-Savart law, we show that non-straight bundles of quantized vortex lines in HeII are structurally robust and can reconnect with each other maintaining their identity. We discuss vortex stretching in superfluid turbulence in many cases. We show that, during the bundle reconnection process, Kelvin waves of large amplitude are generated, in agreement with previous work and with the finding that helicity is produced by nearly singular vortex interactions in classical Euler flows. The reconnection events lead to changes in velocities, radius, number of points and total length. The existence of reconnections was confirmed by other authors using the model of nonlinear Schrödinger equation (NLSE). Our results are agreed with the finding of other authors and extension to our numerical experiments.
1. Introduction
It has been realised that the disordered motion of a tangle of quantized vortices play an important part in the behavior of superfluids. The flow is generally turbulent for high-velocity or high Reynolds number flows. Although turbulence has been studied intensely in many fields, it is still not yet well understood because it is a complicated dynamical phenomenon with strong nonlinearity [1]. Vortices are not well-defined for a typical classical fluid, and the relationship between vortices and turbulence remains indistinct. The liquid state of 4He exists in two phases: Helium I and Helium II [2]. The boundary between these phases is called the lambda line, which occurs at the critical temperature T = Tλ = 2.1768 K [3]. Characteristic phenomena of superfluidity were discovered by Kapitza et al. in 1930s. Superfluid heluim 4He is described by the two-fluid model, where the system consists of a viscous normal fluid has density 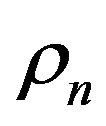 and an inviscid superfluid has density
and an inviscid superfluid has density 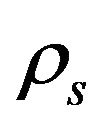 with two independent velocity vn and
with two independent velocity vn and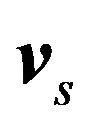 . The superfluid velocity field is given by
. The superfluid velocity field is given by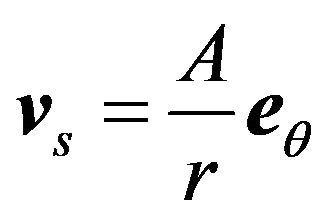 , where
, where  is some constant determined by assuming that the action of a single helium atom in the fluid to be quantized in units of
is some constant determined by assuming that the action of a single helium atom in the fluid to be quantized in units of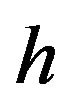 Planck’s constant,
Planck’s constant, 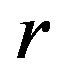 is the distance from the vortex axis and
is the distance from the vortex axis and  is the unit vector in the tangential direction [4,5]. The circulation of the vortices is quantized as
is the unit vector in the tangential direction [4,5]. The circulation of the vortices is quantized as
![]() (1)
(1)
where 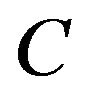 is a path around the axis of the vortex and the constant
is a path around the axis of the vortex and the constant  is called the quantum of circulation
is called the quantum of circulation
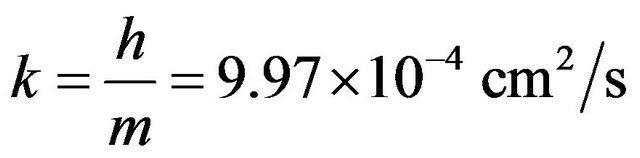 (2)
(2)
and ![]() is the mass of a 4He atom. The constant
is the mass of a 4He atom. The constant  is given by
is given by
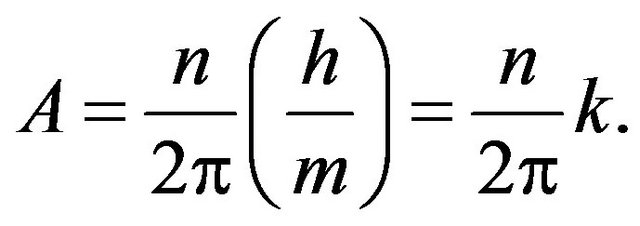 (3)
(3)
From Equation (1), it follows that the superfluid velocity field around the vortex is
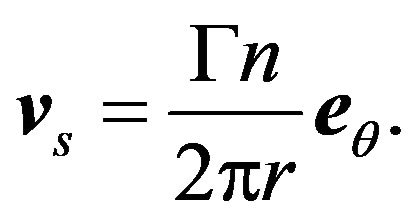 (4)
(4)
A quantived vortex is different from a vortex in a classical fluid where the circulation is quantized, which is contrary to a classical vortex that can have any value of circulation [6].
The dynamics of quantized vortices can be described by the Gross-Pitaevski (GP) model [7],
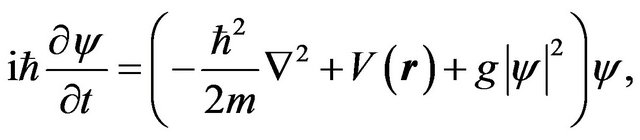 (5)
(5)
where 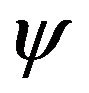 is the order parameter filed,
is the order parameter filed, 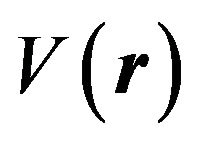 is an external potential,
is an external potential, ![]() is a coupling constant, and
is a coupling constant, and ![]() is the mass of each particle. This description is most applicable in the limit of
is the mass of each particle. This description is most applicable in the limit of , where the normal fluid is absent. This model can also be used to explain phenomena related to vortex cores, such as nucleation and reconnection. However, the GP model is applicable to Bose-Einstein condensation of a dilute atomic Bose gas. It is, however, not applicable quantitatively to superfluid 4He, which is not a weakly interacting Bose system. For more details, we refer to Refs. [8-10].
, where the normal fluid is absent. This model can also be used to explain phenomena related to vortex cores, such as nucleation and reconnection. However, the GP model is applicable to Bose-Einstein condensation of a dilute atomic Bose gas. It is, however, not applicable quantitatively to superfluid 4He, which is not a weakly interacting Bose system. For more details, we refer to Refs. [8-10].
The second formulation for studying the dynamics of quantized vortices is called the vortex filament model. The aim of this work is to use this model under the full Biot-Savart law to make numrical simulations to examine the dynamics of inviscid vortex filaments, specifically what happens at vortex including reconnection events. This model was pioneered by Schwarz [11,12], where the vortex lines are numerically discretized by a large, variable number of points depends on the local radius of curvature. We will briefly describe this model in the next section.
2. Vortex Filament Model
As we mentioned in the Introduction, the quantized vortex has quantized circulation and the vortex core is very thin. These properties allow a quantized vortex to be considered as a vortex filament. In the vortex filament model a quantized vortex is represented as a filament passing through the fluid. In the case of superfluid 4He, the vortex core radius 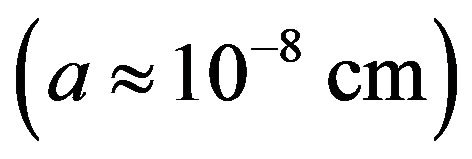 is many orders of magnitude smaller than the average separation between vortices (typically,
is many orders of magnitude smaller than the average separation between vortices (typically, 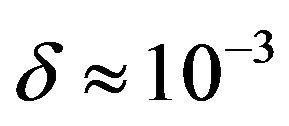 to
to  cm in turbulence experiments), or any other scale of interest in the flow; it is therefore expedient to consider a superfluid vortex filament as a space curve
cm in turbulence experiments), or any other scale of interest in the flow; it is therefore expedient to consider a superfluid vortex filament as a space curve 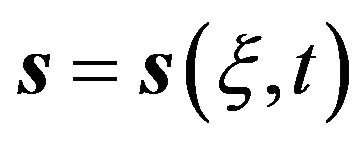 of infinitesimal thickness in three dimensional space, where
of infinitesimal thickness in three dimensional space, where  is the arc length and t is the time. The vortex lines are numerically discretized by a large variable number of points
is the arc length and t is the time. The vortex lines are numerically discretized by a large variable number of points ![]()
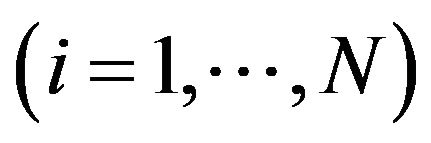 , which are called vortex points [13,14]. The governing equation of motion of the superfluid vortex lines is
, which are called vortex points [13,14]. The governing equation of motion of the superfluid vortex lines is
 (6)
(6)
where 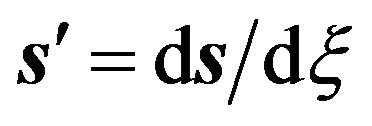 is the unit tangent,
is the unit tangent, 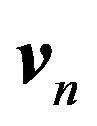 is the normal fluid velocity,
is the normal fluid velocity, ![]() and
and  are temperature-dependent friction coefficients, and the total velocity
are temperature-dependent friction coefficients, and the total velocity 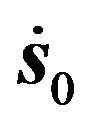 of the vortex filament without dissipation is given by
of the vortex filament without dissipation is given by
 (7)
(7)
where  is the background superfluid velocity field,
is the background superfluid velocity field, ![]() is a cutoff parameter corresponding to radius of the vortex filament,
is a cutoff parameter corresponding to radius of the vortex filament, 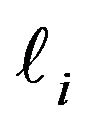 and
and  are the lengths of the two adjacent line elements connected to the point
are the lengths of the two adjacent line elements connected to the point ![]() and
and ![]() represents integration along the vortex line outside the region specified by
represents integration along the vortex line outside the region specified by 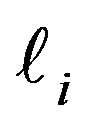 and
and 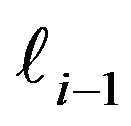 [5,15]. In the absence of normal fluid, vortex lines move with the local superfluid velocity where the friction coefficients,
[5,15]. In the absence of normal fluid, vortex lines move with the local superfluid velocity where the friction coefficients, ![]() and
and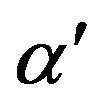 , will be equal to zero. And so, the equation of vortex motion will be
, will be equal to zero. And so, the equation of vortex motion will be
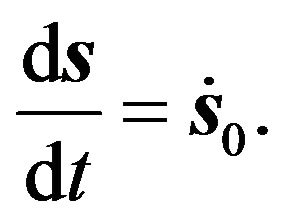 (8)
(8)
3. Numerical Results
In our numerical experiments we use the model of Schwarz which is explained in detail in Ref. [16]. The filaments are discredited into a large variable number of points, N; this (Lagrangian) spatial discretization depends on the local radius of curvature: vortex points are removed in regions where filaments straighten and are added where the local radius of curvature becomes smaller. The time evolution is computed using a fourth order Runge-Kutta scheme with fixed time step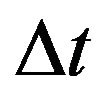 . The first and second derivatives in Equation (8) can be computed by using the central difference formula which is second order in space [17].
. The first and second derivatives in Equation (8) can be computed by using the central difference formula which is second order in space [17].
So, for a vortex configuration modeled by  vortex segments, we must solve a system of
vortex segments, we must solve a system of 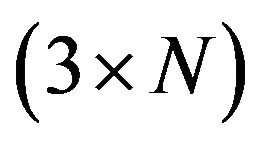 coupled first order differential equations.
coupled first order differential equations.
Our simulations are performed in a cubic box of volume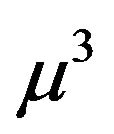 , where
, where  (typically, we chose
(typically, we chose 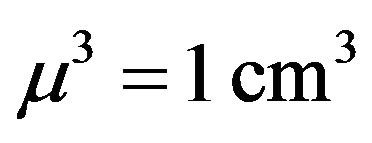 or
or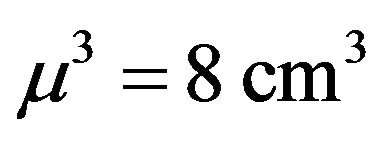 ) with periodic boundary conditions. In this work, we use the vortex filament model in which vortex reconnections are performed by the numerical algorithm (rather than occurring as natural solution of the governing equation, as in the model of nonlinear Schrödinger equation (NLSE)) [18,19]. In our method, we firstly select these points which are candidates for a reconnection. This selection is based on the distance between those points, where the reconnection between two lines can takes place only if they have different directions. For more details, we refer the reader to Refs. [20-22].
) with periodic boundary conditions. In this work, we use the vortex filament model in which vortex reconnections are performed by the numerical algorithm (rather than occurring as natural solution of the governing equation, as in the model of nonlinear Schrödinger equation (NLSE)) [18,19]. In our method, we firstly select these points which are candidates for a reconnection. This selection is based on the distance between those points, where the reconnection between two lines can takes place only if they have different directions. For more details, we refer the reader to Refs. [20-22].
By using the vortex filament method, we study the interaction of two non-straight vortex bundles (with sinusoidally) each one of them contains a given number M of (initially) non-straight parallel vortex strands, set (initially) at ![]() (vortex with antivortex bundles).
(vortex with antivortex bundles).
If two vortex strands become closer to each other than the local discretization along filaments, then, consistently with the orientation of the filaments, our numerical code reconnects the strands, provided that the total length is decreased [16]. As first, we set a single vortex with a single antivortex as shown in Figure 1, and we found that the two vortices trend to each other and the reconnection between them takes place. These results are in agreement with the finding of Koplik and Levine [23], who used the NLSE model.
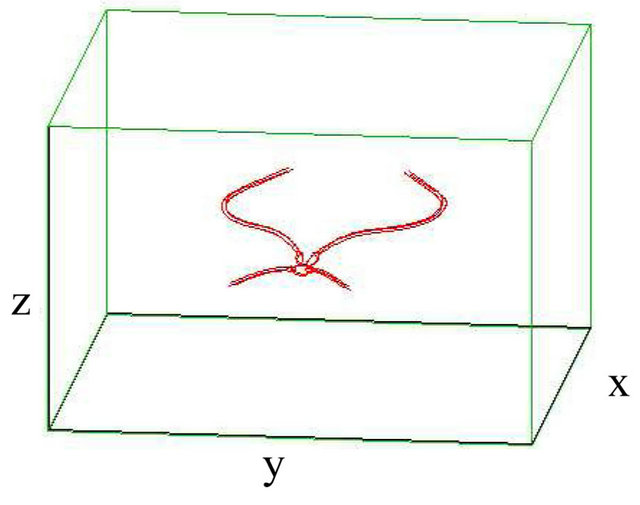
In the case of bundles, the initial position of vortex strands within the same bundles is symmetric, and we found that the reconnection events are still possible in different values of M. When M = 3, we place three vortices at the corner of a equilateral triangle. The interaction between the bundles makes them to bend in the direction of each other, until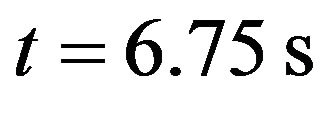 , the first reconnection takes place. With the evolution, the second reconnection is found at
, the first reconnection takes place. With the evolution, the second reconnection is found at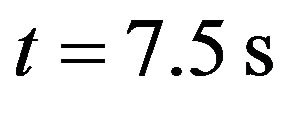 , then they become free from each other at
, then they become free from each other at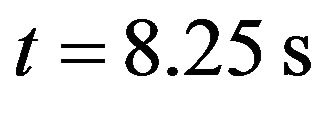 , and move away, see Figure 2.
, and move away, see Figure 2.
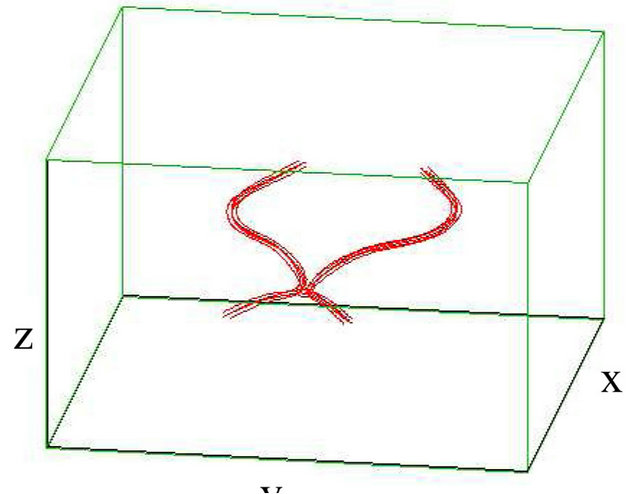
A typical result for two bundles of five non-straight parallel vortex with sinusoidally strands each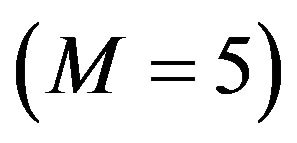 , where one of them against the other (vortex bundle with antivortex bundle), the radius of each bundle A = 0.0155804 cm, the distance between the closest point between the two non-straight bundles
, where one of them against the other (vortex bundle with antivortex bundle), the radius of each bundle A = 0.0155804 cm, the distance between the closest point between the two non-straight bundles  is shown in the upper-left panel of Figure 3. In this case, we place four vortices at the corner of a square lie on a circle and one vortex in the middle. We found, that vortex bundles with sinusoidally are structurally stable structures. To some extent they survive a time longer than their characteristic time of rotation and travel a distance larger
is shown in the upper-left panel of Figure 3. In this case, we place four vortices at the corner of a square lie on a circle and one vortex in the middle. We found, that vortex bundles with sinusoidally are structurally stable structures. To some extent they survive a time longer than their characteristic time of rotation and travel a distance larger
 (a)
(a)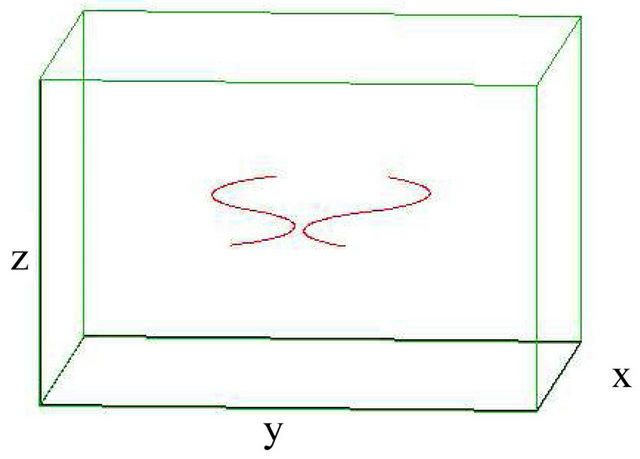 (b)
(b)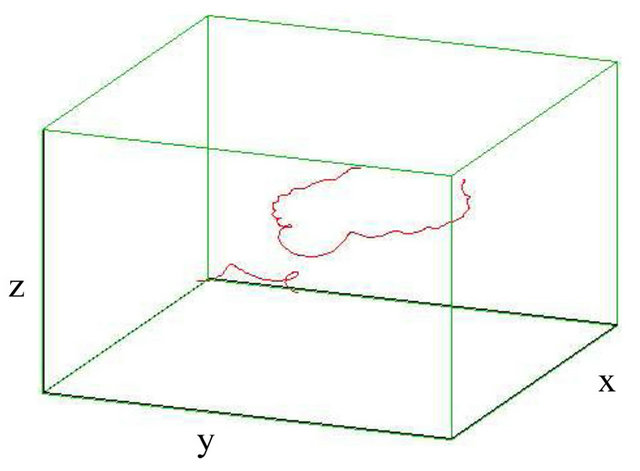 (c)
(c)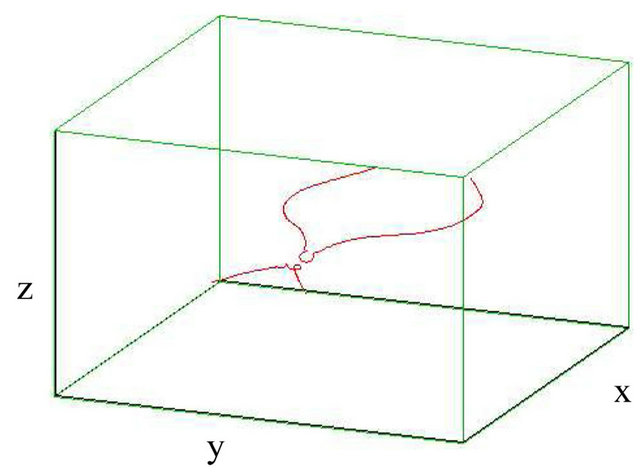 (d)
(d)
Figure 1. Reconnection of single vortex and single antivortex (with sinusoidally) strands each when . (a) t = 0 s; (b) t = 6.75 s; (c) t = 7.5 s; (d) t = 12.5 s.
. (a) t = 0 s; (b) t = 6.75 s; (c) t = 7.5 s; (d) t = 12.5 s.
 (a)
(a)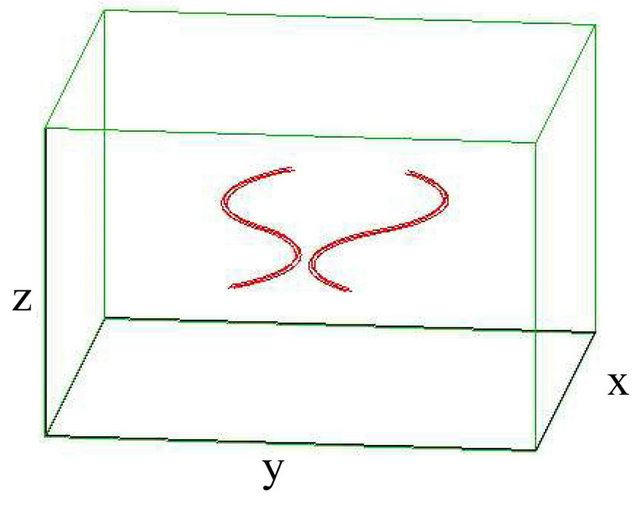 (b)
(b) (c)
(c)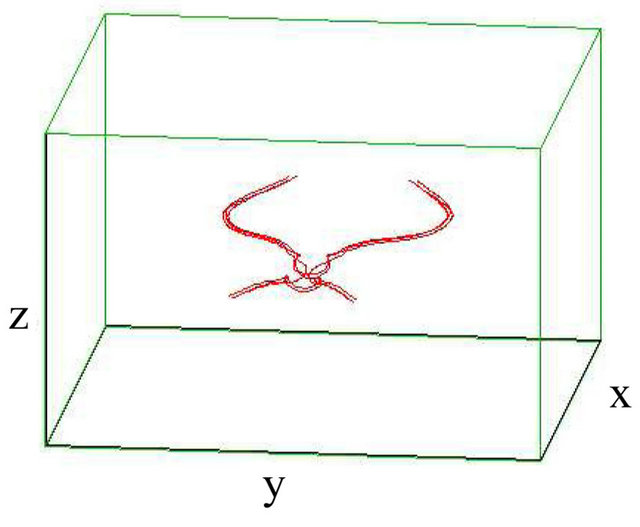 (d)
(d)
Figure 2. Reconnection of vortex bundle and antivortex bundle (with sinusoidally) strands each when 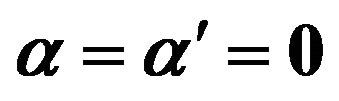 and M = 3. (a) t = 0 s; (b) t = 6.75 s; (c) t = 7.5 s; (d) t = 8.25 s.
and M = 3. (a) t = 0 s; (b) t = 6.75 s; (c) t = 7.5 s; (d) t = 8.25 s.
 (a)
(a)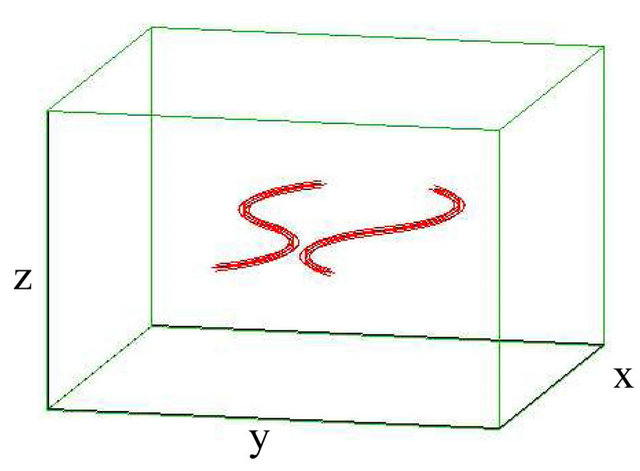 (b)
(b) (c)
(c)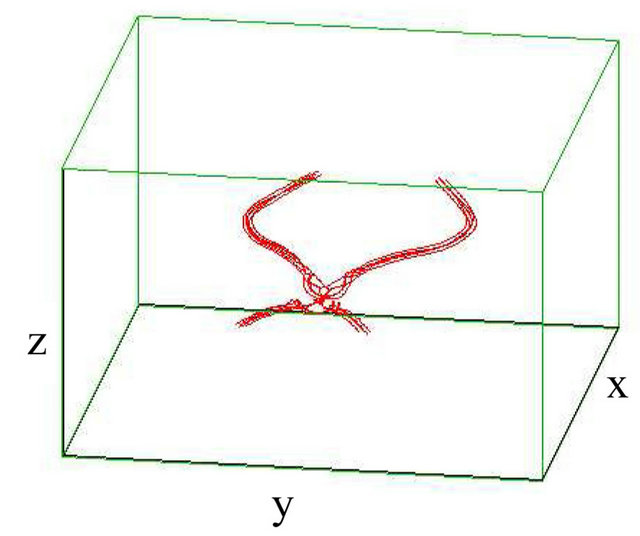 (d)
(d)
Figure 3. Reconnection of vortex bundle and antivortex bundle (with sinusoidally) strands each when 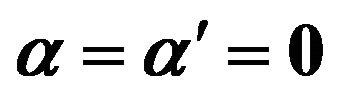 and M = 5. (a) t = 0 s; (b) t = 6.75 s; (c) t = 8.25 s; (d) t = 10 s.
and M = 5. (a) t = 0 s; (b) t = 6.75 s; (c) t = 8.25 s; (d) t = 10 s.
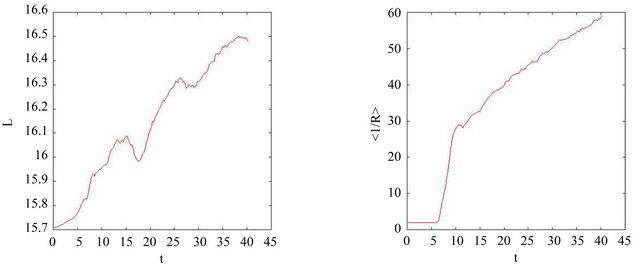
than their size. Remarkably, vortex bundles survive reconnections with other bundles without disintegrating, but rather amplifying their vortex length, where the total length L increases by about 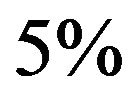 as appear in the upperleft panel of Figure 4. The successive evolution involves the reconnections of all strands, until, at time
as appear in the upperleft panel of Figure 4. The successive evolution involves the reconnections of all strands, until, at time , after which the two bundles separate from each other (lower-right panel of Figure 3) and move away in agreement with Koplik and Levine results [23]. It is clear that Kelvin waves are generated as result of a recon-
, after which the two bundles separate from each other (lower-right panel of Figure 3) and move away in agreement with Koplik and Levine results [23]. It is clear that Kelvin waves are generated as result of a recon-
 (a)
(a) (b)
(b)
Figure 4. Corresponding to the evolution shown in Figure 3. (a) Total vortex length L versus time t; (b) Average inverse radius of curvature 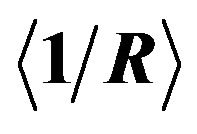 versus time t; (c) Number of discretization points N versus time t; (d) Average velocity of vortex points
versus time t; (c) Number of discretization points N versus time t; (d) Average velocity of vortex points 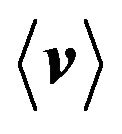 versus time t.
versus time t.
nection, see Figure 3. The upper-right panel of Figure 4 shows the average inverse radius of curvature, 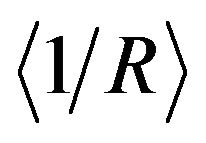 , obtained by computing
, obtained by computing 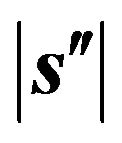 at each discretization point
at each discretization point 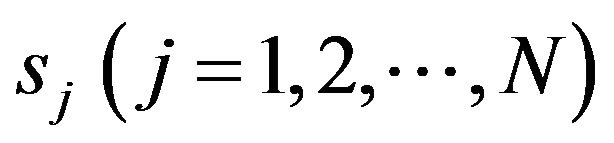 and then averaging over all discretization points. As a result of the increase in
and then averaging over all discretization points. As a result of the increase in ![]() and the decrease of
and the decrease of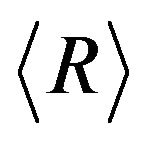 , the number of discretization points (initially
, the number of discretization points (initially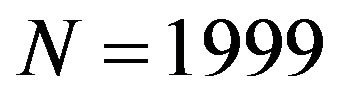 ) grows with time up to
) grows with time up to 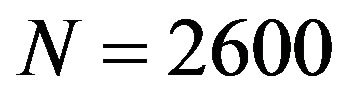 when we stop this particular calculation as shown in the lower-left panel of Figure 4. As shown in the lower-right panel of Figure 4 the decrease of
when we stop this particular calculation as shown in the lower-left panel of Figure 4. As shown in the lower-right panel of Figure 4 the decrease of 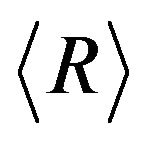 causes the increase in the average velocity of vortex points.
causes the increase in the average velocity of vortex points.
These calculations are performed in a cubic periodic box , where
, where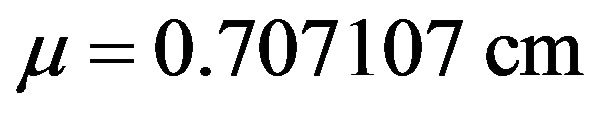 .
.
4. Conclusion
This work deals with the numerical simulation of the motion of inviscid vortex filaments under full BiotSavart law. The calculations presented here were made when the periodic boundary conditions are applied in all axes. The very known fourth order Runge-Kutta method was used for the time evolution. The reconnection and vortex stretching in superfluid turbulence is concerned. The existence of reconnections was proved by Koplik and Levine [23] using the model of nonlinear Schrodinger equation in order to confirm Schwarzs insight that quantized vortices reconnect [11]. We found that the single vortex with single antivortex can be reconnect together by using the vortex filament method as confirmed beforetime by Koplik and Levine [23]. A noteworthy feature of the reconnection between two vortex lines is the ability of their reconnection can be takes place only when they have different directions. Our main finding was that non-straight bundles (with sinusoidally) of quantized vortex lines in He II are structurally robust and can reconnect with each other maintaining their identity. The interaction between two bundles makes them approach each other closely and then the reconnection occurs one by one after which the two bundles separate from each other. This is in agreement with our previous experiments [2]. This leads to increasing in total length, velocity and the number of vortex points and decreasing the average radius of curvature.
5. Acknowledgements
The authors are grateful to Prof. Carlo F. Barenghi and Prof. Eed M. Darwish for useful discussions and a critical reading of the manuscript. This work is supported by the Deanship of Scientific Research at Taibah University (Project No. 1433/1790).
REFERENCES
- R. Aarts, “A Numerical Study of Quantized Vortices in He II,” Ph.D. Dissertation, Eindhoven University, Eindhoven, 1993.
- S. Z. Alamri, A. J. Youd and C. F. Barenghi, “Reconnection of Superfluid Vortex Bundles,” Physical Review Letters, Vol. 101, 2008, Article ID: 215302. doi:10.1103/PhysRevLett.101.215302
- C. F. Barenghi, R. J. Donnelly and W. F. Vinen, “Quantized Vortex Dynamics and Superuid Turbulence,” Springer, Berlin, 2001. doi:10.1007/3-540-45542-6
- R. J. Donnelly, “Quantized Vortices In Helium II,” Cambridge University Press, Cambridge, 1991.
- F. Maggioni, S. Z. Alamri, C. Barenghi and R. Ricca, “Kinetic Energy of Vortex Knots and Unknots,” Il Nuovo Cimento C, Vol. 32, 2009, p. 133.
- W. F. Vinen and J. J. Niemela, “Erratum: Quantum Turbulence,” Journal of Low Temperature Physics, Vol. 129, No. 5-6, 2002, pp. 213. doi:10.1023/A:1020890811263
- A. C. White, C. F. Barenghi and N. P. Proukakis, “Creation and Characterization of Vortex Clusters in Atomic Bose-Einstein Condensates,” Physical Review A, Vol. 86, 2012, Article ID: 013635. doi:10.1103/PhysRevA.86.013635
- C. F. Barenghi, “Turbulent Dissipation near Absolute Zero,” European Journal of Mechanics—B, Vol. 23, No. 3, 2004, pp. 415-425. doi:10.1016/j.euromechflu.2003.10.011
- A. W. Baggaley and C. F. Barenghi, “Condensate Fraction in Neutron Matter,” Physical Review E, Vol. 84, 2011, Article ID: 067301. doi:10.1103/PhysRevE.84.067301
- M. Tsubota, T. Araki and S. K. Nemirowskii, “Dynamics of Vortex Tangle Without Mutual Friction in Superfluid 4He,” Physical Review B, Vol. 62, No. 17, 2000, pp. 11751-11762. doi:10.1103/PhysRevB.62.11751
- K. W. Schwarz, “Three-Dimensional Vortex Dynamics in Superfluid 4He: Line-Line and Line-Boundary Interactions,” Physical Review B, Vol. 31, 1985, pp. 5782-5804. doi:10.1103/PhysRevB.31.5782
- K. W. Schwarz, “Three-Dimensional Vortex Dynamics in Superfluid 4He: Homogeneous Superfluid Turbulence,” Physical Review B, Vol. 38, No. 4, 1988, pp. 2398-2417. doi:10.1103/PhysRevB.38.2398
- A. W. Baggaley and C. F. Barenghi, “Tree Method for Quantum Vortex Dynamics,” Journal of Low Temperature Physics, Vol. 166, No. 1-2, 2012, pp. 3-20. doi:10.1007/s10909-011-0405-6
- A. J. Allen, P. M. Chesler and H. Liu, “Holographic Vortex Liquids and Superfluid Turbulence,” arXiv Preprint [hep-th]: arXiv:1212.0281.
- A. W. Baggaley and C. F. Barenghi, “Turbulent Cascade of Kelvin Waves on Vortex Filaments,” Journal of Physics: Conference Series, Vol. 318, No. 6, 2011, Article ID: 062001. doi:10.1088/1742-6596/318/6/062001
- S. Z. Alamri, “A Numerical Study of Quantum Turbulence,” Ph.D. Dissertation, Newcastle University, Newcastle, 2009.
- M. S. Ismail and S. Z. Alamri, “Highly Accurate Finite Difference Method for Coupled Nonlinear Schrdinger Equation,” International Journal of Computer Mathematics, Vol. 81, No. 3, 2004, pp. 333-351. doi:10.1080/00207160410001661339
- F. Maggioni, S. Z. Alamri, C. Barenghi and R. Ricca, “Velocity, Energy, and Helicity of Vortex Knots and Unknots,” Physical Review E, Vol. 82, 2010, Article ID: 026309. doi:10.1103/PhysRevE.82.026309
- A. W. Baggaley, C. F. Barenghi and Y. A. Sergeev, “Quasiclassical and Ultraquantum Decay of Superfluid Turbulence,” Physical Review B, Vol. 85, 2012, Article ID: 060501(R). doi:10.1103/PhysRevB.85.060501
- M. V. Berry and M. R. Dennis, “Reconnections of Wave Vortex Lines,” European Journal of Physics, Vol. 33, No. 3, 2012, pp. 723-731. doi:10.1088/0143-0807/33/3/723
- D. Holm and R. Kerr, “Transient Vortex Events in the Initial Value Problem for Turbulence,” Physical Review Letters, Vol. 88, No. 24, 2002, Article ID: 244501. doi:10.1103/PhysRevLett.88.244501
- R. Kerr, “Cover Illustration: Vortex Structure of Euler Collapse,” Nonlinearity, Vol. 9, 1996, pp. 271-272. doi:10.1088/0951-7715/9/2/001
- J. Koplik and H. Levine, “Vortex Reconnection in Superfluid Helium,” Physical Review Letters, Vol. 71, No. 9, 1993, pp. 1375-1378. doi:10.1103/PhysRevLett.71.1375
NOTES
*Corresponding author.

