Applied Mathematics
Vol. 4 No. 5 (2013) , Article ID: 31477 , 4 pages DOI:10.4236/am.2013.45114
On the Symmetrical System of Rational Difference Equation 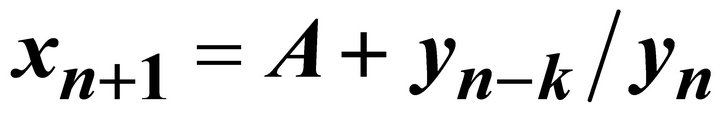 ,
,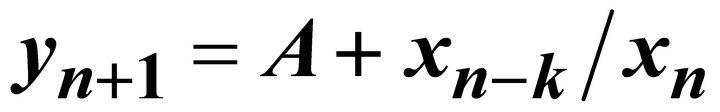 *
*
Institute of Systems Science and Mathematics, Naval Aeronautical and Astronautical University, Yantai, China
Email: #jwqyikeshu@163.com
Copyright © 2013 Decun Zhang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 12, 2013; revised April 12, 2013; accepted April 19, 2013
Keywords: Symmetrical System; Difference Equation; Boundedness; Period-Two Solution
ABSTRACT
In this paper, we study the behavior of the symmetrical system of rational difference equation:
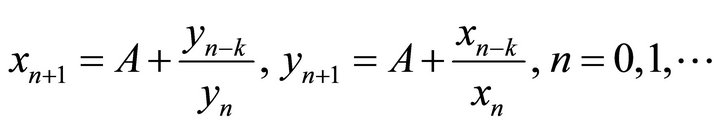
where 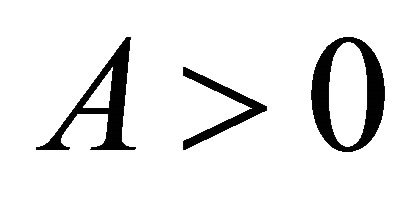 and
and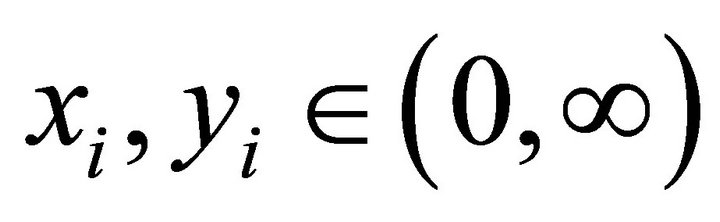 , for
, for .
.
1. Introduction
Recently there has been a great interest in studying difference equations and systems, and quite a lot of papers about the behavior of positive solutions of system of difference equation. We can read references [1-10].
In [1] C. Cina studied the system:
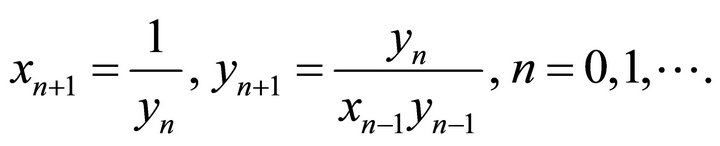 (1)
(1)
In [2] A. Y. Ozban studied the difference equation system:
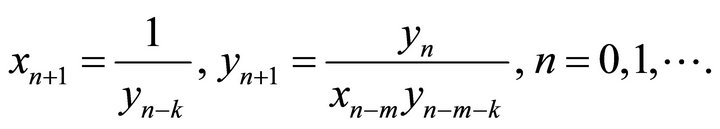 (2)
(2)
In [3] A. Y. Ozban studied the behavior of positive solutions of the difference equation system:
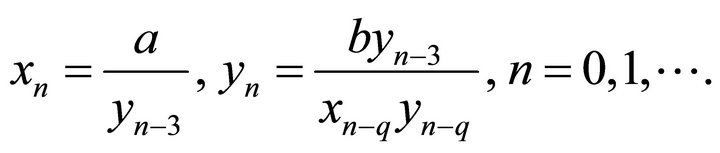 (3)
(3)
In [4] X. Yang, Y. Liu, S. Bai studied the difference equation system:
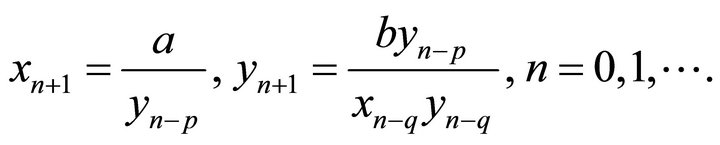 (4)
(4)
We can see in [1-4], they have the same similar character, which is the system can be reduced into a difference equation with 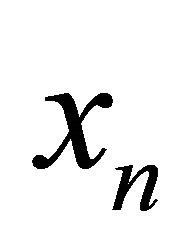 or
or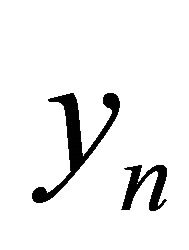 .
.
In [5] G. Papaschinopoulos, C. J. Schinas studied the behavior of positive solutions of the difference equation system:
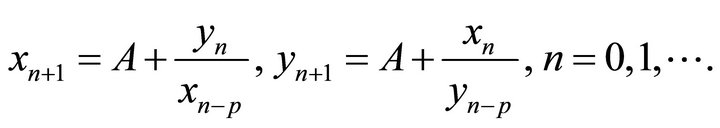 (5)
(5)
In [6] G. Papaschinopoulos, Basil K. Papadopoulos studied the behavior of positive solutions of the difference equation system:
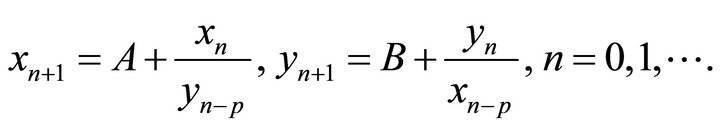 (6)
(6)
In [7] E. Camouzis, G. Papaschinopoulos studied the behavior of positive solutions of the difference equation system:
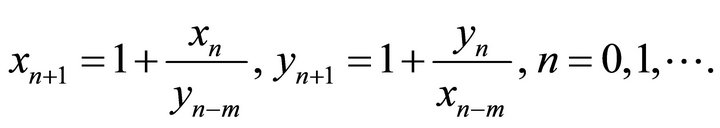 (7)
(7)
In [8] Yu Zhang, Xiaofan Yang, David J. Evans, Ce Zhu studied the behavior of positive solutions of the difference equation system:
 (8)
(8)
Motivated by systems above, we introduce the symmetrical system:
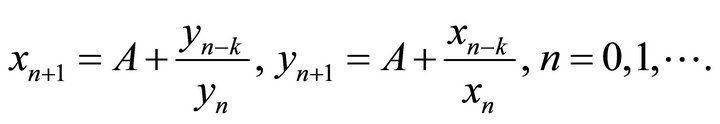 (9)
(9)
with parameter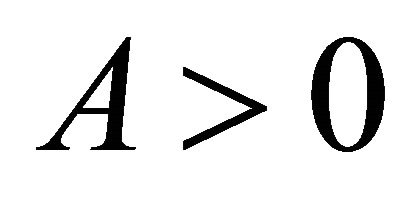 , the initial conditions
, the initial conditions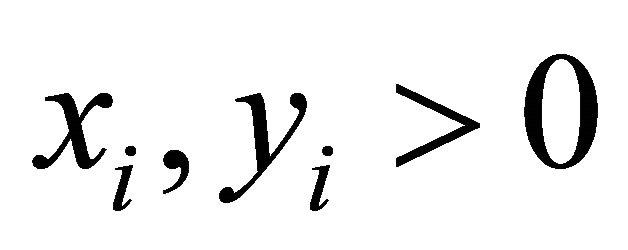 , for
, for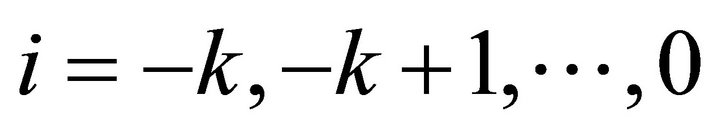 , and
, and 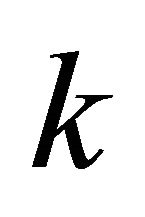 is a positive integer. We can easily get the system (9) has the unique positive equilibrium
is a positive integer. We can easily get the system (9) has the unique positive equilibrium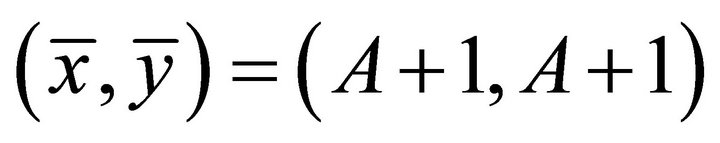 .
.
There are two cases we need to consider:
1) If the initial conditions  in the system (9) for
in the system (9) for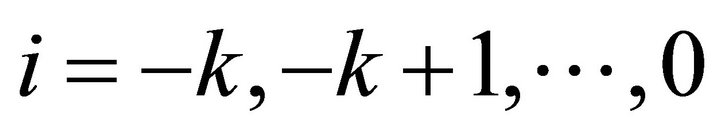 , then
, then 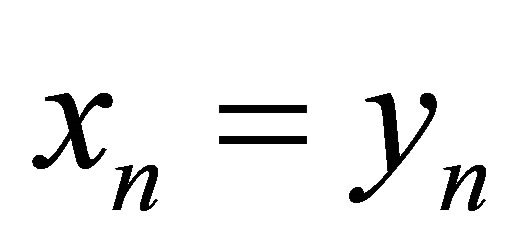 for all
for all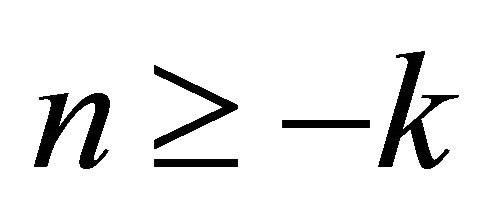 , thus, the system (9) reduces to the difference equation
, thus, the system (9) reduces to the difference equation
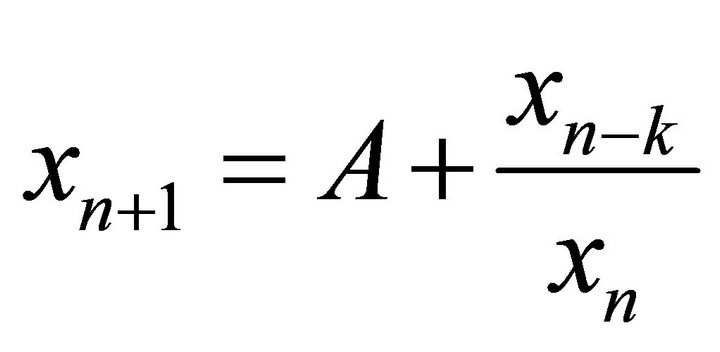
which was studied by El-owaidy in [11].
2) If 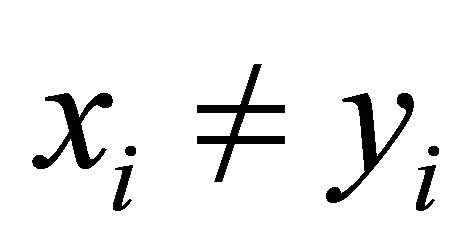 for
for , then the system (9) is similar to the system in [8]. We study the system (9) basing on this condition in this paper.
, then the system (9) is similar to the system in [8]. We study the system (9) basing on this condition in this paper.
In this paper, we try to give some results of the system (9) by using the methods in [8]. We consider the following cases of ,
, 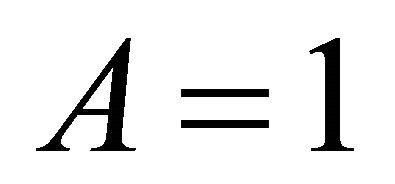 and
and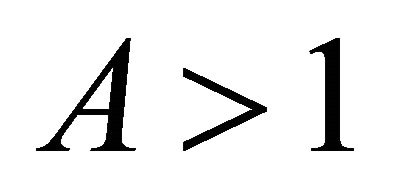 .
.
2. The Case 0 < A < 1
In this section, we give the asymptotic behavior of positive solution to the system (9).
Theorem 2.1. Suppose 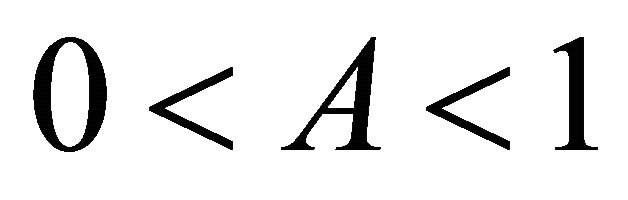 and
and 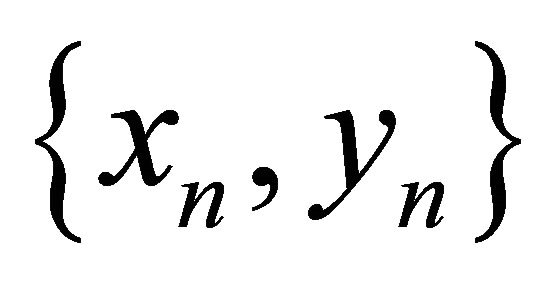 is an arbitrary positive solution of the system (9). Then the following statements hold.
is an arbitrary positive solution of the system (9). Then the following statements hold.
1) If k is odd, and ,
, 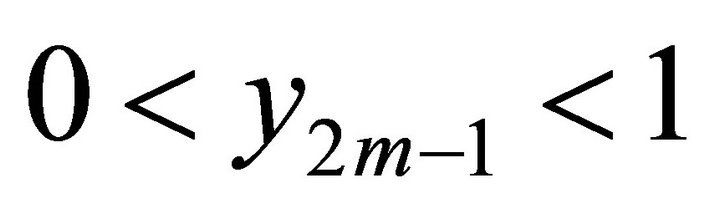 ,
, 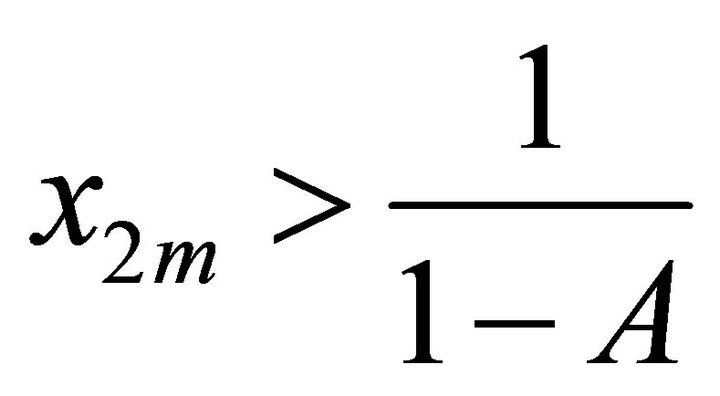 ,
, 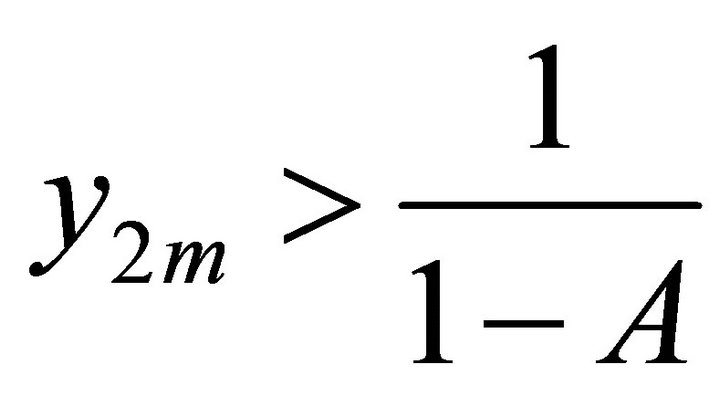 for
for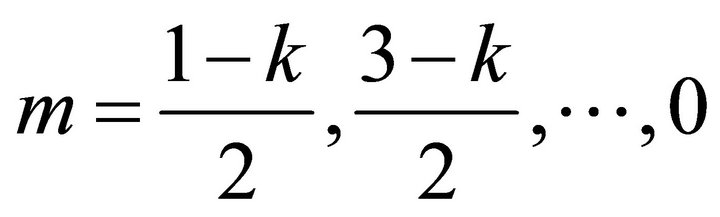 , then
, then

2) If  is odd, and
is odd, and ,
, 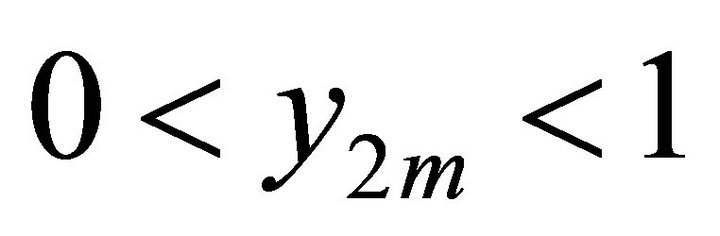 ,
, 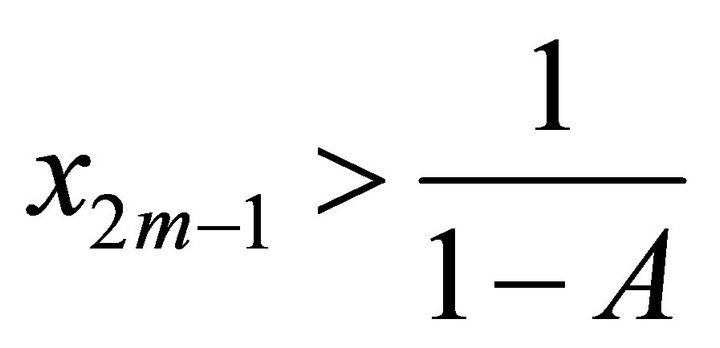 ,
, 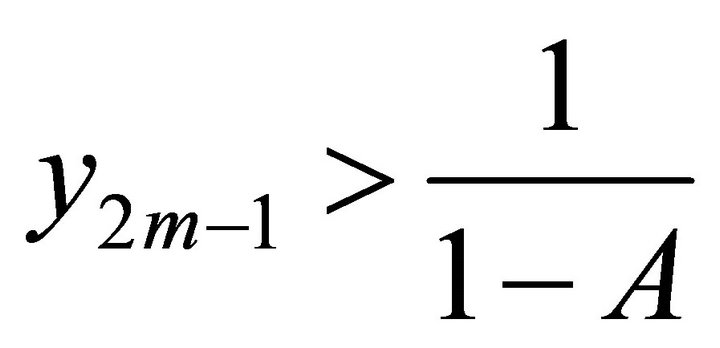 for
for , then
, then

3) If k is even, we can not get some useful results.
Proof: 1) Obviously, we can have
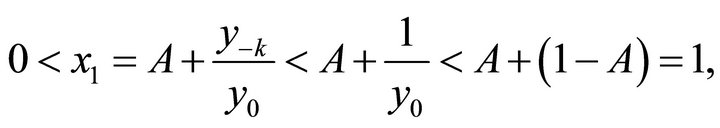
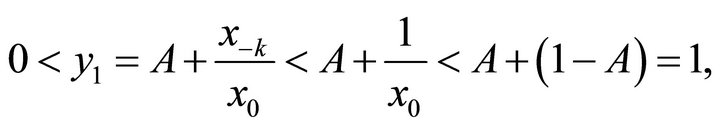
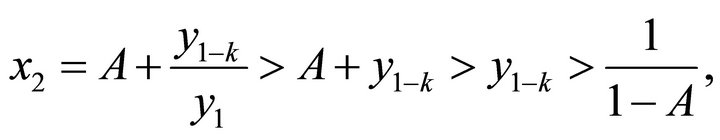
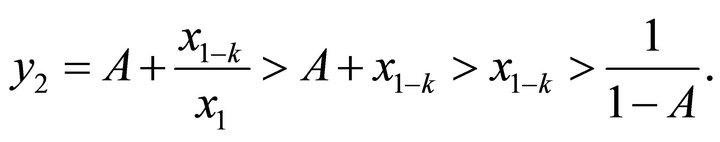
By introduction, we can get
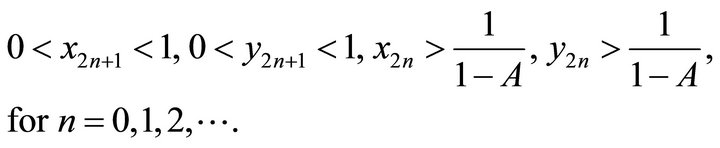
So for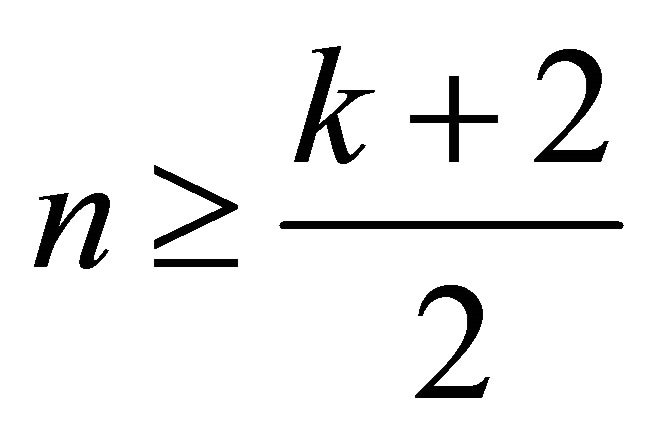 ,
,
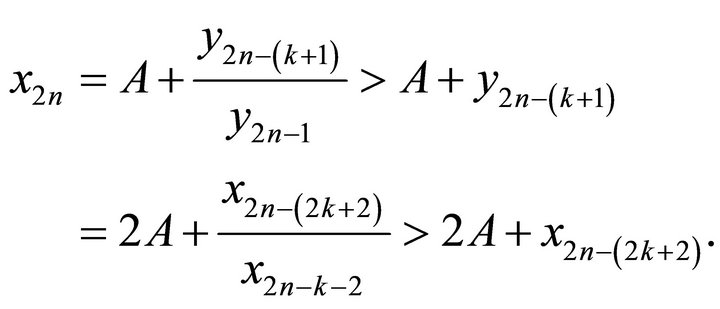
By limiting the inequality above, we can get
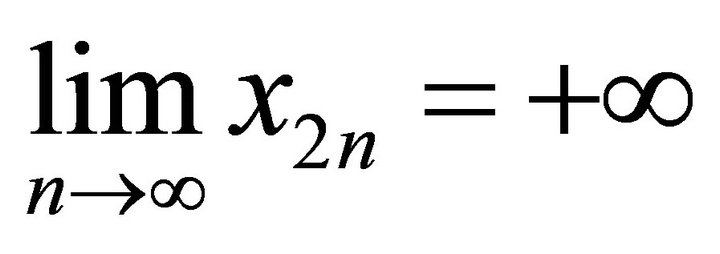 . Similarly, we can also get
. Similarly, we can also get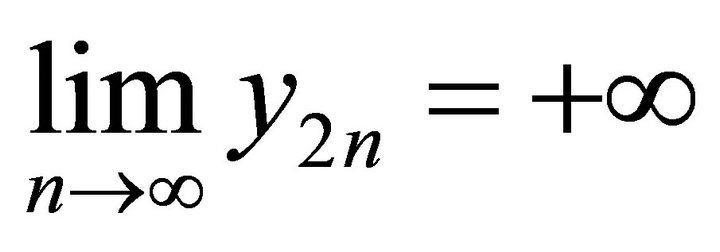 .
.
Taking limits on the both sides of the following two equations
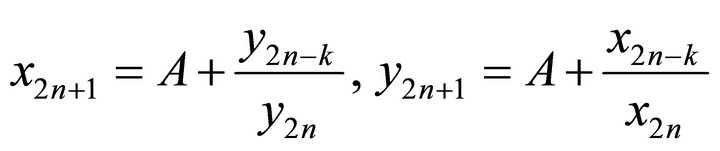
we can obtain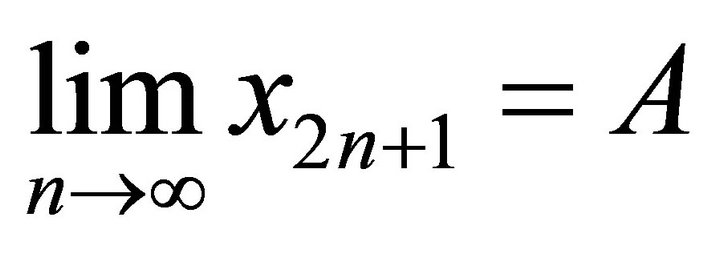 ,
,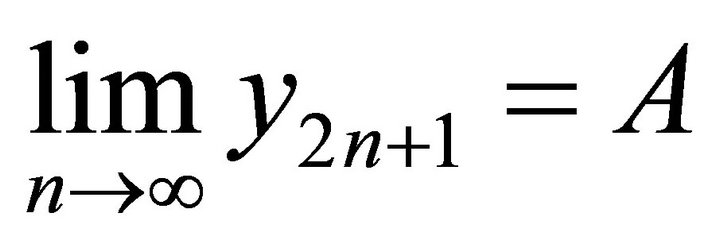 .
.
The proof of 2) is similar, so we omit it.
3. The Case A = 1
In this section, we try to get the boundedness, persistence, and periodicity of positive solutions of the system (9).
Theorem 3.1. Suppose A = 1. Then every positive solution of the system (9) is bounded and persists.
Proof. 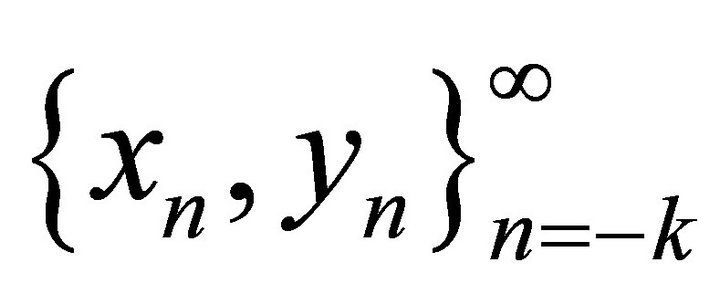 is a positive solution of the system (9).
is a positive solution of the system (9).
Obviously, 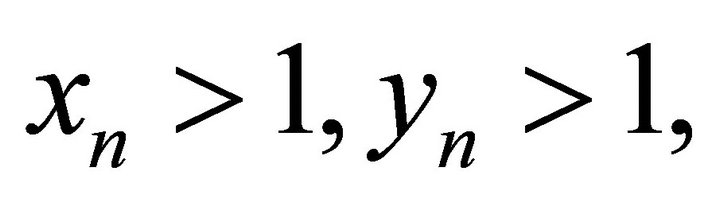 for
for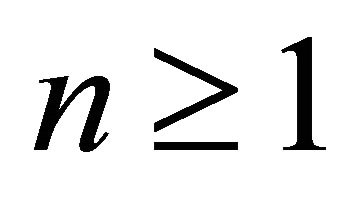 . So we can get
. So we can get
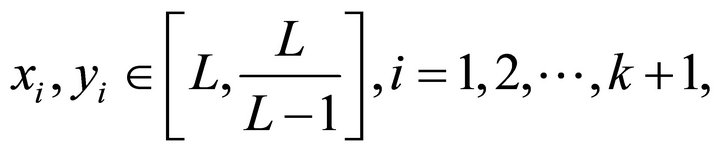
where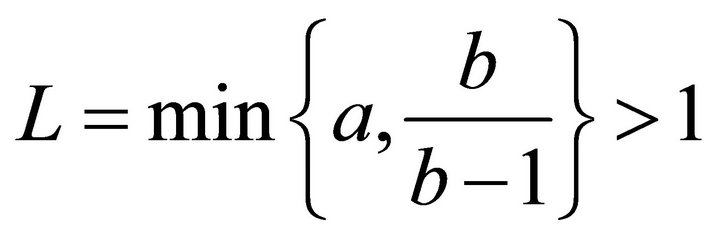 ,
,  ,
,
 , for
, for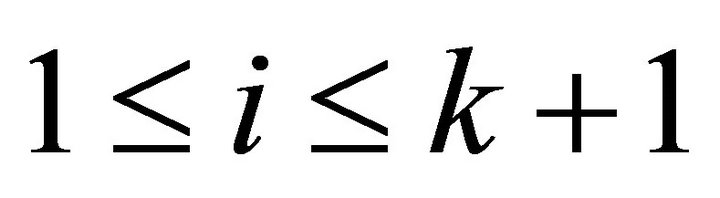 .
.
Then we can obtain
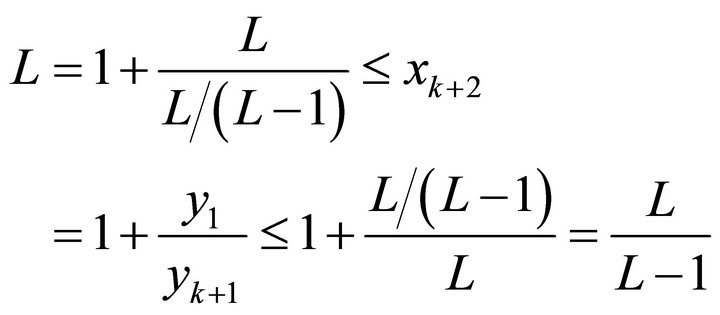
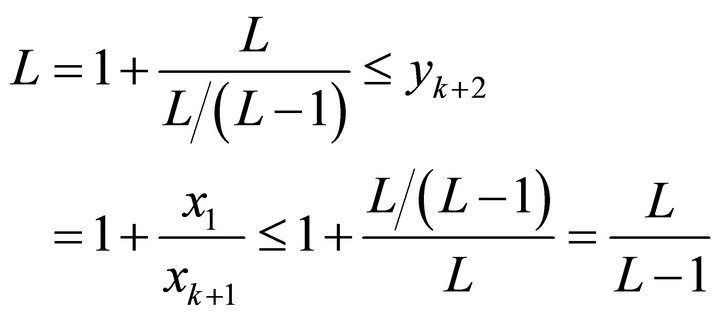
By introduction, we have
 (10)
(10)
Hence, we complete the proof.
Theorem 3.2. Suppose A = 1,  is a positive solution of the system (9). Then
is a positive solution of the system (9). Then
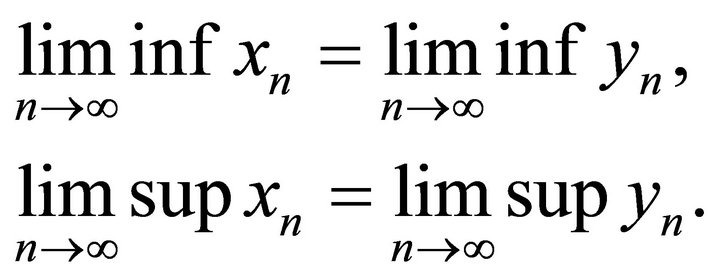
Proof: By (10), we can get

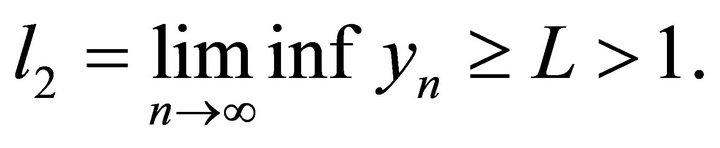
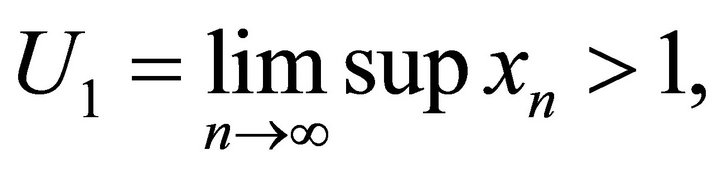

By system (9), we can have
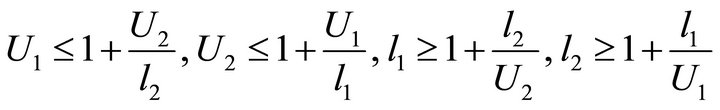
which implies 
Hence, we can obtain
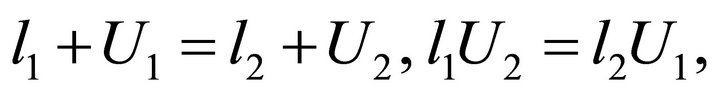
which can be changed into
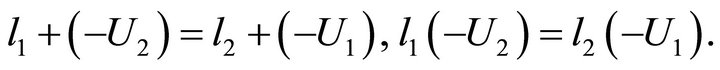
Obviously, 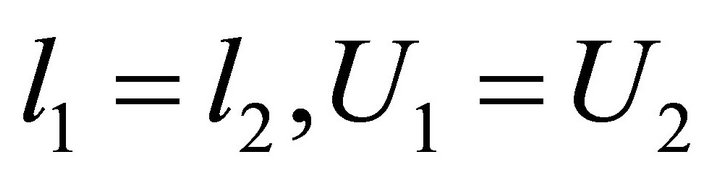 , we complete the proof.
, we complete the proof.
Theorem 3.3. Suppose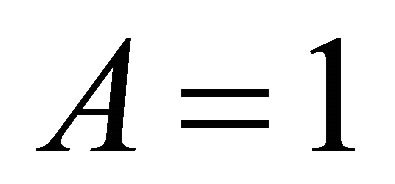 .
.
1) If 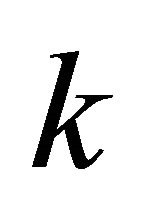 is odd, then every positive solution of the system (9) with prime period two takes the form
is odd, then every positive solution of the system (9) with prime period two takes the form
 (11)
(11)
or
 (12)
(12)
with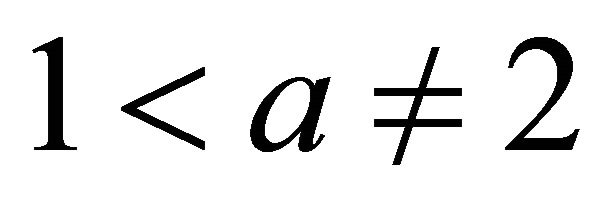 .
.
2) If 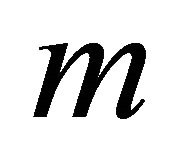 is even, there do not exist positive nontrival solution of the system (9) with prime period two.
is even, there do not exist positive nontrival solution of the system (9) with prime period two.
Proof: 1) As k is odd.
We set 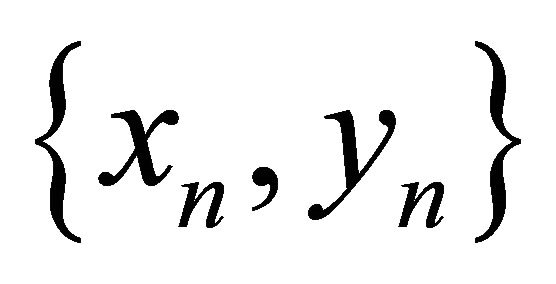 is the solution of the system (9) with prime period two. Then there are four positive number
is the solution of the system (9) with prime period two. Then there are four positive number 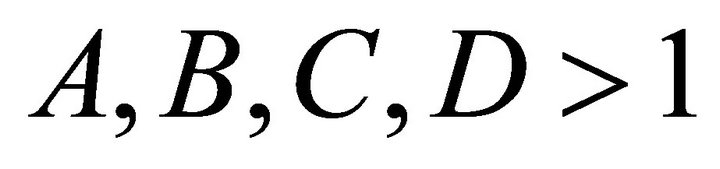 such that
such that
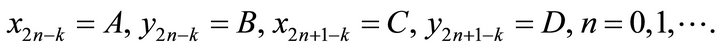
If , by the system (9) we can get
, by the system (9) we can get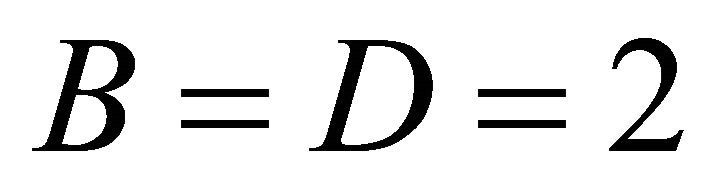 , which is contradiction with the condition
, which is contradiction with the condition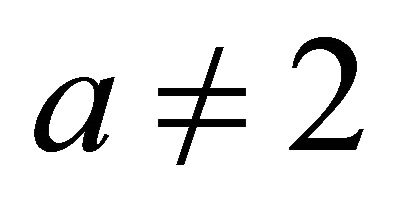 , hence
, hence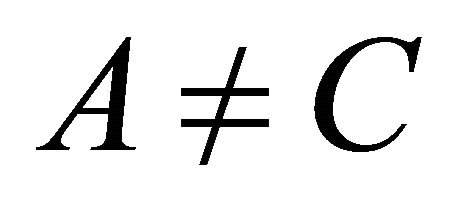 . Similarly, we can get
. Similarly, we can get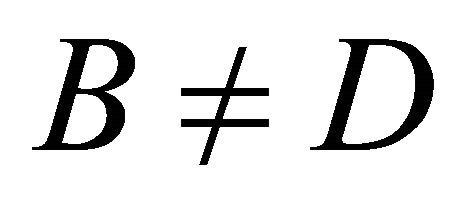 . Then we obtain
. Then we obtain
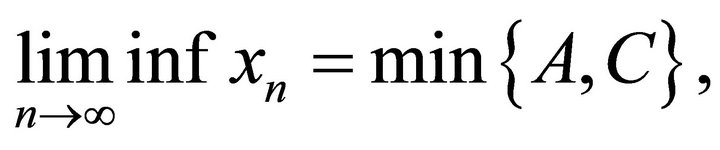
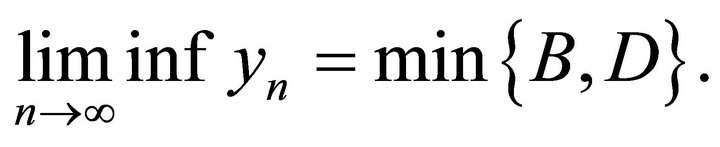
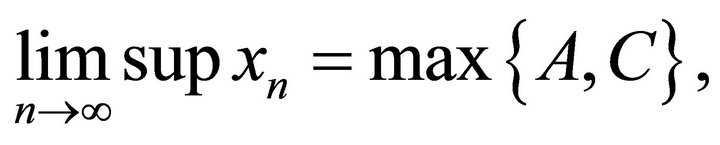
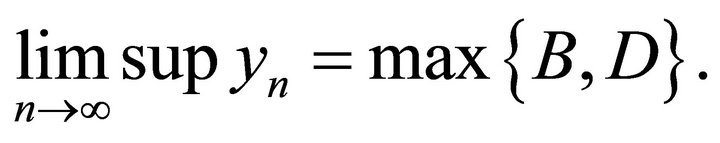
From Theorem 3.2, we can get
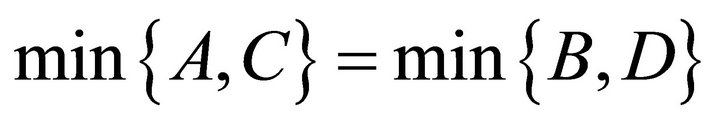
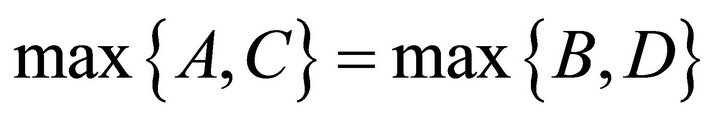
Next, we consider the following possibilities:
Case 1: Either(I) A < C and B < D or (II) A > C and B > D. Then A = B, C = D.
Case 2: Either(I) A < C and B > D or (II) A > C and B < D. Then A = D, B = C.
Therefore by the system (9), we can get 1) holds.
2) Obviously, if k is even, the system (9) just has trival solution with prime period two.
We complete the proof.
4. The Case A > 1
Theorem 4.1. Suppose A > 1. Then every positive solution of the system (9) is bounded and persists.
Proof. Let 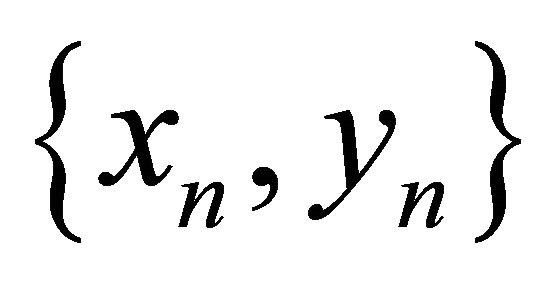 be a positive solution of the system (9). Obviously,
be a positive solution of the system (9). Obviously, 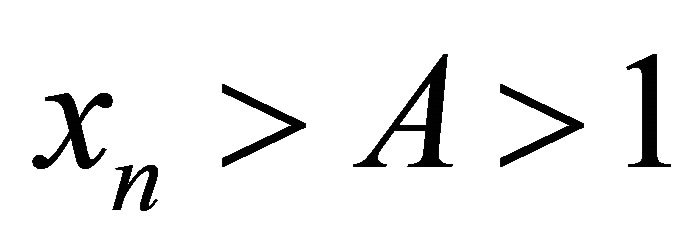 ,
, 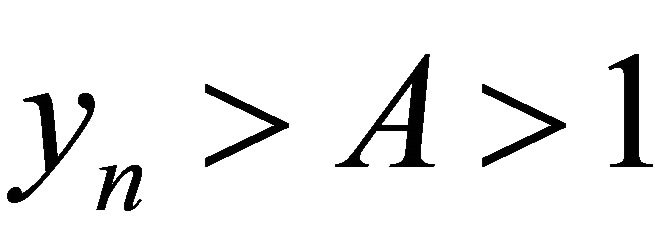 , for
, for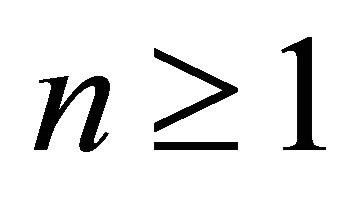 . So we can get
. So we can get
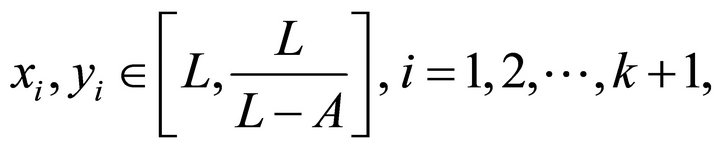
where ,
, 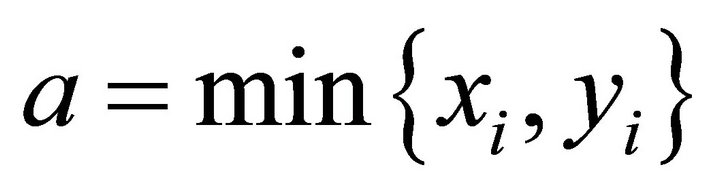 ,
,
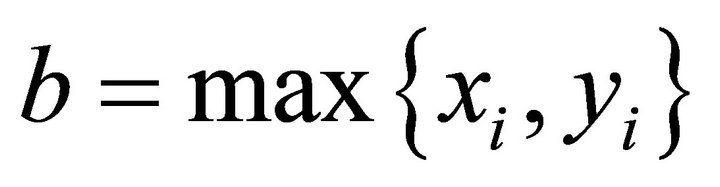 , for
, for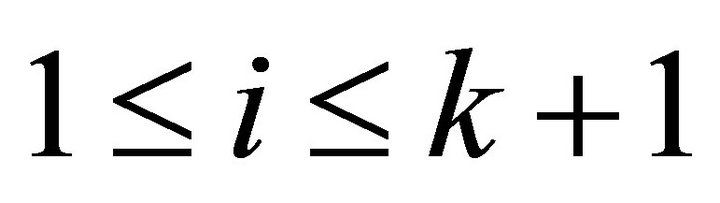 . Then we can obtain
. Then we can obtain

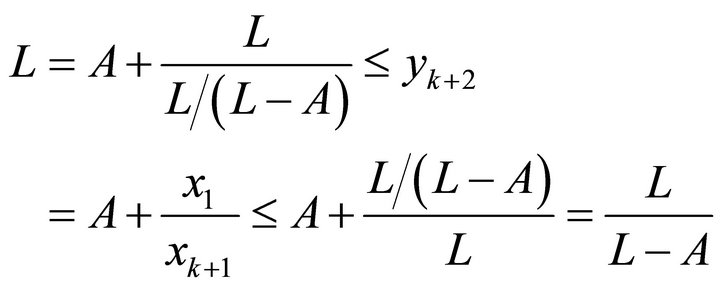
By introduction, we have
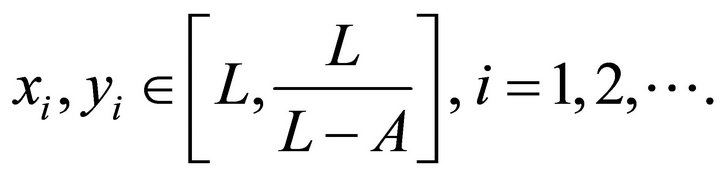 (13)
(13)
We complete the proof.
Theorem 4.2. Suppose A > 1. Then every positive solution of the system (9) converges to the equilibrium as .
.
Proof: By (13), we can get
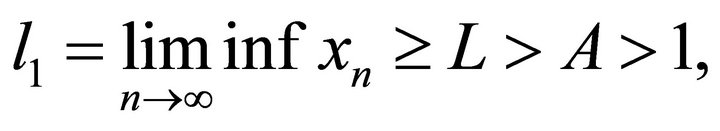
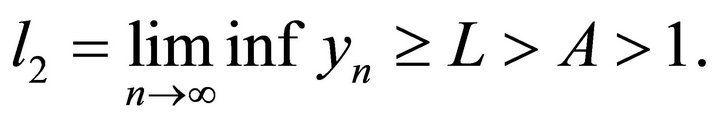
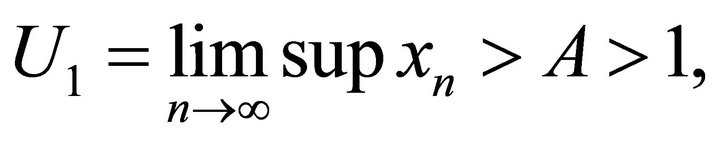
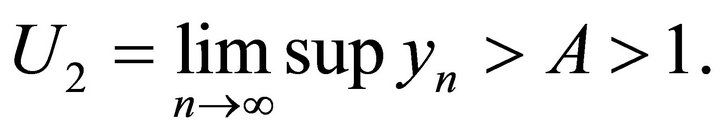
By system (9), we can have
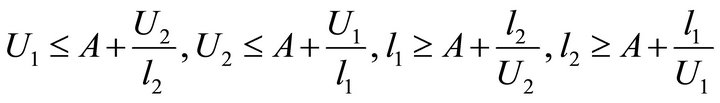
which imply
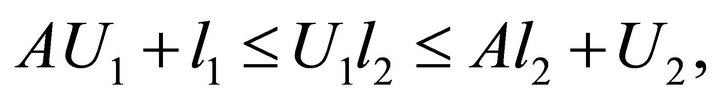
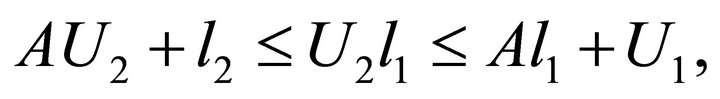
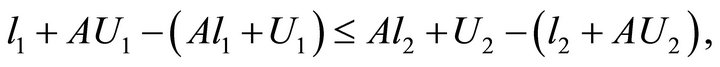
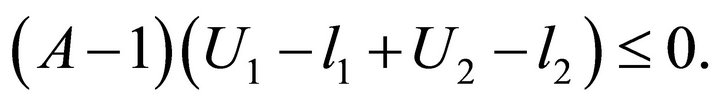
By the condition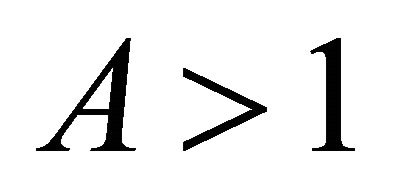 , we can get
, we can get
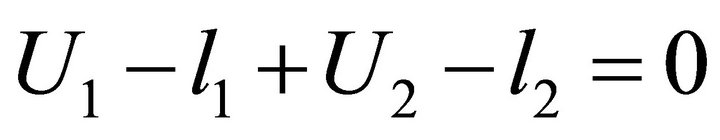
Besides,  and
and , so we can get
, so we can get
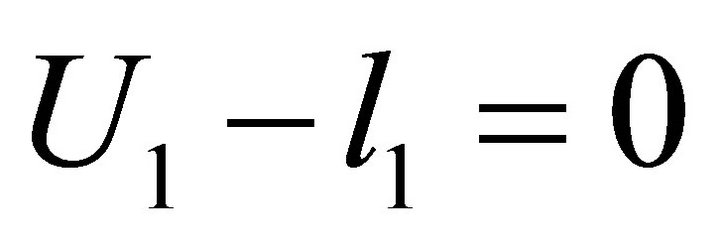 and
and 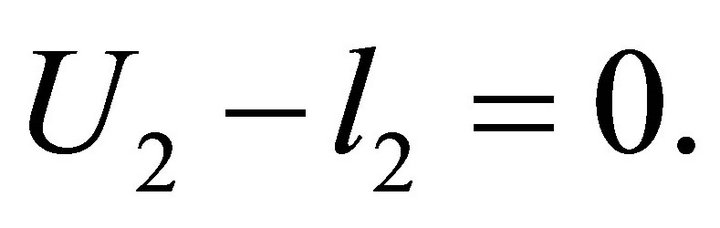
i.e.

we complete the proof.
REFERENCES
- C. Cinar, “On the Positive Solutions of the Difference Equation System

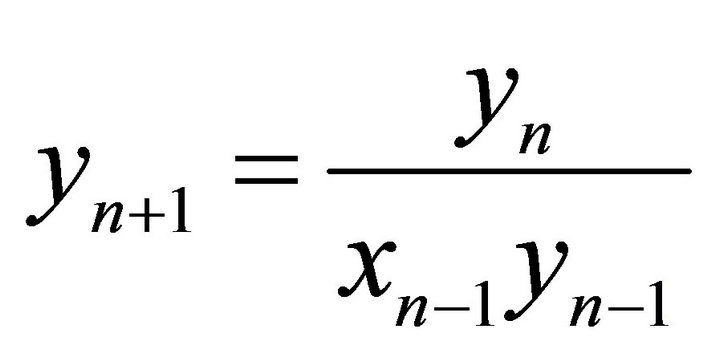 ,” Applied Mathematics and Computation, Vol. 158, No. 2, 2004, pp. 303-305. doi:10.1016/j.amc.2003.08.073
,” Applied Mathematics and Computation, Vol. 158, No. 2, 2004, pp. 303-305. doi:10.1016/j.amc.2003.08.073 - A. Y. Ozban, “On the Positive Solutions of the System of Rational Difference Equations
 ,
, 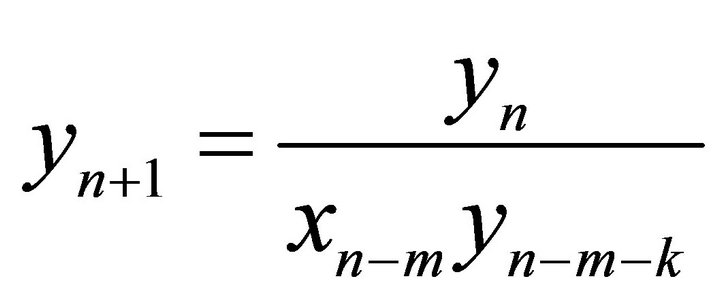 ,” Journal of Mathematical Analysis and Applications, Vol. 323, No. 1, 2006, pp. 26-32. doi:10.1016/j.jmaa.2005.10.031
,” Journal of Mathematical Analysis and Applications, Vol. 323, No. 1, 2006, pp. 26-32. doi:10.1016/j.jmaa.2005.10.031 - A. Y. Ozban, “On the System of Rational Difference Equations
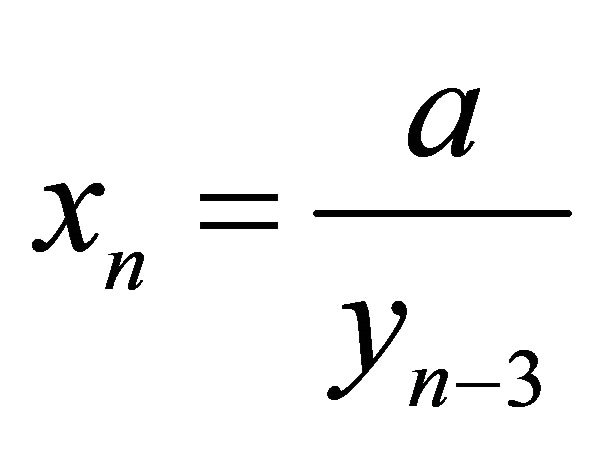 ,
,  ,” Applied Mathematics and Computation, Vol. 188, No. 1, 2007, pp. 833- 837. doi:10.1016/j.amc.2006.10.034
,” Applied Mathematics and Computation, Vol. 188, No. 1, 2007, pp. 833- 837. doi:10.1016/j.amc.2006.10.034 - X. Yang, Y. Liu and S. Bai, “On the System of High Order Rational Difference Equations
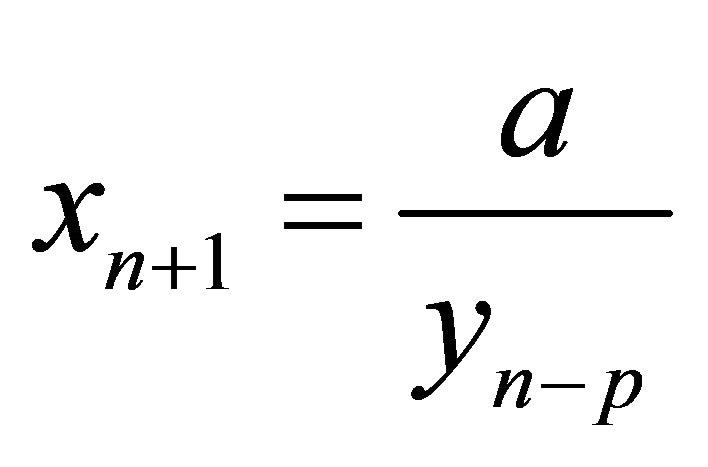 ,
, 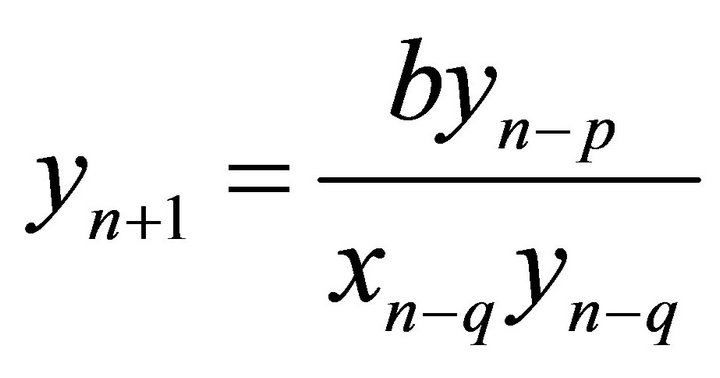 ,” Applied Mathematics and Computation, Vol. 171, No. 2, 2005, pp. 853-856. doi:10.1016/j.amc.2005.01.092
,” Applied Mathematics and Computation, Vol. 171, No. 2, 2005, pp. 853-856. doi:10.1016/j.amc.2005.01.092 - G. Papaschinopoulos and C. J. Schinas, “On a System of Two Nonlinear Difference Equations,” Journal of Mathematical Analysis and Applications, Vol. 219, No. 2, 1998, pp. 415-426. doi:10.1006/jmaa.1997.5829
- G. Papaschinopoulos and B. K. Papadopoulos, “On the Fuzzy Difference Equation
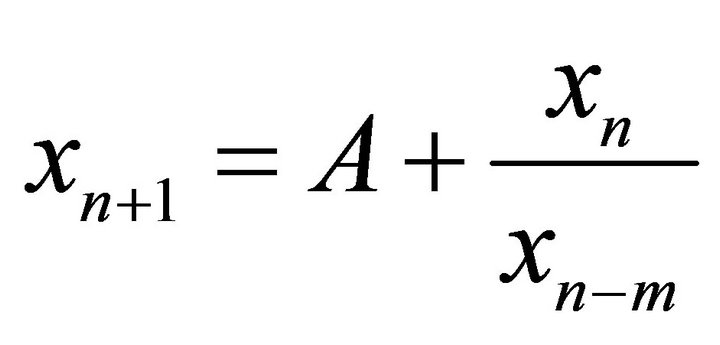 ,” Fuzzy Sets and Systems, Vol. 129, No. 1, 2002, pp. 73-81. doi:10.1016/S0165-0114(01)00198-1
,” Fuzzy Sets and Systems, Vol. 129, No. 1, 2002, pp. 73-81. doi:10.1016/S0165-0114(01)00198-1 - E. Camouzis and G. Papaschinopoulos, “Global Asymptotic Behavior of Positive Solutions on the System of Rational Difference Equation
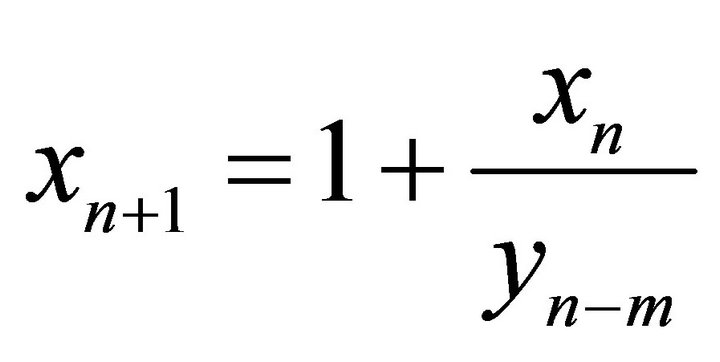 ,
, 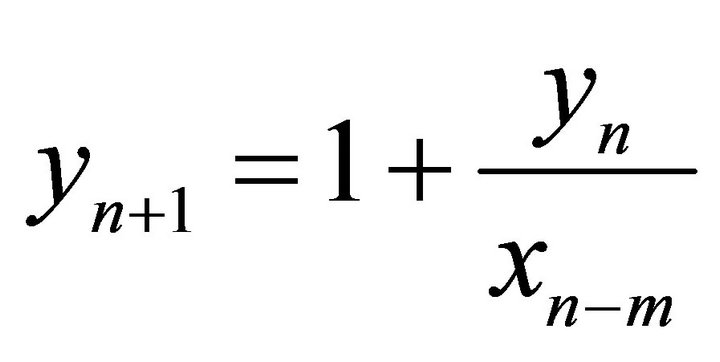 ,” Applied Mathematics and Letters, Vol. 17, No. 6, 2004, pp. 733-737. doi:10.1016/S0893-9659(04)90113-9
,” Applied Mathematics and Letters, Vol. 17, No. 6, 2004, pp. 733-737. doi:10.1016/S0893-9659(04)90113-9 - Y. Zhang, X. F. Yang, D. J. Evans and C. Zhu, “On the Nonlinear Difference Equation System
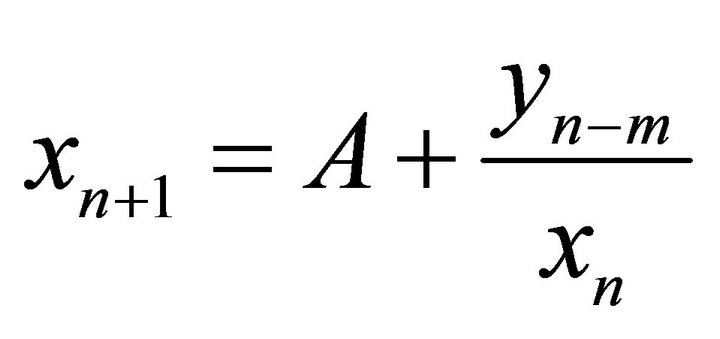 ,
, 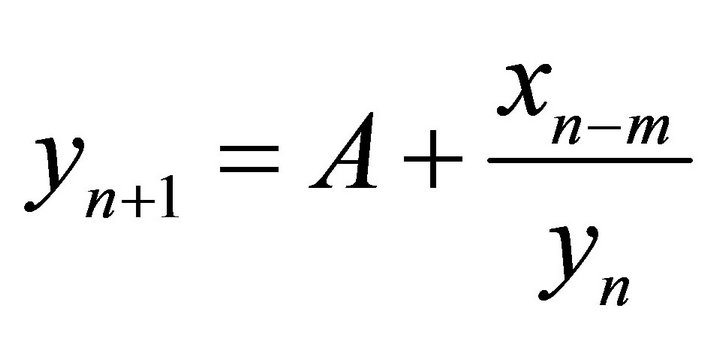 ,” Computers and Mathematics with Application, Vol. 53, No. 10, 2007, pp. 1561-1566. doi:10.1016/j.camwa.2006.04.030
,” Computers and Mathematics with Application, Vol. 53, No. 10, 2007, pp. 1561-1566. doi:10.1016/j.camwa.2006.04.030 - E. Camouzis, C. M. Kent, G. Ladas and C. D. Lynd, “On the Global Character of Solutions of the System:
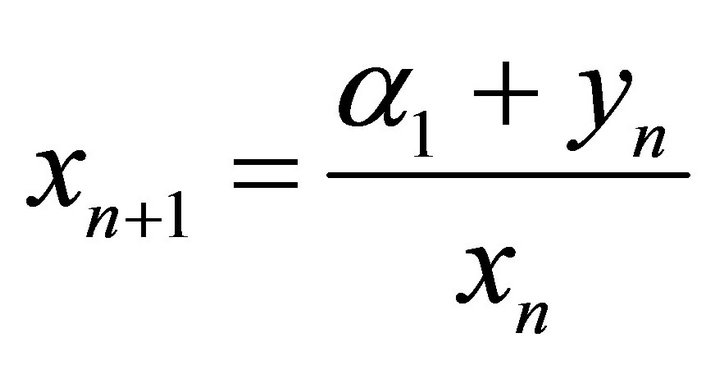 ,
, 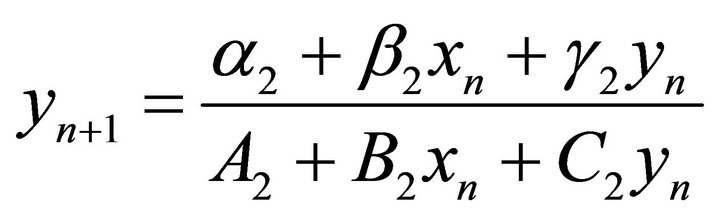 ,” Journal of Difference Equations and Applications, Vol. 18, No. 7, 2012, pp. 1205-1252. doi:10.1080/10236198.2011.555406
,” Journal of Difference Equations and Applications, Vol. 18, No. 7, 2012, pp. 1205-1252. doi:10.1080/10236198.2011.555406 - E. Camouzis, E. Drymonis, G. Ladas and W. Tikjha, “Patterns of Boundedness of the Rational System
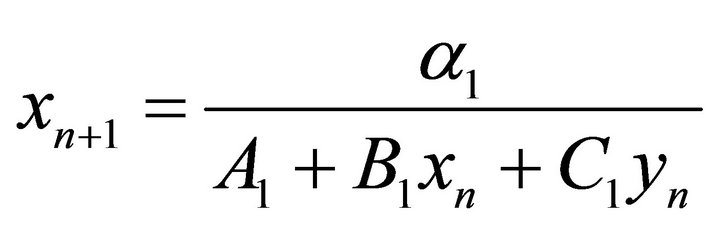 ,
, 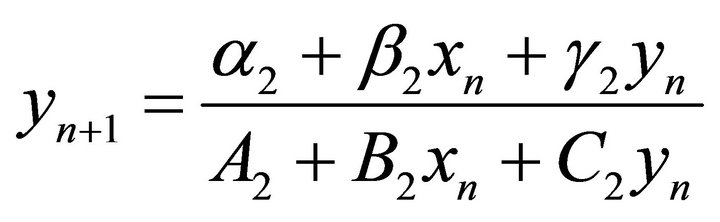 ,” Journal of Difference Equations and Applications, Vol. 18, No. 1, 2012, pp. 89-110. doi:10.1080/10236198.2010.515591
,” Journal of Difference Equations and Applications, Vol. 18, No. 1, 2012, pp. 89-110. doi:10.1080/10236198.2010.515591 - H. M. El-Owaidy, A. M. Ahmed and M. S. Mousa, “On Asymptotic Behavior of the Difference
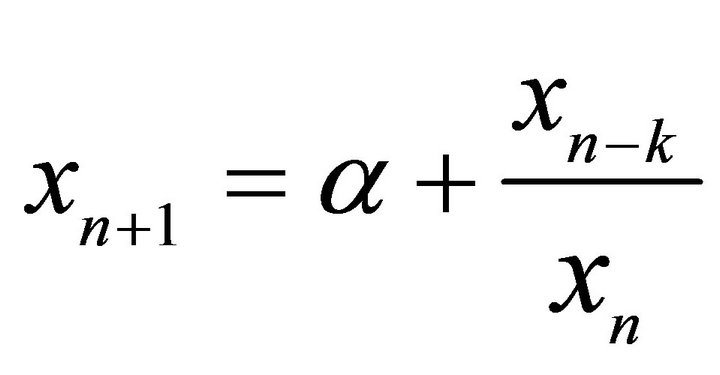 ,” Applied Mathematics and Computation, Vol. 147, No. 1, 2004, pp. 163-167. doi:10.1016/S0096-3003(02)00659-8
,” Applied Mathematics and Computation, Vol. 147, No. 1, 2004, pp. 163-167. doi:10.1016/S0096-3003(02)00659-8
NOTES
*Research supported by Distinguished Expert Foundation and Youth Science Foundation of Naval Aeronautical and Astronautical University.
#Corresponding author.

