Applied Mathematics
Vol.4 No.3(2013), Article ID:28863,5 pages DOI:10.4236/am.2013.43075
The New Approximate Calculation Method for the First Order Reliability*
1School of Engineering, Shijiazhuang University of Economics, Shijiazhuang, China
2Key Laboratory of Water Resources Sustainable Utilization and Exploit, Shijiazhuang, China
3Hebei Color Arima Geotechnical Engineering Co., Ltd., Sanhe, China
Email: hgl920@126.com
Received January 6, 2013; revised February 6, 2013; accepted February 13, 2013
Keywords: Reliability; First-Order Second Moment (FOSM); Direct Searching
ABSTRACT
The new method is presented for computing engineering structure reliability by direct searching the next checking point and accelerating convergence based on the analysis of errors in the center point method and borrowing ideas form the merits of the other First-Order Second Moment (FOSM) methods. The idea of the direct searching method is constructing a new explicit searching formula to make the new checking point being more closed to the failure surface based on the results of the center point method. The new checking point has steepest descent character because the searching path is the gradient of the approximate surface. An example shows that the method presented in this article has well precision. Although the direct searching formula may not reach the globally optimal point, the error can be controlled owing to the locally optimal plan at each searching step.
1. Introduction
There are a lot of uncertainties in the analysis of engineering structure [1], the distribution type of the random variable is various, the functions of the member do not follow the normal distribution, which are generally nonlinear, therefore, it is hard to calculate the reliability index of the structure directly. At the present, the firstorder second moment method (FOSM) is widely used as the approximate calculation method, which is. The common first-order second moment methods are center point method, checking point method, mapping transformation method, practical analysis, design point and gradient optimization method etc. The first-order second moment method is accepted in the engineering due to its simple calculation and the calculation precision can meet the engineering application requirement in the most cases.
Because of its direct and simple characteristic, the center point method is firstly used in the engineering as the primary estimation of the structure reliability. But the center point method does not consider the real distribution of the random variables, which only consider their mean value and variance and implicitly assume the each random variable is normal distribution or logarithmic normal distribution. Both the theory and practice indicate [2,3], the calculation error of the center point method is big for the nonlinear limit state equation, as a result, reliability indexes which obtained from different format of nonlinear limit state equation with the same mechanical meaning differ greatly, it is inconvenient in the real application and could not meet the requirement of engineering accuracy. Both the checking point method and mapping transformation method select the design checking point as the linearization point of the nonlinear function, which could get reliability index with higher accuracy and ensure the uniqueness of reliability index for the same member, but the two methods are implicit and the calculation process are complex, which need several double iteration and the selection of initial values have impact on the iteration process, therefore, they are not easy to be applied in the real engineering. Hence, it should put forward some simplified algorithms with less calculation and good accuracy, there are practical analysis method [4] and design point method [5]. The gradient optimization method [6] is also an implicit method, which calculate the problem as an optimization question, thus, the calculation of the reliability index is convenient, the advantage is more obvious especially for the complex index, it could reduce the calculation effective.
The basic principal of the first order reliability method is the linear expansion of the function, which use the linear function as the former function, so it could get the approximate solution. Hasofer, Lind [7] define the smallest distance between the failure surface point (checking point) and the mean point as the reliability index, which has solved the problem of simple reliability index. Rackwitz, Fiessler [8] has dealt with non-normal distribution of random variables used the equivalent normal variable method. Shinozuka [9] has pointed out the checking point is the largest probability density point on the structure function surface, the search of the checking point could use the ordinary constraint optimization algorithm. Der Kiureghian [10] has put forward the method to deal with many checking points in the optimized analysis. Bjerager [11] has deduced the sensitivity of the first order reliability index used the check point coordinates. There also appear a lot of new reliability calculation methods during the solution of nonlinear function problem, such as the two order reliability method, selective sampling method (Harbitz [12]) etc. Guan [13] has suggested selecting several points on the function surface near the checking point, and constructing multi tangent planes to fit the real nonlinear function surface, the similar idea is such as the method which is proposed by Mahadevan [14]. The improved reliability methods are in the theoretical discussion stage, while the traditional FORM are still used in the real practice.
The computational accuracy of the center point method is not high, even if not considering the influence of the variable distribution pattern, there are two reasons as follows. Firstly, the mean point is assumed as the linearization point for the method, while the mean point is far away from the failure boundary, thus, if the original nonlinear limit state equation is made Taylor series expansion about the point and the reliability index is calculated, the calculation error is larger than taking the expansion point for design checking point. Secondly, the center point method only take a linear cut for the Taylor series expansion and does not consider the influence of higher order, which is also an important reason caused error. Due to the above two reasons, the reliability index is different for the same structure when limit state equations with different format are given. Based on the analysis of the defect of center point method and advantage of other methods, a new approximate calculation method which is suitable for engineering application and with high calculation accuracy is proposed in the paper.
2. Direct Searching Method
Generally, the random variables which have impact on the structure reliability are assumed as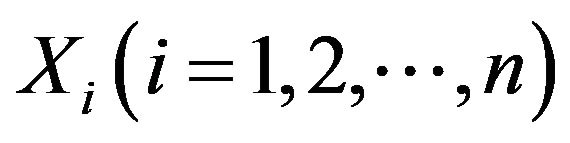 , the function is:
, the function is:
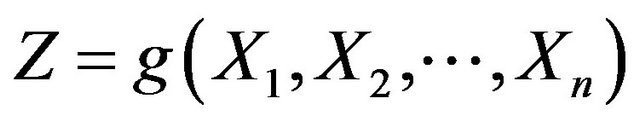 (1)
(1)
Limit state equation is:
 (2)
(2)
The structure function is made Taylor series expansion about the point 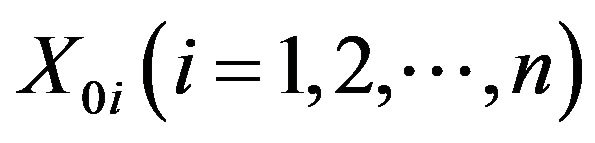 thus,
thus,
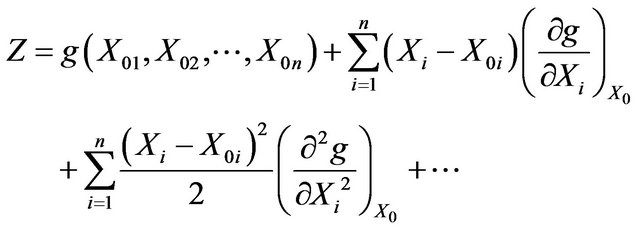 (3)
(3)
Record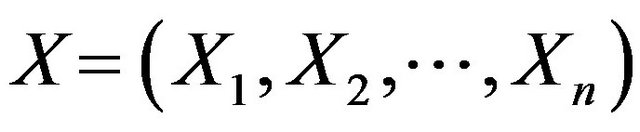 ,
, 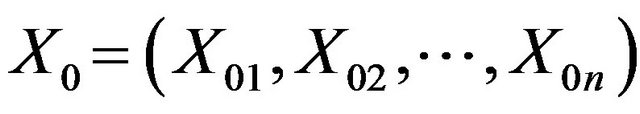 , therefore, the format of Formula (3) could be transformed as follows
, therefore, the format of Formula (3) could be transformed as follows
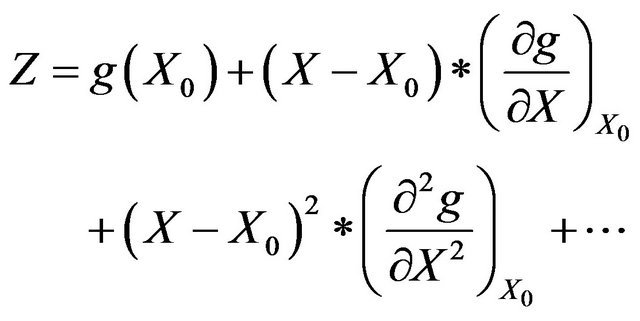 (4)
(4)
where,  is the vector point,
is the vector point, 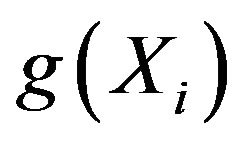 is the function of each component, which is not the overall function of
is the function of each component, which is not the overall function of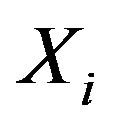 . The symbol
. The symbol  represent the point multiplication operation between components, and the transposed symbol of the component is not used here, a scalar could be obtained through corresponding item multiplication if the two components could be multiplied. The power time of the vector represents each.
represent the point multiplication operation between components, and the transposed symbol of the component is not used here, a scalar could be obtained through corresponding item multiplication if the two components could be multiplied. The power time of the vector represents each.
The simple vector expression is adopted in the following deduction.
The expression of linear structure function could be got through only taking the linear item.
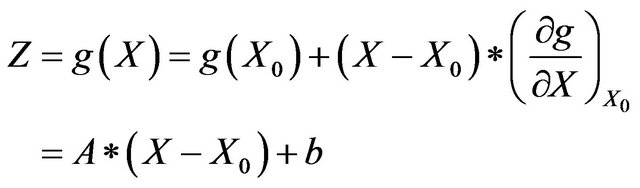 (5)
(5)
where, 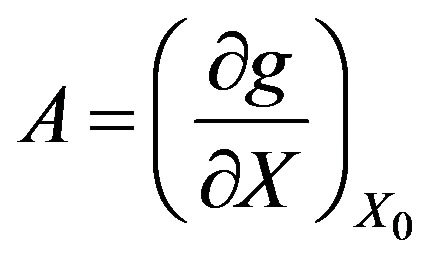 ,
,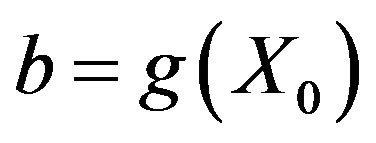 .
.
Take mean value and variance for the Formula (5), thus
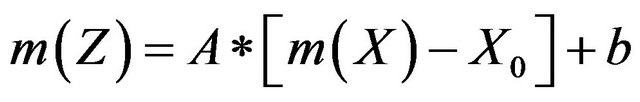 (6)
(6)
 (7)
(7)
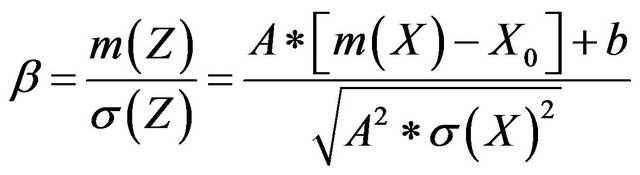 (8)
(8)
The structure function is expanded about the center point at this time, generally speaking, the center point is far away from the failure surface, which cause a large calculation error, so a new checking point would be constructed in the following, which is near the failure surface. In fact, the Formula (5) is the one order approximation for the failure surface, whose geometrical significance is a hyperplane in 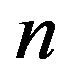 -dimensional space, while the geometrical significance of the failure surface is a curved surface in
-dimensional space, while the geometrical significance of the failure surface is a curved surface in 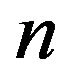 -dimensional space, if a suitable point on the plane is taken as the checking point, it could make the smallest distance between the checking point and the failure surface smaller than the smallest distance between the center point and the failure surface. The structure function is made Taylor series expansion about the checking point again, and the linear item is taken to be analyzed, it could predict that the accuracy of the reliability index is higher than the Taylor series expansion about the center point.
-dimensional space, if a suitable point on the plane is taken as the checking point, it could make the smallest distance between the checking point and the failure surface smaller than the smallest distance between the center point and the failure surface. The structure function is made Taylor series expansion about the checking point again, and the linear item is taken to be analyzed, it could predict that the accuracy of the reliability index is higher than the Taylor series expansion about the center point.
Construct:
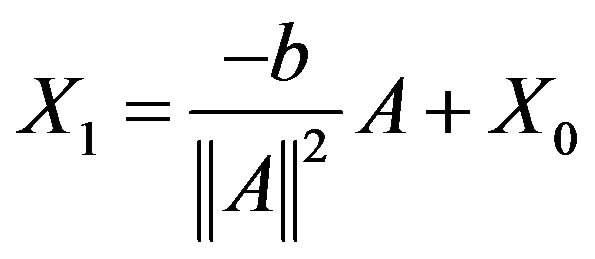 (9)
(9)
Substitute the Formula (9) into Formula (5), it could satisfy
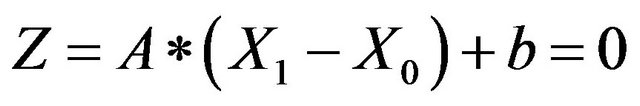 (10)
(10)
Moreover, 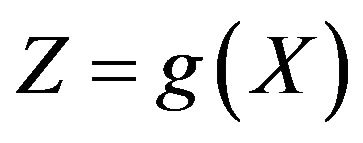 is made Taylor series expansion about the checking point
is made Taylor series expansion about the checking point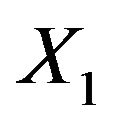 , it could obtain
, it could obtain
 (11)
(11)
Note, here A and b are 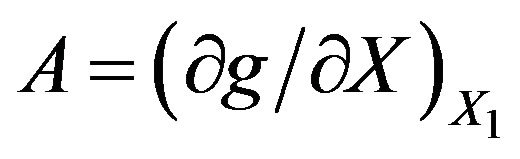 and b = g(X1), respectively, which are not distinguished from
and b = g(X1), respectively, which are not distinguished from and b in the Formula (5) for convenience of writing, in fact, it is not necessary for the careful distinction. Similarly, a new series of expectancy values, variances and reliability indexes of the structure function could be obtained based on the Formula (11).
and b in the Formula (5) for convenience of writing, in fact, it is not necessary for the careful distinction. Similarly, a new series of expectancy values, variances and reliability indexes of the structure function could be obtained based on the Formula (11).
 (12)
(12)
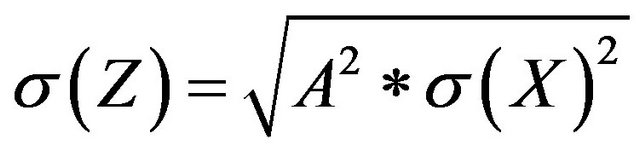 (13)
(13)
 (14)
(14)
The direct search method has finish a iterative process for the reliability index, and it should point out, the iterative process is explicit.
If the obtained reliability index does not meet the accuracy requirement, new checking point could be constructed sequentially
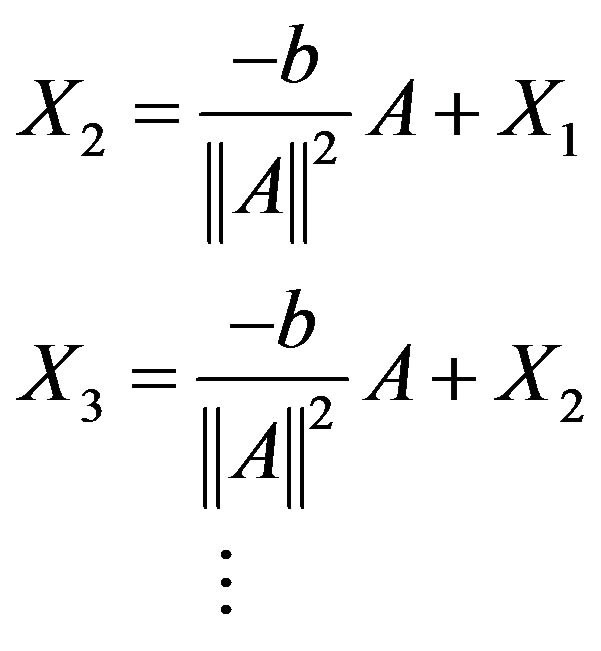 (15)
(15)
The obtained series and
and 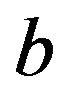 are:
are:
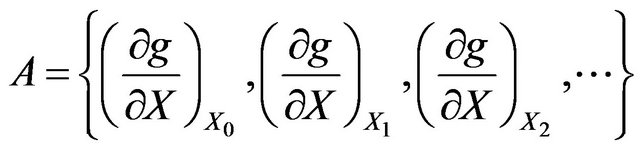 (16)
(16)
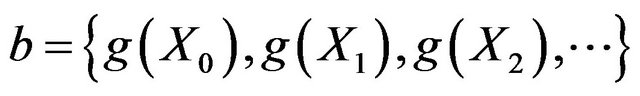 (17)
(17)
We can see that, series is the reflection of structure function for sensitivity index of each random variable, called sensitivity series; while series
is the reflection of structure function for sensitivity index of each random variable, called sensitivity series; while series 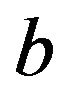 represent the approximation degree between the checking point and failure surface, from the iterative process it could know,
represent the approximation degree between the checking point and failure surface, from the iterative process it could know,
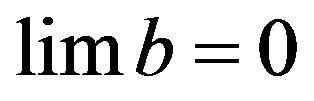 (18)
(18)
It could be called residual series, which is used to judge whether the iterative process is terminated.
3. Analysis of Examples
A straight-bar with circular section, the tension force is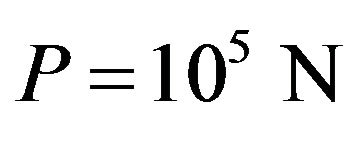 , the diameter
, the diameter and stress yield limit Fy are assumed as the random variables, which the mean value and variance are
and stress yield limit Fy are assumed as the random variables, which the mean value and variance are
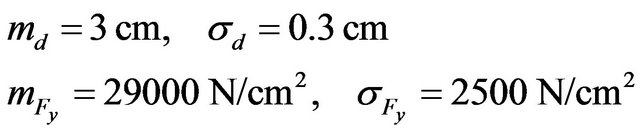
Now calculate the tensile reliability index [15,16].
Internal force and stress were established with representation of the limit state equation of 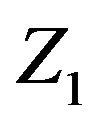 and
and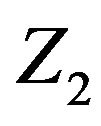 , there is
, there is
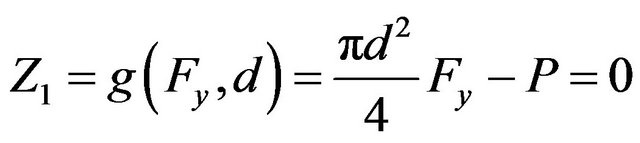 (19)
(19)
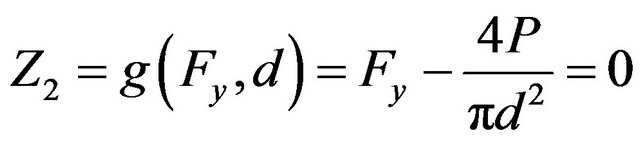 (20)
(20)
When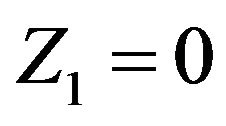 , the iterative results used the direct searching method are seen in Table 1.
, the iterative results used the direct searching method are seen in Table 1.
Tables 1 and 2 indicate, after several simple iterative, the reliability index obtained used the direct searching method converge to a certain value. In the example, the convergent value is same for different structure function. But it should note that, the cases is not always as the above, because the nature of the direct searching method is the searching the point which is most near the failure surface on the approximation failure surface, because the checking point here is not the actual checking point on the failure surface, therefore, the reliability degree for different failure surfaces could converge to different values, but the differences is little, they would distribute in a small neighborhood of the reliability index. The geometric meaning of the reliability index is the smallest distance from the failure boundary to the mean point. Because the direct searching method limit the final searching point almost locate on the failure surface used the scale of b (it take 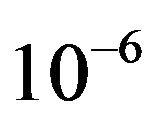 in the example), as a result, the
in the example), as a result, the
Table 1. Iterative results in the direct searching method.
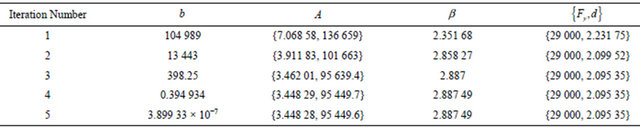
Table 2. Iterative results in the direct searching method.
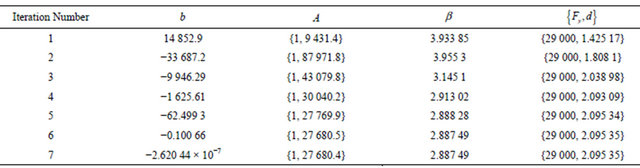
final obtained distance from the approximation failure boundary to mean point is larger than the distance obtained by checking method, therefore, the reliability index obtained by the direct searching method is radical.
Moreover, the proposed method is with good convergence property, and could satisfy the engineering accuracy, it is an explicit calculation method with relatively simple and accurate characteristic.
4. Conclusion
When the structure reliability degree is calculated used the direct method, if the limit state formula is different for the same mechanics problem, generally the structure reliability index is different, which is the insurmountability. Although the searching point obtained by the direct searching method proposed in the paper is not the global optimum, but each step of searching is local optimum, it make the searching result meet the accuracy requirement and with considerable guiding significance. The direct searching method is based on keeping accuracy, because the process of iteration is very simple, direct and vivid, and as a way of displaying the format, which is the checking point method is lacking of.
REFERENCES
- G. F. Zhao, “Theory and Application of Reliability in Engineering Structure,” Dalian University of Technology Press, Dalian, 1996, pp. 1-2. (In Chinese)
- S. W. Wu, “Structural Reliability Analysis,” China Communications Press, Beijing, 1996, pp. 22-31. (In Chinese)
- G. F. Zhao, J. Y. Cao and K. Q. Zhang, “Engineering Structural Reliability,” Wate Conservancy and Hydropower Press, Beijing, 1984, pp. 51-65. (In Chinese)
- Y. G. Li and G. F. Zhao, “The First Order Reliability Method of General Stochastic Space,” Journal of Dalian University of Technology, Vol. S1, 1993, pp. 1-5. (In Chinese)
- G. Q. Li and W. J. Yang, “A Simplified Calculating Method on Reliability,” Journal of Changsha Communications Universrty, Vol. 15, No. 3, 1999, pp. 62-67.
- Q. X. Wu, T. R. Lv and S. W. Wu. “Computing of Structural Reliability Index for Correlated Variables,” Applied Mathematics: A Journal of Chinese Universities, Vol. 3, 1987, pp. 323-329.
- A. M. Hasofer and N. C. Lind, “Exact and Invariant Second-Moment Code Format,” Journal of the Engineering Mechanics Division, Vol. 100, No. 1, 1974, pp. 111-121.
- R. Rackwitz and B. Fiessler, “Structural Reliability under Combined Random Load Sequences Computers and Structures,” Computers and Structures, Vol. 9, No. 5, 1978, pp. 489-494. doi:10.1016/0045-7949(78)90046-9
- M. Shinozuka, “Basic Analysis of Structural Safety,” Journal of Structural Engineering, Vol. 109, No. 3, 1983, pp. 721-740. doi:10.1061/(ASCE)0733-9445(1983)109:3(721)
- A. Der Kiureghian and T. Dakessian, “Multiple Design Points in First and Second-Order Reliability,” Structural Safety, Vol. 20, No. 1, 1998, pp. 37-49. doi:10.1016/S0167-4730(97)00026-X
- P. Bjerager and S. Krenk, “Sensitivity Measures in Structural Reliability Analysis,” Reliability and Optimization of Structural Systems, Proceedings of the First IFIP WG 7.5 Working Conference, Springer-Verlag, Aalborg, 1987, pp. 459-470.
- A. Harbitz, “An Efficient Method for Probability of Failure Calculation,” Structural Safety, Vol. 3, No. 2, 1986, pp. 109-115. doi:10.1016/0167-4730(86)90012-3
- X. L. Guan and R. E. Melchers, “Multi-Tangent-Plane Surface Method for Reliability Calculation,” Journal of Engineering Mechanics, Vol. 123, No. 10, 1997, pp. 996- 1002. doi:10.1061/(ASCE)0733-9399(1997)123:10(996)
- S. Mahadevan and P. Shi, “Multiple Linearization Method for Nonlinear Reliability Analysis,” Journal of Engineering Mechanics, Vol. 127, No. 11, 2001, pp. 1165- 1173. doi:10.1061/(ASCE)0733-9399(2001)127:11(1165)
- Q. X. Wu, “Structural Reliability Analysis and Random Finite Element Method,” China Machine Press, Beijing, 2005, pp. 63-73. (In Chinese)
- W. T. Liu, “Design Handbook for Structural Reliability,” National Defense Industry Press, Beijing, 2008, pp. 493- 501. (In Chinese)
NOTES
*This work was jointly supported by Hall of Hebei province science and technology, China (11213947) and (11276733).

