Applied Mathematics
Vol.4 No.2(2013), Article ID:28212,4 pages DOI:10.4236/am.2013.42053
Super Cyclically Edge Connected Half Vertex Transitive Graphs*
College of Mathematics and System Sciences, Xinjiang University, Urumqi, China
Email: hnjiangsd@163.com, #mjx@xju.edu.cn, tianyzhxj@163.com
Received October 21, 2012; revised December 26, 2012; accepted January 3, 2013
Keywords: Cyclic Edge-Connectivity; Cyclically Optimal; Super Cyclically Edge-Connected; Half Vertex Transitive Graph
ABSTRACT
Tian and Meng in [Y. Tian and J. Meng, 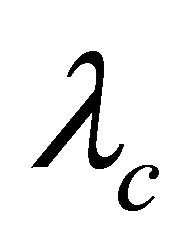 -Optimally half vertex transitive graphs with regularity
-Optimally half vertex transitive graphs with regularity , Information Processing Letters 109 (2009) 683-686] shown that a connected half vertex transitive graph with regularity
, Information Processing Letters 109 (2009) 683-686] shown that a connected half vertex transitive graph with regularity 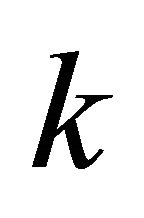 and girth
and girth 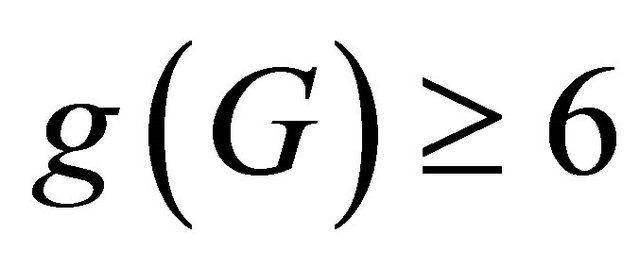 is cyclically optimal. In this paper, we show that a connected half vertex transitive graph G is super cyclically edge-connected if minimum degree
is cyclically optimal. In this paper, we show that a connected half vertex transitive graph G is super cyclically edge-connected if minimum degree 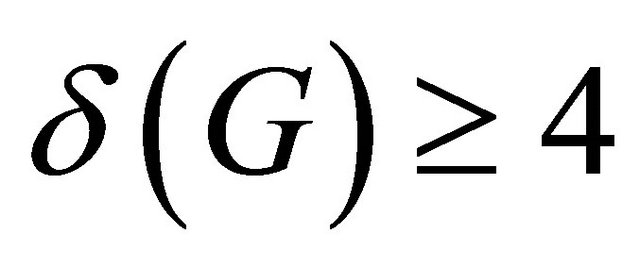 and girth
and girth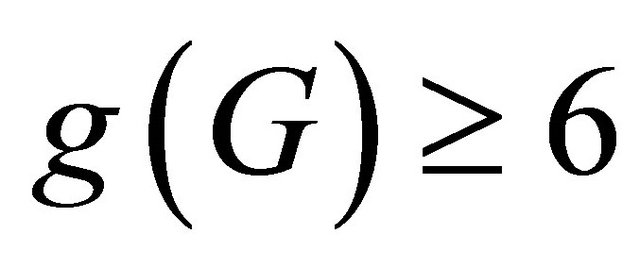 .
.
1. Introduction
The traditional connectivity and edge-connectivity, are important measures for networks, which can correctly reflect the fault tolerance of systems with few processors, but it always underestimates the resilience of large networks. The discrepancy incurred is because events whose occurrence would disrupt a large network after a few processors, therefore, the disruption envisaged occurs in a worst case scenario. To overcome such a shortcoming, Latifi et al. [1] proposed a kind of conditional edgeconnectivity, denoted by , which is the minimum size of edge-cut
, which is the minimum size of edge-cut ![]() such that each vertex has degree at least
such that each vertex has degree at least 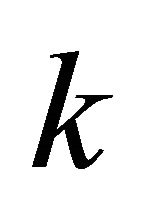 in
in .
.
Throughout the paper graphs are undirected finite connected without loops or multiple edges.
Let 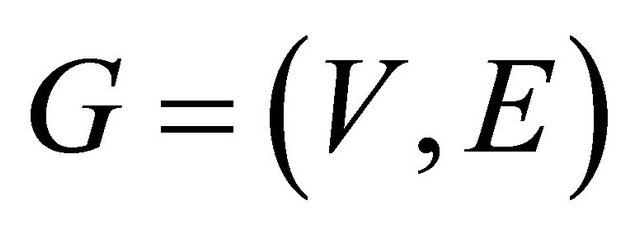 be a graph, an edge set
be a graph, an edge set  is a cyclic edge-cut if
is a cyclic edge-cut if 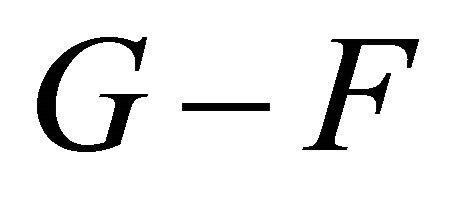 is disconnected and at least two of its components contain cycles. Clearly, a graph has a cyclic edge-cut if and only if it has two vertexdisjoint cycles. A graph
is disconnected and at least two of its components contain cycles. Clearly, a graph has a cyclic edge-cut if and only if it has two vertexdisjoint cycles. A graph 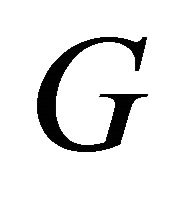 is said to be cyclically separable if
is said to be cyclically separable if 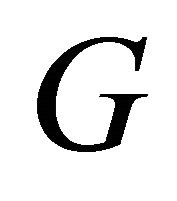 has a cyclic edge-cut. Note that Lovász [2] characterized all multigraphs without two vertex-disjoint cycles. The characterization can also be found in Bollobás [3]. So, it is natural to further study the cyclically separable graphs. For a cyclically separable graph
has a cyclic edge-cut. Note that Lovász [2] characterized all multigraphs without two vertex-disjoint cycles. The characterization can also be found in Bollobás [3]. So, it is natural to further study the cyclically separable graphs. For a cyclically separable graph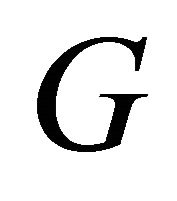 , The cyclic edge-connectivity of
, The cyclic edge-connectivity of , denoted by
, denoted by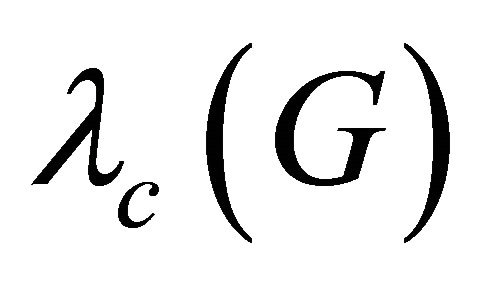 , is defined as the minimum cardinality over all cyclic edgecuts of
, is defined as the minimum cardinality over all cyclic edgecuts of  by following Plummer [4]. The concept of cyclic edge-connectivity as applied to planar graphs dates to the famous incorrect conjecture of Tait [5].
by following Plummer [4]. The concept of cyclic edge-connectivity as applied to planar graphs dates to the famous incorrect conjecture of Tait [5].
The cyclic edge-connectivity plays an important role in some classic fields of graph theory such as Hamiltonian graphs (Máčajová and Šoviera [6]), fullerence graphs (Kardoš and Šrekovski [7]), integer flow conjectures (Zhang [8]), n-extendable graphs (Holton et al. [9]; Lou and Holton [10]), etc.
For two vertex sets 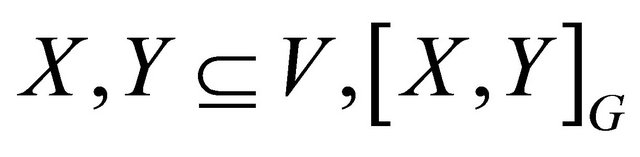 is the set of edges with one end in
is the set of edges with one end in 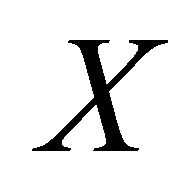 and the other end in
and the other end in![]() . For any vertex set
. For any vertex set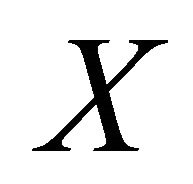 ,
,  is the subgraph of
is the subgraph of  induced by
induced by ,
, 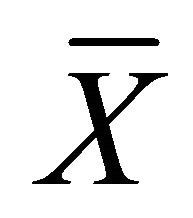 is the complement of
is the complement of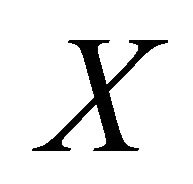 . Clearly, if
. Clearly, if  is a minimum cyclic edge-cut, then both
is a minimum cyclic edge-cut, then both
 and
and 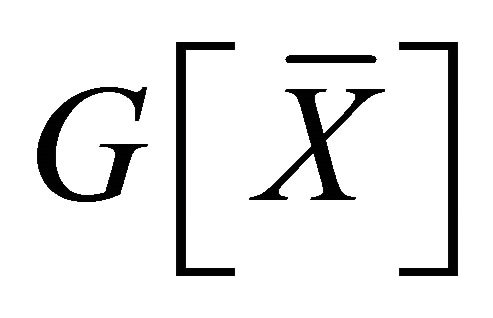 are connected. We set
are connected. We set
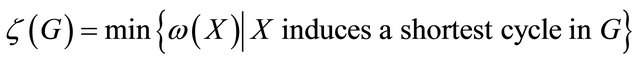 where
where 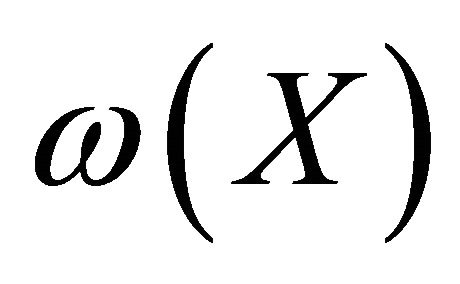 is the number of edges with one end in
is the number of edges with one end in  and the other end in
and the other end in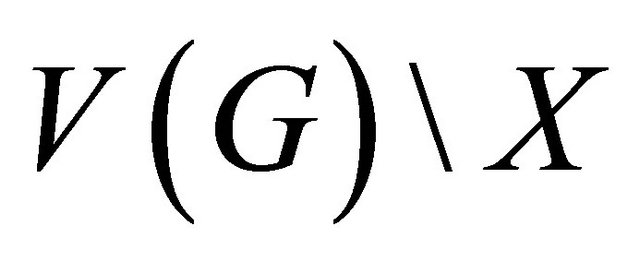 . It has been proved in Wang and Zhang [11] that
. It has been proved in Wang and Zhang [11] that 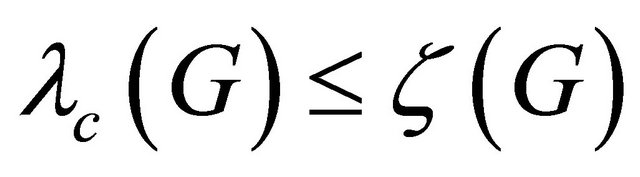 for any cyclically separable graph. Hence, a cyclically separable graph G is called cyclically optimal, in short,
for any cyclically separable graph. Hence, a cyclically separable graph G is called cyclically optimal, in short,  , if
, if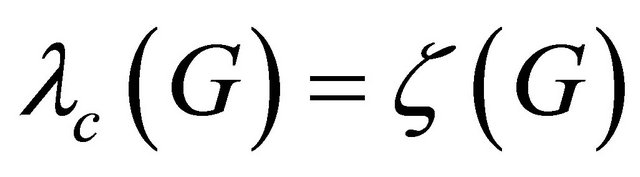 , and super cyclically edge-connected, in short,
, and super cyclically edge-connected, in short,  , if the removal of any minimum cyclic edge-cut of graph
, if the removal of any minimum cyclic edge-cut of graph 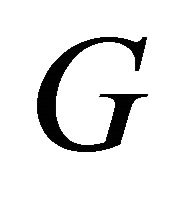 results in a component which is a shortest cycle.
results in a component which is a shortest cycle.
Cyclic edge-fragment and cyclic edge-atom play a fundamental role. A vertex set  is a cyclic edgefragment, in short, fragment, if
is a cyclic edgefragment, in short, fragment, if 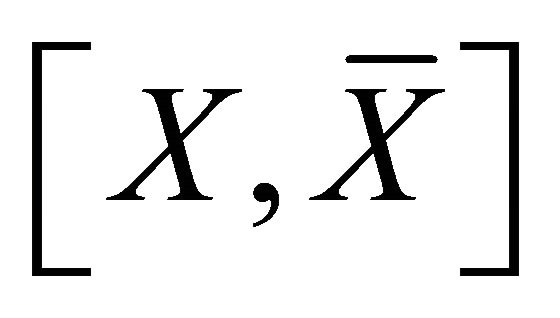 is a minimum cyclic edge-cut. A cyclic edge-fragment with the minimum cardinality is called a cyclic edge-atom, in short, atom. A cyclic edge-fragment of
is a minimum cyclic edge-cut. A cyclic edge-fragment with the minimum cardinality is called a cyclic edge-atom, in short, atom. A cyclic edge-fragment of 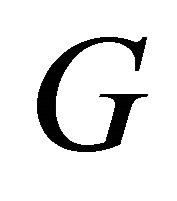 is said to be super, if neither
is said to be super, if neither 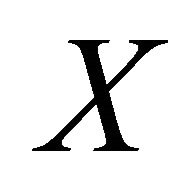 nor
nor  induces a shortest cycle, in short, super fragment. A super cyclic edge-fragment with the minimum cardinality is called a super cyclic edge-atom, in short, super atom. A cyclic edge-fragment is said to be trivial, if it induces a cycle, otherwise it is nontrivial.
induces a shortest cycle, in short, super fragment. A super cyclic edge-fragment with the minimum cardinality is called a super cyclic edge-atom, in short, super atom. A cyclic edge-fragment is said to be trivial, if it induces a cycle, otherwise it is nontrivial.
A graph 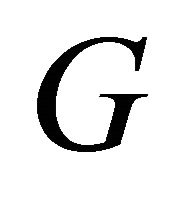 is said to be vertex transitive if
is said to be vertex transitive if 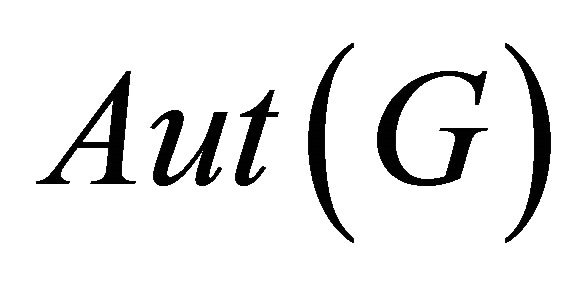 acts transitively on
acts transitively on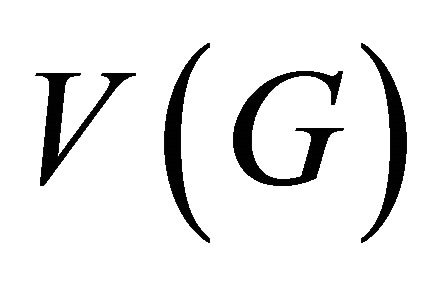 , and is edge transitive if
, and is edge transitive if 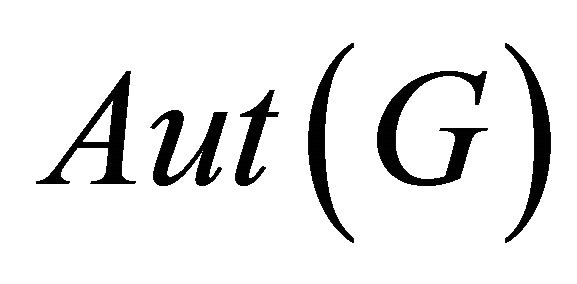 acts transitively on
acts transitively on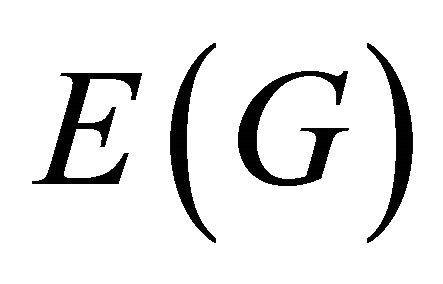 . A bipartite graph is biregular, if all the vertices from the same partite set have the same degree. We abbreviate the bipartite graph as a
. A bipartite graph is biregular, if all the vertices from the same partite set have the same degree. We abbreviate the bipartite graph as a 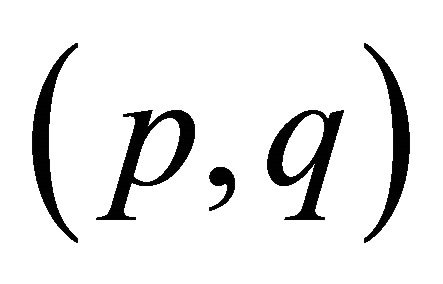 -biregular graph, if the two distinct degrees are
-biregular graph, if the two distinct degrees are ![]() and
and 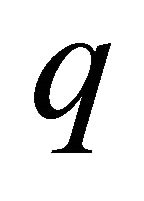 respectively
respectively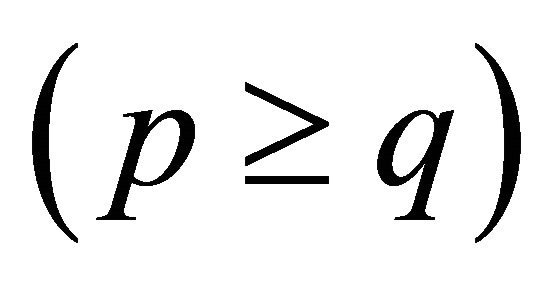 . A bipartite graph
. A bipartite graph 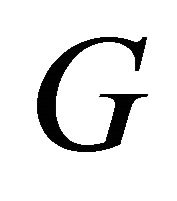 with bipartition
with bipartition 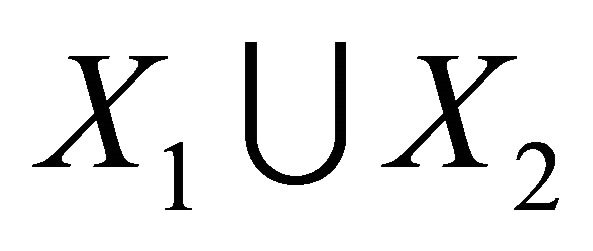 is called half vertex transitive [12], if
is called half vertex transitive [12], if 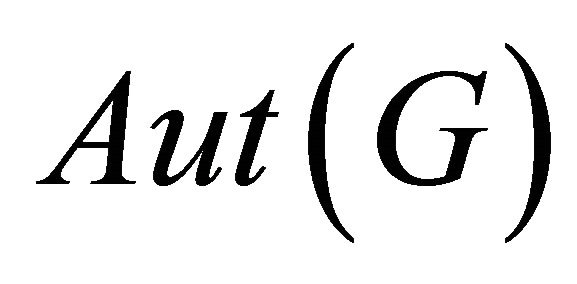 acts transitively both on
acts transitively both on  and
and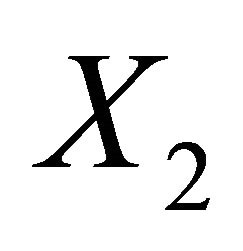 . Clearly, the half vertex transitive graph is biregular graph. Let
. Clearly, the half vertex transitive graph is biregular graph. Let , we call the set
, we call the set 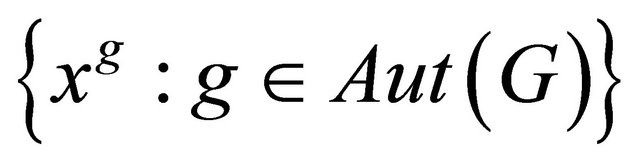
an orbit of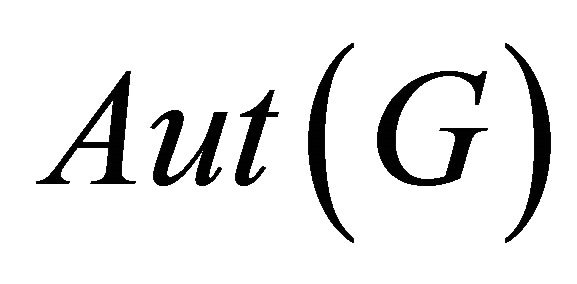 . Clearly,
. Clearly, 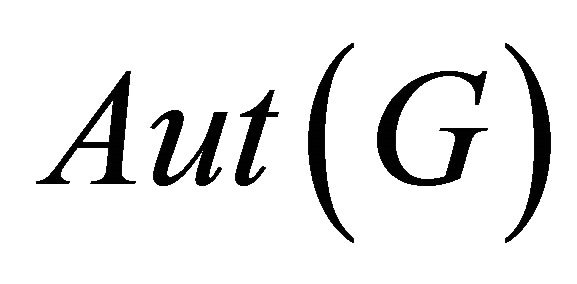 acts transitively on each orbit of
acts transitively on each orbit of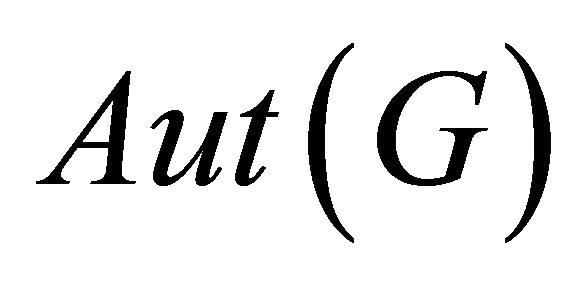 . Transitive graphs have been playing an important role in designing network topologies, since they possess many desirable properties such as high fault tolerance, small transitive delay, etc. [13,14].
. Transitive graphs have been playing an important role in designing network topologies, since they possess many desirable properties such as high fault tolerance, small transitive delay, etc. [13,14].
In Nedela and Škoviera [15], it was proved that a cubictransitive or edge-transitive graph (expect for  and
and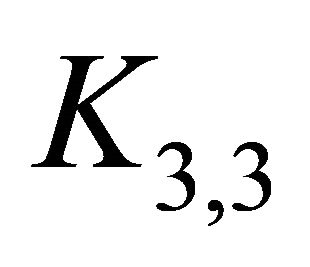 ) is
) is 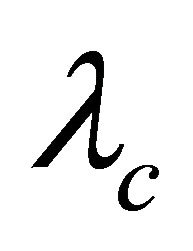 -optimal. From Wang and Zhang [11], Xu and Liu [16], we have known that a
-optimal. From Wang and Zhang [11], Xu and Liu [16], we have known that a 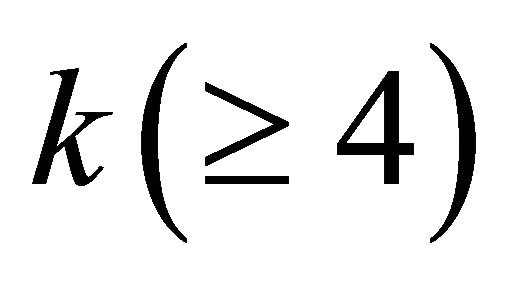 -regular vertex-transitive graph
-regular vertex-transitive graph 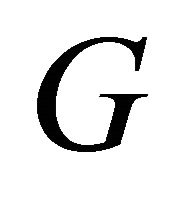 is
is 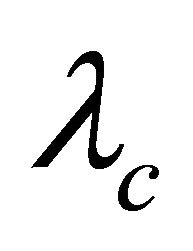 -optimal if it has girth
-optimal if it has girth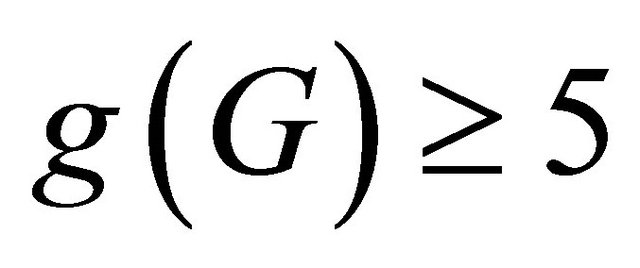 . It was also shown that an edge-transitive graph
. It was also shown that an edge-transitive graph 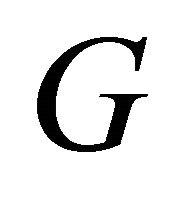 with minimum degree
with minimum degree 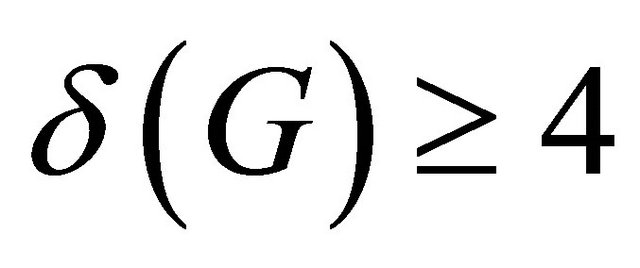 and order
and order 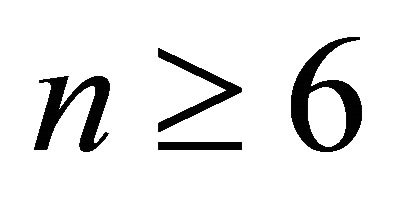 is
is  -optimal in Wang and Zhang [11]. Recently, Zhang and Wang [17] showed that a connected vertextransitive or edge-transitive graph is super-
-optimal in Wang and Zhang [11]. Recently, Zhang and Wang [17] showed that a connected vertextransitive or edge-transitive graph is super-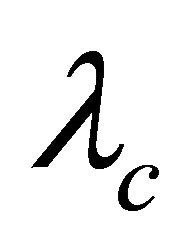 if either
if either 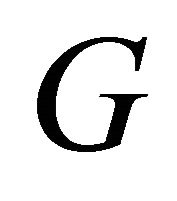 is cubic with girth
is cubic with girth 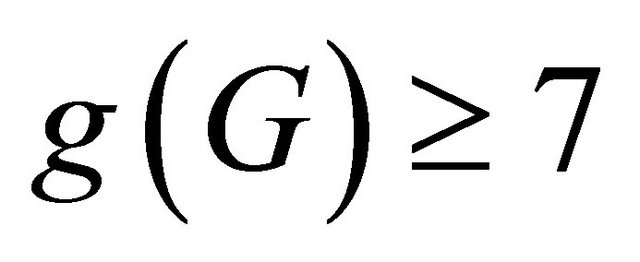 or G has minimum degree
or G has minimum degree 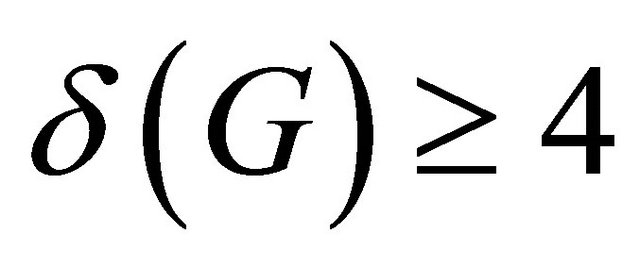 and girth
and girth . Zhou and Feng [18] characterized all possible
. Zhou and Feng [18] characterized all possible 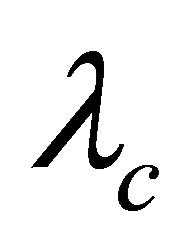 -superatoms for
-superatoms for 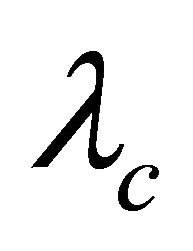 - optimal nonsuper-
- optimal nonsuper- graphs, and classified all
graphs, and classified all 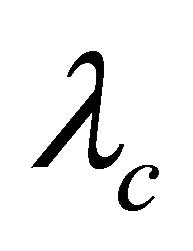 -optimal nonsuper-
-optimal nonsuper- edge-transitive graphs.
edge-transitive graphs.
Theorem 1.1 ([19]) Let G be a 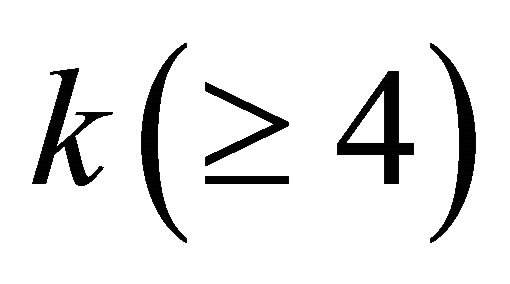 -regular connect half vertex transitive graph with bipartition
-regular connect half vertex transitive graph with bipartition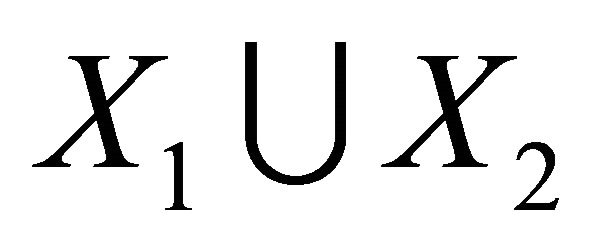 , and girth
, and girth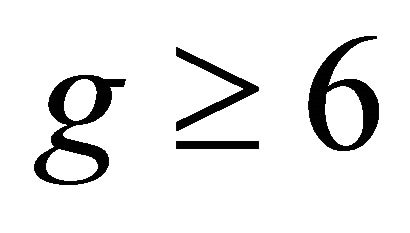 , then G is
, then G is 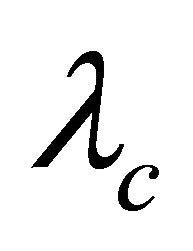 -optimal.
-optimal.
Motivated by the work in Tian and Meng [19], in this article we aim to study a connected half vertex transitive graph, and we show that a connected half vertex transitive graph 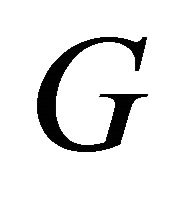 is super cyclically edge-connected if minimum degree
is super cyclically edge-connected if minimum degree 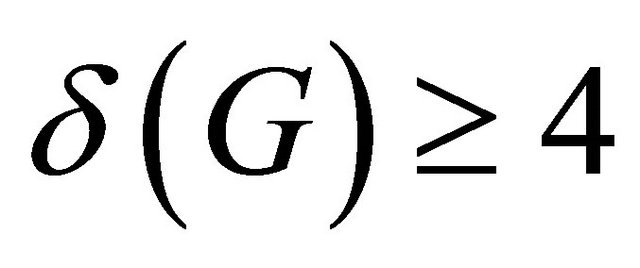 and girth
and girth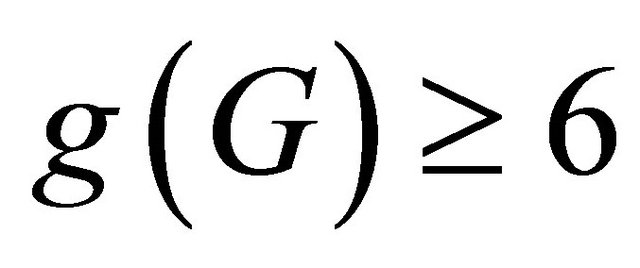 .
.
2. Preliminaries
Lemma 2.1 ([11]) Let G be a simple connected graph with 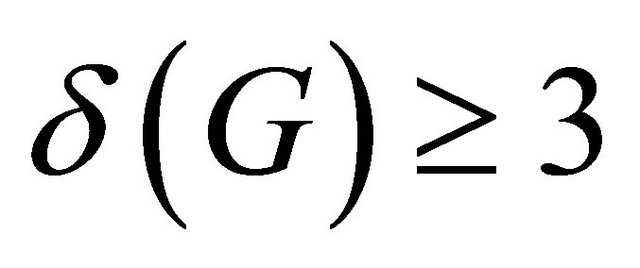 and
and 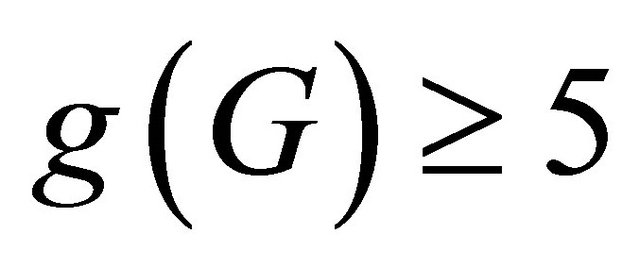 or
or 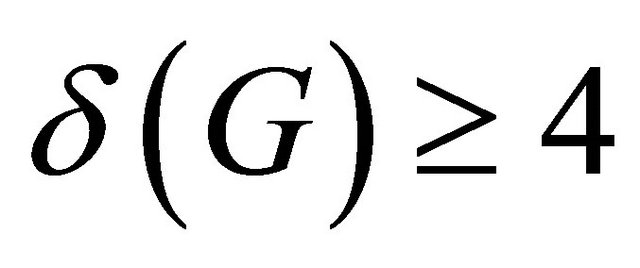 and order
and order . Then G is cyclically separable.
. Then G is cyclically separable.
Lemma 2.2 ([11]) Let G be a cyclically separable (p, q)-biregular graph with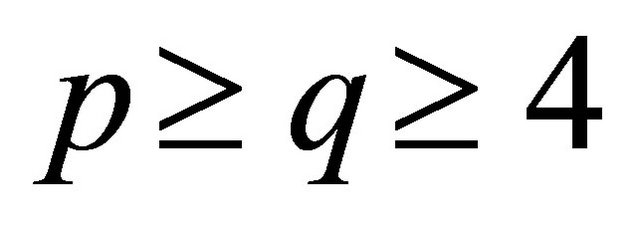 . Suppose G is not cyclically optimal and
. Suppose G is not cyclically optimal and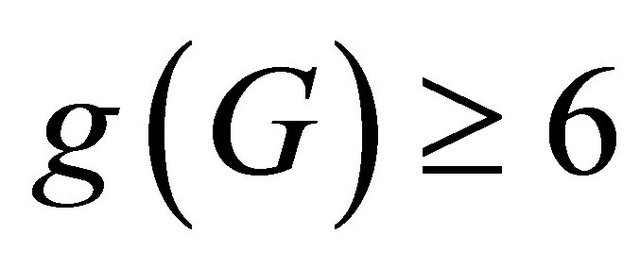 . Then for any distinct atoms X and Y,
. Then for any distinct atoms X and Y,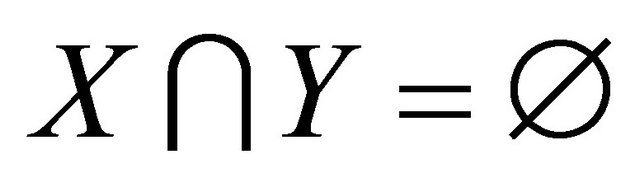 .
.
An imprimitive block of 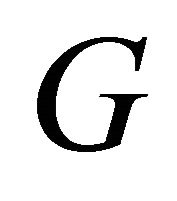 is a proper nonempty subset
is a proper nonempty subset  of
of 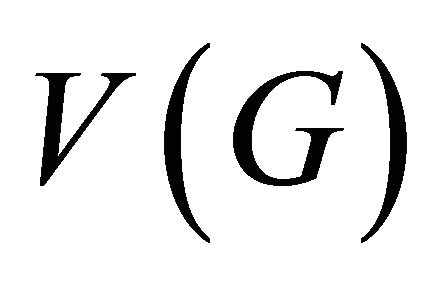 such that for any automorphism
such that for any automorphism , either
, either 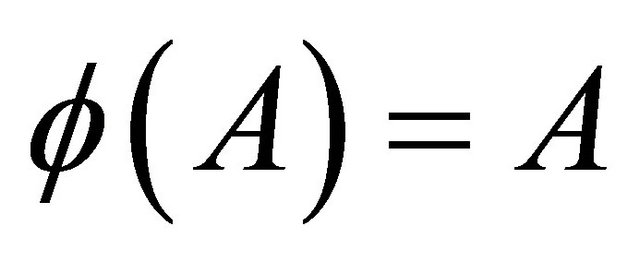 or
or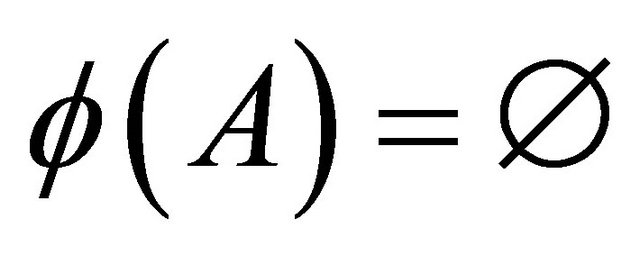 .
.
Lemma 2.3 ([20]) Let 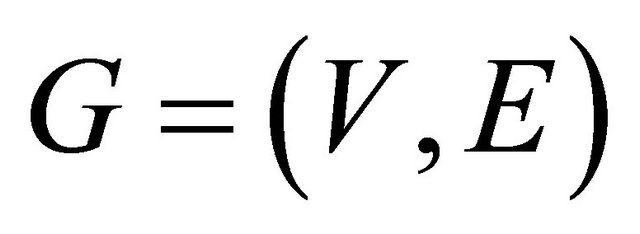 be a graph and let Y be the subgraph of G induced by an imprimitive block A of G. If G is vertex-transitive, then so is Y. If G is edge-transitive, then A is an independent set of G.
be a graph and let Y be the subgraph of G induced by an imprimitive block A of G. If G is vertex-transitive, then so is Y. If G is edge-transitive, then A is an independent set of G.
If X is a super atom, and 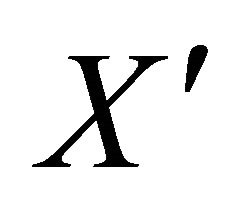 is a proper subset of X such that
is a proper subset of X such that 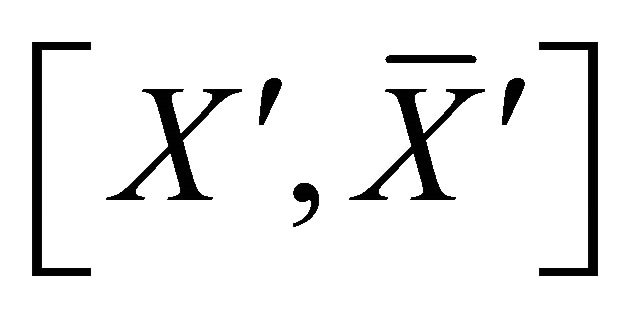 is a cyclic edge-cut and
is a cyclic edge-cut and 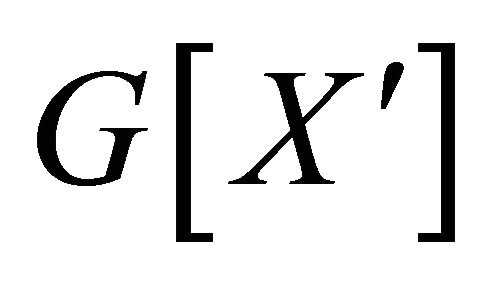 is not a shortest cyclic, then
is not a shortest cyclic, then

The observation is used frequently in the proofs.
Lemma 2.4 ([11]) Let G be a connected graph with 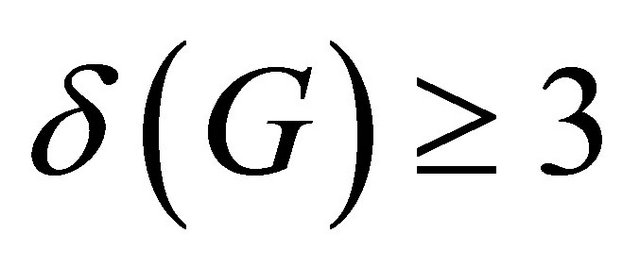 and
and 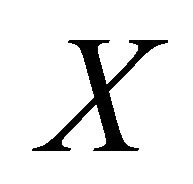 be a fragment. Then
be a fragment. Then
(1)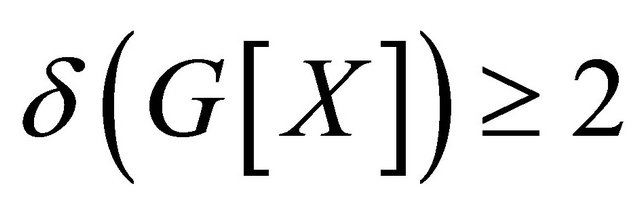 ;
;
(2) If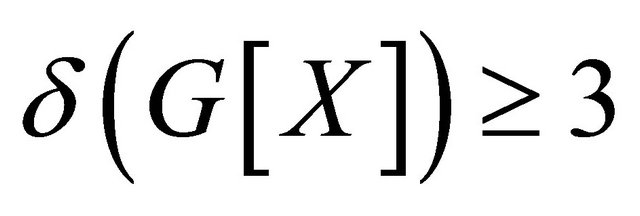 , then
, then 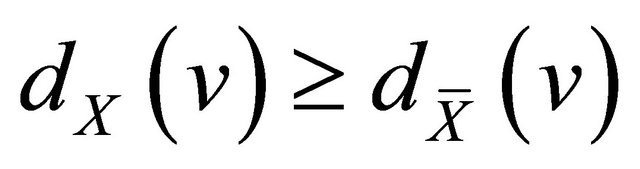 holds for any
holds for any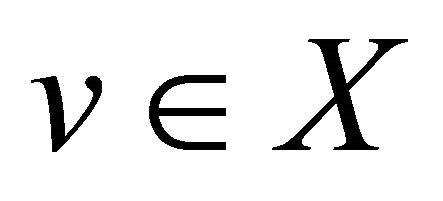 ;
;
(3) If  is not a cycle and
is not a cycle and ![]() is a vertex in X with
is a vertex in X with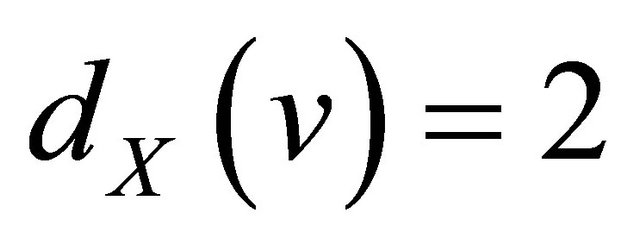 , then
, then 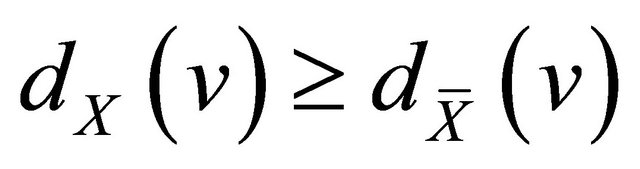 holds for any
holds for any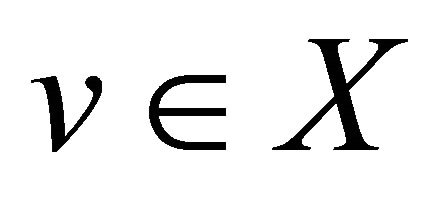 ;
;
(4) If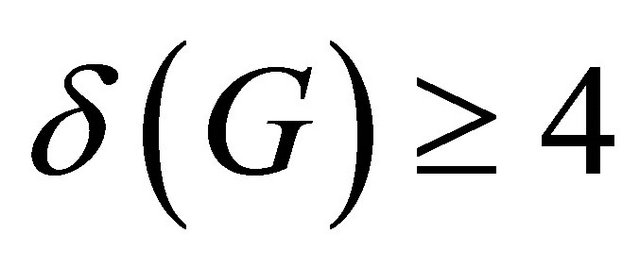 , and X is a non-trivial atom of Gthen
, and X is a non-trivial atom of Gthen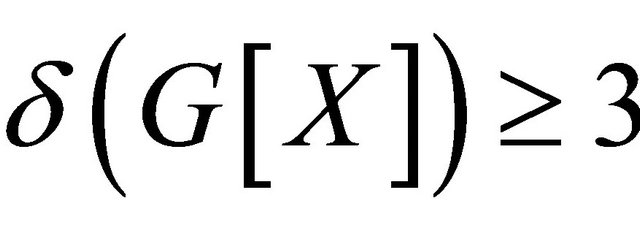 . Furthermore,
. Furthermore, 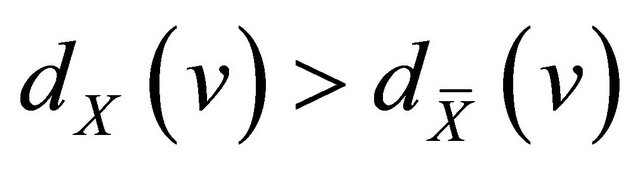 holds for any
holds for any . and
. and  holds for any
holds for any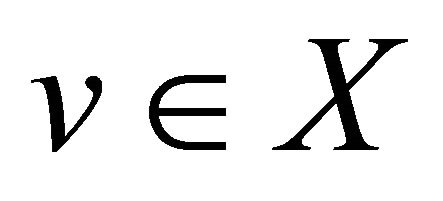 .
.
Lemma 2.5 ([17]) Let G be a connected graph with  and
and . Then G has two vertex-disjoint cycles and
. Then G has two vertex-disjoint cycles and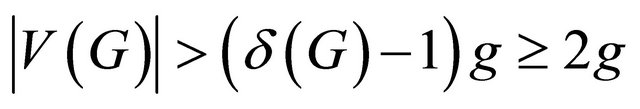 .
.
Lemma 2.6 ([17]) Let G be a (p,q)-biregular graph with 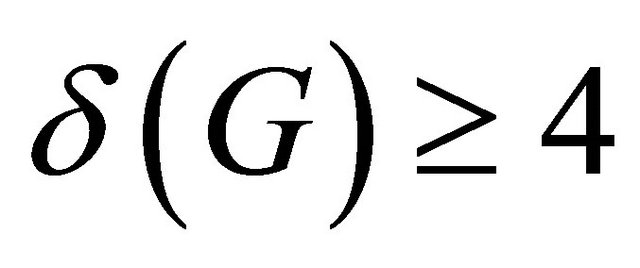 and girth
and girth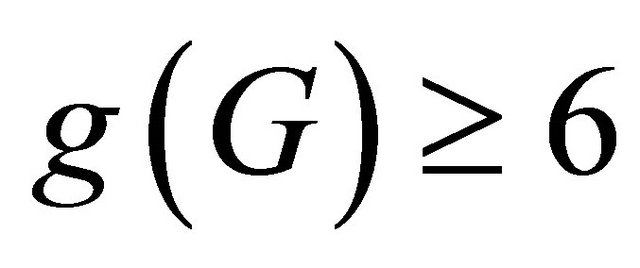 . Suppose G is cyclically optimal but not super cyclically edge-connected. Then any two distinct super atoms X and Y of G satisfies
. Suppose G is cyclically optimal but not super cyclically edge-connected. Then any two distinct super atoms X and Y of G satisfies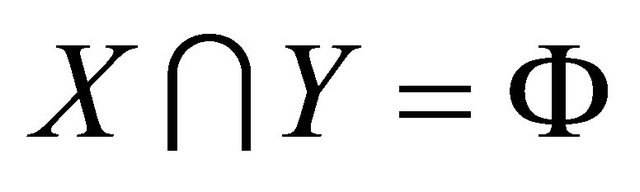 .
.
Lemma 2.7 Let G be a connected (p,q)-half vertex transitive graph with bipartition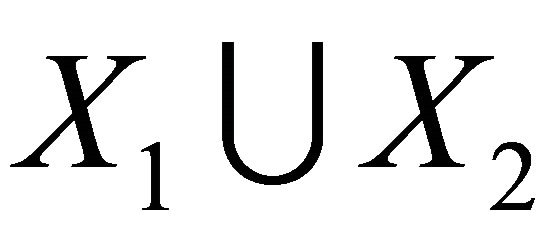 ,
, 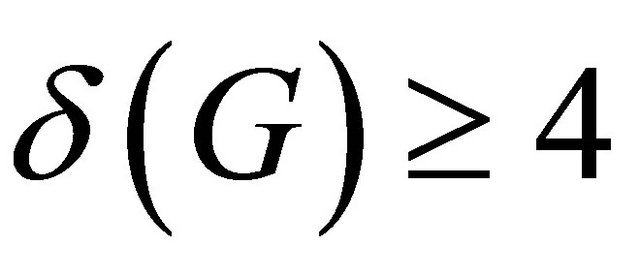 and girth
and girth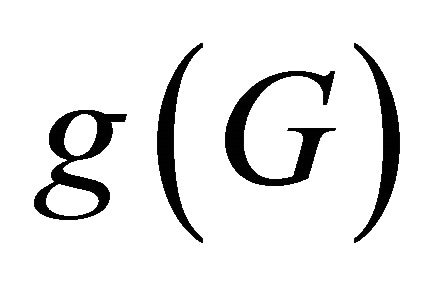 . Suppose A is a atom of G and
. Suppose A is a atom of G and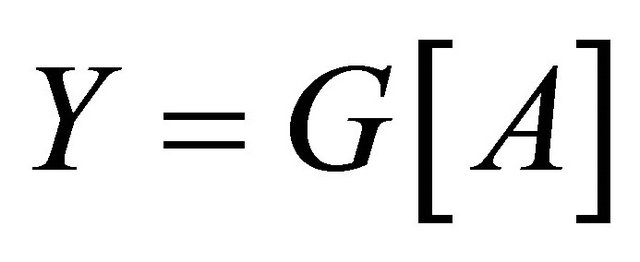 . If G is not
. If G is not 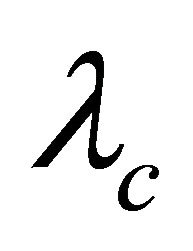 -optimal, then
-optimal, then
(1) 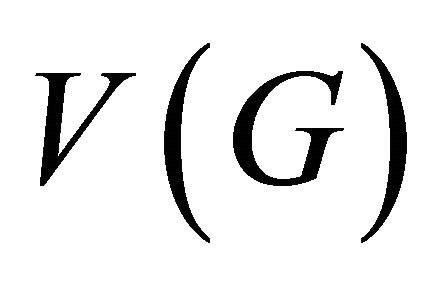 is a disjoint union of distinct atoms;
is a disjoint union of distinct atoms;
(2) Y is a 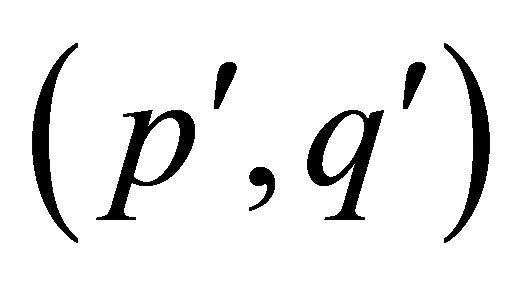 -half vertex transitive graph, where
-half vertex transitive graph, where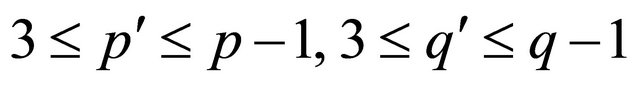 .
.
Proof. Let
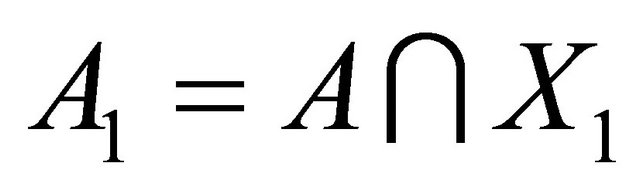 and
and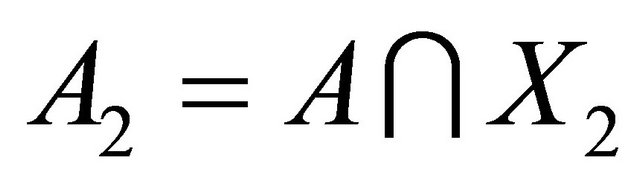 then
then
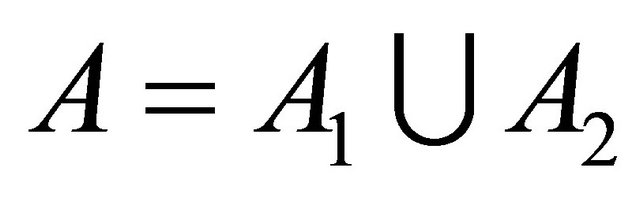 .
.
Since A is a 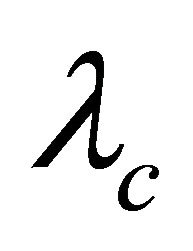 -atom, we have
-atom, we have
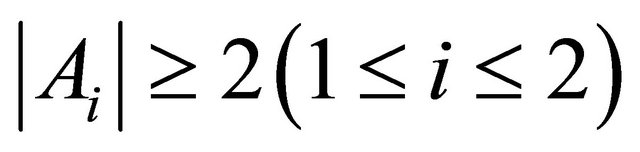 .
.
(1) Since  and Aut(X) acts transitively both on
and Aut(X) acts transitively both on 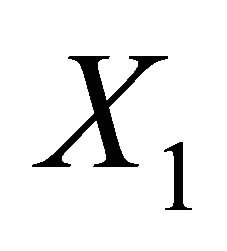 and
and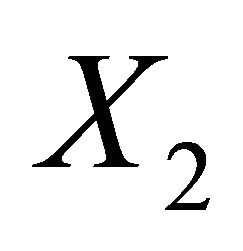 , each vertex of G lies in a
, each vertex of G lies in a 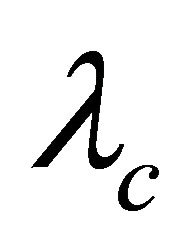 - atom. by Lemma 2.3, we have that
- atom. by Lemma 2.3, we have that 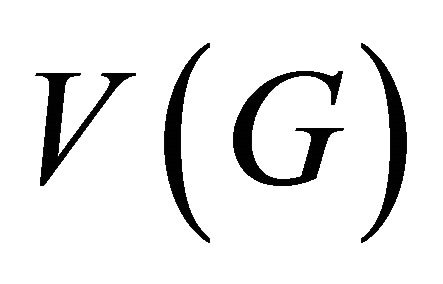 is a disjoint union of distinct
is a disjoint union of distinct 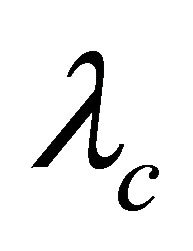 -atoms.
-atoms.
(2) Let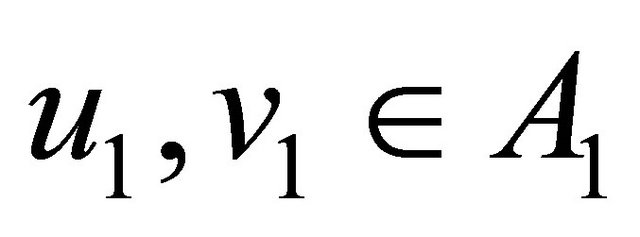 , then there exits an automorphism
, then there exits an automorphism
![]() of G with
of G with 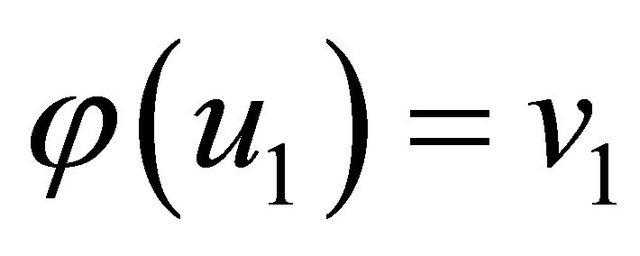 and so
and so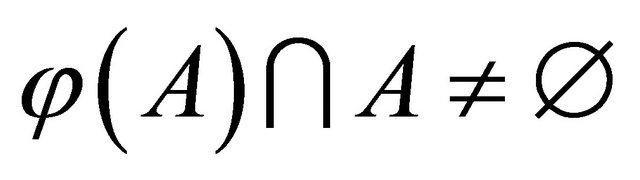 . By Lemma 2.3,
. By Lemma 2.3, . Thus the restriction of
. Thus the restriction of ![]() on A induces an automorphism of Y, and then Aut(Y) acts transitively on
on A induces an automorphism of Y, and then Aut(Y) acts transitively on . Similarly, Aut(Y) acts transitively on
. Similarly, Aut(Y) acts transitively on .
. 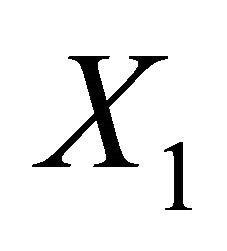 and
and 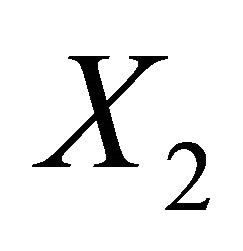 are two orbits of Aut(G). By (1), there exists
are two orbits of Aut(G). By (1), there exists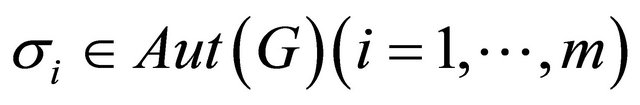 , such that
, such that
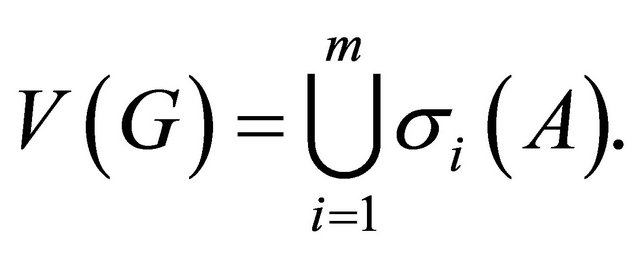
Since Aut(G) has two orbits 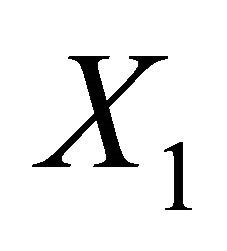 and
and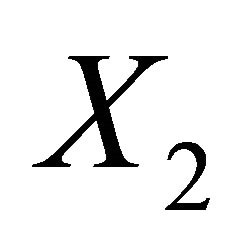 , for any
, for any 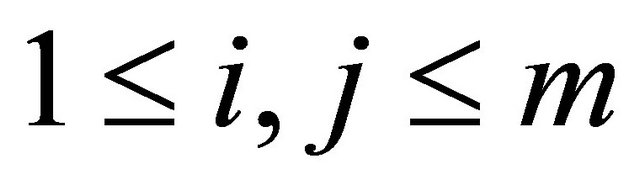 and
and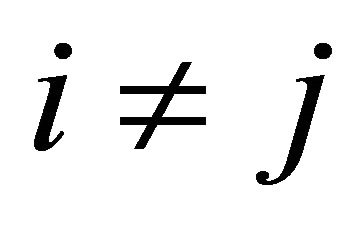 ,
, 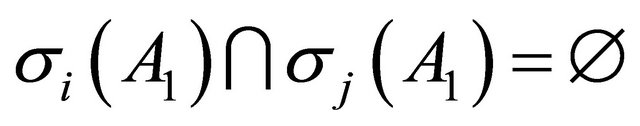 and
and
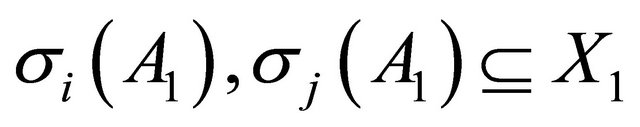 . Thus, we have
. Thus, we have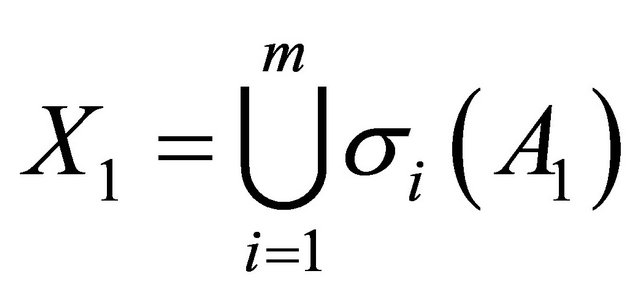 ,
,  , and
, and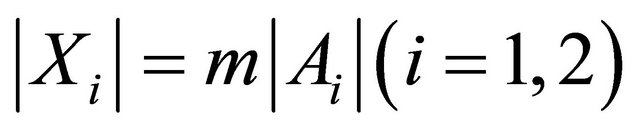 . Thus Y is a
. Thus Y is a
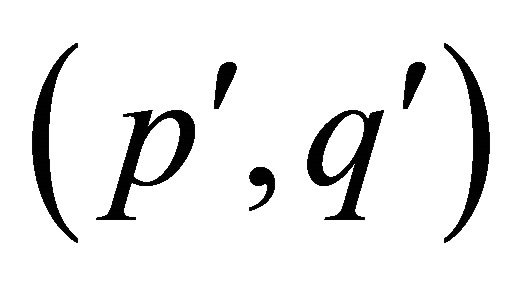 -half vertex transitive graph, where
-half vertex transitive graph, where
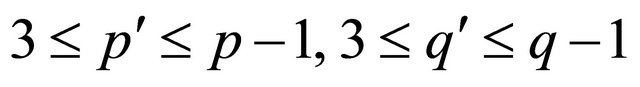 (by Lemma 2.4).
(by Lemma 2.4).
Lemma 2.8 ([17]) A cyclically optimal graph is not super cyclically edge-connected if and only if it has a super atom.
Lemma 2.9 Let G be a connected (p,q)-half vertex transitive graph with bipartition 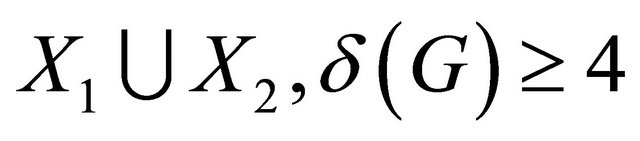 and girth
and girth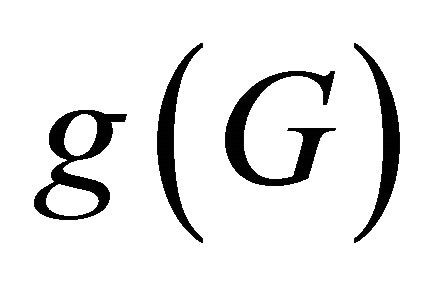 . Suppose A is a super atom of G and
. Suppose A is a super atom of G and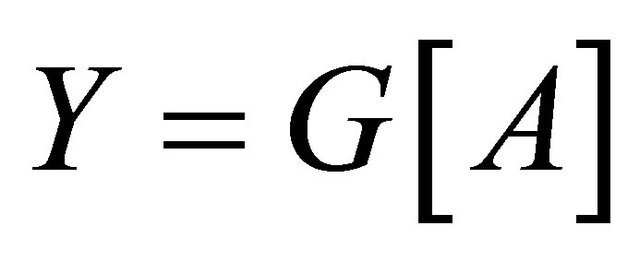 . If G is
. If G is 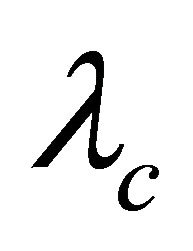 -optimal but not super-
-optimal but not super-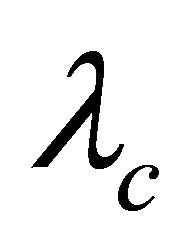 , then
, then
(1) 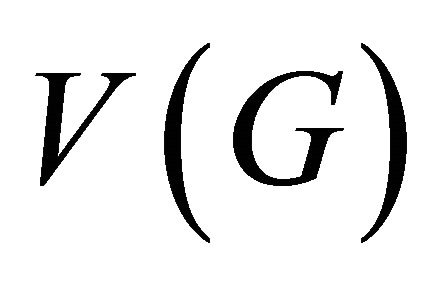 is a disjoint union of distinct super atoms;
is a disjoint union of distinct super atoms;
(2) Y is a 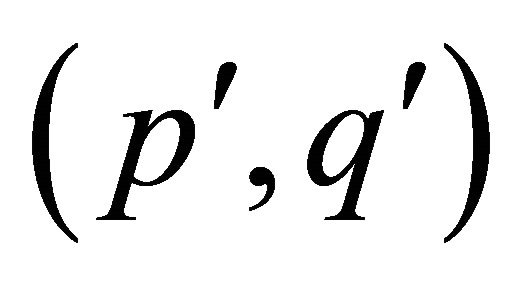 -half vertex transitive graph, where
-half vertex transitive graph, where 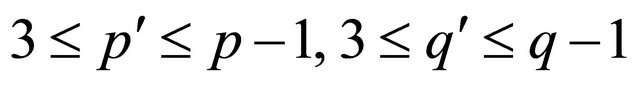
With a similar argument as the proof of Lemma 2.7, we can prove it.
3. Super-λc Half Vertex Transitive Graphs
Theorem 3.1 Let G be a connected (p,q)-half vertex transitive graph with bipartition ,
,  and girth
and girth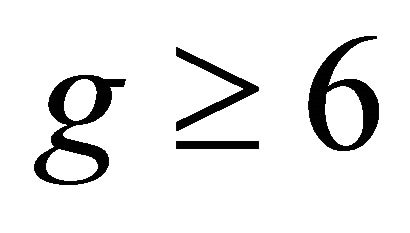 , then G is
, then G is 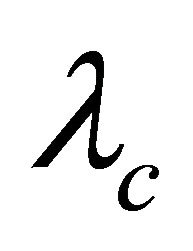 -optimal.
-optimal.
Proof. By Lemma 2.1, G is cyclically separable. Suppose G is not 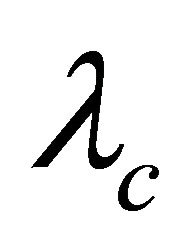 -optimal. By Lemma 2.2, every atom is impimitive block. Let A be a atom of G, by Lemma 2.3,
-optimal. By Lemma 2.2, every atom is impimitive block. Let A be a atom of G, by Lemma 2.3, 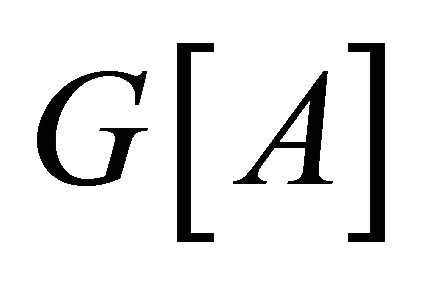 is half-vertex transitive. Let
is half-vertex transitive. Let
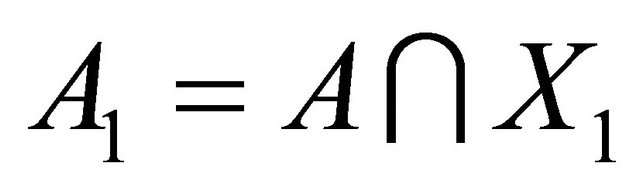 and
and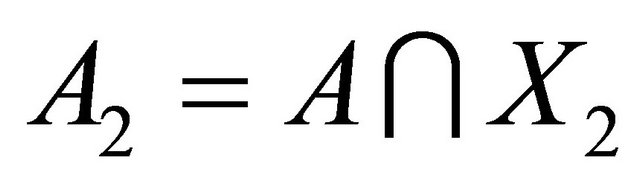 , then
, then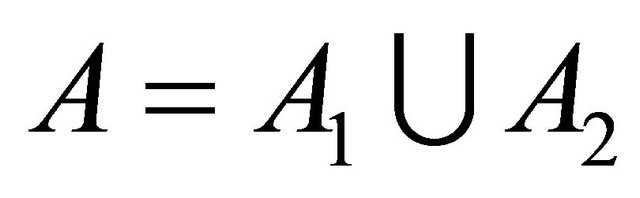 .
.
Suppose  is
is 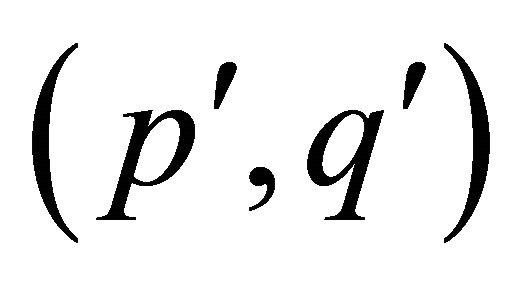 by Lemma 2.4 (2),
by Lemma 2.4 (2),
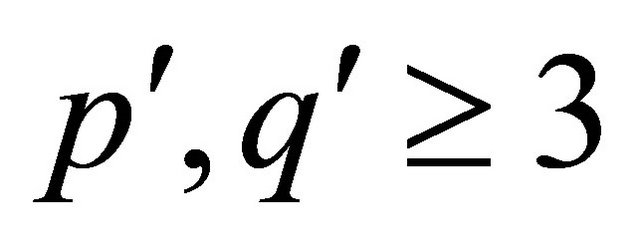 . Let C be a shortest cycle of
. Let C be a shortest cycle of . Then by Lemma 2.4 (2) and Lemma 2.5,
. Then by Lemma 2.4 (2) and Lemma 2.5, 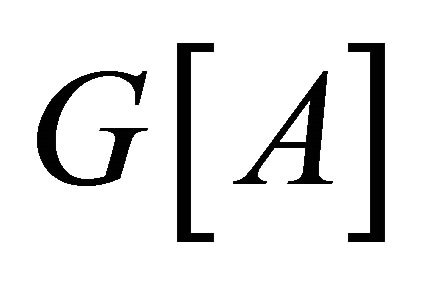 contains two disjoint cycles, and
contains two disjoint cycles, and 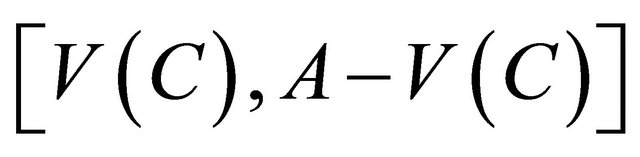 is s cyclic edgecut. Clearly,
is s cyclic edgecut. Clearly, 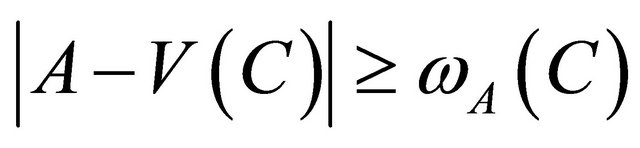 since no two vertices of C have common neighbor in
since no two vertices of C have common neighbor in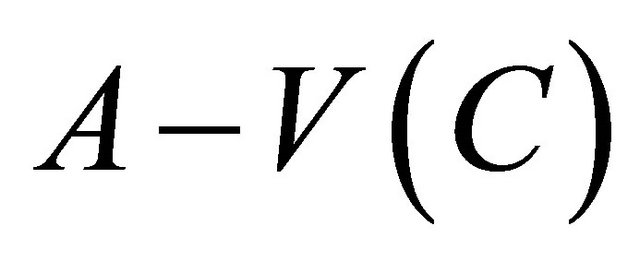 . Then,
. Then,
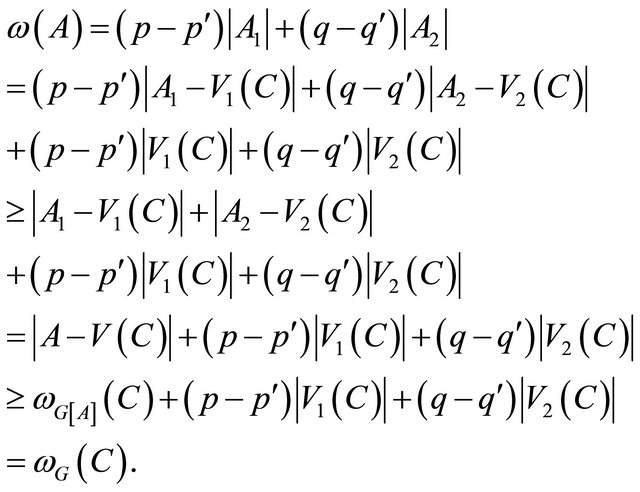
a contradiction.
Theorem 3.2 Let G be a connected 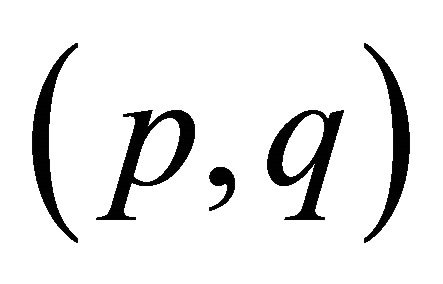 -half vertex transitive graph with bipartition
-half vertex transitive graph with bipartition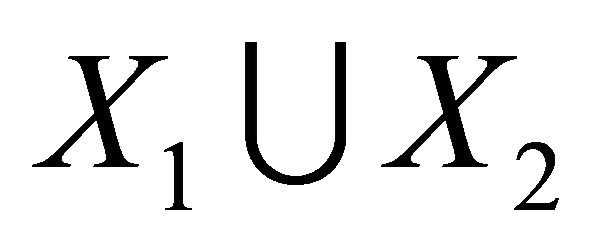 ,
, 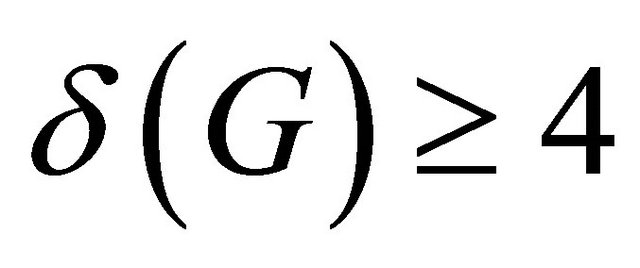 and girth
and girth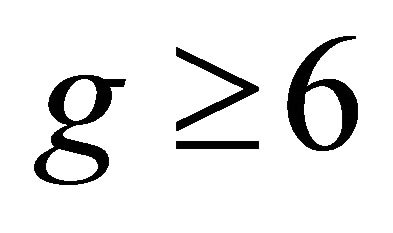 , then G is super-
, then G is super-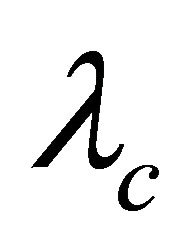 .
.
Proof. By Theorem 3.1, G is 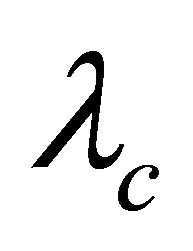 -optimal. Suppose G is not super-
-optimal. Suppose G is not super-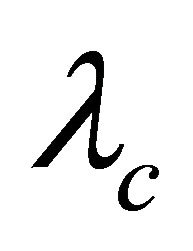 . By Lemma 2.8, G has a super atom. By Lemma 2.9, every super atom is impimitive block. Let A be a super atom of G, by Lemma 2.3,
. By Lemma 2.8, G has a super atom. By Lemma 2.9, every super atom is impimitive block. Let A be a super atom of G, by Lemma 2.3,  is halfvertex transitive. Let
is halfvertex transitive. Let 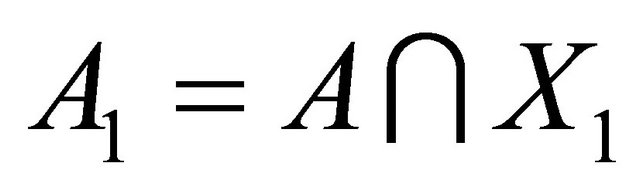 and
and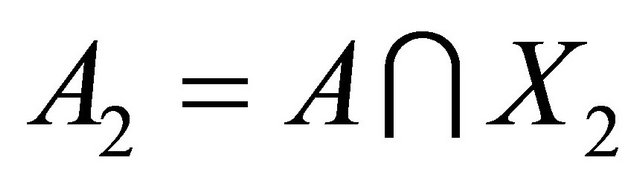 then
then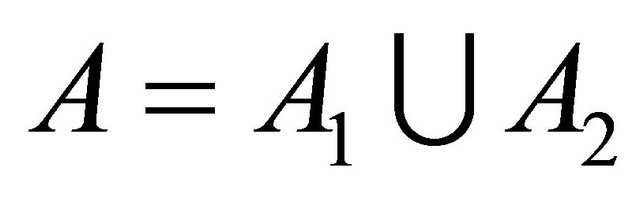 . Suppose
. Suppose 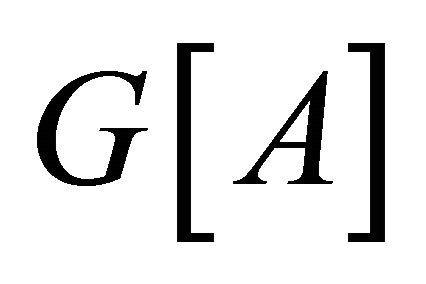 is
is 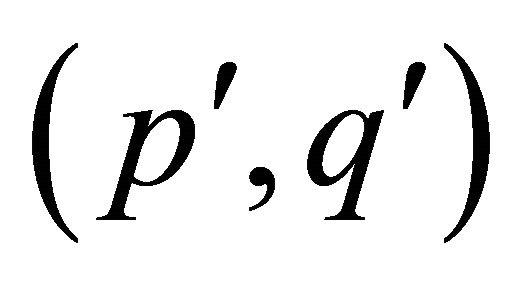 by Lemma 2.4 (2),
by Lemma 2.4 (2),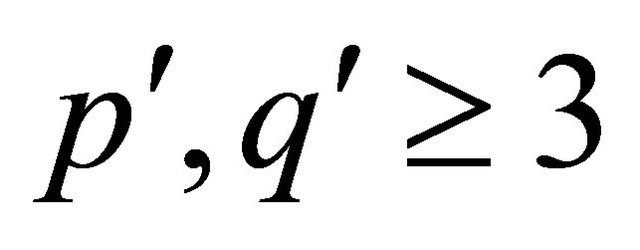 . Let C be a shortest cycle of
. Let C be a shortest cycle of . With a similar proof as Theorem 3.1, we can get
. With a similar proof as Theorem 3.1, we can get
 , a contradiction.
, a contradiction.
4. Acknowledgements
We would like to appreciate the anonymous referees for the valuable suggestions which help us a lot in refining the presentation of this paper.
REFERENCES
- S. Latifi, M. Hegde and M. Naraghi-Pour, “Conditional Connectivity Measures for Large Multiprocessor Systems,” IEEE Transactions on Compututers, Vol. 43, No. 2, 1994, pp. 218-222. doi:10.1109/12.262126
- L. Lovász, “On Graphs Not Containing Independent Circuits,” Matematikai Lapok, Vol. 16, No. 3, 1965, pp. 289- 299.
- B. Bollobás, “Extremal Graph Theory,” Academic Press, London, 1978.
- M. D. Plummer, “On the Cyclic Connectivity of Planar Graphs,” Lecture Notes in Mathematics, Vol. 303, No. 1, 1972, pp. 235-242. doi:10.1007/BFb0067376
- P. G. Tait, “Remarks on the Colouring of Maps,” Proceedings of the Royal Society of Edinburgh, Vol. 10, No. 4, 1880, pp. 501-503.
- E. Máčajová and M. Šoviera, “Infinitely Many Hypohamiltonian Cubic Graphs of Girth 7,” Graphs and Combinatorics, Vol. 27, No. 2, 2011, pp. 231-241. doi:10.1007/s00373-010-0968-z
- F. Kardoš and R. Šrekovski, “Cyclic Edge-Cuts in Fullerence Graphs,” Journal of Mathematical Chemistry, Vol. 44, No. 1, 2008, pp. 121-132. doi:10.1007/s10910-007-9296-9
- C. Q. Zhang, “Integer Flows and Cycle Covers of Graphs,” Marcel Dekker, New York, 1997.
- D. A. Holton, D. Lou and M. D. Plummer, “On the 2-Extendability of Planar Graphs,” Discrete Mathematics, Vol. 96, No. 2, 1991, pp. 81-99. doi:10.1016/0012-365X(91)90227-S
- D. Lou and D. A. Holton, “Lower Bound of Cyclic Edge Connectivity for n-Extendability of Regular Graphs,” Discrete Mathematics, Vol. 112, No. 1-3, 1993, pp. 139-150. doi:10.1016/0012-365X(93)90229-M
- B. Wang and Z. Zhang, “On the Cyclic Edge—Connectivity of Transitive Graphs,” Discrete Mathematics, Vol. 309, No. 13, 2009, pp. 4555-4563. doi:10.1016/j.disc.2009.02.019
- M. Y. Xu, J. H. Huang, H. L. Li and S. R. Li , “Introduction to Group Theory,” Academic Publishes, Beijing, 1999.
- J. X. Meng, “Optimally Super-Edge-Connected Transitive Graphs,” Discrete Mathematics, Vol. 206, No. 1-3, 2003, pp. 239-248. doi:10.1016/S0012-365X(02)00675-1
- J. M. Xu, “On Conditional Edge-Connectivity of Graphs,” Acta Mathematica Applicatae Sinica, Vol. 16, No. 4, 2000, pp. 414-419. doi:10.1007/BF02671131
- R. Nedela and M. Šoviera, “Atoms of Cyclic Connectivity in Cublic Graphs,” Mathematica Slovaca, Vol. 45, No. 5, 1995, pp. 481-499.
- J. M. Xu and Q. Liu, “2-Restricted Edge-Connectivity of Vertex-Transitive Graphs,” Australasian Journal of Combinatorics, Vol. 30, No. 1, 2004, pp. 41-49.
- Z. Zhang and B. Wang, “Super Cyclically Edge-Connected Transitive Graphs,” Joumal of Combinatorial Optimization, Vol. 22, No. 4, 2011, pp. 549-562. doi:10.1007/s10878-010-9304-z
- J. X. Zhou and Y. Q. Feng, “Super-Cyclically Edge-Connected Regular Graphs,” Joumal of Combinatorial Optimization, 2012.
- Y. Z. Tian and J. X. Meng, “
 -Optimally Half Vertex Transitive Graphs with Regularity k,” Information Processing Letters, Vol. 109, No. 13, 2009, pp. 683-686. doi:10.1016/j.ipl.2009.03.001
-Optimally Half Vertex Transitive Graphs with Regularity k,” Information Processing Letters, Vol. 109, No. 13, 2009, pp. 683-686. doi:10.1016/j.ipl.2009.03.001 - R. Tindell, “Connectivity of Cayley Graphs,” In: D. Z. Du and D. F. Hsu, Eds., Combinatorial Network Theory, Kluwer, Dordrecht, 1996, pp. 41-64. doi:10.1007/978-1-4757-2491-2_2
NOTES
*This research is supported by NSFC (10671165) and NSFCXJ (2010211A06).
#Corresponding author.

