Applied Mathematics
Vol. 3 No. 11 (2012) , Article ID: 24513 , 10 pages DOI:10.4236/am.2012.311230
A Novel Pseudo Random Number Generator Based on Two Plasmonic Maps
1Group for Automatic Mesh Generation and Advanced Methods, Gamma 3 Project (UTT-INRIA), University of Technology of Troyes, Troyes Cedex, France
2Network & Information Security, Graduate School of Informatic, Electronic, Automatic (ESIEA), Paris, France
Email: thomas.grosges@utt.fr
Received August 29, 2012; revised September 29, 2012; accepted October 7, 2012
Keywords: Plasmonics; Applied Classical Electromagnetism; Pseudo-Random Number Generator; Randomness; Cryptography; Remeshing Process
ABSTRACT
In plasmonic systems, the response of nanoobjects under light illumination can produce complex optical maps. Such plasmonic or resonant systems have interesting characteristics such as sensitivity on parameters and initial conditions. In this paper, we show how these complex maps can be cryptographically improved and associated in order to design a secure pseudo random number generator.
1. Introduction
Pseudo-random number generators (PRNGs) are fundamental blocks in various domains of applications such as Monte Carlo simulation algorithms, communications and many cryptographic systems which depend on the quality of the pseudo random sequences. The generated numbers are mainly used as simple pseudo random sequences, private or secret keys or secret signatures. The development of PRNGs has impassioned the researchers for few decades and since then, many techniques to produce such PRNGs have been studied [1-9]. The robustness of such pseudo random generators is crucial to ensure secure applications in cryptograhy and to avoid all the various and existing attacks. A large family of PRNGs is based on sequences generated by single chaotic system or combination of chaotic maps [4,8,10,11], through a one-way function. Such a combination of several maps by a one-way function improves the security of the PRNG. In this paper, we propose a PRNG based on the use of complex maps produced by the electromagnetic response of plasmonic systems. The study of plasmonic or resonant systems has shown the possibility to produce complex electromagnetic field patterns, with strong gradients and high confinement, superimposed with interference patterns. These local physic effects have opened the experimental and theoretical ways of designing efficient systems in various new applications (sensors, imaging and burning biomedicine applications, security) [12-15]. For cryptographic applications, the main question concerns the ability of such plasmonic systems, due to their high sensitivities to parameters in the neighbouring of the resonances, to serve as the basis of pseudo random number generator with high efficiency.
Therefore, we propose a method to generate long sequences of numbers, with high quality of randomness, based on the complex nature of plasmon simulations. The nanosystems permit to produce complex optical maps and provide inherent tamper-evidence due to their sensitivities to the initial parameters and initial conditions. We show how these complex maps, through a numerical process, can produce sequences that have high level of randomness, in compliance with the classical tests of randomness on binary sequences [16]. This can be used as a base of secret key between two parties in a symmetric cipher (e.g. One-time pad). The high level of security of this inspired-plasmonic system is related to the number of freedom degrees used to generate the pseudo random sequence and the physical complexity of the plasmonic structures. These degrees of freedom can be grouped into two categories of parameters, of completely different origin. The first one (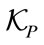 ) can be related to the physical parameters required to model the nanostructures (materials, shapes). From the constructed 3D spatial maps of the electromagnetic field, a second set of parameters (
) can be related to the physical parameters required to model the nanostructures (materials, shapes). From the constructed 3D spatial maps of the electromagnetic field, a second set of parameters (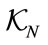 ) can be assigned to a numerical processes consisting in an adaptive remeshing process and a modular transformation. These processes ensure quality targets of a maximum Shannon’s entropy [17] as well as increasing disorder in the sequences. We analyse the randomness quality [16] and the correlation of sets of pseudo random sequences. We show that only weak correlation can be exhibited. This weak correlation between pseudo random sequences is an essential condition to be fulfilled for more secure uses.
) can be assigned to a numerical processes consisting in an adaptive remeshing process and a modular transformation. These processes ensure quality targets of a maximum Shannon’s entropy [17] as well as increasing disorder in the sequences. We analyse the randomness quality [16] and the correlation of sets of pseudo random sequences. We show that only weak correlation can be exhibited. This weak correlation between pseudo random sequences is an essential condition to be fulfilled for more secure uses.
This paper is structured as follows. The description of the method as well as the plasmonic functions analysis are given in Section 2. Section 3 presents results for constructed pseudo random sequences and statistical analysis applied on the sets of generated pseudo random sequences. The security analysis of the PRNG is also discussed, before concluding in Section 4.
2. The Proposed Cryptosystem
The core of the PRNG algorithm is based on the contruction of two plasmonic maps obtained by computing the electromagnetic field interacting with metallic nanoparticles.
2.1. Nanoworld as Source of Complex Maps
The process of production of pseudo random sequences we propose, is based on a model of plasmonic resonance [14,18]. The interest here is the interaction of the coupling of light-matter at a nanometric scale which is kwown to induce strong gradient of the field and complex interference patterns. The resonance of the interaction between light and matter is very sensitive to all physical parameters: size of the nanoobjects, materials and illumination characteristics. The numerical simulated signals on which we work is the total electromagnetic field in the vicinity of such metallic nanostructures. It comes from the numerical resolution of the vectorial Helmholtz’ equation governing the electric field vector and the Maxwell’s equations relating both electric and magnetic field vectors E and H satisfying:
 (1)
(1)
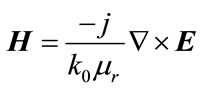 (2)
(2)
with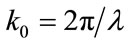 ,
, 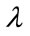 the wavelength in vacuum,
the wavelength in vacuum,  and
and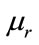 , the relative permittivities and permeabilities, respectively. The electric and magnetic fields E and H satisfy the orthogonality condition
, the relative permittivities and permeabilities, respectively. The electric and magnetic fields E and H satisfy the orthogonality condition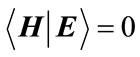 . The resolution of such a system of equations can be achieved numerically in a 3D spatial domain
. The resolution of such a system of equations can be achieved numerically in a 3D spatial domain  and the physical electromagnetic fields
and the physical electromagnetic fields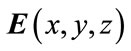 ,
,  and their associated intensities
and their associated intensities
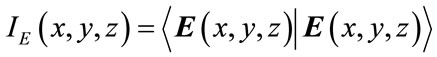 and
and
 are computed. The characteristics of the 3D spatial maps are intrinsically dependent on a large number of parameters which relates to the entire physical system. It is moreover why, the exact reproducibility of this map is almost impossible for an attacker without additional information about the used physical and meshing parameters
are computed. The characteristics of the 3D spatial maps are intrinsically dependent on a large number of parameters which relates to the entire physical system. It is moreover why, the exact reproducibility of this map is almost impossible for an attacker without additional information about the used physical and meshing parameters  and
and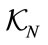 . The physical parameters can be grouped as a key set
. The physical parameters can be grouped as a key set 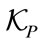 containing:
containing:
1) Optical parameters: the wavelength of the light source 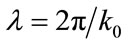 in
in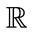 , the incident angle of illumination
, the incident angle of illumination  in
in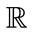 , the choice of material permitivitties
, the choice of material permitivitties 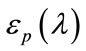 in
in  and
and 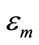 in
in  for the surrounding medium;
for the surrounding medium;
2) Geometrical parameters: the radii of the nanospheres { in
in  }, the number of nano-sphere
}, the number of nano-sphere 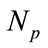 in
in  and their spatial coordinates
and their spatial coordinates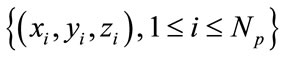 , in
, in .
.
The theoretical dimension of the space of the physical parameters 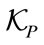 is
is . At this stagethe complex spatial fields
. At this stagethe complex spatial fields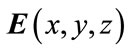 ,
, 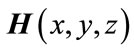 and their associated intensities
and their associated intensities 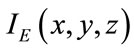 and
and 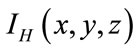 necessitate a specific numerical process in order to transform these maps to an efficient pseudo random sequence
necessitate a specific numerical process in order to transform these maps to an efficient pseudo random sequence . The aim is to obtain a sequence
. The aim is to obtain a sequence  with a high level of randomness and which satisfy the basic cryptographic properties.
with a high level of randomness and which satisfy the basic cryptographic properties.
2.2. Construction of the Generator
The “physical” 3D maps ,
,  ,
, 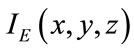 and
and 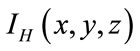 cannot be directly used as pseudo random sequences or secret keys in an encryption scheme, because the distribution of the spatial intensities is not random enough relatively to the requirements of a random sequence. Therefore a renumbering of the spatial nodes is necessary to be able to create more disorder in these intensity maps, which will give us a stronger derived sequence
cannot be directly used as pseudo random sequences or secret keys in an encryption scheme, because the distribution of the spatial intensities is not random enough relatively to the requirements of a random sequence. Therefore a renumbering of the spatial nodes is necessary to be able to create more disorder in these intensity maps, which will give us a stronger derived sequence . A two-steps numerical process is achieved on the field and intensity maps in order to satisfy both criterion of maximum entropy and randomness statistical characteristics.
. A two-steps numerical process is achieved on the field and intensity maps in order to satisfy both criterion of maximum entropy and randomness statistical characteristics.
The first step consists in an homogenization of occurrence of fields and intensities through the redistribution of intensity level by a 3D adaptive meshing process [19] with an a posteriori error estimator based on the maximum entropy. This adaptive scheme of remeshing of the domain 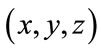 uses selected frequencies of each intensity levels occurrence as target. For this goal, second order polynomials are used to interpolate intensity levels, to generate additional points in the tomography map (or equally to suppress the nodes corresponding to too numerous intensity levels). Each point of the domain
uses selected frequencies of each intensity levels occurrence as target. For this goal, second order polynomials are used to interpolate intensity levels, to generate additional points in the tomography map (or equally to suppress the nodes corresponding to too numerous intensity levels). Each point of the domain  is labeled by an integer
is labeled by an integer 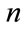 (the node number) and the intensity levels of the maps
(the node number) and the intensity levels of the maps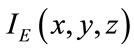 ,
,
 are translated to
are translated to ,
, 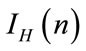 before transformed into the maps
before transformed into the maps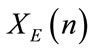 ,
, 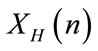 in the basis
in the basis . In this new basis
. In this new basis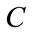 , the maps are given by:
, the maps are given by:
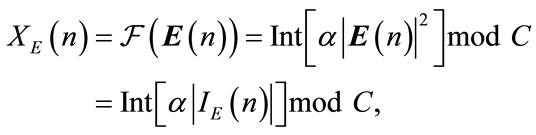 (3)
(3)
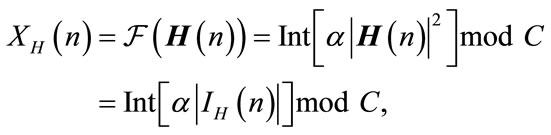 (4)
(4)
with 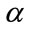 and
and  fixed integers (e.g.
fixed integers (e.g. 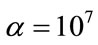 and
and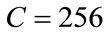 ). This transformation of the maps
). This transformation of the maps 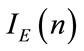 to
to 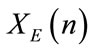 (resp.
(resp. 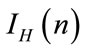 to
to ) drastically affects the internal structure of the sequence. These two maps
) drastically affects the internal structure of the sequence. These two maps 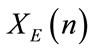 and
and  produce directly random-like images (i.e. images that seem to be random in appearence but not necessarely satisfying cryptographical randomness requirements). That comes from the physics structure of the fields E and H and the remeshing process which were not intended to randomize the initial maps by only to control the occurencies of the intensity levels in respect to the entropy criteria. This part of the space of parameters consists in a set of numerical parameters
produce directly random-like images (i.e. images that seem to be random in appearence but not necessarely satisfying cryptographical randomness requirements). That comes from the physics structure of the fields E and H and the remeshing process which were not intended to randomize the initial maps by only to control the occurencies of the intensity levels in respect to the entropy criteria. This part of the space of parameters consists in a set of numerical parameters  associated to the remeshing process and are summary by:
associated to the remeshing process and are summary by:
the adaptive remeshing process parameters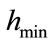 ,
, 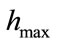 ,
, 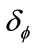 in
in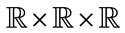 , the minimum, the maximum distance between nodes after remeshing and the maximum tolerance between the levels of signal at two adjacent nodes, respectively. The number of nodes after computation is
, the minimum, the maximum distance between nodes after remeshing and the maximum tolerance between the levels of signal at two adjacent nodes, respectively. The number of nodes after computation is  in
in  and their spatial coordinates
and their spatial coordinates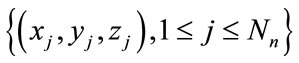 , in
, in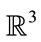 .
.
With such numerical parameters, the dimension of the space  is
is .
.
The second step consists in applying a xor operator by matching 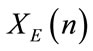 and
and  in order to produce a new map
in order to produce a new map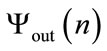 . This matching benefits from the differences between
. This matching benefits from the differences between  and
and  (i.e.
(i.e. 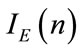 exhibits strong variations whenever
exhibits strong variations whenever 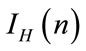 is smother) and coming from the orthogonality between the symmetric and antisymmetric parts of the electromagnetic tensor, respectively. This map is given by:
is smother) and coming from the orthogonality between the symmetric and antisymmetric parts of the electromagnetic tensor, respectively. This map is given by:
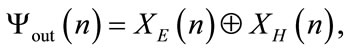 (5)
(5)
Such a produced numerical pseudo random sequence 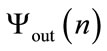 is therefore deduced from the plasmonic process. The complexity of the plasmonic simulated optical signal of nano-objects and the various parameters used are the assets of this cryptosystem and the global set of parameters
is therefore deduced from the plasmonic process. The complexity of the plasmonic simulated optical signal of nano-objects and the various parameters used are the assets of this cryptosystem and the global set of parameters  of dimension
of dimension
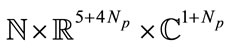 .
.
In principle the physical parameters used seem to take an infinity of values (i.e. ,
,  or
or , even non existing materials can be used in the model). With all this parameters package, the exact reproducibility of the sequence
, even non existing materials can be used in the model). With all this parameters package, the exact reproducibility of the sequence 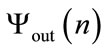 is almost impossible if the exact parameters used are unknown. Indeed, in the vicinity of the plasmon resonance, an error on one of the used parameters can produce enough variations in the produced image map (in term of the exact value of the pixels in the formed image). Due to the high internal complexity and without a robust reverse engineering method, this construction process is now a good candidate for a PRNG permitting to produce a long pseudo random sequence.
is almost impossible if the exact parameters used are unknown. Indeed, in the vicinity of the plasmon resonance, an error on one of the used parameters can produce enough variations in the produced image map (in term of the exact value of the pixels in the formed image). Due to the high internal complexity and without a robust reverse engineering method, this construction process is now a good candidate for a PRNG permitting to produce a long pseudo random sequence.
A fundamental advantage of any kind of PRNG is the quality of pseudo random sequences. According to the Kerckhoffs’ principle [20], the security of a cryptosystem only depends on its keys. In any cryptosystem, a poor key or a limited key space 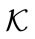 induces a weakness of the cryptosystem (i.e. which can be easily broken by testing all possibilities: brute-force attacks). Indeed, the limit of brute-force attacks on the parameter space depends on the entropy of this space. For a given today’s computer speed-up, it is commonly admise that a key space (space of parameters) of size
induces a weakness of the cryptosystem (i.e. which can be easily broken by testing all possibilities: brute-force attacks). Indeed, the limit of brute-force attacks on the parameter space depends on the entropy of this space. For a given today’s computer speed-up, it is commonly admise that a key space (space of parameters) of size 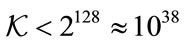 (i.e. smaller than 128 bits) is not sufficiently secure [21]. In the present case, the generated key space
(i.e. smaller than 128 bits) is not sufficiently secure [21]. In the present case, the generated key space  permits to overpass the lower limit of 128 bits of entropy. Each key is corresponding to two kinds of input data related to numerical or physical characteristics.
permits to overpass the lower limit of 128 bits of entropy. Each key is corresponding to two kinds of input data related to numerical or physical characteristics.
3. Results and Discussion
In this section, the results on the produced pseudo random sequences are presented. Moreover, the analysis methods based on the randomness and correlation properties are discussed and applied to the generated sequences.
3.1. Generation of a Subspace of Pseudo Random Sequences
A subspace of pseudo random sequences is produced before analysing. These sequences are obtained from the simulation of a plasmonic device and the numerical remeshing process in the construction of the pseudo random sequence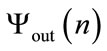 . This analysis puts forward the quality of the outputs produced following a change of consecutive parameters. We consider the electromagnetic images of the interaction of light with gold nano-particles of radius
. This analysis puts forward the quality of the outputs produced following a change of consecutive parameters. We consider the electromagnetic images of the interaction of light with gold nano-particles of radius  in [5.0; 210.0] nm embeded in a surrounding medium of permittivity
in [5.0; 210.0] nm embeded in a surrounding medium of permittivity 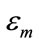 in [0.999; 2.500] under light illumination wavelength
in [0.999; 2.500] under light illumination wavelength  in [480; 1200] nm and incident angle
in [480; 1200] nm and incident angle 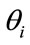 in
in . The number of considered nano-particles is
. The number of considered nano-particles is 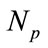 in
in 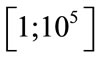 (which can be compared to experimental structures). With the selected parameters of the remeshing process,
(which can be compared to experimental structures). With the selected parameters of the remeshing process, 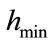 in [0.1; 1.0] nm,
in [0.1; 1.0] nm, 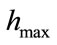 in [2.0; 20.0] nm and
in [2.0; 20.0] nm and 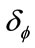 in [0.001; 0.100]the number of computing nodes
in [0.001; 0.100]the number of computing nodes 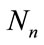 in
in  and the spatial positions of nodes
and the spatial positions of nodes 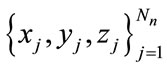 are adapted in order to satisfy the maximum error
are adapted in order to satisfy the maximum error 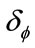 in the whole computational domain
in the whole computational domain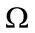 .
.
To illustrate, we consider gold nano-particle of radius  in {10.0, 11.0, 12.0, 13.0} nm embeded in sourrounding medium of permittivity
in {10.0, 11.0, 12.0, 13.0} nm embeded in sourrounding medium of permittivity 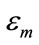 in {0.999, 1.000, 1.001 } illuminated at wavelength
in {0.999, 1.000, 1.001 } illuminated at wavelength  in {500, 501, 502, 503} nm. The gold permitivitty is
in {500, 501, 502, 503} nm. The gold permitivitty is 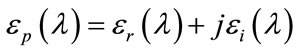 and different values are considered:
and different values are considered: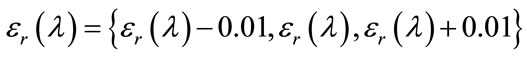 and
and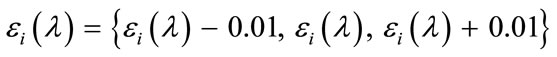 . With such physical parameters and the remeshing parameters
. With such physical parameters and the remeshing parameters ,
, 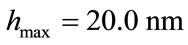 and
and , the total number of nodes is
, the total number of nodes is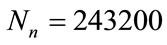 , producing sequences
, producing sequences  of 1,945,600 bits. Therefore, the total number of generated sequences is
of 1,945,600 bits. Therefore, the total number of generated sequences is 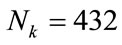 (corresponding to 4 values of
(corresponding to 4 values of , 4 values of
, 4 values of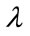 , 3 values of
, 3 values of ,
, 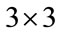 values for both real and imaginary parts of
values for both real and imaginary parts of ). Each sequence has a size of 1,945,600 bits. The produced maps
). Each sequence has a size of 1,945,600 bits. The produced maps ,
, 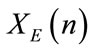 (resp.
(resp. ,
, ) and
) and , can be viewed as vectors made up of all the numbers of nodes ranked in a precise order. Moreover, the elements of these vectors can be viewed on a 2D map (i.e. the corresponding images in gray levels of the generated maps, see Figure 1). Figure 1 shows an example of the corresponding 2D images of the maps
, can be viewed as vectors made up of all the numbers of nodes ranked in a precise order. Moreover, the elements of these vectors can be viewed on a 2D map (i.e. the corresponding images in gray levels of the generated maps, see Figure 1). Figure 1 shows an example of the corresponding 2D images of the maps ,
, 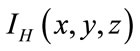 ,
,  ,
, 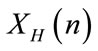 and the pseudo random sequence
and the pseudo random sequence . The Figures 1(a) and (b) let appear low structures and have low Shannon’s entropy. This mainly comes from the fact that there are many missing levels of intensities. We also remark the non regularity in the occurency of the zero-bit value (0) relatively to one-bit value (1) in the corresponding binary sequence of this image (62.51% against 37.49% for the image of Figure 1(a)). The output sequence
. The Figures 1(a) and (b) let appear low structures and have low Shannon’s entropy. This mainly comes from the fact that there are many missing levels of intensities. We also remark the non regularity in the occurency of the zero-bit value (0) relatively to one-bit value (1) in the corresponding binary sequence of this image (62.51% against 37.49% for the image of Figure 1(a)). The output sequence , obtained after a xor operation between
, obtained after a xor operation between 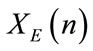 and
and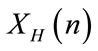 , presents the characteristics of randomnes (see Figure 1(e)) and pass all the NIST tests successfully (see Section 3.2.1).
, presents the characteristics of randomnes (see Figure 1(e)) and pass all the NIST tests successfully (see Section 3.2.1).
3.2. Statistical Analysis
In order to analyse the qualities of the produced pseudo random sequences, two approaches are developped and used. These qualities are investigated following both aspects: randomness properties of the individual sequences and correlation between multiple sequences.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e)
Figure 1. The corresponding 2D images, in gray levels, of the maps (a)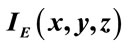 , (b)
, (b) , (c)
, (c)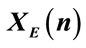 , (d)
, (d)  obtained after renumbering, homogenization and projection in basis C. The map (e)
obtained after renumbering, homogenization and projection in basis C. The map (e)  is obtained from the xor operator between
is obtained from the xor operator between 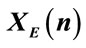 and
and . The total size of each image is 243,200 pixels (
. The total size of each image is 243,200 pixels ( ), each pixel being expanded on 8 bytes (256 levels).
), each pixel being expanded on 8 bytes (256 levels).
3.2.1. Randomness Analysis
The goal of this approach is to evaluate the randomness level of the sequences  produced by the algorithm. The sequences are evaluated through statistical tests suite NIST (National Institute of Standards and Technology of the US Government). The NIST statistical test battery have been chosen for the following reasons. Firstly, it contains many famous tests from the Diehard battery with some extra tests. Secondly, it was used in the AES evaluation process to check the randomness of the output sequences of each candidate algorithm. Moreover, the NIST tests have also shown their ability to ckeck pseudo random number generators in smart cards [22]. This NIST suite consists in a statistical package of fifteen tests developped to quantify and to evaluate the randomness of (arbitrarily long) binary sequences produced by either hardware or sotware based cryptographic random or pseudo random number generators [16]. For each statistical test, a set of
produced by the algorithm. The sequences are evaluated through statistical tests suite NIST (National Institute of Standards and Technology of the US Government). The NIST statistical test battery have been chosen for the following reasons. Firstly, it contains many famous tests from the Diehard battery with some extra tests. Secondly, it was used in the AES evaluation process to check the randomness of the output sequences of each candidate algorithm. Moreover, the NIST tests have also shown their ability to ckeck pseudo random number generators in smart cards [22]. This NIST suite consists in a statistical package of fifteen tests developped to quantify and to evaluate the randomness of (arbitrarily long) binary sequences produced by either hardware or sotware based cryptographic random or pseudo random number generators [16]. For each statistical test, a set of 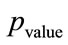 is produced and is compared to a fixed significance level
is produced and is compared to a fixed significance level 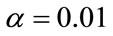 (i.e. only
(i.e. only 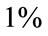 of the sequences are expected to fail). Therefore, a sequence passes a statistical test for
of the sequences are expected to fail). Therefore, a sequence passes a statistical test for 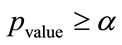 and fails otherwise. In case of testing multiple sequences at the same time, each test define a proportion
and fails otherwise. In case of testing multiple sequences at the same time, each test define a proportion 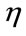 as the ratio of sequences passing succesfully the test relatively to the total number of sequences
as the ratio of sequences passing succesfully the test relatively to the total number of sequences 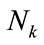 (i.e.
(i.e. ). This proportion
). This proportion  is compared to an acceptable proportion
is compared to an acceptable proportion 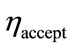 which corresponds to the ratio of sequences which should pass the test [16]. These NIST tests are achieved on the two following kind of sequences: individual sequences and the concatened sequence.
which corresponds to the ratio of sequences which should pass the test [16]. These NIST tests are achieved on the two following kind of sequences: individual sequences and the concatened sequence.
1) Individual sequences: The randomness level of each sequence belonging to a subset of sequences is analysed directly by NIST tests. The 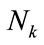 sequences
sequences 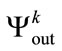 of binary size M (with
of binary size M (with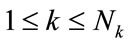 ) are individually tested and the results are given as ratio of success
) are individually tested and the results are given as ratio of success 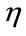 compared to a fixed threshold. The provided information is the randomness of each sequence.
compared to a fixed threshold. The provided information is the randomness of each sequence.
2) Concatened sequence: A new sequence is constructed by concatening all the individual sequences:
 of binary size
of binary size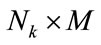 . The randomness quality of this new sequence is also analysed directly by the NIST tests. The provided information is the randomness of the concatened sequence and especially the binary correlation between the produced sequences.
. The randomness quality of this new sequence is also analysed directly by the NIST tests. The provided information is the randomness of the concatened sequence and especially the binary correlation between the produced sequences.
The results obtained on the 432 sequences are given in Table 1. We notice that the results of the tests are satisfactory for the whole set of tested outputs. The sequences pass successfully the NIST tests for individual sequences and for the constructed concatened sequence. These results show the quality of the produced sequences with the PRNG.
3.2.2. Correlation Analysis
In this second approach the purpose is to check the correlation between the produced pseudo random sequences. Compared to the previous approach (Approach 1.2), the correlation between sequences are analysed globally by computing the correlation coefficients of each pair of sequences [23]. Let the two sequences 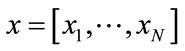 and
and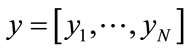 , we have:
, we have:
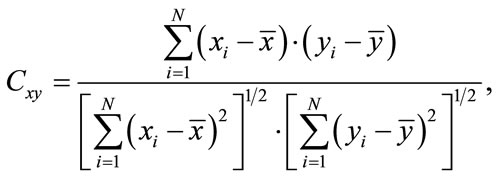 (6)
(6)
where 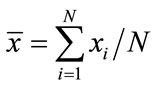 and
and 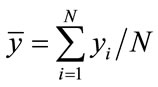 are the mean values of
are the mean values of  and
and , respectively. A strong correlation occurs between two sequences for
, respectively. A strong correlation occurs between two sequences for  and no
and no
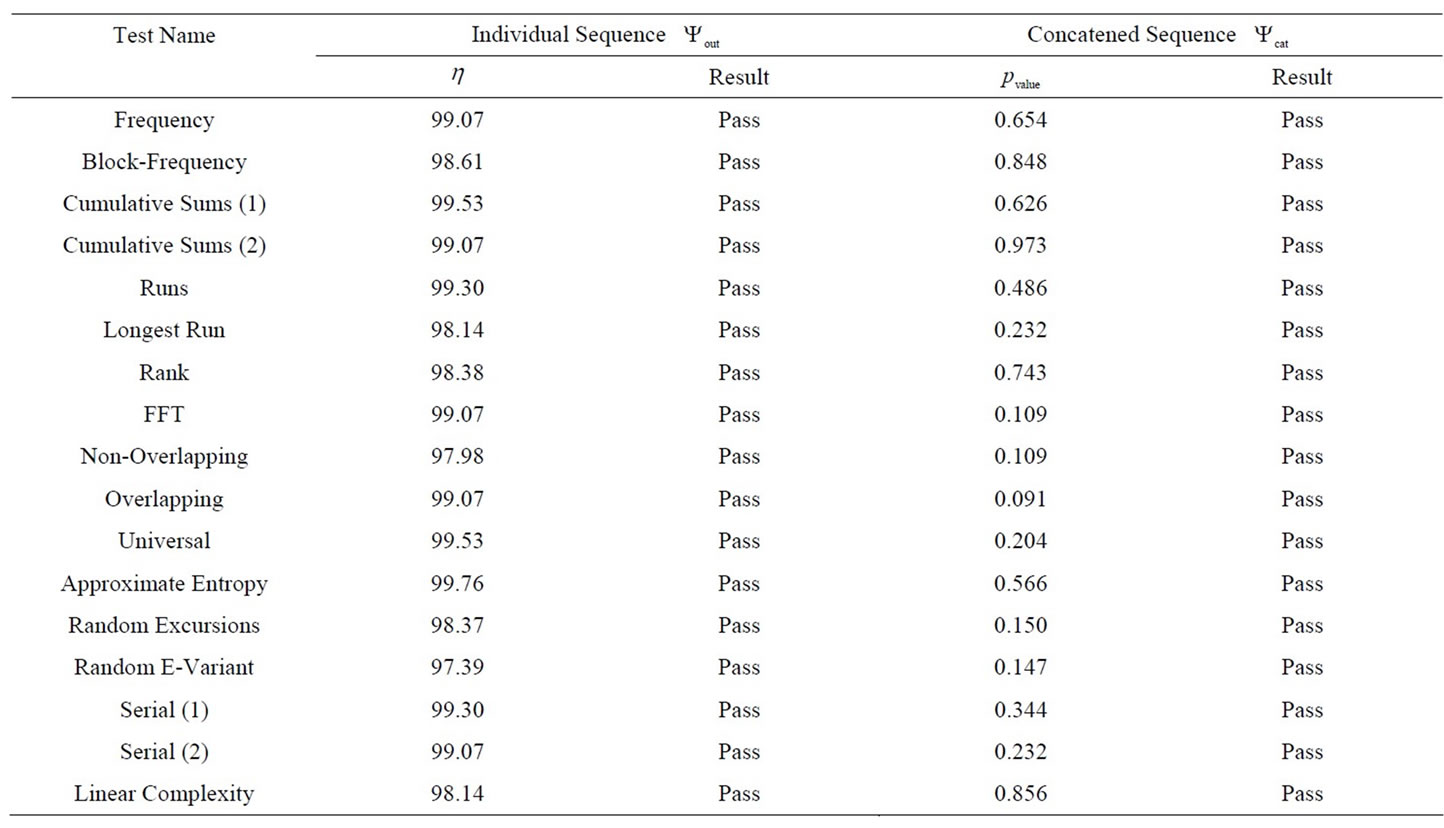
Table 1. Results of the NIST tests using Approach 1 on the 432 generated individual sequences and on the concatened sequence. The ratio  of
of  concerns the individual sequences while the
concerns the individual sequences while the 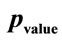 concerns the concatened sequence.
concerns the concatened sequence.
correlation corresponds to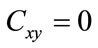 . The coefficients
. The coefficients 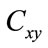 are computed for each pair of sequences and the distribution of their values is presented by a histogram. Therefore the coefficients of correlation between each pair of the 432 generated sequences are computed and the distribution of these coefficients
are computed for each pair of sequences and the distribution of their values is presented by a histogram. Therefore the coefficients of correlation between each pair of the 432 generated sequences are computed and the distribution of these coefficients 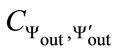 is presented in Figure 2.
is presented in Figure 2.
The result exhibits a very weak correlation between the sequences and 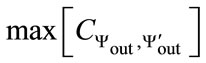 in [–0.008; 0.008].
in [–0.008; 0.008].
This confirms the decorrelation and the randomness quality of the tested individual sequences. Finally, we show, on Figure 2(b), the distribution of occurencies of the 0-bit for each produced pseudo random sequence. This distribution is uniform around the value 0.50. Each sequence 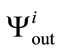 (
(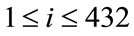 ) can be now viewed as a pseudo random octal sequence. The outputs of PRNG must have both strong quality of randomness and strong independence between these outputs. The results of the analysis, obtained with the two approaches, show the randomness level of the pseudo random sequences and the quasi independence that may exist between a group of produced pseudo random sequences.
) can be now viewed as a pseudo random octal sequence. The outputs of PRNG must have both strong quality of randomness and strong independence between these outputs. The results of the analysis, obtained with the two approaches, show the randomness level of the pseudo random sequences and the quasi independence that may exist between a group of produced pseudo random sequences.
 (a)
(a) (b)
(b)
Figure 2. (a) Histogram of distribution of the correlation coefficients 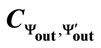 on the interval
on the interval ; (b) Distribution of the 0-bit in the generated pseudo random sequences
; (b) Distribution of the 0-bit in the generated pseudo random sequences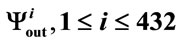 .
.
3.3. Security Analysis
The security analysis of any PRNG should also be evaluated against attacks as well as its application domain. Therefore, the analysis must take into account all the critical points of the cryptosystem and must meet cryptographic requirements [24]. In the present case, the investigated points are: the size of the key space, the key sensitivity, the randomness quality of the ouputs. These points are investigated through the two following attacks: Heuristic Guess-and-Determine Attack [25], Distinguishing Attack [26].
3.3.1. Key Space
A good generator of (pseudo) random sequences should have a large key space in order to make brute-force attacks infeasible. It is generally accepted that a key space of size smaller than 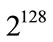 is not secure enough [21]. The theoretical size of the key space given in the (Section 2) is
is not secure enough [21]. The theoretical size of the key space given in the (Section 2) is  or
or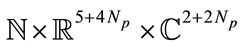 .
.
For , the theoretical entropy of the key space is equal to 448. For real physics measurements, the size of the space of input parameters is smaller. Indeed, the parameters do not take all the possible values in
, the theoretical entropy of the key space is equal to 448. For real physics measurements, the size of the space of input parameters is smaller. Indeed, the parameters do not take all the possible values in ,
,  or
or , which can decrease the size of the key space. In fact, with such limitation of parameter space, we already assure to be in the region of near-field inducing plasmonic effects (i.e. strong resonances and interference patterns in the electromagnetic field). For example, by taking into account the available physical measures (see the sizes of intervals for each parameter given in Section 3.1), the values of parameters can be limited at least on a 12- to 16-bits encoding. With such limited bits encoding, the entropy of the key space is 156 bits (or 224 bits for a 16-bits encoding) with only one considered nano-sphere (i.e.
, which can decrease the size of the key space. In fact, with such limitation of parameter space, we already assure to be in the region of near-field inducing plasmonic effects (i.e. strong resonances and interference patterns in the electromagnetic field). For example, by taking into account the available physical measures (see the sizes of intervals for each parameter given in Section 3.1), the values of parameters can be limited at least on a 12- to 16-bits encoding. With such limited bits encoding, the entropy of the key space is 156 bits (or 224 bits for a 16-bits encoding) with only one considered nano-sphere (i.e. ). This clearly overpass the lower limit of 128 bits. Therefore, the size of the key space is large enough to resist brute-force attacks. Such a large space of keys is a necessary condition, but not sufficient. Indeed, all the keys must be equiprobable and the corresponding outputs must also be cryptographically strong.
). This clearly overpass the lower limit of 128 bits. Therefore, the size of the key space is large enough to resist brute-force attacks. Such a large space of keys is a necessary condition, but not sufficient. Indeed, all the keys must be equiprobable and the corresponding outputs must also be cryptographically strong.
3.3.2. Key Sensitivity
The sensitivity on the key is an essential factor for the pseudo random generation based on optical system. Indeed, only a small deviation in the input should cause a large change in the output. Here, the key is given by various kinds of inputs (physical parameters) such as the radius of the nano particle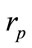 , the permittivity of the materials
, the permittivity of the materials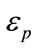 , the number of particles
, the number of particles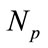 , the permittivity of the surrounding medium
, the permittivity of the surrounding medium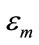 , the illuminating angle
, the illuminating angle 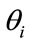 and the illuminating wavelength
and the illuminating wavelength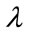 . The numerical parameters (i.e.
. The numerical parameters (i.e.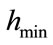 ,
, 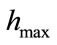 and
and ) define the length of the pseudo random sequences (
) define the length of the pseudo random sequences (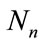 ) and the spatial positions where the fields are computed (
) and the spatial positions where the fields are computed (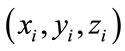 , with
, with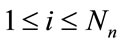 ). The key sensitivity analysis must be normally achieved on all these parameters (physical and numerical parameters). Neverthless, the main sensitive parameters concern physical ones. Therefore, we can limit this analysis to mainly four physical parameters: the radius of the nano-particles
). The key sensitivity analysis must be normally achieved on all these parameters (physical and numerical parameters). Neverthless, the main sensitive parameters concern physical ones. Therefore, we can limit this analysis to mainly four physical parameters: the radius of the nano-particles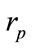 , the surrounding medium
, the surrounding medium , the complex permitivitty
, the complex permitivitty 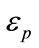 (i.e. the real and imaginary parts
(i.e. the real and imaginary parts ) of the nano-particle material and the illuminating wavelength
) of the nano-particle material and the illuminating wavelength .
.
Actually, in the study of correlation (Section 3), the sensitivity was already indirectly tested due to the selected near values of input parameters. Here, the analysis is achieved on individual physical parameters in order to analyse the sensitivity of these parameters through the computing of the correlation coefficient values. To analyse the sensitivity to the physical parameters, we consider the generation of large pseudo random sequences  of size
of size  (i.e.
(i.e.  bits with hmin = 0.1 nm,
bits with hmin = 0.1 nm,  and
and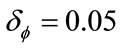 ) obtained for
) obtained for 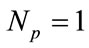 spherical nanoparticle.
spherical nanoparticle.
1) Radius Value Sensitivity:
The first parameter concerns the radius 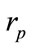 of the nano-particle. The fixed parameters are: the permittivity of the surrounding medium
of the nano-particle. The fixed parameters are: the permittivity of the surrounding medium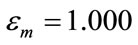 , the permittivity of the gold nano-sphere
, the permittivity of the gold nano-sphere 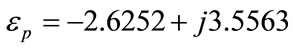 at the illuminating wavelength
at the illuminating wavelength . With three slightly differing radius values
. With three slightly differing radius values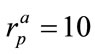 ,
,  and
and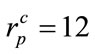 , the produced sequences are
, the produced sequences are ,
, 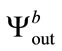 and
and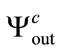 , respectively. If the cryptosystem is sensitive to the radius value then the produced outputs
, respectively. If the cryptosystem is sensitive to the radius value then the produced outputs 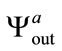 and
and  should be very different from
should be very different from 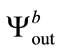 and not correlated. The correlation coefficients between these three produced sequences are presented in Table 2. The produced sequences
and not correlated. The correlation coefficients between these three produced sequences are presented in Table 2. The produced sequences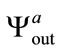 ,
, 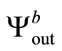 and
and 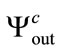 are very different for near radius
are very different for near radius 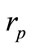 values and only a very weak correlation is detected.
values and only a very weak correlation is detected.
2) Surrounding Medium Permittivity Value Sensitivity:
The second parameter is the value of the surrounding medium permittivity . The fixed parameters are: the radius of the nano-sphere
. The fixed parameters are: the radius of the nano-sphere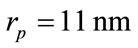 , the permittivity of the gold nano-sphere
, the permittivity of the gold nano-sphere 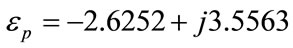 at the illuminating wavelength
at the illuminating wavelength . With these fixed parameters and the three slightly differing permittivity values
. With these fixed parameters and the three slightly differing permittivity values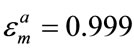 ,
,  and
and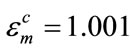 , the produced sequences are
, the produced sequences are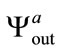 ,
, 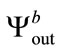 and
and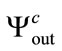 , respectively. The correlation coefficients between these three produced sequences are presented in Table 3. For near permittivity values
, respectively. The correlation coefficients between these three produced sequences are presented in Table 3. For near permittivity values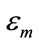 , the produced sequences
, the produced sequences ,
, 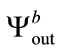 and
and  are also different and only a weak correlation is detected.
are also different and only a weak correlation is detected.
3) Sensitivity of the real part of the material permitivity:

Table 2. Correlation coefficients between the three pseudo random sequences produced with slightly different radius values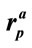 ,
, 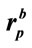 and
and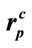 .
.

Table 3. Correlation coefficients between the three pseudo random sequences produced with slightly different surrounding medium values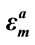 ,
, 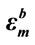 and
and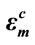 .
.
The third parameter is the value of the real part of the complex permittivity of the gold nano-particle . The fixed parameters are: the radius of the nano-sphere
. The fixed parameters are: the radius of the nano-sphere , the permittivity of the surrounding medium
, the permittivity of the surrounding medium 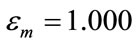 and the imaginary part of the permittivity of gold nano-sphere
and the imaginary part of the permittivity of gold nano-sphere 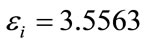 at the illuminating wavelength
at the illuminating wavelength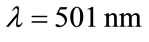 . With these fixed parameters and the three slightly differing real part of the permittivity values
. With these fixed parameters and the three slightly differing real part of the permittivity values 
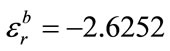 and
and 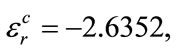 the produced sequences are
the produced sequences are ,
,  and
and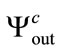 , respectively. The correlation coefficients between these three produced sequences are presented in Table 4. The cryptosystem is also sensitive to the value of real part of the material permitivitty.
, respectively. The correlation coefficients between these three produced sequences are presented in Table 4. The cryptosystem is also sensitive to the value of real part of the material permitivitty.
4) Sensitivity to the imaginary part of the material permittivity:
The fourth parameter is the value of the imaginary part of the complex permittivity of the gold nano-particle . The fixed parameters are: the radius of the nano-sphere
. The fixed parameters are: the radius of the nano-sphere , the permittivity of the surrounding medium
, the permittivity of the surrounding medium 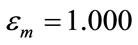 and the real part of the permittivity of gold nano-sphere
and the real part of the permittivity of gold nano-sphere 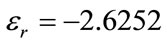 at the illuminating wavelength
at the illuminating wavelength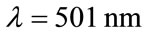 . With these fixed parameters and the three slightly differing imaginary part of the permittivity values
. With these fixed parameters and the three slightly differing imaginary part of the permittivity values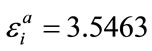 ,
, 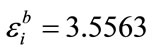 and
and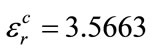 , the produced sequences are
, the produced sequences are ,
, 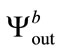 and
and , respectively. The correlation coefficients between these three produced sequences are presented in Table 5. The tested sequences
, respectively. The correlation coefficients between these three produced sequences are presented in Table 5. The tested sequences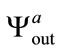 ,
, 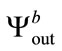 and
and 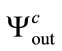 are uncorrelated. The cryptosystem is sensitive to the value of imaginary part of the material permitivitty.
are uncorrelated. The cryptosystem is sensitive to the value of imaginary part of the material permitivitty.
5) Illuminating wavelength value sensitivity:
The last parameter concerns the illuminating wavelength values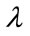 . The fixed parameters are: the radius of the nano-sphere
. The fixed parameters are: the radius of the nano-sphere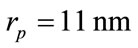 , the permittivity of the surrounding medium
, the permittivity of the surrounding medium 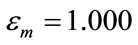 and the complex permittivity of gold nano-sphere
and the complex permittivity of gold nano-sphere . With these fixed parameters and the three slightly differing illuminating wavelength
. With these fixed parameters and the three slightly differing illuminating wavelength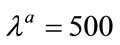 ,
, 

Table 4. Correlation coefficients between the three pseudo random sequences produced with slightly different values of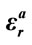 ,
, 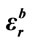 and
and  retated to the real part of the permitivitty of gold nanosphere.
retated to the real part of the permitivitty of gold nanosphere.

Table 5. Correlation coefficients between the three pseudo random sequences produced with slightly different values of ,
, 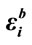 and
and  retated to the imaginary part of the permitivitty.
retated to the imaginary part of the permitivitty.
and , the produced sequences are
, the produced sequences are ,
,  and
and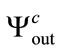 , respectively. The correlation coefficients between these three produced sequences are presented in Table 6.
, respectively. The correlation coefficients between these three produced sequences are presented in Table 6.
These coefficients are closed to 0 then the tested outputs are very different. The results obtained here show that the sequences seem to be very different and also illustrate the sensitivity of the cryptosystem relatively to the wavelength value.
3.3.3. Quality of Pseudo Random Sequences
A mathematical analysis would be necessary to determine is the PRNG is robust or not before being used. Indeed, whichever way the cryptosystem is designed, the produced output must be strong (i.e. random, decorrelated and sensitive). Several and various statistical tests are available for evaluating the randomness of binary sequences. Reference test suites for PRNGs are the NIST suite [16], TestU01 [27] and the DieHARD suites [28]. In this paper, the NIST tests are used to evaluate the randomness level of subset of pseudo random sequences. As previously mentionned, the NIST statistical test battery are chosen because it contains many famous tests from the Diehard battery with some extra tests and used to check the randomness of the output sequences of each candidate algorithm in the AES evaluation process and smart cards [22]. The correlation between such pseudo random sequences was also evaluated (see Statistical analysis in Section 3.2). The sensitivity to the parameters of the key (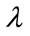 ,
, 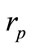 ,
,  ,
,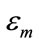 ) was also analysed. All the produced pseudo random sequences pass successfully the tests.
) was also analysed. All the produced pseudo random sequences pass successfully the tests.
3.3.4. Security against Attacks
We also analyse the security of the cryptosystem against two types of attacks: Heuristic Guess-and-Determine Attack and Distinguishing Attacks.
1) Heuristic Guess-and-determine (HGD) attack is a

Table 6. Correlation coefficients between the three pseudo random sequences produced with slightly different wavelength values ,
, 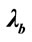 and
and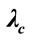 .
.
general attack on stream ciphers [25]. The main idea of this attack is to guess in the first time the value of few unknown variables of the cipher. Next, the remaining unknown variables are deduced by iterating the system a few times and by comparing the produced pseudo random sequence with the original pseudo random sequence. If these two sequences are equal, then the guessed values are correct and the cryptosystem is broken, else the attack should be repeated with new guessed values. We consider that the system is known by the attacker, it seems that the attack discussed in reference [25] can not be applied correctly on the proposed cryptosystem which is not of the same family of involved stream ciphers. In fact, the model and the structure of the proposed PRNG is completely different. An alternative way to apply this attack would be to guess and to fix the values of physical parameters and to iterate the algorithm by searching the remeshing ones to produce the sequence . Once all the comparisons made without success, the first set of input values is guessed again and the process is repeated until success. This process has almost the same complexity than a classic brute-force attack.
. Once all the comparisons made without success, the first set of input values is guessed again and the process is repeated until success. This process has almost the same complexity than a classic brute-force attack.
2) Distinguishing Attacks: Any output of a stream cipher (or PRNG) designed for cryptographic applications, should not be statistically distinguished from a truly random sequence. In fact, distinguishing attacks described in reference [26], try to find traces of the distinguishing property by exploiting the weaknesses of the algorithm related to the linear and non-linear combinations. Here, the generated sequences pass successfully the standard statistical tests for randomness. Moreover, the only linear masking occurs when we applied
 and
and  in Equations (3)
in Equations (3)
and (4). Knowing that the values of 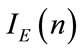 and
and 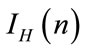 are sensitive from the second or third decimal place, the fact to mulltiply by
are sensitive from the second or third decimal place, the fact to mulltiply by  gives values which the modulo are completely different. Thus, by applying a XOR operation between the two maps
gives values which the modulo are completely different. Thus, by applying a XOR operation between the two maps  and
and 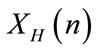 it kills any information on linear dependance then, the attack becomes ineffective.
it kills any information on linear dependance then, the attack becomes ineffective.
4. Conclusion
In this paper, a new PRNG using two plasmonic maps to generate long pseudo random sequences was presented. Such a generator has shown its ability to produce a very large number of pseudo random sequences which can be usefull in several cryptographic applications. The randomness quality on the plasmonic maps is improved through the use of remeshing process and one-way function (xor operator). The advantages of the generator are the size of the key space, the sensitivity to the initial inputs (keys), the quality of pseudo random sequences and the security level against several attacks. Moreover, these produced sequences do not present correlations which ensuring a large variety of pseudo random sequences and a higher security level. Of course, this method can be enriched by increasing the complexity of the nanostructures (including substrates, multi-materials, ...) inducing complex interaction patterns and strong gradients and by considering experimental field measurements.
5. Acknowledgements
Authors thank the Centre de Calcul Intensif ROMEO II for computational facilities, the Région ChampagneArdennes and the Conseil Régional de l’Aube for financial supports.
REFERENCES
- L. Blum, M. Blum and M. Shub, “A Simple Unpredictable Pseudo-Random Number Generator,” SIAM Journal on Computing, Vol. 15, No. 2, 1986, pp. 364-383. doi:10.1137/0215025
- K. W. Wojciechowski, “Pseudorandom Number Generators Based on the Weyl Sequence,” Computational Methods in Science and Technology, Vol. 5, 1999, pp. 81-85.
- N. K. Pareek, V. Patidar and K. K. Sud, “Discrete Chaotic Cryptography Using External Key,” Physics Letters A, Vol. 309, No. 1-2, 2003, pp. 75-82. doi:10.1016/S0375-9601(03)00122-1
- V. Patidar and K. K. Sud, “A Novel Pseudo-Random Bit Generator Based on Chaotic Standard Map and Its Testing,” Electronic Journal of Theoretical Physics, Vol. 6, No. 20, 2009, pp. 327-344.
- S. M. Fu, Z. Y. Chen and Y. A. Zhou, “Chaos-Based Random Number Generators,” Computer Research and Development, Vol. 41, No. 4, 2004, pp. 749-754.
- J. P. Gonzailez and R. Pino, “Random Number Generator Based on Unpredictable Chaotic Functions,” Computer Physics Communications, Vol. 120, No. 2-3, 1999, pp. 109-114. doi:10.1016/S0010-4655(99)00233-7
- V. V. Kolesov, R. V. Belyaev and G. M. Voronov, “A Digital Random-Number Generator Based on the Chaotic Signal Algorithm,” Journal of Communications Technology and Electronics, Vol. 46, No. 11, 2001, pp. 1258- 1263.
- F.-L. Wang, “A Universal Algorithm to Generate PseudoRandom Numbers Based on Uniform Mapping as Homeomorphism,” Chinese Physics B, Vol. 19, No. 19, 2010, p. 090505.
- I. Vattulainen, K. Kankaala, J. Saarinen and T. Ala-Nissila, “A Comparative Study of Pseudo-Random Number Generators,” Computer Physics Communications, Vol. 86, No. 3, 1995, pp. 209-226. doi:10.1016/0010-4655(95)00015-8
- A. B. O. López, G. Á. Marañon, A. G. Estévez, G. P. Dégano, M. R. García and F. M. Vitini, “Trident, a New Pseudo-Random Number Generator Based on Coupled Chaotic Maps,” Advances in Intelligent and Soft Computing, Vol. 85, 2010, pp. 183-190. doi:10.1007/978-3-642-16626-6_20
- N. K. Pareek, V. Patidar and K. K. Sud, “A Random Bit Generator Using Chaotic Maps,” International Journal of Network Security, Vol. 10, No. 1, 2010, pp. 32-38.
- D. Barchiesi, D. Macías, L. Belmar-Letellier, D. van Labeke, M. Lamy de la Chapelle, T. Toury, E. Kremer, L. Moreau and T. Grosges, “Plasmonics: Influence of the Intermediate (or Stick) Layer on the Efficiency of Sensors,” Applied Physics B-Lasers and Optics, Vol. 93, No. 1, 2008, pp. 177-181. doi:10.1007/s00340-008-3173-5
- T. Grosges, D. Barchiesi, T. Toury and G. Gréhan, “Design of Nanostructures for Imaging and Biomedical Applications by Plasmonic Optimization,” Optics Letters, Vol. 33, No. 23, 2008, pp. 2812-2814. doi:10.1364/OL.33.002812
- T. Grosges and D. Barchiesi, “Toward Nanoworld-Based Secure Encryption for Enduring Data Storage,” Optics Letters, Vol. 35, No. 14, 2010, pp. 2421-2423. doi:10.1364/OL.35.002421
- M. François, T. Grosges, D. Barchiesi and R. Erra, “Generation of Encryption Keys from Plasmonics,” PIERS Online, Vol. 7, No. 3, 2011, pp. 296-300.
- A. Rukhin, J. Soto, J. Nechvatal, M. Smid, E. Barker, S. Leigh, M. Levenson, M. Vangel, D. Banks, A. Heckert, J. Dray and S. Vo, “A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications,” National Institute of Standard Technologies Special Publication, Washington DC, 2010, pp. 1-200.
- C. E. Shannon, “A Mathematical Theory of Communication,” Bell System Technical Journal, Vol. 27, No. 3-4, 1948, pp. 379-423, 623-656.
- D. Barchiesi, E. Kremer, V. P. Mai and T. Grosges, “A Poincaré’s Approach for Plasmonics: The Plasmon Localization,” Journal of Microscopy, Vol. 229, No. 3, 2008, pp. 525-532. doi:10.1111/j.1365-2818.2008.01938.x
- H. Borouchaki, T. Grosges and D. Barchiesi, “Improved 3D Adaptive Remeshing Scheme Applied in High Electromagnetic Field Gradient Computation,” Finite Element in Analysis and Design, Vol. 46, No. 1-2, 2010, pp. 84-95. doi:10.1016/j.finel.2009.06.026
- A. J. Menezes, P. C. Van Oorschot and S. A. Vanstone, “Handbook of Applied Cryptography,” CRC Press, Boca Raton, 1996. doi:10.1201/9781439821916
- W. Janke, “NIC Series Volume 10: Quantum Simulations of Complex Many-Body Systems: From Theory to Algorithms,” John von Neumann Institute for Computing, Kerkrade, 2002, pp. 447-458.
- R. N. Akram, K. Markantonakis and K. Mayes, “Pseudorandom Number Generation in Smart Cards: An Implementation, Performance and Randomness Analysis,” The 5th International Conference on New Technologies, Mobility and Security (NTMS), Istanbul, 7-10 May 2012, pp. 1-7. doi:10.1109/NTMS.2012.6208760
- G. Cheng, Y. Mao and C. Chui, “A Symmetric Image Encryption Scheme Based on 3D Chaotic Cat Maps,” Chaos Solitons and Fractal, Vol. 21, No. 3, 2004, pp. 749- 761. doi:10.1016/j.chaos.2003.12.022
- G. Alvarez and L. Shujun, “Some Basic Cryptographic Requirements for Chaos-Based Cryptosystems,” International Journal of Bifurcation and Chaos, Vol. 16, No. 8, 2006, pp. 2129-2151. doi:10.1142/S0218127406015970
- H. Ahmadi and T. Eghlidos, “Heuristic Guess-and-Determine Attacks on Stream Ciphers,” IET Information Security, Vol. 3, No. 2, 2009, pp. 66-73. doi:10.1049/iet-ifs.2008.0013
- D. Coppersmith, S. Halevi and C. Jutlar, “Cryptanalysis of Stream Ciphers with Linear Masking,” CRYPTO ’02 Proceedings of the 22nd Annual International Cryptology Conference on Advances in Cryptology, Vol. 2442, 2002, pp. 515-532.
- P. L’ecuyer and R. Simard, “TestU01: A C Library for Empirical Testing of Random Number Generators,” ACM Transactions on Mathematical Software, Vol. 33, No. 4, 2007, pp. 22-40.
- G. Marsaglia, “Diehard: A Battery of Tests of Randomness,” 1996. http://stat.fsu.edu/geo/diehard.html

