Applied Mathematics
Vol. 3 No. 5 (2012) , Article ID: 19062 , 5 pages DOI:10.4236/am.2012.35073
The Feature Core of Dynamic Reduct*
College of Information Science and Engineering, Central South University, Changsha, China
Email: csuwjy@mail.csu.edu.cn
Received April 1, 2012; revised May 1, 2012; accepted May 8, 2012
Keywords: Decision System; Reduction; Dynamic Core
ABSTRACT
To the reduct problems of decision system, the paper proposes the notion of dynamic core according to the dynamic reduct model. It describes various formal definitions of dynamic core, and discusses some properties about dynamic core. All of these show that dynamic core possesses the essential characters of the feature core.
1. Introduction
KNOWLEDGE reduct is an important step in knowledge discovery, and also a favorable method to extract the more generalized rules. There are a number of research papers [1-3] about reduct problems, but most of them are just for static reduct.
The reduct methods based on standard rough set are effective to some extent, but there are also some problems to be solved in practice. Dynamic data, incremental data and noise data make the analysis results instable and uncertain. All of these limit the application of rough set theory [1].
Standard rough set methods are not always sufficient for extracting laws from decision system. One of the reasons is that these methods are not taking into account the fact that part of the reduct set is chaotic, in other words it is not stable.
Firstly, it gives the definition of dynamic core. Then the properties of dynamic core is certified. All of these show dynamic core possesses the essential characters of the feature core.
2. Dynamic Reduct
To the problems of standard rough set reducts or static reducts, dynamic reducts can put up better performance in very large dataset, and also enhance effectively the ability to accommodate noise data.
The rules calculated by means of dynamic reducts are better predisposed to classify unseen cases, because these reducts are in some sense the most stable reducts, and they are the most frequently appearing reducts in subdecision system created by random samples of a given decision system.
Definition 1: Decision system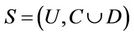 , where
, where 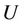 is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe, 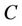 is condition attributes set,
is condition attributes set, 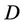 is decision attributes set,
is decision attributes set, 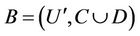 ,
,  ,
, 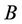 is called the sub-decision system of
is called the sub-decision system of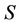 . Let
. Let 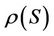 denote the set of all sub-decision system of
denote the set of all sub-decision system of ,
,  is called a F family of decision system
is called a F family of decision system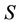 .
.
Definition 2: Decision system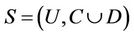 , where
, where 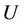 is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe, 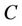 is condition attributes set,
is condition attributes set, 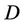 is decision attributes set,
is decision attributes set, 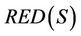 denotes the set which contains all reducts of decision system
denotes the set which contains all reducts of decision system , and
, and  denotes the set which includes all reducts of sub-decision system
denotes the set which includes all reducts of sub-decision system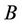 .
.
There is at least one reduct in a decision system, which is just itself, so the set of reduct is not empty. In many cases, there may be several reducts in a given decision system. Each reduct can product a rule set, and it is difficult to justify which is the best rule set. Therefore it is important to search the most stable reduct, dynamic reduct is proposed in this case.
Definition 3: Decision system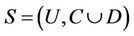 , where
, where 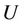 is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe, 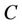 is condition attributes set,
is condition attributes set, 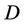 is decision attributes set,
is decision attributes set, 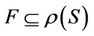 , dynamic reduct of decision system
, dynamic reduct of decision system  is denoted as
is denoted as 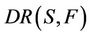 [4], and
[4], and
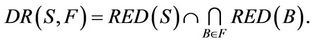
Any element of 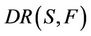 is called an F-dynamic reduct, which describes the most stable reducts in decision system. From the definition of dynamic reduct, it follows that a relative reduct of
is called an F-dynamic reduct, which describes the most stable reducts in decision system. From the definition of dynamic reduct, it follows that a relative reduct of  is dynamic if it is also a reduct of all sub-decision system from a given family F by random sampling.
is dynamic if it is also a reduct of all sub-decision system from a given family F by random sampling.
The reducts in a decision system are not stable, sensitive for sample data [5]. Bazan gives the concept and method about dynamic reduct [4], which grounds the most stable reduct of decision system in theory, then the dynamic core is put forward in the paper.
3. Dynamic Core
Attributes reduct is the basic problem in rough set theory, and the computation of feature core is especially important for resolving this problem. All attributes in the feature core will be present in any reduct, otherwise discernible relation in decision system can not be ensured. Many reduct algorithms are based on the feature core. According to the feature core one can construct reduct heuristically, and the efficiency of reduct can be improved greatly.
Many references discuss about the feature core of reduct [2,3], but it is just static reduct. For dynamic reduct the feature core still need to be probed in a further step.
Given decision system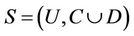 , where
, where 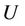 is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe, 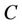 is condition attributes set,
is condition attributes set, 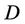 is decision attributes set, we know that the feature core of decision system
is decision attributes set, we know that the feature core of decision system 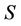 in static reduct is
in static reduct is

the feature core of sub-decision system 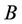 is
is

Definition 4: Decision system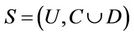 , where
, where 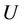 is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe, 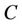 is condition attributes set,
is condition attributes set, 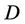 is decision attributes set,
is decision attributes set,  , the dynamic core of
, the dynamic core of 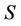 based on family F is defined by
based on family F is defined by

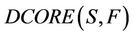 is called F-dynamic core of decision system
is called F-dynamic core of decision system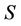 .
.
Theorem 1: Decision system , where
, where  is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe,  is condition attributes set,
is condition attributes set, 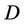 is decision attributes set,
is decision attributes set, 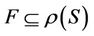 , then the intersection of F-dynamic reduct contains F-dynamic core, that is
, then the intersection of F-dynamic reduct contains F-dynamic core, that is
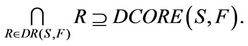
Proof: According to the definition of dynamic reduct [5], it follows
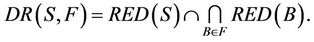
For any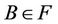 ,
, 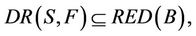
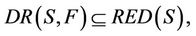
then,
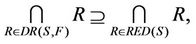

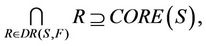
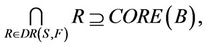
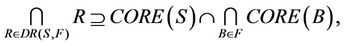
therefore,

Theorem 1 means that each attribute in F-dynamic core is included by all F-dynamic reducts. Dynamic reducts is the most stable reducts of decision system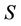 , then dynamic core is the most stable core of decision system
, then dynamic core is the most stable core of decision system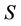 , which represents a stable unreducted attribute set.
, which represents a stable unreducted attribute set.
4. (F-λ)-Dynamic Core
F-dynamic core can be sometimes too much restrictive so here applies a generalization of F-dynamic core. It will be more suitable for noise data.
Definition 5: Decision system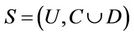 , where
, where 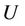 is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe, 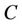 is condition attributes set,
is condition attributes set,  is decision attributes set,
is decision attributes set, 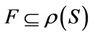 ,
, 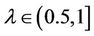 , the (F-λ)-dynamic core of decision system
, the (F-λ)-dynamic core of decision system  based on family F is defined by
based on family F is defined by

 is precision coefficient, and the value of
is precision coefficient, and the value of 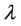 decides which attribute belongs to (F-λ)-dynamic core
decides which attribute belongs to (F-λ)-dynamic core .
.
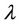 approaches 1,
approaches 1, 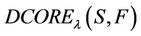 will be closed to
will be closed to , while
, while 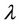 approaches 0.5,
approaches 0.5,
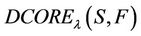 is more rough compared with
is more rough compared with 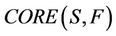 , but
, but  will comprise more attributes.
will comprise more attributes.
Theorem 2: Decision system , where
, where 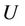 is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe, 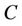 is condition attributes set,
is condition attributes set, 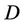 is decision attributes set,
is decision attributes set,  , we have the following propositions.
, we have the following propositions.
1) If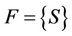 , then
, then 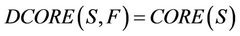
In this case dynamic core is just the feature core of decision system .
.
2) 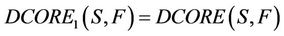
Actually, when 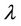 increases from 0.5 to 1, the dynamic core will change from
increases from 0.5 to 1, the dynamic core will change from 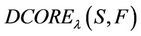 to
to  .
.
3) If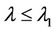 , then
, then
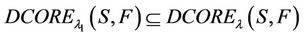
Obviously, for any , there will be
, there will be
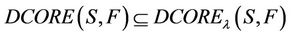 .
.
Theorem 3: Decision system , where
, where 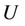 is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe,  is condition attributes set,
is condition attributes set, 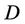 is decision attributes set,
is decision attributes set, 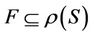 ,
, 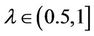 , then the intersection of (F-λ)- dynamic reduct contains (F-λ)-dynamic core.
, then the intersection of (F-λ)- dynamic reduct contains (F-λ)-dynamic core.
Proof: According to the definition of (F-λ)-dynamic core, it follows
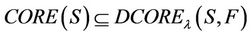
(F-λ)-dynamic reduct is
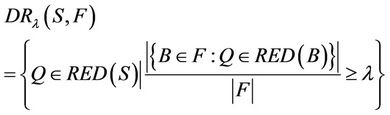
It is obviously that
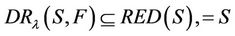
then,
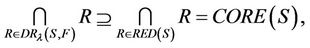
therefore,
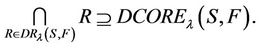
5. Generalized Dynamic Core
According to the definition of dynamic core, if some feature attributes of any sub-decision system in F family are comprised by dynamic core, then it is certainly a feature attribute of decision system . This notion sometimes can not be convenient because we are interested in useful sets of attributes which are not necessarily reducts of the decision system. Therefore we have to generalize the notion of a dynamic core.
. This notion sometimes can not be convenient because we are interested in useful sets of attributes which are not necessarily reducts of the decision system. Therefore we have to generalize the notion of a dynamic core.
Definition 6: Decision system , where
, where  is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe,  is condition attributes set,
is condition attributes set, 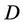 is decision attributes set,
is decision attributes set, 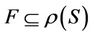 , then
, then
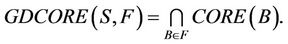
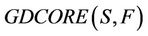 is called the generalized dynamic core of decision system
is called the generalized dynamic core of decision system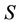 .
.
Definition 7: Decision system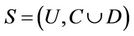 , where
, where  is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe, 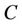 is condition attributes set,
is condition attributes set, 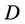 is decision attributes set,
is decision attributes set, 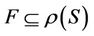 ,
,  , then
, then
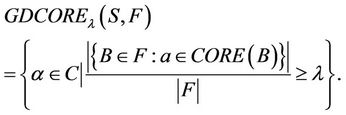
The  is called the (F-λ)-generalized dynamic core of decision system
is called the (F-λ)-generalized dynamic core of decision system .
.
Theorem 4: Decision system , where
, where 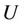 is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe, 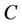 is condition attributes set,
is condition attributes set, 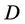 is decision attributes set,
is decision attributes set, 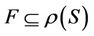 ,
,  , we have the following propositions.
, we have the following propositions.
1) 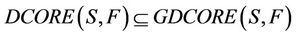
By definitions 6 and 7 we know that it is obviously true.
2) 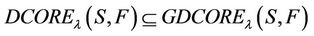
By 1) it is also obviously true.
3) If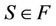 , then
, then

when F family contains decision system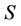 , then generalized dynamic core will be just dynamic core.
, then generalized dynamic core will be just dynamic core.
Theorem 5: Decision system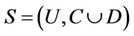 , where
, where  is a non-empty, finite set called the universe,
is a non-empty, finite set called the universe, 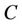 is condition attributes set,
is condition attributes set, 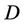 is decision attributes set,
is decision attributes set, 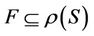 ,
, 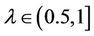 , then 1) The intersection of F-generalized dynamic reduct contains F-generalized dynamic core Proof: According to the definition of F-dynamic reduct [5], it follows
, then 1) The intersection of F-generalized dynamic reduct contains F-generalized dynamic core Proof: According to the definition of F-dynamic reduct [5], it follows
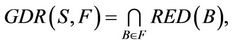
for any ,
, 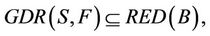
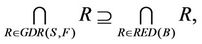
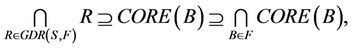
then,

2) The intersection of (F-λ)-generalized dynamic reduct contains (F-λ)-generalized dynamic core Proof: For any attribute , it satisfies
, it satisfies 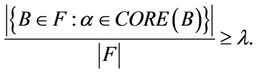
It might as well suppose that attribute  exists in core of
exists in core of  sub-decision systems,
sub-decision systems,

We have
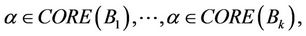
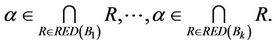 (1)
(1)
According to the definition of (F-λ)-generalized dynamic reduct [5],

because of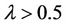 , any reduct
, any reduct 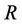 in (F-λ)-generalize dynamic reduct satisfies:
in (F-λ)-generalize dynamic reduct satisfies:
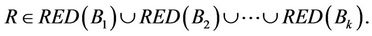
By (1), for any attribute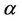 , we can infer:
, we can infer:

then,
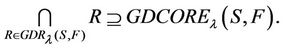
Actually, supposes 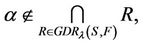
therefore it exists 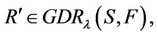 and
and 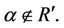
By (1), it follows
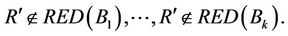 (2)
(2)
If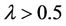 , then (2) is contradiction with hypothesis, then
, then (2) is contradiction with hypothesis, then
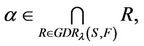
only when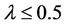 , it may be true for the hypothesis, but we have fixed
, it may be true for the hypothesis, but we have fixed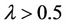 , so it is impossible.
, so it is impossible.
6. Quality of Family F
We can not calculate the family of all subtables of universal decision information table, therefore we construct family F to estimate universal decision information table. General speaking, if family F contains more elements then the stability of the calculated reduct will be better.
Extracting too much subtables inevitably cause enormous computation. From the thought of Bernoulli’s theorem we know that if the extracted subtables is adequate, continuing to extract other subtables has litter relate with reduct stability coefficient. So a minimum value of |F| can be determined.
However the computation of sample of dynamic reduct should emphasize the other important aspect, namely the influence of sampling distribution to the validity of the dynamic reduct. We generally assume that the sample is random. The basic thought of evaluate the quality of family F is proposed. It can be used to weight the equalization of family F and reflect the validity of the dynamic reduct.
Definition 7 (entire sample): Decision system 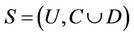 , where
, where 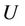 is universe,
is universe,  is condition attributes set,
is condition attributes set, 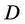 is decision attributes set,
is decision attributes set,  , and
, and

 is named entire sample set.
is named entire sample set.
Definition 8 (central sample): Decision system 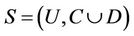 , where
, where 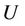 is universe,
is universe,  is condition attributes set,
is condition attributes set,  is decision attributes set,
is decision attributes set, 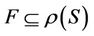 , and
, and
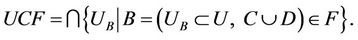
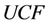 is named central sample set.
is named central sample set.
Taking simple random sampling as a precondition, firstly we will consider the equalization of family F and give two radios to weight it.
1) Entire Sampling Rate The entire sampling rate is denoted by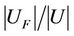 . It is easy to observe that
. It is easy to observe that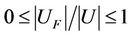 . If
. If  takes a too small value then the sample is too centralized. So it can not reflect the character of the original decision information system, and reduce the confidence degree of dynamic reduct.
takes a too small value then the sample is too centralized. So it can not reflect the character of the original decision information system, and reduce the confidence degree of dynamic reduct.
We think the sample of family F is deficient when the value of 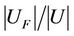 less than 0.5. A threshold value can be established. The sample conforms to the requirement and the result of dynamic reduct is effective if
less than 0.5. A threshold value can be established. The sample conforms to the requirement and the result of dynamic reduct is effective if 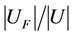 is bigger than the threshold value.
is bigger than the threshold value.
2) Entire Balanced Degree The entire balanced degree is denoted by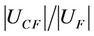 and It is easy to observe that
and It is easy to observe that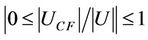 . If
. If 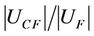 takes a too big value then the sample may too repetitious. So it can not reflect the character of object of the original decision information system, and reduce the confidence degree of dynamic reduct.
takes a too big value then the sample may too repetitious. So it can not reflect the character of object of the original decision information system, and reduce the confidence degree of dynamic reduct.
We think the sample of family F is unbalanced when the value of 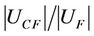 is bigger than 0.5. A threshold value can be established. The uniformity of sample distribution is better and the result of dynamic reduct is effective if
is bigger than 0.5. A threshold value can be established. The uniformity of sample distribution is better and the result of dynamic reduct is effective if  is lower than the threshold value.
is lower than the threshold value.
Just evaluating the performance of entire sample is not enough, we should also avoid the abnormal phenomenon of individual decision table in family F. The influence of individual subtables to the distribution must be not too much. For example, we extract 100 subtables. If the radio of central sample set constructed by 99 subtables of them is larger than 0.5, when a subtable is brought into the central sample set, the radio decline sharply. For another example, if the radio of entire distribution is acceptable, but the difference among half of the subtables is small. It indicates the distribution of sampling is not balanced.
We can calculate the degree that central sample set contains each of the subtables and the degree that entire sample set contains each of the subtables. The two parameters can be used to evaluate the equalization of subtables.
3) Partial Sampling Rate
The partial sampling rate is denoted by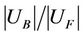 . It is easy to observe that
. It is easy to observe that . If
. If  of some subtables take a higher value then the sample may be unbalanced. Even the entire balanced degree is permissible, but most of the subtables overlap, this reduces the confidence degree of dynamic reduct.
of some subtables take a higher value then the sample may be unbalanced. Even the entire balanced degree is permissible, but most of the subtables overlap, this reduces the confidence degree of dynamic reduct.
4) Partial Balanced Degree The partial balanced degree is denoted by .
.
It is easy to observe that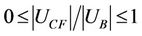 . If
. If  of some subtables takes a higher value then the sample is too centralized. Even the entire balanced degree is permissible, but most of the subtables overlap.
of some subtables takes a higher value then the sample is too centralized. Even the entire balanced degree is permissible, but most of the subtables overlap.
7. Conclusion
The notion of dynamic core is actually based on dynamic reducts in the paper. Dynamic core consists with the most stable attributes which can not be reducted, and describes the set of feature attributes. At the same time it is proved that the intersection of dynamic reducts contains dynamic core, which is suitable for all kinds of definitions about dynamic reducts. All of these show that the dynamic core possesses the essential properties of the feature core in deed. We can say that dynamic core expresses the feature attributes in a more general way.
REFERENCES
- Z. Pawlak, “Rough Sets (Periodical Style),” International Journal of Computer and Information Sciences, Vol. 11, No. 5, 1982, pp. 341-356. doi:10.1007/BF01001956
- X. H. Hu and N. Cercone, “Learning in Relational Databases: A Rough Set Approach (Periodical Style),” International Journal of Computational Intelligence, Vol. 11, No. 2, 1995, pp. 323-338.
- J. Jelonek, K. Krawiec and R. Slowinski, “Rough Set Reduction of Attributes and Their Domains for Neural Networks (Periodical Style),” Computational Intelligence, Vol. 11, No. 2, 1995, pp. 339-347. doi:10.1111/j.1467-8640.1995.tb00036.x
- J. G. Bazan, “A Comparison of Dynamic and Non-Dynamic Rough Set Methods for Extracting Laws from Decision Tables (Published Conference Proceedings Style),” In: L. Polkowski and A. Skowron, Eds., Rough Sets in Knowledge Discovery 1: Methodology and Applications, Physica-Verlag, Heidelberg, 1998, pp. 321-365.
- J. G. Bazan, A. Skowron and P. Synak, “Dynamic Reducts as a Tool for Extracting Laws from Decision Tables, in: Methodologies for Intelligent System (Published Conference Proceedings Style),” Proceedings of 8th International Symposium ISMIS’94, Vol. 869, Springer-Verlag, Berlin, 1994, pp. 346-355.
NOTES
*The project supported by National Natural Science Foundation of China, Grant No. 61173052.
The project supported by Hunan Provincial Natural Science Foundation of China, Grant No. 11JJ5040.

