Applied Mathematics
Vol. 3 No. 6 (2012) , Article ID: 20280 , 4 pages DOI:10.4236/am.2012.36088
A New Family of Nonlinear Fifth-Order Solvers for Finding Simple Roots
Department of Mathematics, Kermanshah University of Technology, Kermanshah, Iran
Email: b.ghanbary@yahoo.com
Received August 26, 2011; revised April 26, 2012; accepted May 3, 2012
Keywords: Iterative Methods; Simple-Root of Nonlinear Equations; Newton’s Method
ABSTRACT
In this paper, we present a new family of iterative methods for solving nonlinear equations. It is proved that the order of convergence of this family is five. Two functions and two derivative evaluations should be computed per iteration. To demonstrate convergence properties of the proposed family of methods, some numerical examples are given. Further numerical comparisons are made with several other existing fifth-order methods.
1. Introduction
In this study, we consider the iterative methods to finding a simple root of a nonlinear equation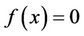 , say
, say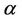 , such that we have
, such that we have 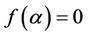 but
but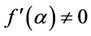 .
.
Newton’s method is one of the best known and probably the most used method for solving the above problem, giving by
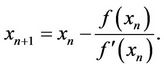 (1)
(1)
In recent years, a lot of effort has been devoted to present some new modifications of the Newton method [1-4].
This paper is structured as follows: In Section 2, we consider a general iterative scheme, analyze it to present a family of fifth-order methods. Then we show that it contains several know fifth-order methods. Section 3 is devoted to numerical comparisons between the results obtained in this work and some known iterative methods. Finally, conclusions are stated in the last section.
2. Development of Method and Convergence Analysis
Motivated and inspired by the recent activities in this direction, in this paper, we are also concerned with developing high-order methods.
Our approach is based on fifth-order method defined in [5] as:
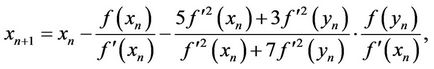 (2)
(2)
where
 (3)
(3)
Throughout the rest of this paper 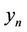 is defined by (3).
is defined by (3).
The iterative scheme (2) can be viewed as a special case of the following general iterative scheme
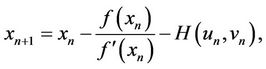 (4)
(4)
with 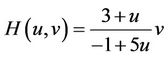 where
where 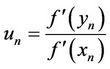 and
and 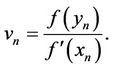
So, the main idea of present paper is to determine the necessary conditions for the two-dimensional function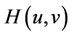 , such that the iterative methods defined by (4) have the fifth-order of convergence.
, such that the iterative methods defined by (4) have the fifth-order of convergence.
Now, for the iterative scheme (4), we have the following convergence results.
Theorem 1. Let 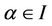 be a simple root of a sufficiently differentiable function
be a simple root of a sufficiently differentiable function 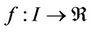 on an open interval which contains
on an open interval which contains 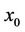 as a close initial approximation to
as a close initial approximation to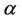 .
.
If 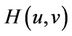 satisfies the conditions
satisfies the conditions
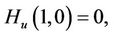
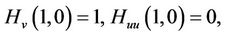
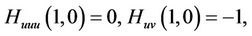
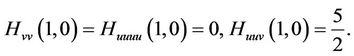
then the method defined by (4) is of order at least five.
Proof. Let 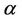 be a simple zero of f. Consider the iteration function F defined by
be a simple zero of f. Consider the iteration function F defined by
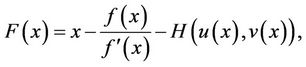
where 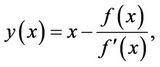
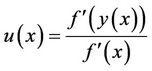 and
and 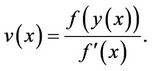
We employ the symbolic computation of the Maple package to compute the Taylor expansion of 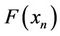 around
around 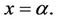 We find after simplifying that
We find after simplifying that
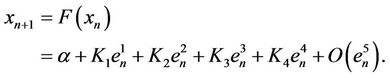
where

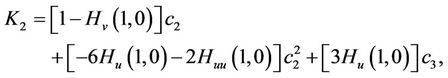
It can be easily verified that if
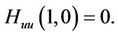
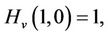
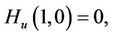 (4)
(4)
To be satisfied, then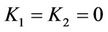 .
.
Substituting of (4) into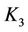 , leads to
, leads to
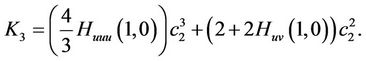
This can be vanished, for
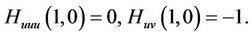 (5)
(5)
Setting (4), (5) in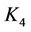 , it turns to
, it turns to
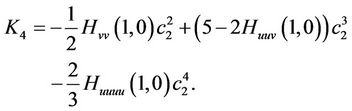
So, the proof is complete if we have

The main point that should be mentioned here is that the order of Newton’s method is improved three units with additional evaluations of the one function and one derivative. So the order of convergence and computational efficiency of the method are greatly improved.
Family (4) with some special choices for 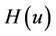 leads to the some known fifth-order methods, as follows.
leads to the some known fifth-order methods, as follows.
Case 1. For the function H giving by
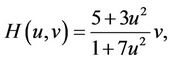
we obtain the fifth-order scheme (2).
Case 2. For the function H, as
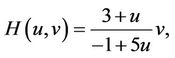
in (4), a fifth-order method is obtained which has been introduced by Ham et al. [6] .
Case 3. For the function H giving by
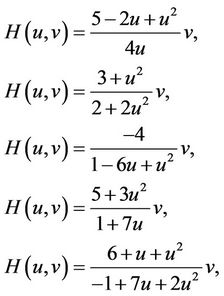
fifth-order methods which have been introduced by Fang et al. in [7] is obtained.
Case 4. For the function H giving by
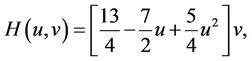
and
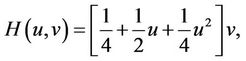
we respectively obtain the following fifth-order methods

and
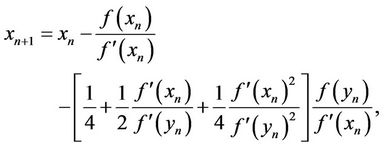
which have been proposed by Biazar et al. in [8].
For obtaining a more general family, let’s consider the function H, as
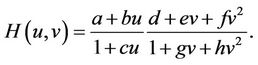 (6)
(6)
It can easily be shown that 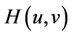 satisfies the conditions of Theorem 1, when
satisfies the conditions of Theorem 1, when
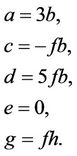 (7)
(7)
Substituting (7) in (6), yields to
 (8)
(8)
where g, h are real parameters that can be freely chosen.
If we take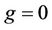 ,
, 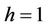 in (8), we obtain the following fifth-order method
in (8), we obtain the following fifth-order method
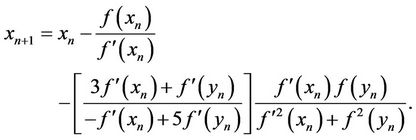 (9)
(9)
If we take ,
, 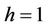 in (8), we obtain the following fifth-order method
in (8), we obtain the following fifth-order method
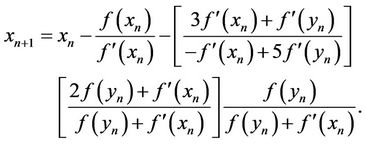 (10)
(10)
Per iteration in the methods defined by (4) requires two function and two first derivative evaluations. If we consider the definition of efficiency index [9] as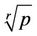 , where p is the order of the method and r is the number of functional evaluations per iteration required by the method, we have that the iteration formula defined by (9) and (10) has the efficiency index equal to
, where p is the order of the method and r is the number of functional evaluations per iteration required by the method, we have that the iteration formula defined by (9) and (10) has the efficiency index equal to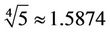 , which is better than the one of Newton’s method
, which is better than the one of Newton’s method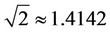 .
.
3. Numerical Examples
In this section, some numerical test of some various rootfinding methods as well as our new methods and Newton’s method are presented. Compared methods were Newton’s method (1) (NM), Fang’s method (2) (FM), the Grau et al. method (GM) [10] defined by
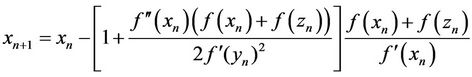 where
where
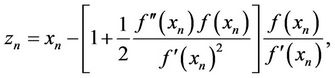
the method of Kou et al. (KM) [11] defined by
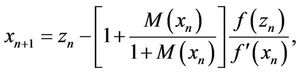
where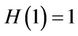 ,
,  ,
, 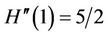 and
and

and
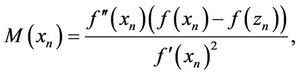
with the new presented methods by Equations (9) (BGM1) and (10) (BGM2), introduced in this contribution. All computations were done using Maple with 128 digit floating point arithmetics (Digits = 128). Displayed in Table 1 are the number of iterations and functional evaluations required such that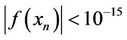 . The following functions [11,12], are used for the comparison.
. The following functions [11,12], are used for the comparison.


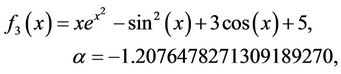
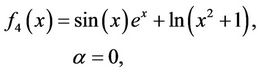


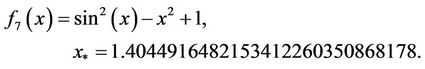
The results presented in Table 1 show that for the functions we tested, the new methods introduced in this contribution need reduce the number of iterations and
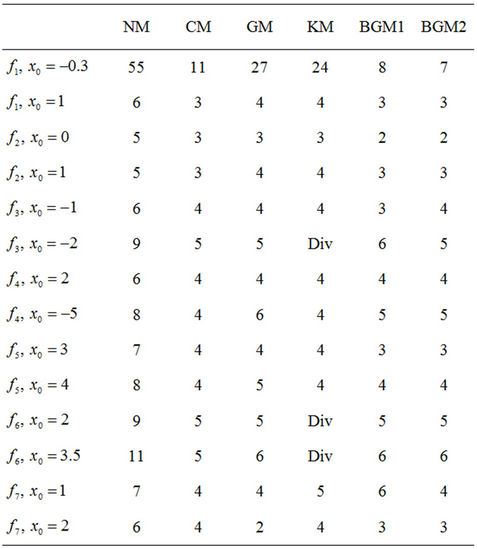
Table 1. Comparison of number of iterations of various fifth-order convergent iterative methods.
needed functional evaluations show that this family can be competitive to the known fifth-order methods and Newton’s method and converge more quickly than the other compared methods.
4. Conclusions
In this paper, we have constructed a new iterative family of methods of order five, for finding a simple root of nonlinear equations. This proposed iterative family contains several well-known methods as special cases.
It also seems that proposed methods can be competitive to the known fifth-order methods and Newton’s method and converge more quickly than the other compared methods.
Applying the idea of this paper, one can suggest and analyze higher-order iterative methods for solving nonlinear equations.
REFERENCES
- J. F. Traub, “Iterative Methods for the Solution of Equations,” Prentice Hall, Upper Saddle River, 1964.
- C. Chun, “Some Variants of King’s Fourth-Order Family of Methods for Nonlinear Equations,” Applied Mathematics and Computation, Vol. 190, No. 1, 2007, pp. 57- 62. doi:10.1016/j.amc.2007.01.006
- A. M. Ostrowski, “Solution of Equations in Euclidean and Banach Space,” Academic Press, New York, 1973.
- B. Ghanbari, “A New General Fourth-Order Family of Methods for Findingsimple Roots of Nonlinear Equations,” Journal of King Saud University—Science, Vol. 23, No. 1, 2011, pp. 395-398.
- L. Fang, L. Sun and G. He, “An Efficient Newton-Type Method with Fifth-Order Convergence for Solving Nonlinear Equations,” Computational Applied Mathematics, Vol. 27, No. 3, 2008, pp. 269-274.
- Y. M. Ham and C. Chun, “A Fifth-Order Iterative Method for Solving Nonlinear Equations,” Applied Mathematics and Computation, Vol. 194, No. 1, 2007, pp. 287-290. doi:10.1016/j.amc.2007.04.005
- L. Fang and G. He, “Some Modifications of Newton’s Method with Higher-Order Convergence for Solving Nonlinear Equations,” Journal of Computational and Applied Mathematics, Vol. 228, No. 1, 2009, pp. 296-303. doi:10.1016/j.cam.2008.09.023
- J. Biazar and B. Ghanbari, “Some Higher-Order Families of Methods for Finding Simple Roots of Nonlinear Equations,” General Mathematics Notes, Vol. 7, No. 1, 2011, pp. 46-51.
- W. Gautschi, “Numerical Analysis: An Introduction,” Birkhäuser, Boston, 1997.
- M. Grau and J. L. Diaz-Barrero, “An Improvement of the Euler-Chebyshev Iterative Method,” Journal of Mathematical Analysis and Applications, Vol. 315, No. 1, 2006, pp. 1-7. doi:10.1016/j.jmaa.2005.09.086
- Y. M. Ham, C. Chun and S. Lee, “Some Higher-Order Modifications of Newton’s Method for Solving Nonlinear Equations,” Journal of Computational and Applied Mathematics, Vol. 222, No. 2, 2008, pp. 477-486. doi:10.1016/j.cam.2007.11.018
- J. Kou and Y. Li, “The Improvements of ChebyshevHalley Methods with Fifth-Order Convergence,” Applied Mathematics and Computation, Vol. 188, No. 1, 2007, pp. 143-147. doi:10.1016/j.amc.2006.09.097

