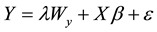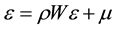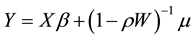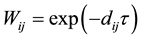Modern Economy
Vol.06 No.06(2015), Article ID:57468,11 pages
10.4236/me.2015.66073
The Role of the Composition of the Human Capital on the Economic Growth: With the Spatial Effect among Provinces in China
Ying Wang, Chao Ni
School of Government, Beijing Normal University, Beijing, China
Email: xjtuwy@sina.com, nichao2011@126.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 June 2015; accepted 23 June 2015; published 26 June 2015
ABSTRACT
Based on the data of China’s 28 provinces and regions during 1987-2007, this paper is trying to explore the role of the composition of the human capital on the economic growth with the spatial effect among provinces. The results indicate that there are significant spatial effects of human capital and economic growth in China; there is a significant positive correlation between the GDP per capita and the average schooling years; when the education of human capital is divided into primary education, secondary education and higher education, only the higher education and the primary education show significantly positive correlation with the GDP per capita.
Keywords:
Economic Growth, Human Capital, Spatial Spillover

1. Introduction
It is commonly agreed that high-level human capital can improve labor productivity, and furthermore enhance the overall national strength. For a country, the most important problem of education development strategy is to decide what kind and what level of education should be developed, and also it closely relates to the efficiency and effectiveness of public expenditure. The relevant theoretical problems are: what is the relationship between education and economic growth? What kind of education has the greatest contribution to economic growth? For example, the Chinese government began to give priority to the development of education especially higher education from 1990s, and the number of freshmen admitted by college entrance exam increased with an average annual growth rate of 15.2%. Is this education development strategy beneficial to economic growth?
With the development (Romer, 1986, 1987) [1] [2] of new economic growth theory, the externalities from technology spillover are considered to be the main source of sustainable growth. As a key problem of the research on economic growth, the internal relationship between economic growth and human capital gains widespread attention. Some scholars believe that the development of educational human capital can promote economic growth (Wolff [3] , 2000; Angel de la Fuente [4] , 2003). However, some others believe that human capital doesn’t have positive impact on economic growth or there is no clear relationship between them (Pritchett [5] , 1999; Krueger and Lindahl [6] , 2000; Vandenbussche [7] , 2006; Mamuneas [8] , 2006).
One reason is that space is not considered. It is well known that large-scale population movements provide rich laborforce, promote the development of the economy and society, lead to the proliferation and spread of technology, and produce social economic effects. Each province is no longer an independent economic entity. Instead, all provinces have become an economic community and have mutual influence on each other. Thus, the space among provinces is an indispensable factor which should be considered in both theoretical research on human capital and economic growth.
In addition, the selection of indicators of human capital is a key issue affecting the determination of the relationship between human capital and economic growth. Becker [9] (1962) divided human capital investment into different forms such as education, training, health care and migration. Different human capital investments form different types of human capital, and show the hierarchical development from the lower forms to higher forms. Besides, health is a form of human capital. If human capital was narrowly equated to education, it would underestimate the impact of human capital on economic growth and overestimate the role of education.
This paper attempts to examine the relationship between China’s human capital and economic growth by using different variables and constructing different weight matrixes. In this paper, educational human capital is divided into the capital of primary education, secondary education and higher education, and meanwhile health human capital is taken into consideration to study the effect of different types of human capital. This dissertation applies geography weight matrix which reflects provincial location adjacency. Owing to space spillover effects caused by the geographical distance among China’s eastern, central and western regions, the distance attenuation matrix is set and spatial lag model and spatial error model for specific analysis are applied as well.
2. Literature Review
Rey and Mountuori (1999) [10] first applied cross-section data spatial econometric model to study the convergence of the economy in United States over the period of 1929-1994. They investigated the influence of spatial correlation of adjacent region’s economic growth to the convergence of regional economy, using spatial lag model and spatial error model. Durlauf & Quah (1999) [11] and De La Fuente (1997) [12] started to study the overflow of human capital and technology diffusion, but they didn’t take the influence of geographical position into account. Besides, some scholars study regional economic growth convergence from spatial spillover perspective. Conley and Ligon (2002) [13] , Ertur et al. (2006) [14] and Moreno Trehan (1997) [15] measured economic growth spillover among different nations through geographic and economic distance.
Chinese scholars believe that there is significant positive correlation between China’s human capital and economic growth. As a carrier of knowledge expansion and technology progress, human capital has strong spatial spillover effect on regional economic growth. Researchers (Xiao Zhi-yong [16] , 2010; Li Meng [17] , 2007; Lin Guang-ping [18] , 2005) studied spatial correlation and convergence, especially regional economic convergence and knowledge spillover, using provincial panel data spatial econometric model. Other than study provincial economic convergence, Wu Yu-ming (2007) [19] investigated county economy agglomeration in China during 2002, and Sun Yang (2009) [20] studied regional spatial convergence effect of Pearl, Yangtze River Delta and Bohai Rim over the period of 1990-2006 through spatial econometric model. Using China’s county-level data during 2000, Gu Jia-feng (2008) [21] believe that educational human capital has significant spatial aggregation effect. Bian Ya-jing and Shen Li-sheng (2004) [22] established a production function model using China’s provincial panel data, pointing out that compared to eastern areas, western regions have weak position in both investment and stock of physical capital and human capital.
With regard to the studies of human capital in China, most of empirical literatures treated human capital as a homogeneous concept. Some papers incorporated human capital in the growth accounting and found a positive relationship between growth and education (Fleisher & Chen [23] , 1997), while several studies which included human capital in the regressions to explain regional growth disparity in China found an insignificant effect of human capital on growth (Chen & Fleisher [24] , 1996; Wei, Liu, Song, & Romilly [25] , 2001). However, there are several recent papers which investigated the relationship between different educational levels and growth in China. Chi [26] (2008) concluded that tertiary education has a positive and larger impact on GDP growth than primary and secondary education. Fleisher, Li and Zhao [27] (2010) found that workers with more than elementary school education have a much higher marginal product than labor with no higher than elementary schooling.
In summary, a huge progress has already been made in both the direction and the depth of the research. There is still much room for research on spatial econometric model.
First, this paper plans to use spatial lag model and spatial error model which are commonly used to conduct the research. In doing so, the most important thing is to set spatial structure and an appropriate spatial structure weight matrix is the key. In current empirical studies, most of researchers would use spatial adjacency to set weight which is very simple. However, the spatial spillover of human capital is not limited only between adjacent areas. Interactions also exist between locations that are not adjacent but close. Therefore, this paper not only set geographic weighting matrix considering the adjacency of the geographic location, but also set distance decay matrix considering that the eastern, the central and the western regions are actually three overalls, and that the spatial effect caused by geographic distance also exist between these three huge regional economies.
Besides, educational human capital is divided into primary education, secondary education and higher education in this paper. The author is trying to investigate whether these three types of education have spatial spillover effect; and if it does, is it positive or negative? The results could offer a reference for government’s policies on education and educational resource distribution. By conducting empirical analysis with those two space models and those two spatial weight matrix models mentioned above, the real relationship between human capital, spatial spillover and economic growth can be studied more accurately.
In addition, this paper also considers educational human capital and health human capital. As an important part of human capital, the impact of population’s health status and its change on economic growth should not be neglected.
3. Model, Variable and Data
The data used in this paper involves population and economic variables of 28 provinces in Chinese mainland over the period of 1987-2007. Although there are 31 provincial-level regions in mainland China, Hainan and Tibet are excluded for missing data, and Because Chongqing became a municipality city drawn from Sichuan Province in 1997, Chongqing and Sichuan are accounted as one province.
The form in this paper is different from the original Solow model since it has introduced education and health human capital in the economic growth model. Adopting production function of Cobb-Douglas, we can get the expanded Solow model consisting with human capital, whose form is:
 (1)
(1)
where Y represents total output, A represents technology stock, K represents physical capital stock, H represents human capital stock which consists educational human capital E and health human capital M.
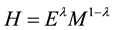
where 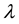 is the parameter, and the substitution elasticity of educational human capital and health human capital in the process of generating human capital is 1. Taking logarithm of both sides of the Equation (1), we can get:
is the parameter, and the substitution elasticity of educational human capital and health human capital in the process of generating human capital is 1. Taking logarithm of both sides of the Equation (1), we can get:
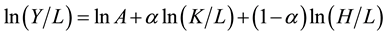 (2)
(2)
This can also be written as:
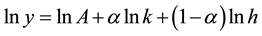 (3)
(3)
where y represents per capita GDP of labor population, k represents per capita physical capital of labor population, h represents per capita human capital which consists of the average years of schooling and life expectancy.
 (4)
(4)
Taking (4) into (3), we can get:
 (5)
(5)
where m represents per capita health capital, 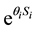 represents per capita education capital (
represents per capita education capital (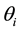 represents the coefficient of education at i level, and
represents the coefficient of education at i level, and 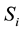 represents the years of being educated at i level, i = (1, 2, 3), Each stands for primary education, secondary education and higher education respectively. We denote output (Y) by Per capita GDP, and all the per capita GDP data is provided by statistical databases of China’s economic and social development. Capital stock (K) data is taken from the capital stock database estimated by China Center for Economic Study of Fudan University (Zhang Jun, Wu Gui-ying and Zhang Ji-peng [28] , 2004). Data over the period of 2001-2005 are figures estimated by Professor Zhang Xueliang from Shanghai University of Finance and Economics, adapting from Zhang Jun’s method. We use the perpetual inventory method as the specific calculation method for physical capital
represents the years of being educated at i level, i = (1, 2, 3), Each stands for primary education, secondary education and higher education respectively. We denote output (Y) by Per capita GDP, and all the per capita GDP data is provided by statistical databases of China’s economic and social development. Capital stock (K) data is taken from the capital stock database estimated by China Center for Economic Study of Fudan University (Zhang Jun, Wu Gui-ying and Zhang Ji-peng [28] , 2004). Data over the period of 2001-2005 are figures estimated by Professor Zhang Xueliang from Shanghai University of Finance and Economics, adapting from Zhang Jun’s method. We use the perpetual inventory method as the specific calculation method for physical capital
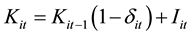
where i represents the i-th province, t represents the t-th year. I refers to the investment of the year, and its indicator is the gross fixed capital formation (data from the National Bureau of Statistics Database: http://www.stats.gov.cn); δ represents the economic depreciation rate (calculate as 9.6%); Additional capital investment for the year will be converted to a constant price, using the price index of investment in fixed asset published by “China’s Statistical Yearbook”.
Health human capital is measured by life expectancy (M) in this paper. As China’s Statistical Yearbook only contains data for every ten years, so this paper applies liner interpolation method to obtain the estimates. In this article, the average year of schooling is used to measure educational human capital. Each provincial data of the average level of education and data of the proportion of the higher educated, the secondary educated and the primary educated are provided by Chen Zhao and other scholars’ research results.
In accordance with China’s education system, we divided the workforces who are beyond age of 15 into 5 groups according to their educational level. Namely, the population of tertiary and higher education H1, the population of high school education H2, the population of junior high school education H3, the population of primary school education H4, and the population of illiterate and semiliterate H5. According to the years of schooling, the author sets weights for each group. Specifically: 0 for illiterate and semiliterate, 6 for primary school education, 9 for junior high school education, 12 for high school education, and 16 for tertiary and higher education. At last, calculate the total stock of human capital with weighted sum method. It can be expressed as:
Total stock of human capital = (human capital stock of higher education H1 + human capital of high school education H2 + human capital of secondary education H3 + human capital of primary education H4 + human capital of illiterate and semiliterate H5) = Σ (the population of different education level × weight) = 16 × H1 + 12 × H2 + 9 × H3 + 6 × H4 + 0 × H5.
Dividing the total stock of human capital by the number of educated people at different level, we can get the average stock of human capital (the average years of schooling for working population). Expressed in formula is:
The average stock of human capital = the total stock of human capital/the population of different education level.
4. Analysis
Using China’s provincial administrative panel data, this paper is trying to construct a spatial econometric model to interpret the correlation between China’s provincial economic growth and human capital. We assume that the economic growth of each province in China depends not only on the level of human capital and physical capital, but also relies on the human capital level of adjacent regions, that is to say, both education human capital and health human capital have spatial “spillover effect” either within the region or between regions. Moran I index is a common method to test whether spatial autocorrelation exist between region variables. In order to determine whether spatial autocorrelation exist between the variables, this paper tested all the variables with Moran method before the empirical spatial econometric analysis. The formula of Moran I is:
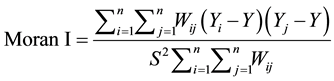
where,  ,
, 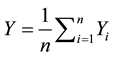 , Yi represents the observed value of the i-th region, n is the total
, Yi represents the observed value of the i-th region, n is the total
number of regions, 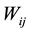 is binary adjacent spatial weights matrix, using adjacency standard or distance standard, which aims to define the adjacent relationship between spatial objects. The general adjacency standard is: the value of adjacent regions is 1, otherwise 0. Moran I values range from −1 to 1. When the value is above 0, it indicates a positive spatial correlation between regions, and the larger the value is, the stronger the positive correlation becomes. When the value is below 0, the spatial correlation is negative. While when the value is 0, there is no spatial correlation between regions.
is binary adjacent spatial weights matrix, using adjacency standard or distance standard, which aims to define the adjacent relationship between spatial objects. The general adjacency standard is: the value of adjacent regions is 1, otherwise 0. Moran I values range from −1 to 1. When the value is above 0, it indicates a positive spatial correlation between regions, and the larger the value is, the stronger the positive correlation becomes. When the value is below 0, the spatial correlation is negative. While when the value is 0, there is no spatial correlation between regions.
The specific variables of Moran I index are shown in Table 1, we can see that the coefficients of seven variables over the period of 1987-2007 are positive, reaching a significant level of 0.10. Therefore, the spatial autocorrelation test proved that per capita GDP, life expectancy, physical capital, educational human capital and the geographical distribution of various educational levels are not random, but showing significant positive spatial correlation. Lin Guang-ping [18] (2005)’s research results also confirmed that since 1992, with the deepening reform of economic system, the economic ties between regions have gradually grown stronger and the neighboring provinces have been showing strong spatial correlation. Gu Jia-feng [21] (2008) found that most of the indicators are significant among the Moran I index of Chinese provincial economic, society and the migrant population variables, which means economy, society and migrant population also has significant geographic aggregation. Therefore, it is necessary to take spatial correlation into account when we conduct researches on the relationship between regional economic and human capital.
Table 1. Moran I index of each year.
Note: ***, **, * respectively denotes the significance level of statistical measurement test results 1%, 5%, 10%.
According to different reflection methods of model setting for “space”, there are two kinds of spatial econometric models: SAR and SEM. The first model (SAR) is mainly used to study situations when the behavior of neighboring institutes or regions has an impact on other institutes or regions within the whole system. The specific formula is:
W is spatial weight matrix of N-N order, namely a matrix which shows the web-structured relationship of several (N) institutes or regions. The weight matrix W need to be standardized to make the sum of each row in the weight matrix equals 1. Wy is the spatial lag of the dependent variable, 
In the second model (SEM), the relationship between organization or regions are reflected through the error term. This model is often used when the interaction between organizations or regions varies with different relative positions. The specific formula is:
where y is the dependent variable, X is exogenous explanatory variable matrix, 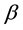
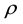
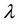
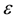
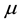
This article uses two kinds of spatial weights matrix to do empirical analysis, the first one is the geo-spatial weight matrix; the weight of geographic adjacent area is 0, while non-adjacent areas is 1; the second one is the distance decay weight matrix, which uses distance decay function to construct spatial weights matrix. The specific formula is:
where, i, j, represent any two different regions; 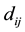
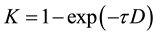
Taking spatial matrix of all regions in china as an example, the form is as follows:
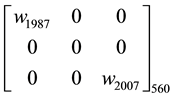
where,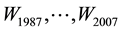

5. Results and Analysis
In this paper, four aspects were considered while constructing the spatial econometric model. First, we divided human capital into two categories and constructed two models respectively. One model measured the educational human capital by the average years of schooling. Another model subdivided the educational human capital into primary education, secondary education and higher education. Besides, the spatial econometric panel model setting consists of SAR Panel Data and SEM Panel Data; in addition, the spatial weights matrix setting includes distance decay weights matrix and geographic weights matrix; at last, the error component of spatial panel data model includes unfixed effect, spatial fixed effect, time fixed effect and temporal-spatial fixed effect. In summary, there can be 2 × 2 × 2 × 4 = 32 aspects.
Models were separated into two categories in this paper. First, we consider the model which measures the educational human capital by the average years of schooling. More details can be seen in Table 2 and Table 3. At first, Table 2 tested the spatial correlation of the distance decay weights. According to the results in Table 2, we can see that spatial autocorrelation exist in the regression error term and it applies to both spatial lag panel model and spatial error panel model. Spatial correlation test of panel data based on geographic weight matrix shows almost the same significance.
Measuring the educational human capital by the average years of schooling, Table 1 presents two spatial panel models, one of which is based on distance decay weights and the other one is based on geographic weights. We can get the following results:
Table 2. Spatial correlation test of distance decay weights.
Table 3. Table of spatial panel model based on the average years of schooling.
Note: ***, **,* respectively denotes the significance level of statistical measurement test results 1%, 5%, 10%.
In all cases, the absolute values of the log-likelihood function estimated by the equation are relatively large. The largest absolute value is in the unfixed effect model and the smallest is in the temporal-spatial fixed effect model. The R-squared which represents the goodness-of-fit of the model is significant high in temporal-spatial fixed effect. Besides, the goodness-of-fit of spatial lag panel data in space fixed effect is higher than it in time fixed effect. In spatial error panel data, the situation is the same. The R-squared of temporal-spatial effect model almost remains the same either in spatial lag panel model or spatial error panel model.
Since estimates of the W*dep.var which marks the spatial dependence and estimates of the Error Spat.aut. both reached a significant level of 1%, it further confirmed the spatial correlation among data. On the whole, in panel data models, the coefficient estimates based on distance decay weights matrix is larger than the ones based on geographic weights matrix. (For example, in the unfixed effect model which belongs to the spatial error model, the value of Spat.aut. based on distance decay weights is 0.814, yet the Spat.aut. value based on geographic weights is 0.790) This probably because that the spillover and diffusion of human capital are limited by geographical positions in some degree, and they (the spillover and diffusion effect) will decay with the increase of spatial distance (Keller [29] , 2002; Miao Fu [30] , 2009), however, such diffusion is not only confined to adjacent areas. Interplay and radiation still exist between regions that are not geographically adjacent. Therefore, the distance decay weights matrix considered the distance between capitals when it reflects the neighbor relations. The weight setting is more even, and the reflection to reality becomes more accurate.
According to the four spatial lag regression models, the R-squared value and the Log-likelihood value affected by spatial and time fixed effect shows significant improvement. Meanwhile, other regression variables are also significant, even the spatial lag term passed the test. In light of this, we can conclude that not only spatial fixed effect, but also time fixed effect exists between regions. It also shows us that some ignored factors such as the regional production technology, management abilities, have strong diffusion effect on surrounding areas. In the spatial error regression model, the fitting efficiency of temporal-spatial fixed effect is the optimal among the four kinds of effects.
In the spatial lag panel model and the spatial error panel model, the coefficients of explanatory, namely the average years of schooling, physical capital and life expectancy, show significant positive influence. The average years of schooling is positively correlated with economic growth. This conclusion is similar with the results of Marcelo Soto, Daniel Cohen [31] (2007)’s research. It proves the endogenous growth theory at an empirical level. Romer Model believes that some countries have long been at a low level growth path for a long time is because of the insufficient investment in knowledge production sectors and the low technological progress rate. Therefore, we should encourage the investment in knowledge production. Lucas believes that human capital is mainly obtained by learning and education. Due to the different accumulation of human capital in different countries, the economic growth and GDP per capita is correspondingly different. Physical capital is the material basis and conditions for economic growth and development, and the correlation between them is undeniable. Either the classical theory of economic growth or the new theory of economic growth, they all regard physical capital as an important factor for economic growth. While other forms of capital all depend on a certain amount of physical capital as carrier to achieve the accumulation, such as human capital and social capital. It will be difficult to sustain the economic growth if lacking physical capital as a carrier. Life expectancy has a positive impact on economic growth is mainly because that healthy people can work much longer and they are relatively stronger both in physical, mental and cognitive abilities, which directly enhances the productivity of labors in family and the market. Long life expectancy encourages individuals in production phase to save, which helps to reserve more money capital for economic investment and then further promote the income and economic growth. Moreover, with healthier workforce, more foreign investment will be attracted.
Then consider models of the second category. Among the explanatory variables, educational human capital is measured by primary education, secondary education and higher education. The specific results are shown in Table 4 and Table 5.
Based on results in Table 4, we can see that spatial autocorrelation exist in the regression error term, and it applies to both spatial lag panel model and spatial error panel model. The spatial correlation test of panel data based on geographical weights matrix also shows the same significance.
Diving educational human capital into primary education, secondary education and higher education, Table 4 presents two spatial panel models, one of which is based on distance decay weights and the other one is based on geographic weights. We can get the following results:
In spatial lag panel data model, the R-squared values of temporal-spatial fixed effect are 0.920 and 0.922
Table 4. Spatial correlation test of distance decay weights.
Table 5. Spatial panel model based on three different education level.
Note: ***, **, * respectively denotes the significance level of statistical measurement test results 1%, 5%, 10%.
respectively, and the log-likelihood values are −92.28 and −87.37. Compared to the un-fixed effect, spatial fixed effect and time fixed effect, these values are the greatest, which indicates that the temporal-spatial fixed effect model has better goodness-of-fit than any other effect model. Therefore, this paper lays a lot of emphasis on the results of temporal-spatial fixed effect model.
From the temporal-spatial fixed model in spatial lag panel data model, we can find out that the coefficient of primary education and higher education are both positive, and that p values are both below the significance level of 5%. Therefore, we can conclude that there is a significant positive correlation between these two different levels of education and economic growth. Where, the coefficient of higher education in distance decay matrix and geographical weights matrix are 11.304 and 11.152 respectively. The coefficient of secondary education is not significant in distance decay matrix, while it is significant in geographical weights matrix as its value is 0.250. The coefficient of primary education in distance decay matrix is 6.452, while 6.379 in geographical weights matrix. The results indicate that the workforce who received higher education contributes the most to economic growth, and workforce who received primary education comes second while workforce who received secondary education contribute the least. There are several reasons for this result. First, as one kind of “mature” labor force, workforce who received higher education can adapt to the liquidity faster and better, which is good for the technology innovation for the inflow area, moreover, they have better abilities in learning new technology, which further promotes economic growth. As for the workforce who only received primary education, they are usually engaged in labor-intensive industries due to their low education level. The liquidity increases since they have to move around to get better opportunities, and finally attributes a lot to economic growth. According to Cai Fang’s research, rural migrant workers are usually not the ones who have received secondary or higher education, because rural workforce who have received better education have already had a good occupation in rural areas, so the motive to migrant to other places is weak. This explained why the spatial spillover effect of secondary education is not significant.
The result of spatial error model is similar to the result of spatial lag model. It is also presented as a result that the temporal-spatial fixed effect model is the best. The coefficient and significance of the three different education levels agree with the ones in spatial lag panel model, from which we can conclude that higher education contributes the most to economic, primary education comes second and secondary education contributes least.
6. Conclusion and Suggestion
Through the spatial statistics based on data provided by China’s 28 provinces, municipalities and autonomous regions over the period of 1987-2007 and the empirical results of econometric analysis, we can conclude that: the spatial dependence between Chinese human capital and economic growth is statistically significant; among the empirical results of different fixed effect model settings, the magnitude and direction of correlation between human capital and economic growth vary, not only including the positive impact of the development of human capital in time dimension, but also involving the negative impact of regional differences of human capital in space dimension; through the spatial lag model, we can see that the provincial human capital will affect the provincial economic growth, and the effect will be further passed to the economic growth of the neighboring provinces or even the whole region. Compared to the traditional statistical model, spatial statistical model and spatial panel data model can reveal the spatial autocorrelation and spatial clustering of human capital much deeper since it includes both the vertical movement and the horizontal differences in time and space dimensions.
In order to further promote the free flow of human capital among the eastern region, central region and western region of China, to realize the rational allocation of human capital, to make full use of the positive spatial spillover effect of human capital, and finally to contribute to economic growth, the government should make efforts from the following aspects:
First, the government should make full use of spatial spillover effect and promote the coordinated regional development of human capital. Only flow capital can produce benefits, so does human capital. The flow of human capital directly affects its operational efficiency. Seeing from the perspective of space transfer, a certain transaction cost must be paid if human capital is about to migrate or flow to other regions or industries. However, this cost is also a kind of “investment” because the migration for better opportunities is the payment for higher “future income”, and this kind of flow has influence on the operational efficiency of human capital. Meanwhile, liquidity also denotes the merit and maturity of the economic system. According to the analysis above, we can see that the spatial mobility of workforce will always have positive impact on economic growth regardless of the different education levels. Currently, the household registration system reform hasn’t been completed yet. When rural labors move out for off-farm employment, they can’t transform their identity to citizenship at the same time. Therefore, the movement of rural labors is inadequate and incomplete, which is not conducive to motivate the enthusiasm of rural labors. Moreover, it also leads to the co-existence of labor mobility and income disparities. So, the government should continue the reform of the household registration system, break down the spatial mobility barrier of elements, product and workforce, and resolve the spatial structure problem through the interaction between people and material. Specifically, first of all, the household registration system reform must continue under the auspices of central government and a series of unified household registration management laws and regulations must be established so that the comprehensive and effective management can be conducted. Population migration and flow are individual’s rational economic behavior since it is a measure that an individual takes to seek for better opportunities. However, due to the imbalanced distribution of public goods in local areas, the population flow is also imbalanced, which requires more financial support for the backward regions from the government so that the supply of public goods can be improved. The government also needs to narrow the inter-regional differences at maximum and avoid some population flow that is not necessary. Meanwhile, the government should use some economic leverage to regulate the population flow to large cities, such as tax and the price of real estate. Namely, under the premise of non-discrimination, the government should use macroeconomic measures to increase the cost of migration, in case the density of urban population becomes too high and the healthy development of the city gets affected. As for the population that has already migrated to other regions, government should ensure they have equal welfare with local people, and also ensure that their accumulation can be transferred to the resettlement place. By doing so, migrant labors will be motivated to work harder in the new places, and the probability of occurrence of mass incidents will be reduced, which has positive impact on the maintenance of social stability and harmony.
Besides, while making policies of human capital investment, government should take spatial correlation into consideration, pay attention to the spatial association between the central western inland areas and the eastern coastal areas, and strengthen the economic interaction between the eastern, the central and the western areas. Compared to the eastern region, the central and western regions are at a disadvantage in economic development, employment environment and development opportunities, which not only makes it difficult to attract high-qual- ity talents from outside, but also makes it hard to keep their own talents. To solve this problem, it is imperative to establish a long-term mechanism of human capital mobility and introduction. It is also important to improve both hard and soft conditions for talent development and growth through the implementation of a variety of policies. On one hand, we can introduce foreign talents into our country. But more importantly, we should build a long-term mechanism of nurturing internal talent to inject new vitality to our economy. The central government should further strengthen the financial support for the central and western regions, such as increasing transfer payments, supporting the education in rural underdeveloped areas and ethnic minority areas, strengthening the key areas and weak links, and solving outstanding problems.
All in all, as to promote the development of Chinese human capital and achieve economic growth by making full use of the spatial spillover effect of human capital, we need to establish a multi-level policy framework from government and society down to individuals, and all relevant policies and measures must be combined with the determinants of economic and social development of human capital.
References
- Romer, P. (1986) Increasing Returns and Long-Run Growth. Journal of Political Economy, 94, 1002-1037. http://dx.doi.org/10.1086/261420
- Romer, P. (1987) Growth Based on Increasing Returns Due to Specialization. American Economic Review, 77, 56-62.
- Wolff, E.N. (2000) Human Capital Investment and Economic Growth: Exploring the Cross-Country Evidence. Structural Change and Economic Dynamics, 11, 433-472. http://dx.doi.org/10.1016/S0954-349X(00)00030-8
- de la Fuente, Á. and Ciccone, A. (2003) Human Capital in a Global and Knowledge-Based Economy―Final Report. Office for Official Publications of the European Communities, Luxembourg.
- Pritchett, L. and Filmer, D. (1999) What Education Production Functions Really Show: A Positive Theory of Education Expenditures. Economics of Education Review, 18, 223-239. http://dx.doi.org/10.1016/S0954-349X(00)00030-8
- Krueger, A.B. and Lindahl, M. (2000) Education for Growth: Why and for Whom? Journal of Economic Literature, 39, 1101-1136. http://dx.doi.org/10.1257/jel.39.4.1101
- Vandenbussche, J., Aghion, P. and Meghir, C. (2006) Growth, Distance to Frontier and Composition of Human Capital. Journal of Economic Growth, 11, 97-127. http://dx.doi.org/10.1007/s10887-006-9002-y
- Mamuneas, T.P., Savvides, A. and Stengos, T. (2005) Economic Development and the Return to Human Capitals: A Smooth Coefficient Semi-Parametric Approach. Journal of Applied Econometrics, 21, 111-132. http://dx.doi.org/10.1002/jae.813
- Becker, G.S. (1962) Investment in Human Capital: A Theoretical Analysis. Journal of Political Economy, 70, 9-49. http://dx.doi.org/10.1086/258724
- Rey, S.J. and Montouri, B.D. (1999) US Regional Income Convergence: A Spatial Econometric Perspective. Regional Studies, 33, 146-156. http://dx.doi.org/10.1080/00343409950122945
- Durlauf, S.N. and Quah, D.T. (1999) Chapter 4. The New Empirics of Economic Growth. In: Taylor, J.B. and Woodford, M., Eds., Handbook of Macroeconomics, Vol. 1, Part A, Elsevier, Amsterdam, 235-308.
- de la Fuente, A. (1997) The Empirics of Growth and Convergence: A Selective Review. Journal of Economic Dynamics and Control, 21, 23-73. http://dx.doi.org/10.1016/0165-1889(95)00925-6
- Conley, T.G. and Topa, G. (2002) Socio-Economic Distance and Spatial Patterns in Unemployment. Journal of Applied Econometrics, 17, 303-327.
- Ertur, C. and Koch, W. (2006) Regional Disparities in the European Union and the Enlargement Process: An Exploratory Spatial Data Analysis, 1995-2000. The Annals of Regional Science, 40, 723-765. http://dx.doi.org/10.1007/s00168-006-0062-x
- Moreno, R. and Trehan, B. (1997) Location and the Growth of Nations. Journal of Economic Growth, 2, 399-418. http://dx.doi.org/10.1023/A:1009741426524
- Xiao, Z.-Y. (2010) Human Capital, Spatial Spillover and Regional Economic Growth. Finance & Economics, 3, 61-68.
- Li, M., Zhang, Y.-L. and Zhang, G.-P. (2007) An Empirical Study on Regional Distributing Disparities of Chinese Human Capital. Education & Economy, 1, 12-17.
- Lin, G.-P., Long, Z.-H. and Wu, M. (2005) A Spatial Analysis of Regional Economic Convergence in China: 1978- 2002. China Economic Quarterly, No. S1, 67-82.
- Wu, Y.-M. (2007) Agglomeration and Differences of County Economic Growth: An Empirical Analysis of Spatial Econometrics. World Economic Papers, No. 2.
- Sun, Y. (2007) Strategies of Industrial Development and Spatial Convergence: A Comparative Analysis of “Chang San Jiao”, “Zhu San Jiao” and “Huanbohai” Districts. Nankai Economic Studies, No. 1.
- Gu, J.-F. (2008) Spatial Analysis of Education Development and Economy Development. China Population Resources and Environment, No. 6.
- Bian, Y.-J. and Shen, L.-S. (2004) Empirical Analysis of the Impact of Human Capital on Economic Growth in East and West. Quantitative & Technical Economics, No. 12.
- Fleisher, B.M. and Chen, J. (1997) The Coast-Noncoast Income Gap, Productivity, and Regional Economic Policy in China. Journal of Comparative Economics, 25, 220-236. http://dx.doi.org/10.1006/jcec.1997.1462
- Chen, J. and Fleisher, B.M. (1996) Regional Income Inequality and Economic Growth in China. Journal of Comparative Economics, 22, 141-164. http://dx.doi.org/10.1006/jcec.1996.0015
- Wei, Y.-Q., Liu, X.-M., Song, H.-Y. and Romilly, P. (2001) Endogenous Innovation Growth Theory and Regional Income Convergence in China. Journal of International Development, 13, 153-168. http://dx.doi.org/10.1002/jid.721
- Chi, W. (2008) The Role of Human Capital in China’s Economic Development: Review and New Evidence. China Economic Review, 19, 421-436. http://dx.doi.org/10.1016/j.chieco.2007.12.001
- Fleisher, B., Li, H.-Z. and Zhao, M.-Q. (2010) Human Capital, Economic Growth, and Regional Inequality in China. Journal of Development Economics, 92, 215-231. http://dx.doi.org/10.1016/j.jdeveco.2009.01.010
- Zhang, J., Wu, G.-Y. and Zhang, J.-P. (2004) The Estimation of China’s Provincial Capital Stock: 1952-2000. Economic Research Journal, 10, 35-44.
- Keller, A., Nesvizhskii, A.I., Kolker, E. and Aebersold, R. (2002) Empirical Statistical Model to Estimate the Accuracy of Peptide Identifications Made by MS/MS and Database Search. Analytical Chemistry, 74, 5383-5392.
- Fu, M. (2009) Geographical Distance and Technological Spillover Effects: A Spatial Econometric Explanation of Technological and Economic Agglomeration Phenomena. China Economic Quarterly, 8, 1549-1566.
- Cohen, D. and Soto, M. (2007) Growth and Human Capital: Good Data, Good Results. Economic Growth, 12, 51-76. http://dx.doi.org/10.1007/s10887-007-9011-5