Journal of Biophysical Chemistry
Vol.2 No.3(2011), Article ID:6733,9 pages DOI:10.4236/jbpc.2011.23034
Spin effects govern DNA/RNA nucleotide polymerization
AstraZeneca Pharmaceuticals, Södertälje, Sweden; *Corresponding Author: atulub@yahoo.co.uk
Received 8 November 2010; revised 10 March 2011; accepted 8 April 2011.
Keywords: Radical Polymerization; Nucleotides
ABSTRACT
A new radical mechanism of nucleotide polymerization is found. The finding is based on the Car-Parrinello molecular dynamics computations at 310 K with an additional spin-spin coupling term for 31P and 1H atoms and a radical pair spin term included. The mechanism is initiated by a creation of a high-energy spin-separated Mg-ATP complex in a triplet state in which the Mg prefers an uncommon chelation to the O2-O3 oxygens of the ATP. The cleavage of the complex produces the (AMPand (Oradicals. The latter captures a proton from acidic solution (the Zundel cation) that converts it into the (OH radical. The process agrees with the protoncoupled electron transfer (PCET) mechanism. Through interacting with the HO-C3’ group of the deoxyribose/ribose the (OH radical captures its hydrogen atom. The process is accompanied by producing water and the (AMP radical. The (AMPand (AMP radicals then interact yielding a dimer. The described mechanism is easily generalized for a bigger number of adjoining nucleotides and their type. The radical mechanism is highly sensitive to the (AMP-(OH radical pair spin symmetry and the radius of the (OH diffusion. This confines the operation of the radical mechanism: it is applicable to nucleotide polymerization through the HO-C3’ group of deoxyribose/ribose (DNA/RNA polymerization) and inapplicable through the HO-C2’ group of ribose (RNA)—a result that nature has developed over evolution.
1. INTRODUCTION
In a living cell a polynucleotide synthesis proceeds along a chain of DNA nucleotides with a special holoenzyme—DNA polymerase [1,2]. The enzyme’s action is closely related to the activity of associated with its structure Mg2+ cations whose role in the polynucleotide synthesis is still unclear [3-7]. It is proved that the adjoining of a new nucleotide to the growing polynucleotide chain occurs through the cleavage of a corresponding nuclesidetriphosphate (NTP; N = Аde, Gua, Cyt, Тhy) to nucleisidemonophosphate (NMP) [2,3]. The cleavage is commonly assumed to be a purely hydrolytic (ionic) process yielding the NMP in a {ВR(PaO4)H2} (В-base, R-deoxyribose/ribose) form with the phosphorrus atom Pa bound to four oxygen atoms [3]. The diester bond formation between the adjoining nucleotide and the polynucleotide chain (polymerization) is also viewed as a hydrolytic process yielding as a side product a water molecule arising through interaction between the negatively charged ОН– group of NMP and the proton Н+ of the ribose hydroxyl. We have outlined this, widely accepted mechanism of the diester bond formation [1-4], to stress its purely ionic nature that initially excludes any spin effect: the initial, intermediate and final products are in the same singlet (S) state. Everything seems fine, but why the presence of Mg (without it no cleavage or synthesis occurs [5-7]) is that essential? The question has no answer and serves the topic of vigorous disputes [8,9]. If the role of Mg is reduced only to polarization of P-O bonds that favors the NTP hydrolysis (the common view), then the Mg could be easily replaced by other cations, say Ca, Ве, Zn, Мn or Fe, because the triphosphate core of NTP is flexible enough to adjust to chelation with each of the said cations showing the similar polarization effect on the P-O bonds [1,3,8]. The unique nature of Mg is traced not only in polynucleotide chain synthesis but in many other NTP-involved reactions like Polymerase Chain Reaction (PCR) [10], tubulin assembly into microtubules [11], myosine dynamics [12,13], and intra-, inter-cellular signaling [2,14].
Besides the ionic mechanism of NTP cleavage there is an alternative one—the radical mechanism [15]. It is initiated by altering spin symmetry of the Mg2+ upon its excitation from the lowest in energy S state into the lowest in energy triplet (T) state. The mechanism was recently revealed in quantum computer experiments [15,16] and indirectly proved by the Chemically Induced Dynamic Nuclear Polarization (CIDNP) on 31P nuclei [15]. The excitation into the T state that proceeds in vitro in a femtosecond interval results in producing the two ion-radicals, ·Mg+ and ·NТP3– (the dot stands for a radical), with the latter showing a rapid decomposition into the ·NМP–. Totally, the process spans over the 1.25 ´ 102 picosecond interval, reaction (1), if the latter thought in the water bulk of 78 water molecules (the corresponding water box is 12.17 ´ 8.17 ´ 21.18 Å3 that includes the ATP molecule (N = Ade) with the first-second water shell around it and the (H2O)6Mg2+ initially distanced from the O2-ATP by 8 Å; water molecules imitate the real solution, for details see [15]):
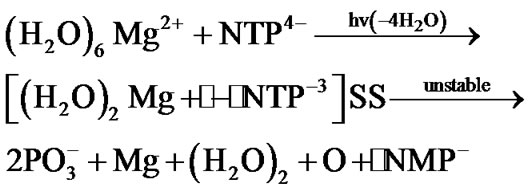 (1)
(1)
The most time-consuming stage in (1) is the Coulomb approach between the (H2O)6Mg2+ and NTP4–, their reorientation and the loss of four of the six initially bound to the Mg water molecules. The cleavage of the [(H2O)2Mg+· – ·NТP–3]SS (SS stands for a spin-separated state with one electron on the Mg and the rest on the NTP) is, on the contrary, highly rapid, ~5 ps [15,16]. At this very point one must make it clear that the ~5 ps interval assumes the pure decomposition time when the Mg cation is just chelated by the O2-O3 fragment of the ATP and the chelate is energetically unstable (the difference in the total energy for the separated ATP+ (water shell) molecule and the (H2O)6Mg2+ and their chelate is around 20 kcal/mol) that allows it to show such a fast decomposition. The total decomposition time as it is said above is two orders higher.
A strong contrast between the radical and the ionic cleavage is that the first mechanism yields a highly active radical - ·NMP– - while the second gives a purely inert ionic form - NMP2–. In addition, the structure of ·NMP– and NMP2– shows a remarkable difference—in the ·NMP– the phosphorus atom Pa is bound to three oxygen atoms while in the NMP2– (hereinafter NMP) it is bound to four oxygens. Reaction (1) assumes its further progress involving the attack of its radical products, see below, their potential cellular targets—the inert NMPs or their strings—polynucleotide chains.
The paper aims to prove that:
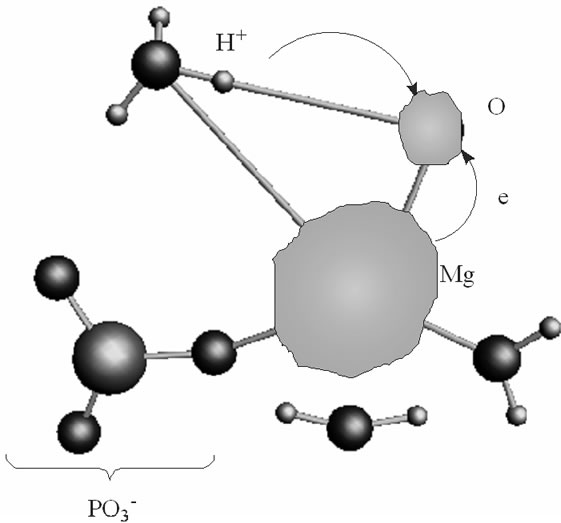
1) The AMP polymerization (without loss of generality, in our computational experiment NTP/NMP º ATP/ AMP) has the radical nature: it originates from the cleavage of the unstable [·Mg+(H2O)2 – ·AТP3–]SS complex with two unpaired electrons located on the Mg and ATP subsystems (Figure 1, left), followed by the production of two highly active radicals - ·OH and ·AMP–, which successively attack the inert AMP/(AMP chain) (Figure 1, right) by converting it, first, into an active radical and, second, by adding to this newly produced radical the ·AMP– radical via a spin-sensitive radicalradical interaction.
2) The radical mechanism of nucleotide polymerization occurs only through attacking the ·OH and ·AMP– radicals the HO-С3’ group of deoxyribose/ribose (DNA/ RNA) and not through the HO-С2’ group of ribose (RNA), Figure 1, leaving the latter exposed only to the ionic polymerization mechanism.
The results come from the Car-Parrinello Molecular Dynamics (CPMD) simulations [17] at 310 K.
2. GEOMETRY PARAMETERS AND COMPUTATIONS
The initial geometry of the high-energy [·Mg+(H2O)2–

Figure 1. Structural formulae of the [·Mg+(H2O)2 – ·ATP3–]SS complex (left) and the AMP (right).
·AТP3–]SS complex (see section 1), Figure 1 (left), was obtained previously with the DFT:B3LYP, 6-311G** basis set, computations [15,16]. In this complex the Mg atom chelates the O2 oxygen atom (r[Mg-O2] = 1.98 Å) and the O3 oxygen atom (r[Mg-O3] = 2.67 Å). It should be put upfront that this way of chelation differs from that known in a stable complex [Mg2+(Н2О)4 – АТP4–] where the Mg binds with the O1 and O2 oxygen atoms. This uncommon chelation results from the interaction between the Mg2+(Н2О)4 complex in the lowest T state (that is a very important thing!) and the ATP4–, for details see [15,16]. The difference in the total energy between the {[·Mg+(H2O)2 – ·AТP3–]SS + 2H2O + water solution} and the [Mg2+(Н2О)4 –АТФ4– + water solution] is ~20 kcal/mol. The initial geometry of AMP was obtained from the DFT: B3LYP, 6-311G** basis set and fits perfectly into the reported one [18].
In a cell, the polynucleotide synthesis to occur the ATP and AMP should be distanced in a range ~8 - 4 Å [3]. This is achieved by a combined action of a holoenzyme, which activates ATP and pushes it forward to the AMP, and a template that locates the AMP (or the growing polynucleotide chain) in a fixed volume to guarantee the attack of ATP products on the AMP ribose hydroxyls [1-3]. In computations the proximity between the ATP and AMP and the AMP location is reached by a volume fixation, in which the both molecules are trapped and not allowed to escape. At the same time they are allowed to approach each other, change their configuration, and interact. Figure 2 displays the way the ATP and AMP face each other in a volume (periodic box) 16.0 ´ 9.0 ´ 18.0 Å3. The displayed arrangement, according to the previous CPMD computations [19], is thermodynamically the most favorable among all the possible configurations. Region ii spans over the diphosphate part of the ATP (it leaves the ribose of the AMP sideways; the angle Pg-Pa(ATP)-O(ribose AMP) is 67˚), and region i—the monophosphate part (the Pa(ATP)-O(ribose AMP) distance is 5.75 Å).
Forty four water molecules (the above named box assumes the presence of 132 water molecules; because of the computational limits the number is reduced to 44 by leaving only the first water shell around the ATP and the first-second shell in ii and i regions) and the Zundel cation,  , (they are not shown in Figure 2) create a water subvolume around the triphosphate tail of the ATP, the ribose and the {PO4} group of the AMP, and the region between the Ade bases. The Zundel cation, located at the interface of i and ii regions, is introduced into the subvolume to give a chance for the ·O– radical, see below, to interact with the proton and to imitate the acidic properties of living cell media. The distances between the water molecules in the periodic box, including
, (they are not shown in Figure 2) create a water subvolume around the triphosphate tail of the ATP, the ribose and the {PO4} group of the AMP, and the region between the Ade bases. The Zundel cation, located at the interface of i and ii regions, is introduced into the subvolume to give a chance for the ·O– radical, see below, to interact with the proton and to imitate the acidic properties of living cell media. The distances between the water molecules in the periodic box, including
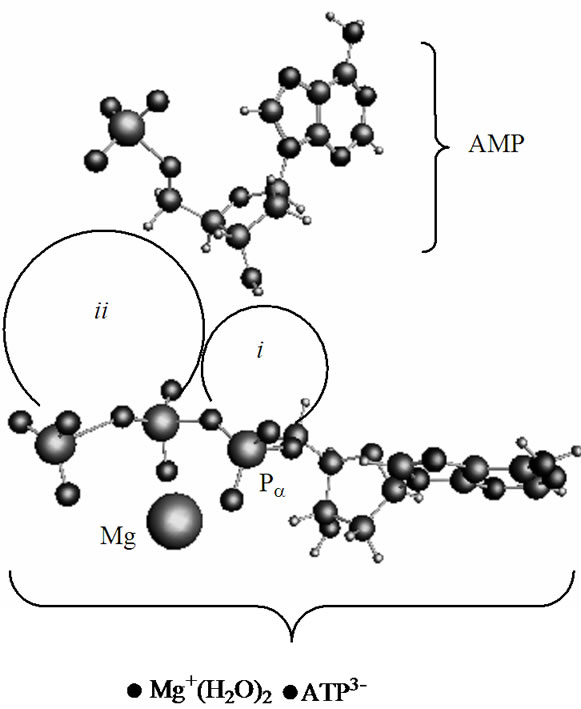
Figure 2. The energetically favorable arrangement of the [·Mg+(H2O)2 – ·ATP3–]SS complex and AMP. The ii and i regions indicate the PgO4-PbO3 diphosphate and the PaO3 monophosphate groups, respectively.
the Zundel cation, are in the range 2.3 - 2.5 Å. Such a created system ([·Mg+(H2O)2 – ·AТP3–]SS + AMP + 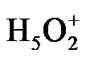 + 44 water molecules) is then slowly heated from 0 to 310 K, for details see our previous works [15,16]. Over the heating the ([·Mg+(H2O)2 – ·AТP3–]SS complex is forced to conserve its initial geometry to prevent its premature decomposition, Figures 1, 2.
+ 44 water molecules) is then slowly heated from 0 to 310 K, for details see our previous works [15,16]. Over the heating the ([·Mg+(H2O)2 – ·AТP3–]SS complex is forced to conserve its initial geometry to prevent its premature decomposition, Figures 1, 2.
The spin effects in the nucleotide polymerization initially assumed, the standard energy functional requires its enlargement by adding two specific terms: the hyperfine coupling (HFC) term and the radical pair RP term [20-23]. The inclusion of the HFC term is highly considerable, specifically for the phosphorus atoms, which active spin nuclei show a 100% natural abundance [24] and strongly affect the behavior of unpaired electrons in the PO(OR)2 and 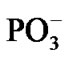 radical fragments [25]. The same is valid for the active nuclear spins of hydrogen atoms (natural abundance of 1H atoms with the active nuclear spin is 99.985%24) in water molecules and the ribose hydroxyls. In our computations the HFC for the named atoms includes the both isotropic and anisotropic terms; their analytical expressions might be found elsewhere [20-22]. The RP term includes the spin-spin electron coupling terms [22,23,26-28] arising from the interaction between the ·AMP–, ·OH and hydrogens of water molecules and ribose hydroxyls. The interaction occurs through the exchange (2) and the dipole-dipole (3) terms:
radical fragments [25]. The same is valid for the active nuclear spins of hydrogen atoms (natural abundance of 1H atoms with the active nuclear spin is 99.985%24) in water molecules and the ribose hydroxyls. In our computations the HFC for the named atoms includes the both isotropic and anisotropic terms; their analytical expressions might be found elsewhere [20-22]. The RP term includes the spin-spin electron coupling terms [22,23,26-28] arising from the interaction between the ·AMP–, ·OH and hydrogens of water molecules and ribose hydroxyls. The interaction occurs through the exchange (2) and the dipole-dipole (3) terms:
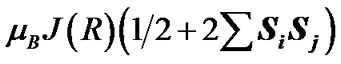 (2)
(2)
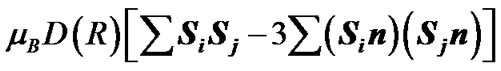 (3)
(3)
where mB is Bohr’s magneton,  and
and 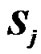 are the unpaired electron spins i and j located on the appropriate atom (group of atoms); the summation spans over all possible i and j. The functions J(R) and D(R) describe the strength of the exchange and dipolar couplings and are assumed, as is often done, to take the simple functional forms
are the unpaired electron spins i and j located on the appropriate atom (group of atoms); the summation spans over all possible i and j. The functions J(R) and D(R) describe the strength of the exchange and dipolar couplings and are assumed, as is often done, to take the simple functional forms
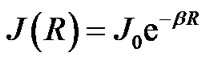 (4)
(4)
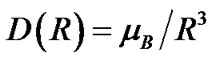 (5)
(5)
In Eqs.2-5 R is the edge-to-edge distance between the radicals, J0 is the exchange coupling constant, n is the unit vector in the direction of R and β is the range parameter. One can see that the exchange and dipolar coupling parameters decrease rapidly with the distance between the radicals and can be neglected if the distance between the radicals is sufficiently large. The characteristic distances can be estimated from the mutual geometry of ATP and AMP, see above. Their initial values are as follows: R(PaO3(ATP)-HO-C3’(AMP)) = 5.75 Å, R(PaO3(ATP)-HO-C2’(AMP)) = 9.02 Å, and R(PaO3(ATP)-·OH) = 10.8 Å (these values allow the ·OH to diffuse through the water volume at large distances). Note that varying R(PaO3(ATP)—HO-C3’ (AMP)), see above, automatically affects the other distances. The values for J0 and β, typical for radical pairs in solution, are taken from the previous works [25,26] and correspond to J0 = 7 × 109 G and β = 2.15 Å−1. The estimated values for the dipolar coupling parameters are D(R(PaO3(ATP) - ·OH) = 75 G, D(R(PaO3(ATP) - HO-C3’ (AMP)) = 20 G, and D(R(PaO3(ATP) - HO-C2’ (AMP)) = 5 G. Despite the fact that these values are much smaller than those for J(R) their contribution however is still remarkable at small distances.
The CPMD simulations are performed using the CPMD code, version 3.9.1 [29,30]. The gradient-corrected BLYP functional [30] is used with a plane-wave basis (cutoff: 70.0 Ry) and norm-conserving pseudopotentials of Troullier-Martins type [20-22]. The temperature of the simulation is set to 310 K. For the solvated system like ours the thermostatting is accomplished by rescaling the kinetic energy of the nuclei whenever the temperature is deviated more than a specific tolerance [30] (±10 K) from the desired 310 K temperature. The CPMD runs, totaling 120 (this is done to accumulate representative statistics), span over the time interval 10–6 s and are performed on the ultra-dense massively parallel computer, the IBM BlueGene/L [31] (University of Minnesota, Rochester). Additionally, the implemented CPMD method includes the nonadiabatic evolution, the so-called surface hopping method [32], when the potential energy surfaces (PESs) are as close as £2.5 kcal/ mol.
3. RESULTS AND DISCUSSION
As soon as the geometry of the [·Mg+(H2O)2 – ·AТP3–]SS complex is unfixed (the system is thermostatted at 310 K), the complex begins to decompose. The decomposition in the water environment spans over 5.4 ps and practically does not affect the geometry of AMP (we stress here again that this time interval is the pure ATP decomposition, when the chelate with the Mg is formed; the total CPMD run interval is much longer, 10–6 s, see section 2, and includes the separation of the produced fragments, their repulsion, approach, diffusion etc.). Except for the two  molecules of ionic nature the rest products of the [·Mg+(H2O)2 – ·AТP3–]SS cleavage are highly reactive. The charge on the Mg atom in the {O3Pb – Mg(H2O)2} fragment (Figure 3(a)), one of the decomposition products, reaction (1), is not exactly 1.0 but 0.49, Table 1. The {O3Pb-Mg(H2O)2} fragment is not stable: the Mg undergoes a reduction (the charge on the Mg atom progressively increases from +0.49 to +1.48, Table 1) accompanied by transferring the electron density onto the initially uncharged atomic oxygen O, for details see, [15] thus producing the ·O– radical. The electron transfer is coupled with the proton transfer from the Zundel cation onto the ·O–, Figures 3(a), (b) (structure-1, 2, Table 1). The coupled electron/proton transfer (CEPT) however is not instantaneous. At the very beginning of the process the Mg atom is slightly charged, q(Mg) = 0.49, and begins to lose its primarily bound ligands: the two H2O molecules and the
molecules of ionic nature the rest products of the [·Mg+(H2O)2 – ·AТP3–]SS cleavage are highly reactive. The charge on the Mg atom in the {O3Pb – Mg(H2O)2} fragment (Figure 3(a)), one of the decomposition products, reaction (1), is not exactly 1.0 but 0.49, Table 1. The {O3Pb-Mg(H2O)2} fragment is not stable: the Mg undergoes a reduction (the charge on the Mg atom progressively increases from +0.49 to +1.48, Table 1) accompanied by transferring the electron density onto the initially uncharged atomic oxygen O, for details see, [15] thus producing the ·O– radical. The electron transfer is coupled with the proton transfer from the Zundel cation onto the ·O–, Figures 3(a), (b) (structure-1, 2, Table 1). The coupled electron/proton transfer (CEPT) however is not instantaneous. At the very beginning of the process the Mg atom is slightly charged, q(Mg) = 0.49, and begins to lose its primarily bound ligands: the two H2O molecules and the  fragment (the Coulomb attraction between the positively charged Mg and the negatively charged oxygens is decreased). This, specifically, is displayed in lengthening the bond distances between the Mg atom and the OH2 molecules, 2.14 and 2.18 Å, and the –O3Pb fragment, 2.64 Å, Table 1. The electron transfer onto the O increases the charge on the Mg atom up to 1.48 that in turn assists accumulation of a water coat around the Mg (the Coulomb attracttion between the Mg and oxygens increases, but not with the
fragment (the Coulomb attraction between the positively charged Mg and the negatively charged oxygens is decreased). This, specifically, is displayed in lengthening the bond distances between the Mg atom and the OH2 molecules, 2.14 and 2.18 Å, and the –O3Pb fragment, 2.64 Å, Table 1. The electron transfer onto the O increases the charge on the Mg atom up to 1.48 that in turn assists accumulation of a water coat around the Mg (the Coulomb attracttion between the Mg and oxygens increases, but not with the  which to that moment is 3.77 Å distanced from the Mg). This is, specifically, observed in approaching the water molecules to the Mg (structure-2), Figure 3(b), Table 1, and adding new water molecules from the water reservoir (not shown), see section II, that favors restoring the most stable in water Mg(H2O)6 configuration [16]. The restoring of the Mg(H2O)6 is not directly coupled with the electron pumping onto the O and the proton transfer on it from the Zundel cation, Figures 3(a), (b). The processes are separated in time: the first acquires milliseconds, while the latter proceeds
which to that moment is 3.77 Å distanced from the Mg). This is, specifically, observed in approaching the water molecules to the Mg (structure-2), Figure 3(b), Table 1, and adding new water molecules from the water reservoir (not shown), see section II, that favors restoring the most stable in water Mg(H2O)6 configuration [16]. The restoring of the Mg(H2O)6 is not directly coupled with the electron pumping onto the O and the proton transfer on it from the Zundel cation, Figures 3(a), (b). The processes are separated in time: the first acquires milliseconds, while the latter proceeds
 (a)
(a)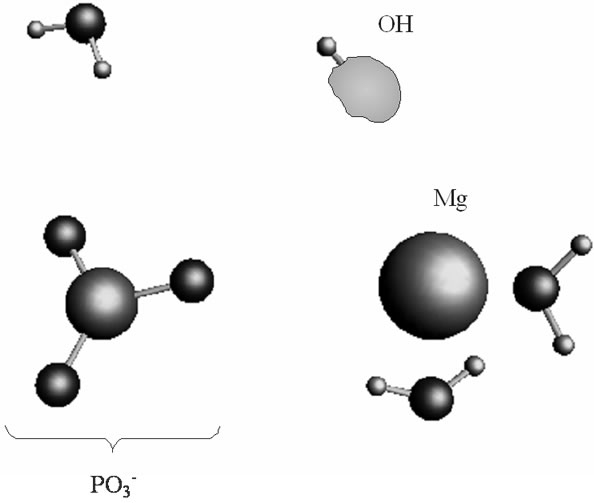 (b)
(b)
Figure 3. The proton coupled electron transfer in the Mg(H2O)2 - Zundel cation (H5O2+, only its H3O+ fragment is shown)-O– (oxygen radical) fragment: (a) the initial stage of the process; (b) the final stage of the process, when the proton from the Zundel cation is transferred onto the oxygen radical. In green is shown a spin density distribution.

Table 1. Interatomic distances (Å) and the charge (Löwdin) on the Mg atom in the structures 1 and 2, Figures 3(a), (b).
in a picosecond—nanosecond interval [15,16]. Figure 3(a) shows that initially the spin density (green) is redistributed between the Mg and O atoms with the Mg slightly bound to the water molecules and the . As the electron density is pumped on the O, the spin density shows its localization right on the said atom, Figure 3(b), which becomes a radical ·O–. The formation of the radical assists the capture of the proton initially belonged to the Zundel cation, Figures 3(a), (b). The fast PCET process avoids a high-energy intermediate and undergoes a concerted mechanism [33-37] that is still valid for our system. The barrier of 1.25 kcal/mol arises from the elongation of the bond length between the H+ and H2O in the Zundel cation (0.96 Å ® 1.07 Å). The elongation is accompanied by the electron pumping on the O. All in all, the decrease in total energy on arising ·OH equals to –5.87 kcal/mol. This, specifically, is achieved through separating the Mg and
. As the electron density is pumped on the O, the spin density shows its localization right on the said atom, Figure 3(b), which becomes a radical ·O–. The formation of the radical assists the capture of the proton initially belonged to the Zundel cation, Figures 3(a), (b). The fast PCET process avoids a high-energy intermediate and undergoes a concerted mechanism [33-37] that is still valid for our system. The barrier of 1.25 kcal/mol arises from the elongation of the bond length between the H+ and H2O in the Zundel cation (0.96 Å ® 1.07 Å). The elongation is accompanied by the electron pumping on the O. All in all, the decrease in total energy on arising ·OH equals to –5.87 kcal/mol. This, specifically, is achieved through separating the Mg and , Table 1. Without separation the total energy decrease is much smaller, –0.65 (a pure CPET process), and still close to that of the thermal motion, which could make the process reversible. The separation between the Mg and the
, Table 1. Without separation the total energy decrease is much smaller, –0.65 (a pure CPET process), and still close to that of the thermal motion, which could make the process reversible. The separation between the Mg and the  spans over 45 ps with regard to the solvent-reactant reorganization, which in our case includes the approach of two water molecules to the Mg atom (Figure 3(b)), Table 1, and the approach of two
spans over 45 ps with regard to the solvent-reactant reorganization, which in our case includes the approach of two water molecules to the Mg atom (Figure 3(b)), Table 1, and the approach of two  fragments with further production of PPi (milliseconds) [1-3,15], partly it is seen in Figures 4(a), (b).
fragments with further production of PPi (milliseconds) [1-3,15], partly it is seen in Figures 4(a), (b).
Though the separation between the Mg and  is a crucial process in decreasing the total energy of the system it cannot guarantee recombination between the ·AMP– (reaction (1)) and ·OH. The recombination is thermodynamically favorable: the energy gain via the recombination equals to –7.87 kcal/mol. This value is lower than the previously named one –5.87 kcal/mol, see above. If the recombination occurs, instead of two highly reactive radicals we have an inert anion—a traditional AMP. The mechanism that prevents recombination lies in the spin symmetry of the ·AMP– - ·OH radical pair where the spins on the ·AMP– and ·OH get the identical orientation, the T- energy state [38,39]. When in ‘cage’, such a radical pair with the identically oriented electron spins prefers being separated rather than being recombined [38-40]. The reason for keeping the spins parallel on the both radicals is in the highly large HF constant a, produced by the ·AMP– radical [25]. According to our computations (CPMD, section II), the value of a reaches 0.078 T. The strong magnetic coupling between the 31P atom and the unpaired electron on the AMP– aligns the spin of ·OH (the a in the ·OH-(5H2O) complex at 310 K is 0.036 T—a result of the ·OH magnetic field enhancement by surrounding water molecules [41]) in the identical direction to that on the ·AMP–, and the environment cannot destroy the effect in the distance range 4.75 - 1.50 Å between the ·AMP- and ·OH. The finding is crucial for the radical polymerization to occur, see below. Moreover, the unpaired spins in the T– state experience repulsion while the oppositely oriented spins, T0 state, show attraction [39,40].
is a crucial process in decreasing the total energy of the system it cannot guarantee recombination between the ·AMP– (reaction (1)) and ·OH. The recombination is thermodynamically favorable: the energy gain via the recombination equals to –7.87 kcal/mol. This value is lower than the previously named one –5.87 kcal/mol, see above. If the recombination occurs, instead of two highly reactive radicals we have an inert anion—a traditional AMP. The mechanism that prevents recombination lies in the spin symmetry of the ·AMP– - ·OH radical pair where the spins on the ·AMP– and ·OH get the identical orientation, the T- energy state [38,39]. When in ‘cage’, such a radical pair with the identically oriented electron spins prefers being separated rather than being recombined [38-40]. The reason for keeping the spins parallel on the both radicals is in the highly large HF constant a, produced by the ·AMP– radical [25]. According to our computations (CPMD, section II), the value of a reaches 0.078 T. The strong magnetic coupling between the 31P atom and the unpaired electron on the AMP– aligns the spin of ·OH (the a in the ·OH-(5H2O) complex at 310 K is 0.036 T—a result of the ·OH magnetic field enhancement by surrounding water molecules [41]) in the identical direction to that on the ·AMP–, and the environment cannot destroy the effect in the distance range 4.75 - 1.50 Å between the ·AMP- and ·OH. The finding is crucial for the radical polymerization to occur, see below. Moreover, the unpaired spins in the T– state experience repulsion while the oppositely oriented spins, T0 state, show attraction [39,40].
After the ·OH production, it begins to move away from the ·AMP– toward the HO-C2’ group of the AMP deoxyribose/ribose (the initial distance between the produced ·OH and ·AMP– is 1.85 Å). The diffusion is accompanied by multistep structural rearrangements of the ·OH radical in the ‘water tube’ (2.65 Å in length) of 11 (the first and second shells) water molecules. These rearrangements are the result of hydrogen bond forming/ breaking between the ·OH and water molecules; the O-H bond length in the radical varies in the interval— rmax(O-H) = 1.12 Å, rmin(O-H) = 0.96 Å—that coincides with the previously observed data [41]. When the ·OH is as close to the HO-C2’ as 1.54 Å, the H-O bond in the HO-C2’ displays a progressive lengthening. This is partly due to the electron density pumping on the H from the ·OH and the AMP. The ·OH diffusion and the H-O lengthening are accompanied by a solvent-reactant reorganization (the reorganization spans over 85 ps after the production of ·OH), which finally yields the structure shown in Figure 4(a). In this structure the Pa-O-C2’ bond is 4.51 Å, the HO·-H-O-C2’ bond is 1.23 Å, and the H-O bond in the HO-C2’ is 1.07 Å. The Mg atom is separated from the 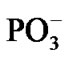 by 4.03 Å and the two
by 4.03 Å and the two 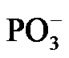 fragments are quite close to each other (the Pb-Pg bond is 2.37 Å). The further approach by 0.1 Å between the ·OH and the AMP results in an instantaneous hopping of the hydrogen atom on the ·OH, Figure 4(b). One can see that the hopping does not practically affect the solvent-reactants geometry. The hydrogen atom detachment from the deoxyribose/ribose ring is energetically favorable, –2.37 kcal/mol. This is in agreement with other theoretical findings upon the action of ·OH on DNAbase fragments [42].
fragments are quite close to each other (the Pb-Pg bond is 2.37 Å). The further approach by 0.1 Å between the ·OH and the AMP results in an instantaneous hopping of the hydrogen atom on the ·OH, Figure 4(b). One can see that the hopping does not practically affect the solvent-reactants geometry. The hydrogen atom detachment from the deoxyribose/ribose ring is energetically favorable, –2.37 kcal/mol. This is in agreement with other theoretical findings upon the action of ·OH on DNAbase fragments [42].
The hydrogen atom detachment from the deoxyribose/ ribose converts the AMP into a radical, ·О-С3’(АМP), denoted hereinafter as ·AMP, Figure 4(b), according to reaction (2).
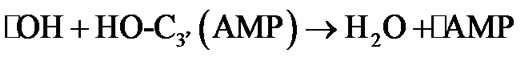 (2)
(2)
The spin orientation on the both radicals, ·AMP– and ·AMP, is opposite, the T0 state,39 that according to the radical pair theory serves the basis for their mutual approach via a diffusion mechanism [39,40]. The diffusion is the most time-consuming part of the process: it spans over 2.7 ns. The final stage of the process proceeds as following. The ·АМP– attacks by its phosphorus atom Рa (q = 1.15) the oxygen atom of the ·О-С3'(АМP) fragment (q(O) = –0.87) thus forming the adenine (Ade) dinucleotide {АМP-AMP}3– of non-radical nature, Figure 5, 6. The T2 state (the T2 and S2 states stand for the
 (a)
(a)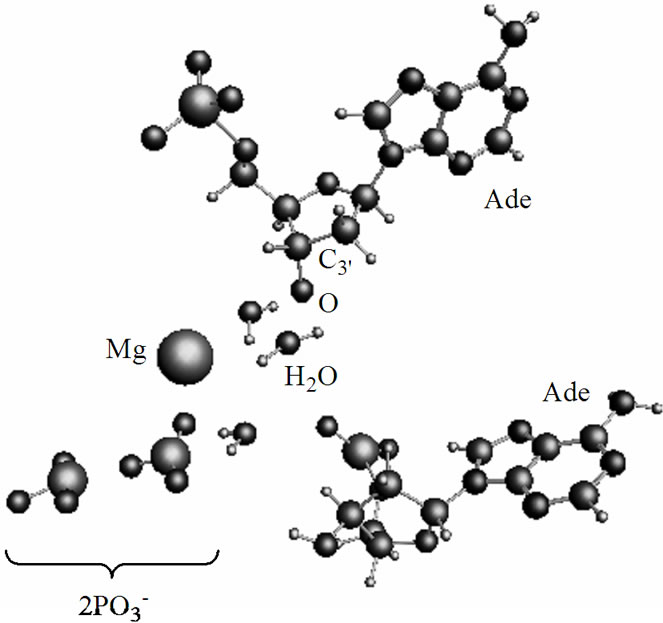 (b)
(b)
Figure 4. The arrangement of the [·Mg+(H2O)2 – ·ATP3–] cleavage products and the AMP. (a) the ·OH radical comes close to the H-O-C3’ group of the ribose; (b) the same picture when the hydrogen atom is detached from the H-O-C3’ group and transferred onto the ·OH radical with the production of water.
dinucleotide, Figure 6, in which the spins are still unpaired and located at the Ade bases, is higher in energy than the S2 state by 7.13 kcal/mol, a value comparable to hydrogen bonding between the complementary nucleotides in DNA. The presence of unpaired spins on the Ade bases in the T state is closely linked to complementtary recognition of nucleotides upon formation of DNA duplex and spin nature of the genetic code [43]. In Figure 5 one can see that the Ade bases are essentially parallel. The further stabilization of the dimer (the process show a little decrease in the total energy of the dimer over the time) assumes the solvent reorganization around

Figure 5. Formation of the adenine dinucleotide in the singlet (S2) state, for details see text and Figure 6.
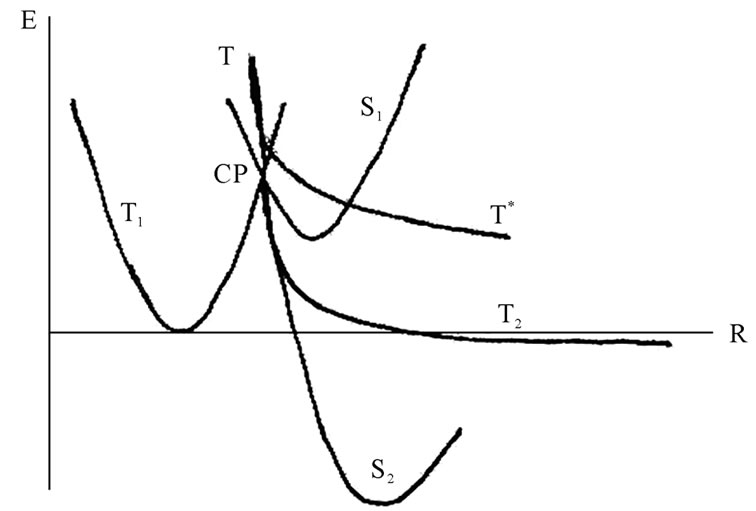
Figure 6. The potential energy surface (PES) projections onto the energy (E)—atomic configuration (R) plane, for details see text. The blurring around the solid lines indicates “on the fly” deviations in the CPMD computation runs. CP stands for a S1-T1-T crossing point.
it and formation of hydrogen bonds favoring stacking between the Ade bases. This is the time-consuming process that spans in general over the millicecond interval (this interval is beyond the accepted computational interval and might be thought as an imaginary asymptotic limit). The ssame is valid for the PPi formation of the two 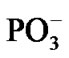 fragments and complete magnesium oxidation accompanied by producing the stable Mg2+(H2O)6 complex (see above) [44,45] that is able to act anew as a catalyst in ATP cleavage [16].
fragments and complete magnesium oxidation accompanied by producing the stable Mg2+(H2O)6 complex (see above) [44,45] that is able to act anew as a catalyst in ATP cleavage [16].
The replacement of deoxyribose by ribose (DNA nucleotide ® RNA nucleotide), which besides the HO-С3’ group possesses the additional HO-С2’ group, basically opens the way for attacking the latter by the ·ОН radical. But this does not occur, and the background for this is not only in a steric hindrance. The point is that the removing of the ·ОН from the ·АМP– results in the loss of the initial strong spin-spin coupling between the two radicals as the distance between them increases (Eq.4, 5). The weakening of the spin-spin coupling allows the hydrogen spins of surrounding water molecules to invert the initial ·ОН radical spin direction. With such an inverted spin, the ·ОН tends through the reverse diffusion to recombine with the ·АМP– to form a non-radical AMP molecule that blocks the radical polymerization mechanism. The said shows the difference in operating the HO-С3’ and HO-С2’ groups: the former is a lucky target for the radical polymerization while the latter is still unlucky. Supposedly, the nature has made its choice in favor of the HO-С3’ group not occasionally. The idea finds its explanation in Figure 6. The S state of AMP, S1, lies lower than the T state, T1, DES-T = –4.3 kcal/mol. Note that this value drastically differs from that observed earlier in quantum chemistry computations for pure bases (DES-T equals to several eV that corresponds to the vertical excitation with no rearrangement in geometry of nucleotides) stripped off their phosphate groups and the deoxyribose/ribose ring [46,47]. The explanation is quite simple: the attached phosphate groups and the solvent hugely affect the monophosphate nucleotide geometry making the S and T states come closer [16]. The S1 and T1 states have a crossing, DE = 6.28 kcal/mol, that is exposed to an additional crossing from the T curve corresponding to the produced ·АМP– – ·ОН radical pair. Because of the instability nature of the latter product the T curve goes straight down, and after passing the crossing point displays the formation of a dinucleotide of the T2 (unstable state) or S2 symmetry (stable state). The combined T-T1-S1 crossing occurs only when the polymerization proceeds through the HO-С3’ group. When the HO-С2’ group, instead of the T curve we have the T* curve that goes above the T, crosses the S1 and T1 curves and does not lead to a dimer production, Figure 6. The appearance of the T-T1-S1 crossing (CP point in Figure 7) is highly essential because at this very crossing point the redistribution of spins occurs as shown in Figure 7. Initially, at the T1-S1 crossing the both triplet and singlet states are degenerated. The attack on this state from the ·ОН leads to electron detachment with the production of the ·АМP radical that experiences an immediate attack by the ·АМP– radical spin, Figure 7 (right). This produces the S2 and T2 reaction paths, which initially go together and then break down into the stable and unstable

Figure 7. Spin orientation (spins like in classical physics are shown with arrows) in the vicinity of the crossing point (CP). Above the CP we have the T state coming from the identical orientation of spins located on the ·OH and ·AMP–. At the CP we have the S1 and T1 states, for details see text and Figure 6. The spins in the box form the singlet state (indicated with the horizontal arrow) corresponding to production of the H2O molecule. When the latter is removed (the ·OH had interacted with the AMP) we have four spins corresponding to the S2 and T2 states that lie below the CP (Figure 6).

Figure 8. The optimized geometry (CPMD computations) of the Mg2+(Asp)2 fragment embedded into the DNA-polymerase hydrophobic pocket. The arrow indicates the direction of the Mg ion (within the complex) attack on ATP.
states, Figure 6. The T* curve reveals no T*-T1-S1 crossing point at which an adequate interspin shuffling might occur.
4. CONCLUDING REMARKS
The outlined radical mechanism of nucleotide polymerization, which is realized through the HO-C3’ bond but not through the HO-C2’ bond, is seen more natural than the alternative ionic/hydrolytic mechanism. First, it proceeds much faster than the ionic mechanism and includes highly reactive species, which production in a living cell under certain conditions is a common thing. Second, it is reasonable to assume that the nature has developed this radical mechanism over a huge period of evolution with a great thought: the mechanism is highly specific and sensitive to the environment and local electromagnetic fields, which are able to switch the course of reaction and direct its progress over one or other potential energy surfaces. This, in particular, is observed in the case of the Mg2+(Asp)2 complex embedded into the DNA-polymerase hydrophobic pocket, Figure 8. The computations (CPMD) show that the T state of the said complex is 0.04 kJ/mol smaller than the S state; this allows the complex to interact with the ATP according to the radical mechanism. Third, the radical mechanism was not found earlier for a very simple reason: to detect this mechanism new computational methods and experimental techniques, like a combined femtosecond laser-CIDNP method (FL-CIDNP) [15,16], are required—they were unavailable as early as decades ago (though the current work is purely computational, our recent works [15,16] that use this highly sophisticated FL-CIDNP method show the effect of nuclear polarization on the 31P caused by the presence of the short-living radicals in the Mg-ATP complex; one can anticipate that the 31P polarization might be detected as well on the assembling NMPs with this FL-CIDNP technique). Fourth, the final products in the ion-radical and pure ionic mechanisms are absolutely identical: these products are water, a polynucleotide, and a regenerated Mg cofactor. Fifth, the time to complete the polymerization cycle takes milliseconds. If this time is multiplied by a number of polymerizing units, the rate of assembling nucleotides per second gives a value of 50 - 70 that fully agrees with the experiment [1-3].
REFERENCES
- Kirschning, A. (2004) Immobilized catalysis. Springer Verlag, Berlin.
- Harvey, F.L., Berk, A., Keiser, C.A., Krieger, M., Scott, M.P., Bortscher, A. and Ploegh, H. (2008) Molecular cell biology. W. H. Freeman Publishers, New York.
- Metzler, D.E. (1977) The chemical reactions of living cells. Academic Press, New York.
- Cowan, J.A. (1995) Introduction to the biological chemistry of magnesium. VCH, New York.
- Black, C.B. and Cowan, J.A. (1995) Magnesium-dependent enzymes in general metabolism. In: Cowan, J.A., Ed., The Biological Chemistry of Magnesium, VCH, New York, pp. 54-87.
- Yang, L., Arora, K., Weard, W.A., Wilson, S.H. and Schlick, T. (2004) Critical role of magnesium ions in DNA polymerase closing and active site assembly. Journal of the American Chemical Society, 126, 8441-8453. doi:10.1021/ja049412o
- Beechero, J.M., Otto, M.R., Bloom, L.B., Eritja, R., Reta-Krantz, L.J. and Goodman, M.F. (1998) Exonuclease-polymerase active site partitioning of primer-template DNA strands and equilibrium Mg2+ binding properties of bacteriophage T4DNA polymerase. Biochemistry, 37, 10144-10155. doi:10.1021/bi980074b
- Kornberg, A. and Baker, T.A. (2005) DNA Replication. 2nd Edition, Nuclear Acid Science Books, New York.
- Tsai, C.S. (2007) Biomacromolecules. Introduction to structure, function and informatics. John Wiley & Sons Inc., Hoboken.
- Mullis, K.B. (1998) The polymerase chain reaction. Nobel Prize lecture: 1993. World Scientific Publication, Singapore.
- Lopus, M., Yenjerla, M. and Wilson L. (2009) Microtubule dynamics (advanced review). In: Wilson, L., Ed., Wiley Encyclopedia of Chemical Biology, Wiley & Sons, New York, 153-168.
- Engelhardt, W.A. and Ljubimova, M.N. (1939) Myosine and adenosinetriphosphatase. Nature, 144, 668-669. doi:10.1038/144668b0
- Kachur, T.M., Pilgrim, D.B. (2008) Myosine assembly, maintenance and elongation in muscle: Role of the chaperon unc-45 in myosine thick filament dynamics. International Journal of Molecular Sciences, 8, 1863-1875.
- Cowan, J.A. (2002) Structural and catalytic chemistry of magnesium-dependent enzymes. BioMetals, 15, 225-235. doi:10.1023/A:1016022730880
- Tulub, A.A. (2008) Mg spin affects adenosinetriphosphate activity. PMC Physics B, 1, 1-18.
- Tulub, A.A. (2006) Molecular Dynamics DFT-B3LYP study of guanosinetriphosphate conversion into guanosinemonophosphate upon Mg(2+) chelation of alpha and beta oxygens of the triphosphate tail. Physical Chemistry Chemical Physics, 8, 2187-2192.
- Car, R. and Parrinello, M. (1985) Unified approach to molecular dynamics and density-functional theory. Physical Review Letters, 55, 2471-2474. doi:10.1103/PhysRevLett.55.2471
- Furmanchuk, A., Isayev, O., Shishkin, O.V., Gorb, L. and Leszczynski, J. (2010) Hydration of nucleic acid bases: A Car-Parrinello molecular dynamics approach. Physical Chemistry Chemical Physics, 12, 3363-3375.
- Tulub, A.A. (2009) Magnesium-associated proteins in drug design. AstraZeneca—Annual Reports, Stockholm, London, New York, Tokyo.
- Asher, J.R. and Kaupp, M. (2007) Car-Parrinello molecular dynamics simulations and EPR property calculations in aqueous ubisemiquinone radical ion. Theoretical Chemistry Accounts, 119, 477-487.
- Asher, J.R. and Kaupp, M. (2007) Hyperfine coupling terms of benzosemiquinone radical anion from the Car-Parrinello molecular dynamics. Chemical Physics, 117, 69-79.
- Asher, J.R., Doltsinis, N.L. and Kaupp, M. (2005) Extended Car-Parrinello molecular dynamics and electronic g-tensors study of benzoquinone radical. Magnetic Resonance in Chemistry, 43, 237-247. doi:10.1002/mrc.1669
- Matta, C.F. (2010) Quantum biochemistry. Wiley-VCH Verlag, Weinheim. doi:10.1002/9783527629213
- Freeman, R. (1988) A handbook of nuclear magnetic resonance. Longman Science & Technical Publishing, London.
- Koptyug, I.V., Sluggett, G.W., Ghatlia, N.D., Landis, M.S., Turro, N.J., Ganapathy, S. and Bentrude, W.G. (2000) Magnetic field dependence of the 31P CIDNP in the photolysis of a benzyl phosphate. Evidence for a T-S mechanism. The Journal of Physical Chemistry, 100, 14581-14583. doi:10.1021/jp9619705
- Solov’ev, I.A. and Schulten, K. (2009) Magnetoreception through cryptochrome may involve superoxide. Biophysical Journal, 96, 4804-4813.
- Prabhakar, R., Siegban, P.E.M., Minaev, B.F. and Agren, H. (2002) Activation of triplet dioxygen by glucose oxidase: Spin-orbit coupling in the superoxide ion. The Journal of Physical Chemistry, 106, 3742-3750
- Van Santen, R.A. and Saulet, P. (2009) Computational methods in catalysis and materials science. Wiley-VCH Verlag, Amsterdam. doi:10.1002/9783527625482
- Hutter, J. and Curioni, A. (2005) Car-Parrinello molecular dynamics on massively parallel computers. A European Journal of Chemical Physics and Physical Chemistry, 1, 1-12.
- Rapacioli, M., Barthel, R., Heine, T. and Seifert, G. (2007) Car-Parrinello treatment for an approximate densityfunctional theory method. Journal of Chemical Physics, 126, 124103-115. doi:10.1063/1.2566510
- Allsopp, N., Follows, J. and Hennecke, M. (2005) Unfolding the IBM & server blue gene solutions. International Business Machines Corporation, IBM Redbooks.
- Doltsinis, N.L. and Marx, D. (2002) Non-adiabatic CarParrinello dynamics. Physical Review Letters, 88, 166402- 1-4. doi:10.1103/PhysRevLett.88.166402
- Marcus, R.A. (1982) Electron, proton and coupled transfers. Faraday Discussions of the Chemical Society, 74, 7-15. doi:10.1039/dc9827400007
- Reece, S. T. and Nocera, D.C. (2009) Proton-coupled electron transfer in biology. Annual Review of Biochemistry, 78, 673-699. doi:10.1146/annurev.biochem.78.080207.092132
- Kumar, A. and Sevilla, M.D. (2010) Proton-coupled transfer in DNA on formation of radiation-produced radicals. Chemical Reviews, 10, 1021-1043.
- Hammes-Schiffer, S. (2009) Theory of proton-coupled electron transfer in energy conversion processes. Accounts of Chemical Research, 42, 1881-1889. doi:10.1021/ar9001284
- Mayer, J.M. and Rhile, I.J. (2004) Thermodynamics and kinetics of proton-coupled electron transfer: stepwise vs concerted pathways. Biochimica et Biophysica Acta, 16, 51-58.
- Goez, M. (1997) Photochemically induced dynamic nuclear polarization, Advances in Photochemistry, 23, 63-163. doi:10.1002/9780470133545.ch2
- Nakagura, S. and Hyashi, H. (2004) Dynamic spin chemistry. John Wiley & Sons, New York.
- Jones, J.A. and Hore, P.J. (2010) Spin-selective reactions of radical pairs act as quantum measurements. Chemical Physics Letters, 488, 90-93. doi:10.1016/j.cplett.2010.01.063
- Lee, J.J., Oka, T. and Hirada, T. (2010) OH radical in water studied by quantum beats on positron annihilation—The effect of water liquid structures. Journal of Physics: Conference Series, 1, 225-228.
- Wu, Y., Mundy, C.J., Colvin, M.E. and Car, R. (2004) On the mechanism of OH radical induced DNA-base damage: A comparative quantum chemical and Car-Parrinello molecular dynamics study. The Journal of Physical Chemistry A, 108, 2922-2929. doi:10.1021/jp0363592
- Tulub, A.A. (2007) Triplet-singlet spin communication between DNA nucleotides serves the basis for quantum computing. Chemical Physics Letters, 436, 258-262. doi:10.1016/j.cplett.2007.01.054
- Fox-Beyer, B.S., Sun, Z., Balteanu, I., Balay, O.P. and Beyer, M.K. (2005) Hydrogen formatin in the reaction of Zn(H2O)n with HCl. Physical Chemistry Chemical Physics, 7, 981-985.
- Pavlov, M., Siegban, P.E.M. and Sandstrom, M. (1998) Hydration of beryllium, magnesium, calcium, and zinc ions using density functional theory. The Journal of Physical Chemistry A, 102, 219-228. doi:10.1021/jp972072r
- Sobolewski, A.L. and Domcke, W. (2004) Ab initio studies on the photophysics of the guanine-cytosine base pair. Physical Chemistry Chemical Physics, 6, 2763-2771.
- Ohno, K., Esfarjani, K. and Kawazoe, Y. (1999) Computational materials science. From ab initio to Monte Carlo Methods. Springer-Verlag, Berlin.
- Tulub, A.A. (2004) Activation of tubulin assembly into microtubules upon a series of repeated femtosecond laser impulses. Journal of Chemical Physics, 121, 11345-11350. doi:10.1063/1.1814056

