Journal of Environmental Protection
Vol.06 No.09(2015), Article ID:59827,17 pages
10.4236/jep.2015.69094
Towards Urban Resource Flow Estimates in Data Scarce Environments: The Case of African Cities
Paul Currie1*, Ethan Lay-Sleeper2, John E. Fernández2, Jenny Kim2, Josephine Kaviti Musango3
1School of Public Leadership, Stellenbosch University, Stellenbosch, South Africa
2Department of Architecture, Massachusetts Institute of Technology, Cambridge, USA
3School of Public Leadership, and the Centre for Renewable and Sustainable Energy Studies (CRSES), Stellenbosch, South Africa
Email: *paulkcurrie@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 July 2015; accepted 20 September 2015; published 23 September 2015
ABSTRACT
Data sourcing challenges in African nations have led many African urban infrastructure developments to be implemented with minimal scientific backing to support their success. In some cases this may directly impact a city’s ability to reach service delivery, economic growth and human development goals, let alone the city’s ability to protect ecosystem services upon which it relies. As an attempt to fill this gap, this paper describes an exploratory process used to determine city-level demographic, economic and resource flow data for African nations. The approach makes use of scaling and clustering techniques to form acceptable and utilizable representations of selected African cities. Variables that may serve as the strongest predictors for resource consumption intensity in African nations and cities were explored, in particular, the aspects of the Koppen Climate Zones, estimates of average urban income and GDP, and the influence of urban primacy. It is expected that the approach examined will provide a step towards estimating and understanding African cities and their resource profiles.
Keywords:
Urban Metabolism, Resource Flows, African Cities, Data Scaling, City Clustering

1. Introduction
Humans have become an urban species. As of 2008, more than half of the human population occupies urban hives of activity [1] [2] . This has happened through two major urbanization waves. The first occurred between 1750 and 1950, in which the urban population increased from 15 million to 423 million [3] . The continents affected by the first wave were mainly Europe and North America. The second urbanization wave is occurring now and expects that an additional 2.4 billion people will be living in African and Asian cities by 2050 [4] .
Cities are concentrators of people and economic production, and therefore require large inputs of resources to fuel their development and growth. Common consensus suggests that cities currently produce roughly 80% of the global GDP and consume approximately 75% of global energy and materials. The concentration of resources forms large quantities of pollutants and wastes which, despite having originated in other global regions are typically exported into the local environment, threatening natural systems as well as the ecosystem services upon which the city relies [5] . Satterthwaite [6] argues that while cities may be blamed for about 80% of global carbon emissions, only about 35% are emitted within city boundaries. Rising consumption levels, not population growth, are identified as the real driver of climate change, and with that, understanding the differing consumption levels within cities is the key to understanding urbanization’s role in climate change. Satterthwaite [6] remarks that cities may offer great opportunities to decouple greenhouse gas emissions from high-quality lifestyles, particularly in low- or middle-income countries. Ozbekhan’s [7] problematique and Morin and Kern’s [8] polycrisis are apt terms to describe the emergent issues of overpopulation, pollution, ecosystem degradation, biodiversity loss, scarcity of materials, social inequality, climate change and a loss of human connection to the natural world. As concentrators of the global polycrisis, cities are where the desire for a sustainable existence should also be fostered.
The polycrisis is directly linked to resource flows: the sourcing, conversion, use and discharge of resources in various forms. These flows of resources are intimately related to the social makeup and processes of cities [9] , the totality of which has been referred to as the urbanmetabolism. One definition of urban metabolism is the “sum total of the technical and socioeconomic processes that occur in cities, resulting in growth, production of energy, and elimination of waste” [10] . The concept of urban metabolism is recognized as useful for developing sustainable cities and urban areas [11] [12] . Indeed, analysis of the resource flow mechanisms in cities is necessary for understanding how cities may develop in the future and how they can support a growing population.
Practical application of the concept of urban metabolism within urban systems requires quantification of the input flows and output flows in cities. These measures are sought to understand how urban systems function, the implication of these flows on the city’s hinterland and the biosphere, and their interactions with the operations of the social sphere [13] . In addition, studies of urban metabolism fall within the scope of sustainable development, and may involve constructing indicators, identifying special targets for sustainability, and developing decision support tools towards dematerialization or decarbonization [14] . To achieve an understanding and assessment of the nature and intensity of urban metabolism, there are a number of methods that have been utilized at city-level, including among others, 1) material flow analysis [15] [16] ; 2) ecological footprint analysis [17] [18] ; and 3) system dynamics modeling [19] .
The primary methodological approach for establishing the urban metabolism of a city is material flow analysis (MFA) which makes use of a standardized framework for data collection, processing, and resource flow calculation developed by Eurostat [20] . However, the framework was formulated on the basis of national data availability and requirements of European member states. Recent studies of urban metabolism acknowledge the need for developing a comprehensive and standardized framework for metabolic flow analysis in the urban context, which not only includes increased data collection but also some degree of consensus on parameters that should be part of basic level reporting [21] . While this argument is put forward, major data challenges and limitations exist in most regions of the world and in relation to most cities. The situation is the same for cities on the African continent which include: 1) unavailability of data at city-level; 2) inconsistent formats of available data, reducing the ability for automatic use of conventional methods; 3) data confidentiality, making it difficult to access relevant data; 4) quality of data, particularly when information is not from credible sources; and 5) informality, in which significant proportions of resource flows occupy an undocumented informal sector.
Some studies are developing approaches to deal with data challenges elsewhere. For instance Baynes and Bai [22] utilized a downscaling approach to reconstruct energy data for Melbourne city. Niza et al. [16] devised a method that could be utilized to extrapolate data from a country or region based on number of inhabitants, commuters, workers, sales, or produced waste. While these are useful city-level contributions to the field of urban metabolism, the limitation is that detailed data and information are required to undertake these analyses. The implication is that, only cities with the most available data can be investigated. It would thus be challenging to apply these methodologies to the large number of cities in which data are limited, including most African cities.
Questions have also been voiced about the most appropriate way to compare cities, particularly around the limitations of using a per-capita baseline. Differences in population distribution, social make-up, or city function are not fully recognized by a per capita measure, allowing quite different cities to show similar traits. Other mechanisms for comparing cities, such as with a per-unit-GDP baseline, may be required.
Given the above data related challenges, there has been a lack of data-supported decision making in planning and managing cities. As such, many of the African urban infrastructure programmes are implemented with minimal scientific backing to support the success of these interventions. This may directly impact a city’s ability to reach service delivery, economic growth, and human development goals, as well as its ability to protect ecosystem services which support the city. This is aggravated by the fact that governments in African cities are (necessarily) more focused on delivery of basic services than on environmental protection or resource efficiency agendas [23] and have yet to prepare for the expected increase in population of the second wave of urbanization. This preparation is further undermined by a threefold denial of urbanization, present in many African governments, namely: 1) denial that urbanization is happening; 2) denial that natural-births are the primary source of urban growth, resulting in an anti-migratory policy focus instead of a city-betterment one; or 3) a denial as to the benefits of urbanization, propagated by multiple popular and scientific writings, which often refute each other’s results, particularly around the question of “inevitable economic growth with urbanization” [24] .
This paper thus provides the exploratory approach that was used as an initial step towards estimating resource flows in data scarce environments such as African cities. The approach has its basis from Saldivar-Sali [25] and Fernandez et al. [26] who developed a Global Typology of Cities, providing a first categorization of global cities by resource consumption profile. The primary argument regarding the typology of cities is: 1) that it is possible to track some of the important resources that urban dwellers consume using a limited number of attributes, and 2) that cities can be classified into different types based on the similarity of their metabolic profiles [25] . Further, a typology demands less research time and funding than individual city analysis and allows the examination of cities’ relative consumption. The typology acknowledges that while all cities demonstrate unique consumptive behaviors, cities do share many behaviors [26] . To this end, grouping “like cities” enables recommendation of multiple scenarios for achieving urban sustainability. The formation of an African city typology aims to provide insights into the more subtle differences between cities on this continent, which are overshadowed in comparisons with cities of developed countries. It can also assist decision-makers in African cities in making informed decisions about future infrastructure development and configurations, in order to improve resource access and flows.
2. The Form of African Cities
The second wave of urbanism is expected to increase the vast expanses of slums surrounding most cities in Africa, spaces in which people must tap into informal flows of resources for their survival [3] . This represents the central challenge of planning African cities: providing adequate services to their populations and encouraging economic growth, while contending with the pressures of climate change, resource scarcity and social inequality. To this end, finding a way to represent the disparities of resource access throughout nations and cities may prove useful to addressing it.
At the national level, African countries tend to demonstrate “urban primacy”, a legacy of colonial times in which one city became and continues to be the administrative and economic driver of the country [24] . As a result, population, resources and productivity are focused in these single complex entities. Rosen and Resnick [27] remark that urban primacy is a useful indicator of the form of government, with primacy relating to authoritarian systems and distributed populations demonstrating more democratic governance. To better handle the rapidly increasing population, UN-Habitat [28] recommends that national governments encourage the development of satellite cities that can share the burden. Attempts at decentralization have already been observed in Nigeria shifting its capital from Lagos to Abuja, Cote d’Ivoire’s shift from Abidjan to Yamoussoukro, or Tanzinia’s shift from Dar es Salaam to Dodoma. These shifts have had variable practical success.
In order to discover if a relationship between urban primacy and resource consumption exists in African cities, an indicator of urban primacy was created1. UN-Habitat and UNEP [29] build their indicator as the population of the largest city divided by the population of the second largest. While this is a good first step to demonstrating urban primacy, this method ignores countries that have two or three apex cities, and overlooks the proportion of the country’s population inhabiting these prime centers. To form a more inclusive indicator, this paper calculates urban primacy as the average population of the second and third largest cities divided by the population of the largest city, further divided by the percent of the urban population residing in the largest city.
African countries with the largest cases of urban primacy include Liberia, Djibouti, Mauritania, Guinea-Bissau and Burundi. Those with low urban primacy include Mozambique, Ghana, Mauritius, Tunisia, Cameroon and Algeria. In examining whether primacy has any impact on economic performance of African nations, there was no correlation found between primacy and per capita GDP. While a correlation between primacy and aggregate GDP exists, this may primarily be due to the population of each nation as smaller countries are more likely to exhibit urban primacy. No correlation was found between primacy and resource consumption. However, if primacy remains an important factor for considerations of good governance, it may be more indicative of resource access, than of consumption.
3. Exploratory Method for Estimating Resource Consumption Profiles for African Cities
For situations in which data are available, the process for analysing the physical requirements of cities and producing resource profiles is as follows: data collection, data analysis and finally, discussion (see Figure 1).
Figure 1. Exploratory pathways for developing urban resource consumption profiles.
However, in data scarce environments, innovative ways to estimate data at city-level based on national data becomes essential. The following sub-sections discuss the processes that were utilised to estimate African city- level data, in particular, data that was essential to begin investigating resource consumption profiles of African cities.
3.1. Acquiring National Data
The first step involved collecting socio-economic and resource profiles data for the 54 countries in Africa. The data were categorised according to type: geographic, demographic, socio-economic, energy, materials, wastes, and renewables and reserves. The respective specific data indicators for each category are detailed in Table 1. The data collected were for 2011, as this was the most recent year in which complete data for most indicators were available.
Table 1. List of the data categories collected for African nations.
Relatively consistent data for demographics, socio-economic and resource production or consumption are available at the national-level for all African nations. Demographic, geographic and economic data were sourced from the World Bank [30] . Energy related data were sourced from US Energy Information Administration [31] and material consumption data, based on trade information, was sourced from a new online portal, materialflows.net, administered by the Sustainable Europe Research Institute (SERI) and Vienna University of Economics and Business (WU) [32] .
Climate data were approximated from the Koppen climate zone classification [33] . Most countries contain multiple climate types, so the climate associated with the largest swath of land area one was utilized. Climate determinations are more precise at the city-level. Kottek et al. [33] have extended Wladimir Koppen’s original 1900 classification into a three-part designation of climate zone, temperature and precipitation. In order to allow numerical comparison of these designations, the 14 zones present in Africa were organized on a medium from equatorial, hot and wet to desert, cold and dry, and ranked from 0 to 100. Thus Uganda (equatorial, hot and humid) is more similar to Ethiopia (temperate, warm summer and humid) than to Chad (steppe, hot and arid). At city-level, climate data were collected from degreedays.net in the form of heating and cooling degree days. These variables measure the number of degrees above or below a baseline temperature over a period of time. This is useful for estimating the energy required for thermal regulation, typically the largest proportion of energy consumption in cities [34] . However, the extent and intensity of thermal regulation will vary greatly between African cities as it is a function of affluence as much as climate.
In order to predict urban resource consumption, a distinction between urban and rural consumption is necessary. Where differential resource data are limited, income of GDP can be used as a proxy. However, city-specific GDP and income data were also particularly difficult to find for African cities. Hence, attempts were made to estimate the average urban income from available national data. The first method used data for national income, ratio of urban to rural population, and the percentages of urban and rural poverty, with the World Bank prescribed poverty line of $1.25 per day. It was stated that each person in poverty made $1.25 per day, or $456.25 per year. This offered usable numbers for income of the urban and rural poor, allowing the remaining amount of national income to be divided by urban and rural “affluent” populations. Finally, the urban affluent income and poor income were summed to provide national urban income. Below is a list of key equations used to estimate urban income for African countries:
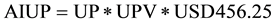 (1)
(1)
 (2)
(2)
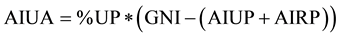 (3)
(3)
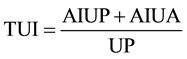 (4)
(4)
where AIUP is the annual income of the urban poor, AIRP is the annual income of the rural poor, AIUA is the annual income of the urban affluent, and TUI is the total urban income. UP is the urban population, %UP is the urban population as a proportion of nation population, RP is the rural population, UPV is the percentage of urban population living in poverty, RPV is the percentage of rural poverty.
As expected, the urban income estimates were predominantly larger than the nation’s average income2. However, the flaw with this method involves determining an appropriate poverty threshold. Many nations, such as Liberia or Burundi, showed average income far below $456.25 per year, suggesting that most of the nations’ population were below the $1.25 a day threshold. This is judged by a global comparison and does not reflect relative poverty within a nation. This method for estimating income seems robust, but would require identification or a more appropriate monetary poverty threshold in each country, given differences in lifestyle and cost of living. This is not to say that poverty is limited to monetary considerations, but it may be a useful metric for this estimation method.
The second method to ascertain urban income made use of an old USAID [35] approach. They suggest that urban income may be determined from the proportion of non-agricultural domestic production. As many African nations’ economies include a large proportion of mineral extraction, this activity was important to include. For their urban income estimation method, the Indian Ministry of Statistics and Programme Implementation (MOSPI) [36] suggests that above ground mining predominantly takes place in urban areas, while underground mining takes place away from large settlements. For this method, unclear as to the form of mining in many countries, it was stated to be rural. MOSPI further suggests that the oil industry is a predominantly urban one. With a stated assertion that all non-extractive economic production takes place in the city, the percent of GDP derived from urban activities is stated as the total GDP minus the proportion of GDP from agriculture and mining activities, excluding those related to oil production. This assertion produces the following equations:
 (5)
(5)
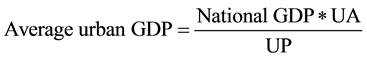 (6)
(6)
where UA is the proportion of GDP derived from urban activities and UP is the urban population of a nation.
This process produced higher urban incomes for all countries with available data, almost doubling the per capita national income, on average. Larger changes are visible in those with lower percentages of extractive industry contributions to GDP as well as for those with lower urban populations. The results of this method were utilized for further analysis of cities.
In order to ensure different per capita values for cities of the same nation, both the urban gross domestic product and urban income were distributed using the city scaling methods described below. Urban GDP and urban income used scaling exponents of 1.15 and 1.12 respectively, which were observed by Bettencourt et al. [37] .
3.2. National Clustering
Taking advantage of relatively abundant national data, clusters of African nations were formed. The data were prepared for comparison by normalizing the data first by population and then into a 0 - 100 index. It is acknowledged that comparing nations or cities using a per-capita measure may oversimplify what is happening in each space. A per-capita measure essentially shows the resource intensity of a nation’s population. If the analysis were to use a per-unit-GDP measure, it would be examining the resource intensity of the nation’s economy. Results of both methods require further speculation as to their meaning, as low intensity could indicate either resource poor nations or resource efficient nations. These national clusters give us our first indication for how their respective cities might also cluster.
The resulting list of data that was used in clustering included national: 1) Climate zone; 2) area; 3) population; 4) population density; 5) proportion of urban population; 6) degree of urban primacy; 7) GDP; 8) GNI; 9) urban poverty; 10) rural poverty; 11) proportion of slum urbanites; 12) carbon emissions (CO2); and 13) consumption of: biomass (Bio), fossil fuels (FF), total energy (TE), electricity (EL), industrial and construction materials (IndCon), total materials (TM) and water (H2O).
The values for each variable were initially normalized on a 0 to 100 index as a percentage of the largest value. Such a scaling demonstrated the comparative magnitude of each country for that variable. However, this resulted in skewed results: For example, South Africa’s net electricity consumption was 218 Billion kWh, far exceeding both the average of 10 Billion kWh, and the median value of 1.3 Billion kWh. The electricity consumption of other African countries’ was therefore insignificant when compared to South Africa’s. As the point of clustering is to determine how similar (or dissimilar) each nation is to each other, the data were scaled by shifting the median value to 50. This provided a more even distribution of values for each variable, such as with a log distribution, yet while remaining on a 1 to 100 index. This method does not, however, display relative magnitude. The key steps to enable median normalization of the values are:
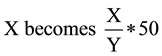 (7)
(7)
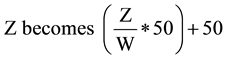 (8)
(8)
where X is less than the median value (Y), Z is larger than Y, and W is the largest value in the indicator’s dataset. This method is still imperfect as values higher than the median may still be skewed by a large outlier.
National clustering was analyzed in R software, and clusters were formed using the ward. D method of hclust and euclidian method of dist. Scree analysis suggested an optimum of 15 separate clusters. However, some of these were outliers of single countries and between 9 and 12 groups proved effective, depending on which data were processed. The first run of clustering used all available variables to group the most similar countries into nine clusters. However, five countries were left as outliers, too dissimilar to properly cluster. A second run, comparing only socio-economic and geographic data, provided 10 groups and three single-country outliers. The final run, comparing only resource consumption or emission indicators, produced 11 groups with one outlier. Table 2 shows the three sets of groupings completed using the median-normalized data. Radar charts were created for each group to visualize and explain the group members’ similarity. Further examination of the differences between variables will be described in a forthcoming publication.
Some uncertainty existed as to which variables were the most important determinants of resource consumption. Krausmann et al. [38] and Fernandez et al. [26] identify population, population density, affluence and climate as the most important indicators of industrialization, and the resource consumption intensity correlated to it. With this in mind, values for resource indicators were designated high, medium or low levels of intensity. Classification trees were then used to determine the relative importance of four variables in predicting this level of resource intensity. Table 3 shows that per capita GDP is the most important predictor of energy consumption and related carbon emissions, while density is an important predictor of water and total material consumption, potentially referring to ease of access to resources. Population is the strongest predictor of biomass consumption, suggesting that biomass is a consistent human need across countries.
3.3. Determining National to City Scaling Relationships
A number of approaches were explored to determine plausible scaling relationships that could be utilised to estimate city data from the available national data. Zipf’s law or more specifically, Gibrat’s law for cities suggests that a certain homogeneity of city processes exists, demonstrating that the size distribution of cities fits a power law [37] [39] . In this way, cities can be conceptualized as scaled versions of each other. The rank-size relationship demonstrated with Gibrat’s law demonstrates that the number of cities with a population greater than S is
Table 2. Groups of African nations by all available variables, socio-economic variables, and resource variables.
Table 3. Relative importance of indicators in predicting resource consumption or emission.
proportional to 1/S [39] . This has been empirically demonstrated for cities of the US, India and China, and holds true for many African nations.
Determination of average scaling coefficients and exponents for a country requires either a comparison of city size and attribute between cities of one nation at the same point in time, or a comparison between different points of time for one city, essentially tracking its growth over time.
Figure 2 shows the rank-size relationship for cities in a number of African countries. The slope of the distribution is expected to be close to −1. Typically, the upper parts of the distribution show this slope, while the lower part, formed of larger cities, tends to deviate. This is visible in Figure 2 and is primarily due to the deviation of the large or prime cities from this linear pattern. Nigeria is an interesting exception as, despite the size of Lagos, the urban population seems well distributed through other cities. This does not hold true for Kinshasa, Cairo and Nairobi, which remain quite prime cities in their respective countries. Angola’s overall slope may indicate a poor accuracy of available population data which hasn’t been updated recently. Rosen and Resnick [27] explain that Zipf’s law is more accurately portrayed when using population data for urban agglomeration instead of city proper.
Bettencourt et al. (2007) take Zipf’s scaling relationships further and represent it in the following equation:
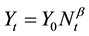 (9)
(9)
where: Y is the indicator to be understood (anything from resource consumption to social attributes) represented as a function of N, city size, at time t. Y0 is the normalizing coefficient (or the Y when t is 1 and N is at its smallest or initial value) and β is the scaling exponent which describes the relationship between Y and N.
Bettencourt et al. [37] processed a large amount of data to determine the way in which multiple attributes change as cities do. They explain three types of relationships and the city attributes which fall in each category. First is a sublinear relationship (β < 1), which demonstrates the benefits of an agglomeration economy, an economy of scale: as it grows, a city may need less material infrastructure to support a larger population. Second is a linear relationship (β = 1), which includes attributes related to individual human needs, such as housing, household water or electricity consumption. Finally, superlinear relationships (β > 1) are categorized by attri- butes which demonstrate the outcomes of urban agglomeration, such as increases of knowledge production, total energy consumption, cases of disease, and affluence.
With abundant population and electricity consumption data for urban settlements of South Africa, the scaling relationship of electricity consumption for the years 2001 and 2005 is demonstrated in Figure 3. Bettencourt et al.’s offer a scaling exponent of 1.07 to describe electricity consumption and the exponents for these graphs as smaller. It was noted that the variance becomes more visable as the smaller cities are added to the graph. This is a clear indication of how larger cities have deviated from the average power law. The outliers may also potentially be a product of using city-proper data instead of agglomeration data, or an indication of their function. For instance, Durban and Johannesburg have higher than average electricity consumption, which is perhaps indicative of larger industrial or business sectors. Durban is South Africa’s largest port, which may demand more electricity to function. For a more indicative scaling exponent, more cities must be included in analysis.
In theory, this scaling relationship could be determined through the growth of one city over time. However, the resulting scaling exponent from a sample of one city may not be as empirically robust or transferable as one
Figure 2. Rank-size relationships for selected African countries.
Figure 3. Relationship of city population to electricity consumption in the nine largest South African cities for 2001 and 2005.
observed from multiple cities. This is particularly true of larger cities which deviate from the average. The growth of population and electricity consumption for Bloemfontein and Cape Town was tracked from 1996 to 2007. The smaller city shows a scaling exponent closer to those demonstrated by multiple cities, yet both exponents are much larger than expected. An ideal situation would be if there were data spanning a larger space of time; this would smooth out any natural fluctuations of electricity consumption, expected due to climate or social changes. Further exploration will entail a comparison of city-proper, agglomeration and municipal data, as well as finding scaling exponents for different groups of cities, perhaps by size or primary function. A more detailed analysis of South African city scaling will be forthcoming elsewhere, in which the relationships between population, GDP and electricity between 1996 and 2011 are explored.
3.4. Estimating City Resource Data from National Data
The discussion in the previous section shows how to scale when reasonable city-level data are available. In the context of data scarcity at city-level, the question that arises is how to go about scaling with the least available data. This is where the use of national data can become useful in providing initial city resource consumption estimates. Using electricity scaling as an illustration, Bettencourt et al. [37] suggest that most cities will follow a β of 1.07 yet South Africa demonstrates lower βs of 1.038 to 1.027 in 2001 and 2005 respectively. A faulty assumption in scaling is that all cities or all attributes scale in the same way. Bettencourt et al.’s [37] equation only provides an average relationship between size and the desired attribute and that relationship is not necessarily transferrable between cities. So how can a more indicative average for each city be determined?
It could be assumed that countries of similar demographic, economic and climate parameters might use resources similarly, and demonstrate similar patterns of scaling. With this in mind, groups of nations can be generated, as above, hence enabling the use of proxy scaling relationships for all members of the group. What is required for each cluster is to determine the scaling coefficients and exponents for a minimum of two relationships: sublinear, indicative of material consumption, and superlinear, indicative of energy consumption. This may be done in the same way as demonstrated by the South African cities example above: that is, analyzing multiple cities at one point in time or a single city over an extensive time. With this minimal additional data, a much more plausible representation of cities using only a few scaling relationships can be generated.
While awaiting more precise scaling relationship data, the following procedure was followed to estimate African cities’ levels of consumption or emission for each resource indicator based on national data:
1) The first step was to establish the nation’s urban average consumption or emission for each indicator. Consumption of total energy, fossil fuels, electricity, total materials, and construction materials, as well as carbon emissions showed positive linear relationships to GDP, so the proportion of urban consumption was determined similarly to urban income and urban product:
 (10)
(10)
where UR is the average urban resource consumption or emission, NR is the national resource consumption or emission, UA is the proportion of GDP derived from urban activities and UP is the urban population.
For fossil fuels, coal was excluded from urban consumption, as it would primarily be used for thermal electricity generation away from cities. Industrial materials and ores were stated to be wholly consumed in cities, so the urban average was determined as the total national consumption of industrial minerals and ores divided by urban population. For biomass and water consumption, which showed no clear relationship to GDP or other indicators, such as biomass and water, the national average was utilized as the urban average.
2) Distributing this average between the cities of each nation utilized Equation (9). Until more specific scaling relationships could emerge, a scaling exponent (β) of 1.07 was used for each resource. Using the population of the largest city in each nation, the normalization constant (Y0) for each nation was determined with this equation:

where CPi is the largest city’s population. The additional multiplication by the scaling exponent was used to increase or decrease the Y0 by a factor, as the consumption in the largest city would tend to be higher or lower than the urban average. Without this extra multiplication, the total resource consumption would not be fully distributed to cities, and the total urban consumption would come up short. This is an imperfect way to solve the problem, but it returns more complete values for total urban consumption.
3) Deriving the value for resource consumption for each city then becomes a matter of returning to the original equation:

where CPj is the city population and CRj is the city’s consumption or emission.
With the derived city resource consumption data, it was possible to form resource consumption profiles and cluster the African cities by similarity of profile. This formed the first iteration of an African city typology, with the second iteration awaiting more accurate scaling relationships.
4. Clustering of Selected African Cities
While it has been demonstrated that scaling methods have been used to determine the resource impact of cities, socioeconomic and geographic variables can also be utilized to predict the resource consumption intensity of cities. From a datasheet of 687 African cities collected since March 2014, a smaller list of cities was distilled. To remain representative, it included three cities per country, where applicable. The criteria used in selecting the three cities per country were: 1) country capital, 2) largest remaining city and 3) remaining city with the most available data. Certain countries, such as the Cape Verde, Djibouti and Seychelles did not lend the full three cities to the list, as there were few choices present in these countries. Any remaining cities of over one million were also included to produce a list of 160 cities. This was further reduced to a list of 120 cities which had complete data for four predictor variables to be used, namely population, population density, income and climate. A preliminary clustering of these cities produced an optimum of 10groups which are shown in Table 4. Though population growth wasn’t used in the clustering process, it is included in the description of clusters. Similarities can be seen between many equatorial cities as well as island cities. Some affinity exists between northern and
Table 4. 120 cities clustered according to similarity of population, density, climate and per capita income.
southern cities (with higher incomes and HDI, and low prevalence of slums), as well as some groupings of industrial cities, and of port cities.
As with the global cities typology [25] [26] , predictor variables can be used to loosely estimate resource consumption intensity (high, medium and low) for each city. Future work includes forming decision trees to sort cities by level of resource intensity, as suggested by the predictors. This is a more qualitative form of clustering and will still require use of some scaled data to form training classification trees.
5. Conclusions
This paper presents an exploratory approach utilized as first step towards estimating resource consumption profiles in data scarce urban environments such as African cities. Specific city-level data on resource consumption and material flow analysis are difficult to establish because such data are non-existent in Africa cities. This makes it more challenging to directly apply standard urban metabolism approaches.
What has emerged from the analysis is that it is possible to make use of scaling and national clustering to group like cities, which in turn can support recommendations for multiple situations towards achieving urban sustainability. With 11 reasonable clusters of countries already generated, it is possible to utilize scaling relationships discovered in one country for other countries of the same cluster, reducing the number of scaling relationships to determine. This brings us a step closer to forming more accurate scaling relationships to estimate resource consumption behaviors, based on similar socio-economic makeup of countries. Within each cluster, the search for data can be simplified to either: 1) energy and material consumption in multiple cities of one country at the same point in time; or 2) energy and material consumption of one city over an extended period of time.
A first iteration of an African City Typology has been produced and the second iteration is underway, with the results expected to be presented in future publications. Future work will involve 1) an exploration as to the benefits of using a “per unit GDP” measure as baseline with which to compare cities and 2) a qualitative estimation of city resource consumption using classification trees. This method is expected to offer some initial representations of material and energy consumption, and will be corroborated with more precise quantitative estimations from scaled national data.
Cite this paper
PaulCurrie,EthanLay-Sleeper,John E.Fernández,JennyKim,Josephine KavitiMusango, (2015) Towards Urban Resource Flow Estimates in Data Scarce Environments: The Case of African Cities. Journal of Environmental Protection,06,1066-1083. doi: 10.4236/jep.2015.69094
References
- 1. Grim, N.B., Faeth, S.H., Golubiewski, N.E., Redman, C.L., Wu, J., Bai, X. and Briggs, J.M. (2008) Global Change and the Ecology of Cities. Science, 319, 756-760.
http://dx.doi.org/10.1126/science.1150195 - 2. UNEP (2011) Decoupling Natural Resource Use and Environmental Impacts from Economic Growth.
http://www.unep.org/resourcepanel/decoupling/files/pdf/decoupling_report_english.pdf - 3. Pieterse, E. (2008) City Futures: Confronting the Crisis of Urban Development. Zed Books, London and New York.
- 4. UN-DESA (2013) World Population Prospects: The 2012 Revision, Highlights and Advance Tables. Working Paper No. ESA/P/WP.228.
http://esa.un.org/wpp/ - 5. Bai, X. (2007) Industrial Ecology and the Global Impacts of Cities. Journal of Industrial Ecology, 11, 1-6.
http://dx.doi.org/10.1162/jie.2007.1296 - 6. Satterthwaite, D. (2009) The Implications of Population Growth and Urbanization for Climate Change. Environment and Urbanization, 21, 545-567.
http://dx.doi.org/10.1177/0956247809344361 - 7. Ozbekhan, H. (1970) The Predicament of Mankind: A Quest for Structured Responses to Growing World-Wide Complexities and Uncertainties. Proposal to the Club of Rome.
- 8. Morin, E. and Kern, A.B. (1999) Homeland Earth: A Manifesto for the New Millennium. Hampton Press, London.
- 9. Hall, M.H.P. (2011) A Preliminary Assessment of Socio-Ecological Metabolism for Three Neighborhoods within a Rust Belt Urban Ecosystem. Ecological Modelling, 223, 20-31.
http://dx.doi.org/10.1016/j.ecolmodel.2011.08.018 - 10. Kennedy, C., Cuddihy, J. and Engel-Yan, J. (2007) The Changing Metabolism of Cities. Journal of Industrial Ecology, 11, 43-59.
http://dx.doi.org/10.1162/jie.2007.1107 - 11. Brunner, P.H. (2007) Reshaping Urban Metabolism. Journal of Industrial Ecology, 11, 11-13.
http://dx.doi.org/10.1162/jie.2007.1293 - 12. Kennedy, C., Pincetl, S. and Bunje, P. (2011) The Study of Urban Metabolism and Its Applications to Urban Planning and Design. Environmental Pollution, 159, 1965-1973.
http://dx.doi.org/10.1016/j.envpol.2010.10.022 - 13. Baccini, P. and Brunner, P. (2012) Metabolism of the Anthroposphere: Analysis, Evaluation, Design. MIT Press, Cambridge.
- 14. Walsh, C., McLoone, A., O’Regan, B., Moles, R. and Curry, R. (2006) The Application of the Ecological Footprint in Two Irish Urban Areas: Limerick and Belfast. Irish Geography, 39, 1-21.
http://dx.doi.org/10.1080/00750770609555863 - 15. Barles, S. (2009) Urban Metabolism of Paris and Its Region. Journal of Industrial Ecology, 13, 898-913.
http://dx.doi.org/10.1111/j.1530-9290.2009.00169.x - 16. Niza, S., Rosado, L. and Ferrao, P. (2009) Urban Metabolism: Methodological Advances in Urban Material Flow Accounting Based on the Lisbon Case Study. Journal of Industrial Ecology, 13, 384-405.
http://dx.doi.org/10.1111/j.1530-9290.2009.00130.x - 17. Best Foot Forward Ltd. (2002) City Limits—A Resource Flow and Ecological Footprint Analysis of Greater London. Best Foot Forward, Oxford.
www.citylimitslondon.com/ - 18. Gasson, B. (2002) The Ecological Footprint of Cape Town: Unsustainable Resource Use and Planning Implications. Paper Presented at the National Conference of the South African Planning Institution, Durban, 18-20 September 2002.
- 19. Abou-Abdo, T., Davis, N.R., Krones, J.S., Welling, K.N. and Fernandez, J.E. (2011) Dynamic Modeling of Singapore’s Urban Resource Flows: Historical Trends and Sustainable Scenario Development. 2011 IEEE International Symposium on Sustainable Systems and Technology (ISSST), Chicago, 16-18 May 2011, 1-6.
- 20. EUROSTAT (2001) Economy-Wide Material-Flow Accounts and Derived Indicators: A Methodological Guide. Eurostat, European Commission, Luxembourg.
http://epp.eurostat.ec.europa.eu/cache/ITY_OFFPUB/KS-34-00-536/EN/KS-34-00-536-EN.PDF - 21. Kennedy, C. and Hoornweg, D. (2012) Mainstreaming Urban Metabolism. Journal of Industrial Ecology, 16, 780-782.
http://dx.doi.org/10.1111/j.1530-9290.2012.00548.x - 22. Baynes, T.M. and Bai, X. (2012) Reconstructing the Energy History of a City. Journal of Industrial Ecology, 16, 862-874.
http://dx.doi.org/10.1111/j.1530-9290.2012.00567.x - 23. Ferrão, P. and Fernandez, J. (2013) Sustainable Urban Metabolism. MIT Press, Cambridge.
- 24. Parnell, S. and Pieterse, E. (Eds.) (2014) Africa’s Urban Revolution. Zed Books, London.
- 25. Saldivar-Sali, A.N.D. (2010) A Global Typology of Cities: Classification Tree Analysis of Urban Resource Consumption. Master’s Thesis, Massachusetts Institute of Technology, Cambridge.
- 26. Fernandez, J.E., Novia, K.M., Kalmykova, Y. and Saldivar-Sali, A. (2013) City Typologies: Derivation and Results from Phases I and II. Massachusetts Institute of Technology, Cambridge.
- 27. Rosen, K. and Resnick, M. (1980) The Size Distribution of Cities: An Examination of the Pareto Law and Primacy. Journal of Urban Economics, 8, 165-186.
http://dx.doi.org/10.1016/0094-1190(80)90043-1 - 28. UN-Habitat (2014) The State of African Cities 2014: Re-Imagining Sustainable Urban Transitions.
http://www.ruaf.org/sites/default/files/Habitat%20state%20of%20African%20cities.pdf - 29. UN-Habitat and UNEP (2010) The State of African Cities 2010: Governance, Inequality and Urban Land Markets. UN Habitat & UN Environment Programme, Nairobi.
http://mirror.unhabitat.org/pmss/getElectronicVersion.aspx?nr=3034&alt=1 - 30. World Bank (2014) World Bank Databank.
http://data.worldbank.org/ - 31. EIA (2014) US Energy Information Administration Data.
http://www.eia.gov/countries/data.cfm - 32. SERI and WU (2014) Global Material Flows Database.
http://www.materialflows.net/home - 33. Kottek, M., Grieser, J., Beck, C., Rudolf, B. and Rubel, F. (2006) World Map of the Koppen-Geiger Climate Classification Updated. Meteorologische Zeitschrift, 15, 259-263.
http://dx.doi.org/10.1127/0941-2948/2006/0130 - 34. Weisz, H. and Steinberger, J.K. (2010) Reducing Energy and Material Flows in Cities. Current Opinion in Environmental Sustainability, 2, 185-192.
http://dx.doi.org/10.1016/j.cosust.2010.05.010 - 35. USAID (1980) Review of Household Income Estimates for Nairobi, Lima and Tunis, and Preliminary Description of Methodology for Estimating Household Incomes. Office of Housing, Agency for International Development, Washington DC.
- 36. MOSPI (2007) Estimation of Rural and Urban Income. National Accounts Statistics-Sources & Methods. [Online]. Ministry of Statistics and Programme Implementation.
http://mospi.nic.in/rept%20_%20pubn/ftest.asp?rept_id=nad09_2007&type=NSSO - 37. Bettencourt, L.M.A., Lobo, J., Helbing, D., Kuhnert, C. and West, G. (2007) Growth, Innovation, Scaling, and the Pace of Life in Cities. Proceedings of the National Academy of Sciences of the United States of America, 104, 7301-7306.
http://dx.doi.org/10.1073/pnas.0610172104 - 38. Krausmann, F., Erb, K.H., Gingrich, S., Lauk, C. and Haberl, H. (2008) Global Patterns of Socioeconomic Biomass Flows in the Year 2000: A Comprehensive Assessment of Supply, Consumption and Constraints. Ecological Economics, 65, 471-487.
http://dx.doi.org/10.1016/j.ecolecon.2007.07.012 - 39. Gabaix, X. (1999) Zipf’s Law for Cities: An Explanation. The Quarterly Journal of Economics, 114, 739-767.
http://dx.doi.org/10.1162/003355399556133
Supplemental Material
Table S1. Urban primacy and its determinants, from most prime at top, to least prime at bottom.
Table S2. Estimations of average urban income and their determinants.
NOTES
*Corresponding author.
1Dataset available in Supplemental Material (Table S1).
2Dataset available in Supplemental Material (Table S2).








