Energy and Power Engineering
Vol. 4 No. 4 (2012) , Article ID: 20229 , 9 pages DOI:10.4236/epe.2012.44037
Evaluation of Operating Domains in Power Systems
SEC Chair in Power System Reliability and Security, King Saud University, Riyadh, KSA
Email: melkady@ksu.edu.sa
Received April 29, 2012; revised May 31, 2012; accepted June 17, 2012
Keywords: Power Systems; Dynamic Security; Operating Parameters; Performance Optimization
ABSTRACT
This paper presents the results of a recent major industry-supported study with the aim to provide power system operators with more meaningful and effective means to quickly identify feasible operating boundaries as well as more flexibility to select alternate operating scenarios. In this regard, the paper outlines the main theoretical basis and computational framework for the development of innovative computerized schemes capable of identifying and processing various system integrity domains. The novel framework allows system operators to determine—in a fast and reliable manner—the most favorable operating scenarios which maintain system security, reliability and operating performance quality. For demonstration purposes, and without loss of generality, an emphasis is given to the dynamic system security problem where the Transient Energy Function (TEF) method is used to define quantitative measures of the level (degree) of system security for a given operating scenario. Nonetheless, the framework presented is applicable quite as well to other system performance functions and criteria that may be considered. A demonstrative application is presented for a 9-bus benchmark system, widely used in the literature. In addition, a practical application is also presented for the Saudi Electricity Company (SEC) power system where the operating security domain was evaluated in the operating parameter space spanned by two major interface flows in the system.
1. Introduction
Power system operators often make operating decisions based on two basic objectives, namely: 1) ensure system integrity (security, reliability and quality); and 2) minimize operating costs. In real life situations, these two objectives are in conflict with each other and the power system operator has, in many cases, to analyze and check—in a trial and error manner—operating scenarios, which are thought to be most economical, against the system security, reliability and quality requirements and, consequently, reject those operating scenarios which do not meet the system integrity constraints [1,2]. In the case where dynamic system security is at stake, the automated identification of the system dynamic security boundaries would be of great help to system operators as it would provide them with a practical way of identifying the dynamic operating security modes of the system in a fast, accurate and reliable manner [3-7].
Due to the critical importance of electric energy and the rising cost of its production, power utilities around the world are compelled to minimize production cost while, in the mean time, operating within acceptable system integrity limits such as operating security constraints, reliability thresholds, voltage profile and VAR guidelines, supply-demand balance requirements, etc. The complexity of the overall problem and the multi-discipline nature of the research involved have resulted in division of the research into two main areas, namely power system performance quality and operational economy. The objective in the operational economy area is to determine the optimum schedule of utility generating units that minimizes the total operation cost subject to constraints and limitations on equipment and system control devices. On the other hand, the objective of system performance assessment is to ensure the system ability to withstand some unforeseen, but probable, disturbances with the minimum disruption of service or reduction of service quality [8-10]. In recent years, the loading of transmission network and the amount of power transfer between interconnected systems has increased to the point where power system security and reliability constraints started to influence the generation commitment and loading decisions. This is because in real power systems, any redistribution of generator power output to minimize fuel and other operational costs would also influence the system static and dynamic behavior when a contingency occurs [11-13].
In a recent major industry-supported study, extensive research and development work was conducted with the aim to provide power system operators with more meaningful and effective means to quickly identify feasible operating boundaries as well as more flexibility to select alternate operating scenarios. In this regard, this paper outlines the main theoretical basis and computational framework for the development of innovative computerized schemes capable of identifying and processing various system integrity domains and, therefore, allowing system operators to determine—in a fast and reliable manner—the most favorable operating scenarios which maintain system security, reliability and operating performance quality. The methodology adopted in this work includes the development of advanced, highly efficient computerized algorithms for fast identification of the system integrity domains, including feasible dynamic operating security and reliability modes of power system. One of the salient outcomes of this work is the development of a novel framework for identification and representation of the system integrity domains as well as evaluation of the security, reliability and performance quality levels associated with different operating scenarios. The system integrity constraints are in fact domains (boundaries) that surround all potentially acceptable operating modes (scenarios) of the power system. In other words, these domains form the feasible operating region— in the parameter space spanned by various operating variables—within which the system can safely be operated. The identification of the system feasible operating domains can be performed using various available numerical techniques including artificial intelligence (artificial neural networks, genetic algorithms, fuzzy logic, etc.), pattern recognition, non-linear optimization-based methods for centering, tolerance and tuning, etc. For a given operating scenario, the associated system integrity level is measured by the position of the operating point with respect to the feasible operating domain boundary, measured either as a simple “distance” (for example, the Euclidean norm) in the decision parameter space or using an operating performance merit function (e.g., security margin).
While the concepts and principles presented are general, the work of this paper is confined to the interpretation of the system integrity as maintaining acceptable levels of system security, reliability and operating performance quality. For demonstration purposes, an emphasis is given to the dynamic system security problem where the Transient Energy Function (TEF) method is used to define quantitative measures of the level (degree) of system security for a given operating scenario [14-16]. Nonetheless, the framework presented is applicable quite as well to other system performance functions that may be considered. A practical application to the Saudi Electricity Company (SEC) power system is also presented in the paper.
2. Theoretical Formulation
2.1. System Integrity Domains
Consider Figure 1 which provides schematic representation to illustrate the concept of the system integrity domains, where the level of system integrity (security, reliability or quality) associated with different operating scenarios is measured in terms of how far the location of the operating point is from the system integrity boundaries. The concepts and principles outlined in this section are applicable to both single and multi (interacting) system integrity domains of either one or more operating functions.
In the general formulation of the problem on hand, the field of real numbers is denoted by  while the field of complex numbers is denoted by C. The vector space over Â, of n-tuples (z1, z2, ∙∙∙, zn), zi Ì Â is denoted by Ân. We classify the problem variables into two groups, namely the dependent (state) variables xi Ì Ân, which are grouped into the n-dimensional column vector x, and the independent (control) decision variables uk Ì Âm, which are grouped into the m-dimensional column vector u.
We note that the states xi are those variables which are of interest to the problem but can only be observed (for example, transmission line flows), while the controls uk are those variables which can be adjusted (manipulated) in practice (for example, plant output powers, transformer tap-settings, controlled bus voltages, var additions, etc.). The state and control variables are related through as set of n equality constraints h (x, u) = 0 representing, for example, the network flow equations.

Figure 1. System integrity domains.
2.2. Operating Scenarios and Integrity Indices
A set of potential operating scenarios ψs (u), s =1, 2, ∙∙∙, NS, where NS denotes number of scenarios, are defined to represent different groupings of the control variables associated with particular operating decisions that cause the power system to reside in a particular mode of operation. In other words, ψs (u) defines a particular setting {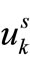 ∈ Rm} of the system operating modes resulting from certain operator decisions.
∈ Rm} of the system operating modes resulting from certain operator decisions.
Now, the problem on hand is formulated in terms of one (or more) System Integrity Index fℓ (x, u) which measures the distance in the control parameter space, in terms of a particular norm (for example, Euclidean norm), between certain system operating scenario {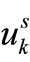 ∈ &Rm} and the system integrity domain Φℓ (u), ℓ = 1, 2, ∙∙∙, NL, where NL denotes the number of integrity domains considered in the problem. In some study cases, several system integrity domains are considered to either represent multi-criteria such as system security, reliability, etc. or denote different potential contingencies and/or operating schemes that are likely to occur during actual system operation. The system integrity domain Φℓ (u) is the feasible space spanned by the problem variables within which all operating scenarios are considered feasible (acceptable). Therefore, a security domain Φℓ (u) is defined, in general, by a number of inequality constraints gℓ (x, u) ³ 0, which may include—as special case—simple upper and lower bounds on the state and control variables xL ≤ x ≤ xU & uL ≤ u ≤ uU. In the present work, the system security index fℓ (x, u) will be defined as the minimum of the distance functional norms between a feasible operating scenario and all relevant inequality constraints defining the integrity domain Φℓ (u). In other wordsfℓ (x, u) = Minimum {over j} of
∈ &Rm} and the system integrity domain Φℓ (u), ℓ = 1, 2, ∙∙∙, NL, where NL denotes the number of integrity domains considered in the problem. In some study cases, several system integrity domains are considered to either represent multi-criteria such as system security, reliability, etc. or denote different potential contingencies and/or operating schemes that are likely to occur during actual system operation. The system integrity domain Φℓ (u) is the feasible space spanned by the problem variables within which all operating scenarios are considered feasible (acceptable). Therefore, a security domain Φℓ (u) is defined, in general, by a number of inequality constraints gℓ (x, u) ³ 0, which may include—as special case—simple upper and lower bounds on the state and control variables xL ≤ x ≤ xU & uL ≤ u ≤ uU. In the present work, the system security index fℓ (x, u) will be defined as the minimum of the distance functional norms between a feasible operating scenario and all relevant inequality constraints defining the integrity domain Φℓ (u). In other wordsfℓ (x, u) = Minimum {over j} of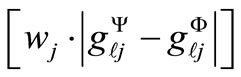 , where
, where 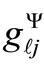 is the value of the j-th inequality constraint evaluated at the operating scenario Ys (u),
is the value of the j-th inequality constraint evaluated at the operating scenario Ys (u), 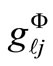 is the value of the boundary (threshold) value of the j-th inequality constraint at Φℓ (u) and wj is a weighting factor associated the jth element of fℓ (x, u). Obviously large values of fℓ (x, u) would indicate more secure operating modes while small values of fℓ (x, u) would indicate less secure modes.
is the value of the boundary (threshold) value of the j-th inequality constraint at Φℓ (u) and wj is a weighting factor associated the jth element of fℓ (x, u). Obviously large values of fℓ (x, u) would indicate more secure operating modes while small values of fℓ (x, u) would indicate less secure modes.
2.3. Reduced Gradients
In order to deal with the presence of the state variables in the problem formulation in an efficient and proper mathematical manner, the concept of reduced gradients (total derivatives) could be employed. The reduced gradients of the system integrity index fℓ (x, u) with respect to the control variables u are denoted by dfℓ/du and, therefore, represent the sensitivity of the system integrity index fℓ (x, u) with respect to u in the sub-space spanned solely by the control variables. The reduced gradients can be calculated using the method of Lagrange multipliers, in which the partial derivatives of fℓ (x, u) with respect to both x and u are denoted by 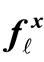 = [∂fℓ/∂x] and
= [∂fℓ/∂x] and 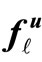 = [∂fℓ/∂u], respectively, while the partial derivatives of the equality constraints h (x, u) with respect to both x and u are denoted by Hx = [∂hT/∂x]T and Hu = [∂hT/∂u]T, respectively. The Lagrange multipliers are obtained by solving the set of linear equations
= [∂fℓ/∂u], respectively, while the partial derivatives of the equality constraints h (x, u) with respect to both x and u are denoted by Hx = [∂hT/∂x]T and Hu = [∂hT/∂u]T, respectively. The Lagrange multipliers are obtained by solving the set of linear equations  λℓ =
λℓ =  and are then used to calculate the reduced gradients as dfℓ/du = [
and are then used to calculate the reduced gradients as dfℓ/du = [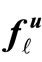 –
–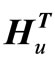 λℓ]. It is important to note that the reduced gradients dfℓ/du represent a powerful means for measuring the sensitivity of the system integrity index (for example, security level) with respect to various operating decision variables. In other words, they provide invaluable information on how the system integrity is impacted by various operating decisions made by the system operators.
λℓ]. It is important to note that the reduced gradients dfℓ/du represent a powerful means for measuring the sensitivity of the system integrity index (for example, security level) with respect to various operating decision variables. In other words, they provide invaluable information on how the system integrity is impacted by various operating decisions made by the system operators.
3. Dynamic Security Domains
3.1. Background
The importance of efficient and secure operation of the power grid has always been acknowledged by the electric power utilities. In this regard, power system operation aims, in principle, at maintaining reliable and secure supply of electricity while minimizing the total cost of operation. In theory, there are two main objectives that could be considered, namely the maximization of system security and the minimization of total operating cost of supplying energy. In practice, however, the security requirements are included as constraints rather than formulating the problem as a security maximization mandate. The system security constraints are in fact boundaries that surround all possible operating modes (scenarios) of the power system. In other words, these boundaries form the feasible operating domain—in the parameter space spanned by various operating variables—within which the system can safely be operated.
For a given operating scenario, the associated security level is measured by the “distance” (for example, the Euclidean norm) of the operating point from the security domain boundary. Alternatively, the security level could also be measured in terms of the energy margin value (see the TEF formulation in the next sub-section) at the operating point.
Security constraints could either be “static” or “dynamic”. The term “static security” means that all constraints reflect steady-state quantities such as steady-state bus voltage violations and steady-state transmission line overloading. In conventional approaches, the dynamic security constraints are either neglected or checked subsequently and independent of the operating cost minimization scheme. In real power system operations, however, any re-distribution of generator powers to minimize fuel costs (economic dispatch) would also influence the system dynamic behavior (stability) when a contingency occurs (for example, a fault which is cleared by a transmission line outage). Modeling complexity as well as the multi-discipline nature of the research required have traditionally prevented the inclusion of the dynamic system security constraints in the overall optimization procedure, which would include both static and dynamic security constraints. While the static security constraints ensure that the system integrity is maintained during the steadystate operation, the dynamic security constraints ensure that the system would maintain its dynamic robustness during contingency situations. In addition to static and dynamic security constraints, other boundaries are defined, for example, in terms of equipment physical constraints.
This section focuses on the use of the transient energy function (TEF) method in order to define quantitative measures of the level (degree) of system security for a given operating scenario.
3.2. Transient Energy Function (TEF)
Until recently, transient stability analysis has been performed by power utilities using exclusively numerical integration techniques to calculate the synchronous generator response to a given disturbance. Transient Energy Function (TEF) method provides an alternative approach to the conventional transient stability analysis. In contrast to the time-domain approach, TEF method determines the system stability directly based on energy functions. The TEF method not only avoids the time-consuming step-by-step time-domain solutions, but it also provides a quantitative measure of the degree of system stability known as the Energy Margin (EM). Positive values of EM indicate a stable system while negative values indicate unstable system.
The EM and its sensitivities with system operating parameters make the TEF method very attractive when stability limits must be calculated quickly. Although the direct methods have a long development history, it was until recently thought to be impractical for large-scale power systems analysis. However, recent developments have made the direct method quite suitable for stability analysis of large-scale power systems.
The TEF can be formulated directly using the Center of Inertia (COI) frame of reference, which has the advantage of removing the energy change associated with the motion of the system COI. The COI is defined as
 (1)
(1)
where NG is the number of generator busses, qi is the generators bus voltage angle, wi is the generator speed, Mi is the moment of inertia and
 (2)
(2)
The bus angles as well as generator internal angles qi and rotor speeds expressed in the COI frame of reference, are given by
 (3)
(3)
Also
 (4)
(4)
where the over ~ denotes quantities in the synchronous frame of reference.
Converting loads to constant shunt admittances and transforming rotor angles and speed to the COI reference, the swing equation of the NG generators can be written in the following compact form
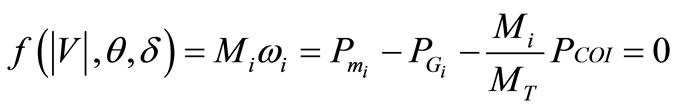 (5)
(5)
where 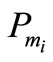 and
and 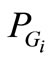 are the mechanical power input and generation power output respectively, V is the bus voltage magnitude and
are the mechanical power input and generation power output respectively, V is the bus voltage magnitude and
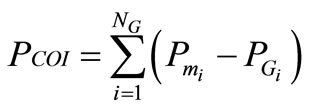 (6)
(6)
The equilibrium points of the system are the points where the right hand side of Equation (5) is equal to 0. Among such equilibrium points, the Stable Equilibrium Point (SEP) and the controlling Unstable Equilibrium Point (UEP) are of interest for the purpose of the transient stability analysis. The only difference between the determination of the SEP and the UEP is the initial condition provided to the solution algorithm. For the SEP, the condition at fault clearing is used while, for the UEP, the so-called “ray point” is normally used unless for stressed systems in which more robust techniques are needed to solve for the UEP.
Having solved for the SEP and the UEP, the transient energy function V (q, ω) is expressed as
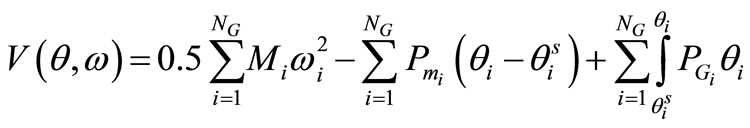 (7)
(7)
in which the three RHS terms represent the kinetic energy, position energy and magnetic and dissipation energy of the system, respectively.
The stability assessment is done by comparing two values of the transient energy V. These are value of V computed at the end of disturbance (e.g., at fault clearing) Vcl and the critical value Vcr which is the potential energy at the controlling UEP, for the particular disturbance under investigation. Substituting for Vcr and Vcl in (7) and using the concept of kinetic energy correction, the energy margin can be obtained as
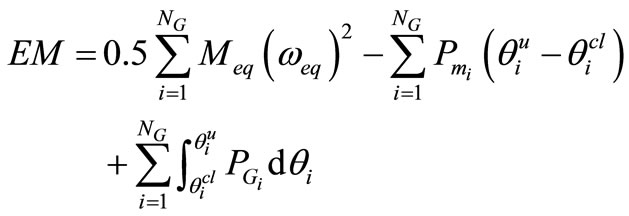 (8)
(8)
in which ωcl and 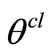 are calculated using either the step-by-step method or directly assuming constant acceleration. The dissipation energy term can be evaluated only if the system trajectory is known. The fairly accurate approximation, assuming the so-called linear angle path, is used in the present analysis.
are calculated using either the step-by-step method or directly assuming constant acceleration. The dissipation energy term can be evaluated only if the system trajectory is known. The fairly accurate approximation, assuming the so-called linear angle path, is used in the present analysis.
3.3. Problem Variables and Indices
The specific formulation for the identification of dynamic security domains involves the following:
1) The set of control (decision) variables involve, in general, plant power outputs, interface-flows, controlled bus voltages, under-load transformer tap settings, injected VAR from controlled reactive power devices, and other decision variables on interest to power system operators.
2) The set of potential operating scenarios Ys (u), s = 1, 2, ∙∙∙, NS, involve various groupings of the control variables associated with particular operating decisions under different identified contingency cases.
3) A system integrity (security) index fℓ (x, u), which associated with a given system integrity (security) domain Fℓ (u), is used to measure the degree of system security in terms of compliance (or violation) of a set of inequality constraints representing security boundaries, on of which is a minimum threshold on the energy margin value.
4. Illustrative Application
As an illustrative application, consider the popular Western System Coordinated Council (WSCC) 3-machine, 9-bus system shown in Figure 2 [17], which is widely used in the literature [18]. The detailed system and machine data is listed in [17,18]. The system has been simulated with a classical model for the generators and one disturbance is considered where a three-phase fault occurs near bus 7 at the end of line 5 - 7. The fault is cleared by opening line 5 - 7. In this demonstrative application scenario, two control variables are considered representing, respectively, the overall system loading (per-unit) level (pPd) and the generator voltage at Bus #2 (Vg2).
The base values for these two control variables are [18]
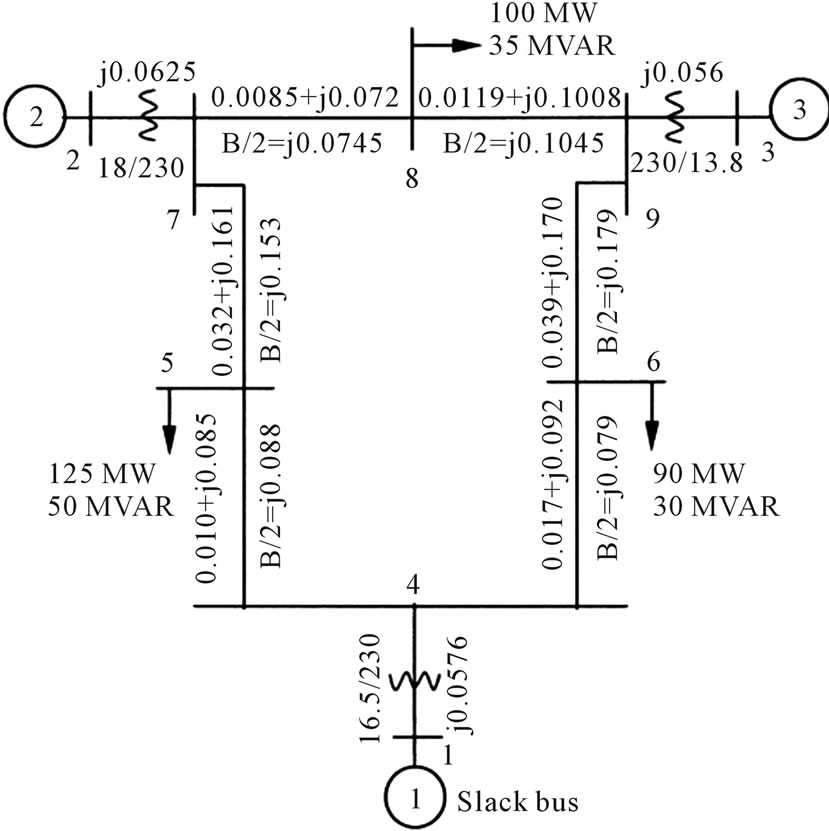
Figure 2. WSCC 3-machine, 9-bus system (all impedances are in pu on a 100 MVA base) [17].
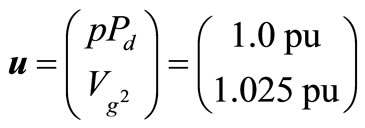
One system integrity domain F1 (u) is considered in this application defining a security criterion in terms of both the transient energy margin (EM) and the minimum incidental load bus voltage in the system (Vmin) in addition to practical upper and lower bounds on the control (decision) variables (u). In other words, the system integrity (security) domain F1 (u) is, in this application, a system security domain defined by four inequality constraints, namely
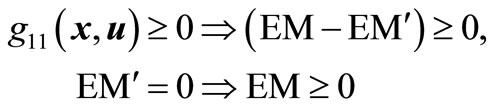
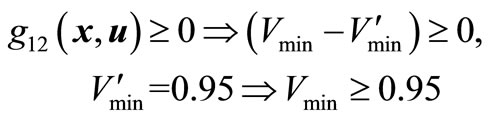
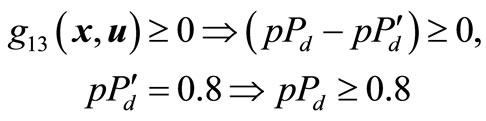
and
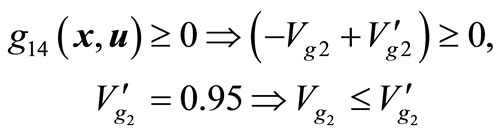
where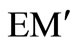 ,
,  ,
, 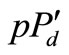 and
and 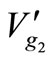 represent, respectively, the security limit (threshold) values associated with the transient energy margin (EM), minimum bus voltage (Vmin), system loading level (pPd) and voltage at generator bus #2 (
represent, respectively, the security limit (threshold) values associated with the transient energy margin (EM), minimum bus voltage (Vmin), system loading level (pPd) and voltage at generator bus #2 (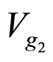 ). Therefore, the system integrity (security) index f1 (x, u) in this application is measured for any operating scenario Ys (u) as:
). Therefore, the system integrity (security) index f1 (x, u) in this application is measured for any operating scenario Ys (u) as:

or
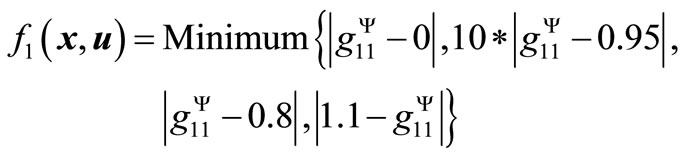
Observe that weighting factors of 10, 5 and 5 are assumed for the second, third and forth elements of f1 (x, u), respectively, to account for different measurement units and/or relative importance (severity/concern) of each component from the operating perspective. Figure 3 depicts the operating security domain of the sample power system in the parameter space spanned by the two control parameters (pPd and Vg2). For demonstration purpose, three operating scenarios (Y1 (u), Y2 (u) and Y3 (u)), as shown in the figure, are examined in this application, representing three operating points in the control parameter space spanned by pPd and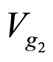 , namely
, namely

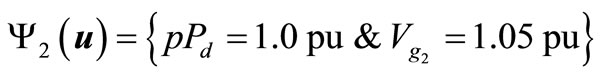

Table 1 shows the values of the inequality constraints g1 (x, u) = {g11 (x, u), g12 (x, u), g13 (x, u)} defining the system integrity (security) domain F1 (u) for the three operating scenarios Y (u) = {Y1 (u), Y2 (u), Y3 (u)} as well as the resulting values of the system integrity (security) index f1 (x, u). It is clear from the results obtained that the first two operating scenarios (Y1 (u) and Y2 (u))
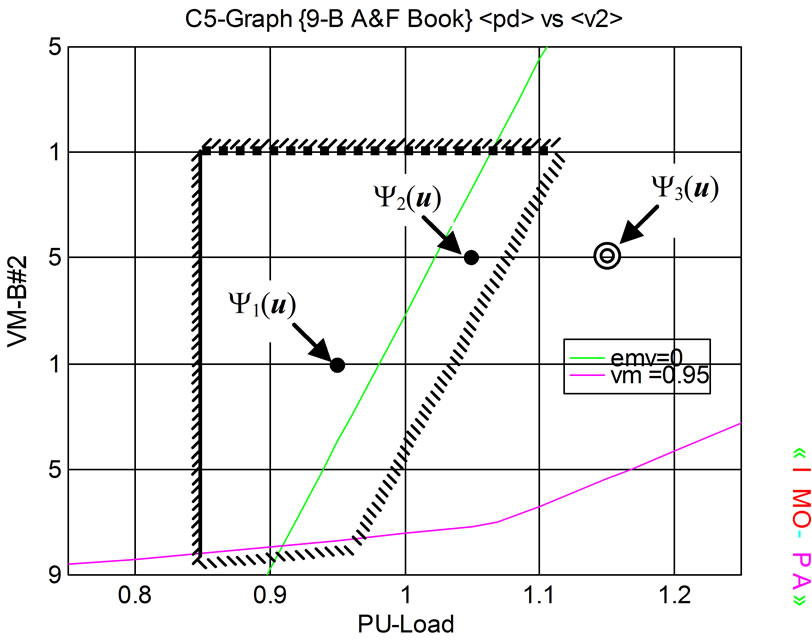
Figure 3. Operating security domain of 9-bus system in two operating parameter space.
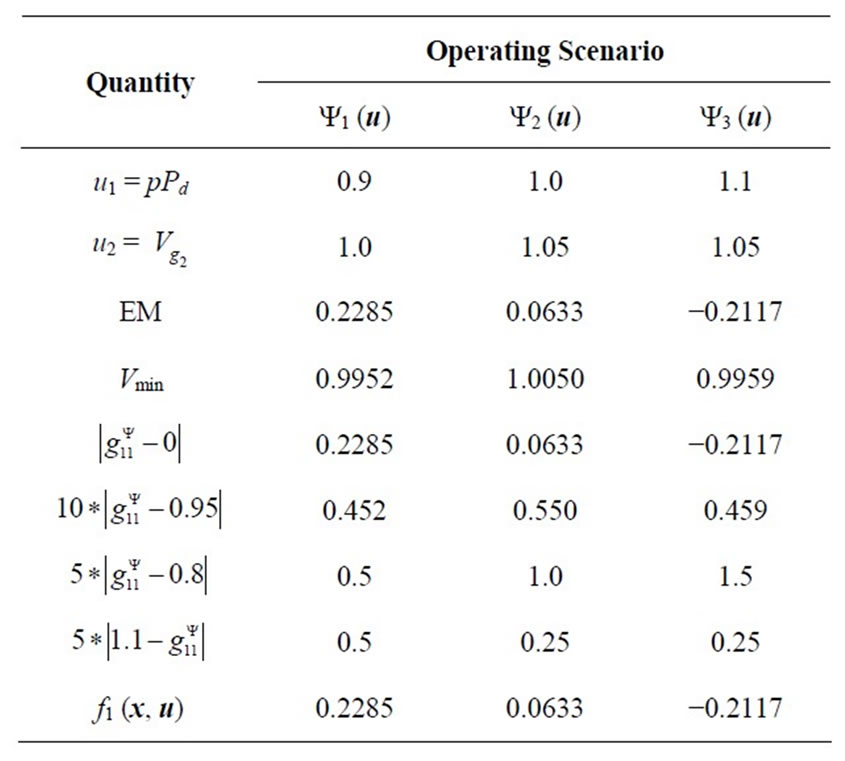
Table 1. System security index at three operating scenarios of the 9-bus system.
are secure while the third operating scenario (Y3 (u)) is insecure with a negative energy margin of −0.2117.
The two secure operating scenarios have, however, different levels of security as determined by the system security index f1 (x, u). While the operating scenario Y1 (u) enjoys a security index value of 0.2285, the operating scenario Y2 (u) has a security index value of only 0.0633 (relatively closer to the security boundary).
5. Application to Saudi Power System
5.1. System Model
In this section, a practical application is presented using the actual Saudi electricity system grid. The power system used in the application is a dynamically reduced model of the full-interconnected Saudi Electricity Company (SEC) power grid, which consists of two main regions, namely the SEC-C (Central Region) and SEC-E (Eastern Region). The two SEC systems are interconnected through two 380 kV and one 230 kV doublecircuit lines.
In the original (unreduced) system model, the interconnected SEC bulk electricity system comprises 150 generator buses, 637 load buses, a total of 1168 transmission lines and transformers. In order to prepare a meaningful system model, which is suitable for the present security assessment study, a coherency-based reduced network model derived from the original base-case is used, which comprises 119 buses (19 generators, 100 loads), 334 lines and 122 transformers.
This system model will be referred to as the 19-Generator model. The nineteen generators are distributed as 11 in the SEC-C area and 8 in the SEC-E area as shown in Figure 4.
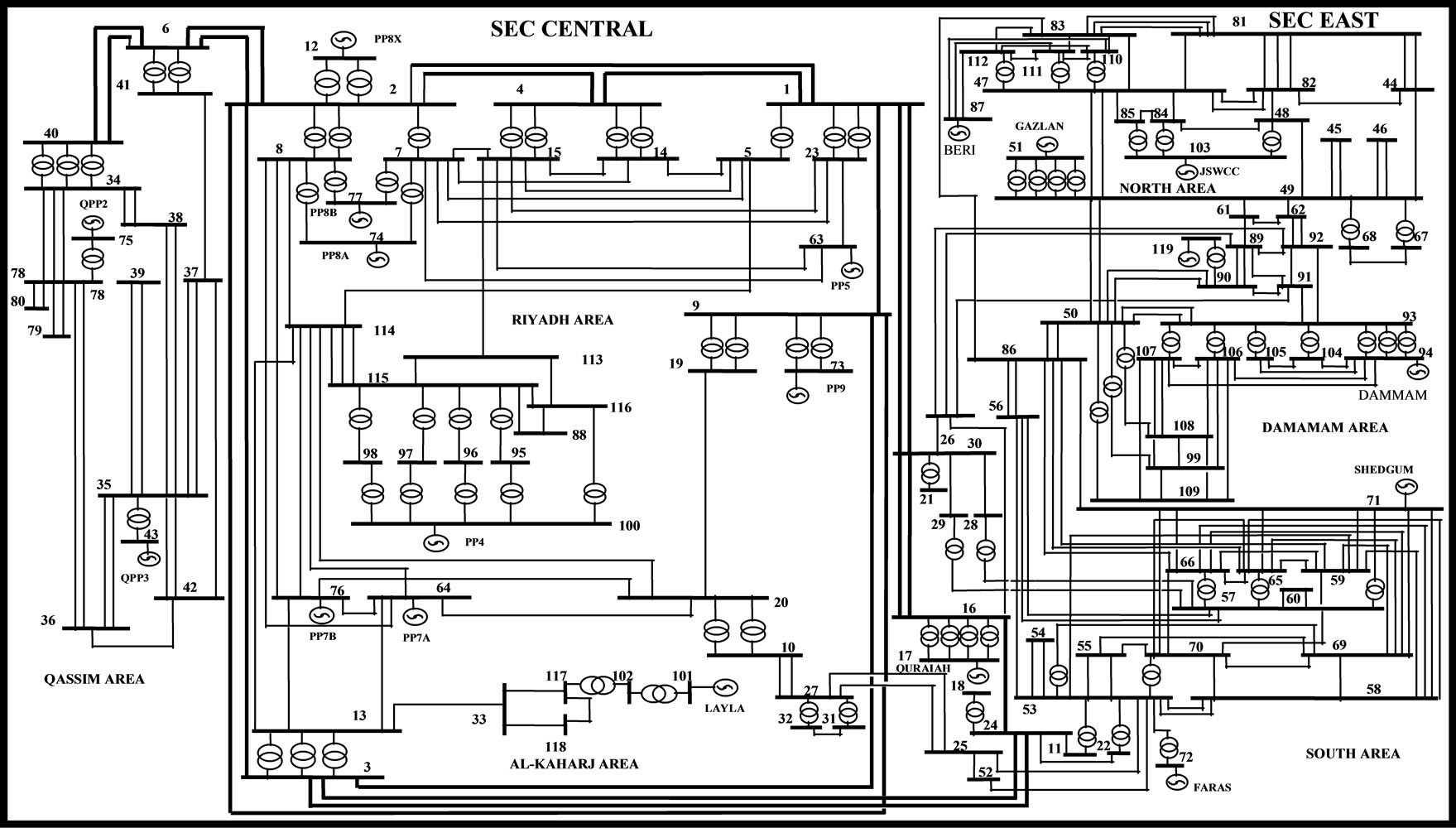
Figure 4. SEC 19-generators system model.
5.2. System Security Assessment
In this practical application, two control variables are considered representing, respectively, the East-to-Central interface flow level (Flow-E) and the Central-to-Qassim interface flow level (Flow-Q), both measured in MW. The base values for these two control variables are
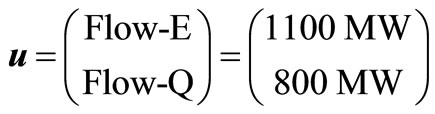
One system integrity domain F1 (u) is considered in this application defining a security criterion in terms of both the transient energy margin (EM) and the minimum incidental load bus voltage in the system (Vmin) in addition to lower bounds on the control (decision) variables (u). In the present application, a three-phase fault close to a major power plant (PP8A at bus #74 of Figure 4) is considered resulting in the complete outage of this power plant. The upper bounds on control variables (maximum interface flows) represent inactive constrains and would not impact on the security domain of this application. In other words, the system integrity (security) domain F1 (u) is, in this application, a system security domain defined by four inequality constraints, namely EM ≥ 0 and Vmin ≥ 0.95, Flow-E ≥ 0 and Flow-Q ≥ 0.
While the stability-limit (zero value) is considered in this application to indicate the security domain, a slightly higher value is normally considered in practice by power utilities as an “operating security limit”. Figure 5 depicts the Operating security domain of SEC interconnected system in the two operating parameters’ space. Four operating scenarios, Y1 (u), Y2 (u), Y3 (u) and Y4 (u), are examined in the present application as shown in Figure 5, representing four operating points in the control parameter space spanned, namely
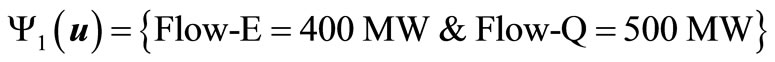
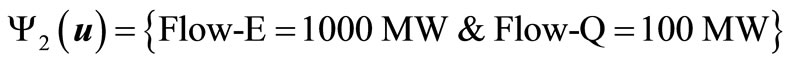

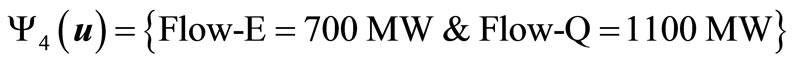
The first two operating scenarios (Y1 (u) and Y2 (u)) are secure as they fall within the security domain depicted in Figure 5. The energy margin values associated with these operating scenarios are 0.61 pu and 1.59 pu, respectively, which are both above the boundary limit of 0. On the other hand, the minimum occurring load voltage associated with these operating scenarios are 1.01 pu and 0.93 pu, respectively, which are also above the boundary limit of 0.9 pu.
The third and forth operating scenarios, Y3 (u) and Y4 (u) are insecure as they fall outside the operating security domain of Figure 5. The operating scenario Y3 (u), although enjoying a positive EM value of 0.62 pu, which is almost the same as the first scenario Y3 (u), is insecure because the minimum load voltage is only 0.81 pu which

Figure 5. Operating security domain of SEC inter-connected system in two operating parameter space.
is below the boundary value of 0.9 pu. The fourth operating scenario Y4 (u), on the other hand violates both energy margin and minimum voltage limits where the energy margin is 0.93 and the minimum load voltage is 0.78.
5.3. Discussion of Results
The electricity flow from the Eastern region (which has most of the generation resources) to the Central region in the interconnected Saudi power system is essential to cover the relatively large demand in the Central region which suffers from generation shortage in relation to its required load. More East-to-Central flow would also relief some power plants in the Central region from having to operate at full capacity during high-demand coupled with adverse weather conditions during which increased possibility exists for major contingencies close to the massive load centers. In other words, avoiding extreme high output from power plants in the Central region (by increasing the support from Easter region) would improve the stability of the system, where more East-toCentral flow would improve the energy margin for a given Qassim demand value. For a Central-to-Qassim flow level of 800 MW, a drop in the East-to-Central from 1100 MW to 750 MW would be sufficient to bring the energy margin down from 1 to 0. On the other hand, because of the long East-Central tie-lines as well as the relatively long “electrical” distances, which electricity has to go from Eastern region to reach the major load centers in the Central region, the incidental minimum load voltage would suffer as the East-to-Central flow increases. For example, for a Central-to-Qassim flow level of 400 MW, an increase in the East-to-Central from 600 MW to 1200 MW would be sufficient to bring the minimum occurring voltage in the system down from 0.95 to 0.85 pu.
The Qassim region depends on the Central region for supplying a portion of its demand. Therefore, electricity flows in normal cases from the Central region to Qassim region in the west. In other words, the Central region sees Qassim as an added load to be supplied. Higher Qassim demand levels would degrade both system stability and minimum occurring voltage magnitude. For an East-to-Central flow level of 800 MW, an increase in the Central-to-Qassim from 460 MW to 1150 MW would be sufficient to bring the energy margin down from 1 to 0. On the other hand, for an East-to-Central flow level of 800 MW, an increase in the Central-to-Qassim from 150 MW to 680 MW would be sufficient to bring the minimum voltage in the system down from 0.95 to 0.85 pu.
6. Conclusions
This paper presents the results of a recent major industrysupported study which has addressed one of the important issues currently of concern to power system operation and management, namely the identification of operating security domains within which the system can operate safely in order to maintain reliable and secure supply of electricity to the consumers. The paper has outlined the main theoretical basis and computational framework for the development of innovative computerized schemes capable of identifying and processing various system integrity domains and, therefore, allowing system operators to determine—in a fast and reliable manner— the most favorable operating scenarios which maintain system security, reliability and operating performance quality.
For demonstration purposes, and without loss of generality, an emphasis was given in the paper to the dynamic system security problem where the Transient Energy Function (TEF) method is used to define quantitative measures of the level (degree) of system security for a given operating scenario. Nonetheless, the framework presented is applicable quite as well to other system performance functions and criteria that may be considered. The applications presented for the Saudi electricity system have revealed several important findings, which demonstrate the powerful features and usefulness of the present methodology. In this regard, the East-to-Central flow has contradicting impacts on the overall system security. While more East-to-Central flow would improve the energy margin (for a given Qassim demand level) due to relieving power plants in the Central region from having to operate at full capacity, it would however cause degradation to the minimum occurring voltage because of the relatively long distances, which electricity has to go from Eastern region to reach the major load centers in the Central region. On the other hand, the Central region sees Qassim as an added load to be supplied and, therefore, higher Qassim demand levels would degrade both system stability and minimum occurring voltage magnitude.
7. Acknowledgements
This work was supported by Saudi Electricity Company.
REFERENCES
- D. P. Popovic, D. M. Dobrijevic, N. A. Mijuskovic and D. J. Vlaisavljevic, “An Advanced Methodology for SteadyState Security Assessment of Power Systems,” ETEP, Vol. 1, No. 4, 2001, pp. 227-233. doi:10.1002/etep.4450110403
- M. S. Owayedh and M. A. El-Kady, “Integration of Economy and Quality Requirements: Practical Application to Power System Operation,” Proceeding of the 7th Saudi Engineering Conference, Riyadh, 26-28 November 2007, Paper # SEC-013.
- J. Aghaei, H. A. Shayanfar and N. Amjady, “Joint Market Clearing in a Stochastic Framework Considering Power System Security,” Applied Energy, Vol. 86, No. 9, 2009, pp. 1675-1682. doi:10.1016/j.apenergy.2009.01.021
- M. A. El-Kady, “Direct Analysis of Transient Stability for Large Power Systems,” Final Report, No. EL-4980, EPRI Project No. 2206-1, Iowa State University, Ontario Hydro, 1986.
- J. Srivani and K. S. Swarup, “Power System Static Security Assessment and Evaluation Using External System Equivalents,” Electrical Power and Energy Systems, Vol. 30, 2008, pp. 83-92. doi:10.1016/j.ijepes.2007.06.008
- Y. Zeng, P. Zhang, M. Wang, H. Jia, Y. Yu and S. T. Lee, “Development of a New Tool for Dynamic Security Assessment Using Dynamic Security Region,” Proceeding of the 2006 International Conference on Power System Technology, Chongqing, 22-26 October 2006, 5 p. doi:10.1109/ICPST.2006.321756
- M. A. El-Kady and E. A. Al-Ammar, “Framework for Identification of Power System Operating Security Regions,” Proceedings of 3rd International Conference on Network and System Security, Gold Coast, 19-21 October 2009. doi:10.1109/NSS.2009.16
- U. D. Annakkage and B. Jayasekara, “Ensuring Power System Security against Contingencies,” Proceeding of the 2nd International Conference on Industrial and Information Systems, Sri Lanka, 8-11 August 2007, pp. 559-564. doi:10.1109/ICIINFS.2007.4579239
- M. A. El-Kady, B. A. Alaskar, A. M. Shaalan and B. M. Al-Shammri, “Composite Reliability and Quality Assessment of Interconnected Power Systems,” International Journal for Computation and Mathematic in Electrical and Electronic Engineering, Vol. 26, No. 1, 2007, Paper SSD05-PES-12.
- K. Tomsovic, D. E. Bakken, V. Venkatasubramanian and A. Bose, “Designing the Next Generation of Real-Time Control, Communication, and Computations for Large Power Systems,” Proceeding of the IEEE, Vol. 93, No. 5, 2005, pp. 965-979. doi:10.1109/JPROC.2005.847249
- M. A. El-Kady, M. S. El-Sobki and N. K. Sinha, “Reliability Evaluation for Optimally Operated Large Electric Power Systems,” IEEE Transactions on Reliability, Vol. R-35, No. 1, 1986, pp. 41-47. doi:10.1109/TR.1986.4335340
- Z. Benguo, W. Dapeng, L. Lei, X. S. Niu, H. Z. Zang and Y. S. Zhao, “Research of Incentive Revelation Mechanism in Power System Optimal Security Control,” Proceeding of the 2006 International Conference on Power System Technology, Chongqing, 22-26 October 2006, 5 p.
- M. A. El-Kady, B. D. Bell, V. F. Carvalho, R. C. Burchett, H. H. Happ and D. R. Vierath, “Assessment of Real-Time Optimal Voltage Control,” IEEE Transactions on Power Systems, Vol. PWRS-1, 1986, pp. 98-107. doi:10.1109/TPWRS.1986.4334912
- T. Athay, R. Podmore and S. Virmani, “A Practical Method for Direct Analysis of Transient Energy Stability,” IEEE Transactions on Power Apparatus and Systems, Vol. 98, No. 2, 1979, pp. 573-584. doi:10.1109/TPAS.1979.319407
- M. A. El-Kady, C. K. Tang, V. F. Carvalho, A. A. Fouad and V. Vittal, “Dynamic Security Assessment Utilizing the Transient Energy Function Method,” IEEE Transactions on Power Apparatus and Systems, Vol. PWRS-1, No. 3, 1986, pp. 284-291.
- M. A. El-Kady and R. W. D. Ganton, “Fast Decoupled Transient Stability,” Canadian Electrical Engineering Journal, Vol. 14, No. 2, 1989, pp. 63-66.
- R. Patel, T. S. Bhatti and D. P. Kothari, “MATLAB/ Simulink-Based Transient Stability Analysis of a Multimachine Power System,” International Journal of Electrical Engineering Education, Vol. 39, No. 4, 2002, pp. 320-336.
- P. M. Anderson and A. A. Fouad, “Power System Control and Stability,” Iowa State University Press, Ames, 1977.

