World Journal of Condensed Matter Physics
Vol.05 No.03(2015), Article ID:59055,4 pages
10.4236/wjcmp.2015.53025
Entanglement: A Modern Aspect of Nature
Jens Cordelair
Birkenweg 2, Elmenhorst, Germany
Email: Jens.Cordelair@freenet.de
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 July 2015; accepted 22 August 2015; published 25 August 2015
ABSTRACT
The intention of this paper is to provide an easy to understand introduction to the peculiarities of entangled systems. A novel description for strong (mass entanglement) and weak (spin-or-bital and thermal entanglement) quantum entangled particles is discussed and applied to the phenomena of superconductivity, superfluidity and ultracold gases. A brief statement about how to represent the physical reality of quantum-entanglement as Quantum-Field-Theory (QFT) is noted.
Keywords:
Quantum Entanglement, Superconductivity, Wave Particle Duality, Cooper-Pairs, Superfluidity, Ultracold Gases

1. Introduction
The word “nature” is derived from the Latin word natura with the physical meaning of “essential quality” or “innate disposition”. In this sense I would like to show you how conservation laws and entanglement are inevitable parts of our physical thoughts.
A conservation law states that a particular measurable property of a physical system doesn’t change as the system evolves, where entanglement describes the correlated evolution of the whole physical system to retain these conservation laws. In classical physics conservation of energy, momentum, angular momentum, mass and electric charge are common conservation laws. In particle physics other conservation laws such as baryon number, lepton number and strangeness apply to properties of subatomic particles that are invariant during an interaction.
In the following I want to introduce a novel description for strong (mass entanglement) and weak (spin-orbital and thermal entanglement) quantum entangled particles and to present some applications for the concept of quantum entanglement. In case of strong entangled particles the entanglement can’t be shared with its environment, while weak entangled particles such as cooper-pairs or Bose-Einstein-condensates (BEC) can easily change its shape, where only the overall entanglement stays the same.
2. Particle Definition on the Basis of Entanglement
2.1. Mass Entanglement and Wave-Particle Duality
A fundamental aspect of physical thoughts is the principle of a homogeneous time development. As a result its influence on the interpretation of natural phenomena is very imperative. Formally the principle of a homogeneous time will be represented by the law of conservation of energy. Einstein showed in his theory of special relativity [1] , that the mass m of a body is equivalent to the energy E in a proper measure, where c is the speed of light
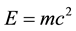 . (1)
. (1)
This means one can convert mass into energy (nuclear fission in the sun) and energy into mass (particle generation in high energy physics).
Another aspect of matter and energy was postulated by Louis de Broglie [2] in 1924 where he stated that matter should behave like light waves, also featuring interference. The simplest type of these matter waves is a plain and monochrome wave, where the energy- and momentum-distribution is restricted to a single value with ħ the Plank constant, P the momentum, ω the angular frequency and k the wave vector
 (2)
(2)
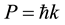 . (3)
. (3)
Figure 1 shows, as virtual holography-experiment, how the topological split-up due to the presence of a wire lead to interference of a single particle like an electron with itself.
A single electron, injected from the top, can pass the thin wire to the right and to the left. Accordingly the entangled matter-wave Ψ underneath the wire can be written as
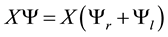 (4)
(4)
where X is a symbol to denote the strong entanglement due to mass conservation.
The probability to find a punctual interaction of the mass entangled matter-wave with the screen at point x is equivalent to the square of the matter-wave. Due to the fact that Ψr, Ψl differ in their path and phase, the phenomenon that a single electron can interfere with itself, occur. In case of an interaction the entire entangled matter wave interact as a whole to preserve mass conservation. This is the well known wave-particle duality.
Entangled matter-waves are the most appropriate representation for masses, where the particulate characteristic is caused by mass conservation. Correspondingly a single photon is composed of energy entangled waves with a continuous energy and direction distribution, thus a single photon can also interfere with itself, showing wave-particle duality.
Figure 1. Interference between matter-waves of a single particle like an electron.
2.2. Spin Entanglement
In spacious systems the spin entanglement induces a spooky distant effect [3] [4] . If, for example, a two atomic molecule gets dissociated by an excitation (Figure 2), the atoms may remain entangled by their spins. If we measure the spin of both Atoms, one will show spin +1/2 and the other −1/2, but it is not possible to predict which one will have the positive and negative sign.
If we carefully align the spin of one atom in a magnetic field, the other must be oriented simultaneously in the opposite direction to conserve the total spin of both atoms, even though it is not in the vicinity. In other words, you can play with Schrödinger’s cat while it’s in the box. This “alignment” doesn’t act as a force, where the first spin turns the second around, only the information about which state has to interact is “transferred” to the second spin to preserve the total spin of the entangled system.
2.3. Thermal Entanglement
At 0 ˚K almost all matter is in the lowest energy-state possible which I call the coherent state. In this state a system must interact as a whole, for example a solid shows a perfect Mößbauer effect or a fluid becomes a superfluid. Increasing the temperature result in distortions of the system and part of the system lose their coherence due to thermal chaos, where only the overall entanglement stays the same. The system gets split into coherent and normal phases where the length of coherence indicates the average size of coherent areas.
3. Applications
3.1. Electrical Superconductivity
The electrons in an atom are fragmented into paired wave-functions (orbitals) of constant energy but antipodal spin (entangled spins), which induces a partly bosonic characteristic [5] . This is why I would like to call these orbitals bound Cooper-pairs. In a solid these orbitals are shared with neighboring atoms (directed binding e.g. ceramics) or more spread out (metallic binding).
At 0 ˚K the orbitals of all atoms in a flawless crystal are perfectly spin entangled and the width of an energy band is reduced to a single value (BEC ground state for this energy band). The material is in the superconducting state.
Increasing the temperature result in distortions of the lattice and part of the orbitals lose their entanglement (bosonic characteristic) due to thermal chaos, where only the overall spin stays the same. The body gets split into coherent and solid phases. Below a critical temperature Tc the coherent phases are interconnected, forming a percolating superconducting backbone. Above Tc the density of the coherent phases is to low to form up a percolating backbone and the body is in the normal conducting state.
Figure 2. Spin entanglement between two atoms.
Figure 3. Entangled flow of superfluid Helium.
3.2. Superfluidity
The effect of superfluidity was first discovered in 1937 by Pyotr Kapitsa, John F. Allen and Don Misener at temperatures as low as 2.2 ˚K [6] [7] . In this variety of matter the thermally entangled coherent state of aggregation has zero viscosity and can show different quantum mechanical behavior on large scales. For example liquid helium can creep up walls and barriers to take up an energetically favorable state (Figure 3).
In a cavity superfluid Helium can flow over a barrier into a second basin with a lower gravitational potential. Responsible for this phenomenon is a thin superfluid layer (Rollin film) covering everything within the cavity. In the entangled state of aggregation an atom at A is thermally entangled with an atom at B. Both can only move the same way (coherent motion) and analog to the principle of corresponding pipes a flow takes place toward the basin with the lower gravitational potential.
3.3. Ultracold Gases
Ultracold gases are produced by a sequence of different cooling steps. Usually a couple of atoms are cooled using a laser. These atoms can be caught in a magneto optical trap. To reach the lowest possible temperature of the gas, the trap is adjusted so that the atoms with the highest temperature can evaporate out of the gas [8] .
Depending on the temperature where the aggregation takes place, different gases can be generated.
When the temperature is high enough, the entanglements of the particles can be transferred to the gas. This gas is able to form a BEC.
If the aggregation temperature of the gas is to low to break the long ranged entanglements of the particles with its source, no BEC can be formed. The gas behaves like a perfect fermionic gas.
4. Conclusions
Some scientists may say that a quantum mechanical system is defined by the states their elements can reach and after assigning occupation probabilities they know everything about it. I hope I am able to show you that this is not in general the case. I don’t believe that a quantum mechanical system where entanglement is present can be separated into elemental parts, where their fundamental properties like the entropy can be simply added up. Only the system as a whole defines measurable states. In general the system is in all these states simultaneously and the entanglement forces that a measurement gives a value for one state. A more fanciful opinion may say that Schrödinger’s cat exists in an entangled quantum-multiverse until it is forced to interact at which the entanglement defines a single universe. With respect to the observed pattern in Figure 1, this illustrative model may be completed by adding the capability of interference in the space of the quantum-multiverse. Accordingly the symbol X in Equation (4) denotes that the state Ψ is not an element of an Hilbert space but a state representing a quantum-multiverse.
I wonder if it is possible to understand for example the exchange of virtual photons in quantum-electrody- namics (QED) as information exchange in an entanglement driven sense. Due to an interaction (in QED described by the exchange of a virtual photon), the quantum-multiverse is forced to define a single universe. With this in mind, Quantum Field Theories provide a suitable mathematical abstraction for the physical reality of quantum entanglement.
Cite this paper
JensCordelair, (2015) Entanglement: A Modern Aspect of Nature. World Journal of Condensed Matter Physics,05,244-248. doi: 10.4236/wjcmp.2015.53025
References
- 1. Einstein, A. (1905) Zur Elektrodynamik bewegter Körper. Annalen der Physik und Chemie, 17, 891-921.
http://dx.doi.org/10.1002/andp.19053221004 - 2. de Broglie, L. (1929) The Wave Nature of the Electron. Nobel Lecture, 12.
- 3. Einstein, A., Podolsky, B. and Rosen, N. (1935) Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review, 47, 777-780.
http://dx.doi.org/10.1103/PhysRev.47.777 - 4. Afriat, A. and Selleri, F. (1999) The Einstein, Podolsky, and Rosen Paradox in Atomic, Nuclear, and Particle Physics. Plenum Press, New York.
http://dx.doi.org/10.1007/978-1-4899-0254-2 - 5. Cordelair, J. (2014) Superconductivity. World Journal of Condensed Matter Physics, 4, 241-242.
http://dx.doi.org/10.4236/wjcmp.2014.44026 - 6. Kapitza, P. (1938) Viscosity of Liquid Helium below the λ-Point. Nature, 141, 74.
http://dx.doi.org/10.1038/141074a0 - 7. Fairbank, H.A. and Lane, C.T. (1949) Rollin Film Rates in Liquid Helium. Physical Review, 76, 1209-1211.
http://dx.doi.org/10.1103/PhysRev.76.1209 - 8. Hau, L.V. (2001) Frozen Light. Scientific American, 285, 52-59.
http://dx.doi.org/10.1038/scientificamerican0701-66




