World Journal of Condensed Matter Physics
Vol.3 No.1(2013), Article ID:28333,9 pages DOI:10.4236/wjcmp.2013.31013
Drift Mobility, Diffusion Coefficient of Randomly Moving Charge Carriers in Metals and Other Materials with Degenerated Electron Gas
![]()
Physics Faculty, Vilnius University, Vilnius, Lithuania.
Email: vilius.palenskis@ff.vu.lt
Received October 25th, 2012; revised December 5th, 2012; accepted December 21st, 2012
Keywords: Conductivity; Thermal Noise; Diffusion Coefficient; Drift Mobility; Hall Mobility
ABSTRACT
In this short review some aspects of applications of free electron theory on the ground of the Fermi statistics will be analyzed. There it is an intention to attempt somebody’s attention to problems in widespread literature of interpretation of conductivity of metals, superconductor in the normal state and semiconductors with degenerated electron gas. In literature there are many cases when to these materials the classical statistics is applied. It is well known that the electron heat capacity and thermal noise (and as a consequence the electrical conductivity) are determined by randomly moving electrons, which energy is close to the Fermi energy level, and the other part of electrons, which energy is well below the Fermi level can not be scattered and change its energy. Therefore there was tried as simple as possible on the ground of Fermi distribution, and on random motion of charge carriers, and on the well known experimental results to take general expressions for various kinetic parameters which are applicable for materials both without and with degenerated electron gas. It is shown, that drift mobility of randomly moving charge carriers, depending on the degree degeneracy, can considerably exceed the Hall mobility. Also it is shown that the Einstein relation between the diffusion coefficient and the drift mobility of charge carriers is valid even in the case of degeneracy. There also will be presented the main kinetic parameter values for different metals.
1. Introduction
In this review it is an attempt to call somebody’s attention to some problems of conductivity interpretation of metals, normal superconductors and semiconductors with degenerated electron gas. Every experimenter knows that conductivity of homogeneous materials can be defined by free randomly moving charge carrier (electron) density and by their drift mobility. They also know that electrons obey the Pauli principle and that electrons are described by the Fermi-Dirac statistics. The latter principles let to ones explain the experimental results of the heat capacity of electrons in metals [1-8]. The main conclusions of these investigations were that randomly move only the small part of electrons, which energy is close to the Fermi level, and that electrons, which energy is well below the Fermi level, can not be scattered and change their energy E because the Fermi distribution function f(E) = 1. It is very strange that till now (during about 80 years) in many books [1-8] for solid state physics in expression for conductivity of metals and for superconductors in the normal state [9-13] the total density of free electrons is included. On the other hand, it is well also known that the thermal noise due to random moving of electrons is completely described by the real part of conductance (Nyquist formula) [14,15]. Thus, electron heat capacity and thermal noise of metals unambiguously show that in all kinetic phenomena take place only that part of free electrons, which energy is close to the Fermi level, because only these electrons can change their energy under influence of external fields. There are many questions: how from measurement of the Hall effect of metals we can get the total density of free electrons, how find the density neff of randomly moving electrons, their diffusion coefficient D and drift mobility mdrift, the Fermi energy EF, velocity of electrons vF at the Fermi level, the length of the free pass? These problems are very important for every researcher of solid state materials, especially of superconductors in the normal state and semiconductors with very high doping level. In this work, we try to present the answers to these questions and other related problems.
2. Presentation Details and Analysis
2.1. The Diffusion Coefficient of Randomly Moving Charge Carriers and the Einstein Relation
It is well known that Fermi distribution function for electrons reads as
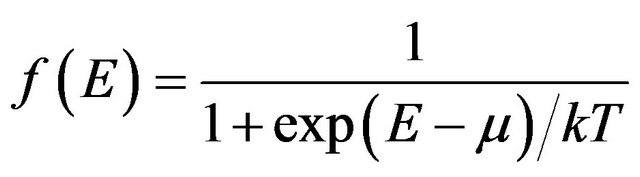 , (1)
, (1)
where E is the electron energy, m is the chemical potential, k is the Boltzmann’s constant, and T is the absolute temperature. This function means the probability that energy E level is occupied by electron.
The total density of valence (free) electrons n in conduction band is
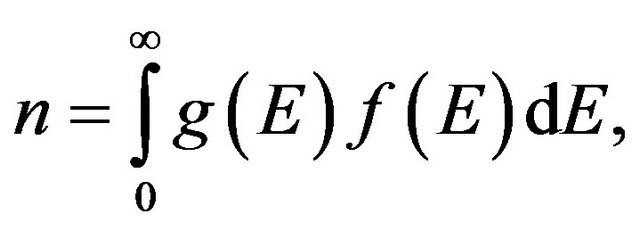 (2)
(2)
where g(E) is the density of states in the conduction band.
The conductivity and the diffusion coefficient D of charge carriers are related by the following expression [16]
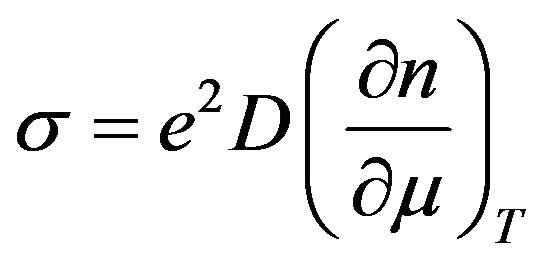 . (3)
. (3)
By simple calculation of the derivative n on parameter (chemical potential) μ we have
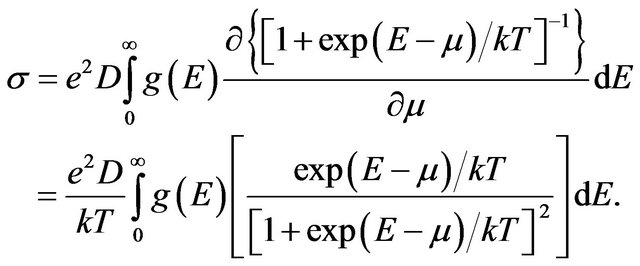 (4)
(4)
On the other hand, it can be shown that the expression in the angle brackets can be replaced by
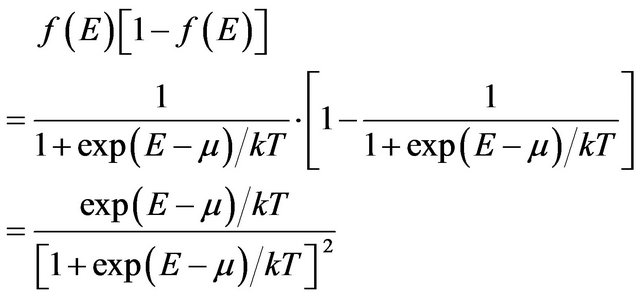 . (5)
. (5)
Thus, the Equation (4), accounting Equation (5), can be presented in the following form
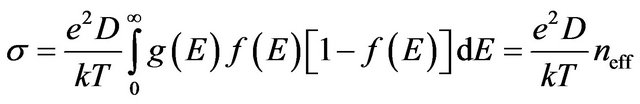 , (6)
, (6)
where
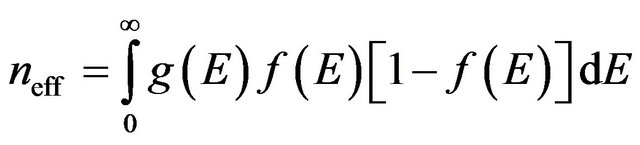 . (7)
. (7)
This expression in comparison to Equation (2) can be named as effective density of randomly moving charge carriers. The Equation (6) unambiguously shows that conductivity in all cases is determined by the effective density of randomly moving charge carriers (Equation (7)), but not by the total free electron density in the conduction band (Equation (2)). The total free electron density for determination of conductivity can be used only for materials with non-degenerated electron gas.
Thus, the conductivity (Equation (6)) can also be presented as
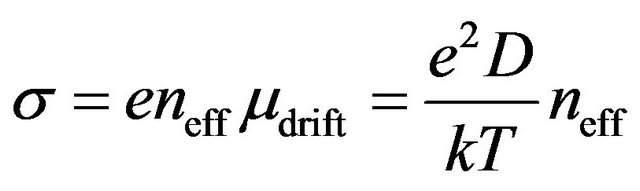 , (8)
, (8)
where mdrift is the drift mobility of randomly moving charge carriers in homogeneous materials with one type of charge carriers (electrons or holes). From this general relationship (Equation (8)) we get the Einstein’s relation
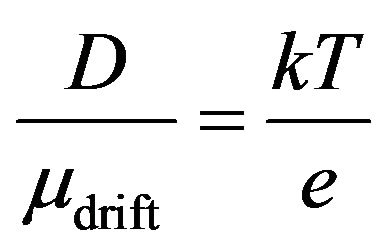 . (9)
. (9)
This expression is true for both degenerated and nondegenerated homogeneous materials with one type of free randomly moving charge carriers (for electrons or for holes). The same conclusion also follows from the thermal noise investigations. The spectral density of the current fluctuations of the thermal noise at low frequencies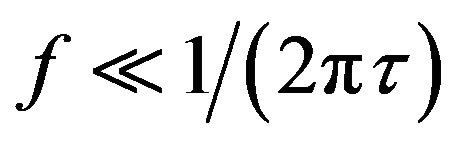 , here τ is the relaxation time of charge carriers) can be presented as [14,17,18]
, here τ is the relaxation time of charge carriers) can be presented as [14,17,18]
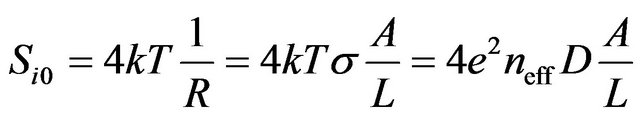 , (10)
, (10)
where R is the resistance of the sample of the test material; A and L are respectively the cross-section and the length of the sample. This relation is right for all homogeneous materials at equilibrium state. The equalities of Equation (10) also can be obtained from the general Kubo formula for conductivity [2,15]
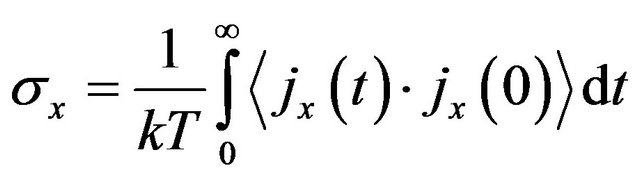 , (11)
, (11)
i.e. in general the conductivity is defined by the correlation function on time 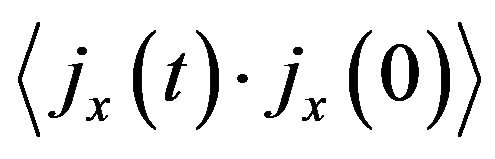 of the current density fluctuation due to random motion of charge carriers. Considering the Wiener-Khintchine theorem and the displacement
of the current density fluctuation due to random motion of charge carriers. Considering the Wiener-Khintchine theorem and the displacement 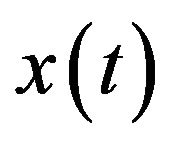 of charge carriers due to Brownian motion during time t, it is possible to obtain both expressions of Equation (10) (See Appendix).
of charge carriers due to Brownian motion during time t, it is possible to obtain both expressions of Equation (10) (See Appendix).
2.2. Effective Density of Randomly Moving Charge Carriers
From Equation (7) directly follows that effective density of randomly moving electrons neff and which causes the conductivity depends not only on the density of states and Fermi function 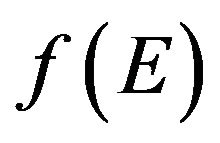 that the energy level E is occupied by electron, but it also depends on the probability
that the energy level E is occupied by electron, but it also depends on the probability 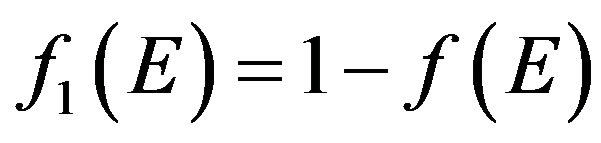 that any of such electron can leave the occupied energy level at a given temperature.
that any of such electron can leave the occupied energy level at a given temperature.
Usually for calculation different kinetic processes in materials instead of probability function  ones use the derivative of the Fermi distribution function
ones use the derivative of the Fermi distribution function 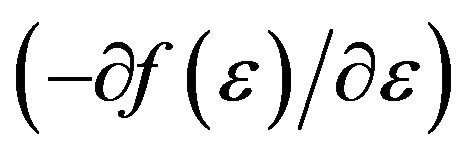 (here
(here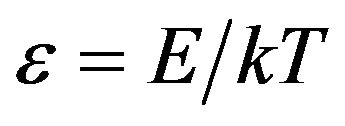 ) [2-6], but
) [2-6], but
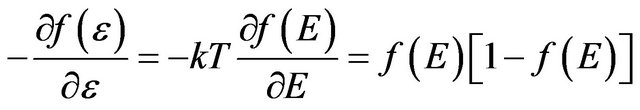 (12)
(12)
The probability function 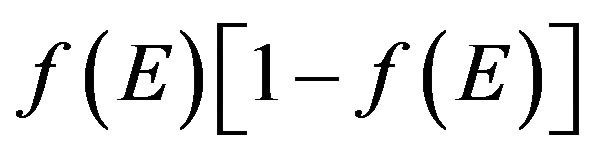 is more understandable in the case of the interpretation of the effective density of randomly moving charge carriers (Equation (7)). Function
is more understandable in the case of the interpretation of the effective density of randomly moving charge carriers (Equation (7)). Function 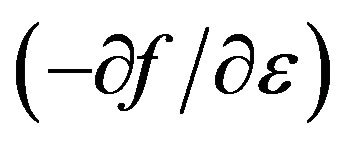 means that only such electrons can be scattered and change its energy for which
means that only such electrons can be scattered and change its energy for which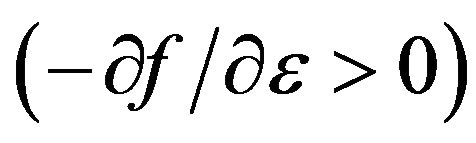 .
.
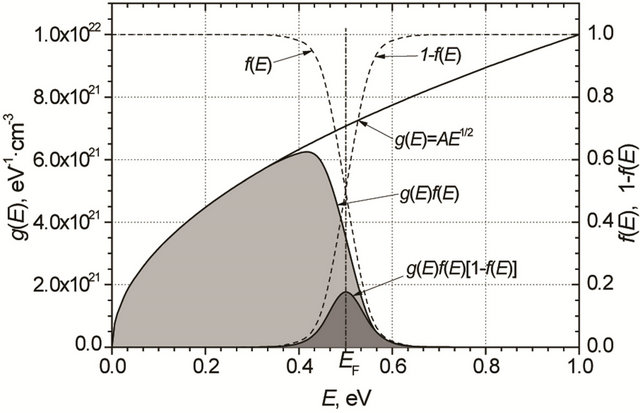
Illustrations of Equations (1), (2) and (7) are presented in Figure 1. From this figure it is clearly seen that the effective density of randomly moving electrons neff (7) is many times smaller than the total density of free electrons n.
Now let ones to evaluate the Equation (7). For non-degenerated materials the probability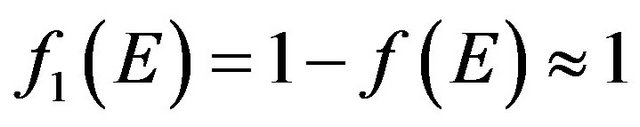 , because
, because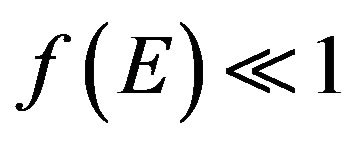 , and, therefore, all electrons in the conduction band n participate in the random motion and in the conduction process
, and, therefore, all electrons in the conduction band n participate in the random motion and in the conduction process
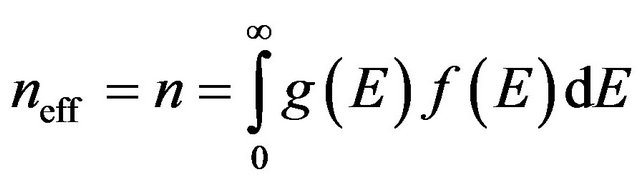 . (13)
. (13)
This is the case where the classical statistics is applicable.
In the case of high degeneracy and considering that Equation (12) has a sharp maximum at the energy E equal to the chemical potential m, the Equation (7) can be written as
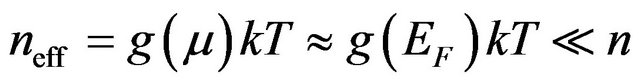 , (14)
, (14)
where 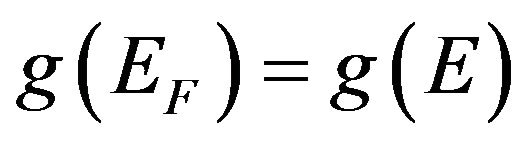 at
at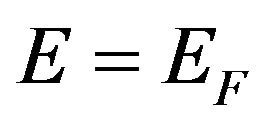 .
.
The chemical potential m and the Fermi energy EF are related by the following relation [5]
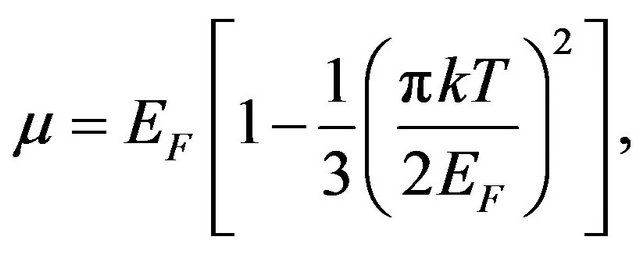 (15)
(15)
and the difference between these quantities is only about
 (a)
(a)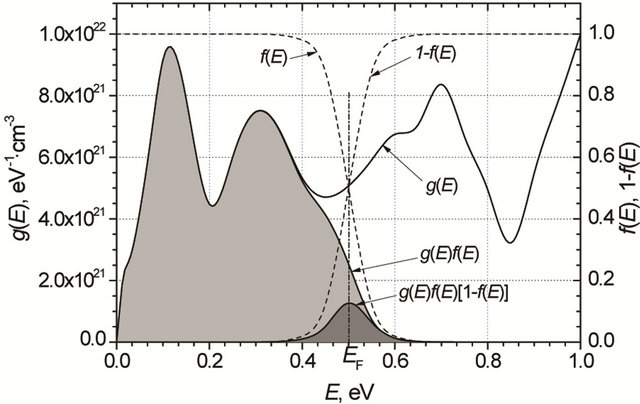 (b)
(b)
Figure 1. Illustration of density of states g(E) and functions 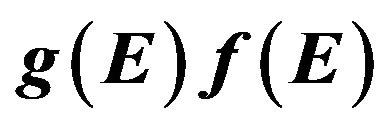 and
and 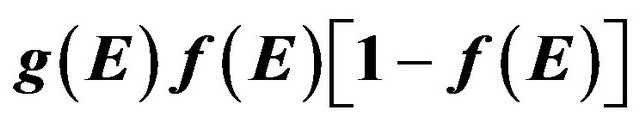 dependency on energy for (a) metals with spherical Fermi surfaces
dependency on energy for (a) metals with spherical Fermi surfaces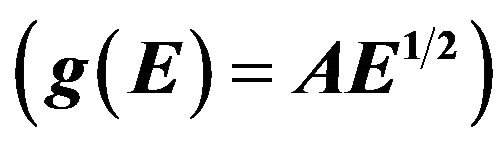 ; (b) for metals and normal state superconductors with composite density of states dependency on energy. The light grey area represents the total density of electrons n (Equation (2)) and the dark grey area represents the effective density of randomly moving electrons neff (Equation (7)). Additionally there are represented the Fermi functions f(E) and
; (b) for metals and normal state superconductors with composite density of states dependency on energy. The light grey area represents the total density of electrons n (Equation (2)) and the dark grey area represents the effective density of randomly moving electrons neff (Equation (7)). Additionally there are represented the Fermi functions f(E) and 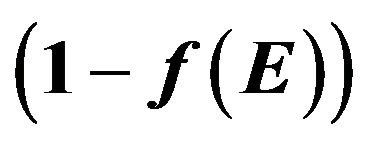 dependency on energy (dashed curves, right scale).
dependency on energy (dashed curves, right scale).
0.01% even at room temperature. So, in many cases for calculation of different quantities ones use the Fermi distribution function in the following form
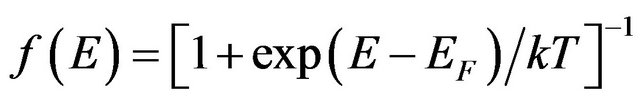 . (16)
. (16)
The density of states at Fermi energy 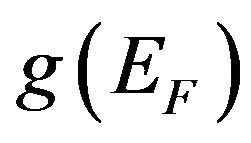 can be determined from of the experimental results of the electron heat capacity [5,6]
can be determined from of the experimental results of the electron heat capacity [5,6]
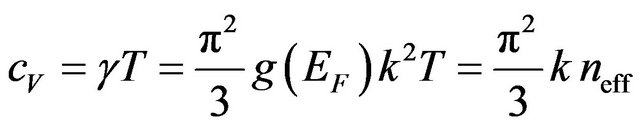 , (17)
, (17)
where
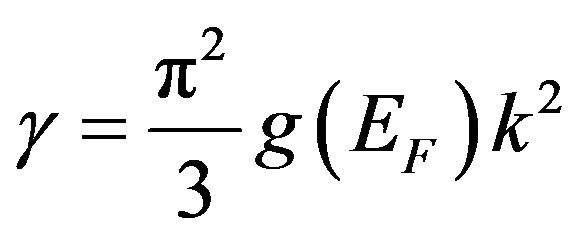 , (18)
, (18)
and
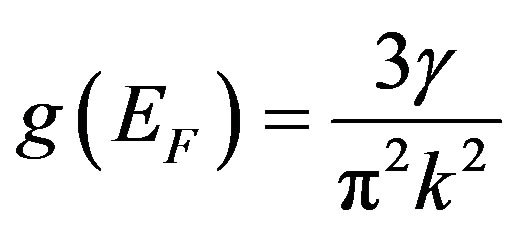 . (19)
. (19)
Thus, for metals and other materials with high degenerated electron gas
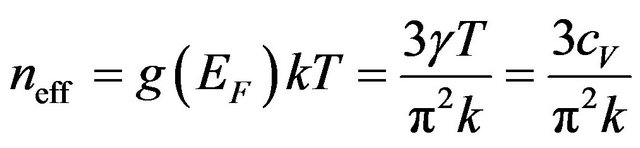 , (20)
, (20)
i.e. neff is proportional to temperature. Experimental results of conductivity and electron heat capacity and calculated effective density neff of randomly moving electrons from the Equation (20) at T = 295 K for different metals are presented in Table 1. The ratio 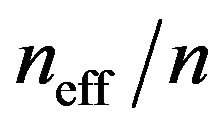 obviously shows that neff amount in the total free electron density n is about a few percents and smaller. From Equation (20) it is seen that the effective density of randomly moving charge carriers neff is completely defined quantity for materials with high degeneracy of electron gas and can be simply obtained from electron heat capacity measurements.
obviously shows that neff amount in the total free electron density n is about a few percents and smaller. From Equation (20) it is seen that the effective density of randomly moving charge carriers neff is completely defined quantity for materials with high degeneracy of electron gas and can be simply obtained from electron heat capacity measurements.
From Equations (8) and (20) for highly degenerated materials we obtain that diffusion coefficient of randomly moving electrons
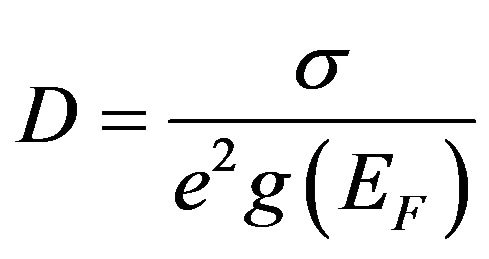 . (21)
. (21)
Thus, on the ground of experimental results of the conductivity and the electron heat capacity we can evaluate the diffusion coefficient D (from Equation (21)) and drift mobility 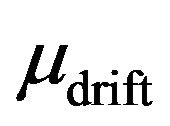 (from Equation (8) or (9)) for randomly moving charge carriers in materials with highly degenerated electron gas. The calculated results for different metals at T = 295 K are presented in Table 2.
(from Equation (8) or (9)) for randomly moving charge carriers in materials with highly degenerated electron gas. The calculated results for different metals at T = 295 K are presented in Table 2.
The diffusion coefficient usually also is determined by the average of square velocity of charge carriers and by their average relaxation time (for metals free pass time)
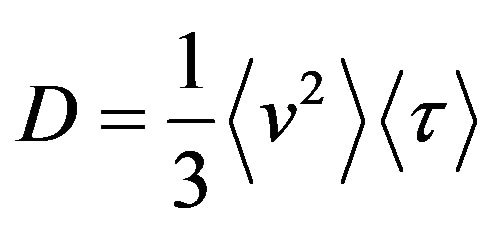 . (22)
. (22)
For highly degenerated electron gas
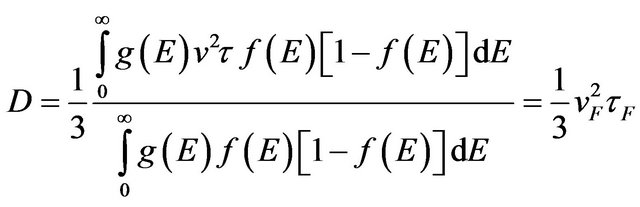 , (23)
, (23)
i.e. the diffusion coefficient is determined by the square velocity and free pass time of randomly moving charge carriers at the Fermi level. From the Equations (21) and (23) follows that conductivity
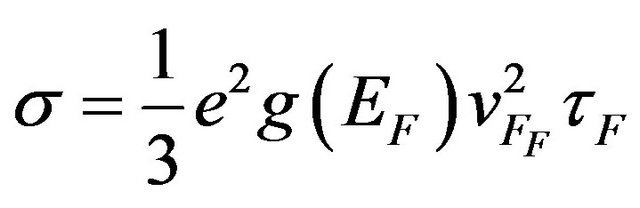 . (24)
. (24)
Table 1. Conductivity and heat capacity parameters of different metals.
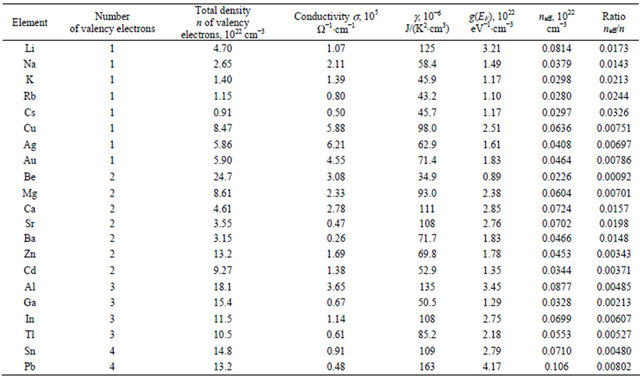
Conductivity and electron heat capacity data are taken from books [5,6,7,19]. Conductivity and neff are presented for T = 295˚ K.
Table 2. Kinetic parameters of different metals.
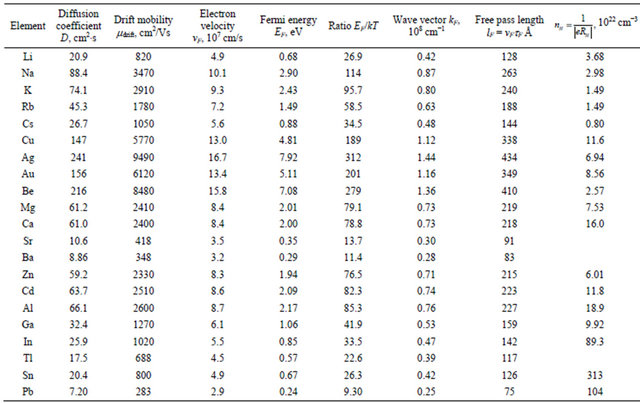
The data for calculation at T = 295 K were used from Table 1. The data of Tables 1 and 2 give the very clear view, why some of metal conductivity is larger than other one. For example, the effective density of randomly moving charge carriers neff of Pb is about two times larger than one of Au, but the conductivity of Au is about ten times larger than that of Pb. It is because the Fermi energy of Au is about twenty times larger than that of Pb, and, as a consequence, the drift mobility of randomly moving charge carriers in Au is about twenty times higher than one in Pb.
This expression is well known for metals and is obtained by solving the kinetic equation [2,3].
The correctness of presented diffusion coefficient and drift mobility values in Table 2 also follows from the electron heat conductivity 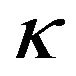 for randomly moving electrons in metals [1-6]
for randomly moving electrons in metals [1-6]
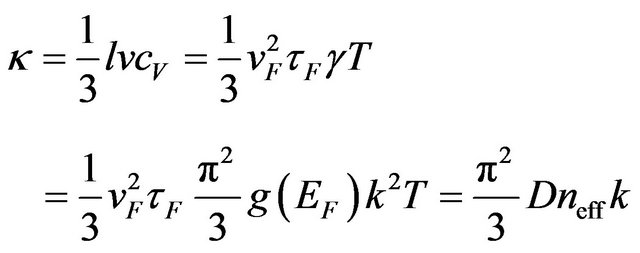 . (25)
. (25)
From Equations (24) and (25) one obtains the well known Wiedemann-Franz law
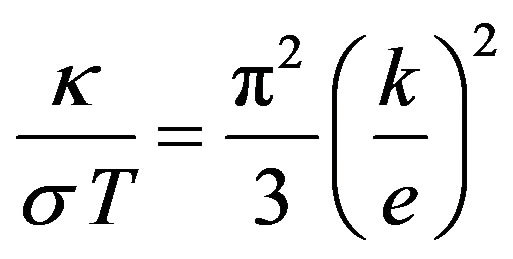 . (26)
. (26)
The diffusion coefficient calculated from Equation (25) gives the same results as from Equation (21). In behalf that Einstein relation also is valid for metals shows this fact that Einstein relation for metals can be obtained from the Wiedemann-Franz law
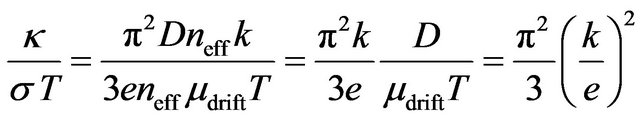 , (27)
, (27)
and now
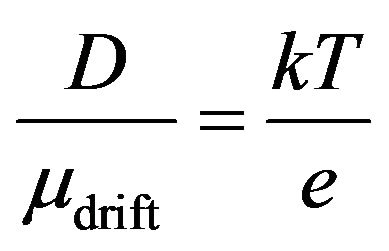 .
.
2.3. Drift Mobility of Randomly Moving Charge Carriers and Conductivity of Homogeneous Materials with Highly Degenerated Electron Gas
From Equations (9) and (22) follows that drift mobility
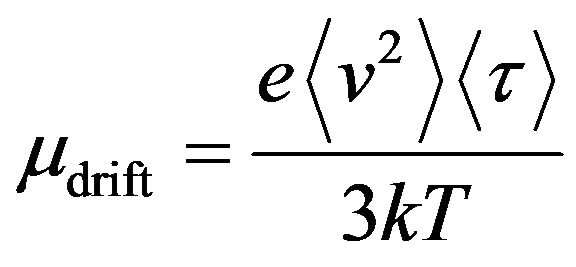 . (28)
. (28)
Including into this relation the effective mass m* of charge carriers the drift mobility can be presented in the following form
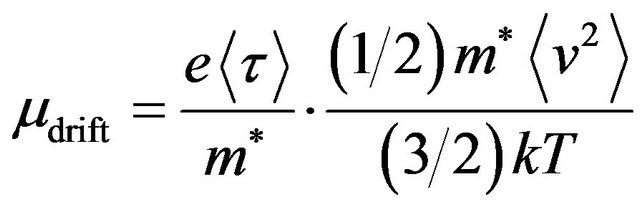 (29)
(29)
or
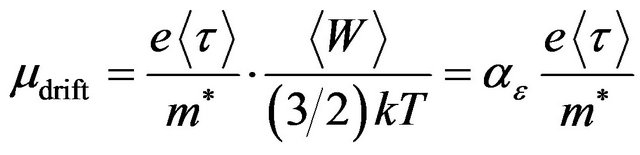 ; (30)
; (30)
where 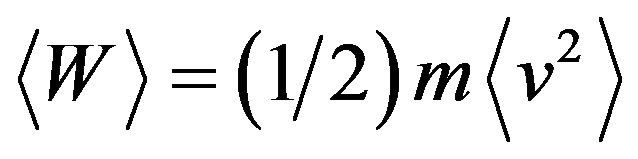 is the average kinetic energy of randomly moving charge carriers. Thus, the Equation (29) is the general relation for drift mobility of randomly moving charge carriers in homogeneous materials with one type of charge carriers (electrons or holes). This relation is true for degenerated and for non-degenerated materials, including metals. The Equation (28) shows that drift mobility of randomly moving electrons in materials is proportional to the square of the electron random velocity, i.e. the electrons with high random velocity contribution into conductivity is larger than that of slow electrons. The factor
is the average kinetic energy of randomly moving charge carriers. Thus, the Equation (29) is the general relation for drift mobility of randomly moving charge carriers in homogeneous materials with one type of charge carriers (electrons or holes). This relation is true for degenerated and for non-degenerated materials, including metals. The Equation (28) shows that drift mobility of randomly moving electrons in materials is proportional to the square of the electron random velocity, i.e. the electrons with high random velocity contribution into conductivity is larger than that of slow electrons. The factor
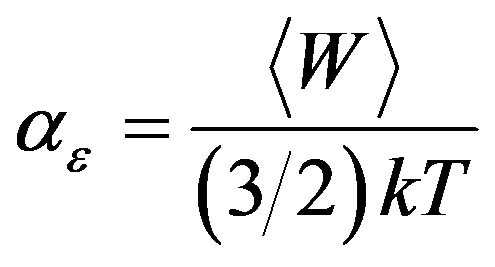 (31)
(31)
shows, how many times the mean kinetic energy 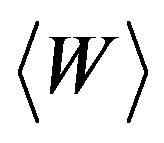 of randomly moving charge carriers is larger than
of randomly moving charge carriers is larger than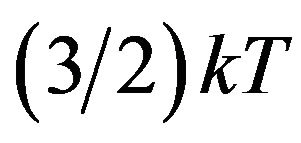 . For non-degenerated material
. For non-degenerated material 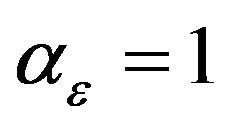 and
and
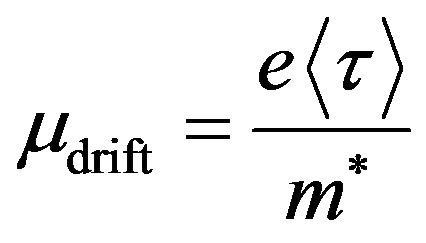 , (32)
, (32)
but for highly degenerated semiconductors, metals and superconductors in the normal state
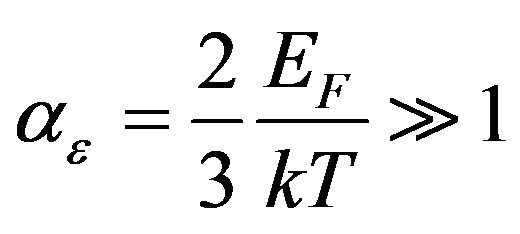 , (33)
, (33)
i.e. the drift mobility (Equation (30)) of random moving charge carriers in metals at room temperature in many cases is about a hundred times larger (see the ratio 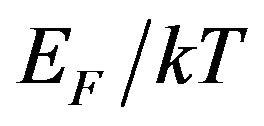 values in Table 2) than it follows from the classical Equation (32).
values in Table 2) than it follows from the classical Equation (32).
From the Equation (29) follows that the drift velocity 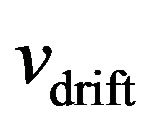 of electrons in the electric field E can be presented as
of electrons in the electric field E can be presented as
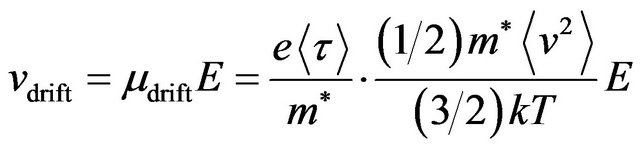 . (34)
. (34)
A very important behavior of electrons in materials follows from this expression: the drift velocity of electrons in the electric field E is proportional to the square velocity of randomly moving electrons. This result in principle can not be explained by application of Newton’s law for calculation of acceleration of electrons in the electric field E in materials.
From the Equations (8) and (30) follows that the general expression for conductivity
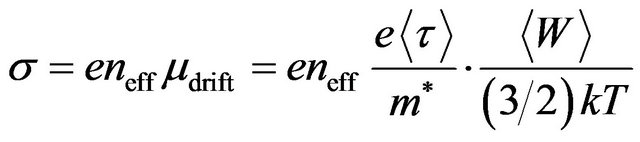 . (35)
. (35)
For non-degenerated material (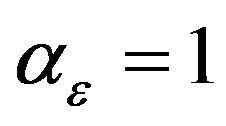 and
and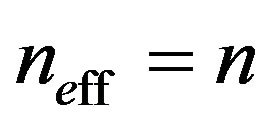 )
)
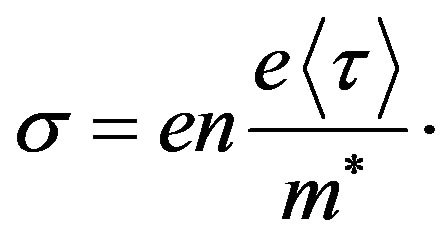 (36)
(36)
but for highly degenerated semiconductors and metals 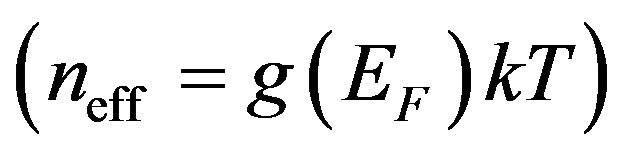
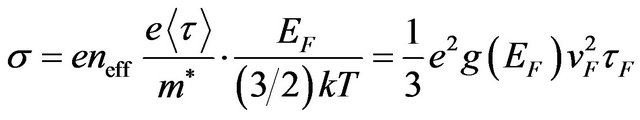 . (37)
. (37)
2.4. Hall Mobility and Its Comparison with the Drift Mobility
Now compare the obtained drift mobility results with that from the Hall effect measurements. On the ground of the Hall effect for highly degenerated materials the Hall mobility [20]
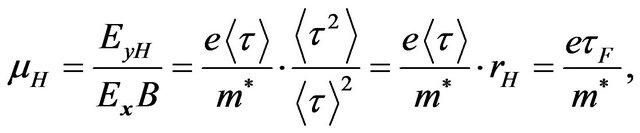 (38)
(38)
where 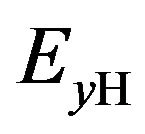 is the Hall electric field strength in y direction perpendicular to the current flow direction;
is the Hall electric field strength in y direction perpendicular to the current flow direction; 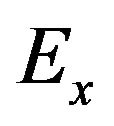 is the applied external electric field strength in x direction;
is the applied external electric field strength in x direction; 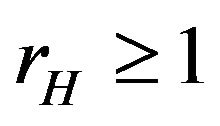 is the Hall factor, which depends on charge carrier scattering mechanism, but for high degenerated charge carriers
is the Hall factor, which depends on charge carrier scattering mechanism, but for high degenerated charge carriers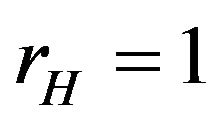 . From Equation (37) it is seen that Hall mobility is determined by average relaxation time of electrons at Fermi level.
. From Equation (37) it is seen that Hall mobility is determined by average relaxation time of electrons at Fermi level.
According to investigations in the work [21], for all homogeneous metals and highly degenerated semiconductors the charge carrier relaxation time at Fermi level at room temperature is general and equal
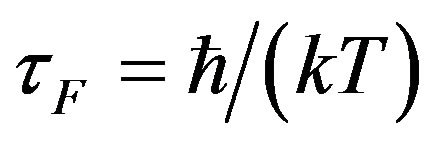 ; (39)
; (39)
where 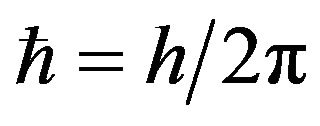 is the Plank constant. At T = 295 K
is the Plank constant. At T = 295 K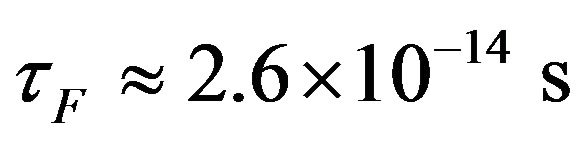 . So, at T = 295 K for m* = m0
. So, at T = 295 K for m* = m0 , while the drift mobility depends also on the kinetic energy of the random moving charge carriers. Now from Equation (23) or from Equation (24) it is possible to find the electron velocity vF at the Fermi level and the Fermi energy EF considering that the effective mass m* of electron is equal to the free electron mass m0, i.e.
, while the drift mobility depends also on the kinetic energy of the random moving charge carriers. Now from Equation (23) or from Equation (24) it is possible to find the electron velocity vF at the Fermi level and the Fermi energy EF considering that the effective mass m* of electron is equal to the free electron mass m0, i.e.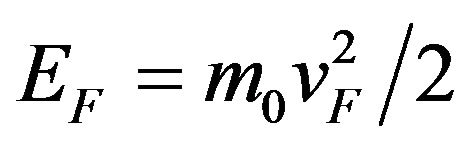 . The calculation results for different metals are presented in Table 2. In this table for different metals there also are presented the free pass length of electron
. The calculation results for different metals are presented in Table 2. In this table for different metals there also are presented the free pass length of electron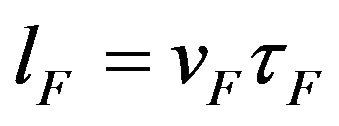 , the latter obtained values are close to experimental data [22].
, the latter obtained values are close to experimental data [22].
Usually for evaluation of the Fermi energy it is considered that Fermi surface is spherical, i.e. [5,15]
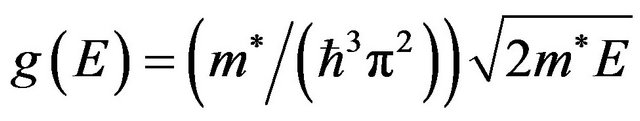 (40)
(40)
and
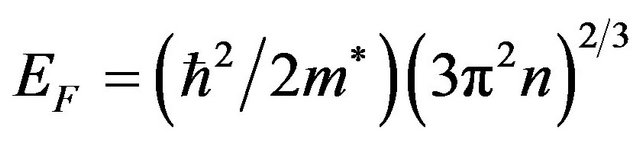 . (41)
. (41)
But for many metals and superconductors in normal state the density of states has composite view (Figure 1(b)), and there is no definite relation between the total density of charge carriers n and the Fermi energy EF. So, as it was mentioned above in order to evaluate the Fermi energy the sure way is from Equation (24) to find the electron velocity at the Fermi level vF and than the Fermi energy EF.
The obtained mobility results clearly show that for high degenerated materials the drift mobility can tens or hundred times be larger than the Hall mobility.
From Equations (37) and (38) the conductivity and Hall mobility for metals are related with the following expression
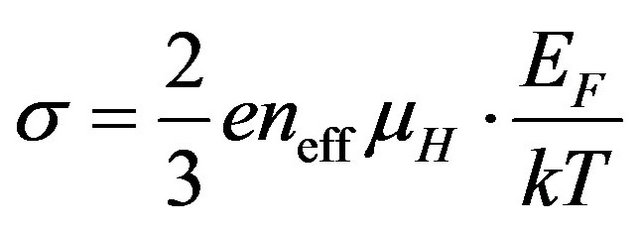 . (42)
. (42)
Thus, the charge carrier density in highly degenerated materials, determined by using the Hall mobility
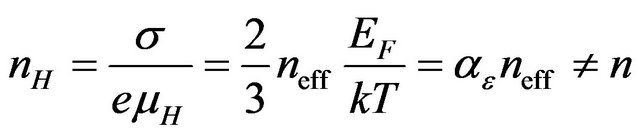 . (43)
. (43)
The charge carrier density nH obtained from Hall effect measurements only in particular cases is equal to the total free charge density for metals with spherical Fermi surfaces, but even in these cases the factor 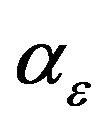 characterizes not the charge density, but the drift mobility. For multivalent metals and superconductors in the normal state with composite density of states dependency on energy there is no definite relation between n and nH.
characterizes not the charge density, but the drift mobility. For multivalent metals and superconductors in the normal state with composite density of states dependency on energy there is no definite relation between n and nH.
Equation (14) shows that the randomly moving charge carrier density 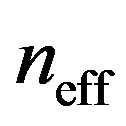 in high degenerated materials is not constant but is proportional to the temperature and the relaxation time close to room temperature
in high degenerated materials is not constant but is proportional to the temperature and the relaxation time close to room temperature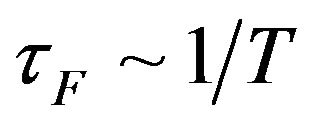 , so in this temperature range the Hall mobility
, so in this temperature range the Hall mobility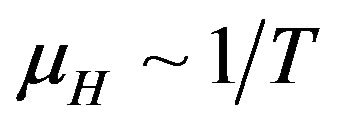 , while the drift mobility
, while the drift mobility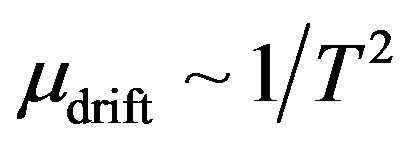 . Hence, one can be very careful in the interpretation of the Hall effect and conductivity measurement results. For example, there are many strange interpretations of charge carrier density and drift mobility of superconductors in the normal state from Hall effect and conductivity temperature measurements [9-13].
. Hence, one can be very careful in the interpretation of the Hall effect and conductivity measurement results. For example, there are many strange interpretations of charge carrier density and drift mobility of superconductors in the normal state from Hall effect and conductivity temperature measurements [9-13].
Considering that Pauli principle and Fermi distribution is known over 80 years, and knowing that only the electrons, which energy is close to the Fermi energy, can be scattered and can change their energy and take part in random moving and in kinetic processes, it is strange that till now in many books of solid state physics the conductivity of metals and superconductors in the normal state is presented in the form of classical expression (Equation (36)? As it is presented in Tables 1 and 2 sometimes the charge carrier density of metals obtained from Hall measurement nH is close to the total density of electrons n, and the conductivity is near to experimental results, but for multivalent metal there is no such coincidence. This conductivity expression gives the increased values of randomly moving charge carriers and decreased values of their drift mobility. Sometimes these two errors compensate one other. In spite of these coincidences the expression (Equation (36)) for metals from the view of the Pauli principle and the Fermi statistics is completely wrong, because the electrical field has no effect to electrons, which are well below the Fermi level.
3. Conclusion
In this review it is tried to call somebody’s attention to problems of conductivity interpretation of metals, normal superconductors and degenerated semiconductors. It is shown that application of classical statistics for these materials in many cases gives the colossal errors in determination of their parameters. On the ground of the Fermi distribution and on the random motion of charge carriers there are presented the general expressions for effective density of randomly moving charge carriers, their diffusion coefficient and drift mobility, and conductivity which are correct for materials without degenerated electron gas, and materials with any degree of degeneracy of electron gas. There also it is presented the approximations of these expressions for materials without degenerated electron gas (classical case), and for materials with high degeneration of electron gas (metals, normal superconductors, highly degenerated semiconductors). The real values of effective density of randomly moving electrons, their diffusion coefficient and drift mobility there are presented for different metals at first time. These parameters were obtained by using the well known conductivity, electron heat conductivity and thermal noise measurement results. There also it is presented the comparison between the Hall and the drift mobility of randomly moving charge carriers, and explained their differences in the case of high degeneration of electron gas. There also is evaluated the Fermi level energy and velocity of electrons at the Fermi energy level for different of metals.
REFERENCES
- Ch. Wert and A. R. M. Thomson, “Physics of Solids,” McGraw-Hill Book Company, New York, 1964.
- J. M. Ziman, “Principles of the Theory of Solids,” Cambridge University Press, Cambridge, 1972.
- A. A. Abrikosov, “Principles of the Theory of Metals,” Nauka Press, Moscow, 1987.
- J. S. Blakemore, “Solid State Physics,” Cambridge University Press, Cambridge, 1985.
- N. Ashcroft and W. N. D. Mermin, “Solid State Physics,” Holt, Rinehart and Winston, New York, 1976.
- Ch. Kittel, “Introduction to Solid State Physics,” John Wiley and Sons, Inc., New York, 1976.
- G. E. R. Schulze, “Metallphysik,” Akademie-Verlage, Berlin, 1967.
- W. A. Harrison, “Solid State Theory,” McGraw-Hill, New York, 1970.
- J. R. Waldram, “Superconductivity of Metals and Cuprates,” Institute of Physics Publishing, London, 1996.
- D. M. Eagles, “Concentrations and Mobilities of Holes and Electrons in a Crystal of a 90 K Oxide Superconductors from Analysis of ab-Plane Resistivity and Hall Data,” Solid State Communications, Vol. 69, No. 3, 1989, pp. 229-234. doi:10.1016/0038-1098(89)90840-5
- A. T. Fiory and G. S. Grader, “Extraordinary Hall Effect in YBa2Cu3O7−x Superconductors,” Physical Review B, Vol. 38, No. 13, 1988, pp. 9198-9200. doi:10.1103/PhysRevB.38.9198
- Y. Lu, Y. F. Yan, H. M. Duan, L. Lu and L. Li, “Hall Coefficient of Single-Crystal Bi2Sr2CaCu2Oy,” Physical Review B, Vol. 39, No. 1, 1989, pp. 729-731. doi:10.1103/PhysRevB.39.729
- J. Clayhold, N. P. Ong, P. H. Hor and C. W. Chu, “Hall Effect of the High-Tc Superconducting Oxides Bi-CaSr-Cu-O and Tl2Ca2Ba2Cu3Ox,” Physical Review B, Vol. 38, No. 10, 1988, pp. 7016-718. doi:10.1103/PhysRevB.38.7016
- A. Van der Ziel, “Noise in Solid State Devices and Circuits,” John Wiley & Sons, Inc., New York, 1986.
- R. Kubo, “Statistical Mechanics,” North-Holland Publishing Company, Amsterdam, 1965.
- V. L. Bonch-Bruevitch and S. G. Kalashnikov, “The Physics of Semiconductors,” Nauka Press, Moscow, 1990.
- H. L. Hartnagel, R. Katilius and A. Matulionis, “Microwave Noise in Semiconductor Devices,” John Wiley & Sons, Inc., New York, 2001.
- V. Palenskis, “Flicker Noise Problem,” Lithuanian Journal of Physics, Vol. 30, No. 2, 1990, pp. 107-152.
- I. K. Kikoin, “Catalogue of Physical Quantities,” Atomizdat, Moscow, 1976.
- R. A. Smith, “Semiconductors,” Cambridge University Press, Cambridge, 1978.
- M. A. C. Devillers, “Lifetime of Electrons in Metals at Room Temperature,” Solid State Communications, Vol. 49, No. 11, 1990, pp. 1019-1022. doi:10.1016/0038-1098(84)90413-7d
- K. L. Chopra, “Thin Film Phenomena,” McGraw-Hill, New York, 1969.
Appendix
The Kubo formula for conductivity in x direction reads as [2,15]
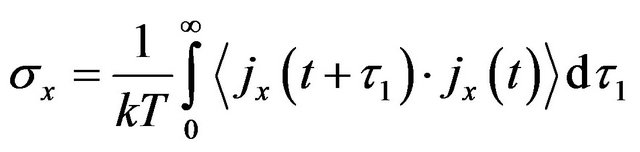 . (A1)
. (A1)
i.e. the conductivity is defined by the correlation function on time 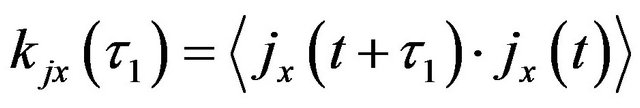 of the current density fluctuations due to random motion of charge carriers. For stationary processes the correlation function depends only on time difference
of the current density fluctuations due to random motion of charge carriers. For stationary processes the correlation function depends only on time difference  Equation (A1) can be presented in the form of Nyquist formula (Equation (10))
Equation (A1) can be presented in the form of Nyquist formula (Equation (10))
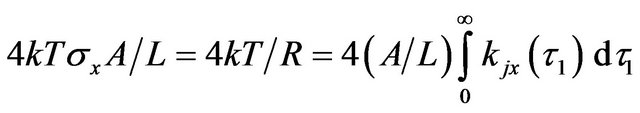 . (A2)
. (A2)
The right side of this expression according to Wiener-Khintchine theorem is the spectral density of the current fluctuations at low frequencies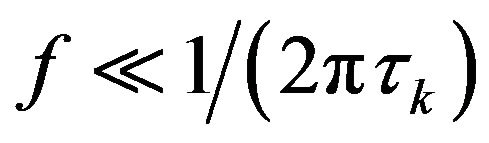 , because
, because 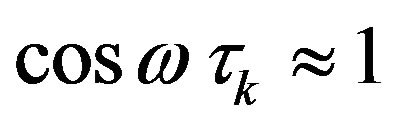 (here
(here 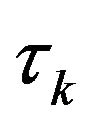 is the correlation time).
is the correlation time).
In Equation (A1), the current density fluctuations can be replaced by the independent charge carrier velocity fluctuations
 (A3)
(A3)
Considering Wiener-Khintchine theorem at low frequencies 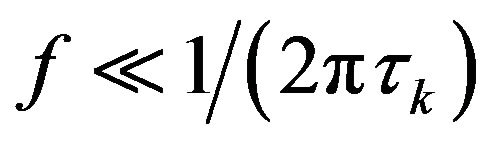 the Equation (A2) can be presented as:
the Equation (A2) can be presented as:
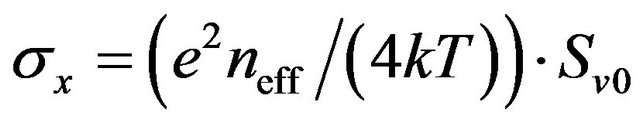 (A4)
(A4)
where 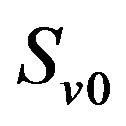 is the spectral density of charge carrier velocity fluctuations at low frequencies
is the spectral density of charge carrier velocity fluctuations at low frequencies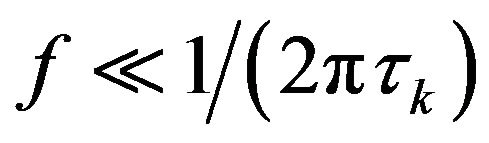 .
.
The particle random (Brownian) motion (the variance of the displacement) during time t can be described by Einstein’s relation:
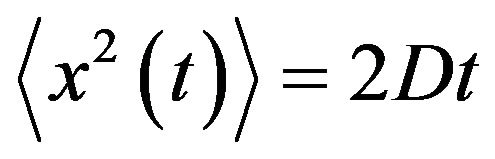 , (A5)
, (A5)
where D is the diffusion coefficient of the particles. If the charge carrier random velocity is v(t), then the displacement
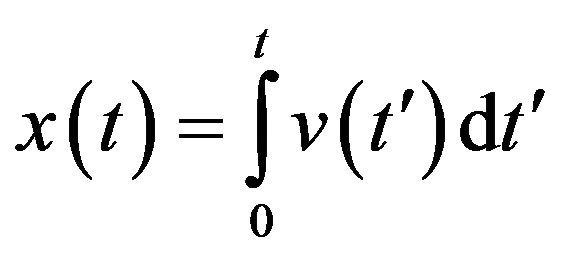 (A6)
(A6)
and
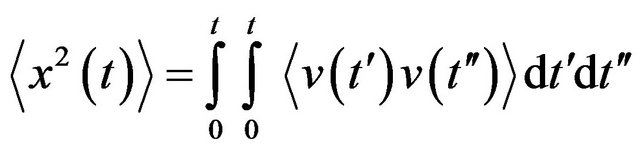 . (A7)
. (A7)
Now one can transform the variables: 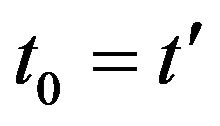 and
and 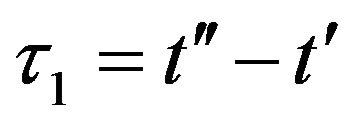
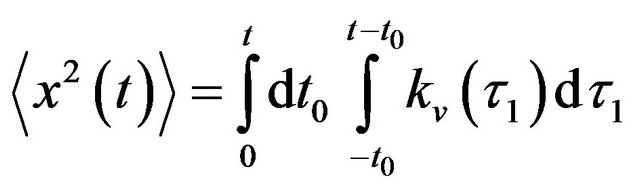 , (A8)
, (A8)
where  is the autocorrelation function of the charge carrier velocity fluctuations. If the observation time is much longer than the correlation time
is the autocorrelation function of the charge carrier velocity fluctuations. If the observation time is much longer than the correlation time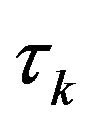 , i.e.
, i.e. 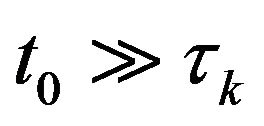 and
and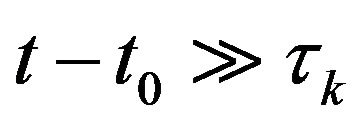 , then
, then
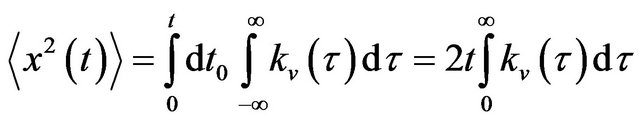 . (A9)
. (A9)
Considering the Wiener-Khintchine theorem the spectral density of charge carrier velocity fluctuations can be expressed as
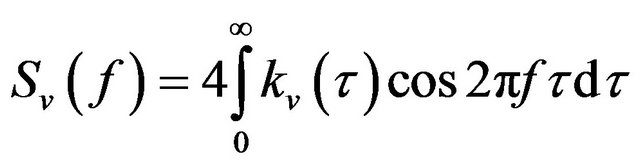 . (A10)
. (A10)
At low frequencies 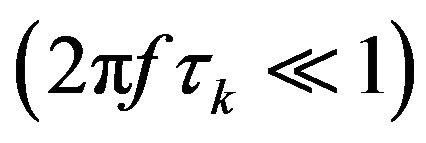
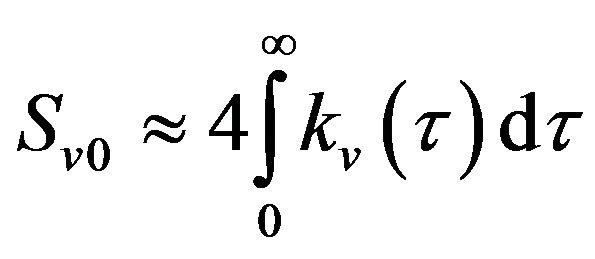 . (A11)
. (A11)
From (A5), (A9) and (A11) follows that
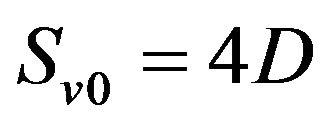 , (A12)
, (A12)
and from (A4) and (A12)
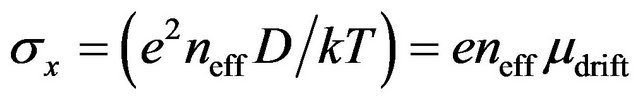 . (A13)
. (A13)
and
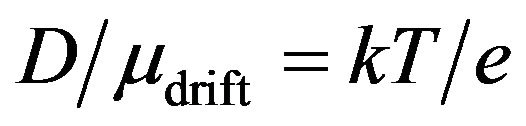 .
.
This derivation once more confirms that Einstein relation (9) is correct for all homogeneous materials with nondegenerated and degenerated electron gas.

