Atmospheric and Climate Sciences
Vol.05 No.03(2015), Article ID:58289,8 pages
10.4236/acs.2015.53024
Impact of the Waves on the Sea Surface Roughness under Uniform Wind Conditions: Idealized Cases for Uniform Winds (Part I)
José Augusto P. Veiga1, Mônica R. Queiroz2
1Department of Meteorology, Institute of Technology, Amazonas State University, Manaus, Brazil
2UNINORTE Laureate International Universities, Manaus, Brazil
Email: veiga.uea@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 February 2015; accepted 21 July 2015; published 24 July 2015
ABSTRACT
The effect of the surface gravity waves over sea surface roughness length (z0) is investigated from several idealized numerical experiments with the Wave-Watch-III (WW3) model. The WW3 model is combined with a simplified model to estimate z0, CD, u* and U10 as function of the sea state. The impacts related to the presence of the ocean waves over z0 are obtained from conditions of growing (young waves) and mature seas (old waves). The wave spectrum is obtained from WW3 model for each idealized simulation under uniform wind conditions. Uniform wind experiments range from 15 to 45 m/s. The simplified algorithm determines z0, CD, u* and U10 for cases of young waves, old waves and by the Charnock method. The results show that when the ocean is characterized by young waves, both z0 and CD (drag coefficient) increase while U10 is reduced. In Charnock case, the values of z0, CD and U10 have no dependence with the presence of gravity waves. Experiments using winds higher than 30 m/s result in young waves’ CD values higher than the CD value for old waves. Even for young waves CD values are high for cases of strong winds. The results also show that in experiments using winds higher than 30 m/s the dependence between CD and wave age becomes stronger, which is in accordance with other studies.
Keywords:
Surface Gravity Waves, Wind Sea, Ocean Waves, Young Waves, Old Waves

1. Introduction
Ocean surface waves are the result of forces acting on the ocean. The characteristics of the waves depend on the controlling forces. Tidal waves are generated by the response to gravity of the Moon and Sun and are rather large-scale waves. Capillary waves are dominated by surface tension in the water. Where the Earth’s gravity is the major determining factor we have the so-called gravity waves. Wind-generated gravity waves are almost always present at sea. These waves are generated by winds somewhere on the ocean. They are also very relevant in climate processes since they play a role in the heat, energy, gases and particles exchange between the oceans and atmosphere. Further, gravity waves can be classified into wind sea and swell. Wind seas are waves that constantly experience the action from the winds. Swells, however, are waves that propagate away from the wind forcing area.
To estimate wind stress over the ocean is one of the most important issues in atmospheric and ocean modeling, including extratropical and tropical cyclones forecasting. In the most operational numerical models the momentum flux at the air-sea interface is parameterized by a nondimensional parameter called surface roughness or Charnock coefficient (zch) [1] . This formulation is used in the most atmospheric models, however over the sea, where the surface experiences constant changes, zch must consider the state of the sea [2] .
A direct dependence between surface roughness and the sea state is suggested in several papers [3] - [10] . The results of these works pointed that the increase of roughness length (z0), a height in meters at which the wind speed becomes zero, occurs in the presence of young waves, while there is a low relationship between old waves and roughness length. [11] showed that roughness length computed as function of the developing sea state better represents the observed sea wave height (SWH). The SWH computed by the Charnock constant overestimates the observed values. This pattern is commonly observed in comparisons between observed and modeled SWH.
From observed and experimental data, [12] evaluated the role of the young waves on the air-sea momentum transfer. It was observed that the relationship between z0 and the waves varies in specific conditions. In addition, it was noted that z0 tends to diminish as the ratio between cp and u* (phase speed at the peak frequency and friction velocity, respectively) decreases. This ratio is a dependent relation between cause (winds) and effect (gravity waves) and is usually called wave age. The parameter wave age indicates the development state of the sea. When the nondimensional value of the wave age is less than 10 the sea is characterized by young waves [13] . The young waves are gravity waves in process of constant growing, once they are continually extracting momentum from the winds. By another way, old waves (wave age greater than 10) are gravity waves that are completely developed. In this case, there is either very weak or any momentum transfer between winds and waves, considering that the winds and waves propagate in the same direction. The term strong (weak) coupling is usually used when the sea is characterized by strong (weak) momentum transfer in the air-sea interface. Strong coupling generally occurs in the presence of young waves, when the winds act as a source of energy to the waves.
[8] investigated the effect of the surface waves on air-sea momentum exchange by combining ocean wave models and a wave boundary layer model. They performed several numerical experiments for constant winds from 10 to 45 m/s to investigate the effect of mature and growing seas on the air-sea momentum exchange. They observed that, for mature seas, the Charnock coefficient is estimated to be about 0.01 - 0.02 and the drag coefficient increases as wind speed increases. With growing seas, results for winds less than 30 m/s show that the drag coefficient is larger for young waves. For winds higher than 30 m/s, however, results show a different trend: very young waves yield less drag.
In this context, the present study evolves a combination of an ocean wave numerical model (WW3) and a very simple algorithm to provide some insight on the effect of the waves on the behavior of some surface variables, including: z0, sea surface drag (CD), wind stress (u*), and wind velocity at 10 meters (U10). These effects are evaluated in conditions of growing and mature sea. A brief outline of the WW3, the simplified algorithm, and the experimental design, used here is introduced in Section 2. Section 3 describes results of the experiments with constant winds from 15 to 45 m/s to investigate roughness length behavior in mature and growing sea conditions. The summary and conclusions are given in Section 4.
2. Methodology
The WW3 runs for all time integration. It outputs SWH, mean wave length (MWL), wave mean period, mean wave direction and peak frequency [14] . The simplified algorithm, based on diagnostic equations, computes z0, CD, u* and U10 from two different manner. In the first, the algorithm uses the Charnock relation (RBULK), which computes z0 considering zch without dependence with waves. In the second case, the parameter wave age
 is included in the place of zch (RWA). In this case, zch takes into account the sea state. The simplified algorithm uses the complete wave spectrum from the WW3 model to compute RBULK and RWA.
is included in the place of zch (RWA). In this case, zch takes into account the sea state. The simplified algorithm uses the complete wave spectrum from the WW3 model to compute RBULK and RWA.
2.1. Wave Model
The WW3 model solves the energy transfer equation for the wave spectrum. The equation describes the variation of the wave spectrum F in space and time due to the advection of energy and local interactions. The wave spectrum is locally modified by the input of energy from the wind, the redistribution of energy due to nonlinear interactions and energy dissipation due to wave breaking. These processes are represented by the source functions Sin, Snl, and Sds, respectively, according to Equation (1).
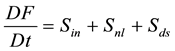 (1)
(1)
The three terms in the right hand side of Equation (1) are called source terms. The source terms of the WW3 use nonlinear wave-wave interaction using a discrete interaction approximation (DIA) modified by [15] , input and dissipation from [15] , and bottom friction from the Joint North Sea Wave Project (JONSWAP) as used in WAM [16] . A detailed description of the model is given by [14] .
2.2. Simplified Algorithm
In most atmospheric, ocean and wave models z0 is determined from the Charnock relation [17] :
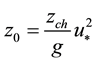 (2)
(2)
where u* is the friction velocity, g the gravity of the Earth, and zch is the Charnock constant with value of 0.0185, which is representative of a sea at equilibrium. Thus, the Charnock conventional formulation does not consider the evolution stage of the sea or its growth.
To include the wave growing effect zch, in simplified algorithm, is replaced by the coupled term wave age. Thus, zch becomes a function of the sea state. The effect of the sea development into z0 can be formulated by two particular ways: the first follows [3] and is related to the wave age parameter: the second, according to [2] , considers the effect of the wave-induced stress (a stress induced by the presence of the waves). Therefore, Equation 2 becomes:
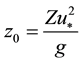 (3)
(3)
where
 and
and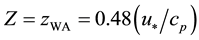 . Here, the subscripts “WA” and “WIS”, refers, respectively, to parameters based on [3] and [18] formulations. The symbols τ, τw, and cp denotes, respectively, total stress, wave-induced stress, and the phase speed at the peak frequency. [13] showed that both schemes (WA or WIS) present similar results in cases of baroclinic systems simulations. For implementation simplicity, it is used the scheme elaborated by [3] .
. Here, the subscripts “WA” and “WIS”, refers, respectively, to parameters based on [3] and [18] formulations. The symbols τ, τw, and cp denotes, respectively, total stress, wave-induced stress, and the phase speed at the peak frequency. [13] showed that both schemes (WA or WIS) present similar results in cases of baroclinic systems simulations. For implementation simplicity, it is used the scheme elaborated by [3] .
The 10 meters level drag coefficient under neutral conditions is given by
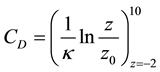 (4)
(4)
in which κ = 0.41 is the von Kármán constant and CD is the drag coefficient.
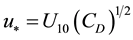 (5)
(5)
where u* is the friction velocity and U10 is the 10 meters wind speed given by
 (6)
(6)
The simplified algorithm solves the Equations (3) to (6), in conventional (RBULK) and nonconventional (RWA) modes, from WW3 outputs. The use of the simplified algorithm allows us to evaluate the impact of the waves on the surface roughness length over the oceans.
2.3. Strategy of the Simulations
The parameters of the WW3 used in this study are 1800 s (time step and wind input interval), 24 directions (directional resolution), 0.2˚ × 0.2˚ spatial grid resolution, and 4000 m (water depth). The grid is regularly spaced by a longitude-latitude grid. It extends 3000 km in the south-north direction and 1500 km in the east-west extent. The wave spectrum is discretized using 25 frequencies extending from 0.041 a 0.42 Hz with a logarithmic increment
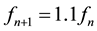 where fn id the nth frequency. The WW3 provides output of two-dimensional directional wave spectra, as well as mean wave parameters such as significant wave heights, mean wave length, mean wave period, mean wave direction, peak frequency, and peak direction.
where fn id the nth frequency. The WW3 provides output of two-dimensional directional wave spectra, as well as mean wave parameters such as significant wave heights, mean wave length, mean wave period, mean wave direction, peak frequency, and peak direction.
Seven experiments are performed for uniform wind conditions ranging from 15 to 45 m/s in all grid space. In the first experiment the uniform winds are 15 m/s, in the second they are of 20 m/s and so on until the last experiment were winds blow with 45 m/s. The simplified algorithm estimates the surface variables for RBULK and RWA for each experiment and in cases of growing and mature seas.
3. Results and Discussions
In this work, the effect of sea state on sea surface roughness length, drag coefficient, wind stress and wind velocity in 10 meters is evaluated. Two distinct cases were analyzed: mature and growing seas. Further, the results are divided into those which consider zch as a constant value of 0.0185 and those which use wave age in the place of zch.
Figure 1 shows sea wave height and mean wave length values for each experiment with uniform wind speedy. The values of sea wave height and mean wave length were obtained for a reference point near the north edge of the domain (not showed). In the first thirty hours of simulation, the wave height and the wave length show right ratio of development when compared with the 42 hours of spin up. This different behavior is due to the strong momentum transfer from the atmosphere to the ocean which occurs in the first hours of simulation [19] . Figure 1 shows that as the wind becomes strong both sea wave height (Figure 1(a)) and mean wave length (Figure 1(b)) increases. This behavior is observed before 24 hours of simulation. This occurs because sea extracts more energy from the atmosphere in the first hours of spin up. In this case the sea is in process of development. After 30 hours of spin up, the waves reaches their peak intensity (or the sea becomes in equilibrium) and no more growth occurs. In this case, the sea wave height is constant due to the fact that the energy gained by the wind equals to the energy loss by dissipative processes Sds (Equation (1)).

Figure 1. Time series of (a) the Significant wave height Hsig and (b) Mean wave length L simulated with spatially homogenous winds from 15 to 45 m/s. From bellow to top the continuous lines in the graphic denotes 45, 40, 35, 30, 25, 20 e 15 m/s.
Figure 2 shows the temporal variability (model time integration) of the wave age term for different wind speed experiments in the same grid point (reference point). When the waves are in process of development the sea is characterized by young waves (wave age less than 15). For mature sea cases (spin up > 30 hours), the sea is dominated by old waves. According to Figure 2 younger waves are related to the strongest winds, while older waves occur in cases of weakest winds. It is also observed that young waves are not produced or observed during weak wind conditions (wind velocity less than 25 m/s).
Figures 3(a)-(d) show scatter plot of z0, CD, and U10 versus wave age for each experiment with uniform wind speed. At this time the sea is completely developed. For RWA case (Figure 3(a)) two different conditions are observed: one with winds less than 30 m/s and other for stronger winds (wind velocity great than 30 m/s). In the first situation, as the waves become older z0 decreases. The ratio of z0 diminishing is more accentuated in cases of strong winds. In the second situation (wind velocity less than 30 m/s), different trends are noted. As the waves become older z0 values keep invariant. This means that old waves (or mature sea) produce slight or any effect on z0, as observed in several studies. Results from RBULK case (Figure 3(b)) show that z0 values are not modified by wave type. This occurs because z0 in RBULK case is kept constant and it does not suffer any modification as the sea or waves growth. In RBULK case the parameter z0 is just forced by wind speed. Because wind speed is it only forcing mechanism one can expected that z0 values are large for experiments with strong winds.
Figure 3(c) shows the scatter plot between CD and wave ages for RWA case. It is noted that the behavior of CD is similar to the observed behavior of z0. For strong wind experiments sea surface drag decreases as the waves become older. In experiments with wind velocity less than 30 m/s, CD suffers slight changes with the sea state. The relation between CD and wave age are more significant for experiments with strong winds. As young waves yields more drag it is expected that wind speed diminish. Expressive reduction of the wind velocity at 10 meters level under strong wind speed and young sea conditions is observed in Figure 3(d). As the winds become strong and the waves become older U10 increases. The values of U10 are not substantially modified with the sea state in cases of experiments with wind speed weaker than 30 m/s. As can be noted, young waves produce more drag and weak winds. However, in experiments with uniform wind speed lower than 25 m/s the relation between U10 and wave ages weak until they become independent. Those results show that significant changes in the planetary boundary layer as well as momentum, heat and moisture fluxes can be expect by considering the sea state.
Figures 4(a)-(c) show the behavior of z0, CD and U10 in the reference point for each experiment with constant
Figure 2. Time series of wave age for numerical simulations with spatially homogenous winds from 15 to 45 m/s. From bellow to top the continuous lines in the graphic denotes 45, 40, 35, 30, 25, 20 e 15 m/s.


Figure 3. Scatter plot of the z0 (a); zch (b); CD (c); and U10 (d) as a function of wave age in all grid points for spatially homogenous winds from 15 to 45 m/s (from bottom to top). All scatter represents the spin up of 56 hours.
wind speed. Further, surface parameters are put in perspective for developing (06 hours) and mature (72 hours) sea conditions (RWA). It is also showed the results from RBULK case. Figure 4(a) shows that young waves yield high values of z0, while old waves are associated to low values of z0. Lowest values of z0 are produced for cases without the sea state influence (RBULK). More discrepancy between z0 values are observed for experiments with strong winds. Results from mature sea conditions and RBULK case show similar z0 values for weak wind experiments (wind velocity less than 35 m/s). An important fact to note is that RBULK case underestimates z0 values in comparison with young and old waves (RWA) for all experiments. This results are in agreement with numerical modeling studies, including complex coupled experiments with atmospheric and ocean wave models [5] [13] [19] [20] .
Figure 4(b) shows that young waves produce more drag (CD) than old waves. Lower values of CD are produced in RBULK case. Differences between CD values for mature and growing sea are more expressive in cases of strong wind conditions (wind velocity greater than 30 m/s). CD values for mature sea conditions are similar to CD values for RBULK cases for weak wind experiments (wind velocity less than 30 m/s). It can be also noted that RBULK case produces the lowest values of CD for all experiments. This results are similar to those observed for z0 (Figure 4(a)). It means that young waves yield more drag than old waves and drag is more accentuated for


Figure 4. Sea surface roughness length (a); drag coefficient (b) and U10 (c) as a function of numerical experiments. Each figure shows the respective variable for mature (72 hours) and developing (06 hours) seas (RWA), and Bulk (RBULK) computed in a reference point near the north edge of the experiment domain.
strong wind conditions. As young waves yield more drag and high values of z0, it can be expected that in conditions of developing sea the wind velocity, near surface, diminish.
Figure 4(c) shows that U10 is lower at sea dominated by young waves than at developed sea. The wind velocity is reduced in developing sea because young waves produce more resistance (or drag) to the wind flow. According to [19] the reduction of wind velocity, under the influence of young waves, can produce less mass and moisture convergence into meteorological systems. It can diminish both the meteorological system intensity and the height of the waves. Further, the velocity of the considered meteorological phenomena (Hurricanes or extratropical systems) can experience a substantial reduction. At developed sea conditions the wind velocity experiences a less reduction. This occurs due the fact that the resistance to the wind displacement is low is this sea condition. This pattern is similar to conditions of RBULK case, where sea is considered completely developed. U10 behaves as in the cases of z0 and CD for experiments under strong wind conditions. However, under strong wind conditions young waves produces weak winds. Our results are in agreement with several works which have showed that when waves are considered to interact with the lower atmosphere they can produce significant impacts on wind field [5] [13] [19] [20] .
4. Conclusions
The effect of waves on sea surface roughness length, sea drag, and wind velocity at 10 meters has been investigated by combining the WW3 model with a simplified algorithm. The combined models estimate the behavior of z0, CD, and U10 for particular sea state situations. To evaluate the sea state effect the wave age coupling term (cp/u*) was included in the algorithm. Several numerical experiments were carried out for constant winds ranging from 15 to 45 m/s. For each numerical experiment, z0, CD, and U10 were computed in terms of mature and growing seas.
The results showed that there is a significant dependency between z0 and the sea state. This relation is strong in cases of developing sea under higher wind speed conditions (wind speed > 30 m/s). This dependency is slight weak in experiments with weak winds (wind speed less than 30 m/s). In addition, it was observed that young waves are related to high values of z0 while old waves are associated to low values of z0. The behavior of CD is very similar to those of z0 values. The wind velocity at 10 meters shows an inverse trend with relation to z0 and CD patterns. As for instance, as the wave age increases, which usually occurs when the sea is reaching an equilibrium condition, U10 also increases. It means that, when the sea is young U10 must decrease because the sea is extremely rough. This pattern is consistent with earlier studies which point out that wind velocity near sea surface is reduced in regions dominated by young waves [5] [19] . This occurs because young waves yield more resistance to the wind displacement and this decreasing in the wind velocity produces significant changes in the heat and moisture fluxes at the air-sea interface.
To evaluate the dependence of z0 on the sea state under mature and developing sea conditions, two cases were carried out. The first (RBULK) considers zch constant in time, while the second one (RWA) admits that zch changes according to the sea state. In RBULK case z0 and CD values present just a slight increase with wind speed in all experiments. However, in the case of RWA, z0 and CD present accentuated and expressive increase as the wind speed in the numerical experiments increases. Despite both z0 and CD obtain a high ratio of increase in the case of RWA, important and notable differences between developing and mature seas are observed. At developing seas z0 and CD increase. In the case of mature sea z0 and CD values are lower than those in the developing sea case. The difference between developing and mature seas increases for experiments with strong winds. This behavior is also valid for the variable U10. However, U10 decreases more for developing sea conditions than for mature stage (RWA). U10 in RBULK cases does not suffer any modification in all experiments. This is due to the fact that the sea state condition does not affect rigorously the flow passing by developing seas, as it occurs in RWA cases.
The present results show important aspects when the sea state is included in the computation of sea surface roughness length. These aspects are related to the change of values of drag and wind velocity near surface, which would bring substantial effects on the life cycle of atmospheric system moving on young sea. Despite the numerical experiments showed that wave state affects the patterns of z0, CD and U10, they are very limited. This limitation is due to the fact that in real conditions the winds will not blow and support constant wind speed too long. Issuing to bring more reality to the results, the second part of this work includes experiments with idealized tropical storms with different intensity and translation speeds.
Cite this paper
José Augusto P.Veiga,Mônica R.Queiroz, (2015) Impact of the Waves on the Sea Surface Roughness under Uniform Wind Conditions: Idealized Cases for Uniform Winds (Part I). Atmospheric and Climate Sciences,05,317-325. doi: 10.4236/acs.2015.53024
References
- 1. Ian, S.F. and Toba, Y. (2001) Wind Stress over the Ocean. Cambridge University Press, Cambridge, 307.
- 2. Janssen, P.A.E.M. (1989) Wave-Induced Stress and the Drag of Air Flow over Sea Waves. Journal of Physical Oceanography, 19, 745-754.
http://dx.doi.org/10.1175/1520-0485(1989)019<0745:WISATD>2.0.CO;2 - 3. Smith, S.D., et al. (1992) Sea Surface Wind Stress and Drag Coefficients: The HEXOS Result. Boundary-Layer Meteorology, 60, 109-142.
http://dx.doi.org/10.1007/BF00122064 - 4. Komen, G.J., Janssen, P.A.E.M., Makin, V. and Oost, W. (1998) On the Sea State Dependence of the Charnock Parameter. Global Atmosphere-Ocean System, 5, 367-388.
- 5. Lalbeharry, R., Mailhot, J., Desjardins, S. and Wilson, L. (2000) Examination of the Impact of a Coupled Atmospheric and Ocean Wave System. Part II: Ocean Wave Aspects. Journal of Physical Oceanography, 30, 402-415.
http://dx.doi.org/10.1175/1520-0485(2000)030<0402:EOTIOA>2.0.CO;2 - 6. Drennan, W. and Hans, C.G. (2003) On the Wave Age Dependence of Wind Stress over Pure Wind Seas. Journal of Geophysical Research, 108, 1-13.
http://dx.doi.org/10.1029/2000JC000715 - 7. Powell, D.M., Vickery, P.J. and Reihold, T.A. (2003) Reduced Drag Coefficient for High Wind Speeds in Tropical Cyclones. Nature, 422, 279-283.
http://dx.doi.org/10.1038/nature01481 - 8. Moon, I.-J., Hara, T., Ginis, I., Belcher, E. and Tolman, H. (2004) Effect of Surface Waves on Air-Sea Momentum Exchange, Part I: Effect of Mature and Growing Seas. Journal of Atmospheric Sciences, 61, 2321-2333.
http://dx.doi.org/10.1175/1520-0469(2004)061<2321:EOSWOA>2.0.CO;2 - 9. Moon, I.-J., Ginis, I., Hara, T. and Belcher, E. (2004) Effect of Surface Waves on Air-Sea Momentum Exchange, Part II: Behavior of Drag Coefficient under Tropical Cyclones. Journal of Atmospheric Sciences, 61, 2334-2348.
http://dx.doi.org/10.1175/1520-0469(2004)061<2334:EOSWOA>2.0.CO;2 - 10. Donelan, M.A., Haus, B.K., Reul, N., Plant, W.J., Stiassenie, M. and Graber, H.C. (2004) On the Limiting Aerodynamic Roughness of the Ocean in Very Strong Winds. Geophysical Research Letters, 31, Article ID: L18306.
- 11. Toba, Y., Iida, N. and Kawamura, H. (1990) The Wave Dependence of Sea-Surface Wind Stress. Journal of Physical Oceanography, 20, 705-721.
http://dx.doi.org/10.1175/1520-0485(1990)020<0705:wdossw>2.0.co;2 - 12. Johnson, H.K., Hojstrup, J., Vested, H.J. and Larsen, S.E. (1998) On the Dependence of Sea Surface Roughness on Wind Waves. Journal of Physical Oceanography, 28, 1702-1716.
http://dx.doi.org/10.1175/1520-0485(1998)028<1702:OTDOSS>2.0.CO;2 - 13. Desjardins, S. Mailhot, J. and Lalbeharry, R. (2000) Examination of the Impact of a Coupled Atmospheric and Ocean Wave System. Part I: Atmospheric Aspects. Journal of Physical Oceanography, 30, 385-401.
http://dx.doi.org/10.1175/1520-0485(2000)030<0385:EOTIOA>2.0.CO;2 - 14. Tolman, H.L. (2002) User Manual and System Documentation of WAVE-WATCH-III Version 2.22. NOAA/NWS/ NCEP/OMB Tech. Note 222, 133.
- 15. Tolman, H.L. and Chalikov, D. (1996) Source Terms in a Third-Generation Wind Wave Model. Journal of Physical Oceanography, 26, 2497-2518.
http://dx.doi.org/10.1175/1520-0485(1996)026<2497:stiatg>2.0.co;2 - 16. WAMDI Group (1998) The WAM Model—A Third Generation Ocean Wave Prediction Model. Journal of Physical Oceanography, 18, 1775-1810.
- 17. Charnock, H. (1955) Wind Stress on a Water Surface. Quarterly Journal of the Royal Meteorological Society, 81, 639-640.
http://dx.doi.org/10.1002/qj.49708135027 - 18. Janssen, P.A.E.M. (1991) Quasi-Linear Theory of Wind-Wave Generation Applied to Wave Forecasting. Journal of Physical Oceanography, 21, 1631-1642.
http://dx.doi.org/10.1175/1520-0485(1991)021<1631:QLTOWW>2.0.CO;2 - 19. Lionello, P., Malguzzi, P. and Buzzi, A. (1998) Coupling between the Atmospheric Circulation and the Ocean Wave Field: An Idealized Case. Journal of Physical Oceanography, 28, 161-177.
http://dx.doi.org/10.1175/1520-0485(1998)028<0161:CBTACA>2.0.CO;2 - 20. Doyle, J.D. (1995) Coupled Ocean Wave/Atmosphere Mesoscale Model Simulations of Cyclogenesis. Tellus, 47-A, 766-778.
http://dx.doi.org/10.1034/j.1600-0870.1995.00119.x


