International Journal of Astronomy and Astrophysics
Vol.04 No.03(2014), Article ID:49717,14 pages
10.4236/ijaa.2014.43049
Analytical Third Order Solution for Coupling Effects of Earth Oblateness and Direct Solar Radiation Pressure on the Motion of Artificial Satellites
Hadia Hassan Selim
Department of Astronomy, National Research Institute of Astronomy and Geophysics, Cairo, Egypt
Email: hassanselim@ yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 June 2014; revised 18 July 2014; accepted 14 August 2014
ABSTRACT
Coupling effects of Earth oblateness and direct solar radiation pressure on the motion of an artificial satellite are evaluated. Secular and periodic terms are retained up to order three and two respectively, where the coefficient
 of the second zonal harmonic of the geopotential is considered of first order. The solution revealed the existence of secular terms at order three that arises from the couplings between terms, of lower orders, resulting from the solar radiation pressure.
of the second zonal harmonic of the geopotential is considered of first order. The solution revealed the existence of secular terms at order three that arises from the couplings between terms, of lower orders, resulting from the solar radiation pressure.
Keywords:
Earth Oblateness-Solar Radiation Pressure-Artificial Satellites

1. Introduction
Analytical theories of celestial mechanics are usually more tractable when tackled within the domain of Hamiltonian mechanics, and fortunately most non-Hamiltonian systems of differential equations can be Hamiltonized by a simple technique [1] [2] . As for as canonical perturbation methods are concerned, the basic demand is a canonical transformation such that the new Hamiltonian has fewer degrees of freedom, which results in integrals of motion equal in number to the number of ingrate coordinated, and thus successive transformations reduce the system to quadratures. If the Hamiltonian is a periodic function of time, a further requirement would be the averaging of the Hamiltonian to eliminate the time.
If the Hamiltonian admits a Taylor series expansion in powers of a small parameter
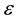 at
at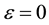 , a generator of the transformation can obtain a series of
, a generator of the transformation can obtain a series of
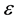 up to any desired power.
up to any desired power.
Many works deal with the effects of solar radiation pressure, Musen (1960) [3] derived first order expansion for the rate of change in the osculating elements using the method of variation of vector elements. Kosai (1961) and Brouwer (1962) [4] [5] used Lagrange’s planetary equations to find the first order solutions with the integration performed between the times of exit from, and entry into, the shadow. The resonance effects produced by the commensurabilities between the different mean motions provided good field for detailed theoretical studies (e.g. Musen, 1960 [3] ; Brouwer, 1962 [5] and Hori, 1966 [6] ). De Moraes (1981) [7] developed semi-ana- lytical theory including the joint effects of direct solar radiation pressure and atmospheric drag for satellites of perigee heights between 500 and 900 Kms. The difficulties arising from solar radiation pressure are analyzed in three very useful and interesting expositions given by Kampos (1968) and Sehnal (1970 and 1975) [8] - [10] . An interesting application is to use solar radiation pressure as means of spacecraft propulsion (solar sailing). The idea is described and its dynamics is studied by Mc Innes and Brouwn (1990) [11] .
It has been repeatedly stated by many authors (e.g. Kampos, 1968; Ferraz-Mello, 1972 and Anselono et al., 1983) [8] [12] [13] that there are no secular or long periodic changes of the semimajor axis and no second order terms (or even, by some author, no secular terms whatever the order). But Geyling and Westerman (1971), Lala (1972) and Sehnal (1975) [10] [14] [15] drew attention to secular terms which appear at higher orders. McMahon, Jay W., (2011) [16] modeled the solar radiation pressure acceleration as a Fourier series which depends on the Sun’s location in a body-fixed frame; a new set of Fourier coefficients are derived for every latitude of the Sun in this frame, and the series is expanded in terms of the longitude of the Sun. Lücking et al. (2012) [17] further explores a passive strategy based on the joint effects of solar radiation pressure and the Earth’s oblateness acting on a high area-to-mass-ratio object. In 2001, Cook found that the most significant effect relating to solar radiation pressure is the changing cross-sectional area of the satellite projected to the Sun [18] .
The present work is concerned with the effects of solar radiation pressure at higher orders to emphasize the effects of the couplings between them and with those resulting from the oblate gravity field of the Earth. The canonical equations of motion are formed in terms of the Delaunay elements augmented with the pair
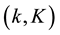 where
where
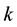 is the mean longitude of the sun. The equations include the radiation pressure force and the geopotential up to
is the mean longitude of the sun. The equations include the radiation pressure force and the geopotential up to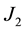 . Two canonical transformations are made to eliminate the short and long period terms in succession respectively. The Hamiltonians and generator are assumed to be expandable as
. Two canonical transformations are made to eliminate the short and long period terms in succession respectively. The Hamiltonians and generator are assumed to be expandable as
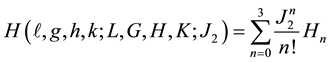
As expected secular terms arise at order 3 from the brackets
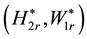 and
and
 where the suffix
where the suffix
 refers to terms arising from solar radiation pressure.
refers to terms arising from solar radiation pressure.
2. Equation of Motion
In terms of the Delaunay variables
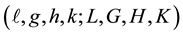 the equations of motion of an artificial satellite about an oblate Earth and perturbed by direct solar radiation
the equations of motion of an artificial satellite about an oblate Earth and perturbed by direct solar radiation
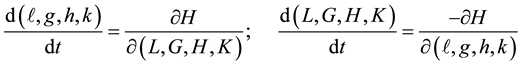 (1)
(1)
With the Hamiltonian [6] [19]
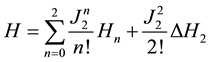 (2)
(2)
 (3)
(3)
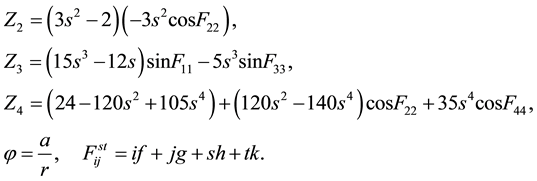 (4)
(4)
And








When deriving the above equations the Sun is assumed moving in a circular orbit so that its mean longitude is

3. Short-Period Perturbations
Since







where



Then

The elements of the transformation are obtained from









Performing the operations described in Equations (6) with the secular and periodic terms retained up to the third and second order respectively, we arrive, after some lengthy manipulations, at the following results. All variables are understood to be single primed but the primes will be dropped out for the sake of simplicity of writing.



At the subsequent orders (order 2 and 3) we will be concerned only with terms arising from the radiation pressure and those due to the coupling between oblateness and radiation pressure effects. We thus separate


where the suffixes




where:


Regarding (6.3) we find that the manipulations at order 3 require evaluating

where:
Evaluating these brackets and performing the averaging process in Equation (6.5) we obtain, after lengthy calculations
(15.1)



So that
(16)
where the





For the elements of the transformations, substituting Equations (10.2) and (12.2) into Equation (8) yields
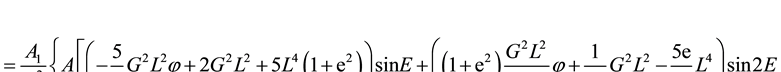









where:
where we note that
Substitution of Equations (18) and (19) into (7) yields the transformation and inverse.
4. Perturbations of Long Period
After the short-period terms have been eliminated the problem is now reduced to the system of canonical equations with Hamitonian 
We now proceed to eliminate the long-period terms, i.e. those periodic in .
The transformation follows the procedure outlined in Equations (6)-(8) but with the averages and integrations, performed over . The basic identities are now


Performing the processes outlined in Equations (16.1),…, (16.6) and (20) to find


4.1. Zero, First and Second Orders
Remembering that at orders 2 and 3, we are concerned only with the terms including radiation pressure effects we have




where:
And
4.2. Third Order
From (20.2)


where:

So, we can write


By following the above scheme, the expressions for


4.3. There Order
4.3.1. Expressions for

From (16), (26) and (27)

Then

Where:
Clearly, Equation (28.2) holds as long as
4.3.2. Expressions for


Equation (26) can be decomposed such that

Regarding





where
And the primes on the summation signs en Equation (33) indicate that the terms

For




where
And
Equation (35) holds true as long as
Finally, for




where:
And
Again, Equation (37) holds true as long as the above conditions hold. Collecting we find that


4.3.3. Expressions for



where
And
For




Finally, for




where:
4.3.4. Expressions for

As

So that
where:
The elements of transformation are easily obtained using Equations (7), (8) with


5. Effects of the Earth’s Shadow
In the proceeding developments, effects of entry into, or exit from, the Earth’s shadow are not taken into considerations.
To account for the shadow effects, we note that:
1) The integration processes to find the generators are not (directly) affected since they are more quadrates without integration limits.
2) What is affected and, indirectly, affects derivation of the generator is averaging process over the mean anomaly, performed to obtain the transformed Hamiltonian. To account for the shadow, let the time of exit from the shadow be




6. Secular Perturbations and Computation of Position and Velocity
After performing the long period transformation, the equation of motions are now reduced to
where

where the constants are be determined from the initial conditions.
Let


1) From the elements of the inverse transformations we compute
2) Having determined



7. Conclusion
Equation (32) reveals that, contrary to previous concept e.g. Kampos (1968) [8] , the direct solar radiation pressure produces secular effects at order 3 as long as the satellite is apart from the earth’s shadow. This emphasizes the importance of taking the effects of the solar radiation pressure into account in high order artificial satellite theories, particularly for those with high area-to-mass ratio flying at high altitudes.
Again, Equation (41) is valid away from the resonant conditions, i.e. as long as



Acknowledgements
The author is grateful to the anonymous referee for helpful comments.
Cite this paper
Hadia HassanSelim, (2014) Analytical Third Order Solution for Coupling Effects of Earth Oblateness and Direct Solar Radiation Pressure on the Motion of Artificial Satellites. International Journal of Astronomy and Astrophysics,04,530-543. doi: 10.4236/ijaa.2014.43049
References
- 1. Kamel, A.A. (1971) Lie Transformation and the Hamiltonian of Non-Hamiltonian Systems. Celestial Mechanics, 4, 397-405. http://link.springer.com/article/10.1007%2FBF01231400
- 2. Giacaglia, G.E.O. (1972) Perturbation Methods in Non-Linear Systems. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-6400-2
- 3. Musen, P.J. (1960) The Influence of the Solar Radiation Pressure on the Motion of an Artificial Satellite. Journal of Geophysical Research, 6, 1391-1396.
http://onlinelibrary.wiley.com/doi/10.1029/JZ065i005p01391/abstract - 4. Kozai, Y. (1961) Effects of Solar Radiation Pressure on the Motion of an Artificial Satellite. Smithsonian Astrophys. Obs. Spec. Re, 56, 25-33.
- 5. Brouwer, D. (1962) Dynamics of Satellites (Roy, M., Ed.). Springer, Berlin.
- 6. Hori, G. (1966) Theory of General Perturbation with Unspecified Canonical Variable. Publications of the Astronomical Society of Japan, 18, 287. http://adsabs.harvard.edu/abs/1966PASJ...18..287H
- 7. De Moraes, R.V. (1981) Combined Solar Radiation Pressure and Drag Effects on the Orbits of Artificial Satellites. Celestial Mechanics, 25, 281-292. http://link.springer.com/article/10.1007%2FBF01228965
- 8. Kampos, B. (1986) Nasa CR1008-Guidance, Flight Mech. and Trajectory Optimization, Vol. IX.
- 9. Sehnal, L. (1970) In Dynamics Satellites (Morando, Ed.). Springer, Berlin.
- 10. Sehnal, L. (1975) In Satellite Dynamics (Giacalia, Ed.). Springer, Berlin.
- 11. McInnes, C.R. and Browen, J.C. (1990) The Dynamics of Solar Sails with a Non-Point Source of Radiation Pressure Celestial Mechanics and Dynamical Astronomy, 49, 249-264.
http://link.springer.com/article/10.1007%2FBF00049416 - 12. Feraz-Mello, S. (1972) Analytical Study of the Earth’s Shadowing Effects on Satellite Orbits. Celestial Mechanics, 5, 80-101. http://link.springer.com/article/10.1007%2FBF01227825
- 13. Anselono, L., Bertotti, B., Farinella, P., Milani, A. and Mobili, A.M. (1983) Orbital Perturbation Due to Radiation Pressure for a Spacecraft of Complex Shape. Celestial Mechanics, 29, 27-43.
http://link.springer.com/article/10.1007%2FBF01358596 - 14. Geyling, F.T. and Westerman, H.R. (1971) Introduction to Orbital Mech. Addison Wesley.
- 15. Lála, P. (1972) Combined Gravitational and Solar Radiation Pressure Effects on The Semimajor Axis of the Earth’s Satellite. Bulletin of the Astronomical Institute of Czechoslovakia, 23, 342.
http://adsabs.harvard.edu/abs/1972BAICz..23..342L - 16. McMahon, J.W. (2011) ProQuest Dissertations and Theses. Ph.D. Thesis, University of Colorado at Boulder, Boulder.
- 17. Lücking, C., Colombo, C. and McInnes, C.R. (2012) A Passive Satellite Deorbiting Strategy for Medium Earth Orbit Using Solar Radiation Pressure and the J2 Effect. Acta Astronautica, 77, 197-206. http://adsabs.harvard.edu/abs/2012AcAau..77..197L http://dx.doi.org/10.1016/j.actaastro.2012.03.026
- 18. Cook, D.G. (2001) Master’s Thesis, AD-A390187; AFIT/GSP/ENY/01M-01 Graduate School of Engineering and Management.
- 19. Selim, H.H. (1991) The Effect of Solar Radiation Pressure on The Motion of Artificial Satellite. M.Sc. Thesis, Cairo University, Giza.
- 20. Deprit, A. (1969) Canonical Transformations Depending on a Small Parameter. Celestial Mechanics, 1, 12-30. http://adsabs.harvard.edu/abs/1969CeMec...1...12D