International Journal of Astronomy and Astrophysics
Vol.4 No.1(2014), Article ID:43577,10 pages DOI:10.4236/ijaa.2014.41013
The Luminosity Function of Galaxies as Modeled by a Left Truncated Beta Distribution
L. Zaninetti
Dipartimento di Fisica, via P.Giuria 1, Turin, Italy
Email: zaninetti@ph.unito.it
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 6 December 2013; revised 5 January 2014; accepted 13 January 2014
ABSTRACT
A first new luminosity function of galaxies can be built starting from a left truncated beta probability density function, which is characterized by four parameters. In the astrophysical conversion, the number of parameters increases by one, due to the addition of the overall density of galaxies. A second new galaxy luminosity function is built starting from a left truncated beta probability for the mass of galaxies once a simple nonlinear relationship between mass and luminosity is assumed; in this case the number of parameters is six because the overall density of galaxies and a parameter that regulates mass and luminosity are added. The two new galaxy luminosity functions with finite boundaries were tested on the Sloan Digital Sky Survey (SDSS) in five different bands; the results produce a “better fit” than the Schechter luminosity function in two of the five bands considered. A modified Schechter luminosity function with four parameters has been also analyzed.
Keywords:Galaxies: Fundamental Parameters; Galaxies: Statistics; Galaxies: Luminosity Function

1. Introduction
The standard luminosity function for galaxies (LF) in the last forty years has been represented by the Schechter LF
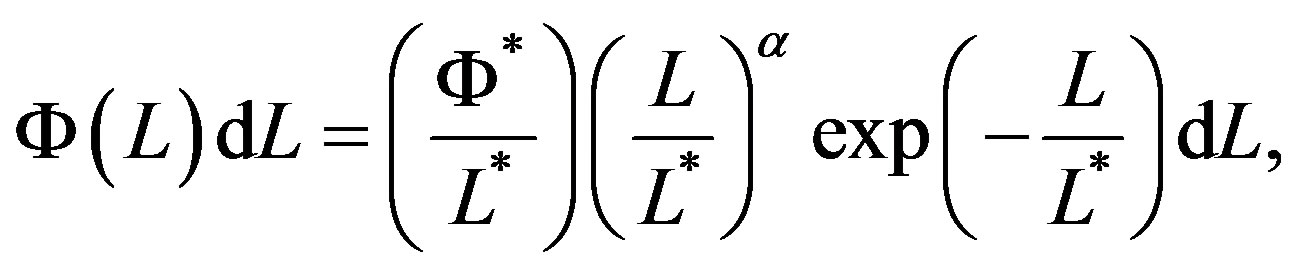 (1)
(1)
where 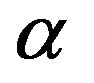 sets the slope for low values of
sets the slope for low values of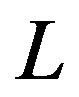 ,
, 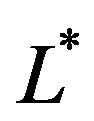 is the characteristic luminosity and
is the characteristic luminosity and  is the normalization, see [1] . This LF is defined in the in the interval
is the normalization, see [1] . This LF is defined in the in the interval 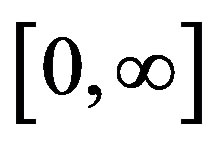 and has replaced other LFs presented by [2] -[5] .
and has replaced other LFs presented by [2] -[5] .
The goodness of the fit can be evaluated by the merit function 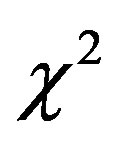
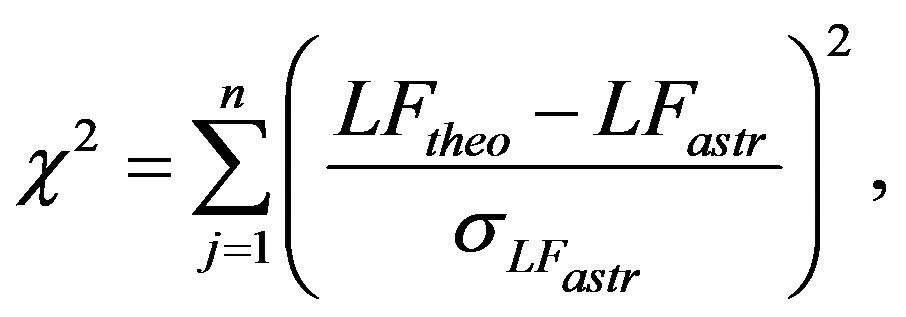 (2)
(2)
where n is number of data and the two indexes 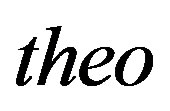 and
and 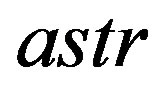 stand for theoretical and astronomical, LF respectively. The value of
stand for theoretical and astronomical, LF respectively. The value of 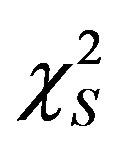 which characterizes the Schechter LF for a given astronomical catalog, i.e. the Sloan Digital Sky Survey (SDSS) in five different bands, represents a standard value to improve. Many new LFs has been derived in the last years and we report some examples. A two-component Schechter-like function is, see [6]
which characterizes the Schechter LF for a given astronomical catalog, i.e. the Sloan Digital Sky Survey (SDSS) in five different bands, represents a standard value to improve. Many new LFs has been derived in the last years and we report some examples. A two-component Schechter-like function is, see [6]
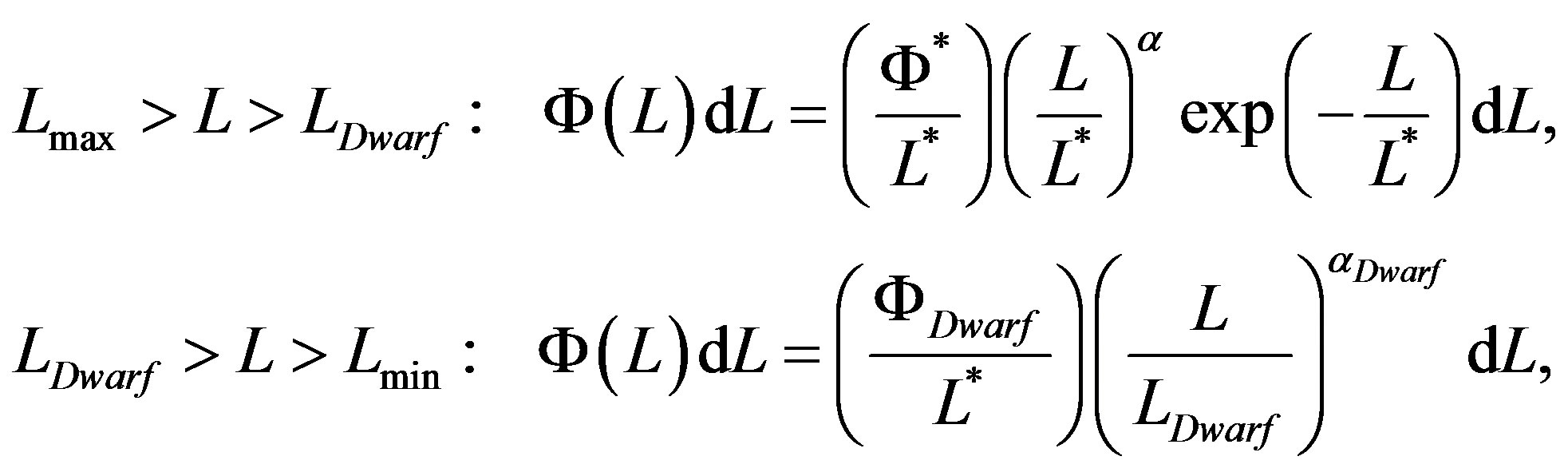
 (3)
(3)
where
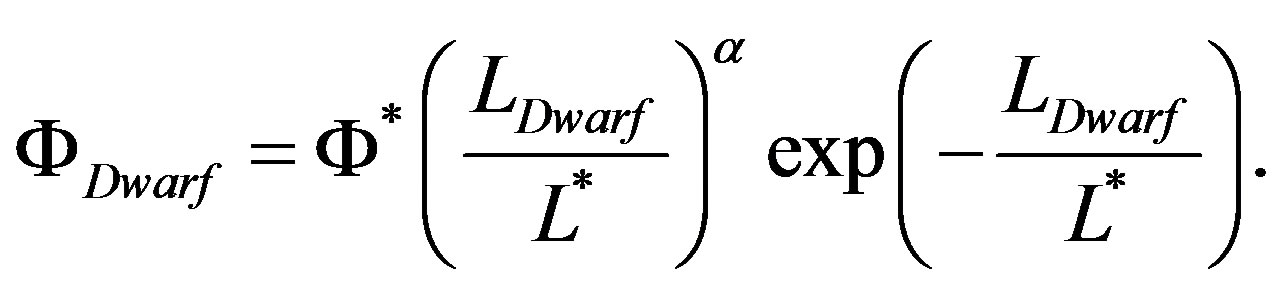
This two-component LF defined between the maximum luminosity, 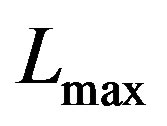 , and the minimum luminosity,
, and the minimum luminosity, 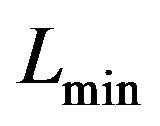 , has five parameters because two additional parameters have been added:
, has five parameters because two additional parameters have been added: 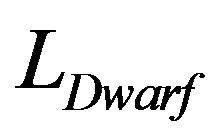 which represents the magnitude where dwarfs first dominate over giants and
which represents the magnitude where dwarfs first dominate over giants and 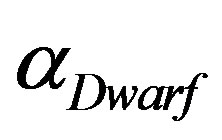 which regulates the faint slope parameter for the dwarf population.
which regulates the faint slope parameter for the dwarf population.
In order to fit the case of extremely low luminosity galaxies a double Schechter LF with five parameters, see [7] , was introduced:
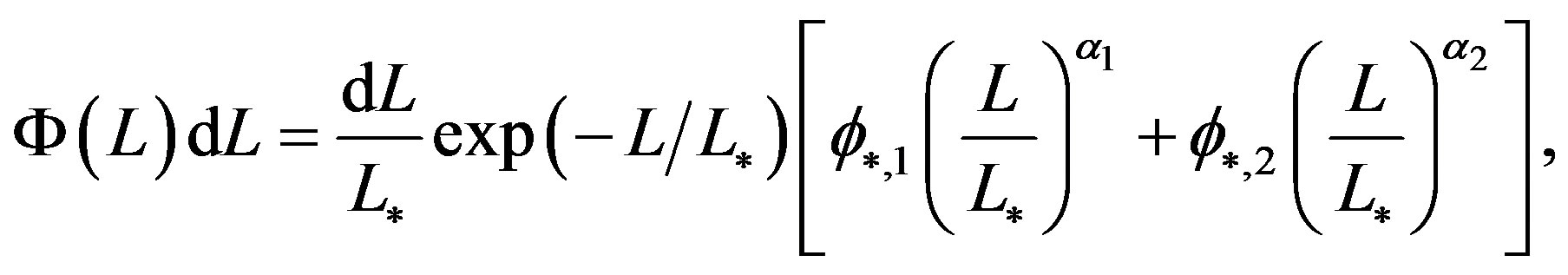 (4)
(4)
where the parameters  and
and  which characterize the Schechter LF have been doubled in
which characterize the Schechter LF have been doubled in 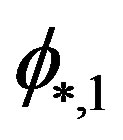 and
and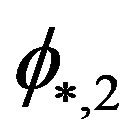 . The strong dependence of LF on different environments such as voids, superclusters and supercluster cores was analyzed by [8] with
. The strong dependence of LF on different environments such as voids, superclusters and supercluster cores was analyzed by [8] with
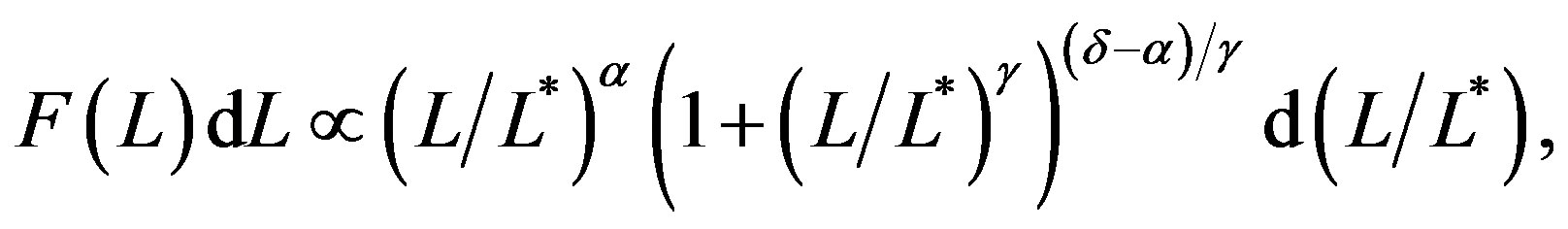 (5)
(5)
where 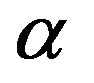 is the exponent at low luminosities
is the exponent at low luminosities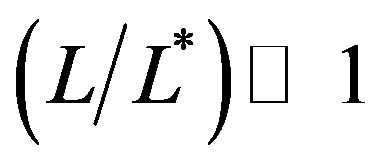 ,
,  is the exponent at high luminosities
is the exponent at high luminosities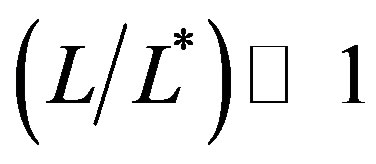 ,
, 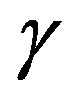 is a parameter of transition between the two power laws, and
is a parameter of transition between the two power laws, and 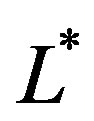 is the characteristic luminosity. Another LF starts from the probability density function (PDF) that models area and volumes of the Voronoi Diagrams and introduces the mass-luminosity relationship, see [9] ; in the SDSS case
is the characteristic luminosity. Another LF starts from the probability density function (PDF) that models area and volumes of the Voronoi Diagrams and introduces the mass-luminosity relationship, see [9] ; in the SDSS case . A last example is represented by three new LFs deduced in the framework of generalized gamma PDF, see [10] ; in the SDSS case
. A last example is represented by three new LFs deduced in the framework of generalized gamma PDF, see [10] ; in the SDSS case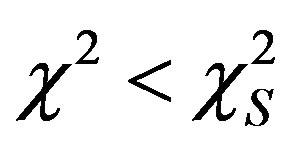 . All the previous LFs cover the range
. All the previous LFs cover the range 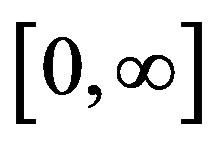 and therefore the analysis of finite upper and lower boundaries can be a subject of investigation. Another interesting observational fact is that at low values of luminosity (high absolute magnitude) the observed LF has an approximate constant value. The left truncated beta with scale PDF recently derived , see Equation (34) in [11] , satisfies the two issues previously raised. In order to explore the connection between LF and evolution of galaxies see [12] -[18] .
and therefore the analysis of finite upper and lower boundaries can be a subject of investigation. Another interesting observational fact is that at low values of luminosity (high absolute magnitude) the observed LF has an approximate constant value. The left truncated beta with scale PDF recently derived , see Equation (34) in [11] , satisfies the two issues previously raised. In order to explore the connection between LF and evolution of galaxies see [12] -[18] .
Here we analyze in Section 2 a left truncated beta LF for galaxies and in Section 3 a left truncated beta for mass which transforms itself in a LF for galaxies through a nonlinear mass-luminosity relationship. Section 4 reports a recent LF for galaxies which has a finite boundary at the bright end.
2. A Linear Mass-Luminosity Relationship
A new PDF, the left truncated beta with scale has been recently derived, see formula (34) in [11] . Once the random variable X is substituted with the luminosity L we obtain a new LF for galaxies, 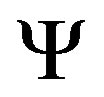 ,
,
 (6)
(6)
where  is a normalization factor which defines the overall density of galaxies, a number per cubic Mpc. The constant
is a normalization factor which defines the overall density of galaxies, a number per cubic Mpc. The constant 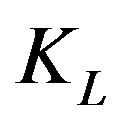 is
is
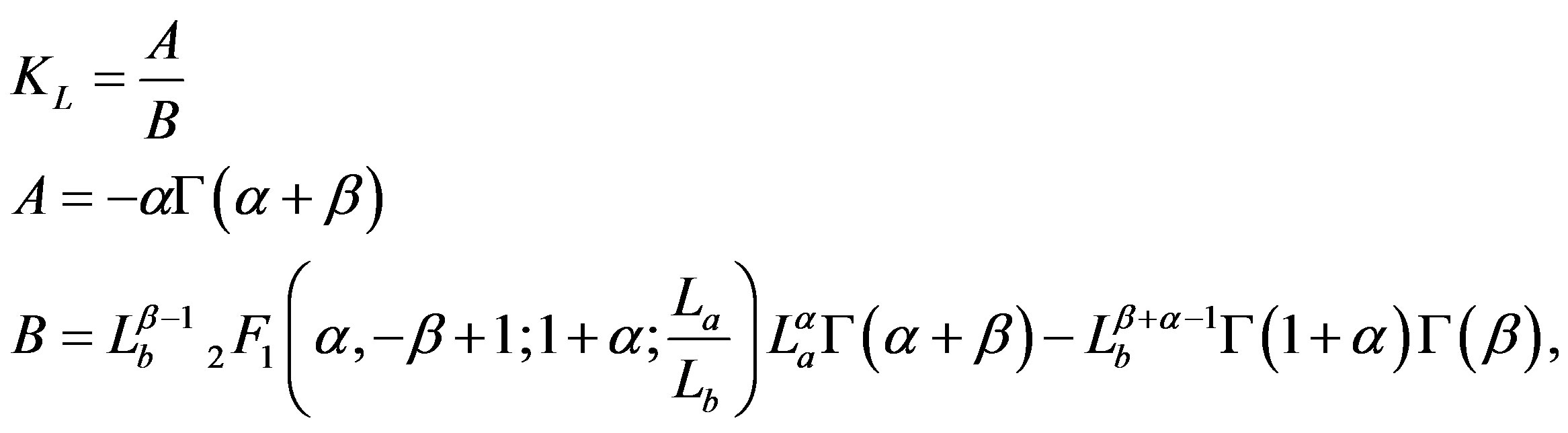 (7)
(7)
and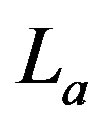 ,
, 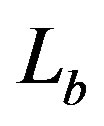 are the lower, upper values in luminosity and
are the lower, upper values in luminosity and 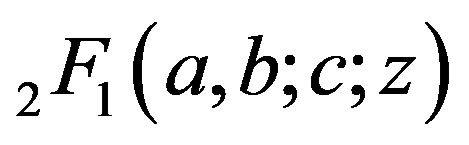 is the regularized hypergeometric function [19] -[23] . The hypergeometric function with real arguments is implemented in the FORTRAN subroutine MHYGFX in [24] . The averaged luminosity,
is the regularized hypergeometric function [19] -[23] . The hypergeometric function with real arguments is implemented in the FORTRAN subroutine MHYGFX in [24] . The averaged luminosity, 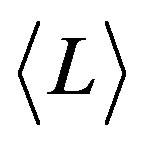 , is:
, is:
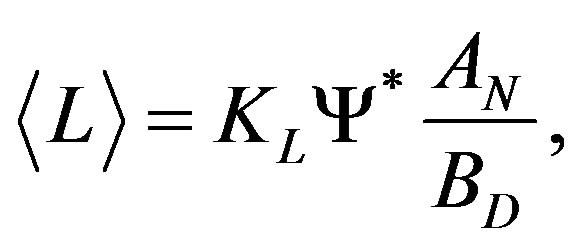 (8)
(8)
where
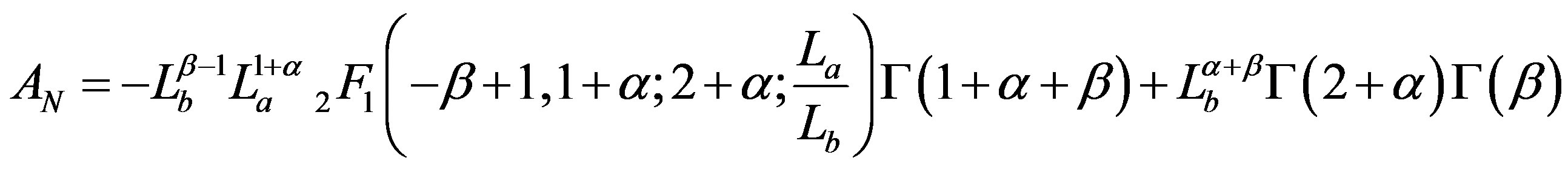
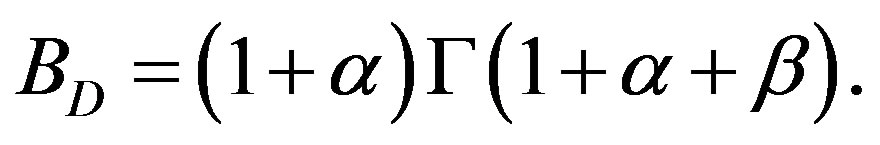
The relationships connecting the absolute magnitude M, 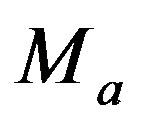 and
and 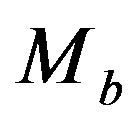 of a galaxy to respective luminosities are:
of a galaxy to respective luminosities are:
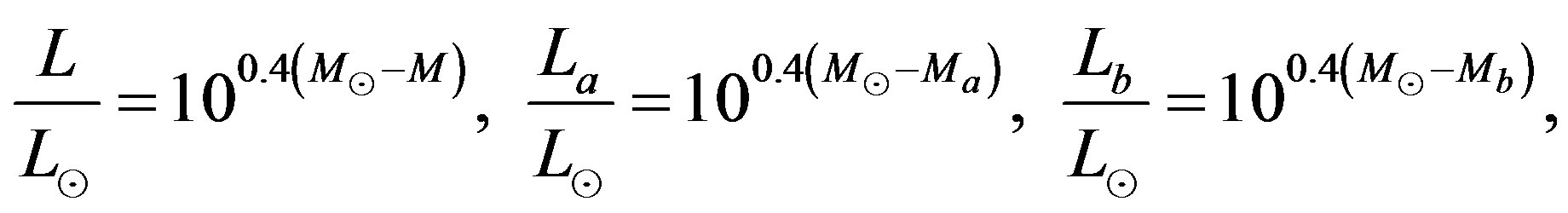 (9)
(9)
where 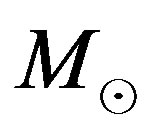 is the absolute magnitude of the sun in the considered band. The LF in magnitude is
is the absolute magnitude of the sun in the considered band. The LF in magnitude is
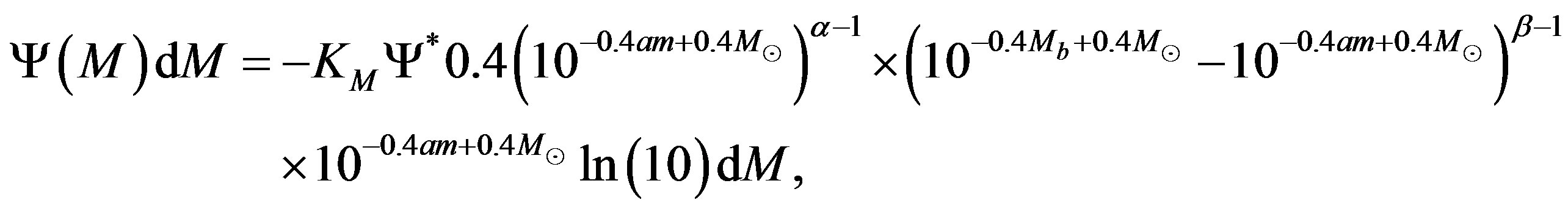 (10)
(10)
where
 (11)
(11)
This data-oriented LF contains the five parameters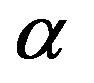 ,
,  ,
, 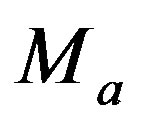 ,
, 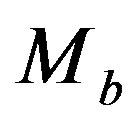 ,
,  which can be derived from the operation of fitting the observational data and
which can be derived from the operation of fitting the observational data and 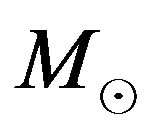 which characterize the considered band. The number of variables can be reduced to three once
which characterize the considered band. The number of variables can be reduced to three once 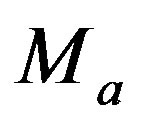 and
and 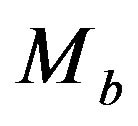 are identified with the maximum and the minimum absolute magnitude of the considered sample. The numerical analysis points toward value of
are identified with the maximum and the minimum absolute magnitude of the considered sample. The numerical analysis points toward value of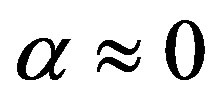 . Once as an example we fix
. Once as an example we fix  we have only to find the two parameters
we have only to find the two parameters 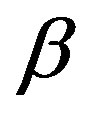 and
and . The test on the new LF were performed on the data of the Sloan Digital Sky Survey (SDSS) which has five bands u*, g*, r*, i*, and z*, see [25] . Table 1 reports the bolometric magnitude, the numerical values obtained for the new LF , the number, N, of the astronomical sample , the
. The test on the new LF were performed on the data of the Sloan Digital Sky Survey (SDSS) which has five bands u*, g*, r*, i*, and z*, see [25] . Table 1 reports the bolometric magnitude, the numerical values obtained for the new LF , the number, N, of the astronomical sample , the 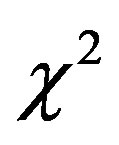 of the new LF, the reduced
of the new LF, the reduced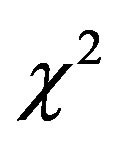 ,
, 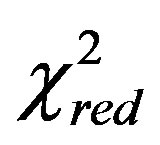 , of the new LF, the
, of the new LF, the 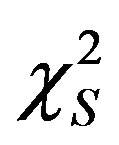 of the Schechter LF, the reduced
of the Schechter LF, the reduced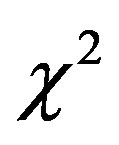 ,
,  , of Schechter LF and the
, of Schechter LF and the 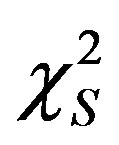 computed as in [25] for the five bands here considered.
computed as in [25] for the five bands here considered.
3. A Non Linear Mass-Luminosity Relationship
We assume that the mass of the galaxies, 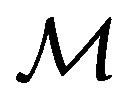 , is distributed with a left truncated PDF as represented by formula (34) in [11] . The distribution for the mass is
, is distributed with a left truncated PDF as represented by formula (34) in [11] . The distribution for the mass is 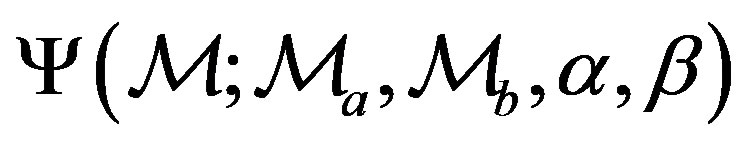 where
where 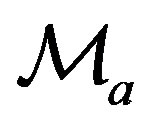 is the lower mass and
is the lower mass and 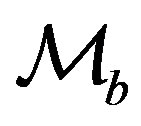 is the upper mass. The mass is supposed to scale as
is the upper mass. The mass is supposed to scale as
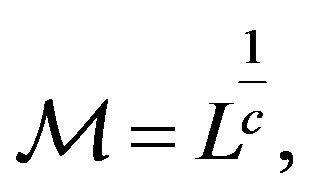 (12)
(12)
where c is the parameter that regulates the non linear mass-luminosity relationship. The differential of the mass is
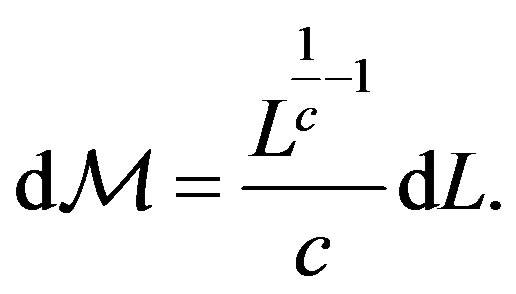 (13)
(13)
As a consequence the LF representing the non linear mass-luminosity relationship is
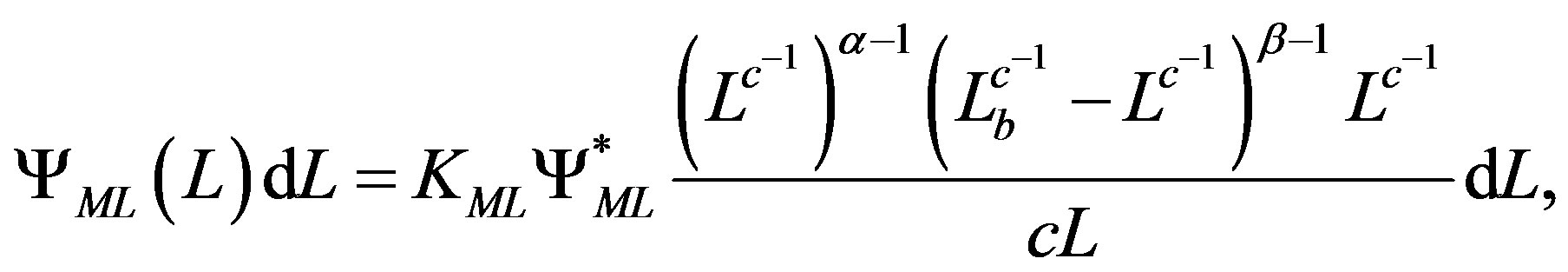 (14)
(14)
where
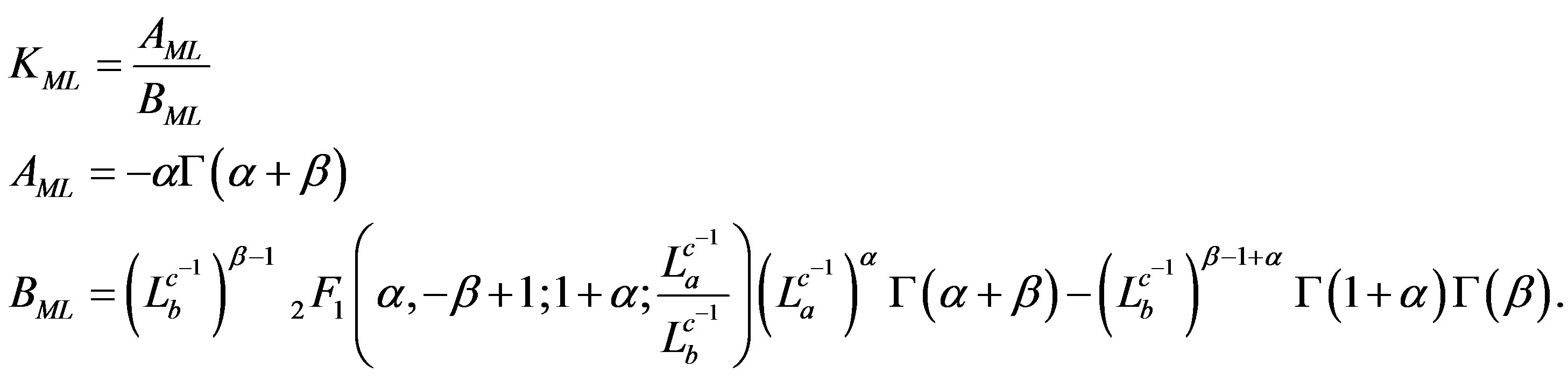 (15)
(15)
The averaged luminosity, 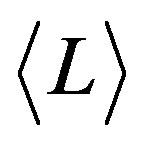 , for the non linear mass-luminosity relationship is:
, for the non linear mass-luminosity relationship is:
Table 1. Parameters of fits in SDSS Galaxies of LF as represented by formula (10) in which the number of free parameters is 5.
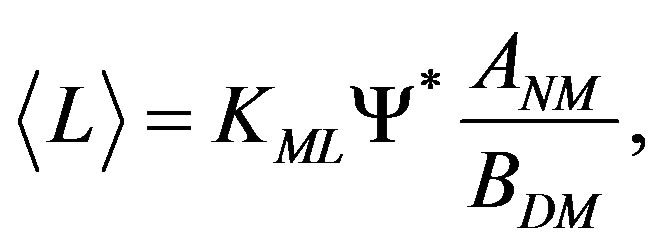 (16)
(16)
where
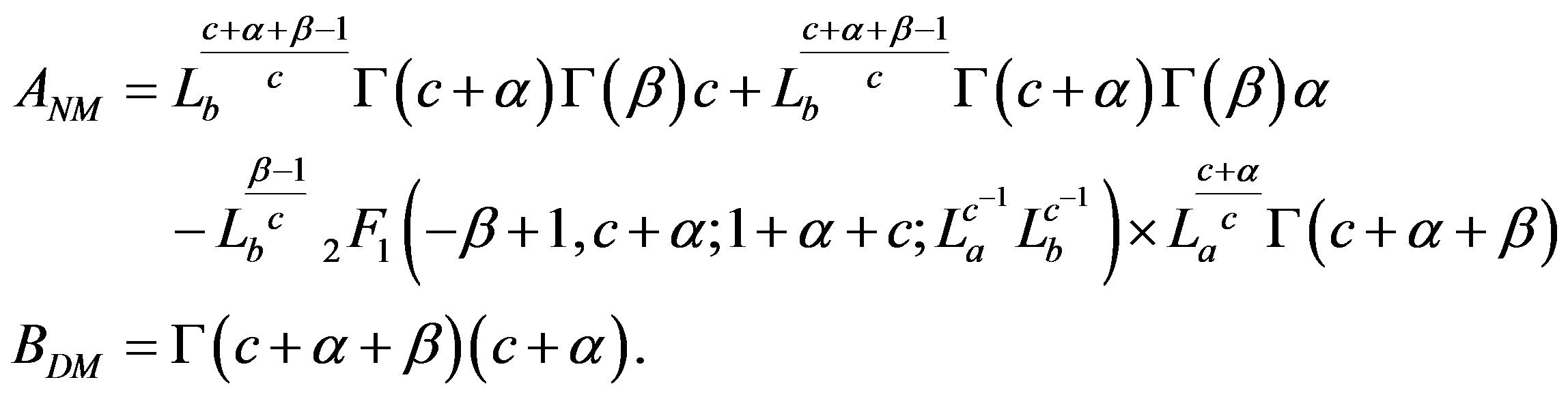
The LF in magnitude for the non linear mass-luminosity relationship is
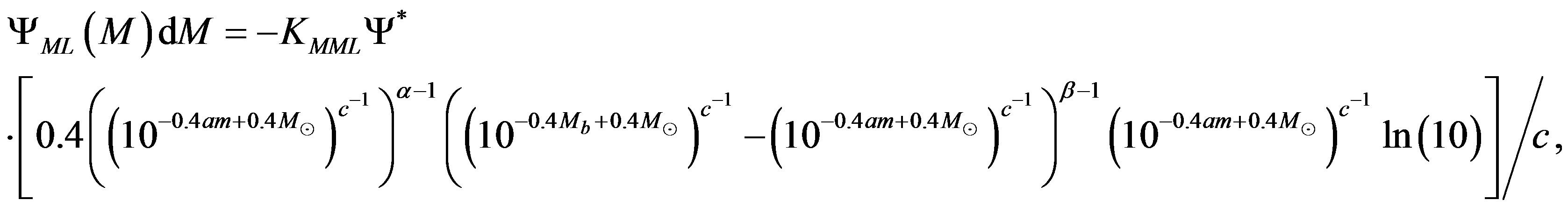 (17)
(17)
where
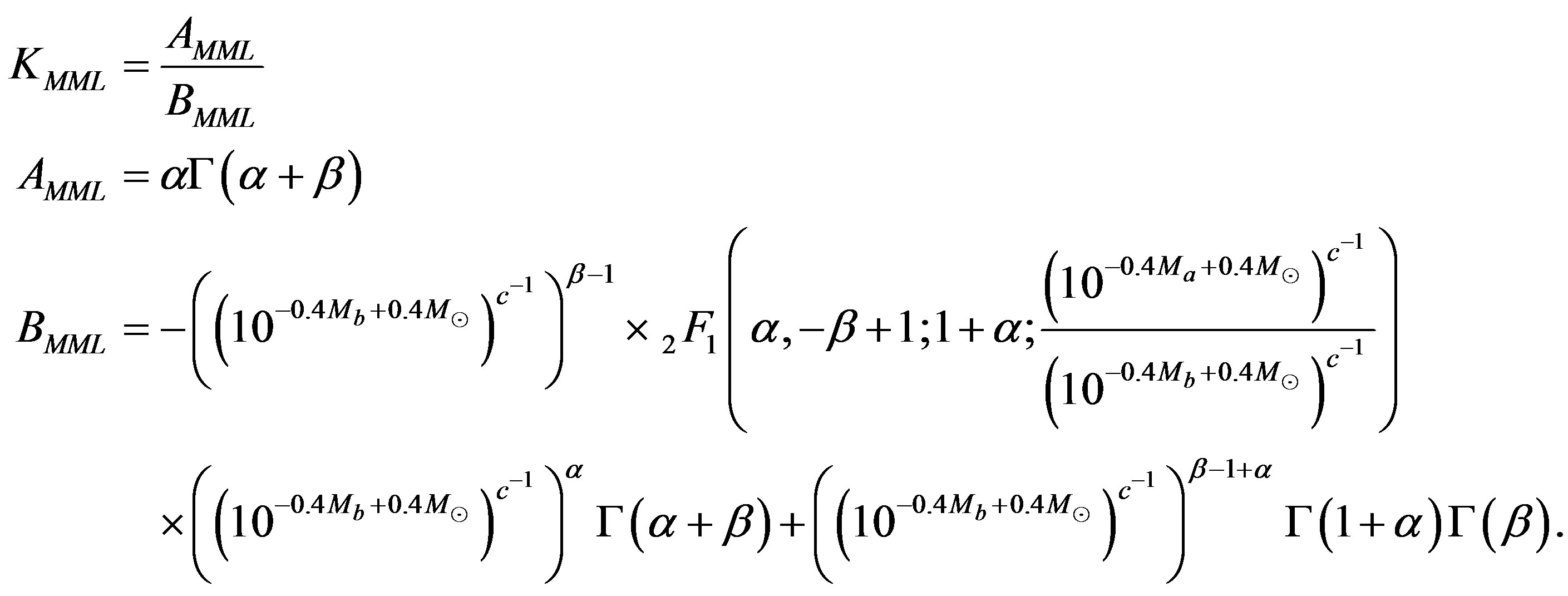 (18)
(18)
Table 2 reports the numerical values obtained for the new nonlinear LF as represented by Equation (17), the  of the new LF and the
of the new LF and the 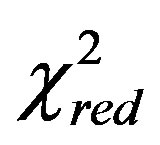 of the new LF in the five bands here considered.
of the new LF in the five bands here considered.
The Schechter LF, the new LF represented by formula (17) and the data of SDSS are reported in Figure 1-5, where bands u*, g*, r*, i*, and z* are considered.
A discussion on the distribution of M/L in all photometric bands can be found in [26] .
4. A Modified Schechter LF
An example of modified Schechter LF is represented by the following function
Table 2. Parameters of fits in SDSS Galaxies of LF as represented by our non linear LF (17) formula (10) in which the number of free parameters is 6.
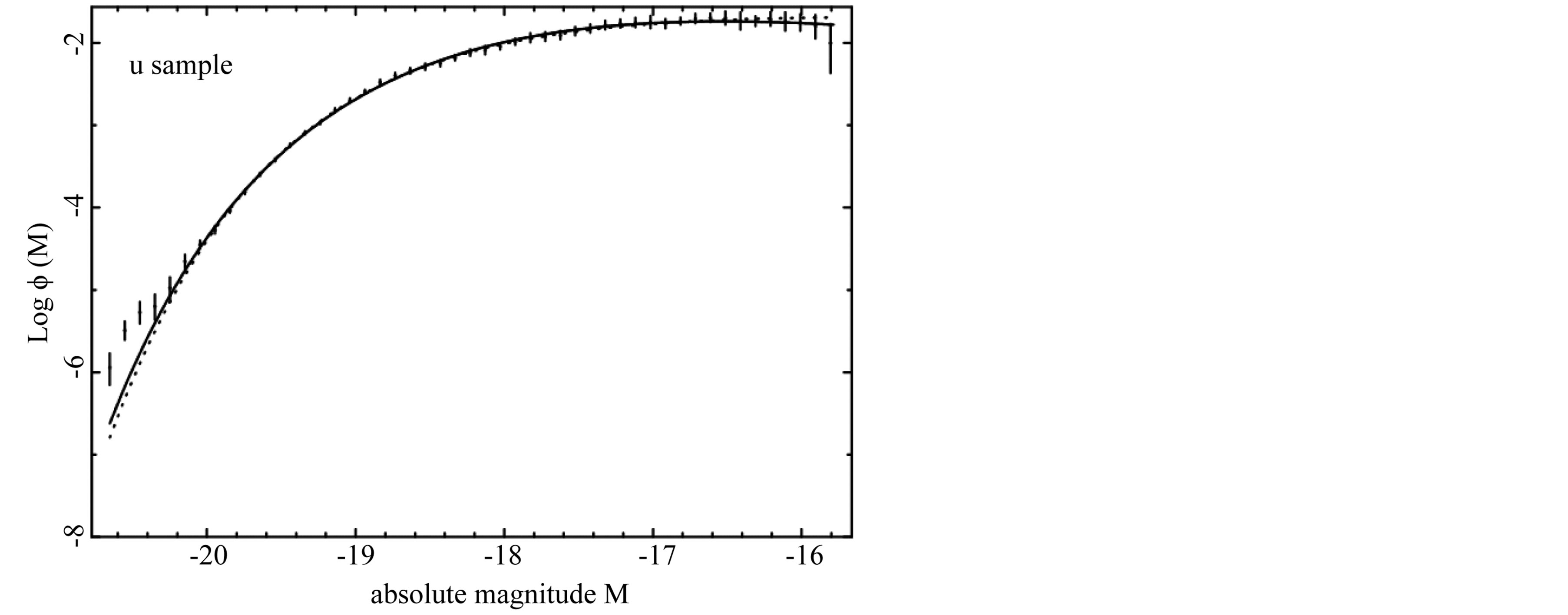
Figure 1. The LF data of SDSS (u*) are represented with error bars. The continuous line fit represents our non linear LF (17) and the dotted line represents the Schechter LF.
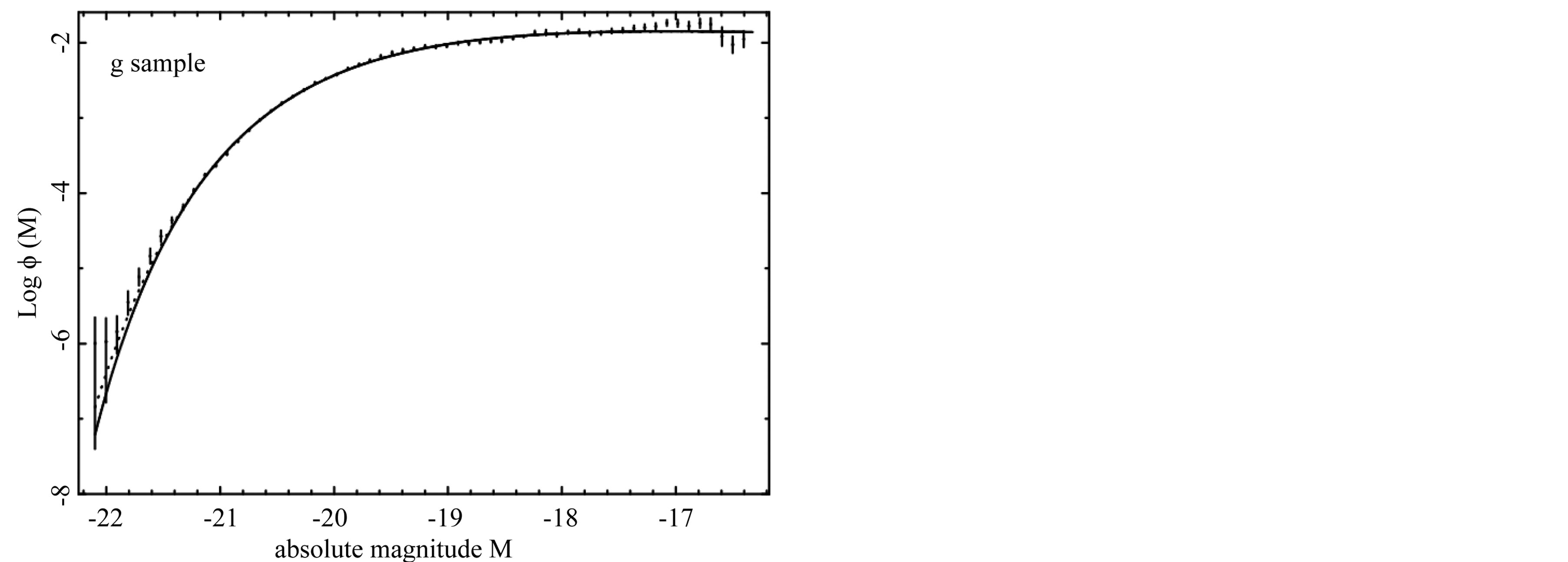
Figure 2. The luminosity function data of SDSS (g*) are represented with error bars. The continuous line fit represents our non linear LF (10) and the dotted line represents the Schechter LF.
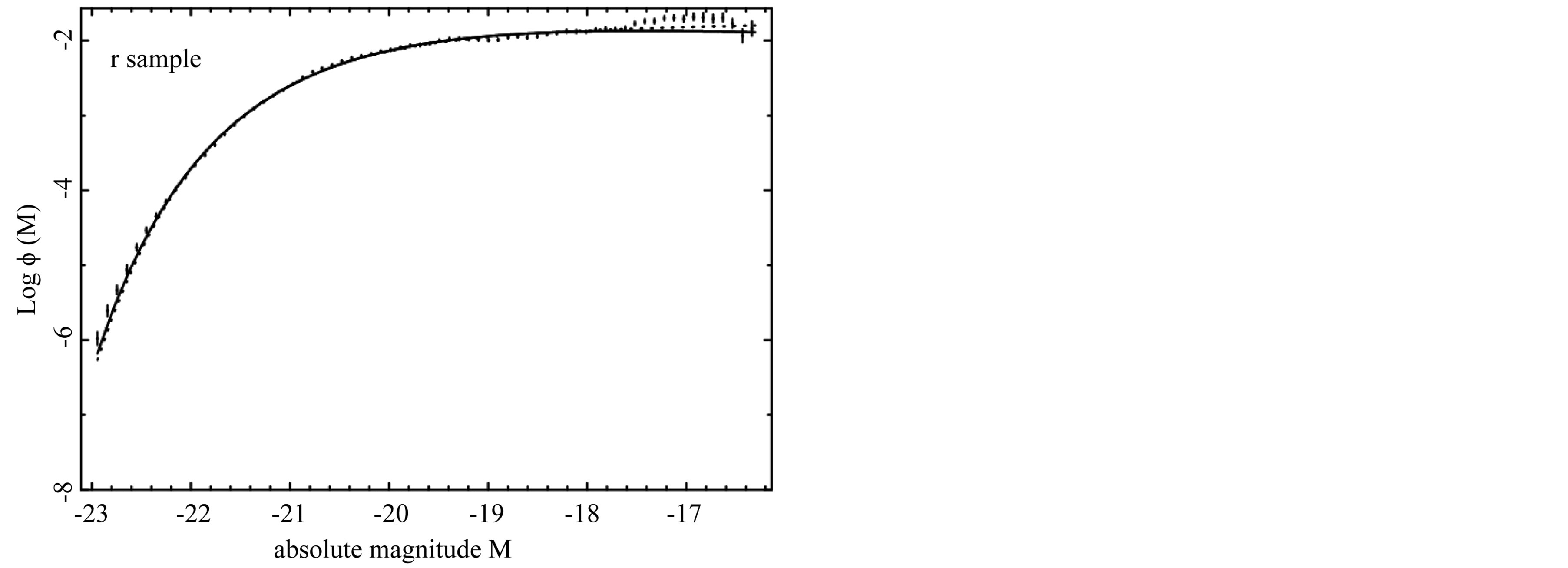
Figure 3. The luminosity function data of SDSS (r*) are represented with error bars. The continuous line fit represents our non linear LF (10) and the dotted line represents the Schechter LF.
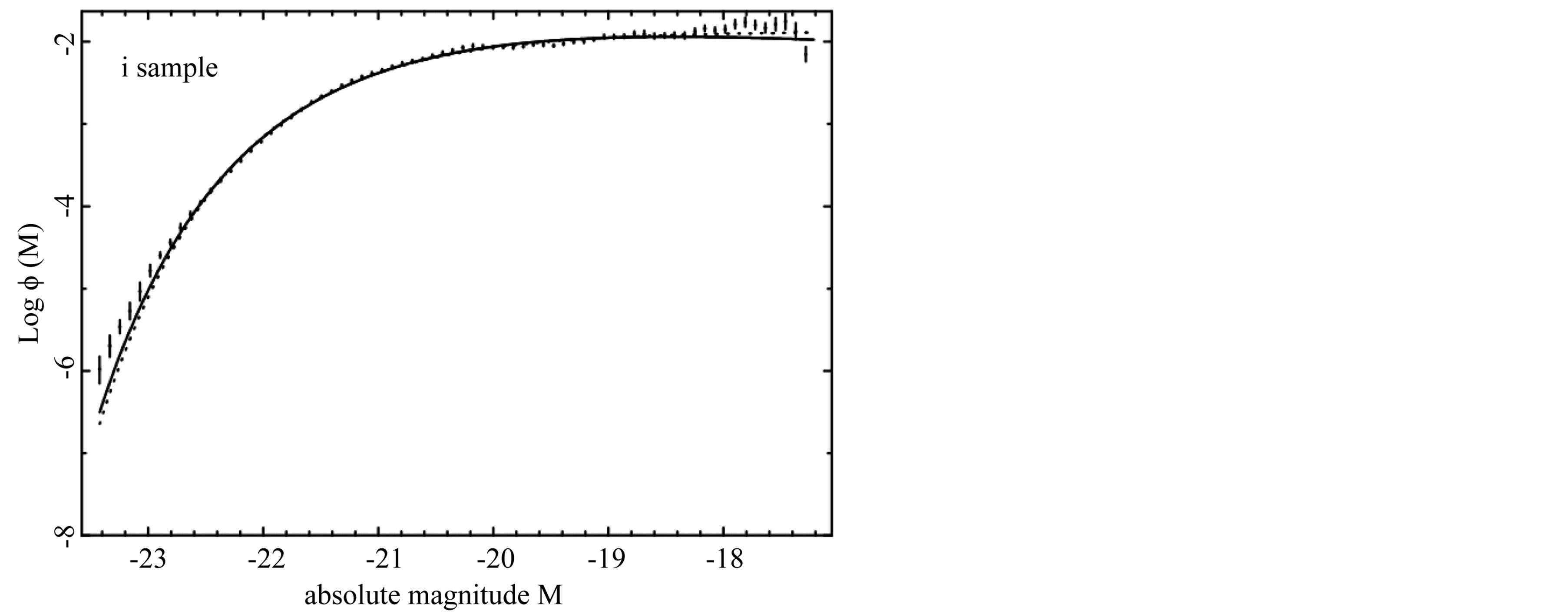
Figure 4. The luminosity function data of SDSS(i*) are represented with error bars. The continuous line fit represents our non linear LF (10) and the dotted line represents the Schechter LF.
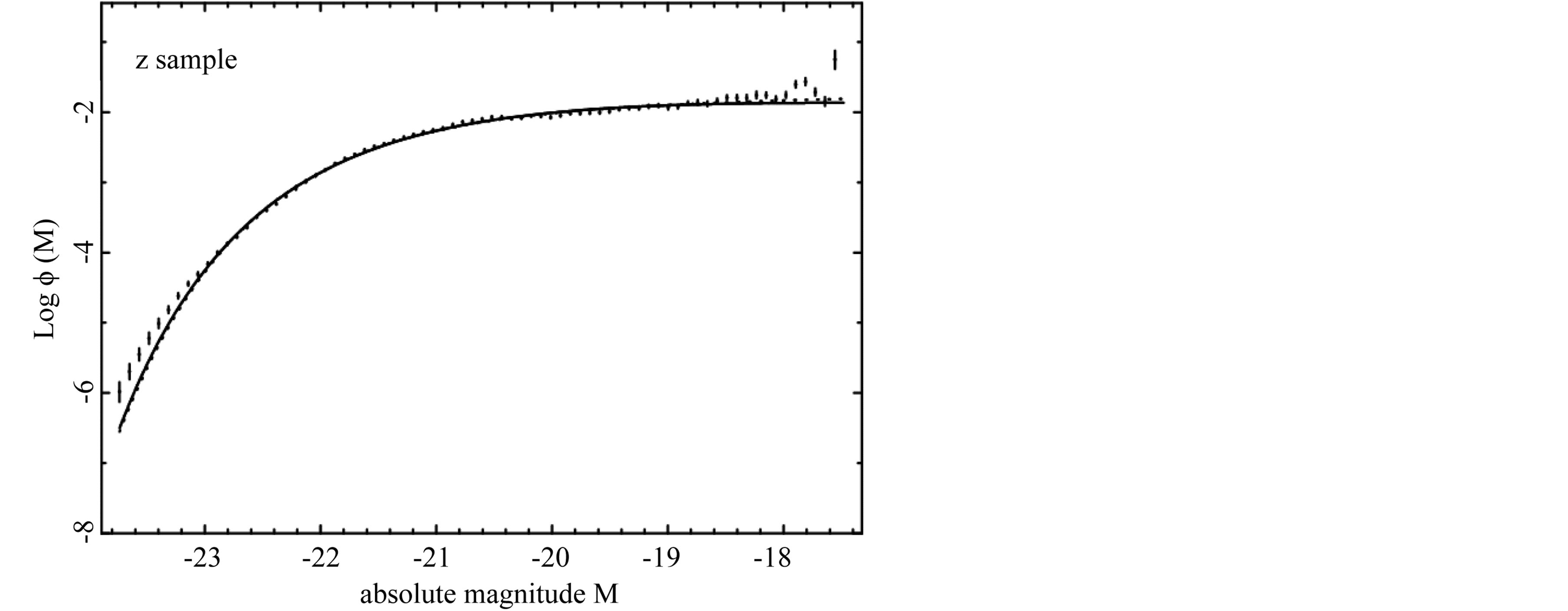
Figure 5. The luminosity function data of SDSS(z*) are represented with error bars. The continuous line fit represents our non linear LF (10) and the dotted line represents the Schechter LF.
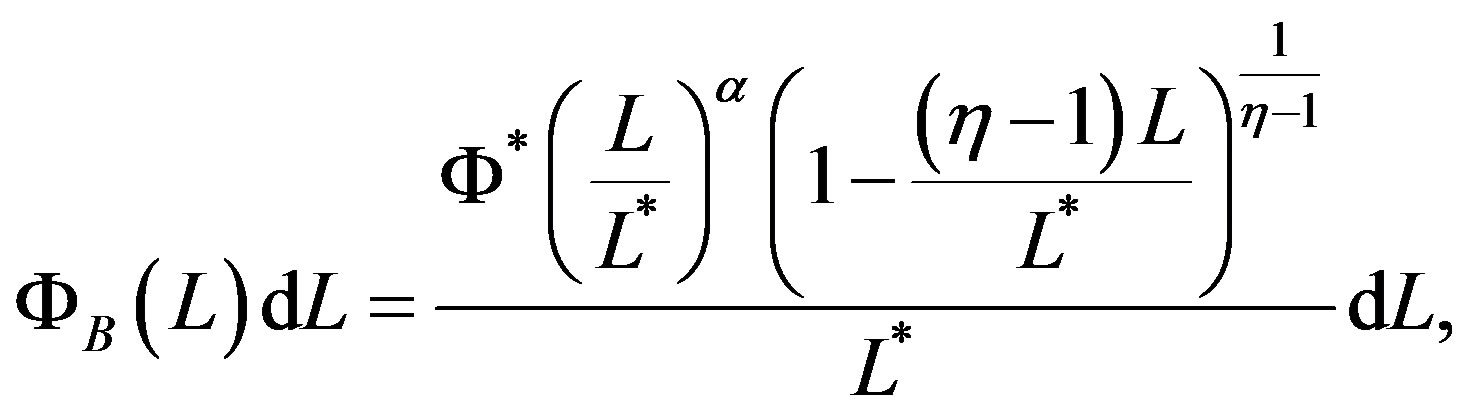 (19)
(19)
where 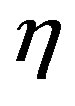 is a new parameter, see [27] . This new LF in the case of
is a new parameter, see [27] . This new LF in the case of 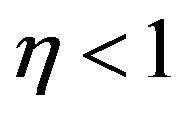 is defined in the range
is defined in the range 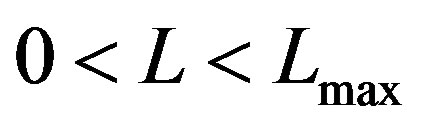
where 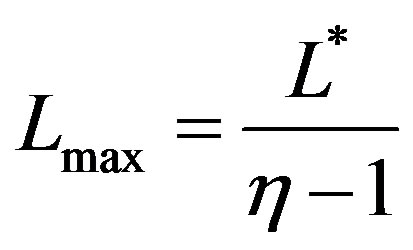 and therefore has a natural upper boundary which is not infinity. In the limit
and therefore has a natural upper boundary which is not infinity. In the limit
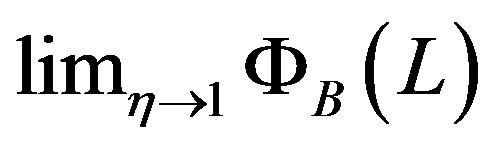 the Schechter LF is obtained. In the case of
the Schechter LF is obtained. In the case of 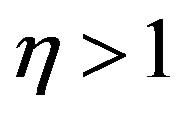 the average value is
the average value is
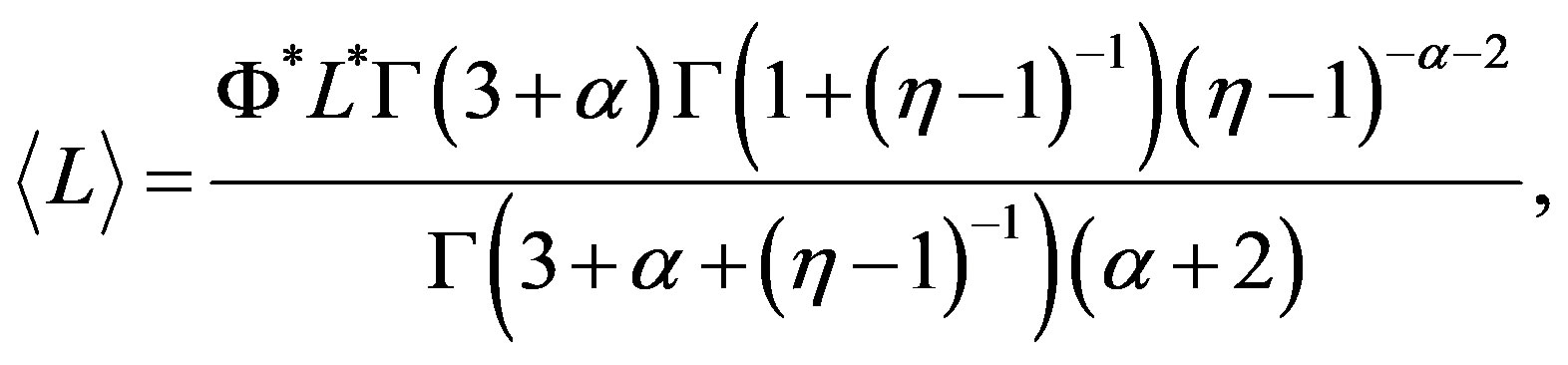 (20)
(20)
and in the case of 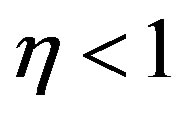 the average value is
the average value is
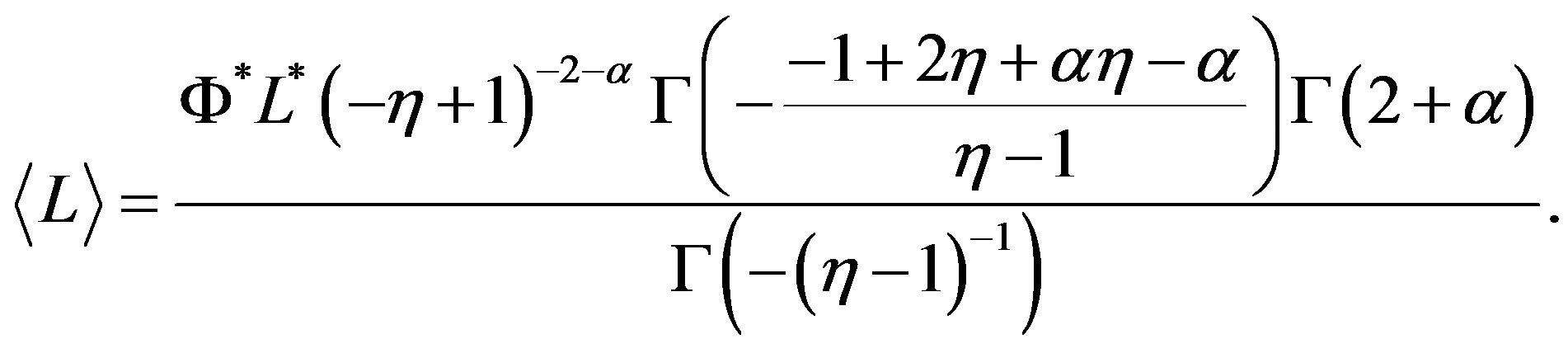 (21)
(21)
The distribution in magnitude is:
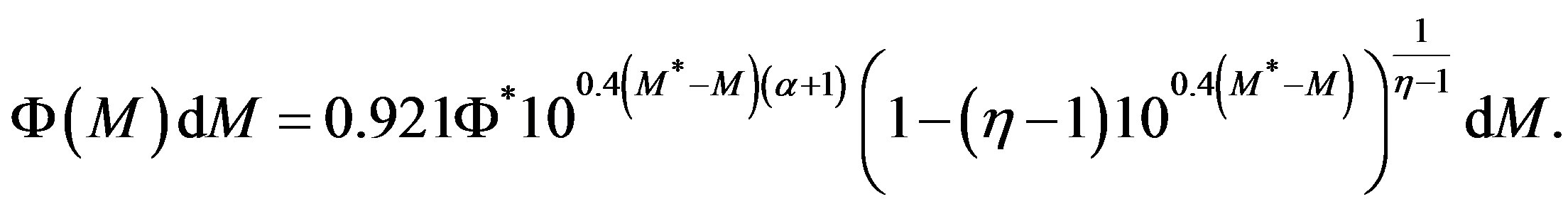 (22)
(22)
As an example the Schechter LF, the modified Schechter LF represented by formula (22) and the data of SDSS are reported in Figure 6 for the u* band and Table 3 reports the results of the fits in all the five bands of SDSS.
5. Conclusions
Motivations The observational fact that the LF for galaxies spans from a minimum to a maximum value in
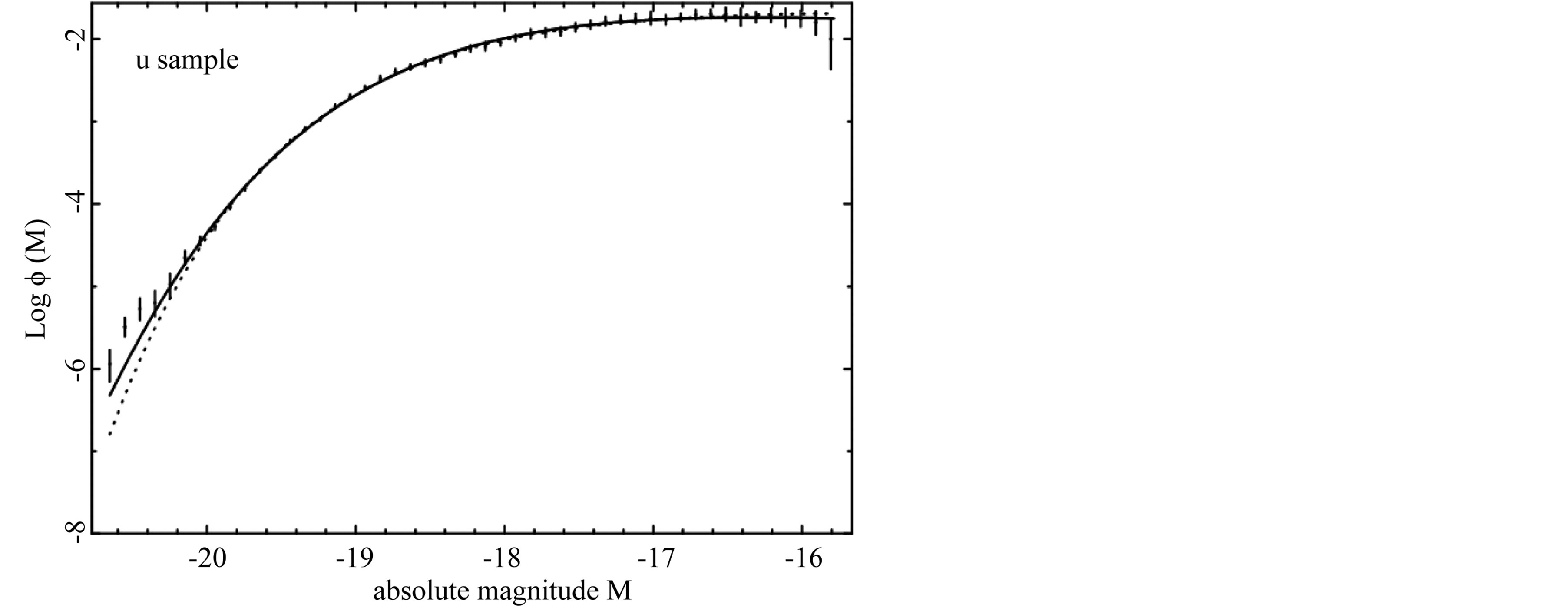
Figure 6. The luminosity function data of SDSS (u*) are represented with error bars. The continuous line fit represents the modified Schechter LF (22) and the dotted line represents the Schechter LF.
Table 3. Parameters of fits in SDSS Galaxies of the modified Schechter LF as represented by formula (22) in which the number of free parameters is 4.
absolute magnitude makes attractive the exploration of the left truncated beta LF. We derived two LFs adopting the framework of the linear M-L relationship, see Equation (10), and the framework of the non linear M-L relationship , see Equation (17).
5.1. Goodness of Fit Tests
We have computed  and
and 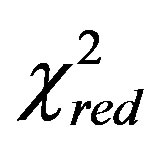 for two LFs here derived and compared the results with the Schechter LF, see Tables 1 and 2. In the linear M-L case
for two LFs here derived and compared the results with the Schechter LF, see Tables 1 and 2. In the linear M-L case 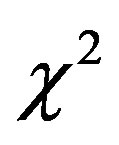 and
and  are greater of that of the Schechter LF. In the non linear M-L case
are greater of that of the Schechter LF. In the non linear M-L case 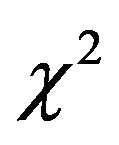 and
and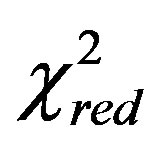 ,
, 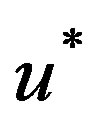 and
and 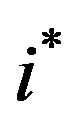 , are smaller in two bands over five in respect to those of the Schechter LF. The non linear case suggests a power law behavior with an exponent
, are smaller in two bands over five in respect to those of the Schechter LF. The non linear case suggests a power law behavior with an exponent 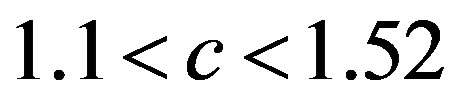 and therefore M-L relationship has an exponent greater than 1 but smaller than 4 , the theoretical value of the stars.
and therefore M-L relationship has an exponent greater than 1 but smaller than 4 , the theoretical value of the stars.
5.2. Modified Schechter LF
The modified Schechter LF when 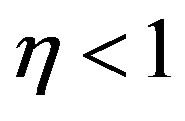 , which is the case of SDSS , has by definition an upper boundary, see 4. The
, which is the case of SDSS , has by definition an upper boundary, see 4. The 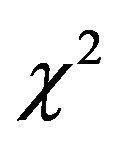 and
and 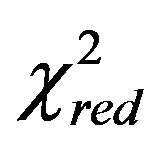 are smaller in five bands over five in respect to those of the Schechter LF. This goodness of fit is due to the flexibility introduced by the fourth parameter
are smaller in five bands over five in respect to those of the Schechter LF. This goodness of fit is due to the flexibility introduced by the fourth parameter 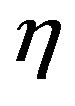 as outlined in [27] .
as outlined in [27] .
5.3. Physical Motivations
The Schechter LF is motivated by the Press-Schechter formalism on the self-similar gravitational condensation. Here conversely we limited ourself to fix a lower and an upper bound on the mass of a galaxy and we translated this requirement in a PDF for mass and then in LF. Finite-size effects on the luminosity of SDSS galaxies has also been explored in [28] .
References
- Schechter, P. (1976) An Analytic Expression for the Luminosity Function for Galaxies. Astrophysical Journal, 203, 297-306. http://dx.doi.org/10.1086/154079
- Zwicky, F. (1957) Morphological Astronomy. Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-87544-1
- Kiang, T. (1961) The Galaxian Luminosity Function. Monthly Notices of the Royal Astronomical Society, 122, 263.
- Abell, G.O. (1965) Clustering of Galaxies. Annual Review of Astronomy and Astrophysics, 3, 1-22.
- Arakelyan, M.A. and Kalloglyan, A.T. (1970) The Luminosity Function of Field Galaxies. Soviet Astronomy, 13, 953.
- Driver, S.P. and Phillipps, S (1996) Is the Luminosity Distribution of Field Galaxies Really Flat? Astrophysical Journal, 469, 529. http://dx.doi.org/10.1086/177801
- Blanton, M.R., Lupton, R.H., Schlegel, D.J., Strauss, M.A., Brinkmann, J., Fukugita, M. and Loveday, J. (2005)The Properties and Luminosity Function of Extremely Low Luminosity Galaxies. Astrophysical Journal, 631, 208.
- Tempel, E., Einasto, J., Einasto, M., Saar, E. and Tago, E. (2009) Anatomy of Luminosity Functions: The 2dFGRS Example. Astronomy & Astrophysics, 495, 37.
- Zaninetti, L. (2008) A New Luminosity Function for Galaxies as Given by the Mass-Luminosity Relationship. The Astronomical Journal, 135, 1264-1275.
- Zaninetti, L. (2010) The Luminosity Function of Galaxies as Modelled by the Generalized Gamma Distribution. Acta Physica Polonica B, 41, 729.
- Zaninetti, L. (2013) The Initial Mass Function Modeled by a Left Truncated Beta Distribution. Astrophysical Journal, 765, 128.
- Van den Bosch, F.C., Yang, X. and Mo, H.J. (2003) Linking Earlyand Late-Type Galaxies to Their Dark Matter Haloes. Monthly Notices of the Royal Astronomical Society, 340, 771. http://dx.doi.org/10.1046/j.1365-8711.2003.06335.x
- Yang, X., Mo, H.J. and van den Bosch, F.C. (2003) Constraining galaxy formation and cosmology with the conditional luminosity function of galaxies. Monthly Notices of the Royal Astronomical Society, 339, 1057. http://dx.doi.org/10.1046/j.1365-8711.2003.06254.x
- Cooray, A. and Cen, R. (2005) The Rise of Dwarfs and the Fall of Giants: Galaxy Formation Feedback Signatures in the Halo Satellite Luminosity Function. Astrophysical Journal, 633, L69.
- Cooray, A. and Milosavljevic, M. (2005) What is L*? Anatomy of the Galaxy Luminosity Function. Astrophysical Journal, 627, L89.
- Cooray, A. and Milosavljevic, M. (2005) Dissipationless Merging and the Assembly of Central Galaxies. Astrophysical Journal, 627, L85.
- Tinker, J.L., Weinberg, D.H., Zheng, Z. and Zehavi, I. (2005) On the Mass-to-Light Ratio of Large-Scale Structure. Astrophysical Journal, 631, 41.
- Tinker, J.L., Norberg, P., Weinberg, D.H. and Warren, M.S. (2007) On the Luminosity Dependence of the Galaxy Pairwise Velocity Dispersion. Astrophysical Journal, 659, 877.
- Abramowitz, M. and Stegun, I.A. (1965) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover, New York.
- Von Seggern, D. (1992) CRC Standard Curves and Surfaces. CRC, New York.
- Thompson, W.J. (1997) Atlas for computing mathematical functions. Wiley-Interscience, New York.
- Gradshteyn, I.S. and Ryzhik, I.M. and Jeffrey, A. and Zwillinger, D. (2007) Table of Integrals, Series, and Products. Academic Press, New York.
- Olver, F.W.J., Lozier, D. W., Boisvert R.F. and Clark C.W. (2010) NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge.
- Zhang, S. and Jin, J. (1996) Computation of Special Functions. Wiley-Interscience, New York.
- Blanton, M.R., Hogg, D.W., Bahcall, N.A., Brinkmann, J. and Britton, M. (2003) The Galaxy Luminosity Function and Luminosity Density at Redshift z = 0.1. Astrophysical Journal, 592, 819.
- Kauffmann, G., Heckman, T.M., White, S.D.M., Charlot, S. and Tremonti, C. (2003) Stellar masses and star formation histories for 105 galaxies from the Sloan Digital Sky Survey. Monthly Notices of the Royal Astronomical Society, 341, 33-53.
- Alcaniz, J.S. and Lima, J.A.S. (2004) Galaxy Luminosity Function: A New Analytic Expression. Brazilian Journal of Physics, 34, 455. http://dx.doi.org/10.1590/S0103-97332004000300026
- Taghizadeh-Popp, M., Ozogány, K., Rácz, Z., Regoes, E. and Szalay, A.S. (2012) Distribution of Maximal Luminosity of Galaxies in the Sloan Digital Sky Survey. Astrophysical Journal, 759, 100.


