International Journal of Astronomy and Astrophysics
Vol.3 No.4(2013), Article ID:40432,8 pages DOI:10.4236/ijaa.2013.34053
An Invitation to El Naschie’s Theory of Cantorian Space-Time and Dark Energy*
1Technical School Center of Maribor, Maribor, Slovenia
2National Engineering Laboratory for Modern Silk, College of Textile and Clothing Engineering, Soochow University, Suzhou, China
Email: leila.marek@guest.arnes.si, hejihuan@suda.edu.cn
Copyright © 2013 Leila Marek-Crnjac, Jihuan He. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 22, 2013; revised October 20, 2013; accepted October 28, 2013
Keywords: Cantorian Philosophy; Nonlinear Dynamics and Relativity; Fractal Einstein Gravity; Dark Energy; Ordinary Energy of the Quantum Particle; Dark Energy of the Quantum Wave
ABSTRACT
The paper is a condensed but accurate account of El Naschie’s theory of Cantorian space-time which was used by him to clarify some major problems in theoretical physics and cosmology. In particular El Naschie’s revision and completion of relativity theory and demystification of dark energy are destined to be two milestones in the history of theoretical physics.
1. Introduction—A Bird’s Eye View of El Naschie’s Theory of Cantorian Space-Time
In the following we will attempt to describe the extraordinary work of El Naschie without going into mathematical analysis in detail.
The work of Mohamed El Naschie was initially an avant garde scientific framework which opens the door for a new way to view nature as testified for by the collection of papers which he edited with Nobel Laureate Ilya Prigogine [1] and later on a book by him, Ilya Prigogine and Otto Rössler [2]. However the latest result of his work in which he put Einstein’s famous formula
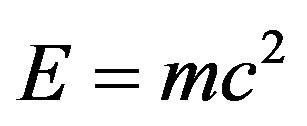 under a set theoretical microscope and dissected it into to the measurable energy of quantum particle and the energy of the quantum wave which cannot be measured directly is a needed scientific earthquake [3-6] which is destined to change the way of thinking about physics and cosmology particularly the quantum wave and dark energy [7-9]. Let us recount this engaging scientific story from the beginning before returning to the issue of dark energy and revising
under a set theoretical microscope and dissected it into to the measurable energy of quantum particle and the energy of the quantum wave which cannot be measured directly is a needed scientific earthquake [3-6] which is destined to change the way of thinking about physics and cosmology particularly the quantum wave and dark energy [7-9]. Let us recount this engaging scientific story from the beginning before returning to the issue of dark energy and revising 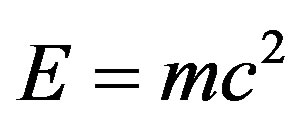 [10].
[10].
Starting from the fundamentals of nonlinear dynamics, deterministic chaos and fractal geometry and by combining that with quantum field theory and the standard model of high-energy particle physics El Naschie created around 1990 the nucleus embryonic form of a novel concept for the physical interpretation of space-time [11]. He replaced the space-time continuum by a transfinite fractal set of points in an infinite dimensional space, thus in particular effectively replacing Euclidean geometry by the geometry of infinite dimensional but hierarchal Cantor set [12,13].
This is a generalization of the so-called transfinite sets initially introduced by the mathematician Georg Cantor who incidentally also invented set theory which is the basis of all modern mathematics as well as the 2000- 2010 period of the work of El Naschie [14]. It is interesting to note that there had been earlier attempts to introduce space-time with dimensions larger than four. The first model of that kind was formulated by the mathematicians Kaluza and Klein with the goal to unify gravity with electromagnetism more than 80 years ago [15]. Their space-time, however, represents merely a continuous manifold. The work on the ten dimensional super string theory is well known and need not be discussed here. The idea of Mohamed El Naschie to use a transfinite set of discrete points in combination with an infinite dimensional space is indeed totally new [16]. The only somewhat similar theories are those of the Canadian physics Professor G.N. Ord and the French cosmologist Dr. L. Nottale but both used continuous Peano-like fractals unlike the totally disjointed Cantor sets of El Naschie [17-25]. There is some correspondence between Richard Feynman and G. Ord which indicates that Feynman was tinkering with the idea of space filling fractal curves but he published nothing on the subject [26]. In the mathematical terminology of the theory of quasi manifolds, El Naschie’s micro space-time is a non-commutative transfinite quotient manifold akin to that developed in the work of the leading French mathematician Alain Connes [27]. From around 1995 onwards El Naschie started developing his ideas to a sophisticated general theory which culminated in 2012 in revising Einstein’s relativity and demystifying the quantum wave as well as the socalled missing dark energy of the cosmos [3-10].
One very interesting point about El Naschie’s spacetime is that viewed at macroscopic resolution it appears as if it were only three plus one or four dimensional, thus mimicking the space-time of classical mechanics and relativity and which agrees in the three plus one case with our daily experience with the macroscopic world [11-25]. In other words the dimensionality of this space-time is resolution dependent and the invariance theorem of dimensions must be relaxed [20-27]. The high dimensional character of space-time starts to become noticeable only at sub-microscopic resolution [25,27]. The near infinite number of dimensions is expected to appear only at interaction energies of 1019 GeV [27]. This is the so-called Planck energy, a fantastically high energy—way out of reach of any conceivable accelerator [28]. This is the energy at which we assume that nature becomes simplest as all fundamental forces unify to a single force, sometimes called super force and we are left with only one hypothetical particle, namely the Planckton, that is to say mini black holes with Planck mass of the order of 1019 GeV [22,23]. El Naschie was able to find an exact value for the coupling constant at the point at which all the forces melt into one. Later on El Naschie succeeded in scaling the Planck scale following an idea due to Nobel Laureate D. Gross [28] and calculated this way the dark energy density of the cosmos. At much lower energies he furthermore could use this to determine important physical effects. By studying particles and their interactions in the framework of his theory El Naschie succeeded to determine the mass spectrum of elementary particles at realistic man made conditions showing that the multitude of elementary particles is nothing but a manifestation of the transfinite discrete fractal structure of the vacuum, i.e. the fine structure of a non-commutative geometry [27]. Because of the inevitable vacuum fluctuations described by quantum mechanics space-time itself represents a fluctuation motion. In a sense the excited states of the fluctuating space-time are what we perceive in our microscopic experiments as elementary particles. While string theory alleges that elementary particles are highly localized vibrations of tiny strings the theory of El Naschie goes even deeper by building the strings themselves from sizzling sets of Cantor points of which spacetime is made [29-31]. Quantum gravity is interpreted accordingly as the effect of the passing of a fractal time [29]. Using this line of reasoning he was able to determine the maximum coupling constant of quantum gravity to be 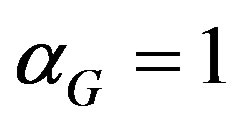 while the largest coupling constant for the unification of all fundamental forces was determined to be
while the largest coupling constant for the unification of all fundamental forces was determined to be 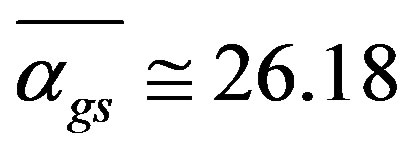 for the super symmetric case in full agreement with numerically obtained estimations using ad hoc theories. For grand unification without gravity and super symmetry he found on the other hand that
for the super symmetric case in full agreement with numerically obtained estimations using ad hoc theories. For grand unification without gravity and super symmetry he found on the other hand that 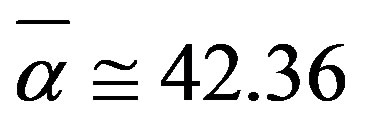 and the Planck mass is reduced to Polyakov—‘tHooft unification magnetic monopol with a mass equal 1016 GeV again in remarkable agreement with many other ad hoc results [12,17,22,23]. From 2011 onwards El Naschie invented a new unit interval physics following the idea of D. Gross to scale the Planck scale mentioned earlier on [27,32].
and the Planck mass is reduced to Polyakov—‘tHooft unification magnetic monopol with a mass equal 1016 GeV again in remarkable agreement with many other ad hoc results [12,17,22,23]. From 2011 onwards El Naschie invented a new unit interval physics following the idea of D. Gross to scale the Planck scale mentioned earlier on [27,32].
El Naschie’s E-infinity theory does not stop here. The theory not only predicts with astonishing precision the mass spectrum of all elementary particles of the standard model, which, by the way, thought not to be possible without additional input and hypothesis, but is also able to determine directly a number of fundamental constants. One example definitely worthwhile to be mentioned is the exact relation between the dimensionless Newton constant and the coupling constants at the electro weak unification. Thus he achieves by using symmetry, dimensionality and other topological invariants which he translates from continuous geometry to the transfinite fractal geometry of his theory. We can now hope that following this methodology we will be able to understand the deep meaning behind certain magical numbers and values of constants of nature which was convincingly revealed by El Naschie’s papers. In fact in a series of relatively recent papers El Naschie was able to give an exact analysis for dark energy of the quantum Hawking-Hartle wave of the cosmos associated with a negative dimension. In the same way the negative sign of the strong coupling found first by ‘t Hooft and independently later on by D. Gross and F. Wilczek is now a proven theorem due to El Naschie’s work.
2. Venturing into Exceptional Lie Groups
Starting from about 2005 El Naschie’s work acquired an even stronger momentum and ventured in new directions culminating in his set theoretical resolution of various fundamental as well as epistemological problems in quantum mechanics, particularly the state vector reduction or wave collapse which provided considerable discomfort to E. Schrödinger and many generations of excellent scientists after him. The research in this direction was particularly motivated by the connection found between the work on non-commutative geometry, quotient manifold and the transfinite version of E8 E8 exceptional Lie groups [14]. Based on the properties of the E-line of exceptional groups, namely E1, E2, E3, E4, E5, E6, E7 and E8 as well as the 17 two and three Stein spaces El Naschie was able to predict the existence of an 8 dimensional Higgs-like field which materializes in at least one or five Higgs particles and a Higgs maximal mass at 169 GeV. Recent experimental findings confirming the reality of the Higgs are not conclusive as far as the weight or the zero spin are concerned. None the less, they did confirm the correctness of the general direction. We could mention on passing some fascinating numerical results connecting a fuzzy Cantorian fractal Ei exceptional Lie group and Stein spaces to the inverse of the electromagnetic fine structure constant 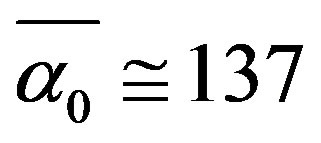 [33-37]. The first result is that the sum of all the fuzzy Ei groups dimensions amount to exactly 4 multiplied with the inverse electromagnetic fine structure constant
[33-37]. The first result is that the sum of all the fuzzy Ei groups dimensions amount to exactly 4 multiplied with the inverse electromagnetic fine structure constant 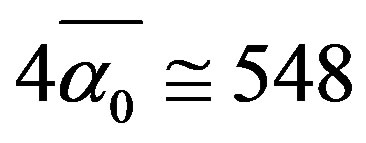 while the sum of all the fuzzy Stein spaces dimension is
while the sum of all the fuzzy Stein spaces dimension is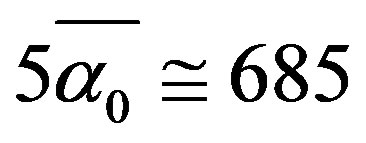 . Based on this result he conjectured against conventional wisdom that there may also exist an E12 exceptional Lie symmetry group with dimension equal (26.18)2 = 685 where (26.18) is the curvature of spacetime [17]. Furthermore he gave the number of gauge gluons on the holographic boundary of his bulk to be equal to the 336 degrees of freedom of Klein’s modular curve plus 3 making a total of 339 particle-like states [17]. In addition El Naschie modeled the quantum wave function as the empty transfinite set with a MengerUrysohn topological dimension equal minus one (−1) and a Hausdorff dimension equal
. Based on this result he conjectured against conventional wisdom that there may also exist an E12 exceptional Lie symmetry group with dimension equal (26.18)2 = 685 where (26.18) is the curvature of spacetime [17]. Furthermore he gave the number of gauge gluons on the holographic boundary of his bulk to be equal to the 336 degrees of freedom of Klein’s modular curve plus 3 making a total of 339 particle-like states [17]. In addition El Naschie modeled the quantum wave function as the empty transfinite set with a MengerUrysohn topological dimension equal minus one (−1) and a Hausdorff dimension equal 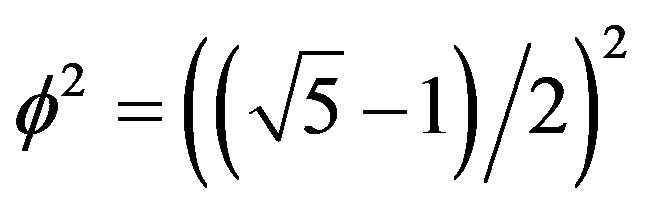 that means the square of the golden ratio [38,39]. By contrast a quantum particle was modeled by the zero set with Menger-Urysohn dimension zero and a Hausdorff dimension
that means the square of the golden ratio [38,39]. By contrast a quantum particle was modeled by the zero set with Menger-Urysohn dimension zero and a Hausdorff dimension 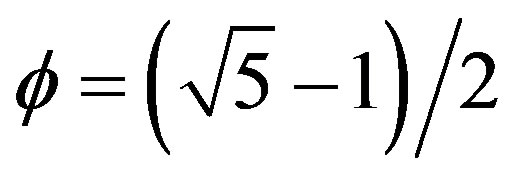 in full agreement with the work on non-commutative geometry of Penrose fractal tiling as well as some experimental work conducted at the Helmholtz Centre, Germany in cooperation with the University of Oxford which found evidence of the golden ratio in quantum mechanics [40] as predicted by El Naschie some 20 years ago [17,38,39]. This identification of the wave function with the empty set and the quantum particle with the zero set is a bold move and a revolutionary discovery with far reaching consequences difficult to assess at the present time for future research. It may be important for the understanding of how the golden mean enters in the theory to know that by a well known mathematical theorem due to Mauldin and Williams, a random Cantor set posses with a probability equal to one a Hausdorff dimension equal to the golden mean [11,12,17]. A space-time geometry based on such random Cantor set as that of El Naschie will therefore have the golden mean at its roots [32].
in full agreement with the work on non-commutative geometry of Penrose fractal tiling as well as some experimental work conducted at the Helmholtz Centre, Germany in cooperation with the University of Oxford which found evidence of the golden ratio in quantum mechanics [40] as predicted by El Naschie some 20 years ago [17,38,39]. This identification of the wave function with the empty set and the quantum particle with the zero set is a bold move and a revolutionary discovery with far reaching consequences difficult to assess at the present time for future research. It may be important for the understanding of how the golden mean enters in the theory to know that by a well known mathematical theorem due to Mauldin and Williams, a random Cantor set posses with a probability equal to one a Hausdorff dimension equal to the golden mean [11,12,17]. A space-time geometry based on such random Cantor set as that of El Naschie will therefore have the golden mean at its roots [32].
To be able to work with totally disjointed point set geometry El Naschie had to develop a mathematical replacement for calculus. He did this by inventing his own quantized calculus, similar to what A. Connes did for non-commutative geometry. El Naschie replaced calculus with Wyle scaling [20,25]. That way integration became scaling up and differentiation a scaling down in the sense of H. Weyl. Following this road El Naschie was able to reproduce Hardy’s quantum entanglement probability  which amounts to almost 9%, as was experimentally confirmed [33,39].
which amounts to almost 9%, as was experimentally confirmed [33,39].
3. Enter Cosmology
There are too many other interesting aspects which El Naschie’s work has covered, in fact too many to be able to mention within this short report. However we could not possibly overlook the fact that his theory is one of the at best two or three general theories which can be used to give theoretical justification for the results of the COBE experiment of the microwave background radiation as well as the WMAP and supernova analysis which was awarded the 2011 Nobel Prize in Physics [23]. Another result connected to cosmology is his analysis that our universe must be a compact manifold as well as his use of the Banach-Tarski theorem all apart from his recent revision of Einstein’s 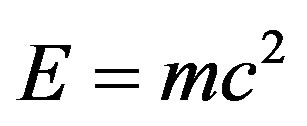 to the sum of ordinary energy
to the sum of ordinary energy 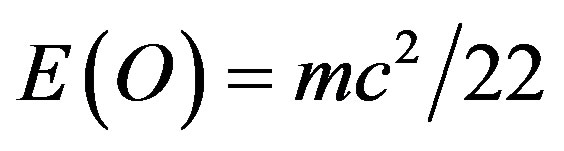 and dark energy
and dark energy
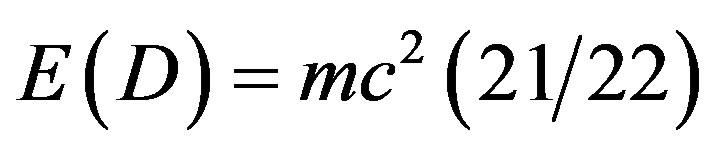 [1-7,41-47].
[1-7,41-47].
El Naschie worked on these fundamental ideas for about 30 years. What appeared at the beginning to be a daring hypothesis has now matured into a fully fledged general theory that convincingly addresses questions which have puzzled scientists around the world for many decades with regard to fundamental aspects of quantum mechanics as well as applications regarding the prediction of new particles and their masses. In fact using his theory El Naschie was able to derive rather than put by hand the inverse electromagnetic fine structure constant  as well as the topological dimensionality of space-time
as well as the topological dimensionality of space-time  the average Hausdorff self similarity dimension
the average Hausdorff self similarity dimension 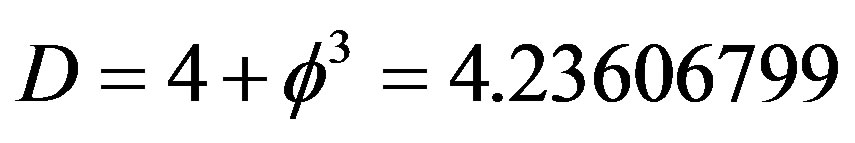 and the spectral dimension of R. Loll and J. Ambjorn D = 4.01999 from first principles. One of the derivations of
and the spectral dimension of R. Loll and J. Ambjorn D = 4.01999 from first principles. One of the derivations of  is based on a neat fundamental equation which is easily reproduced within this report. El Naschie’s fundamental equations say that if the bulk is given by the 496 massless gauge bosons of E8 E8 and particle physics which is 339 gluons lives on the holographic boundary, then adding the 20 principle curvatures or pure gravity of Einsteinthe difference of (496) minus (339 plus 20) must be the (137) of electromagnetism [17]. We know of no simpler derivation than that. To the best of our knowledge this was never achieved before and is the first time ever to derive the most fundamental constant of nature
is based on a neat fundamental equation which is easily reproduced within this report. El Naschie’s fundamental equations say that if the bulk is given by the 496 massless gauge bosons of E8 E8 and particle physics which is 339 gluons lives on the holographic boundary, then adding the 20 principle curvatures or pure gravity of Einsteinthe difference of (496) minus (339 plus 20) must be the (137) of electromagnetism [17]. We know of no simpler derivation than that. To the best of our knowledge this was never achieved before and is the first time ever to derive the most fundamental constant of nature  from a general theory. Using similar fundamental considerations El Naschie was able to show that the exact number of first massless level of particles using his transfinite version of super strings is 8872 and the classical result of the conventional theory, namely 8064 is only an approximation which ignores the fractal fine structure of space-time. The value 8872 could be used as an energy functional in some complex way and by applying Weyl scaling to it, many fundamental results follow. This is all explained in details in the corresponding papers [17-26,28-30]. In our eyes El Naschie’s theory constitutes a grand design to a deeper understanding of nature. We feel that his life-long scientific work is exceptional.
from a general theory. Using similar fundamental considerations El Naschie was able to show that the exact number of first massless level of particles using his transfinite version of super strings is 8872 and the classical result of the conventional theory, namely 8064 is only an approximation which ignores the fractal fine structure of space-time. The value 8872 could be used as an energy functional in some complex way and by applying Weyl scaling to it, many fundamental results follow. This is all explained in details in the corresponding papers [17-26,28-30]. In our eyes El Naschie’s theory constitutes a grand design to a deeper understanding of nature. We feel that his life-long scientific work is exceptional.
On the other hand, in our personal opinion the most astonishing result of Mohamed El Naschie’s theory is his quantum relativity equation  which could be interpreted together with his dark energy equation
which could be interpreted together with his dark energy equation 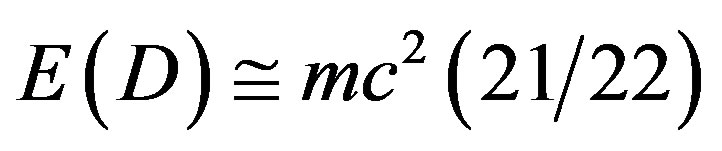 in various ways leading to a complete new understanding of special relativity and opening the door in principle to a new source of energy which constitutes 95.5% of the total energy of the cosmos [45-47].
in various ways leading to a complete new understanding of special relativity and opening the door in principle to a new source of energy which constitutes 95.5% of the total energy of the cosmos [45-47].
4. El Naschie’s Revision of Relativity and Explaining Dark Energy
1) The simplest way to introduce El Naschie’s theory is to start with his latest results obtained not more than two years ago [4,5]. Using this theory he was able to show that Einstein’s iconic equation of 1905
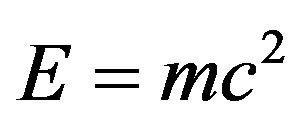 (1)
(1)
where E is the energy, m is the mass and c is the speed of light consists of two components, both of which were not known to Einstein at the time because they belong to a field developed some two decades later, namely quantum mechanics. The first component is 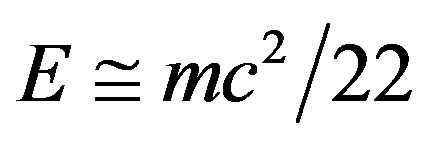 which he was able to show it to be the energy density of a quantum particle. The second component is
which he was able to show it to be the energy density of a quantum particle. The second component is 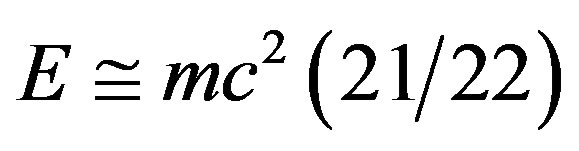 which he deduced from the quantum wave aspect of quantum mechanics. One should also mention at this point that the particle-wave duality is fundamental to quantum mechanics and has no counterpart in classical or relativistic mechanics. The previous two expressions when added together gave him initially a delightful surprise, namely the exact expression derived in Einstein’s special relativity [47]
which he deduced from the quantum wave aspect of quantum mechanics. One should also mention at this point that the particle-wave duality is fundamental to quantum mechanics and has no counterpart in classical or relativistic mechanics. The previous two expressions when added together gave him initially a delightful surprise, namely the exact expression derived in Einstein’s special relativity [47]
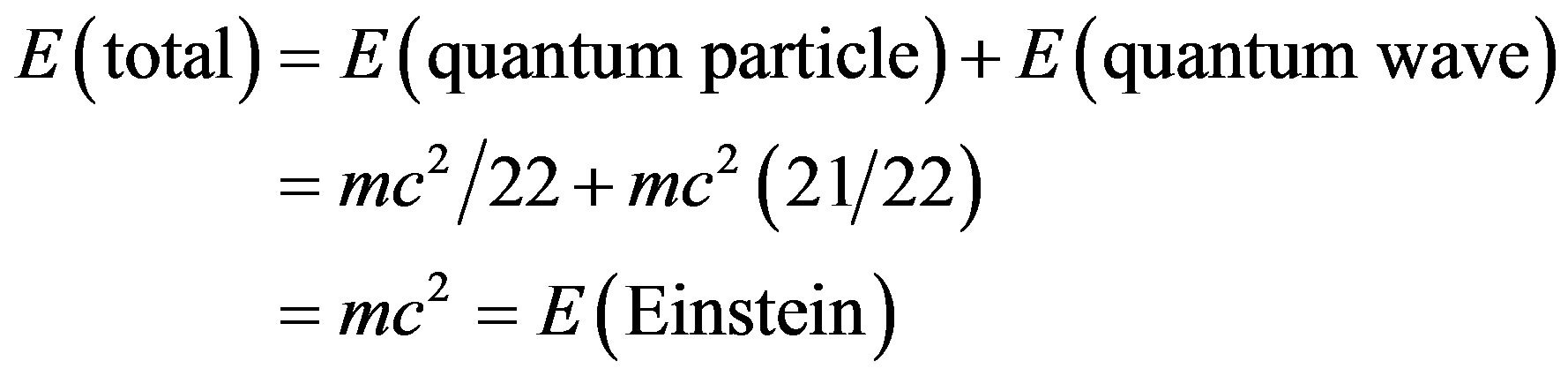 (2)
(2)
Although the above two expressions for the two energy components are only approximate the equality holds for the exact expression, a point which we will postpone discussing for the moment but will come back to later on. Let me condense and summarize this section. Einstein’s formula 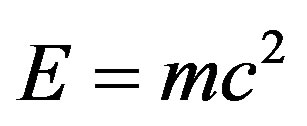 is in fact the sum of the two parts
is in fact the sum of the two parts 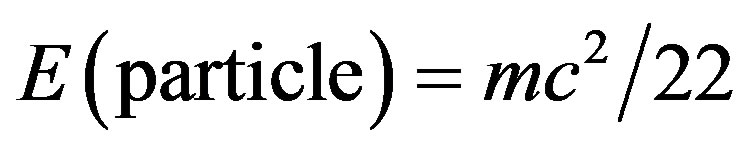 and
and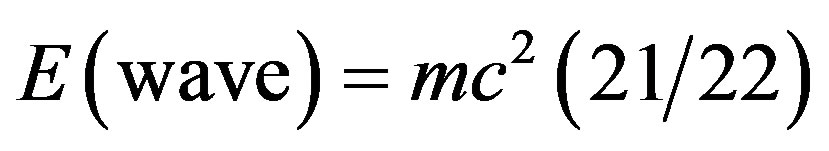 . It is thus a reflection of the well known phenomenon of particle-wave duality of quantum mechanics. The great importance of this discovery stems from the fact that within quantum mechanics a wave is a probability wave and does not possess any form of ordinary energy so one is inclined at first sight to wrongly think that his theory is wrong. However, it is right not only because the mathematics is consistent and makes a great deal of sense but because experimental work confirms El Naschie’s result. This experimental work was actually carried out in a laboratory virtually as large as the entire universe. This is not an imaginative metaphor but seriously a fact. The confirmation that
. It is thus a reflection of the well known phenomenon of particle-wave duality of quantum mechanics. The great importance of this discovery stems from the fact that within quantum mechanics a wave is a probability wave and does not possess any form of ordinary energy so one is inclined at first sight to wrongly think that his theory is wrong. However, it is right not only because the mathematics is consistent and makes a great deal of sense but because experimental work confirms El Naschie’s result. This experimental work was actually carried out in a laboratory virtually as large as the entire universe. This is not an imaginative metaphor but seriously a fact. The confirmation that 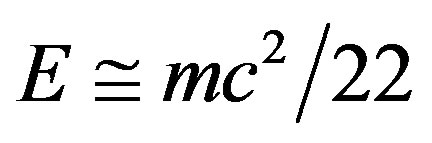 comes directly from the cosmic measurement of WMAP and the analysis of certain supernova effects which earned S. Perlmutter, B. Schmidt and A. Riess the 2011 Nobel Prize in Physics [3-9,41-47]. If
comes directly from the cosmic measurement of WMAP and the analysis of certain supernova effects which earned S. Perlmutter, B. Schmidt and A. Riess the 2011 Nobel Prize in Physics [3-9,41-47]. If 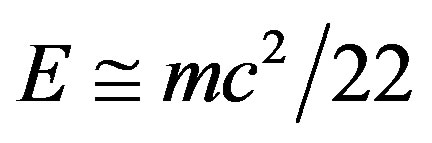 is all what was measured, then
is all what was measured, then 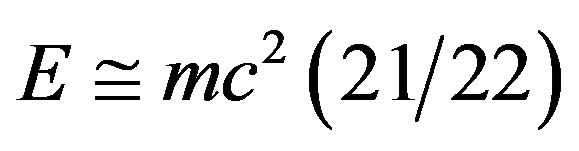 is what could not be found and that is exactly what El Naschie reasoned to be the missing dark energy of the universe. Since he was able to reason that the dark energy of the wave has an opposite sign to that of the measured
is what could not be found and that is exactly what El Naschie reasoned to be the missing dark energy of the universe. Since he was able to reason that the dark energy of the wave has an opposite sign to that of the measured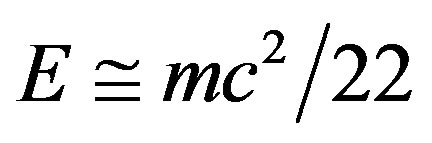 , he concluded that this dark energy is what is causing the observed accelerated expansion of the universe and this conclusion, together with the found numerical value agrees completely and accurately with the measured cosmological red shift of the three Nobel Laureates of 2011. There was one more piece in the jigsaw puzzle, namely why can’t we measure the dark energy directly rather than via its antigravity repulsive effect causing the accelerated cosmic expansion? The reason was very clear and is implied by the measurement problem of quantum mechanics. It is the wave collapse or vector reduction of quantum mechanics. El Naschie’s theory says, that a quantum particle is a zero set in Kaluza-Klein five dimensional space-time. On the other hand a quantum wave is an empty set also in five dimensions. Since measurement will penetrate the wave to find the particle, then the empty set will be rendered non-empty [3-9,41-47]. That is the wave collapse. Since the wave disappears in a manner of speaking, we cannot measure its “energy” that is unless we invent highly sophisticated wave collapse free non-demolition measurement instruments.
, he concluded that this dark energy is what is causing the observed accelerated expansion of the universe and this conclusion, together with the found numerical value agrees completely and accurately with the measured cosmological red shift of the three Nobel Laureates of 2011. There was one more piece in the jigsaw puzzle, namely why can’t we measure the dark energy directly rather than via its antigravity repulsive effect causing the accelerated cosmic expansion? The reason was very clear and is implied by the measurement problem of quantum mechanics. It is the wave collapse or vector reduction of quantum mechanics. El Naschie’s theory says, that a quantum particle is a zero set in Kaluza-Klein five dimensional space-time. On the other hand a quantum wave is an empty set also in five dimensions. Since measurement will penetrate the wave to find the particle, then the empty set will be rendered non-empty [3-9,41-47]. That is the wave collapse. Since the wave disappears in a manner of speaking, we cannot measure its “energy” that is unless we invent highly sophisticated wave collapse free non-demolition measurement instruments.
That way El Naschie solved in one stroke two major fundamental problems in quantum physics and cosmology, namely first that the quantum wave function has negative energy and is the surface, i.e. cobordism of the quantum particle and second that dark energy is nothing but the energy of this quantum wave function which the very act of measurement makes it inaccessible to measure. In the next section we will attempt to explain the basis of the theory which was instrumental in finding out all the preceding results [41-47].
2) It is time to ask how Einstein’s original equation E =  was dissected and opened bare to see inside it and find its quantum mechanical constituent although it is a classical causal equation. The result is so unsuspected and far reaching that it puts the conventional way in which we think about fundamental physics upside down. The quantum is now what is fundamental and relativity is derivable from it. So what did El Naschie change to obtain such a totally unexpected result and why was it not found before? The answer is that he changed the geometry and topology of space-time. El Naschie abandoned the prejudice about the apparent smoothness and continuity of space-time. He looked deeper like Kaluza, Klein, Gross, Green and Witten before him and replaced the Euclidean space and time of Newtonian mechanics as well as the continuously curved differentiable Riemannian manifold of general relativity by a totally disjointed fractal representing a huge Cantor set manifold made of infinite union and intersections of elementary random Cantor sets. Not only that but he also introduced the notion of infinite dimensional but hierarchical topology for this transfinite Cantorian point set manifold with an average expectation value for its dimensionality which turned out to be miraculously exactly 4. Thus Einstein used 4 dimensions, Kaluza and Klein used five, Veneziano and Nambu used 26 dimensions. Superstrings used 10 dimensions. Super gravity and Witten used 11 dimensions. El Naschie used an infinite number of fractal dimensions and made computation using their finite expectation values. Thus he confronted head on the notions of infinity and zero and reaped the fruits of utilizing these concepts rather than regarding them as undesirable “catastrophes” where mathematics breaks down. In other words, the cutting edge research result on the continuum hypothesis from Cantor via Gödel and Cohn to Hugh Wooden, were used to arrive with unheard of simplicity to the present result. A new number system intrinsic to random Cantor sets, namely the golden mean number system played a fundamental role in simplifying calculations to the extent that no computer was needed in any essential way and to a level that we may liken the situation to Turing’s computer which can do any calculation in principle without any hardware and the price for that is time. A Turing virtual machine is extremely slow in doing actual calculation. El Naschie’s golden mean virtual computer by contrast is super fast in doing real calculations with infinite precision although the numbers involved harbour certain infinite decimal expansions being totally irrational numbers [11,14,17,41-48].
was dissected and opened bare to see inside it and find its quantum mechanical constituent although it is a classical causal equation. The result is so unsuspected and far reaching that it puts the conventional way in which we think about fundamental physics upside down. The quantum is now what is fundamental and relativity is derivable from it. So what did El Naschie change to obtain such a totally unexpected result and why was it not found before? The answer is that he changed the geometry and topology of space-time. El Naschie abandoned the prejudice about the apparent smoothness and continuity of space-time. He looked deeper like Kaluza, Klein, Gross, Green and Witten before him and replaced the Euclidean space and time of Newtonian mechanics as well as the continuously curved differentiable Riemannian manifold of general relativity by a totally disjointed fractal representing a huge Cantor set manifold made of infinite union and intersections of elementary random Cantor sets. Not only that but he also introduced the notion of infinite dimensional but hierarchical topology for this transfinite Cantorian point set manifold with an average expectation value for its dimensionality which turned out to be miraculously exactly 4. Thus Einstein used 4 dimensions, Kaluza and Klein used five, Veneziano and Nambu used 26 dimensions. Superstrings used 10 dimensions. Super gravity and Witten used 11 dimensions. El Naschie used an infinite number of fractal dimensions and made computation using their finite expectation values. Thus he confronted head on the notions of infinity and zero and reaped the fruits of utilizing these concepts rather than regarding them as undesirable “catastrophes” where mathematics breaks down. In other words, the cutting edge research result on the continuum hypothesis from Cantor via Gödel and Cohn to Hugh Wooden, were used to arrive with unheard of simplicity to the present result. A new number system intrinsic to random Cantor sets, namely the golden mean number system played a fundamental role in simplifying calculations to the extent that no computer was needed in any essential way and to a level that we may liken the situation to Turing’s computer which can do any calculation in principle without any hardware and the price for that is time. A Turing virtual machine is extremely slow in doing actual calculation. El Naschie’s golden mean virtual computer by contrast is super fast in doing real calculations with infinite precision although the numbers involved harbour certain infinite decimal expansions being totally irrational numbers [11,14,17,41-48].
5. The Most Important Results of El Naschie’s Theory
After the preceding short exposition of the basics of El Naschie’s theory we would like to concentrate in this section on the various results obtained regardless of being of potential practical value or epistemological insight into the way nature works. We divide the results of El Naschie broadly into two parts, namely (A) high energy physics and (B) cosmology [48].
(A)—High energy physics [11,14,17]
Ÿ The fundamental constants of nature as well as the mass spectrum of elementary particles are usually put in by hand in traditional theories. By contrast our theory is the first in which these constants and mass spectrums are derived from first principles. For instance the super symmetric inverse coupling constant of super symmetric unification of all the fundamental interactions was found to be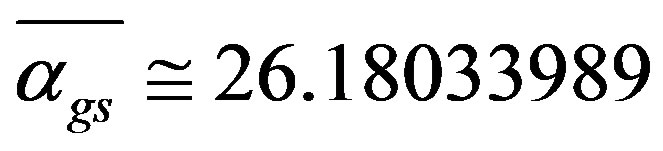 .
.
Ÿ The quantum relativity energy-mass equation is given by the multiplication of Einstein’s equation  with half of Hardy’s quantum entanglement
with half of Hardy’s quantum entanglement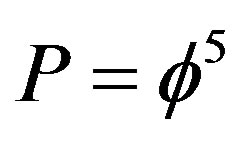 . That means
. That means
 (3)
(3)
in full agreement with observations. This number 26 could be interpreted as the 26 dimensions of bosonic string theory minus the 4 dimensions of Einstein (26 − 4 = 22).
(B)—Cosmology [3-9,41-48]
Ÿ The topological dimension of space-time is exactly DT = 4 while the corresponding Hausdorff dimension is 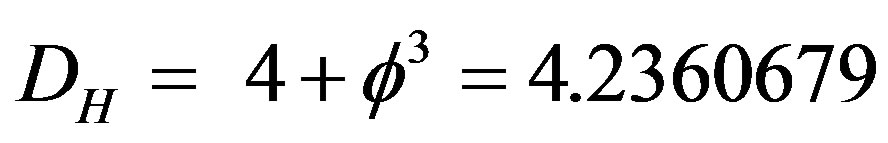 and the spectral dimension is DS = 4.019999.
and the spectral dimension is DS = 4.019999.
Ÿ The speed of light is an expectation value linked to the expectation of DT and DH. Thus its constancy is only apparent. In reality the speed of light is variable but not in the laboratory in our 4D space.
Ÿ The missing dark energy in the universe is the energy of the Hawking-Hartle quantum wave of the universe. Its energy density is given by
 (4)
(4)
This is verified by the WMAP and supernova measurements leading to the 2011 Nobel Prize.
6. Discussion and Conclusion
There are also numerous other results obtained by El Naschie which cross boundaries, for example, Hardy’s quantum entanglement of two quantum particles appears in different forms depending upon the number of particles involved. For instance for 3 particles it is the Immirzi parameter unifying superstring theory with loop quantum gravity. Unruh temperature [7] is also a related effect for which the number of particles is zero or one, i.e. the self entanglement of space-time [45].
The preceding general theory of El Naschie dispenses of many notions regarded as esoteric and supernatural via a truly super ordinary non-classical geometry which on the surface appears classical and ordinary like the permanently calm blue ocean observed from the window of a transatlantic flight. However, as the plane descends, the same ocean may reveal itself as stormy waters with meter high waves. The same effect applies on magnification not only to matter which dissolves under scanning tunneling microscopes as made of crystals and crystals made of atoms and so on, but space is also made of space elementary building blocks. These building blocks are the transfinite random Cantor sets which possess two dimensions, a topological dimension namely zero and a Hausdorff dimension  which is a number well known from art and science ranging from the design of the pyramids, Mona Lisa and Bach music to sun flowers and giant Nano particles called Bucky balls or Fleureen. It seems that this most irrational number of KAM theory of Kolmogorov, Arnold and Moser [14,17] held the key to a transfinite space-time geometry which can unify classical, relativistic and quantum mechanics leading to a rational and deeper understanding of nature. It was the good fortune of El Naschie to be able to contribute to this understanding by adopting this kind of geometry first discovered by G. Cantor and popularized in modern time by B. Mandelbrot and many others with the help of modern computer graphics [11,14,17]. In conclusion we note that El Naschie’s theory influenced research outside of physics and nanotechnology and as far as brain research and consciousness [49].
which is a number well known from art and science ranging from the design of the pyramids, Mona Lisa and Bach music to sun flowers and giant Nano particles called Bucky balls or Fleureen. It seems that this most irrational number of KAM theory of Kolmogorov, Arnold and Moser [14,17] held the key to a transfinite space-time geometry which can unify classical, relativistic and quantum mechanics leading to a rational and deeper understanding of nature. It was the good fortune of El Naschie to be able to contribute to this understanding by adopting this kind of geometry first discovered by G. Cantor and popularized in modern time by B. Mandelbrot and many others with the help of modern computer graphics [11,14,17]. In conclusion we note that El Naschie’s theory influenced research outside of physics and nanotechnology and as far as brain research and consciousness [49].
REFERENCES
- M. S. El Naschie and I. Prigogine, “Time Symmetry Breaking in Classical and Quantum Mechanics,” Chaos, Solitons & Fractals (Special Issue), Vol. 7, No. 4, 1996, pp. 499-503.
- M. S. El Naschie, O. E. Rössler and I. Prigogine, “Quantum Mechanics, Diffusion and Chaotic Fractals,” Pergamon Press/Elsevier, Oxford, 1995.
- J.-H. He, “A Historical Scientific Finding on Dark Energy,” Fractal Space-Time & Non-Commutative Geometry in Quantum & High Energy Phys., Vol. 2, No. 2, 2012, p. 14.
- J.-H. He and L. Marek-Crnjac, “Mohamed El Naschie’s revision of Albert Einstein’s E = mc2: A Definite Resolution of the Mystery of the Missing Dark Energy of the Cosmos,” International Journal of Modern Nonlinear Theory and Application, Vol. 2, No. 1, 2013, pp. 55-59. http://dx.doi.org/10.4236/ijmnta.2013.21006
- L. Marek-Crnjac, “Modification of Einstein’s E = mc2 to E = 1/22 mc2,” American Journal of Modern Physics, Vol. 2, No. 5, 2013, pp. 255-263.
- M. S. El Naschie and A. Helal, “Dark Energy Explained via the Hawking-Hartle Quantum Wave and the Topology of Cosmic Crystallography,” International Journal of Astronomy and Astrophysics, Vol. 3, No. 3, 2013, pp. 318- 343.
- M. S. El Naschie, “The Quantum Gravity Immirzi Parameter—A General Physical and Topological Interpretation,” Gravitation and Cosmology, Vol. 19, No. 3, 2013, pp. 151-155. http://dx.doi.org/10.1134/S0202289313030031
- M. S. El Naschie, “What Is the Missing Dark Energy in a Nutshell and the Hawking-Hartle Quantum Wave Collapse,” International Journal of Astronomy and Astrophysics, Vol. 3, No. 3, 2013, pp. 205-211. http://dx.doi.org/10.4236/ijaa.2013.33024
- M. S. El Naschie, “A Resolution of Cosmic Dark Energy via a Quantum Entanglement Relativity Theory,” Journal of Quantum Information Science, Vol. 3, No. 1, 2013, pp. 23-26. http://dx.doi.org/10.4236/jqis.2013.31006
- M. S. El Naschie, “Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrödinger Quantum Wave,” Journal of Modern Physics, Vol. 4, No. 5, 2013, pp. 591- 596. http://dx.doi.org/10.4236/jmp.2013.45084
- M. S. El Naschie, “Superstrings, Knots and Non-Commutative Geometry in E-Infinity Space,” International Journal of Theoretical Physics, Vol. 37, No. 12, 1998, pp. 2935-2951. http://dx.doi.org/10.1023/A:1026679628582
- M. S. El Naschie, “A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics,” Chaos, Solitons & Fractals, Vol. 19, No. 1, 2004, pp. 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
- M. S. El Naschie, “Topological Defects in the Symplictic Vacuum, Anomalous Positron Production and the Gravitational Instanton,” International Journal of Modern Physics E, Vol. 13, No. 4, 2004, pp. 835-849. http://dx.doi.org/10.1142/S0218301304002429
- M. S. El Naschie, “Average Exceptional Lie Group Hierarchy and High Energy Physics,” In: American Institute of Physics (AIP) Conference Proceedings, Vol. 1018, American Institute of Physics (AIP), New York, 2008, pp. 15-20.
- P. S. Wesson, “Five-Dimensional Physics,” World Scientific, Singapore, 2006.
- P. Weibel, G. Ord and O. Rössler, “Space-Time Physics and Fractality, Festschrift in Honour of Mohamed El Naschie on the Occasion of His 60th Birthday,” Springer, Vienna, New York, 2005.
- M. S. El Naschie, “The Theory of Cantorian Space-Time and High Energy Particle Physics (an Informal Review),” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2635-2646. http://dx.doi.org/10.1016/j.chaos.2008.09.059
- J.-H. He, “Hilbert Cube Model for Fractal Space-Time,” Chaos, Solitons & Fractals, Vol. 42, No. 5, 2009, pp. 2754-2759. http://dx.doi.org/10.1016/j.chaos.2009.03.182
- J.-H. He, et al., “Twenty-Six Dimensional Polytope and High Energy Space-Time Physics,” Chaos, Solitons & Fractals, Vol. 33, No. 1, 2007, pp. 5-13. http://dx.doi.org/10.1016/j.chaos.2006.10.048
- M. S. El Naschie, “From Classical Gauge Theory Back to Weyl Scaling via E-Infinity Space-Time,” Chaos, Solitons & Fractals, Vol. 38, No. 4, 2008, pp. 980-985. http://dx.doi.org/10.1016/j.chaos.2008.05.017
- L. Marek-Crnjac, “The Hausdorff Dimension of the Penrose Universe,” Physics Research International, Vol. 2011, 2011, Article ID: 874302. http://dx.doi.org/10.1155/2011/874302
- J.-H. He, et al., “Transfinite Physics—A Collection of Publications on E-Infinity Cantorian Space-Time Theory,” China Culture & Scientific Publishing, Hongkong, 2005.
- J.-H. He, E. Goldfain, et al., “Beyond the 2006 Physics Nobel Prize for COBE,” China Culture & Scientific Publishing, Beijing, 2006.
- M. S. El Naschie, “Nonlinear Dynamics of the Two-Slit Experiment with Quantum Particles,” Problems of Nonlinear Analysis in Engineering Systems, Vol. 26, No. 2, 2006.
- L. Marek-Crnjac, “A Feynman Path Integral-Like Method for Deriving the Four Dimensionality of Space-Time from First Principles,” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2471-2473. http://dx.doi.org/10.1016/j.chaos.2008.09.014
- M. S. El Naschie, “On ‘tHooft’s Dimensional Regularization in E-Infinity Space,” Chaos, Solitons & Fractals, Vol. 12, No. 5, 2001, pp. 851-858. http://dx.doi.org/10.1016/S0960-0779(00)00138-7
- A. Connes, “Non-Commutative Geometry,” Academic Press, San Diego, 1994.
- M. S. El Naschie, “The Missing Dark Energy of the Cosmos from Light Cone Topological Velocity and Scaling the Planck Scale,” Open Journal of Microphysics, Vol. 3, No. 3, 2013, pp. 64-70. http://dx.doi.org/10.4236/ojm.2013.33012
- M. S. El Naschie, “A Note on Quantum Gravity and Cantorian Space-Time,” Chaos, Solitons & Fractals, Vol. 8, No. 1, 1997, pp. 131-133. http://dx.doi.org/10.1016/S0960-0779(96)00128-2
- M. S. El Naschie, “Remarks on Superstrings, Fractal Gravity, Nagasawa’s Diffusion and Cantorian Space-Time,” Chaos, Solitons & Fractals, Vol. 8, No. 11, 1997, pp. 1873-1886. http://dx.doi.org/10.1016/S0960-0779(97)00124-0
- M. S. El Naschie, “Fractal Gravity and Symmetry Breaking in a Hierarchical Cantorian Space,” Chaos, Solitons & Fractals, Vol. 8, No. 11, 1997, pp. 1865-1872. http://dx.doi.org/10.1016/S0960-0779(97)00039-8
- L. Marek-Crnjac, et al., “Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology,” International Journal of Modern Nonlinear Theory and Application, Vol. 2, No. 1A, 2013, pp. 78-88. http://dx.doi.org/10.4236/ijmnta.2013.21A010
- M. S. El Naschie, “Electroweak Connection and Universality of Hardy’s Quantum Entanglement,” Fractal SpaceTime & Non-Commutative Geometry in Quantum & High Energy Physics, Vol. 1, No. 1, 2011, pp. 25-30.
- M. S. El Naschie, “Fuzzy Multi-Instanton Knots in the Fabric of Space-Time and Dirac’s Vacuum Fluctuation,” Chaos, Solitons & Fractals, Vol. 38, No. 5, 2008, pp. 1260-1268. http://dx.doi.org/10.1016/j.chaos.2008.07.010
- M. S. El Naschie, “Fuzzy Knot Theory Interpretation of Yang-Mills Instantons and Witten’s 5-Brane Model,” Chaos, Solitons & Fractals, Vol. 38, No. 5, 2008, pp. 1349-1354. http://dx.doi.org/10.1016/j.chaos.2008.07.002
- M. S. El Naschie, “Knots and Exceptional Lie Groups as Building Blocks of High Energy Particle Physics,” Chaos, Solitons & Fractals, Vol. 41, No. 4, 2009, pp. 1799-1803. http://dx.doi.org/10.1016/j.chaos.2008.07.025
- M. S. El Naschie, “Fuzzy Platonic Spaces as a Model for Quantum Physics,” Mathematical Models, Physical Methods and Simulation in Science & Technology, Vol. 1, No. 1, 2008, pp. 91-101.
- M. S. El Naschie, S. Olsen, J. H. He, S. Nada, L. MarekCrnjac and A. Helal, “On the Need for Fractal Logic in High Energy Quantum Physics,” International Journal of Modern Nonlinear Theory and Application, Vol. 1, No. 3, 2012, pp. 84-92.
- M. S. El Naschie, “Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry,” Journal of Quantum Information Science, Vol. 1, No. 2, 2011, pp. 50-53. http://dx.doi.org/10.4236/jqis.2011.12007
- R. Coldea, D. A. Tennant, E. M. Wheeler, et al., “Quantum Ratio Discovered in a Quantum World,” Science, Vol. 8, No. 32, 2010, pp. 177-180.
- M. S. El Naschie, “The Hydrogen Atom Fractal Spectra, the Missing Dark Energy of the Cosmos and Their Hardy Quantum Entanglement,” International Journal of Modern Nonlinear Theory and Application, Vol. 2, No. 3, 2013, pp. 167-169. http://dx.doi.org/10.4236/ijmnta.2013.23023
- M. S. El Naschie, “The Hyperbolic Extension of SigalottiHendi-Sharifzadeh’s Golden Triangle of Special Theory of Relativity and the Nature of Dark Energy,” Journal of Modern Physics, Vol. 4, No. 3, 2013, pp. 354-356. http://dx.doi.org/10.4236/jmp.2013.43049
- M. S. El Naschie, “Dark Energy from Kaluza-Klein SpaceTime and Noether’s Theorem via Lagrangian Multiplier Method,” Journal of Modern Physics, Vol. 4, No. 6, 2013, pp. 757-760. http://dx.doi.org/10.4236/jmp.2013.46103
- M. S. El Naschie and L. Marek-Crnjac, “Deriving the Exact Percentage of Dark Energy Using a Transfinite Version of Nottale’s Scale Relativity,” International Journal of Modern Nonlinear Theory and Application, Vol. 1, No. 4, 2012, pp. 118-124. http://dx.doi.org/10.4236/ijmnta.2012.14018
- M. S. El Naschie, “Quantum Entanglement: Where Dark Energy and Negative Gravity plus Accelerated Expansion of the Universe Comes from,” Journal of Quantum Information Science, Vol. 3, No. 2, 2013, pp. 57-77. http://dx.doi.org/10.4236/jqis.2013.32011
- M. S. El Naschie, “The Quantum Entanglement behind the Missing Dark Energy,” Journal of Modern Physics and Applications, Vol. 2, No. 1, 2013, pp. 88-96.
- M. S. El Naschie, “Determining the Missing Dark Energy of the Cosmos from a Light Cone Exact Relativistic Analysis,” Journal of Physics, Vol. 2, No. 2, 2013, pp. 18-23.
- G. Iovane, “Mohamed El Naschie’s E(Infinity) Cantorian Space-Time and Its Consequences in Cosmology,” Chaos, Solitons & Fractals, Vol. 25, No. 3, 2005, pp. 775-779. http://dx.doi.org/10.1016/j.chaos.2005.02.024
- M. Persinger and C. Lavellee, “Theoretical and Experimental Evidence of Macroscopic Entanglement between Human Brain Activity and Photon Emission,” Journal of Consciousness Exploration & Research, Vol. 1, No. 7, 2010, pp. 785-807.
NOTES
*Dedicated to Prof. Dr. Dipl. Ing. M. S. El Naschie on the occasion of his 70th birthday.

