Received 3 October 2014; accepted 24 May 2015; published 28 May 2015

ABSTRACT

Ahmad et al. in their paper [1] for the first time proposed to apply sharp function for classification of images. In continuation of their work, in this paper we investigate the use of sharp function as an edge detector through well known diffusion models. Further, we discuss the formulation of weak solution of nonlinear diffusion equation and prove uniqueness of weak solution of nonlinear problem. The anisotropic generalization of sharp operator based diffusion has also been implemented and tested on various types of images.

Keywords:

Maximal Function, Sharp Function, Image Processing, Edge Detection, Nonlinear Diffusion

1. Introduction

Nonlinear diffusion filtering is a well-established tool for image denoising and simplification. Starting with the pioneering work by Perona and Malik [2] in 1990, it has attracted the attention of many researchers working in the domain of mathematics and image processing (see [3] - [9] , for example). This filter class makes it possible to smooth images while the edges as main source of information are preserved. This leads to an adaptive sim- plification that can be useful for image understanding and interpretation. Among the most effective extensions of the basic method are the anisotropic filters [8] that offer the possibility to remove noise and enhance flow- like structures.

The sharp function, on the other hand, is a well-known functional analytic concept to measure the oscillatory behaviour of functions. It goes back to the maximal function which was introduced by Hardy and Littlewood [10] in 1930 to solve a problem in the theory of functions of complex variables. Based on this idea, John and Nirenberg [11] introduced the concept of bounded mean oscillation (BMO) functions. In 1972, Fefferman and Stein [12] introduced the sharp function (denoted by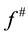) and found that a function was equivalent with. 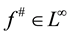The theory of Hardy Spaces received impetus from the work of Fefferman and Stein.

The idea of applying the sharp operator to measure the oscillation and classification of images was first proposed by Ahmad and Siddiqi [1] where it was used to find a suitable compression technique.

In this paper, we propose an alternative way to steer nonlinear diffusion filters via the sharp operator without using derivatives to measure edges. We show that the results of these diffusion filters are comparable to classical versions while the underlying sharp operator has a rich theoretical background. Motivated by the available diffusion processes in image processing, we propose an extension of the sharp operator for measuring aniso- tropic structures. To use this to steer anisotropic diffusion processes, we show how a fast variant of it can be implemented and used in practice.

The paper is organized as follows. Section 2 gives a review of classical nonlinear diffusion filters for image processing. In Section 3, we shortly describe the aspects of the theory for the maximal function, bounded mean oscillation functions, and the sharp function, which are necessary for this paper. The main idea of this paper, namely, the use of the sharp operator in nonlinear diffusion filters and its generalization to the anisotropic setting, is presented in Section 4. To evaluate the methods in practice, Section 6 describes some computational experiments. A summary and an outlook conclude the paper in Section 7.

2. Classical Nonlinear Diffusion Filters

Diffusion is interesting as image processing tool since it is a physical process that equilibrates concentration without creating or destroying mass. The idea behind the use of the diffusion equation in image processing arose from the use of Gaussian filter in multiscale image analysis. It can be founded by a system of several axioms like linearity, translational and rotational invariance, and average grey value preservation, that marks the begin- ning of the scale-space concept [13] - [16] . Convolving an image with a Gaussian filter,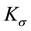

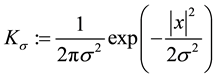
with standard deviation, is equivalent to the solution of the linear homogeneous diffusion equation

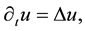(1)

where the given image f is used as initial condition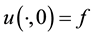. We assume homogeneous Neumann boundary conditions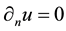, where n denotes the outer normal of the boundary of image domain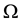. The stopping time t has to be chosen as 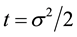for equivalence.

Isotropic nonlinear diffusion. The major drawback of linear diffusion is the delocalisation and blurring of image edges. To circumvent this problem, Perona and Malik [2] introduced the nonlinear diffusion equation

(2)

The diffusivity g is chosen as a decreasing function of the edge detector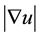. Examples for diffusivity functions can be found in [2] [17] - [19] . Catté et al. [3] introduced a regularisation of the gradient of u to make the process well-posed. They use the equation

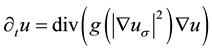(3)

with 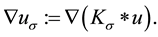A review of this filter class can be found in [20] .

Anisotropic nonlinear diffusion. Nonlinear isotropic diffusion often shows problems to remove noise close to image edges. It can be helpful to use an anisotropic diffusion filter

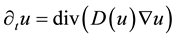(4)

in such cases as proposed by Weickert [8] . The scalar diffusivity function g has been replaced by a matrix here. Depending on the choice of D this allows for smoothing along edges while smoothing across edges is avoided: the so-called edge-enhancing diffusion (EED). Another classical choice of D, depending on the struc- ture tensor [21] [22] , makes enhancement of coherent flow-like structures possible. This process is known as coherence-enhancing diffusion (CED). Details on these filters and their numerical implementation can be found in [8] [23] .

3. The Sharp Operator

In this section, we give a short introduction to the sharp operator and its background. There is a rich theory behind it, and we point out the main results connected to it.

The Hardy-Littlewood maximal function was developed to solve a problem in the theory of functions of complex variable. The analogue for integrals, which is required for the function theoretic applications, is derived in Hardy and Littlewood [10] .

Definition 1. Let be the n-dimensional Euclidean space and be a real valued measurable function on. For such a function f on its Hardy-Littlewood maximal function is defined by the formula

(5)

where the supremum ranges over all finite cubes Q in and is the Lebesgue measure of.

Now we state a Hardy-Littlewood maximal theorem.

Theorem 1. For each function we have

Proof. See ( [24] , p. 142).

The space BMO, i.e. bounded mean oscillation of functions is introduced by John and Nirenberg [11] .

Definition 2. A measurable function f on has bounded p-mean oscillation, , if

(6)

where the supremum ranges over all finite cubes Q in and

is the mean value of the function f on the cube Q.

Fefferman and Stein [12] introduced the “sharp function” that mediates between and spaces. It is defined as follows.

Definition 3. Let f be a locally integrable function on. The sharp function is represented by the formula,

(7)

Of course, is identical with. It is also observed that there are unbounded functions in.

Example 1. The function on is in.

After calculation it comes out to be So, the un-bounded function is in.

It is important to note that it does not matter in which norm we measure the oscillation. This is clear from the following corollary.

Corollary 1. For each p, , there exists a constant such that for each we have

Proof. See ( [24] , p. 156).

In view of the above corollary the spaces are equivalent for all p,.

4. Nonlinear Diffusion with the Sharp Operator

It is clear from the definition of the sharp function that for a pixel z, where f has almost uniform grey level region in an image, will be of very small value. However, for the contrast region we get large values for. The idea is to accrue more diffusion in the regions of lower oscillation whereas to preserve the regions of higher oscillation.

Many isotropic nonlinear diffusivity models in physics and mechanics are governed by the nonlinear parabolic equation, , , , where the diffusion coefficient, , satisfying the condition

depends on the gradient of the function. In the diffusivity model given in [2] , the choice of the diffusivity coefficient is restricted to a subclass of the smooth monotonically decreasing functions with

. Further analysis of the nonlinear diffusivity model for the 1D diffusion equation has been developed in [5] . In particular, rewriting this equation in the form

(8)

where, , Equation (8) is defined to be forward parabolic, when, and

backward parabolic one, when. The assumption in the Perona-Malik diffusivity 1D model, leads to the following condition with respect to the diffusion coefficient:

First of all let us prove that if only the conditions (i)-(ii) hold, then the nonlinear diffusion operator is a monotone potential. For this, we define the nonlinear operator as

in an appropriate Banach space. Introduce the functional

Calculating the first derivative

we conclude that, and hence the above defined functional is the potential of the nonlinear diffusion operator A. Further calculating the second Gateaux derivative

and then substituting here, we conclude that the second Gateaux derivative of the potential is positive, i.e.,

if conditions (i)-(ii) hold. This means that the potential of the nonlinear diffusion operator is a convex functional which implies the strong monotonicity of the nonlinear operator [25] , i.e.,.

Thus for the strong monotonicity of the nonlinear diffusion Equation (8), and hence solvability of an initial

boundary value problem related to the nonlinear diffusion equation, only the conditions (i)-(ii)

are sufficient. However, these conditions are not sufficient for solvability of the corresponding problem related to the 2D diffusivity model. Specifically, one needs to impose the monotonicity condition:, as the theorem shows below. This condition and the above two conditions compose the set of admissible coefficients satisfying the following conditions:

(9)

An analysis of the steady state diffusivity model governed by the nonlinear elliptic equation in has been given in Hasanov et al. [26] . Based on the results given here let us analyze now the 2D diffusivity (Perona-Malik) model

(10)

Here is the domain with the piecewise smooth boundary, , n is the unit outward normal to the boundary. The negative sign in the Neumann condition

means that the diffusion flux, across the part of the boundary, passes from a region of high concentration to one of low concentration.

We will use weak solution theory for nonlinear PDE. For this, let us introduce the following well-known notations [25] . Let

and

where. Here and are the Sobolev spaces with the norms

respectively.

Evidently, the norms and are equivalent due to the homogeneous Dirichlet condition in (10). Identifying the Hilbert space H with its dual we have the triple with dense continuous compact

embedding. To define the weak solution of the nonlinear problem (10), we also need the following spaces, , , where the time derivative needs to be understood in sense of distributions. Evidently, W is the separable reflexive Banach space with the norm defined to be as

. Moreover, it is well-known that, the embedding is

continuous and the embedding is compact. For the convenience we denote the duality in the Banach

space (with its dual) and the norm as follows: and, accordingly.

Now we define the operators,

(11)

It is known that the operator, with the domain, is a maximal monotone operator (see, [25] , Proposition 32.10, p. 855).

For a given coefficient we define the nonlinear operator by the nonlinear functional

(12)

and the linear functional

which is well defined for. Within these definitions the weak solution of the nonlinear problem (10) can be defined as follows: find a function such that

(13)

Theorem 2. Let be the set of admissible coefficients satisfying conditions (9) and. Assume that and. Then the nonlinear problem (8) has a unique solution defined by (13).

Proof. Let us introduce the functional

and calculate the first Gateaux derivative. We have

Hence, as (12) shows. Thus the above defined functional is the potential of

the nonlinear diffusion operator A. Calculating the second Gateaux derivative and then substituting here we obtain:

(14)

Since, , we conclude

Substituting this in (14) and using the condition (ii) of (9), we conclude

Thus the potential of the nonlinear diffusion operator A is a convex functional which implies the strong monotonicity of this operator. Hence is also the strong monotone the operator:

This implies the uniqueness of the weak solution of the nonlinear problem (13). Existence of the solution follows from the results given in [27] [28] .

Remark 1. The assertion of the above theorem holds also for the case when.

Since structures in images often have the highly anisotropic features, for example, lines or corners, we propose some generalization of the presented method to the anisotropic setting. We start with an anisotropic generalization of the sharp operator.

5. Anisotropic Sharp Operator

So far we have only used isotropic nonlinear diffusion filters. In the definition (7) of the sharp operator, all integration domains Q are cubes. Therefore, the sharp function only provides information about local variations of the function, but not about the direction of these local variations. In order to allow for a quantitative descrip- tion of local variations in a certain direction, we propose to use non-symmetric sets instead of cubes. With this concept, an anisotropic extension of the sharp function can be defined as follows:

(15)

The most important in this definition is the set. We propose to use ellipses to measure the variation in several directions. So, one could alternatively define

(16)

In this definition, we take the supremum over all angles. Therefore, with this measure one is not only be able to find out the direction of the variation, but can also find the largest variation in any existing direction. For our later experiments, we start with the model (15) since we want to find the angle of the largest variation in an image.

5.1. Modifications of This Basic Model

For practical calculations, depending on the number of directions used, this measure is computationally very expensive. Thus we propose two simplifications in order to keep the motivation of the sharp operator while obtaining a fast measure of local variations.

Analogously to definition (7), the value is defined as the local mean value of f inside the integration domain, i.e.

Instead of taking this mean value as function of, we use a pre-smoothed version of the function f:

(17)

This changes the definition (15) to

(18)

We notice that in this definition, the difference in the integral is a difference between two functions. This offers the possibility to calculate the second function in one step for the whole domain instead of calculating mean values for each set independently. We notice that with this change, we do not use the same set for both integrations.

The second step is now to write this as a convolution. Instead of an elliptical set, we prefer to use an anisotropic Gaussian kernel here and write:

(19)

And lastly we replace also the outer integral with a convolution with an anisotropic Gaussian,

(20)

This measure can be evaluated in a very efficient way using the methods of Geusebroek et al. [29] for fast anisotropic Gaussian convolution. This makes it possible to incorporate it in an image processing tool as described in the following section.

5.2. Anisotropic Diffusion with the Fast Sharp Operator

Now we want to use the anisotropic variant of the sharp operator to steer an anisotropic diffusion process

as it has been proposed by Weickert [8] . In order to use this concepts for anisotropic diffusion in this formula- tion, we have to define a diffusion tensor based on the anisotropic sharp operator to obtain a process of the form

We define the diffusion tensor as follows: Let a point in the image domain be given, then we search for the direction

where the absolute value of the anisotropic sharp operator is maximal. The eigenvectors of the diffusion tensor are then the unit vectors pointing in this direction and the orthogonal one, i.e.,

The eigenvalues are defined analogously as for edge-enhancing diffusion:

where,

is the maximal sharp value in the point x.

Having these definitions for the diffusion tensor at hand, we can use classical discretisation for anisotropic diffusion filters as described in [8] .

6. Computational Experiments

To compare the sharp operator based diffusion approach with classical derivative based methods, we show filtering examples in Figure 1.

It is clear that the parameters of the anisotropic diffusion process have to be specified in practical situations. The time t is an inherent parameter in each diffusion process that controls the amount of simplification applied

to the data. The variance of evolving image decreases monotonically to zero in time. The contrast parameter allows to steer the edge preservation properties by distinguishing between important edges that should be preserved and smaller edges that are removed. For our discrete sharp operator, there are number of directions as an artificial parameter.

7. Summary and Outlook

We have investigated the use of the sharp operator for image processing applications. We have used the sharp operator to steer diffusion filters. With the classical notion, it is suitable to be used inside the diffusivity of a Perona-Malik filter. For anisotropic filters, we have used fast anisotropic Gauss filters to extend the sharp operator to a fast directional-dependent measure of variation. With the help of this measure, we could construct an alternative diffusion tensor for an anisotropic diffusion process. The results are quite similar to classical anisotropic diffusion filters. We have seen that the sharp operator not only is of theoretical interest but also may be used in practical applications.

References