Journal of Signal and Information Processing
Vol. 3 No. 2 (2012) , Article ID: 19573 , 5 pages DOI:10.4236/jsip.2012.32030
Reducing the PAPR of OFDM Signals Based on SCHT Precoding
![]()
School of Information and Electronic Engineering, Zhejiang University of Science and Technology, Hangzhou, China.
Email: wzp1966@sohu.com
Received February 25th, 2012; revised March 22nd, 2012; accepted April 19th, 2012
Keywords: Complex Hadamard Transform; PAPR; Precoding; OFDM
ABSTRACT
The precoding scheme based on real Hadamard transform is an effective and flexible way for reducing the peak-to-average power ratio (PAPR) of OFDM signals. However, the reduction capacity of PAPR is limited for real Hadamard transform method. In this paper, the new scheme based on complex Hadamard transform is proposed. The simulation results indicate that the proposed scheme may obtain a 1.2 dB PAPR reduction of OFDM signal with only moderate complexity compared with the real Hadamard transform.
1. Introduction
This OFDM (orthogonal-frequency-division multiplexing) plays a significant role in the modem telecommunications for both wireless and wired communication since it provides an efficient means to mitigate the intersymbol interference (ISI) caused by the channel multipalth spread and high data transmission. Now OFDM has been successfully adopted in many standards, such as IEEE802.11 a/g, IEEE802.16e, DAB/DVB etc. It is also being considered for future bradband applications and fourth generation transmission technique. However, OFDM systems have the inherent problem of a high peak-to-average power ratio (PAPR), which causes poor power efficiency or serious performance degradation in the transmitted signal. To reduce the PAPR, many techniques have been proposed [1,2], such as clipping, coding, partial transmit sequence (PTS) [3], selected mapping (SLM), nonlinear companding transforms [4], and Hadamard transforms [5]. Among those PAPR reduction methods, the simplest scheme to use is the clipping process. However, use of the clipping processing causes both in-band distortion and out-of-band distortion, and causes an increased bit error rate (BER) in the system. The SLM scheme is relatively attractive since it can obtain better PAPR by modifying the OFDM signal without distortion. With this technique, the price to pay for a significant decrease in PAPR is a loss in data rate due to the transmission of several side information bits that are required for original data block recovery at the receiver side. The loss of such side information bits during transmission would result in significant error performance degradation at the receiver output since the whole data block would be lost in this case. The powerful channel code has to be used when SLM is applied. This makes the system more complex, increases the transmission delay, and furthermore reduces the data rate.
The most popular PAPR reduction approaches can be classified into categories: the one is PAPR reduction with signal distortion, such as clippig, compandor; the other is PAPR reduction without signal distortion, such as SLM, PTS. As an alternative distortionless approach, precoding is a promising processing technique which is efficient, signal independent and distortionless. The precoder based on real Hardmard is proposed in [5] to reduce the PAPR of OFDM signals. The proposed Hadamard-precoder scheme may reduce the occurrence of the high peaks when compared the original OFDM system. The idea is to use the Hadamard transform to reduce the autocorrelation of the input sequence to reduce the peak to average power problem. In addition, it requires no side information to be transmitted to the receiver. Inspired by the literature [6], we propose an efficient PAPR reducing technique based on a complex Hadamard transform method.
The real Hadamard transform is based on the walsh functions, which form an ordered set of rectangular waveforms taking only two amplitude values (±1). But due to its limitation to the real-valued input data sequences, the compex Hadamard transform, which can process the complex-valued input functions, has been developed in [7,8]. The complex Hadamard transform is based on four complex values . Recently, SCHT has been applied in a DS-CDMA systems as the complex spreading sequences which are derived from the row vectors of an SCHT matrix [8]. However, no work has been presented so far focusing on reducing the PAPR of OFDM signals based on complex Hadamard transform.
. Recently, SCHT has been applied in a DS-CDMA systems as the complex spreading sequences which are derived from the row vectors of an SCHT matrix [8]. However, no work has been presented so far focusing on reducing the PAPR of OFDM signals based on complex Hadamard transform.
This paper aims to apply sequency-ordered complex Hadamard transform (SCHT) to reduce the PAPR of OFDM signals. It is described in detail about the properties, computational complexity and applications of sequency-ordered complex Hadamard transform in [7]. The proposed scheme makes use of the character domain. The data encoded in the OFDM signal are modulated by an IFFT (inverse fast Fourier transform) after being processed with the complex Hadamard transform, which can reduce the PAPR of OFDM signals. This scheme will be compared with the original real hadamad transform for reduction PAPR.
The organization of this paper is as follow. Section 2 presents OFDM signal and PAPR. Section 3, a new reduction PAPR scheme based on complex haramard is proposed. Computer simulation results are presented in Section 4. Section 5 draws conclusions.
2. OFDM Signal and PAPR
An OFDM system with N subcarriers is considered. Let a block of N symbol 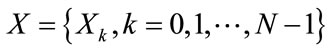 is formed with each symbol modulating one of a set of subcarriers
is formed with each symbol modulating one of a set of subcarriers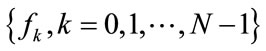 . The N subcarriers are chosen to be orthogonal, that is,
. The N subcarriers are chosen to be orthogonal, that is,  , where
, where 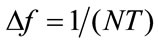 and T is the original symbol period. Therefore, the complex baseband OFDM signal can be written as
and T is the original symbol period. Therefore, the complex baseband OFDM signal can be written as
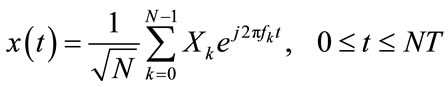 (1)
(1)
In general, the PAPR of OFDM signals 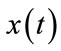 is defined as the ratio period between the maximum instantaneous power and its average power during an OFDM symbol
is defined as the ratio period between the maximum instantaneous power and its average power during an OFDM symbol
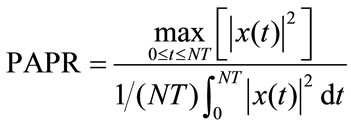 (2)
(2)
Reducing the 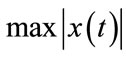 is the principle goal of PAPR reduction techniques. In practice, most systems deal with a discrete-time signal, therefore, we have to sample the continuous-time signal
is the principle goal of PAPR reduction techniques. In practice, most systems deal with a discrete-time signal, therefore, we have to sample the continuous-time signal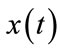 .
.
We can evaluate the performance of PAPR using the complementary cumulative distribution (CCDF) of PAPR of OFDM signal. The CCDF Is the probability that the PAPR of an OFDM symbol exceeds the given threshold PAPR0, it is given by
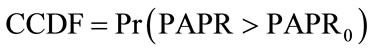 (3)
(3)
3. Basic Definition of SCHT Matrix [7]
The paper, by Park et al., [5] proposes a scheme for PAPR reduction in OFDM transmission using Hadamard transform. The idea to use the Hadamard transform is that the PAPR of OFDM signal is reduced by firstly to reduce the autocorrelation of the input data block. In the section, the definition of SCHT matrix is present. Any SCHT matrix of size 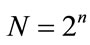 can be generated from complex Rademacher matrices whose row vectors are orthogonal to each other. The complex Rademacher matrices are the discrete versions of complex Rademacher functions (CARD) and they can be generated by sampling the complex Rademacher functions. The
can be generated from complex Rademacher matrices whose row vectors are orthogonal to each other. The complex Rademacher matrices are the discrete versions of complex Rademacher functions (CARD) and they can be generated by sampling the complex Rademacher functions. The 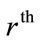 row of complex Rademacher matrix of size
row of complex Rademacher matrix of size 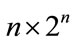 can be defined as
can be defined as
 (4)
(4)
where 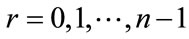 and
and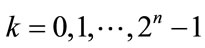 . The row vectors of the complex Rademacher matrices are orthogonal to each other in the complex domain. The CRAD is a complex Rademacher function with period 1. It can be expressed as [7]
. The row vectors of the complex Rademacher matrices are orthogonal to each other in the complex domain. The CRAD is a complex Rademacher function with period 1. It can be expressed as [7]
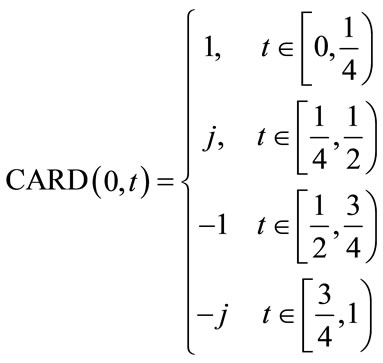 (5)
(5)
and
 (6)
(6)
for non-negative integer r, 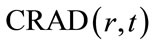 is defined as
is defined as
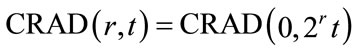 (7)
(7)
where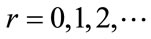 . This means that
. This means that 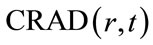 is obtained by compressing
is obtained by compressing 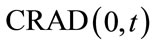 in yhr horizontal direction by a factor of
in yhr horizontal direction by a factor of .
.
With the complex Rademacher matrices defined, Sequency-ordered Complex Hadamard transform matrices, 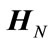 , are constructed as follows:
, are constructed as follows:
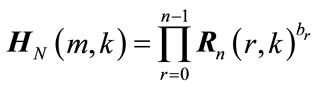 (8)
(8)
where 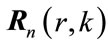 is the (rth, kth) element of the complex Rademacher matrix,
is the (rth, kth) element of the complex Rademacher matrix,
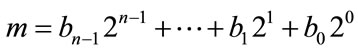 (9)
(9)
and 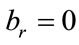 or 1. Let
or 1. Let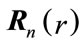 ,for
,for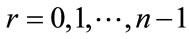 , be the rth row vector of the complex Rademacher matrix, and also, let
, be the rth row vector of the complex Rademacher matrix, and also, let  be the operator for element by element vector multiplication.
be the operator for element by element vector multiplication.
Based on them the complex Rademacher matrices are generated as mentioned in (4). For example, 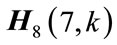 can be expressed as
can be expressed as
 (10)
(10)
since binary number of 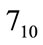 is
is 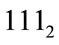 and the row indices 2, 1, 0 refer to ones found in the binary bit positions.
and the row indices 2, 1, 0 refer to ones found in the binary bit positions.
An SCHT matrix of order ,
,  , is a square matrix and it is said to be orthogonal in the complex domain as
, is a square matrix and it is said to be orthogonal in the complex domain as
 (11)
(11)
where  is the transport matrix,
is the transport matrix, 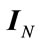 is the unit matrix of N order.
is the unit matrix of N order.
The  is symmetrical, that is
is symmetrical, that is
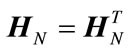 (12)
(12)
The inverse of the SCHT matrix, 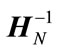 , is related as its complex conjugate transpose matrix,
, is related as its complex conjugate transpose matrix, 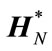 , as follows:
, as follows:
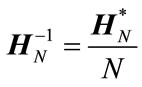 (13)
(13)
Definition: Sequency-ordered complex Hadamard transform of a signal vector 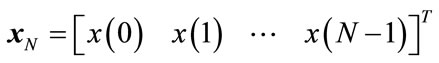 is defined as
is defined as
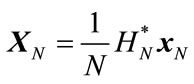 (14)
(14)
where 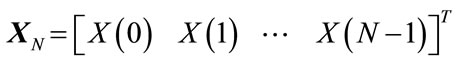 is the transformed column vector. The values of
is the transformed column vector. The values of 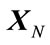 are the complex numbers. The data sequence can be recovered uniquely from the inverse transform, that is
are the complex numbers. The data sequence can be recovered uniquely from the inverse transform, that is
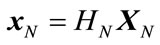 (15)
(15)
After the sequence 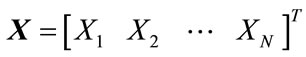 is transformed by Hadamard matrix of N order, the new data sequence is
is transformed by Hadamard matrix of N order, the new data sequence is
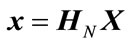 (16)
(16)
4. Proposed Scheme
In this study, we adopt precoder based on SCHT to reduce the PAPR of the OFDM signals with N orthogonal subcarriers. The block of system is showed in Figure 1.
When data block passed by complex Hadamard matrix before IFFT, the autocorrelation coefficients of IFFT input is reduced, then the PAPR of OFDM signal could be reduced. So the main idea of the proposed scheme is the data stream in the transmit end is firstly transformed by complex Hadamard matrix before IFFT signal processing. In the receiver end, the receiver data is firstly transformed by inverse complex Hadamard matrix before FFT signal processing.
5. Simulation Results
In this section, computer simulations are used to evaluate the peak-to-average ratio reduction capability with proposed scheme. The channel is modeled an additive while Gaussian noise (AWGN). In simulation, we research the effect of reduction PAPR based on our proposed scheme under different sub-carriers and modulation format.
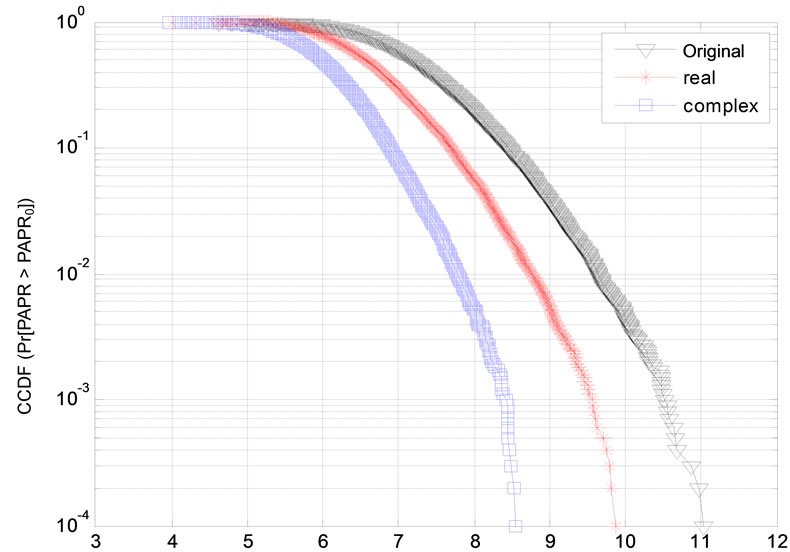
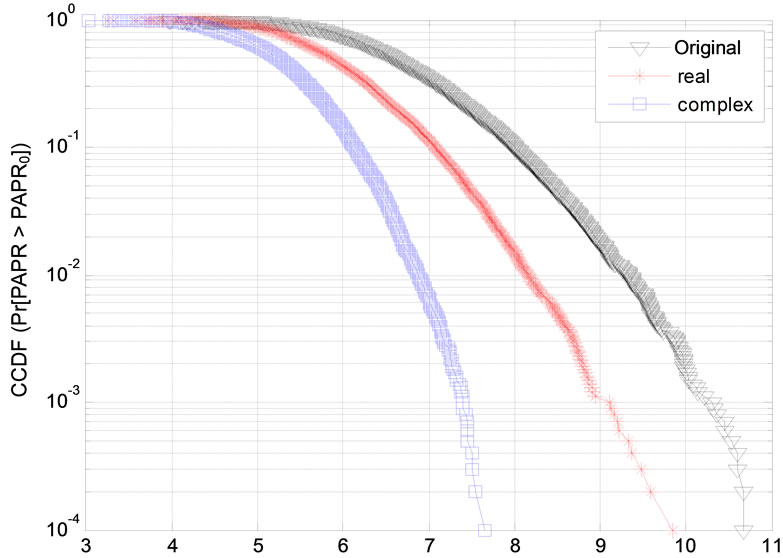
Figure 2 is the reduction PAPR performances of OFDM signal with 128 sub-carriers. The QPSK modulation is applied. We can see that the reduction PAPR performance of OFDM signal is better than original real Hadamard matrix precoding. Figure 3 is the comparision of PAPR about OFDM signals with 64 sub-cairrers and QPSK moudulaton format. We also see the proposed scheme is better than real Hadmard precoder method in terms of PAPR reduction. Figures 2 and 3 show that the PAPR of an OFDM signal using complex Hardmard precoder increases slightly as the number of subcarriers increases. For instance, the PAPR increases by about 1 dB when the subcarrier number increases from 64 to 128 at a CCDF of 10–3.
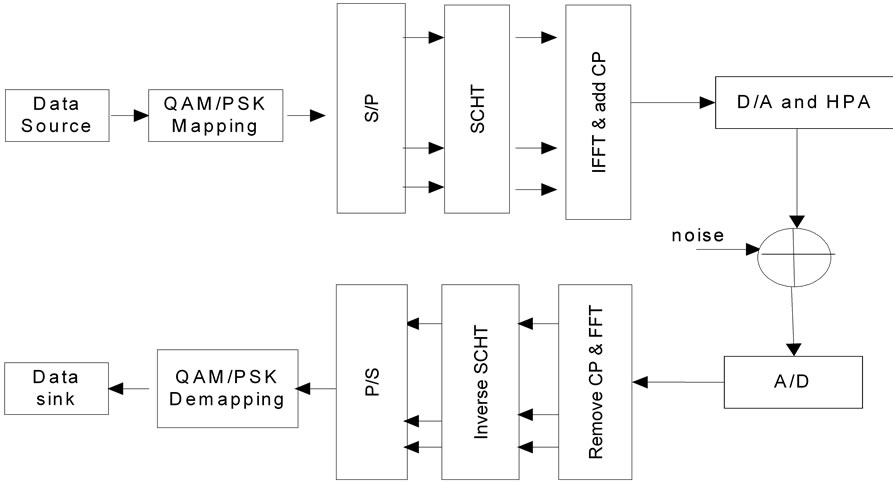
Figure 1. OFDM system block with SCHT precoding.
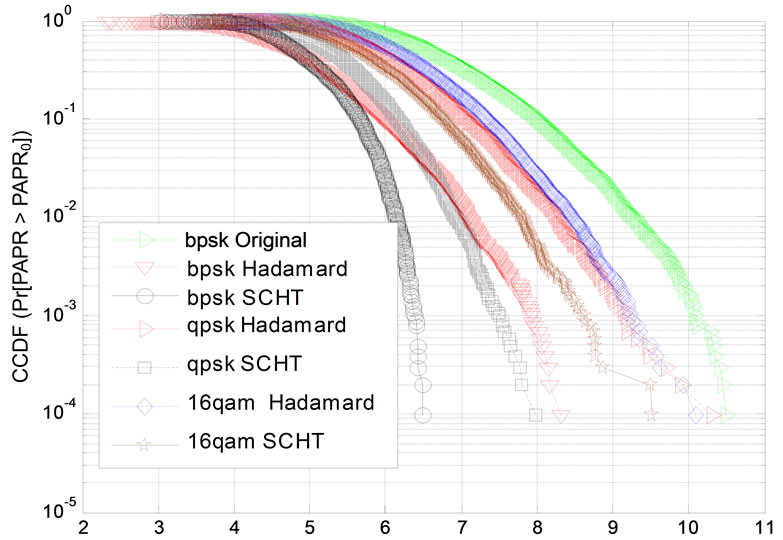
Figure 4 is the PAPR comparision of OFDM signals with different modulation format. We can see the CCDF of PAPR varying order of modulation format. The PAPR of OFDM signal increases slightly as the order of modulation increases. The amount of reduction PAPR is the most high when BPSK modulation format is adopted.
6. Conclusion
In this paper, a PAPR reduction scheme based on SCHT is proposed for the OFDM signal. The PAPR reduction performances of OFDM signals are evaluated by computer simulation. Simulation results state that the PAPR of OFDM signal based SCHT precoder is decreased about 1.2 dB compared to real Hadamard precoder as in literature [5].
7. Acknowledgements
This work is partially supported by the Open Fund of State Key Laboratory of Millimeter Waves (Southeast University, Ministry of Education, China), National Natural Science Foundation of China (Grant No. 71071145) and the Zhejiang Provincial Natural Science Foundation of China (Grant No. Y6090027).
REFERENCES
- T. Jiang and Y. Imai, “An Overview: Peak-to-Average Power Ratio Reduction Techniques for OFDM Signals,” IEEE Transactions on Wireless Communications, June 2008, pp. 56-57.
- A. Zolghadrasli and M. H. Ghamat, “An Overview of PAPR Reduction Techniques for Multicarrier Transimission and Propose of New Techniques for PAPR reduction,” Iranian Journal of Electrical and Computer Engineering, Vol. 7, No. 2, 2008, pp. 115-120.
- S. H. Muller and J. B. Huber, “OFDM with Reduced Peak to Average Power Ratio by Optimum Combination of Partial Transmit Sequences,” IEEE Electronics Letters, Vol. 33, No. 5, 1997, pp. 368-369. doi:10.1049/el:19970266
- R. W. Bauml, R F. Fischer and J. B. Huber, “Reducing the Peak-to-Average Power Ration of Multicarrier Modulation by Selected Mapping,” Electronics Letters, Vol. 32, No. 22, 1996, pp. 2056-2057. doi:10.1049/el:19961384
- M. Park, J. Heeyong, N. Cho, D. Hong and C. Kang, “PAPR Reduction in OFDM Transmission Using Hadamard Transform,” IEEE International Conference of Communications, Vol. 1, 2000, pp. 430-433.
- Z. P. Wang, J. N. Xiao, F. Li and L. Che, “Hadamard Precoding for PAPR Reduction in Optical Direct Detection OFDM Systems,” Optoelectronics Letters, Vol. 7, No. 5, 2011, pp. 0363-0366.
- A. Aung, B. P. Ng and S. Rahardja, “Sequency-Ordered Complex Hadamard Transform: Properties, Computational Complexity and Applications,” IEEE Transactions on Signal Processing, Vol. 56, No. 8, 2008, pp. 3562-3571. doi:10.1109/TSP.2008.923195
- A. Aung, B. P. Ng and S. Rahardja, “Performance of SCHT Sequences in Asynchronous CDMA System,” IEEE Communication Letters, Vol. 11, No. 8, 2007, pp. 641-643.