International Journal of Geosciences
Vol.07 No.03(2016), Article ID:65255,12 pages
10.4236/ijg.2016.73031
Estimation of Hydraulic Conductivity of Soils at a Watershed-Scale Using Porchet’s Method: Application in the Olezoa Waterhed, Yaounde, Cameroon
André Firmin Bon1,2*, Auguste Ombolo3, Guillaume Ewodo Mboudou2,3, Jules Rémy Ndam Ngoupayou2, Georges Emmanuel Ekodeck2
1Department of Climatology, Hydrology and Soil Science, Higher Institute of the Sahel, University of Maroua, Maroua, Cameroon
2Department of Earth Sciences, Faculty of Science, University of Yaounde I, Yaounde, Cameroon
3Department of Hydraulics and Water Control, Higher Institute of the Sahel, University of Maroua, Maroua, Cameroon

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 January 2016; accepted 28 March 2016; published 31 March 2016
ABSTRACT
Contamination analysis of the unsaturated zone requires information on the spatial variability of hydraulic conductivity. Two types of hydraulic tests (variable and constant charge) were identified to estimate the spatial variability of the hydraulic conductivity of the surface portion of the unsaturated zone in the Olezoa watershed. These tests were performed on 100 holes at depths ranging between 50 and 90 cm, spread throughout the watershed. The hydraulic conductivity values obtained at 50 and 90 cm are close to the absolute value for each method. However, they show a difference of 10−1 m/s between the two types of test regardless of the depth of investigation. The representation of data in the graph indicates a staircase quartile distribution for the variable charge test. The test at constant charge, rather presents a log normal distribution which is also supported by the Kolmogorov-Smirnov test. Hydraulic conductivities have a random component and a spatial organization which results from soil and/or morphological factors. This organization thus permits the distinction of zones which could show high pollution risk.
Keywords:
Unsaturated Zone, Quartile Graphs, Hydraulic Conductivity, Olezoa

1. Introduction
The transfer of water in the saturated part of alterites is linked to the hydraulic properties of the overlying unsaturated zone. Their assessment therefore has important applications for the management of irrigation and underground drainage [1] . Hydraulic conductivity can either be estimated in the field, in the laboratory or from models [2] . However, the characteristics relating to the accuracy of the results from each method remains questionable. In fact, the choice of the method depends on the conditions of its implementation, investigation scale, environmental conditions and calibration parameters of the model [3] . For example, laboratory results from reduced volumes of soil are difficult to extrapolate on the field. Hydraulic properties measured in the laboratory can be different from those observed in situ.
The theoretical approaches to these are difficult to implement at the scale of a watershed because they do not account for spatial variability. According [4] , the spatial variability of soil hydraulic properties can cause a problem of heterogeneity irrigation response or underground drainage. The use of predictive models requires the knowledge of certain soil properties [5] . Unfortunately, these do not always better reflect the nonlinearity of hydrodynamic soil properties [5] . Moreover, these models always require the adjustment of the parameters that only in-situ experimental measurements permit to validate. In situ experimentation is time consuming and often requires substantial financial and human investment. These constraints and technical difficulties generally reduce the investigations to the scale of a plot of land. When investigations are made at the scale of a watershed, the measurement distances are wider but in plots, the distances are closer, meanwhile, the unsaturated zone is very heterogeneous [6] [7] .
Several in situ measurement methods for the hydraulic conductivity of the soil surface portion exist but the most commonly used are those of Müntz, Guelph permeameter and that of Porchet [8] . These methods give the saturated hydraulic conductivity field by applying a positive charge on soils [9] . However, Müntz’s method only takes into account a unidimensional vertical flow [10] . The Guelph permeameter method takes into account the horizontal and vertical components of flow. On the other hand, Porchet’s method mainly characterizes horizontal movements [11] . The latter seems more appropriate in urban areas where pollution of groundwater by latrines is generally through lateral transfers. It is also part of the methods used to assess the degree of vulnerability of aquifers and during evaluation of individual sanitation projects [10] . Indeed, in terms of noncollective sanitation, the choice of the treatment process to implement depends on the soil’s ability to receive and dispose off wastewater.
This justifies the choice of Porchet’s method to study the main parameter affecting the movement of water in the soil. The aim of the present work is to hydraulically characterize the upper part of the altered basement of the Olezoa watershed. The hydraulic investigations on the part of the soil near the surface will contribute to better protect water resources in urban areas.
2. Presentation of the Study Area
The Olezoa watershed (3.65 km2) is located in the Yaounde region-Southern Cameroon (Figure 1(A)). This basin has an average altitude of 740 m and has a hilly landscape with tabular summits. Morphological units with higher altitudes are found in the North (770 - 800 m) and the southwest (770 - 780 m) respectively, meanwhile units with moderate altitudes are at the Centre/southeast (740 - 760 m).
It is characterized by an equatorial climate marked by two rainy seasons (March to June and September to November) and two dry seasons (December to February and July to August). The Olezoa watershed has within it, five fish ponds with four being totally eutrophic due to anthropogenic activities (Figure 1(B)). In this watershed is found the University of Yaounde I and other structures such as the military camp, the Mvolye Catholic mission, residences/offices of diplomatic corps and the University Hospital Centre. The population density per hectare is greater than 600 inhabitants/ha against an average of 50 inhabitants/ha in the country. This high concentration is accompanied by uncontrolled land use and the proliferation of wells or springs which are adjacent to latrines. These latrines are dug under the regolith developed on the Pan-African orthogneiss basement [12] . The soil cover consists of red ferrallitic soil at hill flanks and yellow ferrallitic soils in the lower areas of slopes and waterlogged soils in marshy lowlands [13] . The vertical organization ferrallitic soils is composed from bottom to top of an alteration set (isalterite and alloterite), a glebular set and a loose clayey set. This study is specifically concerns the unsaturated part of the latter two sets which vary morphologically (Figure 1(C)).
Figure 1. Location map (A), distribution of observation points (B) soil profiles in the Olezoa watershed (C).
3. Material and Methods
The methodological approach used in this work is based on a spatial estimation of hydraulic conductivity of soils from in situ hydraulic tests. These tests were done on 100 points distributed throughout the watershed (Figure 1(B)). Given the presence of the private owned zones and the high urbanization, it was not possible to carry out systematic transects. However, the topography and the availability of space, guided the selection of measuring points.
Measurement protocols at variable and constant levels were based on Porchet’s method. Details on the classic exploitation of a measurement at the variable charge using Porchet’s method are presented in the works of [10] [11] . In this study, holes with a diameter of 15 cm and depths of 50 cm and 90 cm were dug with a manual auger during the short dry season (July and August 2014). Rainy phases observed during this period of study significantly reduced the time to saturation to about 2 hours, the latter generally being 4 hours or more [11] . The timing of the measurement was set at 30 minutes and the measurement interval was close to 10 seconds at the beginning of the flow and also taking into account the heterogeneity of the soil [14] . However, evaporation phenomena are neglected due to the humid climate. The water flow in the hole is thus expressed by the following equations [11] :
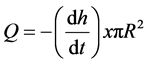 (1)
(1)
with 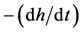 being the rate of descent of the water level and πR2, the infiltration surface.
being the rate of descent of the water level and πR2, the infiltration surface.
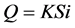 (2)
(2)
with 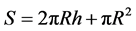 being the infiltration surface; i is the hydraulic gradient of 1 and K is the hydraulic conductivity. Equating these two equations, we obtain:
being the infiltration surface; i is the hydraulic gradient of 1 and K is the hydraulic conductivity. Equating these two equations, we obtain:
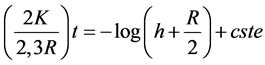 (3)
(3)
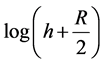 is a linear function of time t. The slope of the line being proportional to K, This can therefore be
is a linear function of time t. The slope of the line being proportional to K, This can therefore be
obtained by the following relationship:
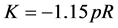 (4)
(4)
with p being the slope of the line and R the radius of the hole (in m).
The constant charge method was realised with a SDEC infiltrometer set (Figure 2). The specification of this
Figure 2. Apparatus for the measurement of constant charge. (A) Infiltrometer set; (B) measurement phase: (a) infiltrometer in pit; (b) reading of water volume passed in the measurement reservoir.
device and the operational procedure can be found in the website http://www.sdec-France.com. In this study, the holes used for the measurements have the same characteristics as those of the variable charge measurements. The saturation reservoir has a capacity of 25 L and that for measurement is 2.5 L, calibrated at 100 ml interval. During the saturation stage, the water level above the bottom of the hole is automatically adjusted to 15 cm by the control level unit which is a stainless steel. The imbibition period of the soil is related to the capacity of the saturation reservoir. It was not therefore evident to determine the saturation time due to interruptions observed during the renewal of the water reserve. This time is known when the saturation bubbles are sufficiently spread out. Immediately the imbibition phase is completed, the level regulator is then connected to the measurement reservoir. The measurement phase, which is done by maintaining the constant level (15 cm) was between 10 and 20 minutes; operating in saturated soil conditions using Darcy’s law whereby hydraulic conductivity is given by the following relationship:
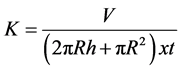 (5)
(5)
with V: the volume of water percolated (in L); R the radius of the hole; h the charge (in m) and t is the time (in second).
Data analysis focused on a comparison of the results from two measurement protocols. These results were correlated with altitude in order to find the filiation between the hydraulic conductivity and morphology. The hydraulic conductivity maps were interpolated in order to assess the spatial variations of this hydrodynamic property of soils. Moreover, tests form data above and below the median and ascending and descending data and the Box-Pierce test were calculated in order to determine the random or non-random character of hydraulic conductivity. The first test counts the number of times the sequence was above or below the median. The second test counts the number of times the sequence has increased or decreased. The third test is based on the sum of squares of the first 24 autocorrelation coefficients.
4. Results
Hydraulic conductivities range from 2.59 × 10−6 and 9.48 × 10−5 m/s and between 3.45 × 10−6 and 7.83 × 10−5 m/s respectively 50 and 90 cm for the variable level method against 6.29 × 10−7 7.83 × 10−5 m/s and between 8.44 × 10−7 and 1.56 × 10−4 m/s at the same depths with the infiltrometer set (Table 1). The conductivities obtained have a constant charge difference of 10−1 m/s with a variable charge test. It shows no difference in an ascending order with respect to the depth of investigation. This difference is significant in maximum value with a constant charge test.
The isopermeabilty maps have distinct morphologies whatever the depth and method of investigation (Figure 3). These maps show a delimitation indicating areas with high hydraulic conductivity. These correspond to areas which are most vulnerable to pollution in the watershed. Constant charge test data show an affiliation with altitude (Figure 4). This is very common at 90 cm depth (Figure 4(B)); high conductivities are common in areas with moderate topographic slopes constituted of lateritic materials (glebular set). Nevertheless, there is a need to remain cautious with this interpretation given the shallow depth of investigation. The data issued from the variable charge method does not indicate an affiliation with altitude whatever the investigation depth (Figure 4). They exhibit hydraulic clouds which correspond to a step-like distribution on quartile graphs whereas those of infiltrometer set show a logarithmic distribution (Figure 5). The distributions observed as such with the infiltometer set correspond to log normal distributions, according to the Kolmogorov-Smirnov test (Figure 6).
Table 1. Hydraulic conductivity values (K (m/s) in the Olezoa watershed.
Note: CV = Variation coefficient.




Figure 3. Maps showing distribution of hydraulic conductivity in the Olezoa watershed at respective depths (A): constant charge at 50 cm; (B): constant charge at 90 cm; (C): variable charge at 50 cm and (D) variable charge at 90 cm. The horizontal grey band shows the logarithmic variation of hydraulic conductivity.


Figure 4. Variation of hydraulic conductivity with altitude. (A): 50 cm depth; (B): 90 cm depth.
Probability values of different tests, obtained with a confidence level of 95.0%, are greater than 0.05, irrespective of the depth of investigation for the infiltrometer set and only at 90 cm depth for variable charge measurement (Table 2). The observed differences between the value obtained (B parameter) and the expected value (C parameter) are small in terms of absolute value. The probability values indicate the randomness of hydraulic conductivity between 0 and 90 cm depth, especially with the infiltrometer set.
5. Discussion
The hydraulic conductivity values obtained in this study show a spatial heterogeneity of the hydrodynamic soil


Figure 5. Graph of quantiles: (A) 50 cm depth; (B) 90 cm depth.
properties [4] . In fact, they show the very heterogeneous nature of the unsaturated zone [7] . This heterogeneity shows the variability and complexity of soil characteristics [6] . This variability can cause a problem of heterogeneity of response to irrigation or underground drainage [4] . However, the spatial variability of hydraulic conductivity can be used to analyse contamination in the unsaturated zone [15] . In this heterogeneous environment, the distribution of hydraulic conductivity obeys the log normal law [16] and hydraulic conductivity presents a strong random component [17] . The absence of a total random character observed in this study could be linked to morphopedologic processes. In fact, the vertical organization of the soil profile shows the transformation of the soil cover in some areas. Profiles undergoing weathering are less thick (southwest profile) unlike those issued from dismantlement of old lateritic systems [18] . According [19] , the heterogeneous spatial distribution of the hydraulic conductivity values indicates a local variation of the emplacement processes (or erosion) of alterites. This distribution is related to the intrinsic soil properties, the nature of the alterite [2] and its topographic position [1] as well as the used protocol [2] [10] [11] . According [10] , testing at constant charge reflects the real characteristics of the soil. The chaotic distribution observed with the variable charge test result from saturation conditions. Indeed the assessment of the saturation of the soil depends largely on the operator contrary to the constant charge test whose saturation is regulated by an automatic device.
6. Conclusion
Two hydraulic in situ tests led to the proposal of a synthetic image of hydraulic conductivity of the surface portion of the unsaturated zone located between 0 and 90 cm depth. The variable charge test shows a hydraulic cloud without significant compartmentalization across the watershed. At this level, the hydraulic conductivities




Figure 6. Histograms distribution of hydraulic conductivity values. (A) Infiltrometer set; (B) Porchet’s method. (a) and (b) = 50 cm depth; (c) and (d) = 90 cm depth.
Table 2. Random character tests of hydraulic conductivity data in the Olezoa watershed.
Note: A = median value; B = Number of data above and below the median; C = Number of awaited data; D = Statistic tests for large samples; E = Probability; F = Number of ascending and descending data.
obtained with the infiltrometer set show a useful zoning in determining the areas which are vulnerable to pollution. These conductivities have a spatial distribution related to the soil and morphological features. Information on the spatial variability of hydraulic conductivity obtained may serve as a basis for analyzing contamination in the unsaturated zone.
Acknowledgements
The authors are thankful to the International Foundation for Science (IFS) for its financial and material support in the realization of this work (Grant No. W/5404-1).
Cite this paper
André Firmin Bon,Auguste Ombolo,Guillaume Ewodo Mboudou,Jules Rémy Ndam Ngoupayou,Georges Emmanuel Ekodeck, (2016) Estimation of Hydraulic Conductivity of Soils at a Watershed-Scale Using Porchet’s Method: Application in the Olezoa Waterhed, Yaounde, Cameroon. International Journal of Geosciences,07,397-408. doi: 10.4236/ijg.2016.73031
References
- 1. McKeague, J.A., Wang, C. and Topp, G.C. (1982) Estimating Saturated Hydraulic Conductivity from Soil Morphology. Soil Science Society of America Journal, 46, 1239-1244.
http://dx.doi.org/10.2136/sssaj1982.03615995004600060024x - 2. Deb, S.K. and Shukla, M.K. (2012) Variability of Hydraulic Conductivity Due to Multiple Factors. AJES, 8, 489-502.
- 3. Tokumoto, I., Heilman, J.L., Mcinnes, K.J. and Morgan, C.L.S. (2014) Hydraulic Properties of Rocky Soils in a Semi-Arid Savanna on the Edwards Plateau. Journal of Arid Land Studies, 24, 77-80.
- 4. Warrick, A.W. and Gardner, W.R. (1983) Crop Yield as Affected by Spatial Variations of Soil and Irrigation. Water Resources Research, 19, 181-186. http://dx.doi.org/10.1029/WR019i001p00181
- 5. Vogel, T., Van Genuchten, M.T. and Cislerova, M. (2001) Effect of the Shape of the soil Hydraulic Functions near Saturation on Variably-Saturated flow Predicitions. Advances in Water Resources, 24,133-144.
- 6. Wanko, A., Tapia, G. and Mosé, R. (2015) Contribution to Numerical Modeling of Water Flow in Variably Saturated, Heterogeneous Porous Media. Revue des Sciences de l’eau, 28, 179-197.
http://dx.doi.org/10.7202/1034007ar - 7. Yeh, T.-C.J. and Harvey, J.D. (1990) Effective Unsaturated Hydraulic Conductivity of Layered Sands. Water Resources Research, 26, 1271-1279. http://dx.doi.org/10.1029/WR026i006p01271
- 8. Chossat, J.C. (2005) La mesure de la conductivité hydraulique dans les sols: Choix des méthodes. Tec et Doc, Hermés-Lavoisier.
- 9. Boivin, P., Touma, J. and Zante, P. (1987) Mesure de l’infiltrabilité du sol par la méthode du double anneau. 1-Résultats expérimentaux. Cahiers Orstom, Série Pédologique, 24, 17-25.
- 10. Lallemand-Barrès, A. and Roux, J.-C. (1999) Périmètres de protection des captages d’eau souterraine destinée à la consommation humaine. Manuels et Méthodes. BRGM, 2ème édition.
- 11. Colombani, J., Lamagat, J.-P. and Thiebaux, J. (1973) Mesure de la perméabilité des sols en place: Un nouvel appareil pour la méthode Muntz. Une extension de la méthode porchet aux sols hétérogènes. Bulletin des Sciences hydrologiques, XVIII, 197-235.
- 12. Toteu S.F., Yongue Fouateu, R., Penaye, J., Tchakounté, J., Seme Mouangue, A.C., Van Schmus, W.R., Deboule, E. and Stendal, H. (2006) U-Pb Dating of Plutonic Rocks Involved in the Nappe Tectonic in Southern Cameroon: Consequence for the Pan-African Orogenic Evolution of Central African Fold Belt. Journal of African Earth Sciences, 44, 479-493. http://dx.doi.org/10.1016/j.jafrearsci.2005.11.015
- 13. Ndjigui, P.-D., Badinane, M.F.B., Nyeck, B., Nandjip, H.P.K. and Bilong, P. (2013) Mineralogical and Geochemical Features of the Coarse Saprolite Developed on Orthogneiss in the SW of Yaoundé, South Cameroon. Journal of African Earth Sciences, 79, 125-142.
http://dx.doi.org/10.1016/j.jafrearsci.2012.11.008 - 14. Dubreuil, P. (1967) Détermination des paramètres du sol influant sur le cycle hydrologique dans les bassins représentatifs et expérimentaux (Protocoles de mesures). Cah. ORSTOM, sér. Hydrol., IV, 3-18.
- 15. Xiang, J., Scanln, B.R., Mullican, W.F., Chen, L. and Goldsmith, R.S. (1997) A Multistep Constant-Head Borehole Test to Determine Field Saturated Hydraulic Conductivity of Layered Soils. Advances in Water Resources, 20, 45-57. http://dx.doi.org/10.1016/S0309-1708(96)00017-6
- 16. Yidana, S.M., Ophori, D. and Banoeng-Yakubo, B. (2007) Hydrogeological and Hydrochemical Characterization of the Voltaian Basin: The Afram Plains Area, Ghana. Environmental Geology, 54, 1751-1762.
- 17. Gascuel-Odoux, C. (1987) Variabilité spatiale des propriétés hydriques du sol, cas d’une seule variable. Revue bibliographique, Agronomie, 7, 61-71. http://dx.doi.org/10.1051/agro:19870108
- 18. Bitom, D., Volkoff, B., Beauvais, A., Seyler, F. and Ndjigui, P.-D. (2004) R?le des héritages et du niveau des nappes dans l’évolution des modelés et des sols en zone intertropicale forestière humide. Comptes Rendus Geoscience, 336, 1161-1170. http://dx.doi.org/10.1016/j.crte.2004.03.019�
- 19. Chaplot, V., Curmi, P., Walter, C. and Bernoux, M. (2000) Analyse de cartes pédologiques pour identifier le r?le du régime tectonique sur la répartition régionale de la perméabilité des altérites. Comptes Rendus de l’Académie des Sciences. Paris, 330, 479-483. http://dx.doi.org/10.1016/s1251-8050(00)00181-6�
NOTES
*Corresponding author.





