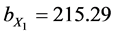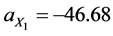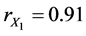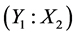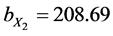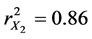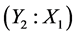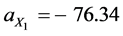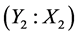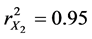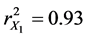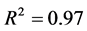Journal of Minerals and Materials Characterization and Engineering
Vol.02 No.05(2014), Article ID:50088,8 pages
10.4236/jmmce.2014.25053
Regression Analysis of Ashaka Clay-Bonded Sand
Aondona-Paul Ihom*, Aniekan Offiong
Department of Mechanical Engineering, University of Uyo, Uyo, Nigeria
Email: *draondonaphilip@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 July 2014; revised 18 August 2014; accepted 29 August 2014
ABSTRACT
Regression Analysis of Ashaka Clay-Bonded Sand has been successfully carried out. The study data were generated at the National Metallurgical Development Centre, Jos Sand Testing Laboratory. The result of the regression analysis showed that both dry compression strength and dry shear strength have a very strong relationship with clay content and moisture content. The correlation coefficient, coefficient of determination and the coefficient of multiple determination in each relationship was very high. The coefficient of multiple determination for the relationship between dry compression strength, clay content and moisture content was 0.91, while that of dry shear strength, clay and moisture content was 0.97. Two mathematical models have been developed for the estimation of dry compression strength and dry shear strength on the shop floor.
Keywords:
Regression, Dry Shear Strength, Dry Compression Strength, Clay-Bonded Sand, Ashaka

1. Introduction
According to Ihom, et al. [1] a model that incorporates several independent variables is known as multiple regression model and in situations where linearity can be assumed, a linear multiple regression model can be used to investigate the possibility that movements in
 the dependent variable are caused by several independent factors and not just one as in the basic model [1] .
the dependent variable are caused by several independent factors and not just one as in the basic model [1] .
Recently, a better understanding of clay bonded sand system for foundry application has been found to be important with the fast development of high speed moulding. The available literature [1] - [6] points out that the shape and size of sand grains, nature and content of clays, moisture and efficiency of mulling the raw materials are important factors that decide the properties and behaviours of the sand moistures. Although classical methods of investigations were helpful in identifying the factors, the optimum formulations of the sand have remained a critical problem for the foundry. It is also a fact that classical tests in themselves do not explain the extent of relationship between the dependent variable and the independent variables. Further, it was recognized that the mulling station is the central point in deciding the properties and behaviours of clay-bonded sands [7] [8] . For many years, sand control was through evaluation of the physical properties of sand mixtures in line with the recommendations made [9] . Later, such practice came under attack and it was felt that the physical properties would be supplemented by complete analysis of mixtures [10] subsequently, a new method of testing sands, and also some type of control were developed which were claimed to be the best sand control vis-à-vis analysis of the sand mixture [1] - [10] . A careful review of the literatures above clearly reveals that most of the methods attempt to establish some type of correlation between the physical properties and the factors of the sand mixtures for the purpose of attaining a satisfactory level of sand control. Several authors have pointed out that considering the number of variable factors involved, sand mixture control and analysis can best be handled through regression analysis and/or with the aid of a computer [1] [2] [10] in view of these observations, and the study of clay- bonded sands by application of statistical design of experiments using multiple regression models seems to be quite justified. Clay content and moisture content variations in clay-bonded sand mixtures play a vital role in determining the properties of the moulding mixtures and the extent and degree of the correlations can be established using regression analysis. Properties can equally be estimated on the shop floor using mathematical models derived from regression analysis without necessary conducting instrumental tests on the moulding mixtures once the variable factors are known [1] - [10] .
The objective of this work is to study Ashaka clay-bonded sand moulding mixture using regression analysis.
2. Materials and Method
2.1. Materials
The equipment and machines used for this work were from National Metallurgical Development Centre, Jos, which has a standard sand research Laboratory, equipped with equipment like; sand mixers, digital weighing balance, universal strength testing machine, green compression testing machine, electric permmeter, mouldability tester, speedy moisture tester, sand rammer, sieve shaker and many others. The materials used for the work included; sand from Ashaka sand deposit, bentonite from Baroid of Nigeria Ltd. Port-Harcourt and water from the laboratory.
2.2. Method
Seven (7) different moulding mixtures were prepared using standard test procedures. After mulling and mixing, the standard specimens of dimension 50 mm × 50 mm (DIN) were prepared using a sand rammer installed with bulk density tester. The numbers of ramming were kept constant at 3 rams. Then the foundry properties of the sand mixtures were determined and the results are given in Table 1. This result which was generated in the sand test laboratory of NMDC as explained above formed the basis of the regression analysis.
Multiple Regression Model Development
The basic two variable models (one dependent and one independent variable) is:
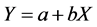 (1)
(1)
Which can be solved using the normal equations thus:
Table 1. Determined foundry properties of the moulding mixtures at constant mulling time and number of rams.
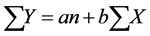 (2)
(2)
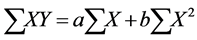 (3)
(3)
From this can be developed models with more than two variables and this is illustrated below using a 3 variable model (one dependent and two independent variables,
 ,
,
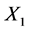 , and
, and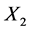 ):
):
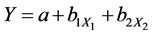 (4)
(4)
This can be solved by the normal equations for a three variable model, as follows:
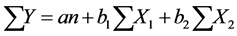 (5)
(5)
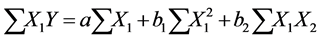 (6)
(6)
 (7)
(7)
The line of best fit gives way to a plane of best fit,
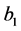 is the slope of the plane along the
is the slope of the plane along the
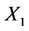 axis,
axis,
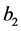 is the slope along the
is the slope along the
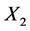 axis and the plane cuts the
axis and the plane cuts the
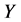 axis at “
axis at “

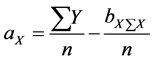
The coefficient of correlation between the variables is given by:




The closeness of fit is measured by the coefficient of multiple determination


Table 2 gives the calculation of separate regressions with Dry compression strength as

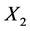
Table 2. Calculation of separate regressions with dry compression strength as
For Regression of Dry Compression Strength


From Equation (8):
From Equation (9):
The regression equation for the relationship of dry compression strength of the moulding mixture with % clay content variation Equation (1) is:
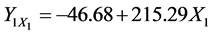
The coefficient of correlation for this relationship in Equation (12) (from Equation (10)) is:
The coefficient of determination



For Regression of Dry Compression Strength


From Equation (8):
From Equation (9):
The regression equation for the relationship of dry compression strength of the moulding mixture with % moisture content variation (from Equation (1)) is:

The coefficient of correlation for this relationship in Equation (13) (from Equation (10)) is:
The coefficient of determination

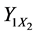
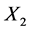
The Multiple Regression (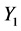
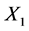

The multiple regression calculations are carried out using the three variable normal equations (Equations (4)- (7)) and this gave rise to a multiple regression equation with best fit with
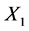
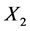

Table 3 shows empirical values of dry compression strength alongside with calculated values using mathematical model of Equation (14).
Coefficient of Multiple Determination,


From Equation (11) the coefficient of Multiple Determination
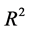
Table 4 gives the calculation of separate regressions with dry shear strength as Y2, clay content as X1 and moisture content as X2.
For Regression of Dry Shear Strength
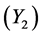
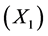
From Equation (8):
From Equation (9):
Table 3. Empirical values of dry compression strength alongside calculated values using Equation (14).
Table 4. Calculation of separate regressions with dry shear strength as
The regression equation for the relationship of dry shear strength of the moulding mixture with % clay content variation from Equation (1) is:

The coefficient of correlation for this relationship in Equation (15) (from Equation (10)) is:
The coefficient of determination



For Regression of Dry Shear Strength

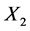
From Equation (8):
From Equation (9):
The regression equation for the relationship of dry shear strength of the moulding mixture with % moisture content variation from Equation (1) is:

The coefficient of correlation

The coefficient of determination

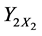

The Multiple Regression (


The multiple regression calculations are carried out using the three variable normal equations (Equations (4)-(7)) and this gave rise to a multiple regression equation with best fit with



Table 5 shows empirical values of dry shear strength alongside with calculated values using mathematical model of Equation (17):
Coefficient of Multiple Determination,
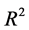

From Equation (11) the coefficient of Multiple Determination

3. Results and Discussion
3.1. Results
The result of the regression analysis is here presented.
Regression of dry compression strength



The coefficient of correlation





Regression of dry compression strength




The coefficients of correlation

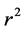
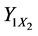


The multiple regression of dry compression strength on



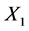
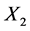

The coefficient of multiple determination,



Table 3 gives the empirical values of dry compression strength alongside calculated values using Equation (14).
The results for regression study of dry shear strength are as follows:
Table 5. Empirical values of dry shear strength alongside with calculated values using Equation (17).
Regression


The coefficients of correlation

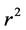

Regression


The coefficients of correlation



The multiple regression (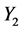
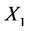


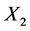

Table 5 shows empirical values of dry shear strength alongside calculated values using Equation (17).
The coefficient of multiple determination,
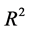

3.2. Discussion
The result above as obtained from the regression analysis is here discussed. Equations (12) and (13) reveal the individual effect of clay content and moisture content variation on dry compression strength of the sand mixture. The two equations can be used to predict the influence of the two variable factors individually on the dry compression strength. The two equations are showing that as the independent variables increase dry compression strength also increases. This is supported by the high positive correlation coefficient and coefficient of determination. For Equation (12) the correlation coefficient for the relationship between dry compression strength and clay content variation is 0.91 while the coefficient of determination is 0.82 which means 82% in movements of dry compression strength is as a result of variations in clay content. For Equation (13) the correlation coefficient for the relationship between dry compression strength and moisture content variation is 0.93 while the coefficient of determination is 0.86, which means 86% in movement values of dry compression strength is as a result of variations in moisture content. This is assuming that there is no other influence from another variable. The above regression results fully agree with the results of several authors who have studied the influence of clay and moisture variations on dry compression strength. Moisture content and clay content increase, all give rise to increase in dry compression strength [11] - [13] .
The multiple regression of dry compression strength on clay content and moisture content variation is given in Equation (14). This equation defines the relationship between the dry compression strength and the two variables of clay content and moisture content. The relationship can be seen in Table 3 as the two variables increase the dry compression strength also increases. This is supported by the strong positive coefficient of multiple determination

The result of regression study of dry shear strength with clay and moisture content shows that the individual regression of dry shear strength on clay content and moisture content is given by Equations (15) and (16). They reveal the individual effect of clay and moisture content on dry shear strength of the moulding mixture. The two equations can be used to predict the influence of the variable factors individually on the dry shear strength. The two equations are showing that as the two independent variables increase, dry shear strength also increases. This is supported by the strong positive correlation coefficients and coefficients of determination. For Equation (15) the correlation coefficient for the relationship between dry shear strength and clay content variation is 0.96 while the coefficient of determination is 0.93, which means 93% in changes of dry shear strength is as a result of variations in clay content assuming clay content is acting alone. For Equation (16) the correlation coefficient for the relationship between dry shear strength and moisture content variation is 0.97 while the coefficient of determination is 0.95, which means 95% in changes in values of dry shear strength is as a result of variations in moisture content assuming it is acting alone. The regression results fully agree with previous works by several authors [7] - [15] including Jain [16] who studied the influence of clay and moisture on dry shear strength. Clay and moisture content increase, both increase the dry shear strength of moulding mixtures.
The multiple regression of dry shear strength on clay content and moisture content variation is given in Equation (17). This equation defines the relationship between the dry shear strength and the two variables of clay content and moisture content. The relationship can be seen in Table 5 as the two independent variables increase the dry shear strength also increase. This is supported by the strong positive coefficient of multiple determination
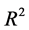
4. Conclusions
The study regression analysis of Ashaka clay-bonded sand has been extensively undertaken. The analysis has led to the following conclusions:
1. Dry compression strength has strong positive relationship with clay content and moisture content. This has been shown in the strong positive correlation coefficient and coefficient of determination that exist between the individual relationship between dry compression strength and the two independent variables.
2. The coefficient of multiple determination for the relationship between dry compression strength and the two variables of clay content and moisture content is a strong positive value of 0.91 which means that 91% of the changes in the value of the dry compression strength is brought about by the changes in the two independent variables.
3. The developed mathematical model of Equation (14) can be used to predict dry compression strength values.
4. Dry shear strength has a strong relationship with clay content and moisture content. This is shown in the strong positive coefficient of correlation and coefficient of determination.
5. Dry shear strength has a strong coefficient of multiple determination in the relationship with clay content and moisture content. The combined influence of these two variables on dry shear strength is very strong.
6. The multiple regression equation of dry shear strength with the two variables of clay content and moisture content can be used to predict dry shear strength values on the shop floor.
Acknowledgements
I wish to acknowledge the contributions of the staff of the sand testing laboratory of National Metallurgical Development Centre, Jos where the data for this work was generated. Their assistance greatly contributed to the success story of this work.
References
- Ihom, A.P., Yaro, S.A. and Aigbodion, V.S. (2006) Application of Multiple Regression-Model to the Study of Foundry Clay-Bonded Sand Mixtures. JICCOTECH, 2, 161-168
- Ihom, A.P., Agunsoye, J., Anbua, E.E. and Bam, A. (2009) The Use of Statistical Approach for Modeling and Studying the Effect of Ramming on the Mould Parameters of Yola Natural Sand. Nigerian Journal of Engineering, 16.1, 186- 192
- Zrimsek, A.H. and Vingas, G.J. (1961) Effect of Moulding Variables Parameters on the Properties of Clay Bonded Sands. Modern Casting, 39, 85.
- Lucey, T. (2000) Quantitative Techniques. 7th Edition, Low Priced Edition Funded by the British Government, London, 99-150.
- Chakoraborty, M. and Dhindaw, B.K. (1979) Utilization of Regression Equations in Optimization of Properties of Clay Bonded Sands. Proceedings of the 41st International Foundry Congress, Liege, 8.
- Chakoraborty, M. and Dhindaw, B.K. (1985) Application of the Statistical Design of Experiments in the Study of Clay-Bonded Sand Mixtures, the British Foundryman. Journal of the Institute of the British Foundrymen, 114-118.
- Eckey, D.C. and Goldress, J.E. (1989) The Design of Experiments in the Sand Casting Foundry. Transactions of the American Foundryman Society, 62, 605.
- Ihom, A.P., Allen, M.A., Nwonye, I.E., Ilochionwu, C. and Ogbodo, N.J. (2014) Investigation of the Accuracy of Non- linear Model in the Study of Green Permeability of Green Sand Moulds. African Journal of Engineering Research, 2, 14-20.
- Ihom, A.P., Ogbodo, J.N., Allen, A.M., Nwonye, E.I. and Ilochionwu, C. (2014) Analysis and Prediction of Green Permeability Values in Sand moulds using Multiple Linear Regression Model. African Journal of Engineering Research, 2, 8-13.
- Ihom, A.P., Agunsoye, J., Anbua, E.E. and Ogbodo, J. (2011) Effect of Moisture Content on the Foundry Properties of Yola Natural Sand. Leonardo Electronic Journal of Practices and Technologies, 19, 85-96.
- Ihom, A.P. (2012) Foundry Raw Materials for Sand Casting and Testing Procedures. 1st Edition, A2P2 Transcendent Publishers, Jos, 71-92.
- Khanna, O.P. (2008) A Text Book of Material Science and Metallurgy. 8th Reprint Dhanpat Rai Publications, India, 51-100.
- Brown, J.R. (1994) Foseco Foundryman’s Handbook. 10th Edition, Pergamon Press PLC, 10-68.
- Heine, R.W., Loper Jr., C.R. and Rosenthal, P.C. (1967) Principles of Metal Casting. 2nd Edition, Tata Mcgraw-Hill Publishing Company Ltd., New Delhi, 100-150.
- Ihom, A.P., Suleiman, U.M. and Nyior, G.B. (2012) Impact of Swelling Indices of Sokoto Clays on the Moulding Properties of the Clays in Sand Mixtures. Journal of Minerals and Materials Characterization and Engineering, 11, 1050-1054.
- Jain, R.K. (2009) Production Technology. 16th Edition, Khana Publishers, Delhi, 153-158.
NOTES
*Corresponding author.