Received 18 June 2015; accepted 25 July 2015; published 28 July 2015

ABSTRACT

Chlorophyll fluorescence parameters such as F_v/F_m, NPQ and Φ_II (Y_II) are widely used to estimate the fitness and photosynthetic activity of plant leaves and non-photochemical dissipation of excessive excitation energy in photosystem II. The effect of chloroplast movement on these fluorescence parameters reduces the accuracy of estimations of the size of de-excitation processes, but there is no method to calculate correct parameters from altered (fluctuated) parameters. Chloroplast movement was recently identified as the “middle” kinetic component of NPQ. In this paper, we devised a complex but reasonable mathematical method to remove the effect of chloroplast movement on fluorescence parameters, based on our previously reported fluorescence theory. The fraction of “S fluctuation” (designated as σ) was estimated from fluorescence observations and used to calculate the non-fluctuated F_s and 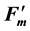fluorescence yields. From the σ values, the fractional change of light absorbance by a leaf caused by chloroplast movement was estimated at 70% - 100%, which varied according to the experimental conditions and plant species. The effect of photoinhibition on fluorescence parameters was also examined in this paper. The photochemical and non-photochemical de-excitation sizes during photoinhibition (measured by the parameters qPI and qSlow) changed on a single regression line. Using this correlation, qPI and qSlow can be predicted from F_v/F_m, and the non-fluctuated F_m and F_o values can be estimated from the fluctuate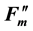d and 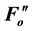values.

Keywords:

Arabidopsis thaliana, Chlorophyll Fluorescence, Non-Photochemical Quenching, Rice

1. Introduction

Typically, 2% of the light energy absorbed by a plant’s chlorophyll is emitted as red fluorescence [1] . The fluorescence intensity (or fluorescence yield) of leaf chlorophyll changes according to light conditions because of the photochemical activities of the quenching processes in photosystem II. Such changes can be relatively easily measured by the pulse amplitude modulation (PAM) method. Several fluorescence parameters such as F_v/F_m, Φ_II (also referred to Y_II in some publications) and NPQ are used to estimate the leaf fitness, rate of photosynthesis, and non-photochemical dissipation of excessive excitation energy [2] [3] . Agricultural applications of fluorescence parameters have also been developed, including the detection of pathogen infection, estimation of stress tolerance in different cultivars, and detection of non-visible symptom of manganese deficiency [4] -[7] . We previously compared the fluorescence parameters of rice cultivars and detected differences in the size of non-photochemical quenching (NPQ: measured by the parameter NPQ) between two subclasses of Indica and Japonica [8] . Although the agricultural significance of the difference in NPQ size is not clear, it may explain the cold tolerance of Japonica cultivars.

Fluorescence is emitted from chlorophyll molecules bound to the photosystem II super-complex. Fluorescence is one of the de-excitation processes of chlorophyll excitation energy. The fluorescence process is classified into ‘basal dissipation,’ together with internal conversion and intersystem crossing. Basal dissipations are intra-molecular de-excitation processes of chlorophyll excitation energy, whereas inter-molecular de-excitation processes (quenching) are divided into two groups: photochemistry and NPQ. Photochemistry represents de-ex- citation by the photosynthetic electron transport chain, especially pheophytin and plastoquinone, and the excitation energy is eventually transferred to photochemistry and used for carbon fixation. NPQ is the sum of the quenching processes except photochemistry. The Lake model approximates the interaction between photosystem II super-complexes. Based on the Lake model, ratios between rate constants of the de-excitation processes can be calculated with the Stern-Volmer approach [9] . By using the simple formula of the Lake model, we previously devised a simple set of calculations to provide more detailed comparisons of rate constants [10] . The fundamental formula of our calculation is as follows:

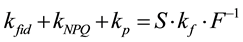(1)

Because the inverse value of fluorescence yield (F) is the key in this formula, Formula (1) is referred to as the “Inverse equation” in this paper, and k_fid, k_p, k_NPQ and k_f are the rate constants for basal dissipation, photochemistry, NPQ and fluorescence, respectively, and S is the sensitivity factor. The S and k_f values are normally constant. Our previous report [10] outlined additional information on this formula. The mathematical relationship between rate constants and fluorescence yields were integrated into a single figure (Figure 1(a)), where qS, qL and NPQ represent ratios between the rate constants, and F_v/F_m, Φ_II, Φ_NPQ and Φ_NO represent quantum yields. Specific formulae for the calculation of fluorescence parameters are described in the materials and methods section. Nomenclature for specific fluorescence yields varies in the literature. In this report, we use F_o, F_m, F_s, 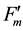, and 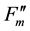for fluorescence yields with or without illumination of a saturating pulse after dark adaptation (F_o and F_m), under actinic illumination (F_s and), and during dark relaxation after actinic illumination (and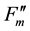) [10] . These fluorescence yields were written as F₀, F_M, F(t), 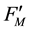, and 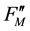in a recent review [3] .

NPQ is absent in the dark and induced by illumination. The NPQ components are divided into three parts (fast, middle and slow kinetics) according to the time span of their relaxation in the dark. Relaxation half-lives of the fast-kinetic, middle-kinetic and slow-kinetic NPQs are approximately 1 min, 10 - 20 min and greater than 1 h, respectively. The fast, middle and slow-kinetic NPQs were originally referred to as qE, qT and qI [11] . The middle component is also referred to as qM [12] , and this term will be used here instead of qT to represent the middle-kinetic NPQ. qE is the main NPQ component in higher plants and regulated by the PsbS protein and xanthophyll cycle [13] [14] . The molecular identity of qI is not clear.

The influence of chloroplast avoidance movement on the apparent NPQ value has been suggested. Light ab-

sorption is decreased after exposure to high light by approximately 10% in Oregon oxalis and approximately 5% in California manroot, whereas light absorption is not significantly influenced by exposure to high light in Japanese holly fern and common sunflower. Thus, chloroplast avoidance movement may increase the apparent NPQ value by reducing the light absorption in plant species such as Oregon oxalis [15] . Mathematically, alterations in the light absorption ratio caused by chloroplast avoidance movement change the S value. When light absorption is decreased by 10%, the S value is also decreased by 10%. Such hypothetical alterations in the S value are referred to as “S fluctuations”, and the influence of S fluctuations on the apparent NPQ size has been mathematically estimated [10] . Arabidopsis (Arabidopsis thaliana) mutants such as phototropin 2 (phot2) and chloroplast unusual positioning 1 (chup1) are defective in chloroplast movement [16] -[18] . phot2 is the blue light receptor for the chloroplast avoidance response [16] , and CHUP1 is a chloroplast-localized actin-binding protein [18] . Recently, a measurement using phot2 detected a clear effect of chloroplast avoidance movement on the apparent NPQ size. Light absorption was clearly decreased in the wild-type plant but not in phot2 mutant plants, and the decrease of light absorption was correlated with the relaxation kinetics of qM. qM is observed under white actinic light but absent under red actinic light, which is consistent with the activity of the phot2 photoreceptor. Thus, qM is caused by chloroplast avoidance movement [12] [19] .

Because qM does not actually quench but rather increases the apparent NPQ size, the influence of qM should not be considered so that the actual NPQ size can be determined. The first goal of this report was to demonstrate how to eliminate such an unfavorable effect of qM on NPQ values through a calculation using the Inverse equation. We were also interested in a mutant analysis and measured the NPQ kinetics in the phot2 and chup1 mutants, although we did not observe a clear effect of chloroplast movement on NPQ. This observation provides insight for an alternative method of minimizing the induction of qM during fluorescence measurements.

Photoinhibition also has similar but different effect on apparent NPQ size. The second goal of this paper was to estimate the effect of photoinhibition on the apparent NPQ size and demonstrate how to eliminate such effects in a series of calculation. Thus this paper collectively suggests novel mathematical processes to calculate actual values of chlorophyll fluorescence parameters from their possibly fluctuated values under various conditions.

2. Materials and Methods

2.1. phot2 and chup1 Mutants

Seeds of wild-type (accession/ecotype Col-0) and phot2-1 and chup1-2 mutants of Arabidopsis thaliana (L.) Heynh. were used. The plants were cultivated on Jiffy-7 (Jiffy International AS, Kristiansand, Norway), a nourished sphagnum peat pellet, for 33 d under an 8 h/16h light/dark scheme using white fluorescent light with a photosynthetic photon flux density (PPFD) of 60 μmol∙m^?2∙s^?1 at 25˚C. Light intensity was made relatively low in order to enhance the effects of chloroplast movement.

2.2. psbS1 Mutant

Wild-type Oryza sativa (cultivar Hwayoung) and a homozygous line of psbS1 mutant (1C-032-61) developed by Gynheung An and obtained from the Pohang University of Science and Technology were selected in a previous report [8] . After germination in a growth chamber, the seeds were grown in nutrient-rich soil (Son-sol no. 1, Sumitomo Chemical, Tokyo, Japan) for 41 d in a partly sun-lit greenhouse. The characteristics of psbS1 were described by [8] .

2.3. Fluorescence Measurement

To measure chloroplast movement, the expanded leaves of Col-0, phot2-1 and chup1-2 (referred to as wild-type, phot2 and chup1, respectively, in the text) were excised, placed on solid media, and dark-adapted for 1 h. After measuring the F_o and F_m, an actinic light (white LED) was illuminated. The F_s and were measured 30 min after the actinic light had been turned on (Table 1). The actinic light was also illuminated for 30 min for the relaxation analysis. The and were measured at 2, 5,10, 15, 20, 25, 30, 35, 40, 45 and 50 min after the actinic light had been turned off (Figure 2).

For photoinhibition, leaf discs were excised from the middle part of the leaf blades of the 6^th leaves of the wild-type and psbS1 mutant and floated on deionized water. The leaves were dark-adapted for 2 h before measuring the F_o and F_m. The F_s and at each light intensity were measured after 5 min of actinic illumination (Figure 3(a) and Figure 3(b)), and photoinhibition was measured every 1 h. Every hour, the high actinic light was illuminated for 55 min and dark-adapted for 5 min before measuring the and. After repeating this process 5 times, the actinic light was turned off so that the photosystem II could recover from photoinhibition (Figure 3(c)). Although the dark adaptation during actinic illumination was only 5 min, the effect of qM (chloroplast movement) would be negligible because the fluorescence was measured with a two-dimensional (2-D) PAM apparatus in rice leaves.

All of the fluorescence yields were measured with the Closed FluorCam (Photon Systems Instruments, Brno, Czech Republic), a 2-D PAM measuring apparatus. The actinic source was a red LED up to a PPFD of 200 μmol∙m^?2∙s^?1 and white LED with a PPFD from 200 to 1500 μmol∙m^?2∙s^?1. Saturating pulses were supplemented for 780 ms with the white LED at a PPFD of approximately 6000 μmol∙m^?2∙s^?1.

^*1PPFD = 400 μmol∙m^?2∙s^?1 for 30 min. ^*2PPFD = 1500 μmol∙m^?2∙s^?1 for 30 min. Underlined data are significantly different from Col-0 by Student’s t-test (P < 0.05). n = 6.

2.4. Fluorescence Parameters

The fluorescence parameters were calculated with the following formulae [10] :

Please refer to the text for the calculation used to determine the fluctuated values and S fluctuation fraction.

3. Results

3.1. Introduction of Chloroplast Movement Effects into the Inverse Equation

The first step for calculating the effect of chloroplast movement on NPQ size is to introduce the effect of chloroplast movement into the Inverse equation. The sensitivity factor in the Inverse equation consists of multiplying several factors. Although there may be additional factors, three factors are usually included: proportion of incident light that is absorbed by the leaf (A_leaf), fraction of absorbed light that is received by photosystem II (fraction_PSII) and instrumental response (Resp) [2] [9] [10] :

(2)

The A_leaf value is changed by chloroplast movement; thus, the S value changes proportionally with changes in the A_leaf value with chloroplast movement. Here, fluctuation-induced changes in the S value are represented as S_(f) to discriminate this value from the S value before fluctuation. The original (non-inverse) equation of the Stern- Volmer approach without S fluctuation is as follows:

(3)

The original equation for the fluctuated S value is as follows:

(4)

The F value changes in proportion to the S value between Formulae (3) and Formulae (4). The inverse versions of these formulae are as follows:

(1)

(5)

The influence of chloroplast movement on the apparent fluorescence intensity can be estimated with the above formulae. The F_o and F_m values are not vulnerable to S fluctuations because these fluorescence yields are measured before illumination by actinic light:

(6)

(7)

The F_s and values, however, are vulnerable to S fluctuations:

(8)

(9)

Please note that F_o, F_m, F_s(f) and are the actual measured fluorescence yields. F_s(f) and are the fluctuations from the original F_s and.

3.2. Calculation of the Fraction of S Fluctuation

Formulae (6)-(9) cannot be directly compared because they have different S values (S and S_(f)). Therefore, the true rate constants are calculated from fluctuated F values by determining the fraction of S fluctuation (σ):

(10)

There are several possible methods of calculating σ from fluorescence yields. Here, let us hypothesize that the non-fluctuated formulae for F_s and is as follows:

(11)

(12)

Comparisons between Formulae (8) and (11) or (9) and (12) provide the σ value:

(13)

The fluctuated and non-fluctuated values of F_s and can be compared with special experimental setups, such as comparisons between the wild-type and phot2 mutant and between white actinic light and red actinic light (as performed by [12] ). In these cases, NPQ fluctuates in the wild-type or under white actinic light, whereas it does not fluctuate in phot2 or under the red actinic light. The non-fluctuated and fluctuated NPQ values (NPQ and NPQ_(f)) can also be used to calculate σ under such experimental setups. The non-fluctuated and fluctuated 1 + NPQ values are as follows:

(14)

(15)

Dividing Formula (14) by Formula (15) produces the following:

(16)

According to observations by [12] , the NPQ value of the wild-type plant (fluctuated NPQ) is approximately 2.3 and that of the phot2 plant (non-fluctuated NPQ) is approximately 1.3 after exposure to actinic light for 1 h. Formula (16) produces an σ value of 0.70 from these data, which indicates that the light absorbance ratio and F_s and fluorescence values of the wild-type plant were decreased by as much as 30% by chloroplast avoidance movement in this experiment. Once the fraction of S fluctuation (σ) is calculated, the actual rate constants of the quenching processes are calculated using the following equations (note S_(f) = σS):

(17)

(18)

Thus, the and values in the fluorescence parameter calculations are replaced by formulae including σ:

(19)

(20)

These alternative formulae for and are shown in Figure 1(a). Again, σ is also proportional to the light absorption ratio (A_leaf), and measuring σ provides a simple method of estimating changes in the light absorption ratio with the PAM equipment.

3.3. Fluorescence Measurement in phot2 and chup1

The effect of chloroplast movement on fluorescence yield was unexpected. We also measured the fluorescence of phot2 and chup1, and Table 1 shows the fluorescence parameters of the wild-type (Col-0), phot2 and chup1 plants. The NPQ values were not significantly different between the wild-type and phot2 plants even after exposure to actinic light (PPFD = 400 or 1500 μmol∙m^?2∙s^?1) for 30 min. In chup1, the NPQ value was only slightly smaller after exposure to high light (PPFD = 1500 μmol∙m^?2∙s^?1) but not significantly different under medium light intensity (PPFD = 400 μmol∙m^?2∙s^?1). Although the F_v/F_m values were high and similar between these genotypes, the Φ_II value was clearly smaller in the phot2 mutant. For unknown reasons, the growth of the phot2 mutant appeared somewhat defective under our growth conditions, which is not the normal growth pattern, although the cylindrical structure of palisade cells is mostly lost in phot2 [20] .

The relaxation kinetics of NPQ after exposure to high light was also observed (Figure 2(a)). NPQ relaxation reached a quasi-plateau in phot2 and chup1 after 10 min in the dark, whereas the NPQ of the wild-type plant gradually decreased after 10 min in the dark. This small but continuous decrease of NPQ appears to represent chloroplast movement-induced S fluctuations. The qE, qM and qI sizes were estimated based on this relaxation analysis. qE is the fraction of NPQ relaxation within 5 min in the dark; qM is the fraction of NPQ relaxation between 5 and 50 min in the dark; and qI is the fraction of NPQ that does not relax after 50 min in the dark in this analysis (Figure 2(b)). The qM size that corresponded to chloroplast movement was slightly but significantly lower in phot2 and chup1 plants than in the wild-type plants, which is consistent with the original report [12] . qE was also slightly higher in the wild-type, which could have been caused by an apparent but not actual increase of qE by chloroplast movement. qI was significantly higher in phot2, reflecting the defective growth of this mutant. The σ value calculated by comparing the NPQ values of the wild-type and chup1 plants after exposure to high light was as high as 0.92, which is in contrast to the estimated value of 0.70 in the original report. Such a reduced induction of chloroplast avoidance movement could have been caused by differences in the PAM equipment (discussed later).

3.4. Photoinhibition in Rice psbS1

Along with chloroplast movement, we were interested in the effect of photoinhibition on the apparent NPQ size. To analyze photoinhibition, we measured a rice (Oryza sativa) psbS1 mutant that cannot induce qE [8] . Figure 3(a) and Figure 3(b) show rate constants of the photochemistry, NPQ and basal dissipation under various light intensities in the wild-type and psbS1 plants, respectively. The fractional difference of the total de-excitation capacity by illumination (qS) in the wild-type rice was approximately 0.6, which was similar to that of the wild-type Arabidopsis [10] . The qS was decreased to less than 0.4 in the psbS1 plant because of the lack of qE induction. The decreased de-excitation capacity of psbS1 caused a hyper-sensitivity to high light. The F_v/F_m values were observed every 1 h for up to 5 h under illumination by high light and then allowed to recover for an additional 14 h in dark conditions (Figure 3(c)). The F_v/F_m values decreased with time under illumination, and the decrease was more severe in the psbS1 than in the wild-type plants. The F_v/F_m values slowly recovered in the dark but did not fully recover within 14 h time period. Although excised leaf discs were used in this experiment, these results indicate that damage by photoinhibition can be carried over until the following day. The lower F_v/F_m values appear to be common in field experiments and analyses of stressed plants. The F_v/F_m values of the undamaged leaves were 0.82 - 0.85.

A reduction in F_v/F_m values by photoinhibition is usually attributed to a decreased rate constant in the dark- adapted photochemistry (k_pi). However, the induction of slow components of NPQ also reduce F_v/F_m, which is the maximum yield of the photochemistry. Figure 1(b) illustrates the changes in the rate constants of the de-excitation processes before and after photoinhibition [10] . The F_o and F_m values after photoinhibition are referred to as and, respectively, because changes in the F_o and F_m values occur after photoinhibition. The rate constant of dark-adapted photochemistry changes from k_pi to with photoinhibition. The ratio between k_pi and (shown by the parameter qPI) represents the fraction of the functional photosystem II reaction center. The parameter qSlow represents the size of qI (the rate constant is denoted as k_I). As shown in Figure 1(b), both a decrease of photochemistry and induction of qI are expected to cause a decrease in the F_v/F_m value.

3.5. Correlation between qPI and qSlow Values

The qPI and qSlow values were calculated for the wild-type and psbS1 leaves. As expected, the qPI value decreased and qSlow value increased under illumination. qPI was smaller in psbS1 plants than in the wild-type plants at the same time points, and qSlow was greater in psbS1. The qPI value gradually increased and qSlow value gradually decreased in the dark. A plot of the qSlow values during illumination and dark recovery against the qPI values (Figure 4(a)) shows that all of the data, including that of the wild-type and psbS1 plants, roughly fit along a single regression curve (R = 0.958 when fitted to a quadratic function):

(21)

If qPI and qSlow are correlated during photoinhibition, then parameters such as F_v/F_m and qSI are naturally correlated with qPI and qSlow.

It is nearly impossible to measure the fluorescence yield of an unstressed state when fluorescence is measured on damaged leaves of stressed plants. Alternatively, a mathematical estimation of fluorescence yield to deter-

mine the F_o and F_m of an unstressed (non-fluctuated) state is possible based on the correlation between the fluorescence parameters observed above. The correlation of F_v/F_m with the parameters qPI, qSI and qSlow during photoinhibition in the wild-type and psbS1 plants are shown in Figures 4(b)-(d). The formulae of the quartic regression functions for these graphs are as follows:

(22)

(23)

(24)

The R² values for these regression lines were 0.993, 0.936 and 0.968. Table 2 shows the values of qPI, qSI and qSlow for each F_v/F_m value (0.30 - 0.83) calculated with these formulae. For example, in a damaged leaf with an F_v/F_m value of 0.70, only 67% of the photochemistry of photosystem II is functional (qPI = 0.67), the total capacity of de-excitation is reduced to 79% (qSI = 0.79), and the relative size of qI compared with that of basal dissipation is 0.36 (qSlow = 0.36). The original F_o and F_m values can also be calculated from the fluctuated and values:

(25)

(26)

One of the potential problems in fluorescence measurements of damaged leaves is underestimating the NPQ size. The actual NPQ is calculated as follows:

(27)

In damaged leaves, the value is smaller than that of the F_m. The fluctuated NPQ value with (NPQ_(f)) is calculated as follows:

(28)

The numerator of the right-most section of Formula (28) is smaller than that of Formula (27), and the denominator is larger than that of Formula (27) because of the value of k_I. Thus, qI decreases the apparent value of NPQ. The actual NPQ sizes can be estimated with the actual F_m calculated with Formula (26). Alternatively, the actual NPQ can be calculated from qSlow and NPQ_(f) as follows:

(29)

4. Discussion

Although a clear effect of chloroplast avoidance movement on NPQ was demonstrated, especially the middle-kinetic NPQ component qT (qM) [12] , the method of removing the effect of chloroplast movement on the apparent NPQ size have not been understood. The key for such calculations is to determine the σ value of light absorbance caused by chloroplast movement because σ is equivalent to the fractional difference of the sensitivity factor S. In this report, we showed a method of calculating σ by comparing the fluctuated and non-fluctuated F_s, or NPQ values. In addition to the comparison of these values, a comparison of NPQ values during dark relaxation, i.e., the NPQ values before and after qM relaxation (approximately 2 min and 45 min), may also roughly estimate the σ value. A further alternative is to compare the apparent k_pi values (non-fluctuated value and fluctuated value) during actinic illumination. In this case, σ is calculated as follows:

(30)

Pleaes note the values are obtained under illumination of far-red light to preferentially excite photosystem I [2] . It is recommended to calculate the σ values to determine the actual sizes of the rate constants and parameters under experimental conditions in which chloroplast avoidance movement is clearly induced, such as observations under high light intensity for a long period (30 min or more). The growth stages and plant species may also influence the degree of chloroplast movement. Notably, rice leaves did not show a decrease of light absorbance under high illumination in a previous report [21] . It is also noteworthy that the middle-kinetic component of NPQ (approximate size = 0.3) is observed even in the npq4 phot2 mutant, which is defective in both qE and qM [19] . The size of the middle NPQ in the npq4 phot2 plant is similar to that observed in the rice leaves [10] , suggesting that the middle NPQ observed in the rice leaves in our previous report was not caused by chloroplast movement. Collectively, the NPQ components cannot be clearly discriminated based on relaxation kinetics; however, qM (chloroplast avoidance movement) and qI (unknown slow NPQ) overlap until 1 h of relaxation in the dark. The size of qI relaxing within 1 h is typically 0.3, and qM would be negligible in rice leaves.

A restricted effect of chloroplast movement was observed on the σ value in our experiment with Arabidopsis phot2 mutant, although this effect was clearly observed in the original report (Figure 2), and the same mutant grown under similar environments was observed under similar measurement conditions in these two experiments. A clear difference between these experiments was the PAM equipment. An ordinary type of PAM fluorometer that measures spots on the leaves (PAM 101, Heinz-Walz GmbH, Effeltrich, Germany) was used in the previous experiment, and a 2-D PAM fluorometer measuring 2-D images (Closed FluorCam, Photon Systems Instruments, Brno, Czech Republic) was used in our experiments. In the measurements with the 2-D PAM, the leaf samples were placed near the bottom of a closed box, and fluorescence was observed with a camera at the center of the ceiling of the box with illumination from LED panels at the edges of the box ceiling. Thus, the leaves are illuminated from two to four sideways angles in 2-D PAM, and this illumination most likely caused a lack of clearly observed chloroplast avoidance movement in our experiments. The σ value was reduced by only 10% in the 2-D PAM, which is approximately one-third of that observed with the ordinary PAM. The measurement with the 2-D PAM is an alternative method of reducing the effect of chloroplast movement on fluorescence yields and parameters.

In addition to NPQ, the qL value can also be affected by S fluctuation caused by chloroplast movement. qL represents the “openness” of the photosystem II photochemistry, and it can be calculated by two different formulae. The first formula (qL₁) includes F_s, and in the calculation as follows [9] [10] :

(31)

The second formula (qL₂) includes F_o, F_m, F_s and in the calculation as follows [10] [22] :

(32)

qL₁ is not affected by S fluctuations because all of the F_s, and values are fluctuated by chloroplast movement. The apparent value of qL₂ is increased by chloroplast avoidance movement because of the 1/σ-fold increase in and values.

In addition to chloroplast movement, the apparent NPQ size also fluctuates during photoinhibition. The correlation and formula of the regression curve between qPI and qSlow was determined (Figure 4(a)). To our knowledge, this is the first examination of correlations in the changes of rate constants between the photochemical and non-photochemical processes during photoinhibition. Further analyses are required to determine whether the regression curves and their formulae for rice leaves are applicable to other plant species or other conditions of photoinhibition. However, the regression curves for the F_v/F_m-qSI and F_v/F_m-qSlow correlations and their values (Table 2) provide a mathematical method of estimating the non-fluctuated F_o and F_m values from the fluctuated and values observed in damaged leaves. The NPQ values of damaged plants reported in other publications were small. For example, the NPQ of a control Physcomitrella patens was 2.82, and the NPQ was curiously decreased to 1.64 when treated with 0.8 M sorbitol [23] . The F_v/F_m values for the control and stressed plants were 0.73 and 0.32, respectively, in this report. The qSlow values corresponding to these F_v/F_m values were 0.265 and 1.523, respectively (Table 2). The fractions of the fluctuation of basal dissipation (1 + qSlow) were 1.265 and 2.523. The non-fluctuated NPQ values calculated from the above data were 3.83 for the control and 5.66 for the stressed plant. Thus, the NPQ was highly induced in the stressed plant; however, the apparent NPQ value was greatly decreased by the fluctuation of basal dissipation.

In this paper, the mathematical methods used to estimate the fluctuation of fluorescence yields and parameter values accompanying chloroplast movement and photoinhibition were derived. The fluctuation of S values by chloroplast movement should be calculated by a direct measurement of leaf absorbance; however, accurate measurements of light transmittance and light reflection in the leaves are difficult to perform. The alternative method of calculating NPQ fluctuations after photoinhibition is to perform a comparison between winter and summer leaves. The fluorescence of winter leaves are affected by photoinhibition, whereas summer leaves are not. A whole-year measurement of pine needles revealed an induction of qSlow (“stable NPQ”) as large as 7 in mid-winter [3] [24] [25] . This method requires special equipment and a long time course.

5. Conclusion

A line of new methods of calculating fluctuations that accompany fluorescence measurements were suggested in this paper. Although these calculations are theoretical biology came simply from mathematical interests and difficult to understand, the calculations in this report may enable rapid estimations of fluctuations and benefit correct description of photosynthetic states of plant leaves in the future.

Acknowledgements

We would like to acknowledge Hirofumi Uchimiya, Maki Kawai-Yamada and the other colleagues for kind supports on this study.

Cite this paper

IchiroKasajima,NoriyukiSuetsugu,MasamitsuWada,KentaroTakahara,11,11, (2015) Collective Calculation of Actual Values of Non-Photochemical Quenching from Their Apparent Values after Chloroplast Movement and Photoinhibition. American Journal of Plant Sciences,06,1792-1805. doi: 10.4236/ajps.2015.611180

References

NOTES

^*Corresponding author.