Journal of High Energy Physics, Gravitation and Cosmology
Vol.02 No.03(2016), Article ID:68917,20 pages
10.4236/jhepgc.2016.23036
Can Thermal Input from a Prior Universe Account for Relic Graviton Production and Imply Usage of the Bogomolnyi Inequality, as a Bridge between Brane World Models and Loop Quantum Gravity in Early Universe Conditions?
Andrew Walcott Beckwith
Physics Department, College of Physics, Chongqing University Huxi Campus, Chongqing, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 April 2016; accepted 21 July 2016; published 25 July 2016
ABSTRACT
The author uses a low temperature and low entropy pre inflation state to create a bridge between String theory and loop quantum gravity. We use this analysis in lieu of the CMB barrier as of z = 1000 since it is our way to come up with a working model of quintessence scalar fields, which permits relic generation of dark matter and dark energy. Not only referencing this bridge, we do it in such a way as to utilize the low entropy condition which the Brane world model of Randal and Sundrum creates, and to show how it is in common with what Caroll and Chen wrote up in 2005., i.e. when the universe was about 1000 times smaller and 100,000 times younger than today.
Keywords:
Branes, Axion Walls, Bogomolnyi Inequality, Four- and Five-Dimensional Cosmological Constant

1. Introduction
Our task is to first answer if there are “vacuum states” created out of “nothing”, and this is done because vacuum fluctuations create dark energy density. The dark energy density is connected with an axion wall, which is dissolved by inflationary expansion. It is given by Weinberg [1] that the process of dissolving that wall occurs when relic background temperature is about 1032 Kelvin, i.e. the high temperature of 1032 Kelvin is the beginning of the onset of quantum gravity [1] . Interesting enough, the pre big bang state may be, as Penrose suggested in [2] , low temperature and low energy. And this is paradoxical since while the pre big bang model has both low temperature and low entropy, the big bang model has high temperature and low entropy.
Still though, as written up by L. Crowell [3] in “Quantum Fluctuations in Space-Time”, we can make a first principle argument as to the uncertainty principle in quantum mechanics being derivable from variations in the space time metric, and especially in the 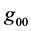 component of the metric
component of the metric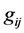 , i.e.
, i.e.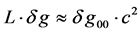 , where L is a unit length for evaluation of quantum fluctuations. From there we can then argue that fluctuations in dark energy density were initially of the form
, where L is a unit length for evaluation of quantum fluctuations. From there we can then argue that fluctuations in dark energy density were initially of the form 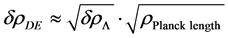 with
with 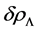 connected with energy density fluctuations due to variations w.r.t. temperature in the Planck “constant” parameter in a formulation first presented by Park et al. [4] . We are assuming that this variation of the Planck “constant” parameter is also connected with relic graviton production. And we use a short time interval quintessence equation of “motion” in order to show a bridge between a pre inflationary quantum bounce thermal inputs of energy and initially cooled down states of matter conditions as postulated by Carroll and J. Chen [5] , 2005 to Guth style quadratic potential inflation.
connected with energy density fluctuations due to variations w.r.t. temperature in the Planck “constant” parameter in a formulation first presented by Park et al. [4] . We are assuming that this variation of the Planck “constant” parameter is also connected with relic graviton production. And we use a short time interval quintessence equation of “motion” in order to show a bridge between a pre inflationary quantum bounce thermal inputs of energy and initially cooled down states of matter conditions as postulated by Carroll and J. Chen [5] , 2005 to Guth style quadratic potential inflation.
Also, relatively recently, quintessence models were for large time scales ruled out, and Padmanabhan [6] in a 2005 world press scientific tome edited by Abbay Ashtekar on pp. 175-204 notes that this is due to the cosmological constant being set to zero for the quintessence models being considered. This is due in part to the classes of potentials offered along the lines of Equation (18) of Padmanabhan’s article [6] , which we did not use, as well as the duration of the quintessence period being far larger than Planck’s time interval. We got about this by using a different scalar model than what Padmanabhan used and also by using a vanishingly small time interval at the onset of the regime just before inflation to have quintessence scalar field evolution. We assume explicitly a collapse of axion walls leading to the chaotic inflationary potential first written up by Guth in the 1980s. As it is, our present paper is in response to suggestions by Dr. Wald [7] (2005), Sean Carroll and Jennifer Chen [5] (2005), with others in the University of Chicago physics department, about a Jeasun stability criteria leading to low entropy states of the universe at the onset of conditions before inflationary physics initiated expansion of inflaton fields. We agree with their conclusions and think it ties in nicely with the argument presented as to a burst of relic gravitons being produced. This is also consistent with an answer as to the supposition for the formation of a unique class of initial vacuum states, answering a question Guth [8] raised in 2003 about if or not a preferred form of vacuum state for early universe nucleation was obtainable. This is in tandem with the addition of gravity changing typical criteria for astrophysical applications of the jeans instability criteria [9] for weakly interacting fields, as mentioned by Penrose [2] .
Contemporary graviton theory states that there is a thermal upsurge which initiates the growth of graviton physics. This is shown in K. E. Kunzes’ well written (2002) article [10] which gives a lucid introduction as to early universe additional dimensions giving a decisive impetus to giving additional momentum to the production of relic gravitons. However, Kunze [10] is relying upon enhanced thermal excitation states, which contradict the Jeans instability criteria which appear to rule out a gravitational field soaked initial universe configuration being thermally excited. Is there a way to get around this situation which appears to violate the Jeans instability criteria for gravitational fields/gravitons in the early universe mandating low entropy states? We believe that there is, and that it relies upon a suggestion given by A. Ashtekar, T. Pawlowski and P. Singh (2006) [11] [12] as to the influence of the quantum bounce via quantum loop gravity mirror imaging a prior universe collapsing into a “singularity” with much the same geometry as the present universe. If this is the case, then we suggest that an energy flux from that prior universe collapse is transferred into a low entropy thermally cooled down initial state, leading to a sudden burst of relic gravitons as to our present universe configuration. The first order estimate for this graviton burst comes from the numerical density equation for gravitons written up by Weinberg as of 1972 [1] with an exponential factor containing a frequency value divided by a thermal value, T, minus 1. If the frequency value is initially quite high, and the input given by a prior universe “bounce”, with an initial very high value of energy configuration, then we reason that this would be enough to introduce a massive energy excitation into a thermally cooled down axion wall configuration which would then lead to the extreme temperatures of approximately 1012 Kelvin forming at or before a Planck interval of time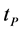 , plus a meltdown of the axion domain wall, which we then says presages’ formations of a Guth style inflationary quadratic and the onset of chaotic inflationary expansion.
, plus a meltdown of the axion domain wall, which we then says presages’ formations of a Guth style inflationary quadratic and the onset of chaotic inflationary expansion.
A way of getting to all of this is to work with a variant of the Holographic principle and an upper bound to entropy calculations. R. Busso and L. Randall (2001) [13] give a brane world variant of the more standard upper bounds for entropy in terms of area calculations times powers of either the fourth or fifth dimensional values of Planck mass (45), which still lead to minimized values if we go near the origins of the big bang itself. Our observations are then not only consistent with the upper bound shrinking due to smaller and smaller volume/area values of regions of space containing entropy measured quantities, but consistent with entropy/area being less than or equal to a constant times absolute temperatures, if we assume at the beginning low temperature conditions prior to the pop up of an inflation scalar field.
Recently, Bo Feng et al. [14] introduced the idea of an effective Lagrangian to compliment the idea of CPT violations as new physics, with a term proportional to the derivative of a scalar field φ (in this case a quintessence field) times the dual of the electromagnetic tensor. What we are supplying is a proof if you are of time dependence of the quintessence scalar field, and Bo Feng et al. [14] inputs into the electric and magnetic fields of this dual of the E & M tensor from the stand point of CMB. It is noteworthy to bring up that Ichiki et al. [15] notes that because standard electromagnetic fields are coupled to gravity, magnetic fields simply dilute away as the universe expands, i.e. we need to consider the role of gravity generation in early universe models. We will, in this document try to address how, via graviton production, we have intense gravity wave generation, and also how to use this as a probe of early universe quintessence fields, and also how to get around the fact that conventional cosmological CMB is limited by a barrier as of a red shift limit of about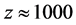 , i.e. when the universe was about 1000 times smaller and 100,000 times younger than today as to photons, i.e. we are confirming as was stated by Weinberg [1] as of 1972 that there is no chance of relic photon generation from the big bang itself and that we are using relic gravitons as a probe to the physics of quintessence fields. We are assuming that our probe may help us answer questions as to the origins of physics matters relevant to the dark matter/dark energy issue.
, i.e. when the universe was about 1000 times smaller and 100,000 times younger than today as to photons, i.e. we are confirming as was stated by Weinberg [1] as of 1972 that there is no chance of relic photon generation from the big bang itself and that we are using relic gravitons as a probe to the physics of quintessence fields. We are assuming that our probe may help us answer questions as to the origins of physics matters relevant to the dark matter/dark energy issue.
In addition this approach accounts for data suggesting that the four-dimensional version of the “cosmological constant” in fact varies with respect to external background temperature. If this temperature significantly varies during early universe baryogenesis, the end result is that there would be a huge release of spin-two gravitons in the early stages of cosmic nucleation of a new universe. It also answers whether “Even if there are 101000 vacuum states produced by String theory, then does inflation produces overwhelmingly one preferred type of vacuum states over the other possible types of vacuum states?” [8] (Guth, 2003).
Also, we also account for the evolution of an equation of motion of a quintessence field, via equations given to us by M. Li, X. Wang, B. Feng, and X. Zhang [16] , which is a first ever model as to the interaction of a quintessence scalar field with baryonic “normal matter” assuming varying contributions to a potential field system with a varying by temperature axion mass contribution to an evolving pre inflationary state, which collapses to a quadratic Guth style inflationary state with a suitable rise in initial inflationary temperatures.
Finally, we can state unequivocally that the typical dark energy SUGRA potential, i.e. for times  or larger
or larger
 (1)
(1)
blends/overlaps well with the finalized Guth style inflationary quadratic potential so derived in our formulation of this problem after we have a thermal input from a quantum bounce which melts axion walls. This is the case only because the intervals of time are so short as to merely indicate that Equation (1) merely indicates the growth behavior of a quantum vacuum state. In addition, we should also mention that the super nova survey, called Essence, has experimentally measured the “dark energy”―the thing that is causing the acceleration of the universe―to better than within 10% accuracy. The feature of this dark energy that was measured is its “equation of state”. So far it looks that the strange acceleration of the expansion of the universe can be explained by Einstein’s “cosmological constant”. Note that in modern terms the cosmological constant is viewed as a quantum mechanical phenomenon called the “energy of the vacuum”, in other words, the energy of empty space. And our work leads to the standard cosmological constant value well within the 1000 year limit of observational accuracy after the big bang, due to thermal cooling off which would occur about the z = 1000 or so red shift limit. This being the case, we will construct the following two tables for outlining the principles involved.
We look at the cosmological constant in 5 dimensions, and after it is given an absolute value give it as in Equation (2) below, we are finding that the absolute value is inversely proportional to temperature, T, as given below.
This is with regards to
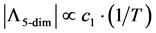 (2)
(2)
Note that the non absolute value version of the contents of Equation (2) is negative valued which is very important, as the negative sign given to Equation (2) contents is put in string theory, to exhibit a different character for the string theory’s version of the cosmological constant than what is given in the four dimensional case.
In comparison, the four dimensional cosmological constant is positive valued we write as
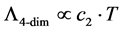 (3)
(3)
In comparison, if we have a temperature decrease of cosmological temperature to 1012 Kelvin, both Equation (2) and Equation (3) exhibit the following claimed linkage as given in Equation (4), noting that if 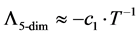 that then we have to an order 1/n that
that then we have to an order 1/n that
 (4)
(4)
It is useful to note a spatial relationship between the four and five dimensional cosmological constant parameters i.e. that the parameterization of the absolute value of the four and five dimensional constant have the following behavior.. I.e. the length scale between the two representations is similar
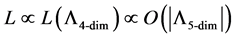 (5)
(5)
So being the case, we get a simple case of where we can analyze vacuum energy density fluctuations in the region of space smaller than the radii given in Equation (5) above, via
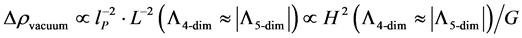 (6)
(6)
This is with respect to working with dimensions of the order of Plancks length, i.e. the volume of space where the volume of space has a radii which is of the order of, for

where initially we have temperatures of the order of 1.4 times 10 to the 32 power Kelvin as a thresh hold for the existence of quantum effects. This would pre suppose answering the issue raised by Weinberg [1] . As of 1972, he wrote that for quantum effects to be dominant in cosmology, with a value of critical energy we will use in setting a template for relic graviton production later on.

This is pre supposing that we have a working cosmology which actually gets to such temperatures at the instance of quantum nucleation of a new universe. And if there is no temperature dependence, in the 5th dimensional cosmological constant set as having magnitude Λ, we still can get a five dimensional line element [17] as given by

2. Fluctuations and Their Linkage to Brane World Physics
We shall reference a simple Lypunov Exponet argument as to adjustment of the initial quantum flux on the brane world picture. This will next be followed up by a description of how to link the estimated requirement of heat influx needed to get the quantum spatial variation flux in line with inflation expansion parameters.
To begin this, we access the article “Quantum theory without Measurements” to ascertain the role of a Lyapunov exponent 

and

Here, we define where a wave functional forms via the minimum time requirement as to the formation of a wave functional via a minimum time of the order of Planck’s time

If we have a specified minimum length as to how to define


3. Why Bother with Talking about Such a Simplified Fluctuation Procedure?
Two reasons First of all, we have that our description of a link of the sort between a brane world effective potential and Guth style inflation has been partly replicated by Sago, Himenoto, and Sasaki in November 2001 [19] where they assumed a given scalar potential, assuming that m is the mass of the bulk scalar field

Their model is in part governed by a restriction of their 5-dimensional metric to be of the form, with l = brane world curvature radius, and H their version [19] of the Hubble parameter

i.e. if we take 

Our difference with Equation (102) of Sago et al. [19] is that we are proposing that it is an intermediate step, and not a global picture of the inflation field potential system. However, the paper they present with its focus upon the zero mode contributions to vacuum expectations 

which assumes one is still working with a modified Gaussian potential all the way through. This is assuming that there exists an effective five dimensional cosmological parameter which is still less than zero, with


It is simply a matter of having

And of making the following identification


of 




The potentials



This is where for low temperatures 
axion walls specified by Kolb’s book [20] about conditions in the early universe (1991) with his Equation (10) and Equation (27) vanishing and collapsing to Guth’s quadratic inflation. i.e. having the quadratic contribution to an inflation potential arise due to the vanishing of the axion contribution of the first potential of Equation (21) above with a temperature dependence of [20]

Here, he has the mass of the axion potential as given by 


So that the axion “matter” will oscillate with a “frequency” proportional to

perature2 

and then relate it to Guth inflationary potential scalar fields [8] later on, and state that 

Or

This axion treatment is similar, in a lower dimensional sense to the work which is presented in [22] [23] physics while the work done by [22] [23] is an elaboration for much of the physics which is done in Equation (24) to Equation (26).
The dissolving of axion walls is necessary for dark matter-dark energy production and we need to incorporate this in a potential system in four dimensions, and relate it to a bigger five dimensional potential systems. We need to find a way to, using brane theory, to investigate how we can have non zero axion mass conditions to begin with. This will be done after we bring up a brief interlude of Quintessence evolution of the scalar field, which for long periods of time is unworkable, but which would be appropriate up to times in the order of magnitude of the Planck’s time coefficient. Note after this description of Quintessence, we will be looking at the mechanism of thermal input leading to the time dependence of the axion mass, as given in Equation (26) above.
4. Dynamics of Axion Interaction with Baryonic Matter, via Quintessence Scalar Field
This discussion is modeled on an paper on Quintessence and spontaneous Leptogenesis (baryogenesis) by M. Li, X. Wang, B. Feng, and Z. Zhang [16] which gave an effective Lagrangian, and an equation of “motion” for quintessence which yielded four significant cases for our perusal. The last case, giving a way to reconcile the influx of thermal energy of a quantum bounce into an axion dominated initial cosmology, which lead to dissolution of the excess axion “mass”. This final reduction of axion “mass” via temperature variation leads to the Guth style chaotic inflationary regime [8] .
Let us now look at a different effective Lagrangian which has some similarities to equations of motion for Quintessence scalar fields, assuming that specifying a non zero value to 


What will be significant will be the constant, 








Here I am making the following assumption about the axion contribution scalar potential system

For low temperatures, we can assume that prior to inflation, as given by Carroll and Chen [5] we have for

And that right at the point where we have a thermal input with back ground temperatures at or greater than 


This entails having at high enough temperatures

Let us now review the four cases so mentioned and to use them to analyze new physics.
CASE I:
Look now at a low temperate slow roll case, which is also true when we get to time

CASE II:
If temperature is T very large and time of the order of Planck time. We ignore slow roll, and we use

We then use the following approximations



CASE III:
T very large and time almost Planck time



Case IV:
T not large, so the Axion mass is not negligible, and time is almost


Then we obtain

This will lead to as the temperature rises we get that the general solution obeys

The upshot is, that we have a real field if the axion mass disappears. First of all, though, we have to understand how the conditions presented by S. Carroll, and J. Chen came about via brane theory.
5. Setting up Conditions for Low Temperature and Low Entropy Bounds via Brane World Physics for the Start of Inflation
Our starting point here is first showing equivalence of entropy formulations in both the Brane world and the more typical four dimensional systems. A Randall-Sundrum Brane world will have the following as a line element and we will continue from here to discuss how it relates to holographic upper bounds to both anti De sitter metric entropy expressions and the physics of dark energy generating systems.
To begin with, let us first start with the following as a 




Furthermore, the 


We can then speak of a four dimensional volume 


And if a Brane world gravitational constant expression 

If we look at an area “boundary” 



We link this to the principle of the Jeans inequality for gravitational physics and a bound to entropy and early universe conditions, as given by S. Carroll and J. Chen (2005) [5] by stating if 

Low entropy conditions for initial conditions, as stated above give a clue as to the likely hood of low temperatures as a starting point via R. Easther et al. (1998) [22] relationship of a generalized non brane world entropy bound, assuming that 


Similar reasoning, albeit from the stand point of the Jeans inequality and instability criteria lead to Sean Carroll and J. Chen [5] (2005) giving for times at or earlier than the Planck time 

We shall next refer to how this relates to, considering a low entropy system as a start an expression Wheeler wrote for graviton production and its implications for early relic graviton production, and its connection to axion walls and how they subsequently vanish at or slightly past the Planck time
6. The Wheeler Graviton Production Formula for Relic Gravitons
We use below the Wheeler black body approximation used in [1] for the production of gravitons, i.e. we obtain

Equation (49) is useful for, in a black body cavity setting for generating a burst of gravitons in a given frequency range. Now, here Equation (49) predicts a surge in gravitons being produced if there is a sharp increase in temperature. If the Early universe prior to the big bang were low temperature in character, with a subsequent build up to Planck temperature, then Equation (49) models an extreme graviton burst.
Here is how we can build up a scenario for just that. Equation (49) suggests that at low temperatures we have large busts of gravitons.
Now, how do we get a way to get the 

We also are as stated earlier, stating that the energy input into the frequency range so delineated comes from a prior universe collapse, as modeled by Ashtekar, A., Pawlowski, T. and Singh, P (2006) [11] [12] via their quantum bounce model as given by quantum loop gravity calculations. We will state more about this later in this document.
The subsequent analysis is for a low temperature axion wall domain wall in early universe structure. This will change, with the axion domain wall being ‘melted’ with a surge to Planck Temperature. We will next then talk more explicitly about Graviton production, aside from using the Wheeler Black Body model, given in Equation (49) above.
7. Graviton Space Propulsion Systems
We need to understand what is required for realistic space propulsion. To do this, we need to refer to a power spectrum value which can be associated with the emission of a graviton. Fortunately, the literature contains a working expression as to power generation for a graviton being produced for a rod spinning at a frequency per second


First of all, we will integrate Equation (50), and also give a Planck length value to the rotating rod, and then we get Equation (51). One can see the results of integrating Equation (50), Note this expression for numerical production of gravitons is extremely sensitive to temperature, T, and se obtain
Table 1. How to outline the existence of a relic graviton burst.

Then, if


Assuming when one does this that the back ground in the initial inflation state causes a thermal heat up of the axion wall “material” due to a thermal input from a prior universe quantum bounce. Our next task will be to configure the conditions via brane world dynamics leading to graviton production. This necessitates using a brane world potential to accommodate the building of a structure accommodating a transition from relic graviton production to the onset of Guth style chaotic inflation.
8. Randall Sundrum Effective Potential
The consequences of the fifth-dimension show up in a simple warped compactification involving two branes, i.e., a Planck world brane, and an IR brane. Let’s call the brane where gravity is localized the Planck brane This construction permits (assuming K is a constant picked to fit brane world requirements) [27] - [29]

Here, what is called 

To use Kaluza-Klein theory, as in [27] , we use an invariant metric on S1 that is the fiber of the U (1)-bundle of electromagnetism. This leads to construction of, by [27] and [28]


Start with

The above in our integral, as in this treatment makes use of the following quadratic approximation. I.e. if Q is a charge, then

Part of the integrand in Equation (54) is known as an action integral,



And

We should note that the quantity 

For convenience we have made the substitution as given in Equation (61).

The upshot is that the following simplification appears to hold as in Equation (62).

All these final steps need to be confirmed in the future by rigorous analysis.
9. Using Our Bound to the Cosmological Constant
We use our bound to the cosmological constant to obtain a conditional escape of gravitons from an early universe brane. To begin, we present conditions (Leach and Lesame, 2005) [29] for gravitation production. Here 

Also there exists an “impact parameter”

This leads to, practically, a condition of “accessibility” via R so defined with respect to “bulk dimensions”


Here, k = 0 for flat space, k = −1 for hyperbolic three space, and k = 1 for a three sphere, while an radius of curvature

This assumes a negative bulk cosmological constant 



This leads to an upper bound with respect to release of a graviton from an anti De Sitter brane (Leach and Lesame, 2005) [29] we write as

In the language of general relativity, anti de Sitter space is the maximally symmetric, vacuum solution of Einstein's field equation with a negative cosmological constant Λ.
How do we link this to our problem with respect to di quark contributions to a cosmological constant? Here we make several claims. These are all from [28] [29]
Claim 1: We reset 
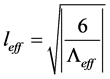
Proof of Claim 1: We are noting that the end result is that

And we take the value of the five dimensional value to be in magnitude presentable as

Note how 



value of the Cosmological Constant. Then

Here, we define 

The upshot is that we have an approaching to the 3 Kelvin background temperature, as in present day Space-time.
This, for potential

Claim 2: 

where L is the physical distance 


This claim 2 breaks down completely when one has a strongly curved space, which is what we would expect in the first instant of less than Planck time evolution of the nucleation of a new universe.
Claim 3: Equation (74) has a first potential which tends to be for a di quark nucleation procedure which just before a defined Planck’s time


Which furthermore

So then that there would be a great release of gravitons at or about time
Claim 4: Few gravitons would be produced significantly after time
Proof of Claim 4: This comes as a result of temperature changes after the initiation of inflation and changes in value of [29]

After this, we need to discuss how this thermal input into the axion wall occurs, leading to these results.
10. Di Quark Potential Systems
Abbay Ashtekar’s quantum bounce results as given in [11] and [12] are redone by Henriques and gives a discrete version of the Wheeler De Witt equation [30] . We begin with the results given in [30]

As well as energy term


This is for a “cosmic” Schrodinger equation as given by [30]

This has 

And

Ashtekar [11] [12] works with as a simplistic structure with a revision of the differential equation assumed in Wheeler-De Witt theory to a form characterized by







This is for a crucial “momentum” value [11] [12] [30]

And

Which leads to, for an initial point in “trajectory space” given by the following relation 

With each 


The existence of gravitons in itself would be able to either confirm or falsify the existence of non LP structure in the early universe. This structure was seen as crucial to Ashtekar, A, Pawlowski, T. and Singh, in their arXIV article [11] [12] make reference to a revision of this momentum operation along the lines of basis vectors 

With the advent of this re definition of momentum we are seeing what Ashtekar [11] [12] works with as a simplistic structure with a revision of the differential equation assumed in Wheeler―De Witt theory to a form characterized by [11] [12]



This in itself would permit confirmation of if or not a quantum bounce condition existed in early universe geometry, according to what Ashtekar’s two articles predict [11] [12] . In addition it also corrects for another problem. Prior to brane theory we had a too crude model. Why? When we assume that a radius of an early universe―assuming setting the speed of light 



This creates problems, so we look for other ways to get what we want. Grushchuk writes that the energy density of relic gravitons is expressible as [32]

where the subscripts i and f refer to initial and final states of the scale factor, and Hubble parameter. This expression though is meaningless in situations when we do not have enough data to define either the scale factor, or Hubble parameter at the onset of inflation. How can we tie in with the Gaussian wave functional 





An appropriate value for a Gaussian representation of an instanton awaits more detailed study. But for whatever it is worth we can refer to the known spaleraton value for a multi dimensional instanton via the following procedure. We wish to have a finite time for the emergence of this instanton from a pre inflation state.
If we have this, we are well on our way toward fixing a range of values for

in order to get a value for



If so, then, most likely, the question we need to ask though is the temperature of the “pre inflationary” universe and its link to graviton production. This will be because the relic graviton production would be occurring before the nucleation of a scalar field. We claim, as beforehand that this temperature would be initially quite low, but then rising to a value at or near 1012 degrees Kelvin after the dissolving of the axion wall contribution given in the dominant value of Equation (21) leading to Equation (22) for a chaotic inflationary potential. And now we shall consider why we need to look at relic graviton production, anyway.
11. Detecting Gravitons as Spin 2 Objects with Available Technology
To briefly review what we can say now about standard graviton detection schemes, as mentioned above, Rothman wrote that Dyson doubts we will be able to detect gravitons via present detector technology [33]

Here, at best, we usually can set

This in part is why we are looking at relic graviton production for early universe models, usually detectable via the criteria developed for white dwarf stars of one graviton for 
Furthermore, 


We should state that we will generally be referring to a cross section which is frequently the size of the

Note that we obtainnn upper bound to the cross section 

M-Planck scale in 4 + n dimensions

iverse extra dimension “square” volume ≈ 10 - 15 mm per side. So, having this limitation, Chongqing University is looking at objects like Neutron stars, as Graviton detection sites, and the like. It is a serious problem, and one which mandates serious choices of GR/ Graviton detection, to be thoroughly vetted by appropriate astrophysical models.
12. Conclusions
Note that if the Rothman analysis [33] is accurate, we need to look at sampling data from Neutron stars and the like as graviton emitter candidates to further increase the likelihood of graviton detection. . We should also note using material from [34] - [42] . Secondly, we state that the idea of using a graviton detector the size of Jupiter as an instrument is absurd. We need to pioneer new Graviton detector technology, rather than what Rothman envisions. Third, we also need to ask how one could go say from 1012 Kelvin as pre Big Bang temperature up to Plank temperatures for observing a graviton burst, i.e. the supposition of Caroll and Chen [5] is very attractive as a model, but the question of how to model such a huge temperature increase is open and needs proper analysis.
We can point to the following as tentative successes of our model which need further elaboration.
Gravitons would appear to be produced in great number in the 


A Randall-Sundrum effective potential, as outlined herein, would give a structure for embedding an earlier axion potential, which would be a primary candidate for an initial configuration of dark energy. This structure would, by baryogenesis, be a shift to dark energy. We need to determine if the sets of JDEM space observations have data which could be configured to determine if WIMPS are in any way tied into the supposed dark energy released after a 
In doing this, we should note the following. We have reference multiple reasons for an initial burst of graviton activity, i.e. if we wish to answer Freeman Dyson’s question about the existence of gravitons in a relic graviton stand point [35] .
We have already found it necessary to avoid the methodology of [36] , for working on the Cosmological constant problem. We wish to obtain, via Parks [4] method of linking, four and five dimensional cosmological constants in a way to obtain a temperature based initial set of conditions for this parameter, which would eliminate the need for the scale factor being appealed to all together.
A lot of work can and should be done to update the power law for graviton production along the lines of an update to the graviton power spectra expression via taking into account a per solid angle expression.
As I was asked about earlier, this does have a directional component which was given by Weinberg in 1972 [1] as the power per solid angle

where we can write 


Getting realistic values of 
Also, the issues raised in [37] need to be settled. Do we have color super conductor type conditions in the early universe as stated by Zhitinisky?
Doing all of this will enable us, once we understand early universe conditions, to be able to initiate de facto engineering work pertinent to power source engineering. We will initiate engineering work so as to allow this concept to become the basis of new space craft technology. Also in order to do this engineering work properly we need to understand the issues raised in [38] - [40] . We will state that details of the four and five dimensional Cosmological constant touches upon Corda’s question as to the ultimate nature of gravity as in [38] . Furthermore, our discussion and analysis should confirm if [39] holds, and if the known experimental constraints of [40] [41] hold. In addition, our analysis has heavily used Ng’s infinite quantum statistics [42] which should be falsified by experiments.
As to reference [43] we refer to confirmation or rejection of the ideas of a causal discontinuity, at the start of cosmological evolution and space-time physics as necessary. Finally, and not least, it is also experimental vetting of the ideas as given in [44] as to the existence, or falsification of an initially non singular universe, as given by Gao et al. We use the Gao’s structure as given in [44] , or we use the non singular start to the universe as given by Non Linear Electrodynamics, as in reference [45] .
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279. I also wish to thank Dr. Christian Corda and Dr. Fangyu Li for motivation, as well as Dr. Xi Yang of Brookhaven laboratory who in the early 2000s helped clean my thinking for my PhD defense as to the intricacies of False vacuum nucleation used in my PhD defense. That methodology has been present for years afterwards.
Cite this paper
Andrew Walcott Beckwith, (2016) Can Thermal Input from a Prior Universe Account for Relic Graviton Production and Imply Usage of the Bogomolnyi Inequality, as a Bridge between Brane World Models and Loop Quantum Gravity in Early Universe Conditions?. Journal of High Energy Physics, Gravitation and Cosmology,02,412-431. doi: 10.4236/jhepgc.2016.23036
References
- 1. Weinberg, S. (1972) Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. John Wiley & Sons, Inc., New York.
- 2. Penrose, R. (1989) The Emperor’s New Mind, Ch. 7. Oxford University Press, Oxford. (And references therein)
- 3. Crowell, L. (2005) Quantum Fluctuations of Space-Time. In: World Scientific Series in Contemporary Chemical Physics, Vol. 25, Singapore.
- 4. Park, D.K., Kim, H. and Tamarayan, S. (2002) Nonvanishing Cosmological Constant of Flat Universe in Brane-Wor Scenario. Physics Letters B, 535, 5-10.
http://arxiv.org/abs/hep-th/0111081
http://dx.doi.org/10.1016/S0370-2693(02)01729-X - 5. Carroll, S.M. and Chen, J. (2005) Does Inflation Provide Natural Initial Conditions for the Universe. General Relativity and Gravitation, 37, 1671-1674.
http://arxiv.org/abs/gr-qc/0505037v1
http://dx.doi.org/10.1007/s10714-005-0148-2 - 6. Padmanabhan, T. (2005) Understanding Our Universe: Current Status and Open Issues. In: Ashtekar, A., Ed., 100 Years of Relativity Space-Time Structure: Einstein and Beyond, World Press Scientific, Singapore, 175-204. http://dx.doi.org/10.1142/9789812700988_0007
- 7. Wald, R.M. (2005) The Arrow of Time and the Initial Conditions of the Universe. Studies in History and Philosophy of Science Part B, 37, 394-398.
https://arxiv.org/abs/gr-qc/0507094
http://dx.doi.org/10.1016/j.shpsb.2006.03.005 - 8. Guth, A.H. (2003) Eternal Inflation.
http://online.itp.ucsb.edu/online/strings_c03/guth/pdf/KITPGuth_2.pdf - 9. Tsiklauri, D. (1998) Jeans Instability of Interstellar Gas Clouds in the Background of Weakly Interacting Massive Particles. The Astrophysical Journal, 507, 226-228.
http://arxiv.org/abs/astro-ph/9805271
http://dx.doi.org/10.1086/306334 - 10. Kunze, K.E. and Sakellariadou, M. (2002) Graviton Production from Extra Dimensions. Physical Review D, 66, Article ID: 104005. http://dx.doi.org/10.1103/PhysRevD.66.104005
- 11. Ashtekar, A., Pawlowski, T. and Singh, P. (2006) Quantum Nature of the Big Bang. Physical Review Letters, 96, Article ID: 141301. http://dx.doi.org/10.1103/PhysRevLett.96.141301
- 12. Ashtekar, A., Pawlowski, T. and Singh, P. (2006) Quantum Nature of the Big Bang: An Analytical and Numerical Investigation. Physical Review D, 73, Article ID: 124038.
http://arxiv.org/abs/gr-qc/0604013 - 13. Buusso, R. and Randall, L. (2001) Holographic Domains of Anti-de Sitter Space. Journal of High Energy Physics, 2002. https://arxiv.org/abs/hep-th/0112080
- 14. Feng, B., Li, M., Xia, J. Chen, Z. and Zhang, X. (2006) Searching for CPT Violation with Cosmic Microwave Background Data from WMAP and Boomerang. Physical Review Letters, 96, Article ID: 221302. http://arxiv.org/abs/astro-ph/0601095
http://dx.doi.org/10.1103/PhysRevLett.96.221302 - 15. Ichiki, K., Takahashi, K., Ohno, H., Hanayama, H. and Sugiyama, N. (2006) Cosmological Magnetic Field: A Fossil of Density Perturbations in the Early Universe. Science, 311, 827-829.
http://dx.doi.org/10.1126/science.1120690 - 16. Li, M., Wang, X., Feng, B. and Zhang, X. (2001) Quintessence and Spontaneous Leptogenesis. Physical Review D, 65, Article ID: 103511.
https://arxiv.org/abs/hep-ph/0112069
http://dx.doi.org/10.1103/PhysRevD.65.103511 - 17. Wesson, P.S. (1999) Space-Time-Matter, Modern Kaluza-Klein Theory. World Scientific, Singapore.
- 18. Kummel, H.G. (2006) Quantum Theory “without Measurement”. International Journal of Modern Physics B, 20, 4982-4991. http://dx.doi.org/10.1142/S0217979206036028
- 19. Susskind, L. (1994) The World as a Hologram. Journal of Mathematical Physics, 36, 6377-6396. https://arxiv.org/abs/hep-th/9409089 http://dx.doi.org/10.1063/1.531249
- 20. Kolb, E.W. and Turner, M.S. (1990) The Early Universe. West View Press, Boulder.
- 21. Balin, D. and Love, A. (2004) Cosmology in Gauge Field Theory and String Theory. Institute of Physics Publishing, Ltd., London.
- 22. Easther, R. and Lowe, D.A. (1999) Holography, Cosmology and the Second Law of Thermodynamics. Physical Review Letters, 82, 4967-4970.
http://arxiv.org/abs/hep-th/9902088
http://dx.doi.org/10.1103/PhysRevLett.82.4967 - 23. Loup, F. (2006) On the 5D Extra-Force according to Basini-Capozziello-Ponce De Leon Formalism and Five Important Features: Kar-Sinha Gravitational Bending of Light, Chung-Freese Superluminal Behaviour, Maartens-Clarkson Black Strings, Experimental Measures of Extra Dimensions on Board International Space Station (ISS) and the Existence of the Particle Z Due to a Higher Dimensional Spacetime. General Relativity and Gravitation, 38, 1423-1506.
http://dx.doi.org/10.1007/s10714-006-0319-9 - 24. Maartens, R. (2005) Brane World Cosmology. In: Papantonopoulos, E. (Ed.), The Physics of the Early Universe, Lecture Notes in Physics, Vol. 653, Springer Verlag, Berlin, 213-249.
- 25. Giovannini, M. (1999) Production and Detection of Relic Gravitons in Quintessential Inflationary Models. Physical Review D, 60, Article ID: 123511. http://dx.doi.org/10.1103/PhysRevD.60.123511
- 26. Fontana, G. (2005) Gravitational Wave Propulsion. In: El-Genk, M.S., Ed., CP746, Space Technology and Applications International Forum-STAIF, American Institute of Physics, Melville.
- 27. Sundrum, R. (2005) Extra Dimensions. SLAC Summer Institute: Gravity in the Quantum World and the Cosmos. http://wwwconf.slac.stanford.edu/ssi/2005/lec_notes/Sundrum1/sundrum1.pdf
- 28. Beckwith, A.W. (2007) How a Randall-Sundrum Brane-World Effective Potential Influences Inflation Physics. AIP Conference Proceedings, 880, 1170-1180.
https://arxiv.org/ftp/physics/papers/0610/0610247.pdf
http://dx.doi.org/10.1063/1.2437564 - 29. Leach, J.A. and Lesame, W.M. (2005) Conditional Escape of Gravitons from the Brane.
http://www.citebase.org/cgi-bin/citations?id=oai:arXiv.org:gr-qc/0502109 - 30. Henriques, A.B. (2006) Loop Quantum Cosmology and the Wheeler-De Witt Equation. General Relativity and Gravitation, 38, 1645-1659.
http://arxiv.org/abs/gr-qc/0601134 http://dx.doi.org/10.1007/s10714-006-0330-1 - 31. Banerjee, B. and Gavai, R. (1993) Super Cooling and Nucleation in Phase Transitions.
http://www.citebase.org/cgi-bin/citations?id=oai:arXiv.org:gr-qc/0603021 - 32. Griskuck, L.P. and Solokhin, M. (1991) Spectra of Relic Gravitons and the Early History of the Hubble Parameter. Physical Review D, 43, 2566-2571.
http://dx.doi.org/10.1103/PhysRevD.43.2566 - 33. Rothman, T. and Boughn, S. (2006) Can Gravitons Be Detected?
http://www.citebase.org/cgi-bin/citations?id=oai:arXiv.org:gr-qc/0601043 - 34. Shapiro, S.L. and Teukolosky, S. (1983) Black Holes, White Dwarfs, and Neutron Stars. John Wiley and Sons, New York.
http://dx.doi.org/10.1002/9783527617661 - 35. Dyson, F. (2013) Is a Graviton Detectable? International Journal of Modern Physics A, 28, Article ID: 1330041.
http://dx.doi.org/10.1142/S0217751X1330041X - 36. Gurzadyan, G. and Xue, S.-S. (2003) On the Estimation of the Current Value of the Cosmological Constant. Modern Physics Letters A, 18, 561-568.
http://dx.doi.org/10.1142/S0217732303008405 - 37. Zhitinisky, A.R. (2002) Dark Matter as Dense Color Superconductor. Nuclear Physics B-Proceedings Supplements, 124, 99-102.
http://arxiv.org/abs/astro-ph/0204218
http://dx.doi.org/10.1016/S0920-5632(03)02087-5 - 38. Corda, C. (2008) Massive Gravitational Waves from the R**2 Theory of Gravity: Production and Response of Interferometers. International Journal of Modern Physics A, 23, 1521-1535.
http://dx.doi.org/10.1142/S0217751X08038603 - 39. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282.
http://arxiv.org/abs/0905.2502
http://dx.doi.org/10.1142/S0218271809015904 - 40. Abbott, B.P., et al. (2016) Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters, 116, Article ID: 061102.
https://physics.aps.org/featured-article-pdf/10.1103/PhysRevLett.116.061102
http://dx.doi.org/10.1103/physrevlett.116.061102 - 41. Maggiore, M. (2008) Gravitational Waves, Volume 1, Theory and Experiment. Oxford University Press, Oxford.
- 42. Jack Ng, Y. (2008) Space-Time Foam: From Entropy and Holography to Infinite Statistics and Nonlocality. Entropy, 10, 441-461. http://dx.doi.org/10.3390/e10040441
- 43. Beckwith, A. (2016) Open Question: Could a Causal Discontinuity Explain Fluctuations in the CMBR Radiation Spectrum? Journal of High Energy Physics, Gravitation and Cosmology, 2, 186-208.
http://dx.doi.org/10.4236/jhepgc.2016.22018 - 44. Gao, C.J. (2012) A Model of Nonsingular Universe. Entropy, 14, 1296-1305.
http://dx.doi.org/10.3390/e14071296 - 45. Camara, C.S., de Garcia Maia, M.R., Carvalho, J.C. and Lima, J.A.S. (2004) Nonsingular FRW Cosmology and Nonlinear Dynamics. Physical Review D: Particles and Fields, 69, Article ID: 063501.








