ABSTRACT

Significant land-use changes in North Dakota have been reported and are widespread over the entire state. Such changing patterns may portend localized impairment to agricultural watersheds. In this study, Land-use Land-cov- er (LULC) change was modeled using geostatistics. The study area was within the Pipestem Creek watershed, a part of the Missouri Watershed James Sub- region of North Dakota, USA. Landsat Thematic mapper images from the years 2007, 2011 and 2015 were used as preliminary data. LULC information for these datasets was acquired from the Global Land-cover facility and Landsat Program. Data analysis, spectral classification and post classification techniques were applied on the datasets. A transition matrix was derived using a Markov chain Monte Carlo (MCMC) model. This study demonstrates that the integration of satellite remote sensing, GIS and statistics may be an effective approach for analyzing the direction, rate, and spatial pattern of land-use change.

Keywords:

Markov Chain, LULC Change, Transition Probabilities

1. Introduction

Over the last decade, a range of models of land-use change have been developed to meet land management needs, and to better assess and project the future role of LULC change in the functioning of the earth system. Modeling, especially if done in a spatially explicit, integrated and multi-scale manner, is an important technique for the projection of alternative pathways into the future, for conducting experiments that test our understanding of key processes, and for describing the latter in quantitative terms [1] [2] [3] . Satellite remote sensing, in conjunction with geographic information systems (GIS), has been widely applied and been recognized as a powerful and effective tool in detecting LULC change [4] - [11] . Multispectral satellite data are cost-effective and the information obtained from them can be used as inputs to build LULC datasets. GIS technology provides a flexible environment for spatial and statistical analyses coupled with modeling. Satellite imagery has been used to monitor discrete land-cover types by spectral classification or to estimate biophysical characteristics of land surfaces via linear relationships with spectral reflectance or indices [12] [13] . With easy accessibility of upgraded remote sensing software and readily available satellite imagery, the change in LULC can be assessed over a period of time [14] . Particularly for applications that link remote sensing with human activity, this differentiation is important because land-use emphasizes the functional role of land in economic activities while land-cover does not [15] . Therefore, confounding land-cover with land-use may generate biased results in these studies [16] . The models of LULC change process fall into two groups: regression-based and spatial transition-based models [17] . The majority of research in LULC utilizes regression-based approach, which relates the locations of LULC change to a set of spatially explicit variables, and uses models such as logistic [18] [19] [20] , and hedonic price models [21] . Cellular automaton simulation models are a type of spatial transition based models which allow for predicting future land development based on probabilistic estimates with Monte Carlo or other methods [22] [23] . One crucial limiting factor to the development of process models is the lack of smart modelling tools for change processes in most software platforms. Equally important is the issue of data availability [24] . Very few studies have attempted to link satellite remote sensing and GIS to stochastic modelling methods in LULC change studies. This paper presents a method that combines satellite remote sensing, GIS, and MCMC modelling to analyze and predict LULC changes in the Pipestem Creek, a part of the Missouri Watershed James Sub-re- gion in North Dakota, USA between 2007 and 2015.

MCMC models are used to examine the stochastic nature of the LULC change data and to prioritize areas of impairment within an agricultural watershed. It is used as a descriptive and interrogative tool to quantify the change in land-use occurring over a human-dominant landscape [25] . MCMC simulation models of LULC change aid in the understanding and analysis of interaction between impacts and natural resource management strategies [26] [27] . Markov analysis of vegetation types tends to focus on a small area of less than a few hectares or on a single small plot. When a few hundred hectares of land are involved, data sampling is usually applied to limit the workload to scattered plots or transects [28] . On the other hand, land-use studies using MCMC models tend to focus on a much larger spatial scale, and involve both urban and non-urban covers [29] - [34] . Most of the studies utilizing MCMC models have used the first order of MCMC which was studied to be most suitable. MCMC have several assumptions. According to [35] , a primary assumption is to consider LULC change as a stochastic process, and different categories are the states of the change which is defined as a stochastic process having the property that the value of the process at time t, X_t, depends only on its value at time t − 1, X_t−1, and not on the sequence of values X_t−2, X_t−3, ···, X₀ that the process passed through in arriving at X_t−1 [36] [37] . For {X_n, n ≥ 0} and

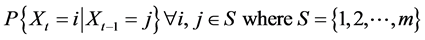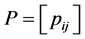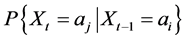then [36] [37] . Reference [37] regarded the change process to be discrete for convenience with incremental time t (t = 0, 1, 2, 3,) values. Likewise, is the transitional probability that makes the transition from state a_i to state a_j in one period of time. The MCMC Model used in this study was of first order homogeneous type. Therefore, 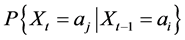can be applied [38] [39] . Here, p_ij can be calculated from observed data by estimating the number of times the particular observed data went from state i to j by adding the number of times the former state occurred. LULC change in itself is very dynamic, thus we cannot expect stationarity in it. However stationary and discrete time has been used in various studies involving forest stands. Thus, MCMC models assume two factors namely time stationarity/homogeneity and time independence. The concept of time stationarity or time homogeneity implies that equal interval in time or consistency between two states is considered within the timeline. Within a stationary MCMC and a set order, the transitional probabilities can be set through maximum likelihood estimation. The probabilities estimated are obtained by maximizing this function [40] . This estimate is just the relative frequency of transitions observed over the entire time period. If the land-use change sequence is a Markov process of order 0, the probability of the random variable X being in state j at time t can be determined [41] . If the MCMC is of order 1, the probability of the random variable X being in state j at time t depends only on the last movement as stated [41] . Thus, testing Markov property is equivalent to testing that the Markov process is of order 1. There are two steps in the testing procedure. First, the null hypothesis that the MCMC is of order 0 versus order 1 is tested; then the order 1 versus order 2 is tested. If the test of order 0 against order 1 is rejected, and the test of order 1 against order 2 is accepted, the process then may be assumed to be of order 1 [41] . In this study, spectral image classification and stochastic methods were utilized to address LULC changes by employing a finite first-order MCMC with stationary transition probabilities.

2. Study Area

The Pipestem 8-Digit Hydrologic Unit Code (HUC) (10160002) sub-basin is approximately 2571 km² covering parts of 4 counties (Foster, Kidder, Stutsman, and Wells) in the Missouri Region-James Sub-Region of North Dakota. Of the 2571 km², Stutsman County contains 65%, Wells 22%, Foster 8%, and Kidder 5%. Human activities affect watersheds by construction of impervious surfaces, which are non-porous. Urban areas are appropriate examples of such surfaces. The amount of runoff is thus increased to foster surface erosion. This could be prevented if a buffer of forests is present in the areas in question. It is difficult to assess the forest cover of North Dakota. This is due to the fact that there are few stands of forests in this region. Most of them are of riparian origin and are found scattered along the river banks [42] . Figure 1 shows the Pipestem Creek watershed map. Figure 2 shows the Land-cover percentage within the Missouri watershed James sub region [43] where the percentage area allotted for cultivated crops is much higher than the forest cover. Table 1 shows the Agricultural Land Suitability within the Missouri Watershed James Sub region in North Dakota indicating a high suitability for grassland.

3. Materials and Methodology

3.1. Image Classification

Landsat 7 ETM+ images (Worldwide Reference System 2, row 027 and path 031) of the study area were acquired from the Global Land-cover Facility and the Landsat Program. These images covered a span of three different years 2007, 2011 and 2015. This freely available data has a ground resolution is 30 m. A thematic RGB band combination of bands 7, 4 & 2 was used. Data obtained was

in the form of individual bands ranging from 1 to 7. Layer stacking created a new multiband file from the input bands which were resampled and re-pro- jected. These datasets were resampled using the nearest neighbor algorithm so that their pixel brightness values were preserved. Upon layer stacking of the Landsat scenes; they were georeferenced to UTM Zone 14 North, WGS-84 Datum, then data calibration was applied which converted the digital numbers of the image to reflectance values as a way of preprocessing the data. Supervised classification was performed using Maximum Likelihood algorithm. We used supervised classification because the data of the study area was available and we had a prior knowledge of the study area. Training site data was derived using digitization which was then converted to polygonal training data. A total of 50 training sites were chosen for each image to ensure that all spectral classes constituting each LULC category were adequately represented in the training statistics. Ten training sites for each of the five classes were chosen as ROIs (regions of interest). The reference data was collected from existing LULC maps that have been field-checked. Change detection statistics was performed on a remote sensing platform to generate a change matrix for the years 2007-2011, 2011- 2015, and 2007-2015. The statistics are presented in a cross tabulation format that compares the change between the two maps, that is, the base map and the final map. We generated change matrices for years 2007 to 2011, 2011 to 2015, and 2007 to 2015. Pixel count and areal extent data for each class within each period was also generated. The maps generated from the change detection statistics were used as inputs to generate confusion matrices as a measure of accuracy assessment. The final change images were overlain with a vector file of the study areas and the final maps were generated.

3.2. Spatial Analyses

Reclassified images of 2007-2011, 2011-2015, and 2007-2015 were imported as raster datasets. The datasets were converted to ASCII using the raster conversion tool to generate the attribute table containing cell values. To estimate the land-use transition from forested land to non-forested land, the datasets were reclassified using spatial analyst. The USGS Anderson Land Classification Scheme [44] was used to classify all the remotely sensed datasets into new values. The categories included: 1) bare soil or barren land, 2) open waters, 3) cropland, 4) forested land, and 5) urban/built-up area. Tables 2-4 represent the areal extent of change within each land-use class for the study period 2007-2015. The amount of positive or negative change for each land-use class is shown in the tables.

3.3. Markov Analysis

The MCMC process was used for describing and projecting land-use information within the watershed from satellite imagery. Data compatibility, stationarity and statistical independence were accessed using the aforementioned MCMC process. The ASCII data generated for each year in the ArcGIS interface was imported into SemGRID 1.6.1 interface as a layer. SemGRID 1.6.1 was used to

generate the transitional probabilities of LULC data for years 2007 to 2011, 2011 to 2015, and finally 2007 to 2015. These probabilities were projected as 3D mesh plots using SigmaPlot® 10.0.

The testing of statistical independence hypothesis involved a procedure that compared the expected change with the actual change. If the number of LULC categories is M, then the statistic to be computed is Pearson’s χ2 with (M − 1)² degrees of freedom [45] . According to the MCMC hypothesis, the transition probability matrix governing the period 2007-2015 can be obtained by multiplying the 2007-2011 and 2011-2015 matrices. Table 5 shows the subset areal extent derived from the Markov Chain model where transition from each class is quantified in hectares as well as percentage value. Transition probability data derived is shown in Tables 6-8. Kappa coefficient of agreement was derived based on [46] [47] . Reclassified Landsat datasets from the years 2007, 2011, and 2015 were combined using the combine function in ArcGIS-Spatial Analyst. Datasets from 2007 and 2011, 2011 and 2015, and finally 2007 and 2015 were combined. The attribute table for each dataset contained the pixel count information for each land-use class. These attribute tables for each datasets were then exported to a database table file in MS-Excel. These were converted to text files and imported into MS-Access where a crosstab query was performed to format and compress the data such that the row and column headings had the same class description as the reclassified datasets. These tables were imported into Excel to derive the Kappa coefficients of agreement for each dataset.

4. Results and Discussion

4.1. LULC Change Statistics

The overall accuracy values based on the post classified images generated for 2007-2011, 2011-2015, and 2007-2015 using change detection statistics in ENVI 4.5® were 91.59 percent, 88.30 percent, and 89.43 percent respectively. Figure 3 shows the graphical representation of LULC change matrix from 2007 to 2011 where a likelihood of increment in 89.69% cropland, 28.81% open waters, and 1.16% urban area was prominent. The likelihood of decrement in forested land appeared to be at 77.16% along with a decrement of 9.06% for bare soil or barren land. Figure 4 represents the graph showing LULC change matrix from 2011 to 2015 where a likelihood of increment in cropland, urban area and bare soil or barren land at 71.17%, 4.09%, and 2.04% respectively was noted. A net negative change in forested land and open waters was observed at 34.27% and 9.24% respectively. Forested land to non-forested land transition was found to be high for 2007 to 2011 period but was slightly lower from 2011 to 2015 period. Positive change in croplands was noted and could be a probable cause to the growing demand for food grains and agricultural products in this area. Figure 5 represents the graph for change matrix from 2007 to 2015. About 89.90% likelihood of increment in agricultural land leading to a 77.44% likelihood of decrement in forested land in the area was noted.

4.2. Validation of LULC Change Process Using Markov Chain

Markov Chain simulations for the Pipestem Creek watershed showed continuity between the trends in change from forested land to other land-use classes (e.g. [47] ). The range of forested land to cropland change was significant. Table 6 represents the transition probabilities of years 2007 to 2011 derived by Markov chain simulation. It represents cropland to cropland transition at 0.36 and

forested land to cropland transition at 0.52. Figure 6 is graphical representations of the transition probability from the year 2007 to 2011 showing significant peak for categories 3 followed by 4 which represent cropland and forested

land respectively. Urban or built-up land generated a low transition probability of 12% from barren land. Table 7 represents the transition probabilities of years 2011 to 2015 derived by Markov chain simulation. Transition from forest to cropland was 44% and cropland to cropland was approximately 50%. Forested land transiting to cropland was relatively higher than that exhibited for the years 2007 to 2011. Barren land to urban area transition probability was high at 22%. Open waters did not show much transition throughout 2007 to 2015. Figure 7 is a visual representation of the tabular data from 2011 to 2015 where the only significant peak that can be seen is for cropland. Table 8 represents the transition probability data 2007 to 2015 in LULC over a period of 9 years where a significant transition probability from forested land to cropland was 41% for years. Figure 8 is a graphical representation of the same data where cropland showed up as a significant peak followed by forested land and urban land, indicating

a likelihood of increment. The Kappa coefficients of agreement for the datasets were at 53.28% for the years 2007 to 2011, 55.74% for the years 2011 to 2015 and 60.24% for the years 2007 to 2015. Figures 9-11 represent LULC maps of the Pipestem Creek in North Dakota for the years 2007-2011, 2011-2015, and 2007-2015 respectively. The western parts of Stutsman and Wells County showed significant transition from forest to cropland. The south-eastern part of Stutsman County showed a significant increase in urban or built-up land attributable to the location of small towns like Jamestown. Reference [47] used error matrices to study similarity between two datasets. A Kappa coefficient value would determine the similarity or dissimilarity between two images. In this study, a low Kappa value is indicative of low similarities between the datasets which could also imply significant transition between various LULC classes. This prediction assumes spatial independence of the area units [48] . Although Markov chains constitute a good tool for describing and projecting LULC quantities, they are insufficient for spatially explicit LULC predictions, because they also assume statistical independence of spatial units. In a similar study made by [48] , it was suggested that Markov transitions

can be used coupled with spatially explicit models like cellular automata and/or linear extrapolation models. The methodology presented in this study incorporated a spatial element along with a temporal model. The projections of future LULC changes on the basis of a MCMC model showed a continuing trend of increase in urban and agriculture land acreages, and the decline in forests and other natural vegetation covers. A similar study was conducted by [47] of statewide North Dakota which depicted a greater likelihood of forest to non-forested land transition especially along north central North Dakota. The prioritization map of North Dakota derived in reference [47] showed that part of the Pipestem Creek watershed was a high priority area for Forest Stewardship Program. The MCMC model transition probabilities estimated from 2007-2015 showing change from forested land to other land-use classes depicted a probability of future change and loss of forest acreage. The test of time homogeneity was performed to determine if that the process of land-use change was stable throughout the full study period. This was done by comparing the data from each sub-period transition matrix i.e. 2007 to 2011, 2011 to 2015 to the full period transition matrix and then comparing the full period of 2007 to 2015. The test of

time dependence in this dataset is evident in Tables 6-8 where the change from forested land to agricultural land was significant from the base year to the transitioning year. The transition probabilities estimated from the full study period with an interval of 4 years was assumed to be time-stationary Markov transition matrix. This may be used to predict the future land-use category distribution to provide answers to management problems as in reference [49] study. Reference [49] also points out that early MCMC models were parameterized using data observed and measured from field surveys and air photography. These data tended to be biased and costly. The use of satellite remote sensing has enabled us to calculate less biased training sites from the full extent of the landscape as in reference [50] . Thus, the issue of obtaining observed training sites is crucial. The Markov chain models have shown the capabilities of descriptive power and simple trend projection for LULC change, regardless of whether or not the trend actually persists. The analysis can serve as an indicator of the direction and magnitude of change in the future as well as a quantitative description of change in the past. However, there are several limitations in LULC change applications. First, these models are difficult to accommodate high-order effects [51] . Reference [51] suggests that these effects can be modeled by redefining the state space, so that new states are defined by both present and preceding states. A second- order model, for instance, would include j² states instead of j states in a first-or- der model [51] . Second, the influence of non-stationary variables cannot be incorporated in the model [51] . Reference [52] shows a method to conditioning changes to the initial states in different sites, as well as in the final states, and therefore introduces spatial dependence into Markov modelling. So higher ordered effects can be studied once the spatial adjustments are made. Table 5 shows results generated with transition states which was corroborated in the transition matrix shown in Tables 6-8 for years 2007 to 2015. Overall, areas used for all forms of agriculture increased by more than 50% of its original level at the first stage. The built-up areas doubled in area compared to the initial stage. The Markov probabilities estimated from the full study period proved to be useful to analyze and predict the distribution of land-use categories, though the land-use change process cannot always be assumed static because of its dynamic nature [52] [53] . The MCMC model, combined with the geospatial analysis proved to capacitate trend projections of the changing land-use [54] . This spatio-temporal model provides not only a quantitative description of change in the past but also the direction and magnitude of change in LULC in the future [55] [56] [57] .

In terms of the quantitative accuracy, error rates for forest and agricultural land are particularly low indicating that nonparametric models can be successfully implemented in a further study of similar agricultural watersheds. In terms of the spatial accuracy for forest, and agricultural land, a confusion matrix generated low accuracy assessment as discussed earlier which were acceptable indicators. This indicates that the MCMC model can predict land-use patterns objectively.

5. Conclusion

The MCMC model performance in predicting LULC distribution from 2007 to 2015 showed that it is possible to project land-use change patterns with small deviations and minimal error. This study integrated land-use pattern changes, MCMC model for the simulation of land-use change. Landscape patterns depict complexities of spatial heterogeneity, and researches have shown that these patterns can influence a variety of ecological phenomena. This methodology combines MCMC model and integrates it with post classification remote sensing techniques. We were able to predict LULC changes from 2007 to 2015. Future research includes the experimentation of spatially explicit models to better understand the LULC dynamics of this area. When facing such severe and rapid LULC changes, one requirement for resource managers is to be able to project future changes under certain assumptions to increase the awareness of ecological consequences. The MCMC model performance reveals the potential and the merit of using this approach for assessing future land-use change in similar arid regions. Future studies are recommended to use more detailed socio-environ- mental variables to improve the understanding of trends of LULC changes within such agricultural watersheds.

Acknowledgements

This study was supported primarily by US Forest Service, award #13-DG-1101- 0000-004, and CFDA Cooperative Forestry Assistance, CFDA Number 10.664, award year FY 2016, and NDSU Project FAR0026072. The research was carried out in a facility that was funded by NSF EAR Division of Earth Sciences Award #: 0963486. This work was conducted at the NDSU Environmental Geomechanics Research Facility.

Cite this paper

Rozario, P.F., Oduor, P., Kotchman, L. and Kangas, M. (2017) Transition Modeling of Land-Use Dynamics in the Pipestem Creek, North Dakota, USA. Journal of Geoscience and Environment Protection, 5, 182-201. https://doi.org/10.4236/gep.2017.53013

References