Journal of Materials Science and Chemical Engineering
Vol.04 No.02(2016), Article ID:64003,15 pages
10.4236/msce.2016.42013
Investigation of the Influence of Annealing Temperature on the Morphology and Growth Kinetic of Ni3Sn4 in the Ni-Sn-Solder System
Mathias Wendt1,2, Andreas Plößl2, Andreas Weimar2, Marcus Zenger2, Klaus Dilger1
1Institut für Füge-und Schweißtechnik, Technische Universität Braunschweig, Braunschweig, Germany
2Osram Opto Semiconductors GmbH, Leibnizstraße 4, Regensburg, Germany

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 November 2015; accepted 25 February 2016; published 29 February 2016
ABSTRACT
The reaction between high purity nickel (99.999%) and high purity tin (99.999%) was investigated in the temperature range of 232˚C - 330˚C, at short periods of annealing (1 - 60 s). The reaction kinetic was studied using cross-sectional scanning electron microscope (SEM) images. The intermetallic compound (IMC) growth was analyzed using the empirical power law and a time dependence in the range of 0.26 to 0.33 was found. The morphology of the IMC was investigated by SEM in the temperature range of 235˚C - 290˚C, at annealing periods of 10 s, 30 s, and 60 s by selectively etching away the remaining elementary tin. The exposed IMC displays a change in morphology with increasing annealing temperature, demonstrating that the growth velocity of certain crystallographic orientations of the IMC is strongly influenced by the annealing temperature. Additionally, coarsening and crumbling of the IMC grains is observed, and will be discussed with respect to the responsible mechanisms.
Keywords:
Lead-Free Solders, Intermetallic Compound Formation, Grain Growth, Coarsening, Solid Liquid Inter-Diffusion (SLID) Bonding

1. Introduction
Producing energy from renewable resources and using energy as efficiently as possible has become a global target and is addressed by politicians worldwide. For instance, the European Council agreed in March of 2007 on their goal to reduce the green house gas emissions by 20% by the year 2020. This can be achieved via two possible ways, either by replacing fossil fuels with renewable energy sources, which can be quite challenging, or by saving energy. Research showed that there was a large potential to save energy in the lighting solutions sector, for example, by using highly efficient light sources, such as LEDs [1] . One key processing step in the manufacturing chain of LEDs is the bonding of wafers, which is used to transfer functional layers from a sapphire wafer to a carrier wafer. A frequently used and well known solder for wafer bonding is the gold-tin-solder (Au Sn). Unfortunately, in the microelectronic industry there is a strong drive to reduce the manufacturing costs of products, which in turn exposes the main disadvantage of the solder, its high price. The drive towards cost reduction in combination with the ban of lead in the microelectronic industry caused a new wave of investigations focusing on lead-free, low-cost soldering processes suitable for surface mount applications or wafer bonding. A suitable candidate for the replacement of Au-Sn solder for wafer bonding is the nickel-tin-solder system (Ni-Sn). Nickel is compared to gold a relatively inexpensive metal which makes it attractive in terms of reducing the cost of the soldering system, but the intermetallic reaction during the soldering process is different. For instance, the dissolution of Au in liquid Sn or Sn-rich alloys is much faster than the dissolution of Ni, additionally the solid Au-Sn intermetallic compound (IMC) forms out of the supersaturated melt while the gold layer dissolves into the molten solder [2] . In the system Ni-Sn the formation of the IMC is driven by a reactive isothermal solidification mechanism which mainly takes place near the Ni-surface and is controlled by the dissolution of Ni into the liquid [3] . Therefore it is of critical importance to understand the growth behavior, reaction kinetics, and the possible influences on them in the Ni-Sn-system in order to achieve similar results to the Au-Sn-system. In order to achieve this goal we need to understand the fundamental processes during the formation of the connection, for instance, in the isothermal solidification of the Ni-Sn-solder the bond connection is formed while the solder system remains at a constant temperature above the melting point of the Sn. The solidification of the solder occurs as a result of the reaction between the Sn and the Ni. This process is often referred to as SLID (Solid-Liquid Inter-Diffusion) or TLP (Transient Liquid Phase) bonding. The reaction between the two materials results in a new phase with an intermediate melting point. In the following processing steps the joint can be exposed to temperatures above the bonding temperature without melting the joint. The details of the influence of temperature on the formation of the connection is only little known. Therefore it is difficult to determine the optimum soldering process for each application. Additionally, most of the current investigations of the Ni-Sn solder system do not focus on the reaction between high purity metals but rather on the reaction between Ni with a certain amount of impurities, as found in electro plated nickel (EP-Ni) or electroless nickel (El-Ni), and Sn-3.5Ag as a solder [4] -[9] . However, in the manufacturing of LEDs and many other microelectronic devices it is important to keep the amount of contaminants in each of the functional layers to a minimum. The contaminants may diffuse to critical junctions during the lifecycle of the LED and cause failure of the device. Since this is unacceptable for a high quality LED used in the automotive industry, high purity metals have to be used for the SLID bonding processes. Therefore this research will focus on the intermetallic compound formation, the grain growth, the morphology of the IMC, and the coarsening mechanisms observed in the reaction between high purity Ni and Sn and the influence of temperature on them.
2. Materials and Methods
The kinetic of the intermetallic phase formation and its microstructural development is studied in the temperature range of 232˚C - 330˚C. All metallic layers were deposited using sputtering techniques in high vacuum. The substrates used are 150 mm, p-doped (boron), single flat silicon wafers with a (100) surface normal. Before the metallisation the wafers were thinned to a thickness of 150 μm using a standard chip-thinning process. The material was removed from the backside of the wafer to retain the high quality front side polishing. Thinning the substrate reduces the thermal mass of the samples. Therefore, giving rise to better accuracy in terms of heat treatment durations by reducing the warm up and cool down time of the samples. After the metal layers were deposited onto the wafers, a low power laser dicing process was used to separate part of the wafers into 1.4 × 1.4 mm square chips. In the heat-affect zone of the nano-second laser dicing process, the metals under study have been melted. Only the regions outside of the heat-affect zone were used for analysis in this research in order not to alter the results of the annealing process.
2.1. The Material System
The materials were deposited in a commercially available PVD cluster tool allowing in-situ cleaning and sputtering without breaking vacuum. Before depositing the metallic layers, the native oxide of the silicon was removed using sputter cleaning with argon as a process gas. In the following step an adhesion layer was deposited on the surface of the wafer, followed by a diffusion barrier and a second adhesion layer, which was made up of 100 nm titanium (Ti). In the initial experiments a 450 nm layer of Nickel (Ni) was deposited on top of the Ti, followed by a 1000 nm thick layer of Tin (Sn). The Sn is covered using a 100 nm thick layer of Ti to prevent the oxidation of Sn once the wafer is exposed to air. The experiments were repeated using the same metal stack with increased Ni (900 nm) and Sn (2000 nm) layer thicknesses, in order to determine the influence of the layer thicknesses on the morphology of the IMC layer. All metals used are grade 5N (99.999% pure) materials. Once the wafer was inserted into the tool used for cleaning and metallisation, vacuum remained uninterrupted to ensure that the silicon and metals are not being oxidized. The scanning electron microscope (SEM) image in Figure 1 displays the metal stack prior to heat treatment.
In order to examine the growth and morphology of the IMC at different stages during the course of its formation, various heat treatment durations and temperatures were selected.
2.2. Sample Preparation for SEM Analysis
Two different methods of sample preparations were used: 1) samples were embedded into an epoxy resin for cross-sectioning, 2) samples were etched in an HCl solution to expose the IMC.
The cross-section samples were used to determine the growth kinetic of the IMC at different temperatures. The etched samples were used to identify the morphology of the IMC at different annealing temperatures and durations.
2.3. Cross-Section Samples
The cross-section samples are 1.4 × 1.4 mm square chips.
2.3.1. Annealing Conditions
The chips were annealed at different temperatures varying between 232˚C - 330˚C (232˚C, 260˚C, 290˚C, 310˚C, 330˚C) and durations between 1 s and 60 s (1 s, 3 s, 5 s, 10 s, 30 s, 60 s). The annealing was conducted using a die bonding tool called heated bond head (HBH), which is traditionally used to bond chips onto lead frames. The tool uses a pick-head to pick up an individual chip, and places it onto a vacuum chuck. Then a heated collet picks
Figure 1. Cross-section SEM image of the as prepared sample, all relevant metal layers identified with element symbols.
the chip off the chuck. The chip remains attached to the heated collet for the desired time period, then it is dropped into a metal beaker for cooling. Since the area of contact between the chip and the heated collet is large, and due to a good thermal contact to the chip, warm up durations are, compared to the annealing times, considered negligible. Similarly, since the thermal mass of the collet is much bigger than the thermal mass of the chip, the temperature change of the collet induced by heating up the chip is considered negligible. Using the HBH, the chips can be heated rapidly, and annealing durations as short as 1 s can be realized. Therefore, this tool is suited to investigate the reaction during short annealing durations (1 s, 3 s, 5 s). The accuracy of the temperature reading of the HBH was determined using the melting point of Sn, bismuth (Bi), and the gold-silicon (Au-Si) eutectic reaction, prior to the experiments.
2.3.2. Cross-Sectioning
After annealing, the samples were embedding into an epoxy resin, then they were ground, polished, prepared using ion milling, and a thin gold-palladium film was deposited on the sample surface to avoid charging during SEM investigation.
2.4. Plan-View Samples
The plan view samples were 1 × 1 cm square pieces; the wafer was separated into the pieces using a diamond tipped stylus.
Annealing Conditions
The heat treatment for the etched samples was conducted using a hotplate (Präzitherm; PZ 28-2T). Selected annealing temperatures and durations were 235˚C, 260˚C, 290˚C and 10 s, 30 s, 60 s. The accuracy of the temperature reading of the hotplate was checked using the melting points of the metals Sn, and Bi prior to the experiments. Following the heat treatment, the Ti surface of the sample was partially ground using sandpaper (grit 4000), and the Sn was selectively etched using an aqueous 38% HCl solution. The selectivity of the Sn etch process was evaluated using over etch experiments in order to ensure that the morphology of the IMC remains unchanged during etching. The samples for the etch experiments were annealed at 260˚C for 10 s using the hotplate. When the samples were etched, hydrogen bubble development terminated after about 20 s, indicating that the Sn not consumed in the reaction with Ni, has been completely dissolved by the HCl. After etching for different durations (25 s, 40 s, 60 s, 80 s) the tip diameters of the IMC grains were measured in top view SEM images for ten grains at each etch duration. A plan-view SEM image of the IMC and the results of the measurements are displayed in the Figure 2.
The data points displayed in Figure 2(b) are the arithmetic mean values of the IMC grain tip diameters for the given etch durations, the error bars represent the error in measurement of the grain tip diameter size. Since the
Figure 2. (a) Top view SEM image of a sample annealed at 260˚C for 10 s, etch duration 25 s, (b) data plot of IMC grain diameter vs. Etch duration in 38% HCl.
selectivity of the Sn etch process is high and the experiments showed that over etching the sample for long periods of time does not alter the grain size, a etch duration of 40 s was selected to ensure that there is no Sn left between the grains or on top of the IMC layer, even at low annealing temperatures and short durations. After etching the samples for 40 s they were placed in an ultrasonic bath, rinsed with DI‑water, and dried under a stream of dry nitrogen. After cleaning the samples, the ones used for cross-sectional images were scratched on the top side using a diamond tipped stylus and mechanically separated into two rectangular pieces. When separating the sample, great care was taken not to damage the delicate grains and forces were applied in a way that the grains of the IMC were pulled apart, as opposed to being pushed together, ensuring that the grains stay attached to the sample and are not being deformed. Preparing the samples in this fashion yields an almost 3-dimensional, unaltered view of the grains and the interface between the Ni and the growing IMC grains, thus exposing their morphology, and the development of new grains at the interface.
2.5. Analytical Methods
The annealing temperature was measured using a thermocouple which was part of the respective tool. The morphology, thickness, and chemical composition of the IMC formed during heat treatment was investigated using a Zeiss Leo Gemini 1530 SEM, and an AMETEK EDAX APOLLO X silicon drift detector. The image analysis was done using the Origin digitizer, the diameter of IMC grains was measured manually and the thickness of the Ni layer used to investigate the growth kinetics was measured using a best fit line along the IMC/Ni interface and the Ni/Ti interface.
3. Results and Discussion
3.1. Growth Kinetics
The growth kinetic of the IMC was studied using cross-sectional samples. Below the melting temperature of the Sn, the growth of the IMC reportedly is slow and occurs in a layer-type morphology [10] . Therefore temperatures below the melting point of Sn are not practicable for a bonding process and were hence not subject of this investigation. When the bonding temperature reaches the melting point of Sn, growth of the IMC becomes faster and relevant for commercially used soldering or bonding processes.
3.1.1. Annealing Samples at 232˚C
Figure 3 displays the cross-sectional SEM images of the sample annealed at 232˚C. At short annealing durations a thin, continuous layer of the IMC develops at the interface of the metals Ni and Sn. With increasing annealing duration the thickness of the developed IMC increases with a non linear dependence on time. After 60 s an about 500 nm thick layer of IMC has formed. The IMC layer contains enclosures, which were analyzed using EDX and it was found that they are made up of elementary Sn.
3.1.2. Annealing Samples at 330˚C
Annealing the samples at 330˚C for 1 s results in a thin, irregular shaped layer of IMC at the interface between the two metals, as seen in Figure 4 (1 s). Parts of the IMC reach far into the Sn, others are only a few hundred nanometers thick, and some seem to lack connection to the underlying IMC. The annealing durations 3 s, 5 s, and 10 s result in an IMC with a similar appearance but continuously increasing thickness. When annealing the samples for 30 s and 60 s, the IMC develops into an almost continuous layer with few Sn enclosures. With increasing time the individual grains, reaching far into the Sn at the beginning of the reaction, seem to connect to form a continuous IMC layer. When examining the images of the late annealing stages, it becomes clear that the layer becomes more continuous and the number of Sn enclosures decreases as the annealing duration increases. Additionally the IMC layer formed during short annealing durations grows rougher as the temperature is increased and the thickness varies more drastically across the inspected region. Various EDX spectra have been recorded at different annealing temperatures and durations. The compositions of the IMC determined using the spectra were closest to Ni3Sn4. Similar results were found in various investigations, which also identified the IMC formed between Ni and Sn in this temperature range to be Ni3Sn4 [4] -[6] [11] . Therefore, we will assume that the compound formed is Ni3Sn4 for all further analysis.
In this study the empirical power law is used to describe the growth of the IMC, Ni3Sn4. This approach is
Figure 3. SEM images of the Ni-Sn interface and the developing IMC at a temperature of 232˚C after 1 s, 3 s, 5 s, 10 s, 30 s, 60 s, magnification 30 kX.
generally used to describe the growth of IMCs [4] -[7] [11] . The following form of the empirical power law is used for analysis:
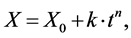 (1)
(1)
where X represents the thickness of the IMC layer at time t, X0 is the initial thickness of the IMC, k is the rate constant of the growth, and n the time exponent. The value of n indicates the rate controlling step of the growth mechanism. Plotting ln(X − X0) vs. ln(t) yields the values of n and ln(k), as the slope and y-intercept, when fitted using a linear regression model. The rate constant k is dependent on activation energy and the temperature, which can be described using the following Arrhenius-type equation:
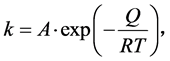 (2)
(2)
where A is the pre-exponential constant, Q is the activation energy, T is the temperature in Kelvin, and R the universal gas constant (8.314 Jmol−1∙K−1). When plotting ln(k) vs. 1/T it is possible to determine Q. In order to determine the time exponent n and the rate constant k, the amount of IMC that developed was determined by measuring the thickness of the nickel layer for each of the annealing durations and calculating the thickness of the IMC layer that developed from the Ni. Measuring the thickness of the Ni is done using lines of best fit at the Ni/Ni3Sn4 interface and at the Ni/Ti interface. In order to determine the resulting IMC thickness, the following assumptions have been made.
1) The solubility of Ni in liquid Sn in the temperature range is low and can, for the purpose of this investigation, be neglected.
2) The decrease in thickness of the Ni layer is directly proportional to the increase of Ni3Sn4.
Figure 4. SEM images of the Ni-Sn interface and the developing IMC at a temperature of 330˚C after 1 s, 3 s, 5 s, 10 s, 30 s, 60 s, magnification 30 kX.
3) The IMC growth during heating and cooling of the sample is negligible.
These assumptions are generally accepted by researchers [7] . If Ni3Sn4 is thermodynamically stable and the only compound formed during this reaction and assumption 1 is valid, then assumption 2 is applicable. The Ni-Sn phase diagram shows that the solubility of Ni in liquid Sn at the temperatures used in this study is less than 1 at% [12] . That makes assumption 1 valid for this study. Furthermore assumption 3 seems valid since the thermal mass of the substrates is small, ensuring short heating and cooling durations for the annealing method used.
Figure 5 displays the ln(X − X0) vs. ln(t) plot of the growing IMC at 232˚C used to determine n and ln(k).
The error bars were determined using a minimum and maximum value for the remaining Ni thickness for each annealing duration and the laws of error propagation. The values of n for all of the investigated temperatures are displayed in Table 1.
Figure 6 displays the graph of ln(k) vs. 1000/T which was used to determine the activation energy Q.
The activation energy was determined to be 33 kJ・mol−1. The error bars in the plot of Figure 6 were derived from the error in y-intercept of the graphs used to determine n.
3.1.3. Discussion of Growth Kinetics: Time Exponent N and Activation Energy Q
A value of n = 0.5 indicates that the reaction is controlled by bulk diffusion and n = 0.33 indicates a reaction controlled by diffusion along grain boundaries [13] . A value of n = 0.41 has been reported for the system electroless Ni and 95.5Sn-4.0Ag-0.5Cu, for the temperatures 260˚C, 280˚C, 300˚C, 320˚C, and 350˚C [7] . Bader et al. determined a value of n = 0.28 for the system sputtered Ni on sputtered Sn at 240˚C [11] . Shen et al. reported a time exponent of n = 0.32 ± 0.013 at 250˚C and n = 0.43 ± 0.011 at 280˚C for the system Ni and Sn-3.5Ag [6] . The values of n determined in our study are slightly lower than the values found for the material systems mentioned above. We found that close to the melting temperature of the Sn, the value of n is higher compared to
Figure 5. Growth of Ni3Sn4 phase plotted for 232˚C.
Figure 6. Arrhenius plot used to determine the activation energy of the Ni3Sn4 growth.
Table 1. Values of n for investigated temperatures, and the associated errors.
temperatures well above the melting point. We suggest that this increase is due to an increase in diffusion flux of Sn caused by the change in IMC morphology and an increased mobility of Sn, both of these effects are a result of the increased temperature, as seen in section “3.2 Dependency of morphology on temperature”. In the works by Gosh et al. the activation energy Q was determined to be 16.936 kJ・mol−1 for the reaction between Sn-3.5Ag and Ni, at a temperature of 230 ˚C and 260 ˚C [7] . Chen et al. determined the activation energy for the reaction between EP-Ni, El-Ni and Sn-3.5Ag to be 25 kJ・mol−1 and 38 kJ・mol−1, respectively [8] . Clearly the value of activation energy found in this study does not vary significantly from the results found by the studies mentioned above. Chen-Chiang et al. determined the activation energy and time exponent for electroplated Ni and Sn on a suttered copper surface in the temperature range of 523 K to 598 K. The resulting time exponent varied between 0.076 and 0.15 and the activation energy was 23.15 kJ・mol−1 [9] . The authors of the study mention that the time exponent varies from the result found by Bader et al. but do not discuss the result further.
3.2. Dependency of Morphology on Annealing Temperature
Since the only parameter changed in the experiments is the annealing temperature and time, we suggest that the morphology of the developing Ni3Sn4 phase displays a distinct dependency on the temperature. This behavior was most pronounced in the early stage of the growth. The lowest annealing temperature used for the etched cross-sectional samples is 235˚C. At this particular temperature the IMC growth occurs in a continuous layer, consisting of individual grains. These grains do not display a clear structure and their shape varies between small whisker-like and large-rounded with irregular shaped edges, as shown in Figure 7.
With increasing annealing time the thickness of the IMC layer increases but the morphology of the grains does not change significantly, as seen in Figure 7 (10 s), (30 s), and (60 s). The grains grow in the horizontal and vertical direction but their shape remains the same. Importantly, the IMC layer displays a homogeneous thickness, similar to the SEM images of the embedded samples annealed at 232˚C. The IMC layer can be divided into two regions, one consisting of large grains which grew early in the reaction, we will call this the primary IMC layer (IMC 1), and another region consisting of a continuous layer of smaller grains that grew between the existing layer and the Ni, which we will call the secondary IMC layer (IMC 2), as seen in Figure 7 (30 s). A similar division into regions of different morphologies was done by Bader et al. which essentially divided the IMC layer into three parts, a fine-grained layer at the Ni interface, a layer consisting of thin whiskers, and a layer consisting of large crystals [11] . Since, according to our results, the thin whiskers continuously change into the large crystals, a clear distinction between the two will not be made here. When the temperature is increased from 235˚C to 260˚C, the growth of the IMC becomes faster, as indicated by a thicker IMC layer in the sample annealed for 10 s (see Figure 8 (10 s)).
It also becomes evident that the grains are more faceted, and shaped like whiskers. This indicates that there are certain crystal orientations whose growth velocity is strongly influenced by the increase in temperature. The growth velocity of this orientation becomes much faster than the velocity of the other orientations. Similar results were found by Bader et al. who discovered that there is an orientation which grows faster than others [11] , but not that temperature has a significant influence on the growth velocities of the Ni3Sn4 crystal orientations.
Figure 7. Side view SEM images of the Ni3Sn4 interface of the etched samples, annealed at 235˚C for 10 s, 30 s, and 60 s, magnification 30 kX.
The spaces between the whiskers are the Sn enclosures which were also seen in the cross-sectional samples. With an increase in annealing time the whiskers develop into large grains and the degree of facetation decreases. This can be observed in samples annealed for 30 s and 60 s (see Figure 8). With an increase in annealing time, a more continuous layer of IMC forms as the Sn enclosures between the whiskers are consumed by the growth of the IMC. At this point in the reaction, a coarsening starts to take place, as the diffusion of the Sn towards the Ni decreases. The images show that the majority of the IMC layer consists of large grains and the whisker like, highly faceted grains have changed. Similar to the samples annealed at 235 ˚C, the SEM images in Figure 8 show an IMC layer consisting of a primary and a secondary layer.
When the temperature is further increased to 290 ˚C the grains become more whisker-shaped and faceted, again attributed to the temperature dependent growth velocity of certain Ni3Sn4 crystal orientations. As the grains become more whisker-shaped, the amount of Sn between them increases, as indicated by the increasing size and number of the Sn enclosure in the primary layer. The secondary layer still forms continuously and the Sn enclosures extend down to this layer. This can be seen in Figure 9.
Figure 8. Side view SEM images of the Ni3Sn4 interface of the etched samples, annealed at 260˚C for 10 s, 30 s, and 60 s, magnification 30 kX.
Figure 9. Side view SEM image of the Ni3Sn4 interface of the etched sample, annealed at 290˚C for 10 s, 30 s, and 60 s, magnification 30 kX.
As annealing time is increased the grains become larger and the degree of facetation decreases. This is due to the fact that the fastest growing crystal faces slowly disappear, as is the case for all crystals with different growth velocities for different crystal orientations. The faces oriented along the fast growing crystal orientations are large at the beginning of the reaction but their size decreases in the course of the growth. Under close inspection it is visible that some of the grains become detached from the underlying IMC layer. This is due to a mechanism called the crumbling mechanism, first observed by Gur and Bamberger [3] . They attribute the detachment of the large grains from the layer of smaller grains beneath them to grain boundary grooving. The grooving separates the grains from each other leading to a complete detachment from the layer beneath and the surrounding grains. The complete detachment from the surrounding grains was rarely observed in this investigation. Additionally, the piling associated with grain boundary grooving was not observed, as seen exemplified in Figure 10.
There are no studies of grain boundary grooving available for Ni3Sn4, but Ni has been studied extensively by Gladstone et al. [14] . They report a good correlation of the experimental data with the model published by Mullins et al. [15] [16] . Gladstone et al. observed a maximum groove depth of 120 nm for cold-rolled Ni tape (4N) when recrystallized in vacuum at 800˚C for 4 h, and a maximum groove depth of 100 nm when recrystallized in Ar-1%H2 at 800˚C for 4 h [14] . Since most grain boundaries seen in our study exceed a depth of 120 nm and the temperature and heat treatment duration are much lower, grain boundary grooving does not supply a reasonable explanation for the crumbling observed in our experiments. Even in view of the melting point of Ni3Sn4 (796˚C) [17] , compared to the melting point of Ni (1453˚C), the amount of grooving necessary to separate the grains appears unreasonably large. We observed that most grains were still attached to some of the smaller or neighboring grains as they became detached from the underlying IMC, giving merit to the hypothesis proposed by Görlich et al. [18] . They claim that the small grains push the larger ones into the liquid phase as they grow in size. In their hypothesis the growth of the Ni3Sn4 phase originates at the Ni/IMC interface and the grain boundaries are the dominant transport path for Sn towards the Ni. This is contradictory to the hypothesis of Gur et al., who claim that Ni diffuses into the Sn and deposits itself onto the Ni3Sn4 grains. They argue that the growth mainly takes place at the Ni3Sn4/Sn interface [13] . In view of our experimental results, we conclude that the crumbling of grains is caused by the mechanism described by Görlich et al. Furthermore we conclude, that the growth of the IMC originates at the Ni/IMC interface and that Sn moves towards the Ni along grain boundaries.
The Effect of Whisker Growth of the Bond Connection
During bonding of chips, the whisker-type growth of Ni3Sn4 at elevated temperatures (290˚C and above) may
Figure 10. Side view SEM image of two grains separated from each other, annealed at 290˚C for 10 s. Arrows are placed on the grains that separated from each other, pointing towards the surface at which separation occurred.
lead to issues in the bond connection. The Ni3Sn4 whiskers will cause a local connection of the two bonding partners, early in the bond process. The majority of the Sn will still be in its elementary form at this point. In the further course of the SLID process, the Sn will be drawn continuously towards the Ni interface, leaving behind cavities. The cavities may lead to a failure of the bond connection when it is subject to loading. Additionally the local connections between the wafers may lead to large stress concentrations when the wafers are pressed together during the bonding process. These stress concentrations may lead to breakage of one of the wafers during bonding. Therefore the selection of the bonding temperature for a Ni/Sn bonding system requires careful consideration and a moderate bond temperature will lead to a more satisfying result in terms of reducing cavities and wafer breakage.
3.3. Coarsening of Grains
Upon inspection of the grain size, it becomes evident that at each of the given temperatures the grains coarsen as the annealing duration increases. There are two main mechanisms causing the coarsening of grains: 1) the large grains may coarsen by consuming smaller grains, this effect is driven by the reduction of free surface energy; 2) grains may also coarsen through the deposition of Ni and Sn onto their surface, this effect is driven by the release of energy from the reaction between Ni and Sn. These two effects may happen simultaneously, but the extent to which they are responsible for the coarsening observed is influenced by the environment in which the grains reside.
We found that grains grow like whiskers at high annealing temperatures (290˚C and above) and short duration (10 s), later on they start coarsening at these particular temperatures (290˚C and above, after 60 s). The diffusion path length along grain boundaries is shorter at short annealing durations (10 s) at this particular temperature, due to the whisker-like growth and Sn enclosures close to the secondary IMC layer. Since Sn is in the liquid state and Ni in the solid, the diffusion of Sn is much faster than the diffusion of Ni in the investigated temperature range. Therefore Sn can move more easily along grain boundaries towards the Ni/IMC interface when the supply of Sn is abundant. This inhibits the diffusion of Ni towards the Sn/IMC interface. If the supply of Sn decreases, Ni is able to diffuse towards the Sn rich side. This allows the Ni3Sn4 grains to grow in the lateral direction by deposition of Ni and Sn out of the liquid phase onto the surface of the existing grains, causing coarsening (type 2). We suggest this coarsening behaviour at high annealing temperature, for instance 290˚C and above.
At low annealing temperatures (235˚C) the IMC grains grow irregular shaped and slowly coarsen as annealing duration increases. The IMC layer grows with a homogeneous thickness and develops very few Sn enclosures. Therefore, the diffusion path length across the IMC layer is almost constant throughout. The supply of Sn is still abundant in this case and Ni cannot diffuse towards the Sn/IMC interface. Therefore grains cannot coarsen through the deposition of Ni and Sn out of the liquid phase (type 2) and the large grains have to coarsen by consuming small grains (type 1). The principle of the diffusion mechanism is drawn schematically in Figure 11.
Görlich et al. also investigated the coarsening of grains in their research. They came to the conclusion that the coarsening is neither well described by Lifshitz-Slezov-Wagner theory (LSW theory) nor by flux-driven ripening theory (FDR theory), since the size distribution of the grains in the experiments and the theoretical predictions did not match [18] . LSW theory assumes that the surface area of the grains undergoing ripening decreases but the volume stays constant [19] [20] . FDR theory takes a more general approach saying that the surface area
Figure 11. Schematic drawing of the diffusion flux of Ni and Sn along the grain the boundaries of the IMC, (a) at an early stage, (b) when Sn supply becomes limited. JSn and JNi represent the diffusion flux of Sn and Ni respectively, the arrows indicate the magnitude and direction of the diffusion flux.
remains constant, while the volume of the phase is growing [21] . A more satisfying result of the theoretical predictions of the grains size distribution may be reached when taking into account that the morphology has an influence on the mechanism causing coarsening.
Our proposed mechanism for coarsening consists of two parts, large grains may coarsen by consuming the smaller grains, and deposition of Ni and Sn onto the existing grains. In this case ripening is controlled by diffusion of the individual species involved in the reaction and the rate of consumption of the small grains by the larger grains. The rate of diffusion of Sn towards Ni/Ni3Sn4 interface and Ni towards the Sn/Ni3Sn4 interface is controlled by the morphology of the IMC, the supply of Sn, and therefore by the annealing temperature. Since it is difficult to determine the contribution of the respective mechanism, the theoretical model has to be adjusted to incorporate the effect of the morphology of the grains undergoing coarsening, and the resulting predictions have to be matched to the experimental results. Vice versa, when FDR theory predictions are matched to experimental results, attention should be paid to the morphology of the grains undergoing coarsening, since the theory assumes scalloped shaped grains, which may only develop at certain annealing temperatures.
3.4. Morphological Difference Due to Increased Temperature
In order to demonstrate that the morphology of the growing IMC depends on temperature, Ni consumption was measured for each of the annealing temperatures 235˚C, 260˚C, and 290˚C. The annealing time was adjusted to achieve equal Ni consumption for each annealing temperature. Figure 12 displays the samples after preparing them by etching.
The images clearly display that the IMC appears different at each of the annealing durations even though the reaction is at the same stage. It becomes evident that the reaction mechanism changes with increasing temperature, resulting in one of the orientations of the grains to grow faster. This effect leads to the highly facetted, whisker like grains with many Sn enclosures, displayed in Figure 12(c), as opposed to the continuous layer, seen in Figure 12(a), with few Sn enclosures. The experiments were repeated with increased Ni and Sn layer thicknesses in order to demonstrate that this effect is independent of the layer thickness. The thickness of the Ni and Sn layers was increased to 900 nm and 2000 nm, respectively. The change in morphology of the Ni3Sn4 grains due to the increase in temperature was observed as well. Figure 13 displays the SEM images of the samples.
4. Conclusion
The reaction between Ni and Sn was studied in the temperature range of 232˚C to 330˚C. The reaction kinetic was studied across the entire temperature range. The morphology of the developing IMC was studied between
Figure 12. Side view SEM images of samples with the same Ni consumption after annealing at (a) 235˚C for 60 s magnification 30 kX, (b) 260˚C for 21 s magnification 25 kX, (c) 290˚C for 7 s magnification 25 kX.
Figure 13. Side view SEM images of samples with increased Ni and Sn layer thicknesses and equal Ni consumption after annealing at (a) 235˚C for 60 s, (b) 260˚C for 21 s, (c) 290˚C for 7 s, magnification 25 kX.
235˚C and 290˚C. The kinetic of the reaction was analyzed using the empirical power law. The time exponent and the activation energy Q were determined. The values of n ranged from 0.26 to 0.33, and the activation energy Q was 33 kJ・mol−1. When studying the morphology of the IMC, it became apparent that it displayed a clear dependence on the annealing temperature, which has not been observed before. At low annealing temperatures (235˚C) the morphology of the IMC grains appears large and rounded. At high annealing temperatures (290˚C) the IMC grains grow with a whisker-type morphology. The fast growing whiskers, which were observed at 290˚C, can have a negative impact on the bonding connection. The whiskers may cause a local connection between the bonding partners early in the SLID process. This may lead to the development of cavities in the bond connection during the further course of the SLID process. The crumbling of large Ni3Sn4 grains into the liquid component cannot conclusively be explained by grain boundary grooving but rather by the growth of smaller grains located at the Ni/Ni3Sn4 interface, pushing the ones formed earlier away from the interface, as proposed by Görlich et al. [18] . Furthermore, we propose a mechanism where coarsening is caused by grains joining each other and the deposition of Ni and Sn out of the liquid Sn onto the grains surface. In particular, the morphology of the IMC at the early stages of the growth has an influence on the coarsening mechanism later in the reaction.
Acknowledgements
We acknowledge the Bundesministerium für Bildung und Forschung for financial support of the “Greight” (project no. 13N10555) project which supplied funding for the research. The authors thank Dipl.-Ing. B. Behr for valuable technical discussions and help in designing experiments.
Cite this paper
MathiasWendt,AndreasPlöβl,AndreasWeimar,MarcusZenger,KlausDilger, (2016) Investigation of the Influence of Annealing Temperature on the Morphology and Growth Kinetic of Ni3Sn4 in the Ni-Sn-Solder System. Journal of Materials Science and Chemical Engineering,04,116-130. doi: 10.4236/msce.2016.42013
References
- 1. OSRAM Executive Summary (2009) Life Cycle Assessment of Illuminants—A Comparison of Light Bulbs, Compact Fluorescent Lamps and LED Lamps. Published by OSRAM Opto Semiconductors GmbH, Regensburg, Germany and Siemens Corporate Technology, Berlin, Germany.
- 2. Laurila, T., Vuorinen, V. and Kivilahti, J.K. (2005) Interfacial Reactions between Lead-Free Solders and Common Base Materials. Material Science and Engineering: R: Reports, 49, 1-60.
http://dx.doi.org/10.1016/j.mser.2005.03.001 - 3. Gur, D. and Bamberger, M. (1998) Reactive Isothermal Solidification in the Ni-Sn System. Acta Materialia, 46, 4917-4923.
http://dx.doi.org/10.1016/S1359-6454(98)00192-X - 4. Shen, J., Chan, Y.C. and Liu, S.Y. (2009) Growth Mechanism of Ni3Sn4 in a Sn/Ni Liquid Solid Interfacial Reaction. Acta Materialia, 57, 5196-5206.
http://dx.doi.org/10.1016/j.actamat.2009.07.021 - 5. Gosh, G. (2000) Coarsening Kinetics of Ni3Sn4 Scallops during Interfacial Reaction between liquid Eutectic Solders and C/Ni/Pd Metallization. Journal of Applied Physics, 88, 6887-6896.
http://dx.doi.org/10.1063/1.1321791 - 6. Alam, M.O. and Chan, Y.C. (2005) Solid-State Growth Kinetics of Ni3Sn4 at the Sn-3.5Ag Solder/Ni Interface. Journal of Applied Physics, 98, Article ID: 123527.
- 7. Jeon, Y.D., Nieland, S., Ostmann, A., Reichl, H. and Paik, K.W. (2002) Studies of the Interfacial Reactions between Electroless Ni UBM and 95.5Sn-4.0Ag-0.5Cu Alloy. Proceedings of the Electronic Components and Technology Conference, San Diego, 31 May 2002, 740-747.
- 8. Chen, H.-Y. and Chen, C. (2012) Kinetic Study of the Intermetallic Compound Formation between Eutectic Sn-3,5Ag Alloys and Electroplated Ni Metallization in Flip-Chip Solder Joints. Journal of Material Research, 27, 1169-1177.
http://dx.doi.org/10.1557/jmr.2012.22 - 9. Yu, C.-C., Su, P.-C., Bai, S.J. and Chuang, T.-H. (2014) Nickel-Tin Solid-Liquid Inter-Diffusion Bonding. International Journal of Precision Engineering and Manufacturing, 15, 143-147.
http://dx.doi.org/10.1007/s12541-013-0317-2 - 10. Mita, M., Kajihara, M., Kurokawa, N. and Sakamoto, K. (2005) Growth Behavior of Ni3Sn4 Layer during Reactive Diffusion between Ni and Sn at Solid-State Temperatures. Journal of Material Science and Engineering A, 403, 269-275.
http://dx.doi.org/10.1016/j.msea.2005.05.012 - 11. Bader, S., Gust, W. and Hieber, H. (1995) Rapid Formation of Intermetallic Compounds by Interdiffusion in the Cu-Sn and Ni-Sn Systems. Acta Metallurgica et Materialia, 43, 329-337.
- 12. Liu, H.S., Wang, J. and Jin, Z.P. (2004) Thermodynamic Optimization of the Ni-Sn Binary System. Calphad, 28, 363-370.
http://dx.doi.org/10.1016/j.calphad.2004.12.002 - 13. Schaefer, M., Fourelle, R.A. and Liang, J. (1998) Theory of Intermetallic Phase Growth between Cu and Liquid Sn-Pb Solder Based on Grain Boundary Diffusion Control. Journal of Electronic Materials, 27, 1167-1176.
http://dx.doi.org/10.1007/s11664-998-0066-7 - 14. Gladstone, T.A., Moore, J.C., Wilkinson, A.J. and Grovenor, C.R.M. (2001) Grain Boundary Misorientation and Thermal Grooving in Cube-Textured Ni and Ni-Cr Tape. IEEE Transactions on Applied Superconductivity, 11, 2923-2926.
http://dx.doi.org/10.1109/77.919674 - 15. Mullins, W.W. (1957) Theory of Thermal Grooving. Journal of Applied Physics, 28, 333-339.
http://dx.doi.org/10.1063/1.1722742 - 16. Mullins, W.W. (1958) The Effect of Thermal Grooving on Grain Boundary Motion. Acta Metallurgica, 6, 414-427.
http://dx.doi.org/10.1016/0001-6160(58)90020-8 - 17. Fields, R.J. and Low, S.R. (2014) NIST Metallurgy Division Research Publication. www.metallurgy.nist.gov
- 18. Görlich, J., Baither, D. and Schmitz, G. (2010) Reaction Kinetics of Ni/Sn Soldering Reaction. Acta Materialia, 58, 3187-3197.
http://dx.doi.org/10.1016/j.actamat.2010.01.027 - 19. Lifshitz, I.M. and Slezov, V.V. (1961) The Kinetics of Precipitation from Supersaturated Solid Solutions. Journal of Physics and Chemisty of Solids, 19, 35-50.
http://dx.doi.org/10.1016/0022-3697(61)90054-3 - 20. Wagner, C. (1961) Theorie der Alterung von Niederschlägen durch Umlösen. Zeitschrift für Elektrochemie, 65, 581-591.
- 21. Gusak, A.M. and Tu, K.N. (2002) Kinetic Theory of Flux-Driven Ripening. Physical Review B, 66, Article ID: 115403.
http://dx.doi.org/10.1103/PhysRevB.66.115403















