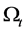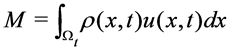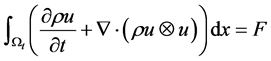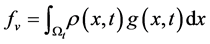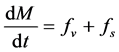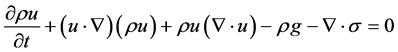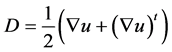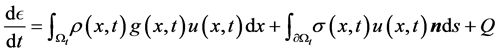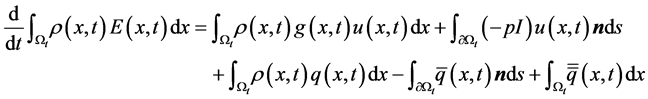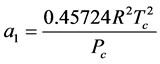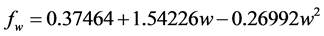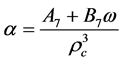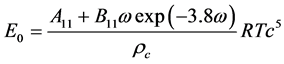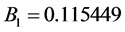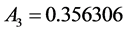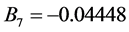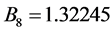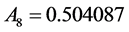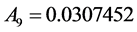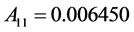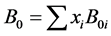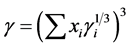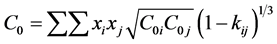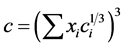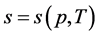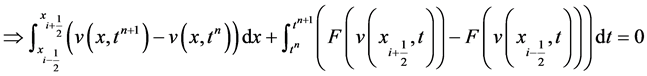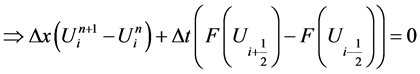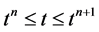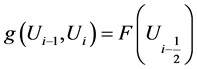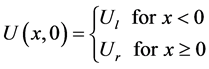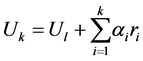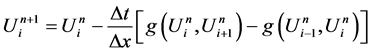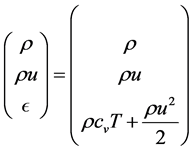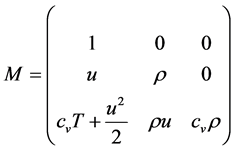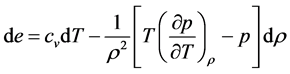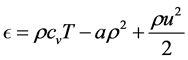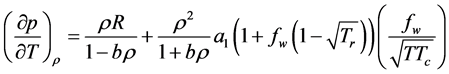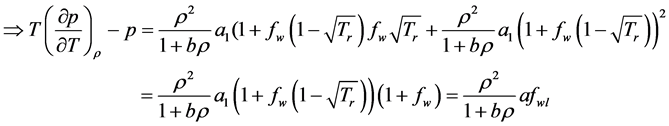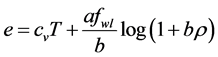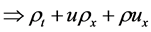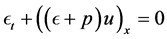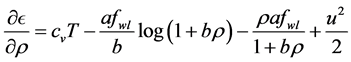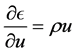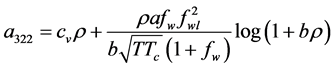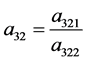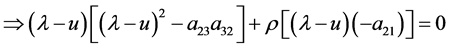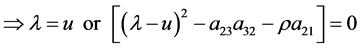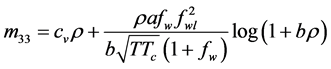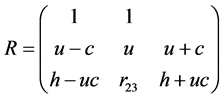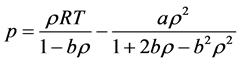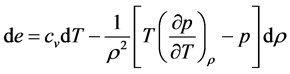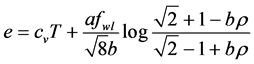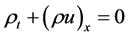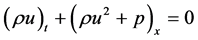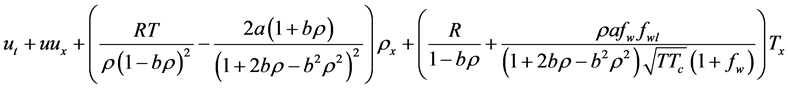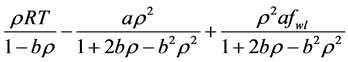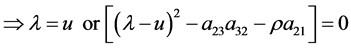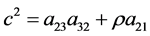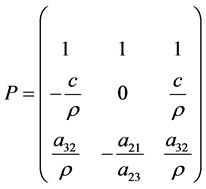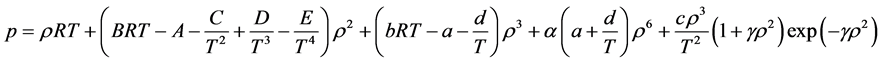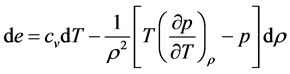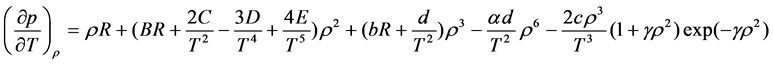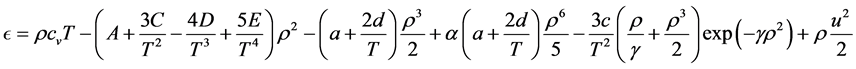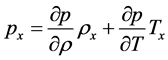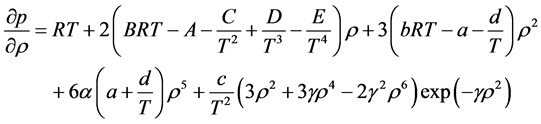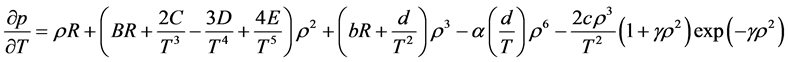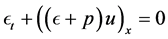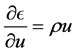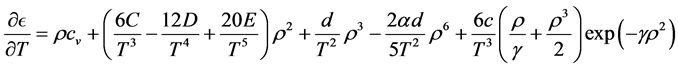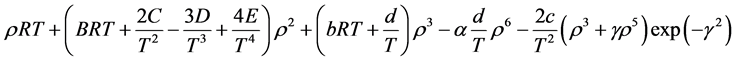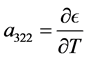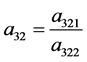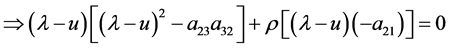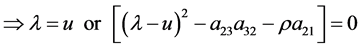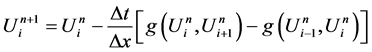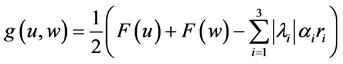Journal of Applied Mathematics and Physics
Vol.04 No.08(2016), Article ID:70200,30 pages
10.4236/jamp.2016.48175
Modeling and Simulation of Real Gas Flow in a Pipeline
Agegnehu Atena, Tilahun Muche
Department of Mathematics, Savannah State University, Savannah, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 July 2016; accepted 27 August 2016; published 30 August 2016
ABSTRACT
In this paper, a mathematical model that describes the flow of gas in a pipe is formulated. The model is simplified by making some assumptions. It is considered that the natural gas flowing in a long horizontal pipe, no heat source occurs inside the volume, transfer of heat due to heat conduction is dominated by heat exchange with the surrounding. The flow equations are coupled with equation of state. Different types of equations of state, ranging from the simple Ideal gas law to the more complex equation of state Benedict Webb Rubin Starling (BWRS), are considered. The flow equations are solved numerically using the Godunov scheme with Roe solver. Some numerical results are also presented.
Keywords:
Gas Flow, Equation of State, Godunov Scheme, Roe Solver, Pipe

1. Introduction
The purpose of this paper is to describe the flow of natural gas in a pipeline by employing the full set of differential equations along with different types of equations of states(EOS), ranging from the simple Ideal gas law to the more complex equation of state, Benedict Webb Rubin Starling (BWRS). The flow equations are derived from the physical principles of conservation of mass, momentum, and energy. More detailed discussion of conservation laws can be found in [1] - [4] . The natural gas is inviscid and compressible. The gas flows in along a horizontal pipe, and then can be considered as one-dimensional flow. It is assumed no heat source occurs inside the pipe and transfer of heat due to the heat conduction is much less than the heat exchange with the surrounding.
In this paper, the results obtained by solving the flow equations along with different types of EOS are compared [5] . The ideal gas equation works reasonably well over limited temperature and pressure ranges for many substances. However, pipelines commonly operate outside these ranges and may move substances that are not ideal under any conditions. The more complicated EOS will approximate the real gas behavior for a wide range of pressure and temperature conditions.
The Godunov scheme with Roe solver [3] is used to solve the Euler equations numerically. The Godunov scheme for conservation laws is known for its shock-capturing capability.
The rest of the article is organized as follows. In Section (2) we review the set of partial differential equations which describe the flow of gas in a pipe. Several equations of states are discussed in this section. In Section (3) a thermodynamical relationships among the physical quantities are presented. One can refer [6] for more thermodynamical relationships. Section (4) contains the discussion of the numerical method used to solve the flow equations together with different types equation of states. Some numerical results are given in this section. Conclusions are deferred to Section (5).
2. Governing Equations of Real Gas Flow in a Pipe
Let us consider a gas occupying a sub domain 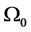 at time
at time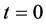 . Let
. Let 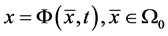 describes the position of the particle
describes the position of the particle 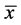 at time t. Then at time t the gas occupies the domain
at time t. Then at time t the gas occupies the domain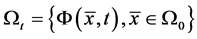 . The velocity of the gas at position x and time t is given by
. The velocity of the gas at position x and time t is given by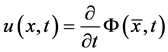 .
.
2.1. Transport Theorem
Let  be some physical quantity transported by the fluid. The total amount
be some physical quantity transported by the fluid. The total amount 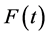 of the quantity f contained in
of the quantity f contained in  a time t is given by
a time t is given by .
.
Notation: 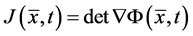
The rate of change of 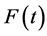 is given by:
is given by:
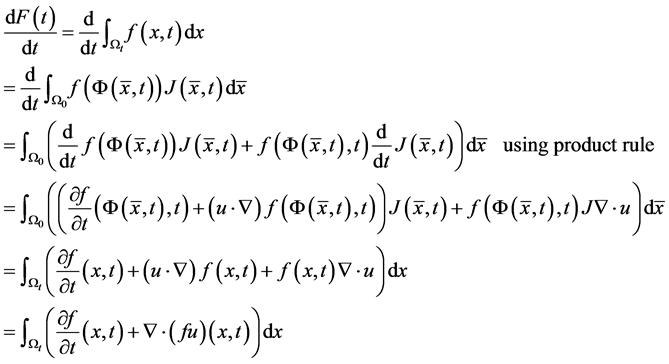
Then we get the transport theorem: . The transport theorem
. The transport theorem
is useful in the derivation of the governing equations.
2.2. Conservation of Mass (The Continuity Equation)
The total mass m in a volume 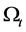 is given by
is given by




Since the above integral holds true for arbitrary region
2.3. Conservation of Momentum (Equation of the Motion)
The total momentum M of particles contained in 
According to Newton’s second law: The rate of change of momentum equals the action of all the forces F applied on
We have two types of forces acting on
1) Volume forces
where g is the gravitational acceleration.
2) Surface forces 



Surface forces are given by
where 
and 


By applying divergence theorem, the second term on the right side of the above equation can be transformed to integral over the domain 

For Newtonian fluid, the stress tensor depends linearly on the deformation velocity, 
where 


For inviscid fluid, friction is neglected and then
Therefore, the equation of motion for inviscid fluid becomes
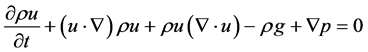
2.4. Conservation of Energy
Conservation of energy accounts for effects of temperature variations on the flow or the transfer of heat with in the flow. The 1st Law of Thermodynamics states that: The total energy of a system and its surroundings remains constant.
Let 






where 

density, and 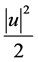
where q is the density of heat sources (per unit mass), and

The transfer of heat by conduction is given by Fourier’s law:






Then the energy equation for inviscid gas flow becomes:
By applying the transport and divergence theorems to the above equation we obtain the following equation:

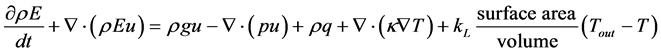
There fore, from the equations (1), (2), (3) we get the following system of equations.

2.5. Simplifications
In practice the form of mathematical model varies with the assumptions made as regards of operation conditions of the pipeline. Simplified models are obtained by neglecting some terms in the basic equations. In our case, we consider natural gas (Methane) flowing in a long horizontal pipeline. Hence we can consider the flow as a one dimensional flow. By assuming the pipe is horizontal, we can neglect the contribution of the gravitational force.
Assume also no heat source occurs inside the volume. For a cylindrical pipe, 
diameter of the pipe. By applying the assumptions we made, (4) is reduced to

Furthermore, Methane gas has the following properties. The specific heat capacity
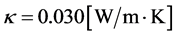





Prandtl number (Pr), defined as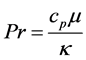
momentum) to that of heat. It is entirely a property of the fluid not the flow. In our case the value of Pr is about 0.7, this enables us to regard the flow as inviscid flow. For gas flow typical values of Pr are between 0.7 and 1. Another dimensionless constant we can use to simplify our system of equations is the Nusselt number (Nu). The
Nusselt number is defined as
of the pipe. The Nusselt number compares convection heat transfer to fluid conduction heat transfer.
For Methane gas flowing through an insulated pipe of diameter 0.5 m buried underground, the value of Nu is approximately 10. If the pipe is exposed to air, it will be around 300. Therefore, the term included in the energy
equation due to heat conduction 


where 
2.6. Equation of State (EOS)
An equation of state is a relationship between state variables, such that specification of two state variables permits the calculation of the other state variables. For an ideal gas, the equation of state is the ideal gas law. More complicated EOS have been formulated by several workers to try to model the behavior of real gases over a range of pressures and temperatures. This includes Van der Waals (VDW), Sovae Redlich Kwong (SRK), Peng Robinson (PR), and Benedict Webb Rubin Starling (BWRS).
2.6.1. Ideal Gas law
The ideal gas law is given by
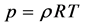
where p is the pressure, 
The ideal gas law is derived based on two assumptions:
The gas molecules occupy a negligible fraction of the total volume of the gas.
The force of attraction between gas molecules is zero.
The ideal gas equation works reasonably well over limited temperature and pressure ranges for many substances. However, pipelines commonly operate outside these ranges and may move substances that are not ideal under any conditions. Hence, we need to look for equation of state with wider validity.
2.6.2. Van der Waals (VDW) EOS
It was observed that the ideal gas law didn’t quite work for higher pressures and temperatures. The first assumption works at low pressures. But this assumption is not valid as the gas is compressed. Imagine for the moment that the molecules in a gas were all clustered in one corner of a cylinder, as shown in the figure below. At normal pressures, the volume occupied by these particles is a negligibly small fraction of the total volume of the gas. But at high pressures (when the gas is compressed), this is no longer true. As a result, real gases are not as compressible at high pressures as an ideal gas. The volume of real gas is therefore larger than expected from the ideal gas equation at high pressures. Van der Waals proposed that we correct for the fact that the volume of real gas is too large at high pressures by subtracting a term from the volume of the real gas before we substitute it in to the ideal gas equation. He therefore introduced a constant b in to the ideal gas equation that was equal to the volume actually occupied by the gas particles. When the pressure is small, and the volume is reasonably large, the subtracted term is too small to make any difference in the calculation. But at high pressures, when the volume of the gas is small, the subtracted term corrects for the fact that the volume of a real gas is larger than expected from the ideal gas equation.
The assumption that there is no force of attraction between the gas particles cannot be true. If it was, gases would never condense to form liquids. In reality, there is a small force of attraction between gas molecules that tends to hold the molecules together. This force of attraction has two consequences: (1) gases condense to form liquids at low temperatures and (2) the pressure of a real gas is sometimes smaller than expected for an ideal gas. To correct for the fact that the pressure of a real gas is smaller than expected from the ideal gas equation, Van der Waals added a term to the pressure in the ideal gas equation. This term contains a second constant a. The complete Van der Waals equation is written as follows:

Or in terms of molar volume
where
R is gas constant, 

We will consider three widely used equations of state that do work reasonably well near the dew point: Sovae-Redlich-Kwong (SRK), Peng-Robinson (PR), and Benedict-Webb-Rubin-Starling (BWRS). In addition to covering a wide range of conditions, these equations also can be expressed in generalized forms with mixing rules that permit the calculation of the coefficients for different compositions.
SRK and PR, along with VDW are called cubic equation of state, because expansion of the equations into a polynomial results in the highest order terms in density (or specific volume) being cubic. BWRS adds fifth and sixth power and exponential density terms. The cubic equation are all of the form

2.6.3. The Sovae-Redlich-Kwong (SRK) EOS
The SRK EOS of state is given by

where
w is the accentric factor which is a measure of the gas molecules deviation from the spherical symmetry, R is
gas constant, 


2.6.4. The Peng-Robinson (PR) EOS
The PR EOS is defined as
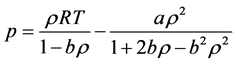
where
2.6.5. Benedict-Webb-Rubin-Starling (BWRS) EOS
Probably because of its ability to cover both liquids and gases and the availability of coefficients and mixing rules for many hydrocarbons in one place, BWRS is the most widely used equation of state for simulation of pipelines with high density hydrocarbons, or with condensation.
Simplicity is not among the good qualities of the BWRS equation of state. The form of the equation is:
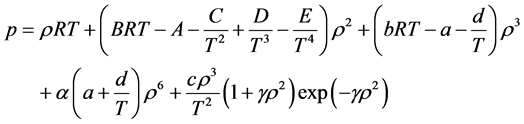
where the eleven coefficients
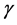




where
BWRS can be adapted for mixtures by the rules:
where 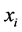
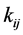
2.6.6. The Universal Gas Law
The universal gas law is 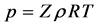
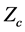
For example the experimental value of 
3. Thermodynamical Relations
In this section we will briefly discuss thermodynamical relations that exist among different physical quantities. First law of thermodynamics states that

The specific total enthalpy is defined as 

Derivative relationships:
Assume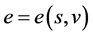

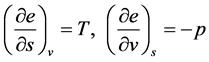
Similarly, assuming 
And comparing the coefficient of this equation with that of Equation (14) we get

Reciprocal relations involving internal energy e and entropy s:
Consider the internal energy and entropy to be a function of temperature and specific volume, i.e, 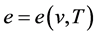

Then

The coefficient of dT, in the first equation, is by definition the heat capacity at constant volume,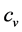

Differentiating the first equation of (18) with respect to T and the second with respect to v gives us
and

Substituting (19) in the first equation of (18) yields

One useful form involving internal energy is obtained by substituting 

Reciprocal relations involving enthalpy h
Assume
Then

The coefficient of dT is by definition the heat capacity at constant pressure,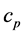

By double differentiating we do get

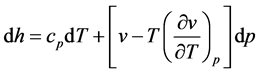
Heat capacities
By equating the difference of (13) and (14) to the difference of (21) and (25) we get

Dividing by 

4. Numerical Methods: Godunov Scheme with Roe Solver
In this section we will consider a numerical scheme to solve homogeneous Euler equation with initial condition by employing different EOS. The Euler equation in vector form:

where
And
One of the methods to solve a 1D nonlinear hyperbolic systems is the Godunov scheme
4.1. Godunov Scheme
Suppose we have subdivided our domain 

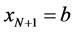
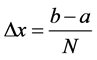
Let us define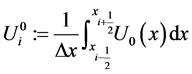

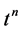


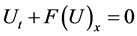

Let us denote the solution by

Then the solution 
Conservation form:
Since v is an exact solution on
where 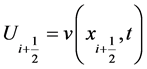
With the numerical flux
This scheme is called Godunov scheme.
Solving a Riemann problem exactly is not always an easy task. Then we may need to consider an approximate solution of the Riemann problem.
4.2. Riemann Problem for a Linear System
Suppose we have a linear system 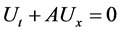
Let 


Then the solution of the Riemann problem is given by
where
A variety of approximate Riemann solvers have been proposed that can be applied more easily than the exact Riemann solver. One of the most popular Riemann solvers currently in use is due to Roe.
Godunov scheme with Roe approximation.
The idea is to replace the non-linear Riemann problem solved at each interface by an approximate one.
where 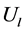




Conservation form of the Roe scheme.
The Roe scheme can be written in conservation form as
where
where 



The main task in the Roe scheme is the determination of the matrix of linearization A.
Now let us consider our equation (28) together with an equation of state of the form
Then we approximate this non-linear system with an approximate linear system as follows:
Define 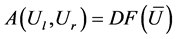
And
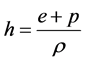

Roe conditions.
To solve our problem with the Roe scheme, we need to calculate the eigenvalues and their eigenvectors of the Jacobian matrix 

Let 

where
Þ the matrices B and 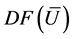
Further more, if 


4.3. Solving Euler Equation Using the Ideal Gas Law
In this section we solve one dimensional Euler equation with Ideal gas EOS. Consider the Euler equation (28) with the ideal gas law
Using (21), the change of internal energy is given by 
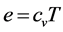


Now let us express (28) in terms of the primitive variables
Continuity equation:
Momentum equation:
Now using
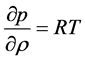

Energy Equation:
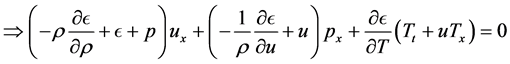
Now, using

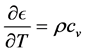
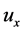
and the coefficient of 
Then equation (29) reduces to

Then the Euler equation in primitive variables is written as

Or in vector form
Eigenvalues and eigenvectors of the coefficient matrix B of (31) are computed as follows.
where the local speed of sound c is given by
The matrix of the corresponding eigenvectors is:
To compute the eigenvectors of the Jacobian 


Hence
The matrix R of eigenvectors of 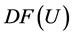
Since the total specific enthalpy h is given by 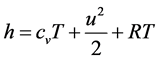
4.4. Solving Euler Equation Using the Van der Waals (VDW) EOS
Here we solve one dimensional Euler equation with VDW EOS. Consider again the euler equation (28) with
VDW EOS 





Again using (21), the change of internal energy is given by:
Here, 


Integrating the above differential equation gives the internal energy
The total energy 
Now let us express (28) in terms of the primitive variables
Continuity equation:
Momentum equation:
Here, 


Hence the momentum equation is reduced to
Energy Equation:

Using


The coefficient of 
and the coefficient of 
Then (32) reduces to

The Euler equation is written as

where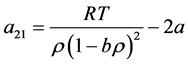
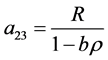

Eigenvalues and eigenvectors of the coefficient matrix B of (34) are computed as follows.
where the local speed of sound c is defined as
The matrix of the corresponding eigenvectors is:
To compute the eigenvectors of the Jacobian 


Hence
The matrix R of eigenvectors of 
where 
Since the total specific enthalpy h is given by 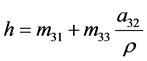
where
4.5. Solving Euler Equation Using the Soave-Redlich-Kwong (SRK) EOS
Let us consider (28) with SRK EOS
where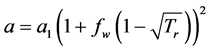



is the accentric factor R is gas constant, 


The internal energy is given by:
where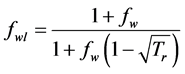
After integrating the differential equation of the internal energy, we get
The total energy 
Continuity equation:
Momentum equation:
using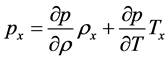


momentum equation is written as
Energy Equation:

The coefficient of 
And the coefficient of 
Notations: Let 



Then Equation (35) reduces to

The Euler equation is written as

where,
Eigenvalues and eigenvectors of the coefficient matrix A of Equation (37) are given as follows.
where
The matrix of the corresponding eigenvectors is:
To compute the eigenvectors of the Jacobian 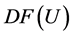
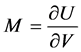

Hence
where
And
The matrix R of eigenvectors of 
Since the specific enthalpy h is given by 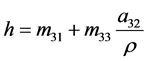
where
4.6. Solving Euler Equation Using the Peng-Robinson (PR) EOS
Let us consider (28) with PR EOS.
where
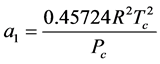

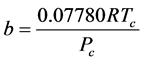
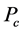
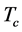
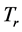
The internal energy is given by:
Here,
where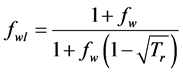
Integrating the above differential equation for internal energy we get
The total energy 
Continuity equation:
Momentum equation:
Using the continuity equation, it is reduced to
Here, 


The momentum equation is written as
Energy Equation:

Using
And
The coefficient of 
And the coefficient of 
Notations: Let 

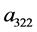
Then (38) reduces to
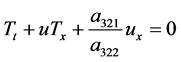
The Euler equation is written as

where,
where
The matrix of the corresponding eigenvectors is:
To compute the eigenvectors of the Jacobian 


Hence
where
and
The matrix R of eigenvectors of 
Since the specific enthalpy h is given by 
where
4.7. Solving Euler Equation Using the Benedict-Webb-Rubin-Starling (BWRS) EOS
Let us consider (28) with BWRS EOS.
The internal energy is given by:
The total energy 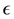
Continuity equation:
Momentum equation:
Let
The momentum equation is written as
Energy Equation:

The coefficient of 
and the coefficient of 
Notations: Let 



Then (41) reduces to
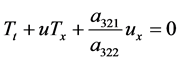
The Euler equation is written as

where,
Eigenvalues and eigenvectors of the coefficient matrix B of Equation (43) are computed as follows.
where
The matrix of the corresponding eigenvectors is:
To compute the eigenvectors of the Jacobian 


Hence
where
and
The matrix R of eigenvectors of 
Since the specific enthalpy h is given by 
where
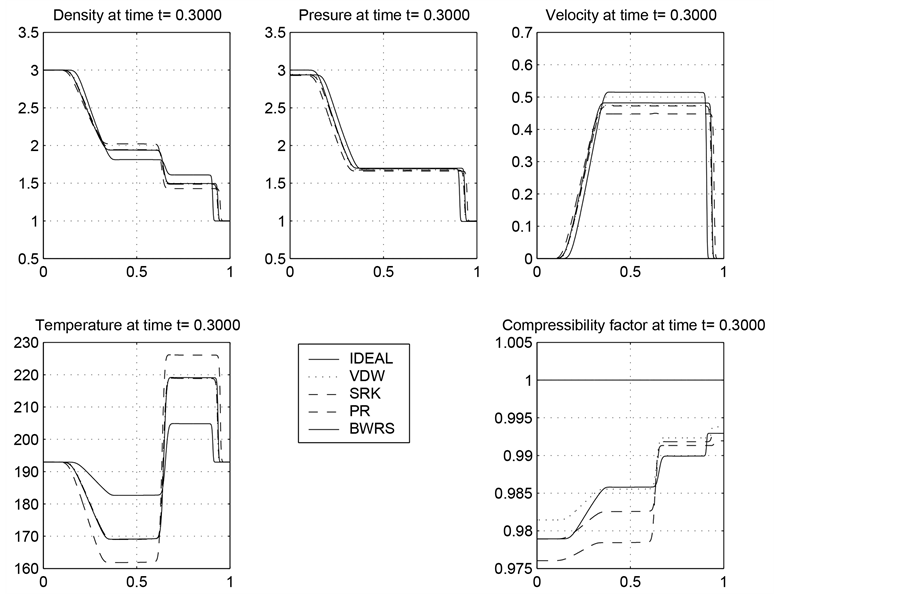
Figure 1. The results obtained by solving the homogeneous Euler equation by employing the ideal gas law and the other four equation of states.
Figure 2. The results obtained by solving the Euler equation (including the source term) by employing the PR and BWRS EOS.
4.8. Application of the Roe solver
Now to apply the Roe scheme on (28), on each cell
where 
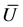
where
where 
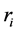

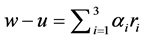
The last equation is a system of simultaneous algebraic equations for the variables
The conservative variables 
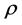
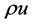
4.9. Numerical Results
In this section we present some numerical results. We consider a tube of length 1, filled by Methane gas, the initial discontinuity is located at







In Figure 1, we have plotted the density, pressure, velocity, temperature, and the real gas compressibility factor computed by using each of EOS we discussed.
Figure 2 depicts results of (6), i.e, the Euler equation with the source term included, obtained by applying PR, and BWRS EOS.
5. Conclusion
The model that describes the flow of gas in a pipe is presented. Simplifications to the equations are made using appropriate assumptions. Several Equations of states that close the system of equations are examined and the results obtained for each equation of state are compared.
Cite this paper
Agegnehu Atena,Tilahun Muche, (2016) Modeling and Simulation of Real Gas Flow in a Pipeline. Journal of Applied Mathematics and Physics,04,1652-1681. doi: 10.4236/jamp.2016.48175
References
- 1. Feistauer, M. (1993) Mathematical Methods in Fluid Dynamics. Longman Scientific & Technical, New York.
- 2. Chorin, A.J. and Marsden, J. E. (1993) A Mathematical Introduction to Fluid Mechanics. Springer, New York.
http://dx.doi.org/10.1007/978-1-4612-0883-9 - 3. LeVeque, R.J. (1990) Numerical Methods for Conservation Laws, Lectures in Mathematics. ETH Zuerich, Birkhaeuser, Basel.
http://dx.doi.org/10.1007/978-3-0348-5116-9 - 4. Kroener, D. (1997) Numerical Schemes for Conservation Laws/John Wiley & Sons Ltd, England and B.G. Teubner, Germany.
- 5. Modisette, J.L. (2000) Equations of State Tutorial. 32nd Annual Meeting PSIG (Pipeline simulation Interest Group), Savanah, Georgia.
- 6. Starling, K.E. (1973) Fluid Thermodynamic Properties for Light Petroleum Systems. Gulf Publ., Houston.