Received 17 October 2015; accepted 24 November 2015; published 27 November 2015

ABSTRACT

In this paper, we study oscillatory properties of solutions for the nonlinear impulsive hyperbolic equations with several delays. We establish sufficient conditions for oscillation of all solutions.

Keywords:

Oscillation, Hyperbolic Equation, Impulsive, Delays

1. Introduction

The theory of partial functional differential equations can be applied to many fields, such as biology, population growth, engineering, control theory, physics and chemistry, see the monograph [1] for basic theory and applications. The oscillation of partial functional differential equations has been studied by many authors see, for example [2] - [7] , and the references cited therein.

The theory of impulsive partial differential systems makes its beginning with the paper [8] in 1991. In recent years, the investigation of oscillations of impulsive partial differential systems has attracted more and more attention in the literature see, for example [9] - [13] . Recently, the investigation on the oscillations of impulsive partial differential systems with delays can be found in [14] - [19] .

To the best of our knowledge, there is little work reported on the oscillation of second order impulsive partial functional differential equation with delays. Motivated by this observation, in this paper we study the oscillation of nonlinear forced impulsive hyperbolic partial differential equation with several delays of the form

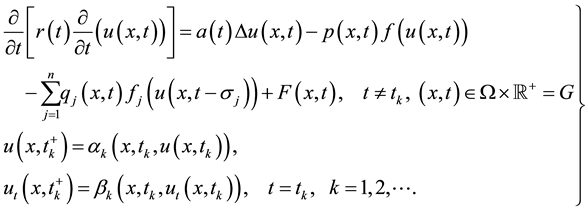(1)

with the boundary conditions

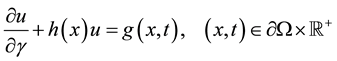(2)

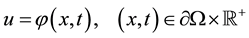(3)

and the initial condition

(4)

Here is a bounded domain with boundary 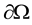smooth enough and 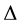is the Laplacian in the

Euclidean N-space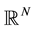, is a unit exterior normal vector of, ,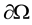

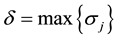In the sequal, we assume that the following conditions are fulfilled:

(H1), is a positive constant, 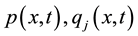are class of functions which are

piece wise continuous in t with discontinuities of first kind only at and left continuous at

(H2); is a positive constant, is a positive constant, for and

(H3) and their derivatives are piecewise continuous in t with discontinuities of first kind only at and left continuous at

(H4) and there exist positive constants and such that for

Let us construct the sequence where and

By a solution of problem (1), (2) ((1),(3)) with initial condition (4), we mean that any function for which the following conditions are valid:

1. If then

2. If then coincides with the solution of the problem (1) and (2) ((3)) with initial condition.

3. If, then coincides with the solution of the problem (1) and (2) ((3)).

4. If, then coincides with the solution of the problem (2) ((3)) and the following equations

or

Here the number is determined by the equality

We introduce the notations:

The solution of problem (1), (2) ((1),(3)) is called nonoscillatory in the domain G if it is either eventually positive or eventually negative. Otherwise, it is called oscillatory.

This paper is organized as follows: Section 2, deals with the oscillatory properties of solutions for the problem (1) and (2). In Section 3, we discuss the oscillatory properties of solutions for the problem (1) and (3). Section 4 presents some examples to illustrate the main results.

2. Oscillation Properties of the Problem (1) and (2)

To prove the main result, we need the following lemmas.

Lemma 2.1. Suppose that is the minimum positive eigenvalue of the problem

and is the corresponding eigenfunction of. Then and Proof. The proof of the lemma can be found in [20] .

Lemma 2.2. Let be a positive solution of the problem (1), (2) in G. Then the functions

are satisfies the impulsive differential inequality

(5)

(6)

(7)

where

has an eventually positive solution.

Proof. Let be a positive solution of the problem (1), (2) in G. Without loss of generality, we may assume that there exists a such that for

For multiplying Equation (1) with, which is the same as that in Lemma 2.1 and then integrating (1) with respect to x over yields

By Green’s formula, and the boundary condition we have

where is the surface element on.

Also from condition (H2), and Jenson’s inequality we can easily obtain

Thus, Hence we obtain the following differential inequality

where

For from (1) and condition (H4), we obtain

According to we obtain

Hence, we obtain that is a positive solution of impulsive differential inequalities (5)-(7).

This completes the proof.

Lemma 2.3. Let be a positive solution of the problem (1), (2) in G. If we further assume that and the impulsive differential inequality (5), and

(8)

(9)

(10)

have no eventually positive solution, then each nonzero solution of the problem (1)-(2) is oscillatory in the domain G.

Proof. Let be a positive solution of the problem (1), (2) in G. Without loss of generality, we may assume that there exists a such that, for

From Lemma 2.2, it follows that the function is an eventually positive solution of the inequality (5) which is a contradictions.

If for then the function

is a positive solution of the following impulsive hyperbolic equation

and satisfies

where

For from (1) and condition (H4), we obtain

According to we obtain

Thus, it follows that the function is a positive solution of the inequality (8)-(10) for which is also a contradiction. This completes the proof.

Now, if we set in the proof of Lemma 2.3, then we can obtain the following lemma.

Lemma 2.4. Let be a positive solution of the problem (1), (2) in G. If we further assume that and the impulsive differential inequality (5), and

(11)

(12)

(13)

has no eventually positive solution, then each nonzero solution of the problem (1), satisfying the boundary condition

is oscillatory in the domain G.

Proof. Let be a positive solution of the problem (1), (2) in G. Without loss of generality, we may assume that there exists a such that for

From Lemma 2.2, it follows that the function is an eventually positive solution of the inequality (5) which is a contradiction.

If for then the function is a positive solution of the following impulsive hyperbolic equation

and satisfies

For from (1) and condition (H4), we obtain

According to we obtain

Thus it follows that the function is a positive solution of the inequality (11)-(13) for which is also a contradiction. This completes the proof.

Lemma 2.5. Assume that

(A1) the sequence satisfies ;

(A2) is left continuous at for

(A3) for and

where, and are constants. PC denote the class of piecewise continuous function from to, with discontinuities of the first kind only at

Then

Proof. The proof of the lemma can be found in [21] .

Lemma 2.6. Let be an eventually positive (negative) solution of the differential inequality (11)-(13).

Assume that there exists such that for If

(14)

hold, then for where

Proof. The proof of the lemma can be found in [22] .

We begin with the following theorem.

Theorem 2.1. If condition (14), and the following condition

(15)

hold, where

then every solution of the problem (1), (2) oscillates in G.

Proof. Let be a nonoscillatory solution of (1), (2). Without loss of generality, we can assume that there exists such that for

From Lemma 2.4, we know that is a positive solution of (11)-(13). Thus from Lemma 2.6, we can find that for

For define

Then we have We may assume that thus we have that for

(16)

(17)

(18)

Substitute (16)-(18) into (11) and then we obtain,

Hence we have

or

From above inequality and condition it is easy to see that the function is nonincreasing for Thus for which implies that

From (12)-(13), we obtain

and

Let

Then according to Lemma 2.5, we have

Since 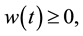the last inequality contradicts condition (15). This completes the proof.

3. Oscillation Properties of the Problem (1) and (3)

Next we consider the problem (1) and (3). To prove our main result we need the following lemmas.

Lemma 3.1. Suppose that is the smallest positive eigen value of the problem

and is the corresponding eigen function of. Then and

Proof. The proof of the lemma can be found in [20] .

Lemma 3.2. Let be a positive solution of the problem (1), (3) in G. Then the function

are satisfies the impulsive differential inequality

(19)

(20)

(21)

where

has the eventually positive solution

Proof. Let be a positive solution of the problem (1), (3) in G. Without loss of generality, we may assume that there exists a such that for

For multiplying equation (1) with, which is the same as that in

Lemma 3.1 and then integrating (1) with respect to x over yields

By Green’s formula, and the boundary condition we have

where is the surface element on.

From condition (H2), we can easily obtain

The proof is similar to that of Lemma 2.1 and therefore the details are omitted.

Lemma 3.3. Let be a positive solution of the problem (1), (3) in G. If we further assume that and the impulsive differential inequality (19), and

(22)

(23)

(24)

have no eventually positive solution, then each nonzero solution of the problem (1), (3) is oscillatory in the domain G.

Proof. The proof is similar to Lemma 2.3, and hence the details are omitted.

Futhermore, if we set, then we have the following lemma.

Lemma 3.4. Let be a positive solution of the problem (1), (3) in G. If we further assume that and the impulsive differential inequality (19), and

(25)

(26)

(27)

has no eventually positive solution, then each nonzero solution of the problem (1), satisfying the boundary condition

is oscillatory in the domain G.

Proof. The proof is similar to Lemma 2.4, and hence the details are omitted.

Using the above lemmas, we prove the following oscillation result.

Theorem 3.1. If condition (14) and the following condition

(28)

hold, where

then every solution of the problem (1), (3) oscillates in G.

Proof. Let be a nonoscillatory solution of (1), (3). Without loss of generality, we can assume that there exists such that for

From Lemma 3.4, we know that is a positive solution of (25)-(27). Thus from Lemma 2.6, we can find that for

For define

Then we have We may assume that thus we have that for

(29)

(30)

(31)

We substitute (29)-(31) into (25) and can obtain the following inequality,

then we have

From (26)-(27), we can obtain

It follows that

Let

Then according to Lemma 2.5, we have

Since the last inequality contradicts (28). This completes the proof.

Theorem 3.2. If condition (14) and the following condition

(32)

hold for some, then every solution of the problem (1), (3) oscillates in G.

Proof. The proof is obvious and hence the details are omitted.

4. Examples

In this section, we present some examples to illustrate the main results.

Example 4.1. Consider the impulsive differential equation

(33)

and the boundary condition

(34)

Here and taking

Moreover

so (14) holds. We take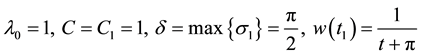, then

thus

Hence (28) holds. Therefore all conditions of Theorem 3.1 are satisfied. Hence every solution of the problem (33), (34) oscillates in In fact is one such solution of the problem (33) and (34).

Example 4.2. Consider the impulsive differential equation

(35)

and the boundary condition

(36)

Here and taking

It is easy to check that the conditions of Theorem 2.1 are satisfied. Therefore, every solution

of the problem (35), (36) oscillates in In fact is one such solution of the problem (35) and (36).

Acknowledgements

The authors thank Prof. E. Thandapani for his support to complete the paper. Also the authors express their sincere thanks to the referee for valuable suggestions.

Cite this paper

VadivelSadhasivam,JayapalKavitha,ThangarajRaja, (2015) Forced Oscillation of Nonlinear Impulsive Hyperbolic Partial Differential Equation with Several Delays. Journal of Applied Mathematics and Physics,03,1491-1505. doi: 10.4236/jamp.2015.311175

References